文章编号: 2096-3203(2022)06-0039-11 中图分类号: TM71
2. 东南大学电气工程学院, 江苏 南京 210096
近年来,电网系统中出现大量分布式资源,其随机性和波动性以及过于分散的特征均增加了系统复杂性和调控难度[1-2],对电网安全可靠运行提出了挑战。但规模化分布式资源的接入也使用户侧具有一定程度的柔性,使用户侧具备参与电网调控的潜力[3]。虚拟电厂(virtual power plant,VPP)可以聚合各类分散的源-荷-储资源,形成资源集群,进行统一调度[4],从而有效发挥分布式电源和储能系统等分散资源的合力,提高电网调控的灵活性、安全性和经济性。因此有必要研究VPP聚合响应能力,辅助参与电力系统调控决策。
研究VPP聚合响应能力,首先要对各类资源分别建模并评估其响应能力。文献[5]建立水电站发电模型,提出其出力表达式和运行约束。文献[6]建立不同燃油流量变化下转速响应的分段线性化模型。文献[7]建立储能系统在平抑波动-峰谷套利两模式下的运行模型及控制策略。文献[8]建立温控负荷运行模型并量化调节能力,同时建立温控负荷集群的频域模型。文献[9]基于参数辨识,提出采用状态分组及动态估计的方法,评估温控负荷集群的响应能力。文献[10]基于参数均一化建立电采暖负荷集群模型,并评估其调控潜力。上述文献为文中对各类资源独立响应能力建模提供了思路,但未对各类资源进行聚合。同时也有文献提出可调资源调度潜力、灵活性、技术性等评估指标并进行权重分析[11-14],但这些指标用于评估响应能力时并不够全面,且文献[11-12]没有给出统一化的评估指标,因而难以聚合各类资源。
此外,国内外对VPP聚合响应能力评估也展开了研究。文献[15]通过构建多个长短期记忆网络建立用户侧需求响应模型,但没有统一的聚合响应模型。文献[16]分析包含温控负荷和电动汽车的VPP的响应特性,计算得到上述2种负荷的接入状态,以及出力的上下边界。文献[17]提出VPP可调能力数学模型,并通过改进粒子群算法进行求解。文献[18]建立VPP聚合模型,并分析快速启动装置带来的响应能力变化。文献[19]提出主动配电系统日前聚合模型,计算其功率上下限、爬坡率和成本曲线。文献[20]建立综合能源系统内部资源的动态模型,对整体进行仿真分析并提出调频方案。文献[21]提出一种VPP主动动态聚合模型来描述其最大可行域。但上述文献均未分析响应时间、持续时间等响应能力。另外,有研究者对分布式资源按某种特性分类再进行聚合[22-23],文献[22]将VPP资源分为有风险和无风险2类,建立聚合后的响应特性模型,但未计算响应能力的值;文献[23]将资源分类并进行标准化建模,分析其综合响应能力。此外也有研究采用数据驱动方法进行调峰潜力评估[24-25],但文献[24]只评估了温度变化带来的调峰潜力,且采用数据驱动的方法存在对以往数据依赖性大,难以处理意外情况的不足。
目前,相关研究中缺少对VPP响应时间等响应能力的分析,也缺少对聚合响应能力指标权重的分析。因此文中首先建立更全面的响应能力评估指标体系;然后在分布式资源独立响应能力模型基础上,建立VPP日前聚合响应能力评估模型,可计算响应能力的多维量化指标,得到聚合资源后的可行调节域;最后考虑聚合后的响应能力不稳定性,对指标权重进行分析并求得聚合响应能力评分。此方法可求得聚合后的可行调节域,为电网调度和控制提供决策辅助,而且聚合响应能力评分可以作为VPP优化配置等其他问题的参考指标。
1 VPP响应能力指标体系为评估VPP整体响应能力,先要对VPP内各类分布式资源进行响应能力评估。分布式资源的响应能力主要体现在输出/吸收功率的水平、速度和可持续时间上。文中采用的响应能力评价指标包括:
(1) 调节方向D,即调节后运行点与运行基点的相对位置,包括向上和向下2个方向。
(2) 调节幅度A,指相对于当前运行点所能达到的最大偏移值,包括向上调节幅度A+和向下调节幅度A-。
(3) 响应时间TR,指从接收到调节指令,直至完全达到调节要求所需的最短时间。
(4) 持续时间TD,指完全达到调节要求后,能保持该状态的最长时间。
(5) 爬坡率R,指调节过程中单位时间Δt内的运行点变化量。分布式资源中运行点指的是运行时资源出力;聚合VPP中运行点所指有所不同,具体可见3.1节。
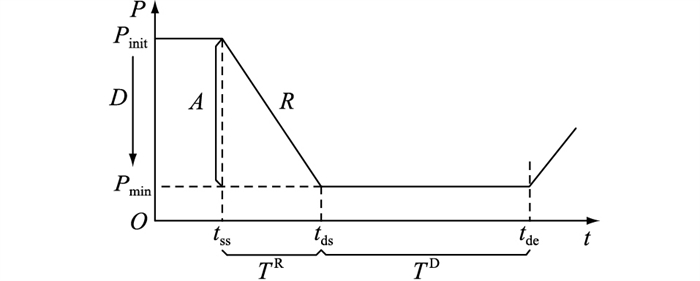
图 1为分布式资源响应能力评估指标示意,以某次VPP内部资源接受上级调度的过程为例。tss时刻指令发出,此时资源出力为Pinit,并根据调度指令开始下降,在tds时刻达到功率最小值Pmin。此时,调节方向D为向下。
|
图 1 VPP内各资源响应能力评估指标示意 Fig. 1 Schematic diagram of response capability evaluation indicators of resources in VPP |
向下调节幅度A-可表示为:
| $ {A^ - } = {P_{{\rm{init }}}} - {P_{\min }} $ | (1) |
响应时间TR可表示为:
| $ {T^{\rm{R}}} = {t_{{\rm{ds}}}} - {t_{{\rm{ss}}}} $ | (2) |
根据调度指令,在tde时刻出力开始上升。持续时间TD可表示为:
| $ {T^{\rm{D}}} = {t_{{\rm{de}}}} - {t_{{\rm{ds}}}} $ | (3) |
同时爬坡率R有以下2种表达形式:
| $ R = \frac{{{P_{{\rm{init}}}} - {P_{{\rm{min }}}}}}{{{t_{{\rm{ds}}}} - {t_{{\rm{ss}}}}}}\Delta t $ | (4) |
| $ R(t) = P(t) - P(t - 1) $ | (5) |
采用第1章所述5个响应能力指标,选取水力发电、燃气轮机、储能系统和温控负荷集群4类VPP内部资源,分别基于发电、用电机理或需求响应模型[26-28]建立各自的响应能力模型,作为聚合响应能力评估的基础。而光伏、风电等其他类型分布式资源响应能力评估模型的相关研究成果较多,可以直接利用文中提出的聚合资源响应能力评估方法进行聚合后的整体响应能力评估。
2.1 水力发电水力发电一般和水流量、水位差有关,水电机组t时刻出力如下:
| $ {P_{\rm{h}}}(t) = KQ(t)H(t) $ | (6) |
式中:Q(t)为t时刻发电引水流量;H(t)为t时刻上下游水位差;K为等效效率。式(7)—式(9)分别为发电引水流量约束、水库蓄水量约束和水量平衡约束。
| $ {Q_{\min }} \le Q(t) \le {Q_{\max }} $ | (7) |
| $ {V_{{\rm{h}}, \min }} \le {V_{\rm{h}}}(t) \le {V_{{\rm{h}}, {\rm{max}}}} $ | (8) |
| $ {V_{\rm{h}}}(t + 1) = {V_{\rm{h}}}(t) + (q(t) - Q(t))\Delta t $ | (9) |
式中:Qmax,Qmin分别为最大、最小发电引水流量;Vh(t),Vh, min,Vh, max分别为水库t时刻蓄水量、最小蓄水量和最大蓄水量;q(t)为t时刻河流平均径流量。
水电机组响应能力总结如下。
(1) 调节方向:可以双向调节。
(2) 调节幅度:可用当前出力Ph(t)和出力上、下限Ph, max,Ph, min表示,表达如式(10)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {A_{\rm{h}}^ + = {P_{{\rm{h}}, \max }} - {P_{\rm{h}}}(t)}\\ {A_{\rm{h}}^ - = {P_{\rm{h}}}(t) - {P_{{\rm{h}}, \min }}} \end{array}} \right. $ | (10) |
(3) 响应时间:水电快调响应时间约为10~20 s,可以达到秒级[29],故后续聚合响应能力时认为响应时间为单位时间Δt。
(4) 持续时间:由式(8)、式(9)的蓄水量约束及动态变化,可得持续时间ThD,计算见式(11)。
| $ T_{\rm{h}}^{\rm{D}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{V_{{\rm{h}}, \max }} - {V_{\rm{h}}}(t)}}{{q(t) - Q(t)}}}&{Q(t) \le q(t)}\\ {\frac{{{V_{\rm{h}}}(t) - {V_{{\rm{h}}, \min }}}}{{Q(t) - q(t)}}}&{Q(t) > q(t)} \end{array}} \right. $ | (11) |
(5) 爬坡率:存在式(12)所示约束条件。
| $ - R_{\rm{h}}^ - \le {R_{\rm{h}}}(t) \le R_{\rm{h}}^ + $ | (12) |
式中:Rh(t)为t时刻水电机组爬坡率;Rh-,Rh+分别为单位时间Δt内出力向下、向上调节最大值。
2.2 燃气轮机燃气轮机的出力曲线是非线性的,因此采用分段线性化的方法分析。而燃气轮机的出力Pg主要由单位时间内输送天然气量ΔVg决定,因此根据ΔVg对Pg的表达式进行分段。可得燃气轮机t时刻的出力表达式为:
| $ {P_{\rm{g}}}(t) = {a_j}\Delta {V_{\rm{g}}}(t) + {b_j}\quad \Delta {V_{\rm{g}}} \in {W_j};j \in {U_{\rm{g}}} $ | (13) |
式中:aj,bj为分段j中线性表达式的常系数;Wj为分段j中ΔVg值的集合;Ug为分段序号的集合。燃气轮机运行时存在出力约束:
| $ {P_{{\rm{g}}, \min }} \le {P_{\rm{g}}}(t) \le {P_{{\rm{g}}, \max }} $ | (14) |
式中:Pg, max,Pg, min分别为燃气轮机出力上、下限。运行时其出力必须大于下限,但可停机使其出力为0。
燃气轮机响应能力总结如下。
(1) 调节方向:可以双向调节。
(2) 调节幅度:向上、向下调节幅度可由式(10)同理得出。
(3) 响应时间:响应时间与调节容量ΔPg和爬坡率有关。由式(13)可知,燃气轮机爬坡率可用ΔVg变化率表示,因此燃气轮机响应时间TgR为:
| $ T_{{\rm{g}}, j}^{\rm{R}} = \frac{1}{{{a_j}}} \cdot \frac{{\Delta {P_{{\rm{g}}, j}}}}{{{\rm{d}}\Delta {V_{\rm{g}}}(t)/{\rm{d}}t}} $ | (15) |
| $ T_{\rm{g}}^{\rm{R}} = \sum\limits_{j \in {U_{\rm{g}}}} {T_{{\rm{g}}, j}^{\rm{R}}} $ | (16) |
式中:Tg, jR为燃气轮机运行在分段j时的响应时间;ΔPg, j为燃气轮机运行在分段j时的出力变化量。
(4) 持续时间:在24 h的运行周期内,燃气轮机可全天维持响应,持续时间为24 h。
(5) 爬坡率:由式(13)可知爬坡率与常系数aj成正比,设爬坡率上下限也近似与aj成正比。因此燃气轮机爬坡率约束可表示为:
| $ - a_j^*R_{\rm{g}}^ - \le {R_{{\rm{g}}, j}}(t) \le a_j^*R_{\rm{g}}^ + \quad j \in {U_{\rm{g}}} $ | (17) |
式中:Rg, j为燃气轮机运行在分段j时的爬坡率;Rg+,Rg-为爬坡率基准值,分别等于分段1的向上、向下爬坡率最大值;aj*为系数aj与系数a1的比值。
2.3 储能系统储能系统的储存电能主要与其初始值和充放电过程相关。而充放电时储存电能的动态变化与充放电功率、充放电效率有关。因此建立储能系统充放电模型如下:
| $ {E_{\rm{b}}}(t + 1) = {E_{\rm{b}}}(t) - {P_{\rm{b}}}(t){\eta _{\rm{b}}}\Delta t $ | (18) |
式中:Eb(t)为t时刻储能系统储存电能;Pb(t)为t时刻充放电功率,以放电功率为正;ηb为充放电效率。
储存电能约束和充放电功率约束如下:
| $ {E_{{\rm{b}}, \min }} \le {E_{\rm{b}}}(t) \le {E_{{\rm{b}}, \max }} $ | (19) |
| $ - {P_{{\rm{bc}}, {\rm{ max }}}} \le {P_{\rm{b}}}(t) \le {P_{{\rm{bd}}, {\rm{ max }}}} $ | (20) |
式中:Eb, max,Eb, min分别为储能系统储存电能的上、下限;Pbc, max,Pbd, max分别为充、放电功率上限。
基于以上模型,储能系统响应能力总结如下。
(1) 调节方向:可以双向调节。
(2) 调节幅度:向上、向下调节幅度计算见式(21)、式(22)。
| $ A_{\rm{b}}^ + = {P_{{\rm{b}}, \max }} - {P_{\rm{b}}}(t) $ | (21) |
| $ A_{\rm{b}}^ - = {P_{\rm{b}}}(t) + {P_{{\rm{b}}, \max }} $ | (22) |
(3) 响应时间:储能系统的响应时间很短,最快可以达到秒级,故后续聚合响应能力时认为响应时间为单位时间Δt。
(4) 持续时间:如果满足调节要求时为充电状态,则充电持续时间TbcD计算见式(23);如果满足调节要求时为放电状态,则放电持续时间TbdD计算见式(24)。
| $ T_{{\rm{bc}}}^{\rm{D}} = \frac{{{E_{{\rm{b}}, \max }} - {E_{\rm{b}}}(t)}}{{ - {P_{\rm{b}}}(t){\eta _{\rm{b}}}}} $ | (23) |
| $ T_{{\rm{bd}}}^{\rm{D}} = = \frac{{{E_{\rm{b}}}(t) - {E_{{\rm{b}}, {\rm{ min }}}}}}{{{P_{\rm{b}}}(t){\eta _{\rm{b}}}}} $ | (24) |
(5) 爬坡率:存在爬坡率约束条件,可由式(12)同理得出。
2.4 温控负荷集群温控负荷在夏季时为制冷空调,冬季时为制热空调或电采暖。文中以夏季制冷空调集群为例,冬季制热空调、电采暖集群也可用类似方法分析。
空调集群运行在稳态时,房间温度Tin可看作保持不变,即空调制冷速率与房间散热速率相等。此时空调集群总功率Pc与空调个数N、空调能效比η、用户房间的等效热阻δ、室内温度Tin、室外温度Tout有关,即:
| $ {P_{\rm{c}}}(t) = NE\left( {\frac{1}{{\eta \delta }}} \right)\left( {{T_{{\rm{out}}}}(t) - E\left( {{T_{{\rm{in}}}}} \right)} \right) $ | (25) |
式中:E(·)表示相应变量的期望。
考虑到人体热舒适性,设某房间设定温度为Tset,温度控制裕量为TΔ,则房间温度Tin的区间为[Tset-TΔ, Tset+TΔ]。因此空调集群的总功率上、下限可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{{\rm{c}}, \max }}(t) = NE\left( {\frac{1}{{\eta \delta }}} \right)\left( {{T_{{\rm{out }}}}(t) - E\left( {{T_{{\rm{set}}}}} \right) + E\left( {{T_\Delta }} \right)} \right)}\\ {{P_{{\rm{c}}, \min }}(t) = NE\left( {\frac{1}{{\eta \delta }}} \right)\left( {{T_{{\rm{out }}}}(t) - E\left( {{T_{{\rm{set}}}}} \right) - E\left( {{T_\Delta }} \right)} \right)} \end{array}} \right. $ | (26) |
η,δ,Tout,Tset,TΔ均看作分布于确定概率密度函数并相互独立的随机变量。
调节过程中,使每个房间的温度Tin同步升高或降低ΔTin,则E(Tin)升高或降低ΔTin,从而使空调集群总消耗功率Pc降低或升高,等效为输出功率-Pc升高或降低。
基于以上分析,空调集群响应能力总结如下。
(1) 调节方向:可以双向调节。
(2) 调节幅度:向上、向下调节幅度计算见式(27)、式(28)。
| $ A_{\rm{c}}^ + = {P_{\rm{c}}}(t) - {P_{{\rm{c}}, \min }}(t) $ | (27) |
| $ A_{\rm{c}}^ - = {P_{{\rm{c}}, \max }}(t) - {P_{\rm{c}}}(t) $ | (28) |
(3) 响应时间:对于所提响应方式,响应时间约为0.5~1 h[6],其主要与ΔTin有关,ΔTin越大,响应时间越长。
(4) 持续时间:对于温控负荷集群,调节后的室内温度期望E(Tin)可一直保持不变,从而全天维持响应,因此持续时间为24 h。
(5) 爬坡率:设Tout和Tin单位时间内变化量为ΔTout和ΔTcr,而ΔTcr存在约束条件| ΔTcr|≤ΔTcr, max,其中ΔTcr, max为房间温度变化最大值。则空调集群等效输出功率的爬坡率Rc存在约束条件如式(29)所示。
| $ R_{\rm{c}}^ - (t) \le {R_{\rm{c}}}(t) \le R_{\rm{c}}^ + (t) $ | (29) |
| $ \left\{ {\begin{array}{*{20}{l}} {R_{\rm{c}}^ + (t) = - NE\left( {\frac{1}{{\eta \delta }}} \right)\left( {\Delta {T_{{\rm{out }}}}(t) - \Delta {T_{{\rm{cr}}, \max }}} \right)}\\ {R_{\rm{c}}^ - (t) = - NE\left( {\frac{1}{{\eta \delta }}} \right)\left( {\Delta {T_{{\rm{out }}}}(t) + \Delta {T_{{\rm{cr}}, \max }}} \right)} \end{array}} \right. $ | (30) |
式中:Rc+,Rc-分别为单位时间Δt内出力变化量上限和下限。
3 VPP聚合响应能力评估 3.1 VPP聚合响应能力评估技术VPP需要在日前市场关闸前分时段上报可调用上行、下行备用容量,在每个备用时段内,该VPP可提供的调整功率不能超过该容量范围,同时其爬坡率、响应时间也应当上报作为电网的调度信息。作为特性各异的资源组成的VPP,需要对其整体响应能力进行有效评估,从而生成生产计划。
实际应用中,由于存在资源出力、爬坡率以及功率基线等限制,VPP的聚合能力应当综合考虑各资源的约束。同时VPP聚合评估需要考虑网架等限制,因此对聚合能力的评估应当是求取优化而不是叠加。
为了得到聚合响应能力的优化模型,可以根据各类资源独立响应能力模型,得到VPP运行约束条件,如3.3节所示,且VPP运行约束条件是聚合响应能力优化模型的一部分约束。
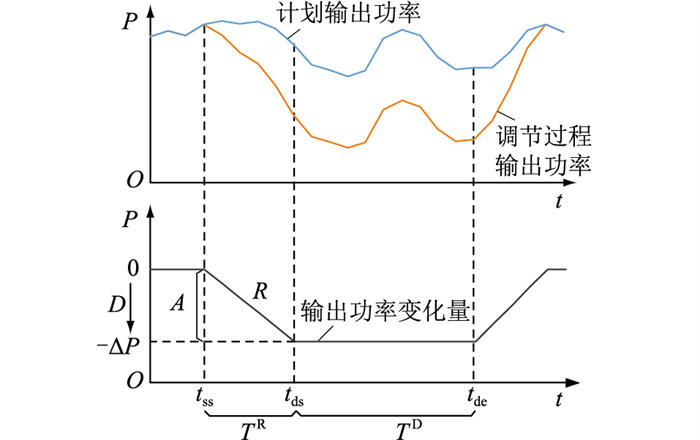
VPP聚合响应能力评估指标定义如第1章所述,需要注意的是,对于分布式资源,评估指标定义中的运行点指的是运行时资源出力;而对于VPP,定义中的运行点指的是运行时输出功率变化量。即分布式资源根据输出功率曲线确定评估指标的值,如图 1所示,而VPP根据输出功率变化量曲线确定聚合响应能力评估指标的值,如图 2所示。图 2中输出功率变化量为计划输出功率与调节过程输出功率的差值,ΔP为调节指令要求的VPP总功率变化量。
|
图 2 聚合响应能力评估指标示意 Fig. 2 Schematic diagram of aggregation response capability evaluation indicators |
VPP内资源聚合后的响应能力可以从联络线功率基线、联络线功率上下限、VPP爬坡率上下限、VPP响应时间几个方面进行评估。文中给出各聚合响应能力指标的具体定义、目标函数及部分约束,具体如下。
(1) 联络线功率基线,即无响应需求时联络线的功率曲线,是基于日前优化调度结果,以总成本最低为目标计算得到的。目标函数如下:
| $ \min \sum\limits_{t \in \psi } {\left( {\sum\limits_{i \in S} {{c_i}} \left( {{p_i}(t)} \right) + {c_{{\rm{tie}}}}(t){p_{{\rm{tie}}}}(t)} \right)} $ | (31) |
式中:ψ为运行时刻集合,文中取1 d,即24个时刻;S为所有设备(包括温控负荷)的集合;i为设备编号;pi(t)为t时刻设备i发出的功率;ptie(t)为t时刻联络线功率,以从上级电网流入VPP为正方向;ci(pi(t))为t时刻设备i的成本函数;ctie(t)为t时刻联络线的购电电价。
(2) 联络线功率上下限,即t时刻联络线功率能达到的最大、最小值。目标函数如下:
| $ \max\ {p_{{\rm{tie }}}}(t)\quad t \in \psi $ | (32) |
| $ \min\ {p_{{\rm{tie }}}}(t)\quad t \in \psi $ | (33) |
(3) VPP爬坡率上下限,即运行在功率基线时,从当前时刻t到下一时刻t+1输出功率增加、减少的最大值。目标函数如下:
| $ \max \left( {\sum\limits_{i \in S} {{p_i}} (t + 1) - \sum\limits_{i \in S} {{p_i}} (t)} \right)\quad t \in \psi $ | (34) |
| $ \min \left( {\sum\limits_{i \in S} {{p_i}} (t + 1) - \sum\limits_{i \in S} {{p_i}} (t)} \right)\quad t \in \psi $ | (35) |
同时此目标函数存在以下约束条件:
| $ \mathit{\boldsymbol{X}}(t) = {\mathit{\boldsymbol{X}}^{{\rm{base}}}}(t) $ | (36) |
式中:X(t)为t时刻决策变量矩阵,包括各设备出力、水电站储水量、储能系统储存电能等;Xbase(t)为已求得的t时刻基线上决策变量的值的矩阵。式(36)代表t时刻各设备的状态与基线上状态相同,即t时刻VPP运行在基线上。
(4) VPP响应时间TaggR,即运行在功率基线时在t时刻收到调节指令,以最短的时间,在时刻t+TaggR所有资源总功率达到调节指令要求的变化量ΔP。目标函数如下:
| $ \min \sum\limits_{m = t}^{t + 25} {{v_{\Delta P, m}}} \quad \Delta P \in {S_{\Delta P}} $ | (37) |
式中:SΔP为ΔP以等间隔取值的集合;m为在求和公式中遍历的时刻;vΔP, m为0-1变量,表征ΔP一定时m时刻是否满足调节指令要求,不满足时为1,否则为0。同时此目标函数存在以下约束条件:
| $ \mathit{\boldsymbol{X}}(t) = {\mathit{\boldsymbol{X}}^{{\rm{base }}}}(t) $ | (38) |
且如果vΔP, m=0,则存在以下2个约束条件:
| $ \sum\limits_{i \in S} {{p_i}} (t) + \Delta P = \sum\limits_{i \in S} {{p_i}} (m) $ | (39) |
| $ {v_{\Delta P, m + 1}} = 0 $ | (40) |
式(39)代表m时刻满足调节指令要求,式(40)代表一旦满足调节指令要求,后续时间均不包含在响应时间内。
3.3 VPP运行约束条件及优化结果处理根据第2章建立的分布式资源响应能力模型,可建立VPP运行约束条件,包括功率平衡约束式(41)、联络线功率约束式(42)、设备运行约束式(43)—式(54)。
| $ \sum\limits_{i \in S} {{p_i}} (t) + {p_{{\rm{tie }}}}(t) = {P_{\rm{D}}}(t)\quad t \in \psi $ | (41) |
| $ {p_{{\rm{tie, }}\min }} \le {p_{{\rm{tie}}}}(t) \le {p_{{\rm{tie}}, \max }}\quad t \in \psi $ | (42) |
| $ {P_{{\rm{h}}, \min , i}} \le {P_{{\rm{h}}, i}}(t) \le {P_{{\rm{h}}, \max , i}}\quad t \in \psi ;i \in {S_{\rm{h}}} $ | (43) |
| $ - R_{{\rm{h}}, i}^ - \le {R_{{\rm{h}}, i}}(t) \le R_{{\rm{h}}, i}^ + \quad t \in \psi ;i \in {S_{\rm{h}}} $ | (44) |
| $ {P_{{\rm{g}}, \min , i}} \le {P_{{\rm{g}}, i}}(t) \le {P_{{\rm{g}}, \max , i}}\quad t \in \psi ;i \in {S_{\rm{g}}} $ | (45) |
| $ \begin{array}{c} - a_{j, i}^ * R_{{\rm{g}}, i}^ - \le {R_{{\rm{g}}, j, i}}(t) \le a_{j, i}^ * R_{{\rm{g}}, i}^ + \\ j \in {U_{\rm{g}}};t \in \psi ;i \in {S_{\rm{g}}} \end{array} $ | (46) |
| $ - {P_{{\rm{bc}}, \max , i}} \le {P_{{\rm{b}}, i}}(t) \le {P_{{\rm{bd}}, \max , i}}\quad t \in \psi ;i \in {S_{\rm{b}}} $ | (47) |
| $ - R_{{\rm{b}}, i}^ - \le {R_{{\rm{b}}, i}}(t) \le R_{{\rm{b}}, i}^ + \quad t \in \psi ;i \in {S_{\rm{b}}} $ | (48) |
| $ {P_{{\rm{c}}, \min , i}}(t) \le {P_{{\rm{c}}, i}}(t) \le {P_{{\rm{c}}, \max , i}}(t)\quad t \in \psi ;i \in {S_{\rm{c}}} $ | (49) |
| $ R_{{\rm{c}}, i}^ - (t) \le {R_{{\rm{c}}, i}}(t) \le R_{{\rm{c}}, i}^ + (t)\quad t \in \psi ;i \in {S_{\rm{c}}} $ | (50) |
| $ {V_{{\rm{h}}, \min , i}} \le {V_{{\rm{h}}, i}}(t) \le {V_{{\rm{h}}, \max , i}}\quad t \in \psi ;i \in {S_{\rm{h}}} $ | (51) |
| $ \begin{array}{c} {V_{{\rm{h}}, i}}(t + 1) = {V_{{\rm{h}}, i}}(t) + \left( {{q_i}(t) - {Q_i}(t)} \right){\rm{\Delta }}t\\ t \in \psi ;i \in {S_{\rm{h}}} \end{array} $ | (52) |
| $ {E_{{\rm{b}}, \min , i}} \le {E_{{\rm{b}}, i}}(t) \le {E_{{\rm{b}}, \max , i}}\quad t \in \psi ;i \in {S_{\rm{b}}} $ | (53) |
| $ {E_{{\rm{b}}, i}}(t + 1) = {E_{{\rm{b}}, i}}(t) - {P_{{\rm{b}}, i}}(t){\eta _{{\rm{b}}, i}}{\rm{\Delta }}t\quad t \in \psi ;i \in {S_{\rm{b}}} $ | (54) |
式中:Sh,Sg,Sb,Sc分别为水电站、燃气轮机、储能系统、温控负荷集群的序号集合;PD为总负荷功率(不包括温控负荷)。
以式(41)—式(54)作为约束条件,配合目标函数式(31)—式(35)、式(37)及其相应的部分约束条件,即可得到优化模型。求解优化模型即可得到相应的聚合响应能力。
值得注意的是,对于联络线功率上下限、VPP爬坡率上下限、响应时间而言,优化结果中目标函数的值即为所求响应能力。但联络线功率基线需要的是各时刻联络线功率,各时刻联络线功率是优化模型中的决策变量,所以须提取其优化结果值作为所求结果。另外,为了更好地分析响应能力,可通过联络线功率基线优化模型求取基线时各资源出力情况,各资源出力是其中的决策变量,同样需要提取其优化结果值。此外,目标函数式(37)在某些ΔP值下优化结果值会大于24 h,此时认为在此ΔP值下无法调节,响应时间不存在。
3.4 聚合响应能力指标权重及评分为了对VPP响应能力进行评分,须对每个响应能力指标进行权重赋值。在设置权重时,考虑VPP响应能力在一天中的稳定性,响应能力越不稳定,则相应指标权重越小,因此采用熵值代表响应能力不稳定性,采用熵值法[30]进行客观赋权。
计算权重时响应能力指标包含向上调节幅度、向下调节幅度、向上爬坡率、向下爬坡率、平均响应时间5个指标。平均响应时间即已确定的调节范围内的响应时间平均值。首先对指标进行标准化:
| $ x_{m, n, t}^\prime = \frac{{{x_{m, n, t}} - \min {x_{m, n}}}}{{\max {x_{m, n}} - \min {x_{m, n}}}} $ | (55) |
| $ x_{m, n, t}^\prime = \frac{{\max {x_{m, n}} - {x_{m, n, t}}}}{{\max {x_{m, n}} - \min {x_{m, n}}}} $ | (56) |
式中:xm, n, t为第m个VPP第n个指标在t时刻的值;x′m, n, t为相应指标标准化后的值。式(55)适用于正向指标,即上述前4个指标;式(56)适用于反向指标,即平均响应时间。第m个VPP的评分Fm计算如下:
| $ {F_m} = \frac{1}{{24}}\sum\limits_{t = 1}^{24} {\sum\limits_{n \in \Gamma } {{w_{m, n}}} } x_{m, n, t}^\prime $ | (57) |
其中:
| $ \left\{ {\begin{array}{*{20}{l}} {{w_{m, n}} = \frac{{1 - {e_{m, n}}}}{{\sum\limits_{n \in \Gamma } 1 - {e_{m, n}}}}}\\ {{e_{m, n}} = - \frac{1}{{\ln 24}}\sum\limits_{t = 1}^{24} {{r_{m, n, t}}} \ln {r_{m, n, t}}}\\ {{r_{m, n, t}} = \frac{{x_{m, n, t}^\prime }}{{\sum\limits_{t = 1}^{24} {x_{m, n, t}^\prime } }}} \end{array}} \right. $ | (58) |
式中:wm, n为第m个VPP第n个指标的权重;Γ为指标的序号集合;em, n为第m个VPP第n个指标的熵值;rm, n,t为t时刻第m个VPP第n个指标的比重。其中评分Fm值域为[0, 1],值越大则响应能力越好。
4 聚合响应能力评估方法的算例验证选取夏季某日的某工业园区为算例,包含水力发电、燃气轮机、储能系统、温控负荷等资源。具体参数见表 1。
|
|
表 1 VPP模型参数 Table 1 Parameters of VPP model |
其余数据比如总负荷功率、分时电价、外界温度、水电站的水位差均通过前一天的数据预测得出。算例中各类资源成本函数采用一次函数近似,输出量为1 h内的成本,水力发电、燃气轮机的成本函数输入量为发电功率,储能系统的成本函数输入量为充放电功率绝对值,温控负荷集群的成本函数输入量为温度偏差量绝对值Tin(t)-E(Tset)。各成本函数系数见表 2和表 3。
|
|
表 2 成本函数一次项系数 Table 2 First-order coefficients of cost functions |
|
|
表 3 成本函数常数项系数 Table 3 Constant coefficients of cost functions |
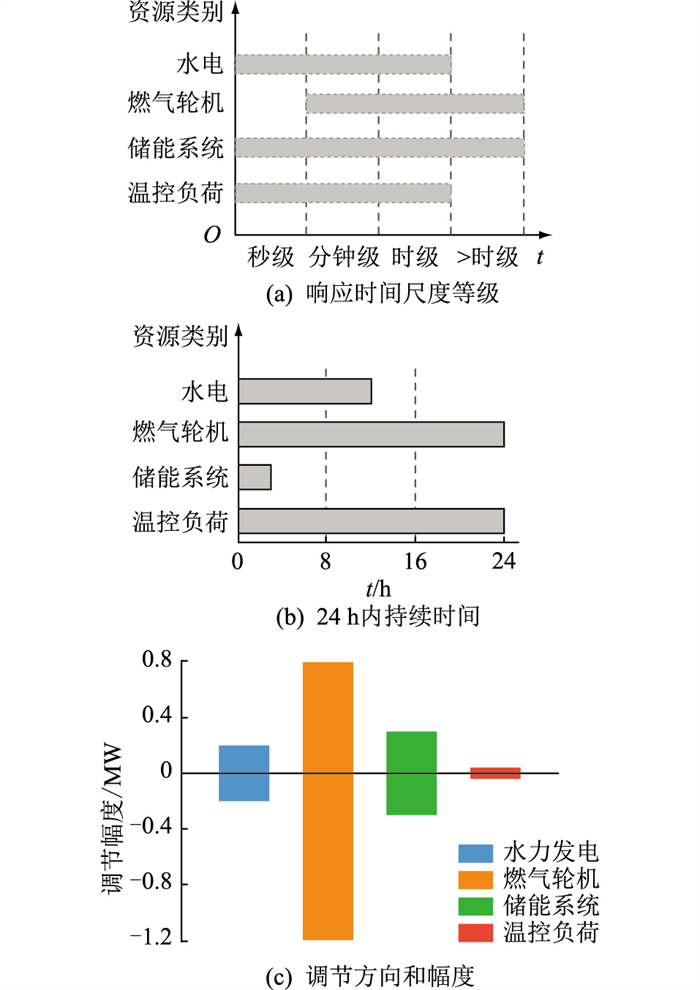
基于各类资源的响应能力模型,结合算例数据,可总结对比各类资源的响应时间尺度、持续时间、调节方向和幅度,如图 3所示。图 3(b)中计算持续时间时,水电站出力取出力上下限的平均值,储水量取最大储水量的50%;储能系统出力取最大充放电功率,储存电能取最大储存电能的50%。图 3(c)中计算调节幅度时,水电站出力取出力上下限的平均值;燃气轮机出力取最大出力的60%;储能系统既不充电也不放电,出力为0;温控负荷温度偏差量Tin(t)-E(Tset)为0。
|
图 3 分布式资源响应能力对比 Fig. 3 Comparision of response capability of distributed resources |
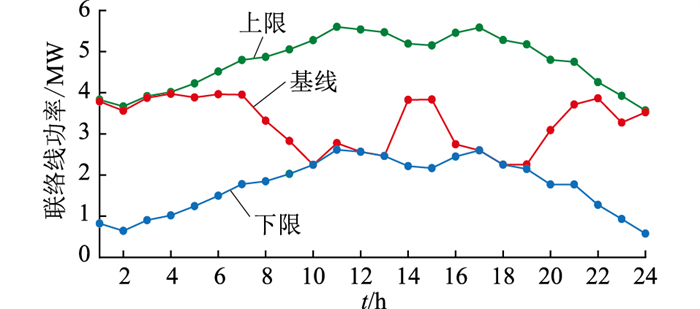
采用文中评估方法,建立VPP聚合模型,使用Gurobi求解响应能力优化模型,得到响应能力值。图 4为VPP聚合后的联络线功率基线和上下限;图 5为运行于基线时各资源分时输出功率。
|
图 4 联络线功率基线和功率上下限 Fig. 4 Tie-line power baseline and upper/ lower limits of power |
|
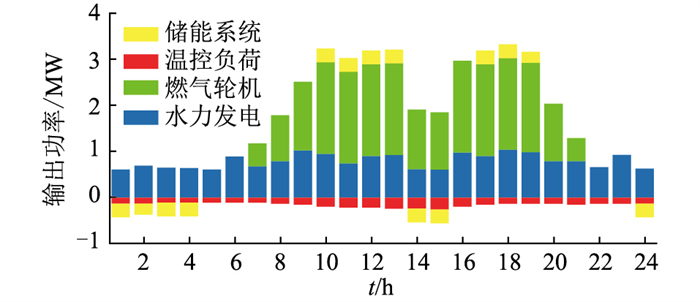
图 5 VPP内部各资源输出功率 Fig. 5 Output power of each resource in VPP |
由图 4可知,0时—5时为低电价段,从电网购电可使成本最小,故联络线基线趋于功率上限;6时—8时为平电价段,联络线功率逐渐下降;9时—13时、16时—19时为高电价段,电网购电减少,故VPP运行基线位于功率下限;14时—15时为位于2个高电价段之间的平电价段,联络线功率有所上升;20时—23时为平电价段,联络线功率逐渐上升。
总体来说,低电价段从电网购电能使成本最低,联络线运行于功率上限;高电价段减少从电网购电能使成本最低,联络线运行于功率下限。平电价段若处于2个高电价段之间,则联络线功率处于适中位置,若处于高、低电价段间则处在上升或下降的过渡阶段。
由图 5可知,储能系统在电价较低时充电,电价较高时放电,实现峰谷套利,达到最低成本;温控负荷调节成本与温度偏差量绝对值成正比,其运行既趋向温度偏差较小,又趋向消耗功率较低,从而达到最低成本。在本算例中,温控负荷在低电价时温度偏差量为0,高电价时温度偏差量达到最大,从而减小消耗功率,达到最低成本。
0时—5时为低电价段,由成本更低的水电满足部分发电需求,VPP从电网购买低价电满足剩余发电需求,储能系统充电,当储能系统储存电能达到上限后,停止充电,此时联络线功率下降;6时—8时为平电价段,故燃气轮机发电功率逐渐上升,电网购电逐渐减少;9时—13时、16时—19时电价较高,燃气轮机功率较大,储能系统放电实现峰谷套利;14时—15时为位于2个高电价段之间的平电价段,燃气轮机、水电发电功率较小,储能系统充电;20时—23时为平电价段,水力发电足以满足发电需求,燃气轮机发电功率下降至0。
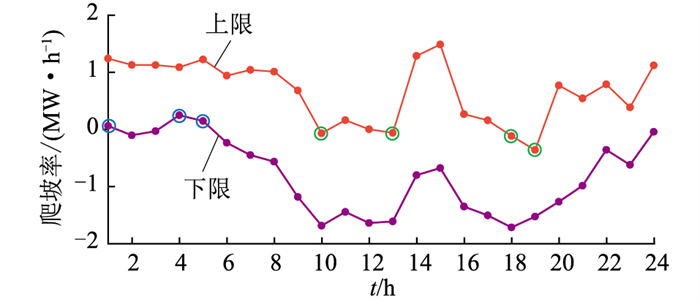
图 6为运行于基线时VPP爬坡率上下限。VPP爬坡率既受到各资源爬坡率约束限制,也受到各资源出力约束、功率平衡约束、联络线功率约束等限制。同时因温控负荷存在,爬坡率上下限的变化也受到温度变化影响,一般来说,温度上升时爬坡率上下限趋向降低,反之亦然。
|
图 6 VPP爬坡率上下限 Fig. 6 Upper and lower limits of climb rate of VPP |
0时—5时联络线功率基线贴近上限、VPP出力贴近下限,难以向下调节,故爬坡率下限较高;6时—8时为平电价段,VPP出力逐渐上升,距下限距离变大,更易于向下调节,同时也因温控负荷的影响,随着温度上升爬坡率趋向下降,故爬坡率上下限均逐渐下降;9时—13时、16时—19时为高电价段,联络线功率基线贴近下限,VPP出力贴近上限,难以向上调节,故爬坡率上限较低;14时—15时为位于2个高电价段之间的平电价段,爬坡率上下限相对较高;20时—23时为平电价段,爬坡率上下限逐渐上升。
图 6中蓝色圆圈标记的时刻下爬坡率下限为正值,而绿色圆圈标记的时刻下爬坡率上限为负值。分析如下:以4时为例,此时总负荷功率逐渐升高,且联络线功率基线贴近上限、VPP出力贴近下限,故受到功率平衡约束限制,难以向下调节,故爬坡率下限较高,甚至为正值,只能向上调节。
爬坡率下限一天内数据的最大、最小值之差为1.95 MW/h,对应的每小时出力可变量大致为全天平均每小时负荷量的43%,爬坡率上限相应的数据则为1.84 MW/h和41%,可以看出VPP爬坡率上下限在一天中变化较大。
VPP爬坡率上限和下限在一天中的平均值分别为-0.80 MW/h和0.66 MW/h,对应的每小时出力可变量大致为全天平均每小时负荷量的18%和15%;VPP在不同时刻爬坡率上下限差值为0.84~2.16 MW/h,对应的每小时出力可变量大致为全天平均每小时负荷量的19%~48%,说明VPP具有较好的爬坡能力。
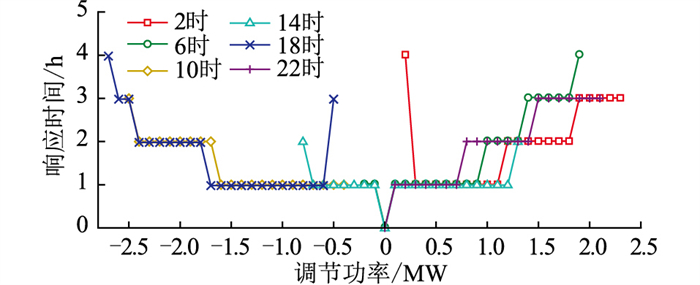
算例选取6个时刻分别评估VPP响应时间,结果如图 7所示。因某些调节功率ΔP下响应时间过长,不适合参与调节,故只展示响应时间在4 h内的情况。其中调节功率ΔP以0.1 MW的间隔取值。同时因算例的程序是在1时—24时这24个时刻优化求解,所以得到的响应时间结果均为整数个小时。另值得注意的是,图 7中某时刻下响应时间为1 h的调节功率范围即为图 6中相同时刻下的爬坡率范围。
|
图 7 不同时刻在不同调节功率下响应时间4 h内的情况 Fig. 7 Response time within 4 hours under different regulating power at different time |
调节过程中,VPP因各资源爬坡率约束、各资源出力约束、功率平衡约束、外界温度变化等而需要一定响应时间才可达到调节指令要求的出力。一般来说ΔP在一定范围内时,响应时间较小,超出这个范围越多,响应时间越大。具体分析如下:
(1) 图 7中6时、14时这2个时刻下ΔP同时存在正值和负值,可以双向调节。以14时为例,此时联络线功率距上下限都有一定距离,有助于VPP双向调节,如响应时间曲线所示,ΔP同时存在正值和负值,可以双向调节,具有较好的调节能力。当ΔP为0时,响应时间为0,不需调节;当ΔP在-0.7~1.2 MW内且不为0时,响应时间为1 h;当ΔP为-0.8 MW或1.3 MW内时,响应时间为2 h;超出这个范围后响应时间超过4 h。
(2) 图 7中2时、10时、18时、22时这4个时刻下ΔP只存在正值或负值,只能向上或向下调节。以18时为例,在18时总负荷逐渐下降,且联络线功率贴近下限,VPP出力贴近上限,所以VPP难以向上调节,如响应时间曲线所示,ΔP没有正值,不能向上调节,只能向下调节。当ΔP在-1.7~-0.6 MW内时,响应时间为1 h;ΔP在-2.4~-1.8 MW内时,响应时间为2 h;超出这个范围后响应时间逐渐上升。
同样的,对2时进行分析,在2时总负荷逐渐上升,且联络线功率贴近上限,VPP出力贴近下限,所以VPP难以向下调节,如响应时间曲线所示,ΔP没有负值,不能向下调节,只能向上调节。当ΔP在0.3~1.1 MW内时,响应时间为1 h;ΔP在1.2~1.8 MW内时,响应时间为2 h;超出这个范围后响应时间逐渐上升。
(3) 2时,6时,10时,14时,18时,22时这6个时刻下响应时间4 h内对应的ΔP范围分别为0.2~2.3 MW、-0.2~1.9 MW、-2.5~-0.4 MW、-0.8~1.3 MW、-2.7~-0.5 MW、0.1~2.1 MW。平均范围长度为2.13 MW,大致为全天平均每小时负荷量的47%,说明VPP具有较好的响应能力。
求取上述指标的权重并对响应能力进行评分。计算平均响应时间时,取功率调节范围为[-1.5 MW, 1.5 MW],结果如下:向上调节幅度、向下调节幅度、向上爬坡率、向下爬坡率、平均响应时间的一天内熵值分别为0.883、0.883、0.950、0.931、0.954;权重分别为0.294、0.294、0.125、0.172、0.115;最后此VPP评分为0.533,说明具有一定的响应能力。
最后,上述已求得的VPP聚合响应能力指标在实际运行中的应用过程如下:联络线功率基线由VPP计算上报,作为结算基准;联络线功率上下限描述了联络线的运行可行域,作为电网调度的约束;当控制中心需要下发调节指令,并计算下一时刻调度方案时,利用VPP爬坡率求得下一时刻的出力可行域,作为下一时刻调度方案的约束;当调节指令要求升高或降低一定的出力时,VPP响应时间即为达到要求所需最短时间,可作为计算调度方案的约束。另外计算得到的聚合响应能力评分也可作为VPP优化配置问题的参考指标,以保证VPP具有足够的响应能力。
5 结论为了有效调度多种分布式资源,文中提出了VPP聚合响应能力评估方法,能够将各类资源聚合为一个整体,优化求解获得其聚合响应能力。算例分析验证了该方法的有效性,得出以下结论:
(1) 文中方法定义了响应能力指标,可用于评估各类资源的独立响应能力以及VPP聚合后的响应能力。对于VPP,上述指标可求解优化模型得到,从而评估聚合响应能力。
(2) 文中方法在评估聚合响应能力方面易于使用且具有较强的通用性,求解得出的聚合响应能力可以上报作为电网的调度信息,参与电力系统调控、电力市场交易决策的制定。
(3) 文中方法考虑响应能力在一天内的不稳定性,采用熵值法求取指标权重,并得到VPP聚合响应能力评分,从而通过评分直观地评价响应能力。
(4) 通过算例对所提方法进行验证,计算出联络线功率基线、功率上下限、VPP爬坡率上下限、平均响应时间,经过分析,上述指标均能正确表现聚合响应能力。最后计算出响应能力评分,验证了此方法的有效性。
| [1] |
李昭昱, 艾芊, 张宇帆, 等. 数据驱动技术在虚拟电厂中的应用综述[J]. 电网技术, 2020, 44(7): 2411-2419. LI Zhaoyu, AI Qian, ZHANG Yufan, et al. Application of data-driven technology in virtual power plant[J]. Power System Technology, 2020, 44(7): 2411-2419. (  0) 0) |
| [2] |
李洁, 孙宏宇, 许椿凯, 等. 参与新型电力系统需求响应的分布式储能资源管理与策略研究[J]. 供用电, 2022, 39(2): 29-35. LI Jie, SUN Hongyu, XU Chunkai, et al. Research on distributed energy storage resource management and strategy participating in demand response of new power systems[J]. Distribution & Utilization, 2022, 39(2): 29-35. (  0) 0) |
| [3] |
田立亭, 程林, 郭剑波, 等. 虚拟电厂对分布式能源的管理和互动机制研究综述[J]. 电网技术, 2020, 44(6): 2097-2108. TIAN Liting, CHENG Lin, GUO Jianbo, et al. A review on the study of management and interaction mechanism for distributed energy in virtual power plants[J]. Power System Technology, 2020, 44(6): 2097-2108. (  0) 0) |
| [4] |
孔英会, 高会生, 张铁峰, 等. 面向虚拟电厂的5G通信技术应用探讨[J]. 电力信息与通信技术, 2020, 18(8): 80-85. KONG Yinghui, GAO Huisheng, ZHANG Tiefeng, et al. Discussion on application of 5G communication technology for virtual power plant[J]. Electric Power Information and Communication Technology, 2020, 18(8): 80-85. (  0) 0) |
| [5] |
毛颖卓. 水-风-光微电网调频与功率平衡控制技术[D]. 广州: 广东工业大学, 2020. MAO Yingzhuo. Fregqency and power balance control technology of microgrids with hydro-wind-solar energy[D]. Guangzhou: Guangdong University of Technology, 2020. (  0) 0) |
| [6] |
杨庆材, 李淑英, 赵宁波, 等. 基于间隙度量的燃气轮机分段线性化建模方法[J]. 热能动力工程, 2018, 33(11): 58-63. YANG Qingcai, LI Shuying, ZHAO Ningbo, et al. Gas turbine piecewise linear model based on gap metric concept[J]. Journal of Engineering for Thermal Energy and Power, 2018, 33(11): 58-63. (  0) 0) |
| [7] |
魏炜, 陈晗, 朱洁, 等. 电池储能系统两模式协调控制策略[J]. 电力系统及其自动化学报, 2021, 33(2): 116-121. WEI Wei, CHEN Han, ZHU Jie, et al. Two-mode coordinated control strategy for battery energy-storage system[J]. Proceedings of the CSU-EPSA, 2021, 33(2): 116-121. (  0) 0) |
| [8] |
惠红勋. 温控负荷参与电力系统动态响应的建模与控制方法研究[D]. 杭州: 浙江大学, 2020. HUI Hongxun. Modelling and control of thermostatically controlled loads for participating in dynamic response of power systems[D]. Hangzhou: Zhejiang University, 2020. (  0) 0) |
| [9] |
崔屹峰, 李珍国, 贾清泉, 等. 基于参数辨识与状态估计的温控负荷响应能力动态评估[J]. 电力系统自动化, 2021, 45(1): 150-158. CUI Yifeng, LI Zhenguo, JIA Qingquan, et al. Dynamic evaluation of response potential of thermostatically controlled load based on parameter identification and state estimation[J]. Automation of Electric Power Systems, 2021, 45(1): 150-158. (  0) 0) |
| [10] |
朱玉杰. 电采暖负荷可调节能力评估与集群控制策略研究[D]. 吉林: 东北电力大学, 2019. ZHU Yujie. Research on electric heating load adjustability evaluation and cluster control strategy[D]. Jilin: Northeast Dianli University, 2019. (  0) 0) |
| [11] |
姜喜燕. 虚拟电厂资源的精细化评估与调度优化研究[D]. 北京: 华北电力大学, 2021. JIANG Xiyan. Research on refined evaluation and scheduling optimization of virtual power plant resources[D]. Beijing: North China Electric Power University, 2021. (  0) 0) |
| [12] |
杨文海. 城市电网需求侧能源资源动态聚合决策及信息系统研究[D]. 北京: 华北电力大学, 2018. YANG Wenhai. Research on dynamic aggregation decision of demand side energy resources in urban power grid and its information system[D]. Beijing: North China Electric Power University, 2018. (  0) 0) |
| [13] |
杨运国, 侯健生, 边晓燕, 等. 面向高比例新能源配电网的灵活性资源综合评价[J]. 供用电, 2021, 38(11): 68-76. YANG Yunguo, HOU Jiansheng, BIAN Xiaoyan, et al. Comprehensive evaluation of flexible resources for high penetration of renewable energy sources integrated to the distribution network[J]. Distribution & Utilization, 2021, 38(11): 68-76. (  0) 0) |
| [14] |
张国梁. 基于灵活性指标的电源规划[D]. 北京: 华北电力大学, 2021. ZHANG Guoliang. Power planning based on flexibility index[D]. Beijing: North China Electric Power University, 2021. (  0) 0) |
| [15] |
陈张宇, 刘东, 刘浩文, 等. 基于精细化需求响应的虚拟电厂优化调度[J]. 电网技术, 2021, 45(7): 2542-2550. CHEN Zhangyu, LIU Dong, LIU Haowen, et al. Optimal dispatching of virtual power plant based on refined demand response[J]. Power System Technology, 2021, 45(7): 2542-2550. (  0) 0) |
| [16] |
屈富敏, 赵健, 蔡帜, 等. 电动汽车与温控负荷虚拟电厂协同优化控制策略[J]. 电力系统及其自动化学报, 2021, 33(1): 48-56. QU Fumin, ZHAO Jian, CAI Zhi, et al. Coordinated optimal control strategy for electric vehicle and thermostatically-controlled load aggregators[J]. Proceedings of the CSU-EPSA, 2021, 33(1): 48-56. (  0) 0) |
| [17] |
龚超, 张轩, 赵越, 等. 考虑虚拟电厂可调能力的综合需求响应市场出清策略[J]. 南方电网技术, 2021, 15(12): 56-65. GONG Chao, ZHANG Xuan, ZHAO Yue, et al. Market clearing strategy of integrated demand response considering adjustable capacity of virtual power plant[J]. Southern Power System Technology, 2021, 15(12): 56-65. (  0) 0) |
| [18] |
ZHAO H T, WANG B, WANG X Y, et al. Active dynamic aggregation model for distributed integrated energy system as virtual power plant[J]. Journal of Modern Power Systems and Clean Energy, 2020, 8(5): 831-840. (  0) 0) |
| [19] |
李泽华, 刘明波. 主动配电系统参与日前电能量市场的聚合模型[J]. 电网技术, 2021, 45(11): 4345-4355. LI Zehua, LIU Mingbo. Aggregation model for active distribution systems participating in day-ahead electricity energy market[J]. Power System Technology, 2021, 45(11): 4345-4355. (  0) 0) |
| [20] |
林曦明. 综合能源系统建模及调频仿真分析[D]. 哈尔滨: 哈尔滨工业大学, 2020. LIN Ximing. Integrated energy system modeling and frequency modulation simulation analysis[D]. Harbin: Harbin Institute of Technology, 2020. (  0) 0) |
| [21] |
ZHAO H T, WANG B, PAN Z G, et al. Aggregating additional flexibility from quick-start devices for multi-energy virtual power plants[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 646-658. (  0) 0) |
| [22] |
云秋晨. 虚拟电厂多类型资源优化组合及运行策略研究[D]. 北京: 北京交通大学, 2021. YUN Qiuchen. Research on optimal combination and operation strategy of multi-type resources of virtual power plant[D]. Beijing: Beijing Jiaotong University, 2021. (  0) 0) |
| [23] |
赵昊天, 王彬, 潘昭光, 等. 支撑云-群-端协同调度的多能园区虚拟电厂: 研发与应用[J]. 电力系统自动化, 2021, 45(5): 111-121. ZHAO Haotian, WANG Bin, PAN Zhaoguang, et al. Research and application of park-level multi-energy virtual power plants supporting cloud-cluster-end multi-level synergetic dispatch[J]. Automation of Electric Power Systems, 2021, 45(5): 111-121. (  0) 0) |
| [24] |
张凯杰. 电力市场环境下虚拟电厂参与调峰的研究[D]. 杭州: 浙江大学, 2021. ZHANG Kaijie. Research on virtual power plant participation in peak regulation in power market environment[D]. Hangzhou: Zhejiang University, 2021. (  0) 0) |
| [25] |
陈新和, 裴玮, 邓卫, 等. 数据驱动的虚拟电厂调度特性封装方法[J]. 中国电机工程学报, 2021, 41(14): 4816-4828. CHEN Xinhe, PEI Wei, DENG Wei, et al. Data-driven virtual power plant dispatching characteristic packing method[J]. Proceedings of the CSEE, 2021, 41(14): 4816-4828. (  0) 0) |
| [26] |
陈宇沁, 曹晓冬, 王俊, 等. 综合能源系统综合需求响应行为研究[J]. 电力工程技术, 2020, 39(6): 89-97. CHEN Yuqin, CAO Xiaodong, WANG Jun, et al. Integrated demand response behavior of integrated energy system[J]. Electric Power Engineering Technology, 2020, 39(6): 89-97. (  0) 0) |
| [27] |
马骏超, 黄弘扬, 楼伯良, 等. 分时电价背景下综合能源需求响应优化建模[J]. 电力工程技术, 2020, 39(5): 99-106. MA Junchao, HUANG Hongyang, LOU Boliang, et al. Optimal modeling of integrated energy demand response under time-shared electricity price[J]. Electric Power Engineering Technology, 2020, 39(5): 99-106. (  0) 0) |
| [28] |
张潼, 于鹤洋, 田江, 等. 基于非侵入式负荷辨识的聚合负荷需求响应能力在线评估[J]. 电力工程技术, 2020, 39(6): 19-25, 65. ZHANG Tong, YU Heyang, TIAN Jiang, et al. Online aggregation monitoring of low-voltage power load demand response capability based on non-intrusive load identification[J]. Electric Power Engineering Technology, 2020, 39(6): 19-25, 65. (  0) 0) |
| [29] |
石渠, 张红丽, 常海军, 等. 水轮机参与西南电网频率紧急控制协调优化方法[J]. 中国电机工程学报, 2018, 38(S1): 93-98. SHI Qu, ZHANG Hongli, CHANG Haijun, et al. Coordinated optimization method of hydropower units involved in frequency emergency control in southwest power grid[J]. Proceedings of the CSEE, 2018, 38(S1): 93-98. (  0) 0) |
| [30] |
周仁和. 高比例新能源电力系统灵活性资源价值评价模型及应用[D]. 北京: 华北电力大学, 2021. ZHOU Renhe. Flexible resources value evaluation model and application of high proportion new energy power system[D]. Beijing: North China Electric Power University, 2021. (  0) 0) |
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2022, Vol. 41
2022, Vol. 41


 蒋正威(1978), 男, 硕士, 研究员级高级工程师, 从事电网调度自动化系统的运行和应用相关工作(E-mail:
蒋正威(1978), 男, 硕士, 研究员级高级工程师, 从事电网调度自动化系统的运行和应用相关工作(E-mail: