文章编号: 2096-3203(2022)06-0109-07 中图分类号: TM732
2. 东南大学电气工程学院, 江苏 南京 210096
随着光伏、风电等可再生能源不断接入配电网,潮流方向的不确定性使得电网发生故障的风险不断提高[1-2]。当配电网发生故障时,快速确定故障区段并及时采取有效的抢修措施是保证配电系统安全稳定运行的关键[3]。
目前配电网故障区段定位研究主要分为2类:一类是基于馈线终端(feeder terminal unit,FTU)遥测数据的方法[4-6],其通过计算所采集数据的相关系数[4]、波形衰减常数[6]等进行区段定位,此类方法需要对采集数据进行特征量提取或数学变换,处理过程繁琐;另一类是基于FTU遥信数据的方法[7-16],其具有数据分析处理简单且快速的优点。传统辐射型配电网发生故障时,故障点至系统电源之间的馈线区段流经故障过电流,而其余区段无故障过电流流过,根据此原理便可以进行故障区段定位[7]。有源配电网发生故障时,系统电源和分布式电源(distributed generation,DG)均会向故障点提供故障过电流[8],导致传统故障区段定位方法失效。文献[9]采取对各个电源分别假定正方向的方法,实现多个电源接入配电网情况下的故障区段定位,但是针对配电网中发生的多重故障,须进行多次计算,因此故障定位的效率较低。
针对有源配电网中多个电源接入的情况,目前常用的处理方法是给整个配电网络仅假定一个正方向[10],以区分故障点上游和下游的故障过电流,从而进行故障区段定位。此类方法主要包括矩阵算法[10-15]和智能优化算法[16-20]。其中,矩阵算法是基于配电网拓扑的一种快速故障定位方法,但该方法容易受到矩阵中数值稳定性的约束,因此容错性较差。文献[12]建立描述节点与节点之间连接关系的矩阵,针对节点FTU信息不完备的情况,仅采用剔除该节点的方法,扩大了故障定位的区域;文献[14-15]建立了节点和区段连接关系的网络描述矩阵,为了提高算法容错性,依靠告警信息之间的逻辑关系对畸变信息进行修改,但此方法处理畸变信息的效率较低。粒子群算法[16]、免疫算法[19]、遗传算法[20]等智能优化算法的原理,是通过求解所建立的评价函数,找出能够最佳解释告警信息的故障区段,从而实现故障定位。此方法具有一定的容错性,但是故障定位速度相对较慢,且迭代过程有一定的局部收敛概率,这一概率与配电网的规模正相关,即在大规模配电网中局部收敛问题更加严重。
针对上述问题,文中提出将矩阵算法和智能优化算法进行优势互补的定位方法,将矩阵算法计算速度快和智能优化算法容错性高的优点相结合。首先,矩阵算法通过FTU上传的实际告警信息得出故障判定结果,然后开关函数根据此结果得出期望的FTU告警信息,通过实际与期望告警信息的比较判断定位结果是否准确。若判断结果正确,直接输出定位结果;否则,运用优化算法求解评价函数,从而输出正确的故障定位结果。矩阵算法的作用在于降低智能优化算法寻优的维度,从而降低局部收敛概率并提高定位速度;而智能优化算法则提高了矩阵算法的容错性。
1 基于矩阵算法的故障区段定位应用图论的有关知识,可以将配电网的结构简单描述为节点与线段之间连接关系的一个图[21]。其中,节点包括隔离开关、断路器、分段开关,线段为连接上述设备的配电线路。
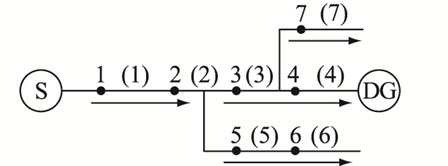
相较于传统的辐射型配电网,有源配电网中功率流向复杂,给故障定位增加了困难。为此,首先设定网络功率由主电源流向各DG及线路末端的方向为正方向,从而将有源配电网的结构等效为传统的辐射型配电网,并定义每个区段中正方向流过的第一个节点为父节点,其余为子节点。以图 1所示7节点有源配电网拓扑为例进行说。图中,箭头方向为规定的正方向;S表示主电源;1—7表示节点编号;(1)—(7)表示区段编号。
|
图 1 7节点有源配电网拓扑 Fig. 1 Topology of 7-node active distribution network |
首先,在假定功率正方向之后,建立n×n型网络描述矩阵D=(Dij),n为节点个数。其实质是描述配电网中所有节点连接关系的不对称邻接矩阵,当节点i和节点j(i≠j)分别为同一区段的父、子结点,且二者为正向连接时,则定义Dij=1,其他情况则定义Dij=0。对于T接区段而言,有1个父节点和2个子节点,特规定其子节点之间的连接关系为0。图 1配电网的网络描述矩阵为:
| $ \boldsymbol{D}=\left[\begin{array}{lllllll} 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] $ | (1) |
由式(1)可知,D为对角元素为0且具有高度稀疏性的不对称矩阵。
其次,建立节点上传的n×1型故障告警信息矩阵G=(Gi1)。有源配电网发生故障后,功率流向发生改变。安装于各节点的FTU将根据是否检测到故障电流以及故障电流的流向与网络正方向是否相同,上传“1,0,-1”3种逻辑信号至配电主站。Gi1取1,0,-1分别表示节点i流过正向故障过电流、节点i不存在故障过电流、节点i流过反向故障过电流。
然后,形成故障判别矩阵P=(Pij)。
| $ P_{i j}= \begin{cases}D_{i j} & i \neq j \\ G_{i 1} & i=j\end{cases} $ | (2) |
为了方便对不同的馈线区段故障进行定位,文中将馈线区段分为T接区段、末端区段和普通区段,例如图 1中区段(2)、(3)为T接区段,区段(4)、(6)、(7)为末端区段,区段(1)、(5)为普通区段,在文献[10]的基础上,形成如下故障判据。
(1) 对Pii=1且Pij=1的j,都有Pjj=0或-1(j≠i);对Pii=-1且Pji=1的j,都有Pjj=0(j≠i);对Pii=0且Pij=1的j, 都有Pjj=-1(j≠i)。满足上述任意一个条件,且节点i和节点j之间的馈线区段为普通区段,则故障发生在节点i与节点j构成的馈线区段内。
(2) 满足判据(1)的任意一个条件,且节点i和节点j之间的馈线区段为T接区段时,由于T接区段有2个子节点j1,j2,若父节点与2个子节点根据判据(1)得出的定位结果相同,则故障发生在该T接区段内。若定位结果相矛盾,且其所有子节点过电流信息均不等于1,则该T接区段有故障,否则该T接区段无故障。
(3) 节点i所在的馈线区段为末端区段,则满足:Pii=1, Pij=0(i≠j)。
最后,利用故障判据对P中的元素进行分析,从而判断出故障区段。
以图 1为例,假定区段(3)故障,则G为:
| $ \boldsymbol{G}=\left[\begin{array}{lllllll} 1 & 1 & 1 & -1 & 0 & 0 & 0 \end{array}\right]^{\mathrm{T}} $ | (3) |
由此得出P为:
| $ \boldsymbol{P}=\left[\begin{array}{ccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] $ | (4) |
运用故障判据对矩阵元素进行分析。P33=1,P34=1,P44=-1,且节点3和节点4之间为T接区段,则首先根据判据(1)得出区段(3)故障。由于区段(3)为T接区段,进一步判断区段(3)的父节点3与另外一个子节点7的矩阵元素,即:P33=1,P37= 1,P77=0。满足故障条件,故障信息不矛盾,因此判断区段(3)故障。
2 开关函数容错判断及优化处理 2.1 开关函数容错判断矩阵算法原理简单,但其定位结果的准确度依赖FTU上传信息的准确度。在实际应用中,FTU安装于户外,易受外界电磁环境的干扰,当配电网发生故障时,告警信息在上传过程中容易发生畸变或漏报,从而影响故障定位结果的准确度。
为了避免矩阵算法在FTU告警信息畸变或漏报的情况下输出错误的定位结果,文中将输出结果代入开关函数进行校验。开关函数反映了节点处FTU告警信息与区段状态之间的逻辑或关系。文中采用的适用于有源配电网中功率双向流动的开关函数为n×1型矩阵G′=(G′i1),G′也为期望故障告警信息矩阵,其中:
| $ \begin{aligned} G_{i 1}^{\prime}=&\left\{\prod\limits_{\mathrm{u}}^{U_{\mathrm{g}}}\left[K_{\mathrm{u}}\left(1-\prod\limits_{i, G_{\mathrm{u}}} S_{i, G_{\mathrm{u}}}\right)\right]\right\} \times \prod\limits_{i, \mathrm{~d}}^{D_{\mathrm{s}}} S_{i, \mathrm{~d}}-\\ &\left\{\prod\limits_{\mathrm{d}}^{D_{\mathrm{g}}}\left[K_{\mathrm{d}}\left(1-\prod\limits_{i, G_{\mathrm{d}}} S_{i, G_{\mathrm{d}}}\right)\right]\right\} \times \prod\limits_{i, \mathrm{u}}^{U_{\mathrm{s}}} S_{i, \mathrm{u}} \end{aligned} $ | (5) |
式中:以开关节点i为分界线且含有主电源的部分为上游,其余部分为下游;Ku,Kd分别为上游和下游的电源接入情况,取1,0表示有、无电源接入;Si,Gu,Si,Gd分别为开关节点i到上游主电源Gu和下游DG Gd之间的馈线区段状态值;Si,u,Si,d分别为开关节点i上游和下游所有馈线区段的状态值;Ug,Dg分别为上游和下游的电源数量;Us,Ds分别为上游和下游所有馈线区段的总数;Π表示逻辑或运算。
在计及FTU上传信息畸变或漏报的情况下,假定式(3)信息畸变为:
| $ \boldsymbol{G}=\left[\begin{array}{lllllll} 1 & 0 & 1 & -1 & 0 & 1 & 0 \end{array}\right]^{\mathrm{T}} $ | (6) |
根据矩阵算法的判定结果,故障区段为区段(1)、(3)、(6),然后将其代入式(5),得到:
| $ \boldsymbol{G}^{\prime}=\left[\begin{array}{lllllll} 1 & 0 & 0 & -1 & 0 & 0 & 0 \end{array}\right]^{\mathrm{T}} $ | (7) |
可见,G′≠G,则判断告警信息发生畸变或漏报,将矩阵算法的输出结果全部纳入可疑故障集合矩阵ρ中。
| $ \boldsymbol{\rho}=\left[\begin{array}{lllllll} x(1) & 0 & x(3) & 0 & 0 & x(6) & 0 \end{array}\right]^{\mathrm{T}} $ | (8) |
式中:ρ的m个元素对应m个区段数,ρ中每个元素为对应区段的故障状态,即变量x(1),x(3),x(6)分别表示区段(1)、(3)、(6)的区段状态,其取值为0,1分别表示区段无故障和有故障。
2.2 灰狼优化算法优化处理为了对ρ中的故障区段进行优化处理,文中构建适用于有源配电网的评价函数,如式(9)所示。该函数为基于逻辑关系的0-1整数规划模型。
| $ \min f(x)=\sum\left(\left\lceil\boldsymbol{G}-\boldsymbol{G}^{\prime}\right\rceil\right)+\beta \sum \boldsymbol{\rho} $ | (9) |
式中:第一部分为寻找最能匹配实际告警信息的故障区段所对应的期望告警信息,
将开关函数校验后得出的可疑故障区段代入式(9),通过求解评价函数便可对上述畸变情况下的故障区段进行优化处理,得出最终的定位结果。综上,文中算法流程如图 2所示。基本步骤如下。

|
图 2 算法流程 Fig. 2 Algorithm flow |
步骤1:建立配电网的网络描述矩阵D,结合节点故障告警信息矩阵G,由式(2)形成故障判别矩阵P,根据故障判据形成初步的故障定位结果。
步骤2:将步骤1中得出的定位结果代入开关函数进行校验,如果校验所得的节点期望故障告警信息矩阵G′与实际故障告警信息矩阵G相同,则直接输出步骤1的定位结果;否则,将上述的定位结果列入可疑故障集合ρ,进行优化处理。
步骤3:构建式(9)的评价函数,将可疑故障集合ρ代入函数中,并运用智能优化算法求解评价函数,求解过程中,保持最优适应度值达到一定次数或达到最大迭代次数时,输出最终定位结果。
文中采用灰狼优化(grey wolf optimization,GWO) 算法求解评价函数。GWO算法是一种基于狼群群体协作捕食机制的智能优化算法[22],其具有结构简单、需要调节的参数少、容易实现等优点。具体参数设置如下:灰狼种群数量为50;灰狼种群维度由可疑故障集合ρ中的变量数决定;r1,r2取0到1之间的随机数;a随着迭代次数的增加,从2线性下降到0。由于矩阵算法大幅降低了GWO算法的寻优维度,一般经过少数几次迭代即可求得最优解,因此设定迭代次数为50。
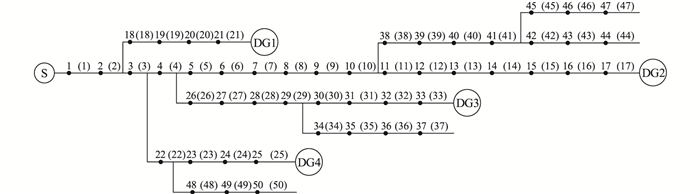
3 算例分析文中以图 3中50节点有源配电网为例进行仿真。
|
图 3 50节点有源配电网拓扑 Fig. 3 Topology of 50-node active distribution network |
首先考虑DG2接入,为了证明文中方法在多区段同时发生故障时的准确定位能力,假定故障区段为区段(12)、(24)、(31)、(37)、(42)、(46)、(50),并伴随节点8,17,35的告警信息畸变或漏报,实际故障告警信息为:
| $ \begin{aligned} &\boldsymbol{G}=\left[\begin{array}{lllllllllllllllll} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \end{array}\right. \\ &\begin{array}{llllllllllllllllllll} 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & -1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \end{array} \\ &\left.\begin{array}{lllllllllllllllllllll} 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \end{array}\right]^{\mathrm{T}} \\ & \end{aligned} $ | (10) |
通过前文所述的矩阵算法得出故障区段为:区段(7)、(12)、(24)、(31)、(34)、(37)、(42)、(46)、(50),将上述故障区段代入式(5),则FTU期望的故障告警信息为:
| $ \begin{aligned} \boldsymbol{G}^{\prime}=& \left[\begin{array}{llllllllllllllllll} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 & -1 & -1 & -1 \end{array}\right. \\ &\begin{array}{llllllllllllllllllll} & -1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & -1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \end{array} \\ &\left.\begin{array}{lllllllllllllllllllll} 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \end{array}\right]^{\mathrm{T}} \end{aligned} $ | (11) |
可见,G′≠G,则判断告警信息上传错误,将矩阵算法的定位结果代入可疑故障集合。
| $ \begin{array}{l} \boldsymbol{\rho}=\left[ {\begin{array}{*{20}{l}} 0&0&0&0&0&0&{x(7)}&0&0&0&0 \end{array}} \right.\\ \begin{array}{*{20}{l}} {x(12)}&0&0&0&0&0&0 \end{array}\\ \begin{array}{*{20}{l}} 0&0&0&0&{x(24)}&0&0&0&0&0&0 \end{array}\\ \begin{array}{*{20}{l}} {x(31)}&0&0&{x(34)}&0&0 \end{array}\\ \begin{array}{*{20}{l}} {x(37)}&0&0&0&0&{x(42)}&0&0&0&0 \end{array}\\ {\left. {\begin{array}{*{20}{l}} {x(46)}&0&0&0&0&{x(50)} \end{array}} \right]^{\rm{T}}} \end{array} $ | (12) |
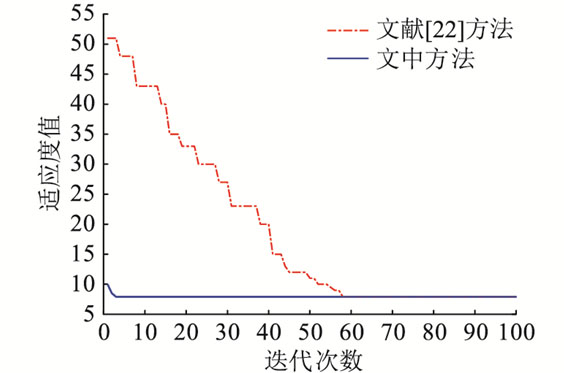
用GWO算法求解式(9),得出x(12)=x(24)=x(31)=x(37)=x(42)=x(46)=x(50)=1,x(7)=x(34)=0,所对应的函数值为7.9,输出故障定位结果为区段(12)、(24)、(31)、(37)、(42)、(46)、(50),定位正确。文中方法与文献[22]中GWO算法的迭代过程对比如图 4所示。
|
图 4 迭代过程对比 Fig. 4 Iteration process comparison |
由图 4可知,文献[22]中GWO算法经过了50多次迭代才正确定位出故障,而文中方法仅通过3次迭代便得出正确结果。出现上述现象的原因在于,包括GWO算法在内的其他智能优化算法,其寻优空间为50个区段,即从250种故障情况中找出唯一的正确解。而文中方法通过矩阵算法和开关函数的联合作用,把上述故障情况缩减为29种。因此,在与GWO算法的配合下,能够迅速得出最优解。文中方法应用于定位大规模配电网的多重故障时,其相对于传统智能优化算法的优势会更加明显。
3.2 单一DG接入配电网假定DG2接入配电网,即对仅有1个DG接入配电网的情况进行仿真,验证文中方法故障定位结果的准确性。
首先,考虑多个节点告警信息畸变或漏报的情况,对DG2接入的情况进行仿真,结果如表 1所示。表 1仿真结果表明,文中方法在有源配电网发生单一或多重故障,并且伴随多个节点故障告警信息畸变的情况下,矩阵算法的定位结果在G与G′的对比过程中被判断为告警信息畸变下的定位结果,因此需进行优化处理,最终输出了正确的故障区段。
|
|
表 1 多节点信息畸变下的故障定位结果 Table 1 Fault location results considering multi-node information distortion |
考虑配电网中DG的不同投切形式对故障定位的影响,对不同DG接入下的故障进行仿真,用开关矩阵K=[k1 k2 … kn]表示n个不同DG的接入情况。矩阵K中的元素取1,0分别表示DG接入和未接入配电网。仿真结果如表 2所示。
|
|
表 2 不同DG接入下的故障定位结果 Table 2 Fault location results considering different DG access |
表 2仿真结果表明,不同DG接入使配电网中功率流向更为复杂的情况下,文中方法仍能准确定位单一或多重故障。
3.4 文中方法与其他方法对比分析为了验证文中方法相较矩阵算法和智能优化算法的优势,分别运用文中方法、文献[10]中矩阵算法、文献[22]中GWO算法对表 2的算例进行50次仿真。
定义定位准确率为:定位的故障区段全部正确的次数与定位总次数的比值。首先,对定位准确率进行对比分析,结果如表 3所示。
|
|
表 3 定位准确率对比 Table 3 Positioning accuracy comparison |
由表 3可知,文献[10]中矩阵算法定位准确率为0,因为在节点告警信息畸变的情况下,其虽然有可能定位出故障区段,但出现了大量的误判区段。文中方法之所以拥有较高的容错性,是因为开关函数的校验作用,使得矩阵算法错误的定位结果能够被及时发现,并在智能优化算法的帮助下得出正确结果,二者的联合起到了修正错误结果的作用,将矩阵算法的定位准确率提高到与智能优化算法同等的水平。
其次,对比3种方法的定位速度。文献[10]中矩阵算法的平均定位时间为0.000 9 s。文献[22]中GWO算法的平均定位时间为1.233 0 s。文中方法采用矩阵算法和GWO算法相结合,在告警信息正确的情况下,平均定位时间为0.000 8 s,而在告警信息错误的情况下,平均定位时间为0.148 0 s。
由以上分析可知,文中方法和矩阵算法相比,在开关函数判断告警信息正确的情况下,定位速度几乎相同;和智能优化算法相比,在告警信息错误的情况下,缩短了故障定位的时间。
为了验证文中方法求解大规模配电网的优点,将有源配电网规模扩大至100、300、500节点,并随机假定每个配电网中的5个末端区段发生故障并伴随五重畸变,运用文中方法(矩阵算法降维)与文献[22]方法(GWO算法,无降维)进行50次仿真,仿真结果如表 4所示。由于文中方法分为2步,采用a,b分别表示矩阵算法的计算维度、智能优化算法的计算维度。
|
|
表 4 大规模配电网下不同方法对比 Table 4 Comparison of different methods under large-scale node distribution network |
由表 4可知,文献[22]中GWO算法进行故障定位时,其计算维度即为配电网的规模,因此配电网维度越大,其寻优空间越大,导致计算速度越慢。而文中首先依靠矩阵算法计算速度快的优点,在节点信息畸变的情况下,快速确定可疑故障区段,实现配电网的降维,减小智能优化算法的寻优空间,从而降低配电网规模对智能优化算法计算速度的影响。
4 结论文中针对传统故障定位方法应用于有源配电网时,存在矩阵算法容错性差、智能优化算法计算速度慢且局部收敛的问题,提出一种矩阵算法和智能优化算法相结合的有源配电网故障定位方法,通过算例分析,得出如下结论:
(1) 文中方法将矩阵算法与智能优化算法的优点相结合,克服了二者单独应用于大规模有源配电网所面临的问题。
(2) 文中的开关函数不仅用于评价函数中与实际告警信息作差以寻找最优解,还能验证矩阵算法所得出的故障区段是否是在故障告警信息错误的情况下所得出的结果。
(3) 在无信息畸变或者漏报的情况下,由矩阵算法单独完成故障区段定位;否则,基于分层处理思想,由矩阵算法确定第一层中可疑故障区段集合,该集合作为第二层的解空间由智能优化算法进行求解。在此过程中,智能优化算法提高了矩阵算法的容错性,避免因矩阵中个别元素错误而输出错误的故障定位结果,而矩阵算法则为智能优化算法降低了配电网维度,从而降低了局部收敛的概率,提高了计算速度。
| [1] |
郝丽丽, 王辉, 王国栋, 等. 含分布式电源配电网运行风险的影响因素溯源[J]. 电力自动化设备, 2021, 41(1): 27-37. HAO Lili, WANG Hui, WANG Guodong, et al. Influence factor tracing of operation risk for distribution network with distributed generations[J]. Electric Power Automation Equipment, 2021, 41(1): 27-37. (  0) 0) |
| [2] |
SINGH M. Protection coordination in distribution systems with and without distributed energy resources-a review[J]. Protection and Control of Modern Power Systems, 2017, 2(1): 1-17. DOI:10.1186/s41601-016-0032-y (  0) 0) |
| [3] |
LIU P H, HUANG C. Detecting single-phase-to-ground fault event and identifying faulty feeder in neutral ineffectively grounded distribution system[J]. IEEE Transactions on Power Delivery, 2018, 33(5): 2265-2273. DOI:10.1109/TPWRD.2017.2788047 (  0) 0) |
| [4] |
苑吉河, 张曦, 黄虎, 等. 基于电流序分量的多源配电网故障定位方法[J]. 电力工程技术, 2020, 39(5): 204-210. YUAN Jihe, ZHANG Xi, HUANG Hu, et al. Multi-source distribution network fault location method based on current sequence component[J]. Electric Power Engineering Technology, 2020, 39(5): 204-210. (  0) 0) |
| [5] |
朱革兰, 李松奕, 兰金晨, 等. 基于零序特征量的配电网接地故障区段定位方法[J]. 电力自动化设备, 2021, 41(1): 34-40, 68. ZHU Gelan, LI Songyi, LAN Jinchen, et al. Fault section location method for grounding fault of distribution network based on zero-sequence characteristic[J]. Electric Power Automation Equipment, 2021, 41(1): 34-40, 68. (  0) 0) |
| [6] |
王晓伟, 张晓, 赵倩宇, 等. 基于暂态零模电流的配电网故障区段定位[J]. 智慧电力, 2021, 49(3): 103-110. WANG Xiaowei, ZHANG Xiao, ZHAO Qianyu, et al. Fault section location in distribution system based on transient zero-mode current[J]. Smart Power, 2021, 49(3): 103-110. DOI:10.3969/j.issn.1673-7598.2021.03.016 (  0) 0) |
| [7] |
杜红卫, 孙雅明, 刘弘靖, 等. 基于遗传算法的配电网故障定位和隔离[J]. 电网技术, 2000, 24(5): 52-55. DU Hongwei, SUN Yaming, LIU Hongjing, et al. Fault section diagnosis and isolation of distribution networks based on genetic algorithm[J]. Power System Technology, 2000, 24(5): 52-55. DOI:10.3321/j.issn:1000-3673.2000.05.013 (  0) 0) |
| [8] |
彭克, 张聪, 徐丙垠, 等. 含高密度分布式电源的配电网故障分析关键问题[J]. 电力系统自动化, 2017, 41(24): 184-192. PENG Ke, ZHANG Cong, XU Bingyin, et al. Key issues of fault analysis on distribution system with high-density distributed generations[J]. Automation of Electric Power Systems, 2017, 41(24): 184-192. DOI:10.7500/AEPS20170609003 (  0) 0) |
| [9] |
卫志农, 何桦, 郑玉平. 配电网故障区间定位的高级遗传算法[J]. 中国电机工程学报, 2002, 22(4): 127-130. WEI Zhinong, HE Hua, ZHENG Yuping. A refined genetic algorithm for the fault sections location[J]. Proceedings of the CSEE, 2002, 22(4): 127-130. DOI:10.3321/j.issn:0258-8013.2002.04.026 (  0) 0) |
| [10] |
胡福年, 张认, 卞小亮. 基于图论的主动配电网故障定位方法[J]. 控制工程, 2021, 28(5): 833-838. HU Funian, ZHANG Ren, BIAN Xiaoliang. Fault location method of active distribution network based on graph theory[J]. Control Engineering of China, 2021, 28(5): 833-838. (  0) 0) |
| [11] |
YAN H Y, WU X Y, LIN C L, et al. A modified matrix algorithm dichotomy for distribution network fault location[J]. E3S Web of Conferences, 2020, 204: 02010. DOI:10.1051/e3sconf/202020402010 (  0) 0) |
| [12] |
胡福年, 孙守娟. 基于图论的矩阵算法在配电网故障定位中的应用[J]. 中国电力, 2016, 49(3): 94-98. HU Funian, SUN Shoujuan. Fault location of distribution network by applying matrix algorithm based on graph theory[J]. Electric Power, 2016, 49(3): 94-98. (  0) 0) |
| [13] |
徐彪, 尹项根, 张哲, 等. 矩阵算法和优化算法相结合的配电网故障定位[J]. 电力系统自动化, 2019, 43(5): 152-158. XU Biao, YIN Xianggen, ZHANG Zhe, et al. Fault location for distribution network based on matrix algorithm and optimization algorithm[J]. Automation of Electric Power Systems, 2019, 43(5): 152-158. (  0) 0) |
| [14] |
王一非, 贾燕冰. 含分布式电源配电网故障定位改进矩阵算法[J]. 计算机仿真, 2018, 35(4): 58-64. WANG Yifei, JIA Yanbing. Fault location of distribution networks with DGs based on an improved matrix algorithm[J]. Computer Simulation, 2018, 35(4): 58-64. (  0) 0) |
| [15] |
刘煜, 王俊江, 焦青, 等. 含分布式电源的配电网故障定位改进矩阵算法[J]. 科学技术与工程, 2019, 19(34): 186-190. LIU Yu, WANG Junjiang, JIAO Qing, et al. An improved matrix algorithm for fault location of distribution networks with distributed generation[J]. Science Technology and Engineering, 2019, 19(34): 186-190. (  0) 0) |
| [16] |
宫宇, 张莲, 杨洪杰, 等. 基于自适应遗传量子粒子群算法的配电网故障定位[J]. 浙江电力, 2021, 40(6): 1-7. GONG Yu, ZHANG Lian, YANG Hongjie, et al. Fault location of distribution network based on adaptive genetic quantum particle swarm optimization algorithm[J]. Zhejiang Electric Power, 2021, 40(6): 1-7. (  0) 0) |
| [17] |
WANG K X, SHAO Y, WANG L M, et al. Distribution network fault diagnosis technology based on intelligent algorithm[C]//2021 6th International Conference on Intelligent Computing and Signal Processing (ICSP). Xi'an, China. IEEE, 2021: 899-903.
(  0) 0) |
| [18] |
LI H R. Research on fault location of power distribution network based on fault data information[J]. Telecommunications and Radio Engineering, 2020, 79(8): 713-722. (  0) 0) |
| [19] |
高锋阳, 李昭君, 袁成, 等. 量子计算和免疫优化算法相结合的有源配电网故障定位[J]. 高电压技术, 2021, 47(2): 396-406. GAO Fengyang, LI Zhaojun, YUAN Cheng, et al. Fault location for active distribution network based on quantum computing and immune optimization algorithm[J]. High Voltage Engineering, 2021, 47(2): 396-406. (  0) 0) |
| [20] |
颜景斌, 夏赛, 王飞, 等. 基于改进遗传算法的有源配电网故障定位分析[J]. 电力系统及其自动化学报, 2019, 31(6): 107-112. YAN Jingbin, XIA Sai, WANG Fei, et al. Analysis of fault location for active distribution network based on improved genetic algorithm[J]. Proceedings of the CSU-EPSA, 2019, 31(6): 107-112. (  0) 0) |
| [21] |
魏然, 张磐, 高强伟, 等. 基于网络树状图的低压配电网故障研判仿真分析[J]. 电力系统保护与控制, 2021, 49(13): 167-173. WEI Ran, ZHANG Pan, GAO Qiangwei, et al. Simulation analysis of low-voltage distribution network fault diagnosis based on tree structure diagram[J]. Power System Protection and Control, 2021, 49(13): 167-173. (  0) 0) |
| [22] |
甄永琦, 蒋伟. 改进灰狼算法在配电网故障定位中的应用[J]. 计算机应用与软件, 2020, 37(11): 200-205. ZHEN Yongqi, JIANG Wei. Application of improved grey wolf algorithm in fault location of distribution network[J]. Computer Applications and Software, 2020, 37(11): 200-205. (  0) 0) |
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2022, Vol. 41
2022, Vol. 41


 梅飞(1982), 男, 博士, 讲师, 研究方向为电气设备在线监测与故障诊断、配电网故障定位(E-mail:
梅飞(1982), 男, 博士, 讲师, 研究方向为电气设备在线监测与故障诊断、配电网故障定位(E-mail: