文章编号: 2096-3203(2022)06-0091-10 中图分类号: TM755
输电线路覆冰会导致严重的覆冰事故,在影响电力系统安全稳定运行的同时还会造成巨大的经济损失[1]。在线监测输电线路的运行状态可用以判断线路是否覆冰,为线路的防冰和覆冰预警提供必要的决策支持,通过及时采取相应的措施可有效减小覆冰造成的危害[2]。
光纤复合相线(optical phase conductor, OPPC)是一种新型的电力专用光缆,具有传输电能和传输光信号的作用[3],在低压配网中具有广阔的应用前景[4]。光纤传感技术通过检测传输光的特征量来实现对光纤的温度、应变等基本量的在线监测[5],具有灵敏度高、抗电磁干扰能力强、检测距离长、无源等优点[6-7]。光纤传感技术在输电线路覆冰监测领域中有着广泛的应用,并取得一定的效果[8]。李成宾等学者提出将光纤传感技术应用到输电线路覆冰的在线监测[9];李永倩等学者利用布里渊光时域分析(Brillouin optical time domain analysis, BOTDA)技术实地监测全介质自承式(all-dielectric self-supporting, ADSS)光缆的温度及应变,并展望BOTDA传感技术在输电线路监测方面的应用前景[10];罗健斌等学者设计基于布里渊散射光纤传感技术的OPPC线芯测温系统,在覆冰实验室和室外分别进行50 km OPPC的温度分布测量试验,系统温度测量精度可达±1.6 ℃[11];覃兆宇等学者所设计的基于布里渊光时域反射(Brillouin optical time domain reflectometer, BOTDR)技术的覆冰识别系统在昭通成功实地监测75 km光纤架空地线(optical fiber composite overhead ground wire, OPGW)的温度分布情况,所设计系统的温度精度达到±2 ℃,监测的覆冰情况与巡线人员观察的覆冰情况一致[12];吴念等学者利用BOTDR技术实现对OPGW的温度监测,在覆冰实验基地证实依据监测所得温度可有效识别线路覆冰情况[13],这表明利用光纤传感技术实现输电线路覆冰监测的可行性、有效性与准确性。文献[11-13]均验证利用光纤传感技术可有效判断线路覆冰状态,并发现导线温度变化趋势将滞后于环境温度变化。在实际运行中,环境温度变化、风速和覆冰厚度等均是影响线路温度的重要因素[14-15],但文献[11-13]在研究影响线路温度因素时存在明显不足,文献[11]在室外和户内对温度-频移之间的线性关系进行标定,所设计的系统可有效测量OPPC导线温度,但未分析覆冰厚度对导线温度的影响;文献[12]的研究仅涉及覆冰厚度10 mm的情况;文献[12-13]所设定的环境温度均以一次函数形式下降变化,难以完全模拟实际运行中的环境温度变化情况。
为解决上述问题,文中利用COMSOL Multi ̄physics有限元软件仿真建立OPPC覆冰模型,改变模型所处的环境温度和覆冰厚度,进行正弦时变温度和不同覆冰厚度的仿真计算。首先,分析OPPC导线覆冰段与未覆冰段的光纤温度在环境温度正弦时变和不同覆冰厚度下的变化特征;其次,利用一段时间内光纤覆冰段温度滞后环境温度的相位判断线路是否覆冰,着重探究覆冰段光纤温度的滞后相位、正弦时变环境温度波动幅值与覆冰厚度之间的关系;再次,得到常见温度变化幅值和覆冰厚度下的滞后相位,提出基于滞后相位的覆冰厚度预测公式;最后,建模计算4种环境温度非严格正弦规律变化下覆冰段温度的滞后相位,分析覆冰判据的可靠性及覆冰厚度预测方法的误差。
1 线路覆冰识别理论OPPC可传输电能,其内置光纤可传递光信号,利用光纤传感对OPPC进行测温,既利用线路资源降低建设成本又有效避免测温通道的重复架设[16]。OPPC导线的设计结构、材质以及运行条件都会影响线路的温度[17],但OPPC导线正常运行时所产生的焦耳热对光纤温度变化的影响较小,基本可忽略。因此,太阳辐射Qs[12]、空气绕流导线的自然对流散热Qc和辐射散热Qr[12]是引起导线温度变化的主要原因,相应的数学表达如式(1)—式(3)所示,其满足的热平衡方程[15]如式(4)所示。
| $ Q_{\mathrm{s}}=\alpha J d_{\mathrm{OPPC}} $ | (1) |
| $ Q_{\mathrm{c}}=\frac{k_{\mathrm{AL}}\left(T-T_{\mathrm{tv}}\right)}{d_{\text {OPPC }}}\left\{0.6+\frac{0.387 R a^{\frac{1}{6}}}{\left[1+\left(\frac{0.559}{P r}\right)^{\frac{9}{16}}\right]^{\frac{8}{27}}}\right\}^2 $ | (2) |
| $ Q_{\mathrm{r}}=\pi d_{\mathrm{OPPC}} \varepsilon_{\mathrm{AL}} \sigma\left[(T+273)^4-\left(T_{\mathrm{tv}}+273\right)^4\right] $ | (3) |
| $ Q_{\mathrm{s}}=Q_{\mathrm{c}}+Q_{\mathrm{r}} $ | (4) |
式中:α为吸热系数;J为太阳辐射率;dOPPC为OPPC线路直径;kAL为铝的导热系数;T为线路温度;Ttv为环境温度;Ra为瑞利数;Pr为普朗特数;εAL为铝的辐射系数;σ为玻尔兹曼常数。
线路覆冰后,太阳辐射Qs-i[12-13]、空气绕流导线的自然对流散热Qc-i和辐射散热Qr-i[12-13]会发生变化,如式(5)—式(7)所示。在不考虑融冰对线路温度影响的情况下,研究线路在不同环境温度和不同覆冰厚度情况下的温度随时间的变化情况,文献[18]指出,影响线路温度的因素主要与线路所处的环境的气象条件有关,于是用瞬态热传导方程进行研究,则线路覆冰时如式(8)所示,线路未覆冰时如式(9)所示。
| $ Q_{\mathrm{s}-\mathrm{i}}=\alpha J\left(d_{\mathrm{OPPC}}+2 b\right) $ | (5) |
| $ \begin{gathered} Q_{\mathrm{r}-\mathrm{i}}=\pi\left(d_{\mathrm{OPPC}}+2 b\right) \varepsilon_{\mathrm{i}} \sigma \times \\ {\left[(T+273)^4-\left(T_{\mathrm{tv}}+273\right)^4\right]} \end{gathered} $ | (6) |
| $ Q_{\mathrm{c}-\mathrm{i}}=\frac{k_{\mathrm{AL}}\left(T-T_{\mathrm{tv}}\right)}{d_{\text {OPPC }}+2 b}\left\{0.6+\frac{0.387 \mathrm{Ra}^{\frac{1}{6}}}{\left[1+\left(\frac{0.559}{\operatorname{Pr}}\right)^{\frac{9}{16}}\right]^{\frac{8}{27}}}\right\}^2 $ | (7) |
| $ \begin{gathered} \left(\rho_{\mathrm{f}} C_{\mathrm{f}}+\rho_{\mathrm{s}} C_{\mathrm{s}}+\rho_{\mathrm{Al}} C_{\mathrm{Al}}+\rho_{\mathrm{i}} C_{\mathrm{i}}\right) \frac{\partial T}{\partial t}+ \\ \left(\rho_{\mathrm{Al}} C_{\mathrm{Al}}+\rho_{\mathrm{i}} C_{\mathrm{i}}\right) \boldsymbol{v} \cdot \nabla T= \\ \nabla \cdot\left[\left(k_{\mathrm{i}}+k_{\mathrm{f}}+k_{\mathrm{AL}}+k_{\mathrm{s}}\right) \nabla T\right]+ \\ Q_{\mathrm{s}-\mathrm{i}}-Q_{\mathrm{r}-\mathrm{i}}-Q_{\mathrm{c}-\mathrm{i}} \end{gathered} $ | (8) |
| $ \begin{aligned} &\left(\rho_{\mathrm{f}} C_{\mathrm{f}}+\rho_{\mathrm{s}} C_{\mathrm{s}}+\rho_{\mathrm{Al}} C_{\mathrm{Al}}\right) \frac{\partial T}{\partial t}+\rho_{\mathrm{Al}} C_{\mathrm{Al}} \boldsymbol{v} \cdot \nabla T= \\ &\nabla \cdot\left[\left(k_{\mathrm{f}}+k_{\mathrm{AL}}+k_{\mathrm{s}}\right) \nabla T\right]+Q_{\mathrm{s}}-Q_{\mathrm{r}}-Q_{\mathrm{c}} \end{aligned} $ | (9) |
式中:ρf,ρs,ρAl,ρi分别为光纤、钢、铝和冰的密度;Cf,Cs,CAl,Ci分别为光纤、钢、铝和冰的比热容;b为覆冰厚度;v为风速向量;kf,ks,ki分别为光纤、钢和冰的导热系数;εi为冰的辐射系数。
由式(5)—式(9)可知,除太阳辐射、对流散热和辐射散热因素会引起线路温度变化外,在瞬态研究过程中线路的比热容与冰的比热容不同,线路材料的密度、冰的密度、环境温度及覆冰厚度均是引起覆冰段与未覆冰段光纤温度变化不同的原因。
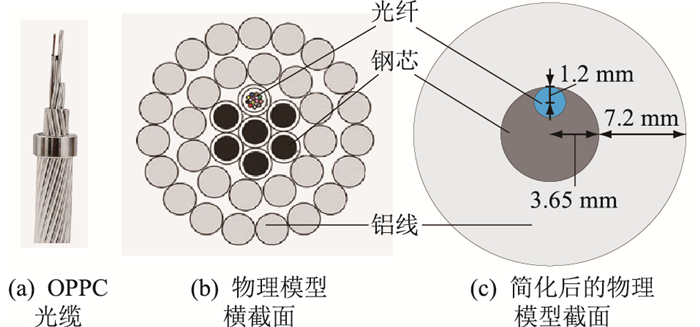
2 线路覆冰光纤温度场模型线路覆冰的温度场涉及环境与线路的热传递和线路各结构间的热传递。文中利用COMSOL Multiphysics有限元仿真软件研究OPPC覆冰与未覆冰线路中的光纤温度变化。模型仿真的OPPC光缆型号为OPPC-24B1-240/30,如图 1(a)所示。在保证计算结果准确的基础上,为提高计算效率,对OPPC线路进行简化[19]:忽略内部的填充油膏,不计内部各部分的距离,材料各向同性,并且将6根钢芯等效为1根嵌套光纤的钢芯,24根铝线等效为1根套筒状的铝线,各部分的导热系数不变。OPPC简化前的物理模型横截面如图 1(b)所示,经过简化后的物理模型截面如图 1(c)所示。在仿真线路覆冰时建立OPPC导线覆冰的三维模型进行研究,参考现有文献的模型以及数据[12],假设此模型中OPPC长5 m,分为3段,假设长度均为1.5 m的第1段和第3段未覆冰,长度为2 m的第2段有覆冰,为便于计算,设冰层均匀覆盖线路[12-13],如图 2所示。仿真计算过程中各结构参数和材料属性在表 1中列出。
|
图 1 OPPC物理模型示意 Fig. 1 The schematic diagram of the OPPC physical model |

|
图 2 物理模型 Fig. 2 Physical model |
|
|
表 1 仿真参数 Table 1 The simulation parameters |
文中为兼顾计算效率以及结果精确性,仿真计算前对所建立的物理模型进行网格划分。理论上网格密度越大,计算值与理论结果越接近,但是容易存在求解不收敛的问题,同时还会减缓计算的速度,因此文中所选网格密度尽可能保证计算结果准确可靠的同时考虑到模型的收敛性与计算时间,选择四面体网格。图 3为具体的网格划分结果示意,求解器模拟线路运行时长为48 h,计算结果收敛。

|
图 3 网格划分示意 Fig. 3 Schematic diagram of meshing |
环境温度是影响覆冰线路温度的因素之一。环境温度变化通常情况为单峰值,即有一个日最高值和一个日最低值,根据大量统计数据研究,气温日变化可以用正弦函数法模拟[20]。正弦函数法模拟日气温时只需要日最高温度值和日最低温度值即可。假设环境温度为正弦函数形式,那么其表达式为:
| $ T_{\mathrm{tv}}(t)=-B+A \cos \left(\frac{\pi(t-14)}{12}\right) $ | (10) |
式中:A为环境温度变化波动幅值;B为环境温度均值的负值;t为时间。
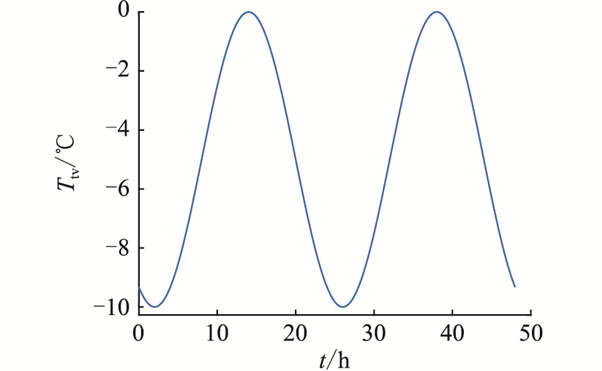
以A和B均为5 ℃为例,时间设定为48 h,如图 4所示。
|
图 4 环境温度 Fig. 4 The ambient temperature |
设定风速为0 m/s,冰层厚度为10 mm,覆冰长度为2 m,模型计算得到覆冰段与未覆冰段在48 h内光纤温度随时间的变化情况,如图 5所示。未覆冰段与覆冰段的光纤温差随运行时间的变化情况如图 6所示。

|
图 5 环境温度与光纤温度 Fig. 5 Ambient temperature and fiber temperature |

|
图 6 未覆冰段与覆冰段光纤温差 Fig. 6 The temperature difference between the icing part and the non-icing part of the optical fiber in the OPPC |
由图 5可知,在3 h时,覆冰段与未覆冰段的温度基本与环境温度相等;随后环境温度上升,覆冰段和未覆冰段的温度也在持续上升,但覆冰段的温度上升速度要慢于未覆冰段的速度;在15 h时,未覆冰段光纤温度达到最大值,之后覆冰段光纤温度持续上升,增幅变小;在16 h之后覆冰段与未覆冰段光纤温度变化曲线皆呈周期性正弦函数变化,覆冰段和未覆冰段的波动幅值较环境温度较小、相位较环境温度滞后;在16.5 h时,环境温度开始下降,覆冰段的温度到达最高,随后随着环境温度下降而下降。由图 6可知,当覆冰段与未覆冰段的温差在第一次达到峰值后,温差在时间尺度上趋于周期性变化,即温差随时间呈正弦函数形式变化。由图 5和图 6可知,假设覆冰期间覆冰情况未出现明显变化,若未及时发现覆冰,且覆冰也未造成大的损失,可观察下一个周期的温度变化曲线以判断是否覆冰。
4 光纤及环境温度与覆冰厚度的关系当环境温度呈正弦函数变化时,不仅环境温度均值及波动幅值对线路造成影响,覆冰厚度也会影响线路温度,因此第4章主要研究光纤温度与环境温度均值、波动幅值和覆冰厚度间的关系。
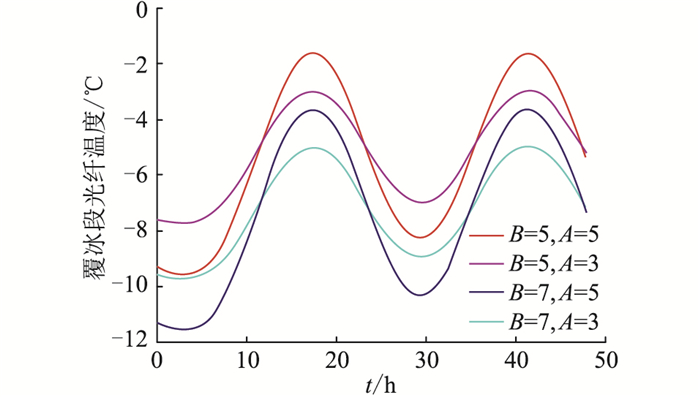
4.1 光纤温度与环境温度均值的关系为研究光纤温度与环境温度均值的关系,4.1节设定B为5 ℃和7 ℃,A为3 ℃和5 ℃,风速为0 m/s,冰层厚度为10 mm,覆冰长度为2 m。模拟运行时长为48 h,得到相同覆冰厚度但不同环境温度均值的光纤温度变化曲线,如图 7和图 8所示。
|
图 7 不同温度均值时的覆冰段光纤温度 Fig. 7 The temperature of the fiber in the icing OPPC at different temperature averages |
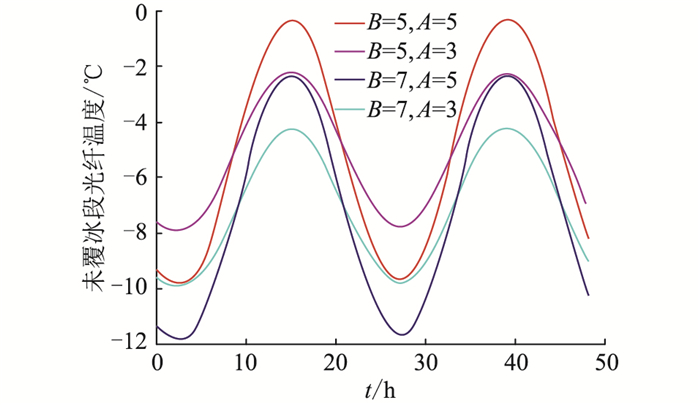
|
图 8 不同温度均值时的未覆冰段光纤温度 Fig. 8 The temperature of the fiber in the OPPC without ice coating at different temperature averages |
由图 7和图 8可知,无论是覆冰段还是未覆冰段,环境温度均值对于光纤温度变化曲线相位的影响基本可忽略。不同环境温度均值不会改变光纤温度曲线随时间的变化特征,即不改变光纤温度变化曲线的相位。
4.2 光纤温度与环境温度波动幅值的关系在4.1节的基础上,研究环境温度波动幅值与光纤温度的关系,假设B与A的数值相等。通过查气象数据资料[21],考虑到寒冷季节的温差变化[22],设定4.2节的A分别为3 ℃、4 ℃、5 ℃、6 ℃和7 ℃,风速为0 m/s,冰层厚度为10 mm,覆冰长度为2 m。模拟线路运行48 h,得到覆冰厚度相同但A不同时的覆冰段与未覆冰段的光纤温度变化曲线,如图 9和图 10所示。

|
图 9 覆冰厚度为10 mm时,不同温度波动幅值时的覆冰段光纤温度 Fig. 9 The temperature of the fiber in the icing OPPC for different fluctuating temperature amplitudes at ice thickness of 10 mm |

|
图 10 覆冰厚度为10 mm时,不同温度波动幅值时的未覆冰段光纤温度 Fig. 10 The temperature of the fiber in the OPPC without ice coating for different fluctuating temperature amplitudes at ice thickness of 10 mm |
由图 9和图 10可知,无论是覆冰段还是未覆冰段,当覆冰厚度为定值时,不同波动幅值对光纤温度变化曲线的峰值大小有一定影响;但对光纤温度第一次到达峰值的时间影响较小,可以忽略。
4.3 光纤温度与覆冰厚度的关系光纤温度变化也与线路的覆冰厚度有关。为研究光纤温度与线路覆冰厚度的关系,4.3节设定覆冰厚度分别为5 mm、10 mm、15 mm、20 mm和25 mm,风速为0 m/s,覆冰长度为2 m,A和B为5 ℃。模拟运行时长为48 h,得到不同覆冰厚度时覆冰段与未覆冰段光纤温度变化曲线,如图 11和图 12所示。
|
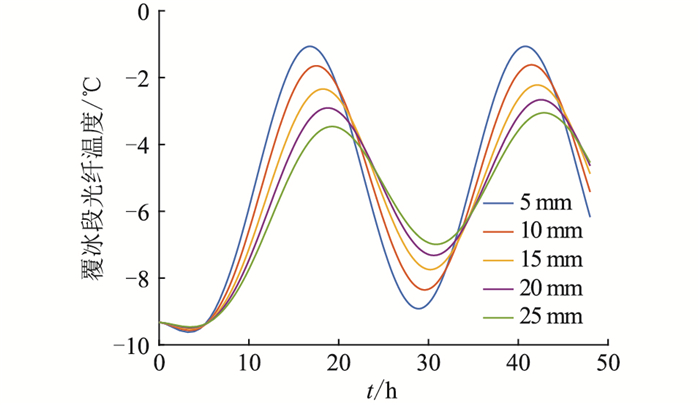
图 11 不同覆冰厚度时的覆冰段光纤温度 Fig. 11 The temperature of the fiber in the icing OPPC with different icing thickness |
|
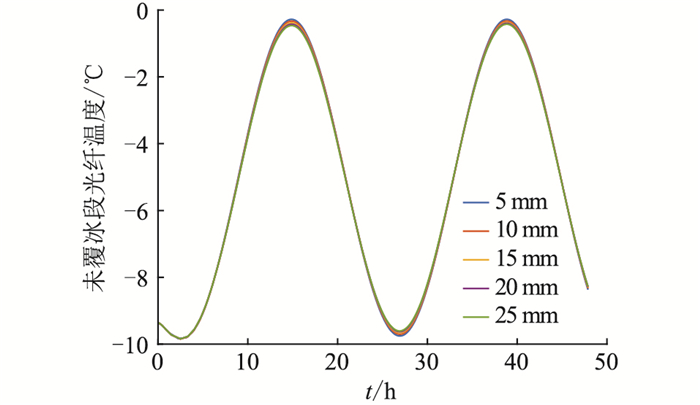
图 12 不同覆冰厚度时的未覆冰段光纤温度 Fig. 12 The temperature of the fiber in the OPPC without ice coating with different icing thickness |
由图 11可知,环境温度波动幅值相同时,覆冰段光纤温度到达峰值的时间随着覆冰厚度的增加而相应提高,这主要是由于覆冰厚度的增加阻碍热传导。由图 12可知,覆冰厚度对未覆冰段光纤温度变化几无影响,这是由于未覆冰段线路温度主要受环境温度的影响,覆冰段虽可通过热传导对其进行影响,但未覆冰段温度达到热平衡所需要时间较短,传热不足,故影响较小。
5 滞后相位、环境温度波动幅值和覆冰厚度的关系在第4章的研究中发现单一考虑环境温度波动幅值或覆冰厚度对未覆冰段的温度变化曲线相位和波动幅值的影响基本上可以忽略,但是对覆冰段的温度变化曲线有着较大影响。如图 9和图 11所示,在不同环境温度波动幅值和覆冰厚度下,覆冰段光纤温度曲线到达峰值的时间不同,曲线大体呈正弦函数形式变化。为方便研究覆冰段光纤温度变化曲线的特征,定义滞后时长td和滞后相位φ,如式(11)、式(12)所示。
| $ t_{\mathrm{d}}=t_{\mathrm{i}}-t_{\mathrm{a}} $ | (11) |
| $ \varphi=\frac{t_{\mathrm{d}}}{t_{1 \mathrm{day}}} \times 360^{\circ} $ | (12) |
式中:ti为覆冰段光纤温度达到最大值时的时间;ta为环境温度到达最大值所需的时间;td为滞后时长;t1day为1 d时长; φ为覆冰段光纤温度滞后相位。
研究过程中发现线路中流过不同大小的电流和环境温度均值对线路温度变化曲线的滞后相位影响较小,可以忽略,因此文中提出基于覆冰段光纤温度变化曲线滞后环境温度的滞后相位作为判断线路是否覆冰的判据。
5.1 滞后相位与环境温度波动幅值的关系根据4.1节和4.2节的研究,5.1节主要研究光纤温度与环境温度波动幅值关系。由图 9可得覆冰厚度为10 mm时覆冰段光纤温度到达峰值的时间,根据式(11)、式(12)计算得到覆冰段光纤温度滞后环境温度的时长及相位,如表 2所示。
|
|
表 2 不同温度波动幅值时覆冰段光纤温度曲线参数 Table 2 Curve parameters of the temperature of fiber temperature in the icing OPPC under fluctuating temperature amplitudes |
由表 2可知,不同波动幅值对覆冰段光纤温度变化曲线的相位影响较小,波动幅值不是影响相位的主要因素。在后续的研究中基本上可以忽略波动幅值的影响,后续的监测过程中少一个监测参数,在工程实际应用中有着重要意义。
5.2 滞后相位与覆冰厚度的关系在4.3节所研究的光纤温度与覆冰厚度关系的基础上,覆冰厚度b分别取0 mm、5 mm、10 mm、15 mm、20 mm和25 mm,环境温度波动幅值为5 ℃,求解得覆冰段光纤温度达到峰值的时间,根据式(11)、式(12)计算得到覆冰段光纤温度曲线滞后环境温度曲线的时长及相位,如表 3所示。
|
|
表 3 不同覆冰厚度时覆冰段光纤温度曲线参数 Table 3 Curve parameters of the temperature of fiber temperature in the icing OPPC with different icing thickness |
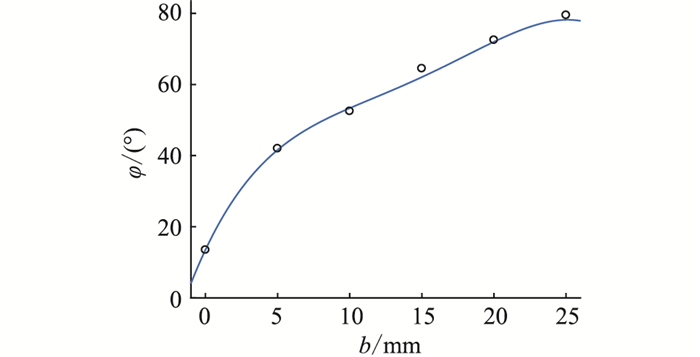
由表 3可知,可拟合得到滞后相位与覆冰厚度的关系,如式(13)所示,拟合效果见图 13,其拟合误差平方和ESSE为1.757,确定系数R为0.999 4,均方根误差ERMSE为0.937 3。
| $ \begin{gathered} \varphi=-0.0006 b^4+0.036 b^3- \\ 0.7603 b^2+8.594 b+13.5 \end{gathered} $ | (13) |
|
图 13 覆冰段温度滞后相位与覆冰厚度的关系 Fig. 13 The relationship between lagging phase of fiber temperature in the icing OPPC and icing thickness |
由表 3和图 13可知,覆冰厚度对覆冰段光纤温度变化曲线相位的影响较大,当覆冰厚度增加时,滞后相位也相应增加。因此,文中所提基于覆冰段光纤温度变化曲线滞后环境温度的相位以判断线路是否覆冰在环境温度波动幅值为5 ℃时是可行的。
5.3 滞后相位与温度波动幅值和覆冰厚度的关系4.2节和4.3节的研究中,考虑的环境温度波动幅值或者覆冰厚度因素单一,故在4.2节和4.3节研究基础上考虑不同环境温度波动幅值和覆冰厚度对覆冰段光纤温度变化曲线的影响。5.1节设定的A等于B,分别为3 ℃、4 ℃、5 ℃、6 ℃和7 ℃,冰层厚度分别取0 mm、5 mm、10 mm、15 mm、20 mm和25 mm,风速为0 m/s,覆冰长度为2 m。模拟运行时长为48 h,得到不同覆冰厚度和不同环境温度波动幅值时覆冰段光纤温度曲线的滞后相位,如图 14所示。
|
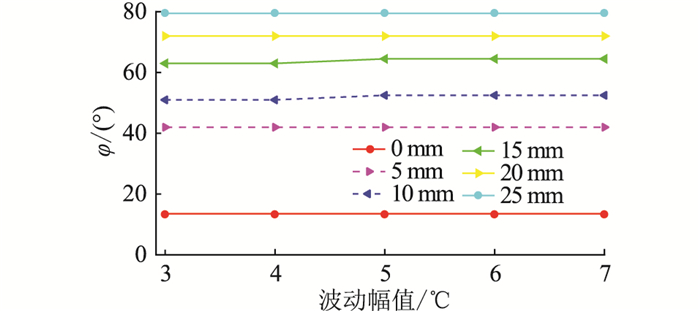
图 14 不同覆冰厚度时,滞后相位与波动幅值间的关系 Fig. 14 The relationship between lagging phase and fluctuating temperature amplitude for different icing thickness |
由图 14可知,波动幅值对滞后相位的影响很小。覆冰厚度为15 mm时,波动幅值为5 ℃、6 ℃和7 ℃时的滞后相位为64.5°,与波动幅值3 ℃和4 ℃时的相位相比滞后1.5°,滞后相位较小,延时时间为0.1 h,延时时间较短,基本上可以认为波动幅值对相位的影响很小,可以忽略,证实4.2节研究结论的正确性,结论有一定的通用性;覆冰厚度对滞后相位的影响,与4.3节研究的结果基本一致,可证实4.3节研究结论的正确性,结论有一定的通用性。
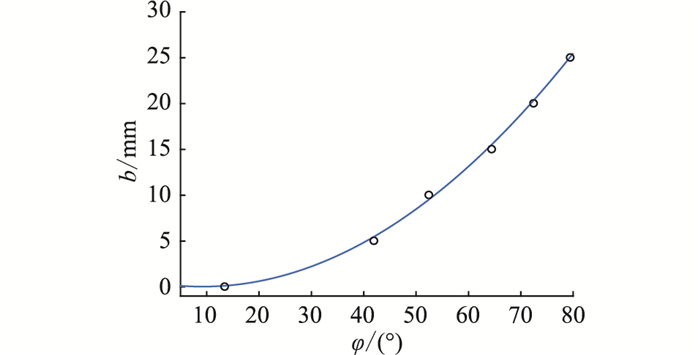
拟合得到基于滞后相位的预测公式,如式(14)所示,拟合效果见图 15。
| $ b=0.00508 \varphi^2-0.09357 \varphi+0.4669 $ | (14) |
|
图 15 覆冰厚度与覆冰段温度滞后相位的关系 Fig. 15 The relationship between icing thickness and lagging phase of fiber temperature in the icing OPPC |
由图 15可知,其拟合误差平方和ESSE数值为0.654 1,确定系数R为0.998 5,均方根误差ERMSE为0.466 9。
根据图 15的结果,考虑测量设备的型号、准确性性能、光纤长度、测量参数和方式的影响,又考虑到输电线路覆冰厚度较小时,覆冰厚度为2 mm时对输电线路的威胁较小甚至可以忽略[7],此时的滞后相位是27.9°,当用滞后相位作为输电线路覆冰判据时,考虑留出一定的裕度,选择角度为常见整数的数值,将滞后相位30°(覆冰厚度为2.2 mm)作为线路覆冰临界相位,若所测得滞后相位达到或者超过30°,则认为输电线路覆冰。
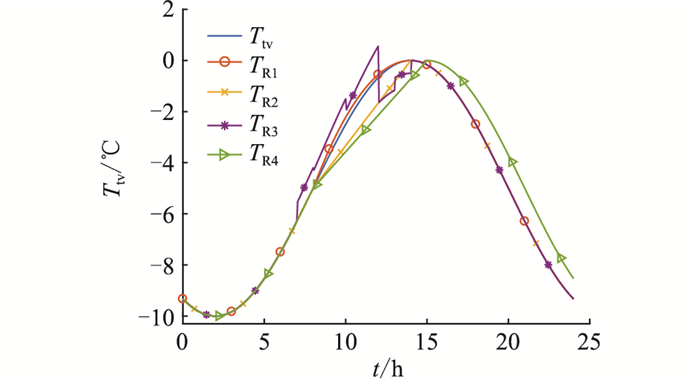
6 覆冰预测方法的仿真验证实际生活中环境温度变化情况并不是完全按照正弦函数形式变化的,因此设置4种非严格正弦形式的环境温度,分别为TR1(t),TR2(t),TR3(t)和TR4(t)进行覆冰验证仿真,如式(15)—式(18)所示。根据前文研究可知,在24 h之前,相位已经可以测出,因此设定模拟运行时长为24 h,验证覆冰判据是否有效,以A和B取5 ℃为例,分别代入TR1(t),TR2(t),TR3(t)和TR4(t),式(15)—式(18)的变化效果如图 16所示。
| $ T_{\mathrm{R} 1}(t)=\left\{\begin{array}{l} T_{\mathrm{tv}}(t) \quad 0 \leqslant t \leqslant 8 \\ \frac{-A}{36} t^2+\frac{7 A}{9} t-\frac{49 A}{9} \quad 8 <t \leqslant 14 \\ T_{\mathrm{tv}}(t) \quad 14<t \leqslant 24 \end{array}\right. $ | (15) |
| $ T_{\mathrm{R} 2}(t)=\left\{\begin{array}{l} T_{\mathrm{tv}}(t) \quad 0 \leqslant t \leqslant 8 \\ \frac{A}{6} t-\frac{7 A}{3} \quad 8 <t \leqslant 14 \\ T_{\mathrm{tv}}(t) \quad 14<t \leqslant 24 \end{array}\right. $ | (16) |
| $ T_{\mathrm{R} 3}(t)=\left\{\begin{array}{l} T_{\mathrm{tv}}(t) \quad 0 \leqslant t \leqslant 7 \\ T_{\mathrm{tv}}(t)+0.1 t \quad 7<t \leqslant 8 \\ T_{\mathrm{tv}}(t)+0.01 t^2 \quad 8<t \leqslant 10 \\ T_{\mathrm{tv}}(t)-0.001 t^3+0.5 \quad 10<t \leqslant 12 \\ T_{\mathrm{tv}}(t)-1 \quad 12<t \leqslant 13 \\ T_{\mathrm{tv}}(t)-0.5 \quad 13<t \leqslant 14 \\ T_{\mathrm{tv}}(t) \quad 14<t \leqslant 24 \end{array}\right. $ | (17) |
| $ \begin{gathered} T_{\mathrm{R} 4}(t)= \\ \left\{\begin{array}{l} T_{\mathrm{tv}}(t) \quad 0 \leqslant t \leqslant 8 \\ \frac{A}{7} t-\frac{15 A}{7} 8 <t \leqslant 15 \\ -B+A \cos \left(\frac{\pi(t-15)}{12}\right) \quad 15<t \leqslant 24 \end{array}\right. \end{gathered} $ | (18) |
|
图 16 非正弦函数形式的环境温度 Fig. 16 The ambient temperature in non-sinusoidal |
由图 16可知,所有滞后相位均大于30°,均可有效监测出覆冰。不同形式的环境温度对覆冰段光纤温度变化有影响,但影响较小,所得到的滞后相位最大相位差为4.5°;TR1(t)曲线与Ttv曲线基本相同,TR1(t)曲线略高于Ttv曲线,覆冰段光纤所吸收的能量略多于Ttv情况,故滞后相位基本上都超前1.5°;TR2(t)曲线整体在Ttv曲线下方,覆冰段所吸收的能量小于Ttv曲线形式的,故相位整体滞后3°及以上;TR3(t)曲线波动较大,无法直接分析所吸收能量的大小,波动较大时,对覆冰厚度较小时有影响,所测出的相位大于Ttv情况,当覆冰厚度较大时则影响较小;TR4(t)曲线温升时长均大于其他曲线,与TR2(t)曲线相比,所得滞后相位稍小,覆冰厚度较小时,滞后相位大于Ttv情况,覆冰厚度较大时,滞后相位基本上与Ttv情况相同。
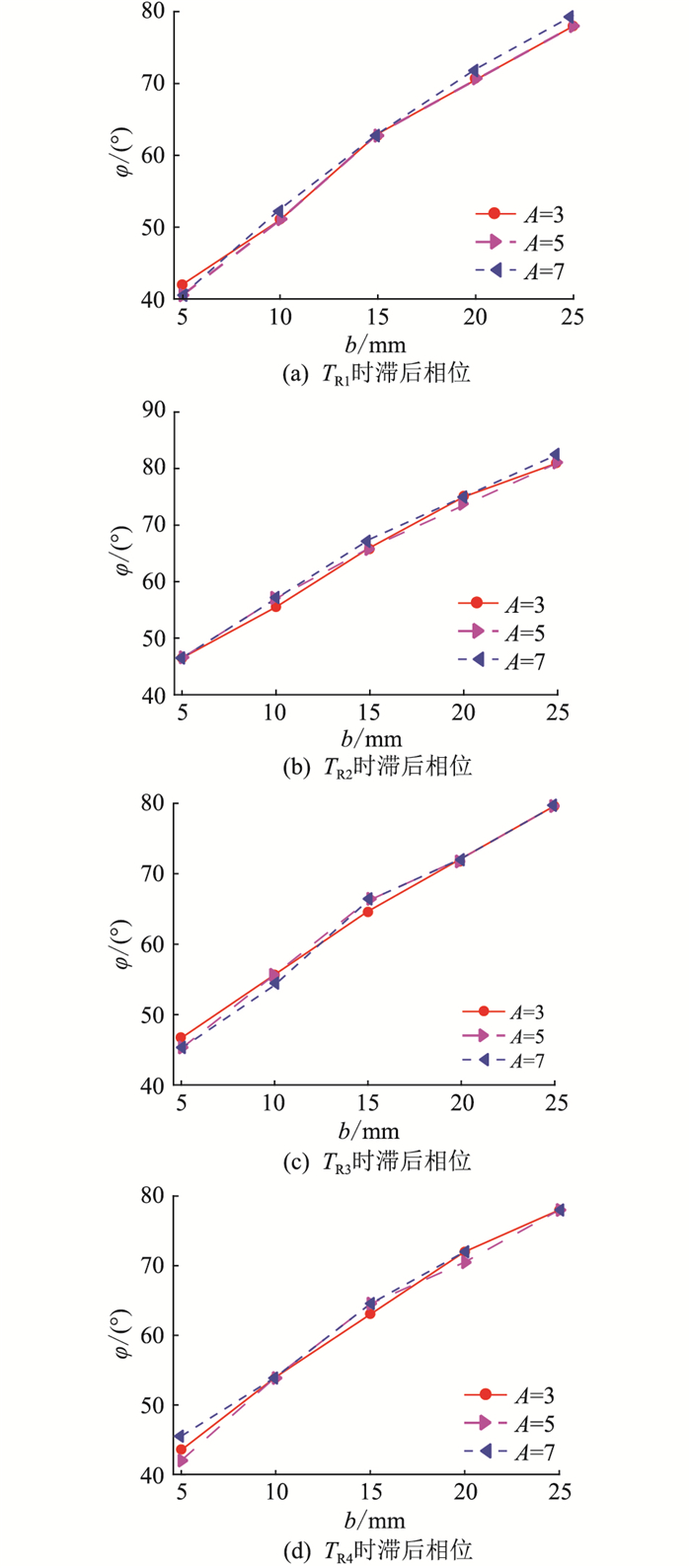
考虑到是验证性试验,根据5.1节的研究结论,故设定A等于B,分别为3 ℃、5 ℃和7 ℃,冰层厚度分别取5 mm、10 mm、15 mm、20 mm和25 mm,风速为0 m/s,覆冰长度为2 m。模拟运行时长为24 h,得到不同覆冰厚度和不同环境温度波动幅值时的覆冰段光纤温度曲线滞后环境温度曲线的相位,如图 17所示。
|
图 17 不同环境温度下的滞后相位 Fig. 17 The lagging phases for different ambient temperatures |
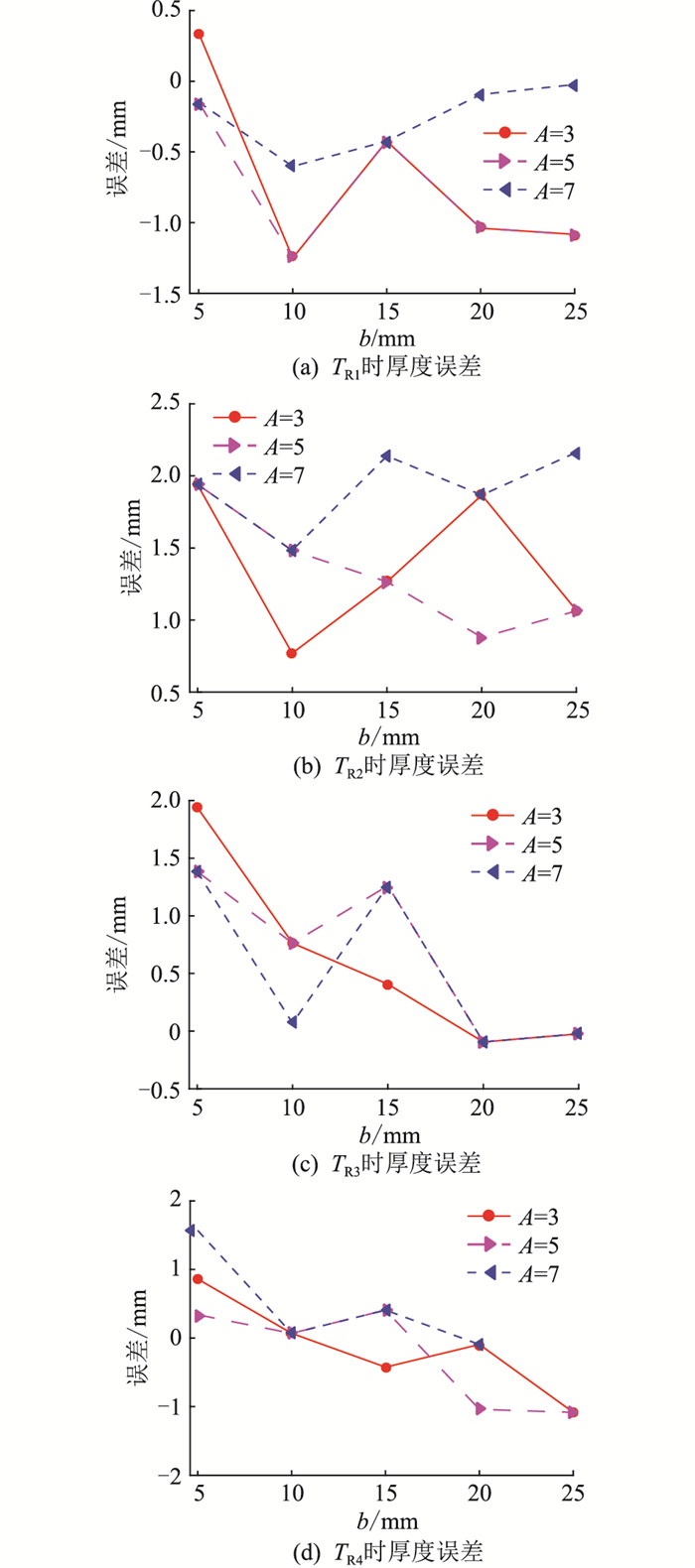
将图 17中的数据代入式(14)可得预测覆冰厚度以及与实际覆冰厚度的误差,如图 18所示,覆冰厚度预测值的绝对误差的最大值为2.164 8 mm,最小值为0.023 3 mm,误差均值为0.828 0 mm,误差标准差为0.659 7 mm。
|
图 18 不同环境温度下的厚度误差 Fig. 18 Thickness errors for different ambient temperatures |
文中图 17和图 18的相关数据由上文分析可知,在4种非正弦函数环境温度变化时,基于滞后相位判据仍可有效判断线路覆冰情况,所预测的覆冰厚度误差较小,可应用于实际运行中的OPPC输电线路覆冰监测。同时,该成果对监测设备选型具有一定的参考价值,根据当地环境条件,结合环境温度波动情况,可判断设备是否可有效监测线路覆冰及预测覆冰厚度。
7 结论文中利用有限元仿真软件建立OPPC架空导线覆冰温度场模型,计算时变环境温度和不同覆冰厚度情况下的覆冰导线温度,得出以下结论:
(1) 环境温度均值和波动幅值对覆冰段光纤温度滞后相位的影响很小,可以忽略;覆冰厚度对滞后相位的影响较大,覆冰厚度在0~25 mm范围内,滞后相位对应在13.5°~79.5°范围内变化;
(2) 提出基于滞后相位的覆冰厚度预测公式和基于滞后相位30°的覆冰判据。
| [1] |
蒋兴良, 常恒, 胡琴, 等. 输电线路综合荷载等值覆冰厚度预测与试验研究[J]. 中国电机工程学报, 2013, 33(10): 177-183, 3. JIANG Xingliang, CHANG Heng, HU Qin, et al. Prediction and experimental study on combined load equivalent ice thickness of overhead transmission line[J]. Proceedings of the CSEE, 2013, 33(10): 177-183, 3. (  0) 0) |
| [2] |
HUANG X B, LI H B, ZHU Y C. Short-term ice accretion forecasting model for transmission lines with modified time-series analysis by fireworks algorithm[J]. IET Generation, Transmission & Distribution, 2018, 12(5): 1074-1080. (  0) 0) |
| [3] |
邓惠华, 张瑞琪, 陈俊武, 等. 基于OPGW光偏振态的雷击定位原理与方法研究[J]. 电瓷避雷器, 2018(1): 148-153. DENG Huihua, ZHANG Ruiqi, CHEN Junwu, et al. Research on principles and methods of lightning strike location based on OPGW light polarization state[J]. Insulators and Surge Arresters, 2018(1): 148-153. (  0) 0) |
| [4] |
迟兴江, 蓝骞, 潘金虎, 等. OPGW光纤传感监测系统的绝缘子覆冰闪络信号分析[J]. 电瓷避雷器, 2019(3): 178-182. CHI Xingjiang, LAN Qian, PAN Jinhu, et al. Insulator icing flashover signal analysis of OPGW optical fiber sensing monitoring system[J]. Insulators and Surge Arresters, 2019(3): 178-182. (  0) 0) |
| [5] |
王敏学, 李黎, 周达明, 等. 分布式光纤传感技术在输电线路在线监测中的应用研究综述[J]. 电网技术, 2021, 45(9): 3591-3600. WANG Minxue, LI Li, ZHOU Daming, et al. Overview of studies on application of distributed optical fiber sensing technology in online monitoring of transmission lines[J]. Power System Technology, 2021, 45(9): 3591-3600. DOI:10.13335/j.1000-3673.pst.2020.1795 (  0) 0) |
| [6] |
李立浧, 阳林, 郝艳捧. 架空输电线路覆冰在线监测技术评述[J]. 电网技术, 2012, 36(2): 237-243. LI Licheng, YANG Lin, HAO Yanpeng. Review of on-line monitoring of ice coating on overhead transmission line[J]. Power System Technology, 2012, 36(2): 237-243. (  0) 0) |
| [7] |
曹春诚, 马超, 张哲民, 等. 基于OPGW的雷击点精确定位研究[J]. 电瓷避雷器, 2021(1): 111-116. CAO Chuncheng, MA Chao, ZHANG Zhemin, et al. Lightning-strike-point location of transmission line based on OPGW[J]. Insulators and Surge Arresters, 2021(1): 111-116. (  0) 0) |
| [8] |
陈天英. 基于光纤传感技术输电线路在线监测的研究[D]. 北京: 华北电力大学, 2015. CHEN Tianying. Research on transmission line online monitoring based on optical fiber sensing technology[D]. Beijing: North China Electric Power University, 2015. (  0) 0) |
| [9] |
李成宾, 杨志, 黄春林. 光纤布里渊传感在输电线路覆冰监测中的应用[J]. 电力系统通信, 2009, 30(6): 37-41. LI Chengbin, YANG Zhi, HUANG Chunlin. Application of optical fiber Brillouin sensor for power transmission lines icing monitoring[J]. Telecommunications for Electric Power System, 2009, 30(6): 37-41. (  0) 0) |
| [10] |
李永倩, 吴飞龙, 徐杰. 基于BOTDA的ADSS光缆监测技术研究[J]. 光通信技术, 2013, 37(2): 38-40. LI Yongqian, WU Feilong, XU Jie. Research on ADSS fiber optic cables monitoring technology based on BOTDA[J]. Optical Communication Technology, 2013, 37(2): 38-40. (  0) 0) |
| [11] |
罗健斌, 郝艳捧, 叶青, 等. OPPC线芯温度的分布式布里渊散射光纤传感技术[J]. 电力系统自动化, 2013, 37(13): 114-120. LUO Jianbin, HAO Yanpeng, YE Qing, et al. A distributed fiber sensing technology based on Brillouin scattering for OPPC wire core temperature measurement[J]. Automation of Electric Power Systems, 2013, 37(13): 114-120. (  0) 0) |
| [12] |
覃兆宇, 刘卫新, 潘哲哲, 等. 光纤布里渊分布式输电线路覆冰识别技术[J]. 光电工程, 2016, 43(10): 6-11. QIN Zhaoyu, LIU Weixin, PAN Zhezhe, et al. Optical Brillouin distributed ice-coating identification technology on transmission line[J]. Opto-Electronic Engineering, 2016, 43(10): 6-11. (  0) 0) |
| [13] |
吴念, 王海涛, 张宗峰, 等. 基于OPGW的输电线路覆冰广域监测方法[J]. 中国电力, 2017, 50(5): 65-70. WU Nian, WANG Haitao, ZHANG Zongfeng, et al. Research of transmission line icing wide-area monitoring based on OPGW[J]. Electric Power, 2017, 50(5): 65-70. (  0) 0) |
| [14] |
念路鹏. 架空输电线路覆冰增长模型关键参数的研究[D]. 广州: 华南理工大学, 2020. NIAN Lupeng. Research on the key parameters of the ice growth model on overhead transmission lines[D]. Guangzhou: South China University of Technology, 2020. (  0) 0) |
| [15] |
陈郑淦哲, 张斌, 范亚洲, 等. 基于高程风速预测的架空导线温度计算方法[J]. 中国电力, 2022, 55(6): 137-145. CHEN Zhengganzhe, ZHANG Bin, FAN Yazhou, et al. An overhead conductor temperature calculation method based on elevation wind speed prediction[J]. Electric Power, 2022, 55(6): 137-145. (  0) 0) |
| [16] |
赵波, 巩锐, 李明. OPPC技术及OPPC光纤测温技术初探[J]. 中国新通信, 2014, 16(1): 97-98. ZHAO Bo, GONG Rui, LI Ming. OPPC technology and OPPC optical fiber temperature measurement technology[J]. China New Telecommunications, 2014, 16(1): 97-98. (  0) 0) |
| [17] |
黄旭峰. 光纤复合架空地线接地方式的改进[J]. 高电压技术, 2010, 36(2): 356-364. HUANG Xufeng. Improvement of the grounding method of OPGW[J]. High Voltage Engineering, 2010, 36(2): 356-364. (  0) 0) |
| [18] |
马覃峰, 姚瑶, 唐建兴, 等. 融合微气象实时监测信息提升架空线路输送能力的研究与应用[J]. 电工技术, 2020(6): 55-57. MA Qinfeng, YAO Yao, TANG Jianxing, et al. Research and application on integrating micrometeorological real-time monitoring information to promote transmission capacity of overhead lines with[J]. Electric Engineering, 2020(6): 55-57. (  0) 0) |
| [19] |
郭振强, 朱超, 王永庆, 等. 基于流-固耦合分析的架空输电线路流场和温度场的数值研究[J]. 电力学报, 2020, 35(4): 302-312. GUO Zhenqiang, ZHU Chao, WANG Yongqing, et al. Numerical study on flow field and temperature field of overhead high voltage line based on fluid-solid coupling analysis[J]. Journal of Electric Power, 2020, 35(4): 302-312. (  0) 0) |
| [20] |
姜会飞, 温德永, 李楠, 等. 利用正弦分段法模拟气温日变化[J]. 气象与减灾研究, 2010, 33(3): 61-65. JIANG Huifei, WEN Deyong, LI Nan, et al. A new simulation method for the diurnal variation of temperature sub-sine simulation[J]. Meteorology and Disaster Reduction Research, 2010, 33(3): 61-65. (  0) 0) |
| [21] |
谢军飞, 许蕊. 北京不同站点气象要素的日与月际变化特征分析[J]. 气象与环境科学, 2014, 37(1): 20-28. XIE Junfei, XU Rui. Variation characteristics analysis of the diurnal and monthly meteorological elements at different stations in Beijing[J]. Meteorological and Environmental Sciences, 2014, 37(1): 20-28. (  0) 0) |
| [22] |
晏海, 曾凤, 董丽. 北京城市局地空气温度时空变化特征分析[J]. 生态环境学报, 2017, 26(5): 816-823. YAN Hai, ZENG Feng, DONG Li. Temporal and spatial variation characteristics of urban local microclimate in Beijing[J]. Ecology and Environmental Sciences, 2017, 26(5): 816-823. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 徐志钮(1979), 男, 博士, 副教授, 研究方向为光纤分布式传感及在电气设备状态监测与故障诊断中的应用(E-mail:
徐志钮(1979), 男, 博士, 副教授, 研究方向为光纤分布式传感及在电气设备状态监测与故障诊断中的应用(E-mail: