文章编号: 2096-3203(2022)05-0021-10 中图分类号: TM46
2. 国网浙江省电力有限公司台州供电公司,浙江 台州 318000;
3. 国网浙江省电力有限公司,浙江 杭州 310007
相较于陆上风电,海上风电因其风能充足、噪音不受限制以及风机利用率高等优点受到了广泛关注[1—3]。随着大型风力发电系统由近海向中远海延伸[4—5],风电场接入电网环境日趋复杂,远距离大容量输电问题对海上风电并网提出了新的挑战。
1994年,王锡凡教授首次提出分频输电系统(fractional frequency transmission system,FFTS)[6],该技术具有降低系统电抗、提高传输容量、经济性好等优势,被广泛应用于海上风电场与电网的并网互联[7—9]。作为FFTS的核心装置,模块化多电平矩阵变换器(modular multilevel matrix converter,M3C)以其高度模块化及易于扩展等优势,成为海上风电FFTS中极具发展前景的变换器方案[10—11]。
现有文献对M3C的数学建模和控制策略已有较多研究[10, 12—14],而对影响M3C及FFTS稳定运行的谐波特性及分布规律还缺乏深入分析。与模块化多电平变换器(modular multilevel converter,MMC)和级联H桥变换器(cascaded H-bridge,CHB)类似,M3C的桥臂电流和模块直流电压存在谐波耦合,谐波特性对变换器内部的环流抑制和外部的阻抗特性均有直接影响。如文献[15]根据MMC桥臂中环流为二倍频的结论,针对性地提出抑制环流的有效策略。此外,具有高波动性和高比例电力电子设备的中远海风力发电及其输电系统,极易发生次/超同步相互作用、谐波谐振等稳定性问题[16—19]。序阻抗模型是交互稳定性分析和宽频振荡抑制的基础,在建模过程中,分析小信号谐波相序及处理不同谐波都须以精确的谐波分析工作为基础。文献[20]以CHB谐波分析为基础,针对谐波分布规律提出一种仅考虑基波与二次谐波的线性化方法,降低了矩阵阶数;文献[21]对MMC进行序阻抗建模时,分析了稳态谐波和小信号谐波的分布规律,将MMC的六桥臂模型简化为单桥臂模型,有效简化了序阻抗建模的分析过程。M3C为直接交-交变换,无公共直流环节,两侧接入不同频率交流系统,存在桥臂电流谐波与模块电压的迭代耦合,导致变换器内部谐波分量丰富,其分布特性和传递规律较MMC和CHB更为复杂。深入研究M3C谐波特性对M3C环流抑制、模块均衡控制以及交互稳定性分析具有重要意义。
目前,仅有少量文献基于模块和桥臂均衡控制需求对M3C系统的谐波特性进行了初步研究。文献[22]研究了电容电压均衡控制策略,比较了不同策略下电容电压纹波幅值的差异,但未给出电容电压纹波的解析式。文献[23]深入分析了电容电压纹波,依据能量守恒建立了电容纹波电压各频率成分的解析式。文献[24]推导了M3C单个桥臂的电流解析式,但没有分析9个桥臂的电流表达式及其与系统电流的关系。文献[25]针对M3C提出一种谐波分析的方法,对20 Hz和60 Hz互联的系统研究了电容纹波电压频率分布,给出了40 Hz的电容纹波电压表达式,推导了桥臂电流谐波分布,讨论了影响电流谐波幅值的主要因素,但研究对象为20 Hz和60 Hz互联的系统,二者具有整数倍关系,且忽略了部分频率信号,模型精度不足,因此所得结果具有特殊性和局限性。
在已有研究的基础上,文中对M3C子模块电容电压和桥臂电流的稳态谐波特性进行分析。首先建立M3C子模块电容纹波电压表达式,对其频率分布情况及耦合成因进行分析。其次,考虑所有电容纹波电压频率分量,推导出不同频率桥臂电流的解析式,并进行谐波特性分析,提出一种零序电流抑制控制策略。利用Matlab/Simulink建立M3C-FFTS的仿真模型,比较投入零序电流抑制前后系统线电流的频谱,验证理论分析的准确性和策略的有效性。
1 M3C基本原理M3C主电路结构如图 1所示,两侧分别连接不同频率的三相交流系统。其中ux,uy分别为输入、输出侧相电压,x=a, b, c,y=u, v, w;ω1, ω2分别为输入、输出侧系统角频率,ω1=2πf1,ω2=2πf2;f1,f2分别为输入、输出侧系统频率;ix,iy分别为输入、输出侧线电流。文中输入侧为分频侧,输出侧为工频侧。M3C共有9个桥臂,每个桥臂由电感L、等效电阻R和N个H桥子模块串联构成。ixy为桥臂电流;Uxy为桥臂电压。M3C正常运行时,通过对桥臂的子模块进行调制,可以使桥臂输出相应的电压,从而实现控制目标。
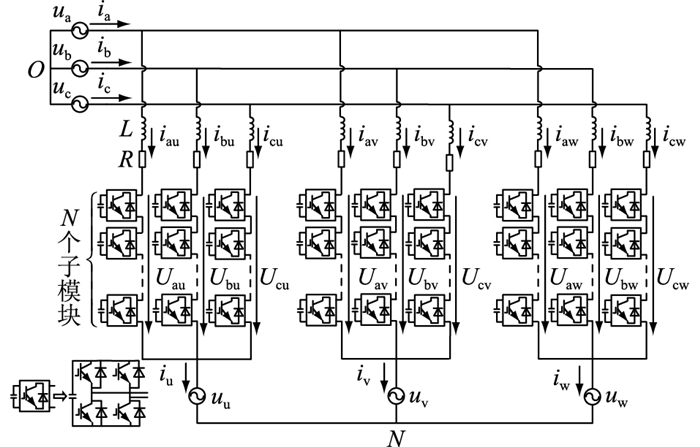
|
图 1 M3C主电路结构 Fig. 1 Main circuit structure of M3C |
定义单个桥臂中第i个子模块的开关信号为:
| $ S_{\mathrm{arm}i}= \begin{cases}0 & \text { 切除 } \\ \pm 1 & \;\;\;\text { 投人 }\end{cases} $ | (1) |
假设所有子模块电容电压均衡,则此时第i个子模块的电流关系式可表示为:
| $ S_{\mathrm{arm} i} i_{\mathrm{arm}}=C \frac{\mathrm{d} U_{\mathrm{dc}}}{\mathrm{d} t} $ | (2) |
式中:iarm为桥臂电流;C为子模块电容;Udc为子模块的电容电压。
则桥臂上所有子模块电流关系式可表示为:
| $ \sum\limits_{i=1}^N S_{\mathrm{arm} i} i_{\mathrm{arm}}=N C \frac{\mathrm{d} U_{\mathrm{dc}}}{\mathrm{d} t} $ | (3) |
| $ n i_{\mathrm{arm}}=N C \frac{\mathrm{d} U_{\mathrm{dc}}}{\mathrm{d} t} $ | (4) |
式中:n为等效投入的子模块数量。
若定义某一时刻桥臂内投入的子模块数量和桥臂总模块数量之比为投切系数Sarm(Sarm=n/N),式(4)可改写为:
| $ S_{\mathrm{arm}} i_{\mathrm{arm}}=C \frac{\mathrm{d} U_{\mathrm{dc}}}{\mathrm{d} t} $ | (5) |
桥臂电压关系式为:
| $ U_{\mathrm{arm}}=N S_{\mathrm{arm}} U_{\mathrm{dc}} $ | (6) |
式(5)、式(6)共同描述了M3C桥臂电压和电流的关系,可知,投切系数Sarm与桥臂电流乘积频率耦合会产生子模块电容纹波电压,电容纹波电压又与Sarm乘积耦合产生桥臂电压以及桥臂电流谐波。该关系式在9个桥臂中均适用。
2 M3C子模块电容纹波电压分析稳态时,两侧系统三相电压、电流在桥臂上均匀分布[26],以桥臂au为例,桥臂电流iau包含有ia/3和iu/3以及部分谐波iarm, h。因此,桥臂电流表达式可写为:
| $ i_{x y}=\frac{1}{3} i_x+\frac{1}{3} i_y+i_{\mathrm{arm}, h} $ | (7) |
首次推导时,忽略谐波分量,则桥臂au电流为:
| $ i_{\mathrm{au}} \approx \frac{1}{3}\left(I_1 \sin \left(\omega_1 t+\beta_1\right)+I_2 \sin \left(\omega_2 t+\beta_2\right)\right) $ | (8) |
式中:I1,β1分别为分频侧系统线电流的幅值和相位;I2,β2分别为工频侧系统线电流的幅值和相位。
根据M3C工作原理,桥臂au子模块的投切系数可定义为:
| $ S_{\mathrm{au}}=m_1 \sin \left(\omega_1 t+\alpha_1\right)-m_2 \sin \left(\omega_2 t+\alpha_2\right) $ | (9) |
式中:m1,α1分别为分频侧系统的调制比和相位;m2,α2分别为工频侧系统的调制比和相位。其余桥臂电流表达式及子模块投切系数与式(8)、式(9)类似,只是存在2π/3的相位差。
对式(5)积分,稳态时桥臂子模块电容电压可表示为:
| $ U_{\mathrm{dc}}=\frac{1}{C} \int S_{\mathrm{arm}} i_{\mathrm{arm}} \mathrm{d} t+U_{\mathrm{dc} 0} $ | (10) |
式中:Udc0为子模块电容电压的直流分量。将iau,Sau代入式(10)可得桥臂au子模块电容电压Udc, au,其表达式为式(11)。采用同样方法可得到其他桥臂子模块的电容电压表达式与式(11)类似,只是存在2π/3的相位差,文中不再给出。
| $ \begin{gathered} U_{\mathrm{dc}, \mathrm{au}}=\frac{1}{6 C}\left(U_{\mathrm{dc} 0}+m_1 I_1 t \cos \left(\alpha_1-\beta_1\right)-\right. \\ m_2 I_2 t \cos \left(\alpha_2-\beta_2\right)-\frac{m_1 I_1 \sin \left(2 \omega_1 t+\alpha_1+\beta_1\right)}{2 \omega_1}+\\ \frac{1}{\omega_2-\omega_1} m_1 I_2 \sin \left(\left(\omega_2-\omega_1\right) t-\alpha_1+\beta_2\right)- \\ \frac{1}{\omega_2-\omega_1} m_2 I_1 \sin \left(\left(\omega_2-\omega_1\right) t+\alpha_2-\beta_1\right)+\\ \frac{1}{\omega_1+\omega_2} m_2 I_1 \sin \left(\left(\omega_1+\omega_2\right) t+\alpha_2+\beta_1\right)- \\ \frac{1}{\omega_1+\omega_2} m_1 I_2 \sin \left(\left(\omega_1+\omega_2\right) t+\alpha_1+\beta_2\right)+\\ \left.\frac{1}{2 \omega_2} m_2 I_2 \sin \left(2 \omega_2 t+\alpha_2+\beta_2\right)\right) \end{gathered} $ | (11) |
观察式(11),由于M3C输入、输出能量守恒,因此式中
桥臂电流和开关函数中均包含ω1和ω2,2种频率分量相互间耦合,因此子模块电容纹波电压含有式(11)中所示的4种频率分量,分别为ω2-ω1(记为ωⅠ),2ω1(记为ωⅡ),ω1+ω2(记为ωⅢ)和2ω2(记为ωⅣ)。对于9个桥臂来说,电容纹波电压所含频率成分一致且相同频率对应的纹波电压幅值相等,该幅值与电容大小和频率成反比。
分析式(11)可发现,分母中存在ω2-ω1和2ω1,这导致M3C存在2种极端运行工况,即ω1→0和ω2-ω1→0。这2种情况均会导致电容电压在低频段产生较大波动,引起系统不稳定。因此,分频侧不能在过小频率下运行,同时也不能和工频侧系统频率过于接近。
3 M3C桥臂电流谐波分析为讨论桥臂电流的谐波特性,文中先根据式(6)推导出桥臂电压,再列写基尔霍夫电压定律(Kirchhoff′s voltage law,KVL)回路电压方程得到桥臂电流,从而进行谐波分析。
将式(9)和式(11)代入式(6),可得到桥臂电压的表达式,所含频率分量如表 1所示。表 1中第一列为桥臂电压含有的频率成分,第二列为该频率成分的耦合成因。如ω2-2ω1频率的桥臂电压耦合成因为:(1) 频率为ωⅠ的电容纹波电压和频率为ω1的开关函数耦合;(2) 频率为ωⅡ的电容纹波电压和频率为ω2的开关函数耦合。
|
|
表 1 桥臂电压频率组成 Table 1 Frequency composition of arm voltage |
表 1中ω1+0和ω2+0是子模块电容电压的直流分量和投切系数耦合得到的分量,是两侧交流系统固有的成分,不属于纹波电压和开关函数耦合得到的谐波,因此不参与谐波特性分析。对桥臂au列写关于表 1中各频率分量的KVL方程,如式(12)所示。
| $ \left\{\begin{array}{l} 0=u_{\mathrm{au}, \omega_2-2 \omega_1}+L \frac{\mathrm{d} i_{\mathrm{au}, \omega_2-2 \omega_1}}{\mathrm{~d} t} \\ u_{\mathrm{a}}=u_{\mathrm{au}, \omega_1}+L \frac{\mathrm{d} i_{\mathrm{au}, \omega_1}}{\mathrm{~d} t} \\ 0=u_{\mathrm{au}, \omega_2}+L \frac{\mathrm{d} i_{\mathrm{au}, \omega_2}}{\mathrm{~d} t}+u_{\mathrm{u}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ 0=u_{\mathrm{au}, 3 \omega_2}+L \frac{\mathrm{d} i_{\mathrm{au}, 3 \omega_2}}{\mathrm{~d} t} \end{array}\right. $ | (12) |
式中:uau,p,iau,p分别为桥臂au频率为p的桥臂电压和桥臂电流(p=ω2-2ω1,ω1,ω2,3ω1,2ω2-ω1,2ω1+ω2,ω1+2ω2,3ω2)。
由于KVL不改变频率特性,因此桥臂电流频率成分与桥臂电压保持一致。根据式(6)、式(9)、式(11)、式(12)可计算出对应频率的电流谐波,分析如下。
3.1 环流谐波分析ω2-2ω1频率的桥臂谐波电流表达式为式(13),该谐波电流在9个桥臂中幅值相等,但存在2π/3的相位差。将xy=au,av,aw时的式(13)相加,结果为0,说明该电流将不能流入a相,同理可知不会流入b相和c相;将xy=au,bu,cu时的式(13)相加,结果同样为0,因此该电流也不会流入u相,同理也不流入v相和w相。
| $ \begin{gathered} i_{x y, \omega_2-2 \omega_1}=k_1\left(-m_1^2 I_2 \sin \varphi_1+m_1 m_2 I_1 \sin \varphi_2\right)+\\ k_2\left(-m_1 m_2 I_1 \sin \varphi_2\right) \end{gathered} $ | (13) |
其中k1,k2如式(14)、式(15)所示,相位φ1,φ2的表达式见表 2。
| $ k_1=\frac{N}{12 C\left(\omega_2-\omega_1\right)\left(\omega_2-2 \omega_1\right) L} $ | (14) |
| $ k_2=\frac{N}{24 C \omega_1\left(\omega_2-2 \omega_1\right) L} $ | (15) |
|
|
表 2 相位φ1和φ2表达式 Table 2 The expressions of phase φ1 and φ2 |
与此特性类似的还有2ω2-ω1,2ω1+ω2,ω1+2ω2频率的桥臂谐波电流分量,其表达式见式(16)、式(19)和式(22)。这4个频率的电流最终既不会流入分频侧系统也不会流入工频侧系统,只在变换器内部循环。
2ω2-ω1频率的桥臂谐波电流表达式为:
| $ \begin{aligned} &i_{x y, 2 \omega_2-\omega_1}=k_3\left(-m_1 m_2 I_2 \sin \varphi_3\right)+\\ &k_4\left(-m_1 m_2 I_2 \sin \varphi_3+m_2^2 I_1 \sin \varphi_4\right) \end{aligned} $ | (16) |
其中k3,k4如式(17)、式(18)所示,相位φ3,φ4的表达式见表 3。
| $ k_3=\frac{N}{24 C \omega_2\left(2 \omega_2-\omega_1\right) L} $ | (17) |
| $ k_4=\frac{N}{12 C\left(\omega_2-\omega_1\right)\left(2 \omega_2-\omega_1\right) L} $ | (18) |
|
|
表 3 相位φ3和φ4表达式 Table 3 The expressions of phase φ3 and φ4 |
2ω1+ω2频率的桥臂谐波电流表达式为:
| $ \begin{gathered} i_{x y, 2 \omega_1+\omega_2}=k_5\left(-m_1^2 I_2 \sin \varphi_5+m_1 m_2 I_1 \sin \varphi_6\right)+\\ k_6 m_1 m_2 I_1 \sin \varphi_6 \end{gathered} $ | (19) |
其中k5,k6如式(20)、式(21)所示,相位φ5,φ6的表达式见表 4。
| $ k_5=\frac{N}{24 C \omega_1\left(2 \omega_1+\omega_2\right) L} $ | (20) |
| $ k_6=\frac{N}{12 C\left(\omega_1+\omega_2\right)\left(2 \omega_1+\omega_2\right) L} $ | (21) |
|
|
表 4 相位φ5和φ6表达式 Table 4 The expressions of phase φ5 and φ6 |
ω1+2ω2频率的桥臂谐波电流表达式:
| $ \begin{gathered} i_{x y, \omega_1+2 \omega_2}=k_7 m_1 m_2 I_2 \sin \varphi_7+\\ k_8\left(m_1 m_2 I_2 \sin \varphi_7-m_2^2 I_1 \sin \varphi_8\right) \end{gathered} $ | (22) |
其中k7,k8如式(23)、式(24)所示,相位φ7,φ8的表达式见表 5。
| $ k_7=\frac{N}{24 C \omega_2\left(\omega_1+2 \omega_2\right) L} $ | (23) |
| $ k_8=\frac{N}{12 C\left(\omega_1+\omega_2\right)\left(\omega_1+2 \omega_2\right) L} $ | (24) |
|
|
表 5 相位φ7和φ8表达式 Table 5 The expressions of phase φ7 and φ8 |
ω1频率的桥臂谐波电流表达式见式(25),将xy=au,av,aw时式(25)的结果相加,和为3iarm,au,ω1,记为iΔ1;将xy=bu,bv,bw时式(25)的结果相加,和为3iarm,bu,ω1,记为iΔ2;将xy=cu,cv,cw时式(25)的结果相加,和为3iarm,cu,ω1,记为iΔ3。观察iΔ1,iΔ2,iΔ3,可知该电流会以正序基波电流的性质流入分频侧系统;将xy=au、bu、cu时式(25)的结果相加,和为0,因此该电流不会流入u相,同理也不会流入v相和w相。
| $ \begin{gathered} i_{x y, \omega_1}=k_9 \mathrm{~m}_1^2 I_1 \sin \varphi_9+\\ k_{10}\left(m_1 m_2 I_2 \sin \varphi_{10}-m_2^2 I_1 \sin \varphi_9\right)+\\ k_{11}\left(-m_1 m_2 I_2 \sin \varphi_{11}+m_2^2 I_1 \sin \varphi_9\right) \end{gathered} $ | (25) |
其中k9,k10,k11如式(26)—式(28)所示,相位φ9,φ10,φ11的表达式见表 6。
| $ k_9=\frac{N}{24 C \omega_1^2 L} $ | (26) |
| $ k_{10}=\frac{N}{12 C \omega_1\left(\omega_2-\omega_1\right) L} $ | (27) |
| $ k_{11}=\frac{N}{12 C \omega_1\left(\omega_1+\omega_2\right) L} $ | (28) |
|
|
表 6 相位φ9和φ10及φ11表达式 Table 6 The expressions of phase φ9, φ10 and φ11 |
与上述分析类似,ω2频率的桥臂谐波电流将会以正序基波电流的性质流入工频侧系统,而不能流入分频侧系统,其表达式见式(29)。
| $ \begin{gathered} i_{x y, \omega_2}=k_{12}\left(m_1^2 I_2 \sin \varphi_{12}-m_1 m_2 I_1 \sin \varphi_{13}\right)+\\ k_{13}\left(m_1^2 I_2 \sin \varphi_{12}-m_1 m_2 I_1 \sin \varphi_{14}\right)+k_{14} m_2^2 I_2 \sin \varphi_{12} \end{gathered} $ | (29) |
其中k12,k13,k14如式(30)—式(32)所示,相位φ12,φ13,φ14的表达式见表 7。
| $ k_{12}=\frac{N}{12 C \omega_2\left(\omega_2-\omega_1\right) L} $ | (30) |
| $ k_{13}=\frac{N}{12 C \omega_2\left(\omega_1+\omega_2\right) L} $ | (31) |
| $ k_{14}=\frac{N}{24 C \omega_2^2 L} $ | (32) |
|
|
表 7 相位φ12和φ13及φ14表达式 Table 7 The expressions of phase φ12, φ13 and φ14 |
3ω1频率的桥臂谐波电流表达式见式(33),仅含有一项,9个桥臂电流的幅值和相位均相等。因此,该电流将以零序电流的性质注入分频侧系统和工频侧系统,若不加以控制,会导致系统电流失真,甚至可能引起稳定性问题。
| $ i_{x y, 3 \omega_1}=k_{15}\left(-m_1^2 I_1 \sin \varphi_{15}\right) $ | (33) |
其中k15如式(34)所示,φ15=3ω1t+2α1+β1。
| $ k_{15}=\frac{N}{72 C \omega_1^2 L} $ | (34) |
与此性质相似的还有频率为3ω2的桥臂谐波电流,其表达式见式(35),最终也以零序电流的形式注入两侧系统,对系统产生不利影响。
| $ i_{x y, 3 \omega_2}=k_{16}\left(-m_2^2 I_2 \sin \varphi_{16}\right) $ | (35) |
其中k16如式(36)所示,φ16=3ω2t+2α2+β2。
| $ k_{16}=\frac{N}{72 C \omega_2^2 L} $ | (36) |
分析各表达式可得到电流谐波大小与电容、电感和系统工作频率有关的结论:观察系数k1~k16可知,电容和电感与谐波大小成反比,且分频侧系统的频率在满足电容电压稳定条件时,其二倍频亦不可与工频过于接近,否则将会导致桥臂电流发散。综上,通过对各桥臂电流谐波分布的详细分析,可汇总各频率谐波分量在分频侧和工频侧系统的谐波情况如表 8所示。为直观表示,当选取算例中分频侧频率f1=20 Hz,工频侧频率f2=50 Hz时,表 4中第二列为桥臂谐波电流的具体频率值。
|
|
表 8 桥臂电流各频率分量与系统电流关系 Table 8 Relationship between the harmonic components of the arm current and the system current |
根据式(13)可以看出,桥臂电流中ω2-2ω1(10 Hz)的电流分量频率较低,幅值较大,同时,通过仿真对此加以证实,因而该电流会再次与投切系数进行耦合(见式(10)),对系统谐波产生影响。因此考虑该频率的桥臂谐波电流,将式(13)代入式(7)中iarm,h,重复进行上述推导分析过程。结果表明,ω2-2ω1频率的桥臂谐波电流会二次耦合产生频率为3ω1-ω2和2ω2-2ω1的子模块电容电压纹波,其表达式为式(37)、式(41)。
3ω1-ω2频率电压纹波表达式为:
| $ \begin{gathered} U_{\mathrm{dc}, 3 \omega_1-\omega_2}=-\frac{1}{2 C}\left(k_{17} \sin \left(\left(3 \omega_1-\omega_2\right) t+3 \alpha_1-\beta_2\right)+\right. \\ k_{18} \sin \left(\left(3 \omega_1-\omega_2\right) t+2 \alpha_1-\alpha_2+\beta_1\right)+\\ \left.k_{19} \sin \left(\left(3 \omega_1-\omega_2\right) t+2 \alpha_1-\alpha_2+\beta_1\right)\right) \end{gathered} $ | (37) |
其中k17,k18,k19如式(38)—式(40)所示。
| $ k_{17}=\frac{k_1 m_1^3 I_2}{3 \omega_1-\omega_2} $ | (38) |
| $ k_{18}=-\frac{k_1 m_1^2 m_2 I_1}{3 \omega_1-\omega_2} $ | (39) |
| $ k_{19}=\frac{k_2 m_1^2 m_2 I_1}{3 \omega_1-\omega_2} $ | (40) |
2ω2-2ω1频率电压纹波表达式为:
| $ \begin{gathered} U_{\mathrm{dc}, 2 \omega_2-2 \omega_1}= \\ -\frac{1}{2 C}\left(k_{20} \sin \left(\left(2 \omega_2-2 \omega_1\right) t-2 \alpha_1+\alpha_2+\beta_2\right)+\right. \\ k_{21} \sin \left(\left(2 \omega_2-2 \omega_1\right) t-\alpha_1+2 \alpha_2-\beta_1\right)+\\ \left.k_{22} \sin \left(\left(2 \omega_2-2 \omega_1\right) t-\alpha_1+2 \alpha_2-\beta_1\right)\right) \end{gathered} $ | (41) |
其中k20,k21,k22如式(42)—式(44)所示。
| $ k_{20}=\frac{k_1 m_1^2 m_2 I_2}{2 \omega_2-2 \omega_1} $ | (42) |
| $ k_{21}=-\frac{k_1 m_1 m_2^2 I_1}{2 \omega_2-2 \omega_1} $ | (43) |
| $ k_{22}=\frac{k_2 m_1 m_2^2 I_1}{2 \omega_2-2 \omega_1} $ | (44) |
同时,该频率的桥臂谐波电流会对首次推导中频率为ω2-ω1和2ω1的子模块电容电压纹波幅值产生影响。这些二次耦合对纹波电压产生影响,进而会对相关桥臂电流谐波产生影响,但影响很小,在后续分析中可忽略。
4 零序电流抑制在工程中,零序电流既可通过接入角接变压器进行隔离,亦可利用控制对其实现抑制作用。
由3.3节可知,分频侧和工频侧的零序电流组成完全一致,均包含3ω1和3ω2分量(式(33)和式(35)),将9个桥臂中的零序电流分量相加,可得M3C系统零序电流izero为:
| $ i_{\text {zero }}=9\left[k_{15}\left(-m_1^2 I_1 \sin \varphi_{15}\right)+k_{16}\left(-m_2^2 I_2 \sin \varphi_{16}\right)\right] $ | (45) |
为了实现系统电流中零序电流分量和正序基波分量的解耦,对其进行Park变换,以分频侧为例,分频侧电流经Park变换后在dq0坐标系下的表达式如式(46)所示。
| $ \left[\begin{array}{c} i_{\mathrm{s} d} \\ i_{\mathrm{s} q} \\ i_{\mathrm{s} 0} \end{array}\right]=\left[\begin{array}{c} I_1 \cos \beta_1 \\ I_1 \sin \beta_1 \\ i_{\text {zero }} \end{array}\right] $ | (46) |
式中:isd,isq,is0分别为分频侧系统的d轴电流、q轴电流和0轴电流。
由式(46)可知,系统dq0坐标系下的dq分量只与三相系统的正序基波有关,与零序分量无关;0轴分量只与系统的零序电流有关,而与正序基波分量无关。因此只需对0轴电流进行控制即可达到零序电流抑制的效果。
文中针对M3C提出一种零序电流抑制控制策略,其框图见图 2。在dq0坐标系下得到分频侧系统的0轴电流is0,给定其参考值is0_ref=0,二者误差经过PI调节器得到0轴补偿电压,加上前馈的分频侧系统0轴电压Us0可得到分频侧0轴电压调制信号U′ s0,再经Park反变换即可得到抑制零序电流的分频侧三相电压调制信号。需要指出的是,如前所述,两侧系统零序电流完全相同,故而使用一个控制器即可对零序电流进行抑制。同时,为有效抑制零序电流分量,PI调节器的控制带宽不能过低。

|
图 2 零序电流抑制控制框图 Fig. 2 Control diagram of the proposed zero-sequence current mitigation controller |
在Matlab/Simulink中搭建如图 1所示的M3C系统模型,对第2章和第3章理论分析结果进行仿真验证。仿真参数为:额定容量为12.5 MW;额定电流为601 A;额定电压为12 kV;M3C桥臂子模块数N为6;子模块电容C为10 mF;桥臂电感L为10 mH;分频侧电压有效值Vs为12 kV,频率f1为20 Hz;工频侧电压有效值Vg为12 kV,频率f2为50 Hz。文中采取的控制方案为:分频侧定交流电压控制,工频侧定子模块平均电容电压控制。控制框图如图 3所示,其中各变量定义见表 9。
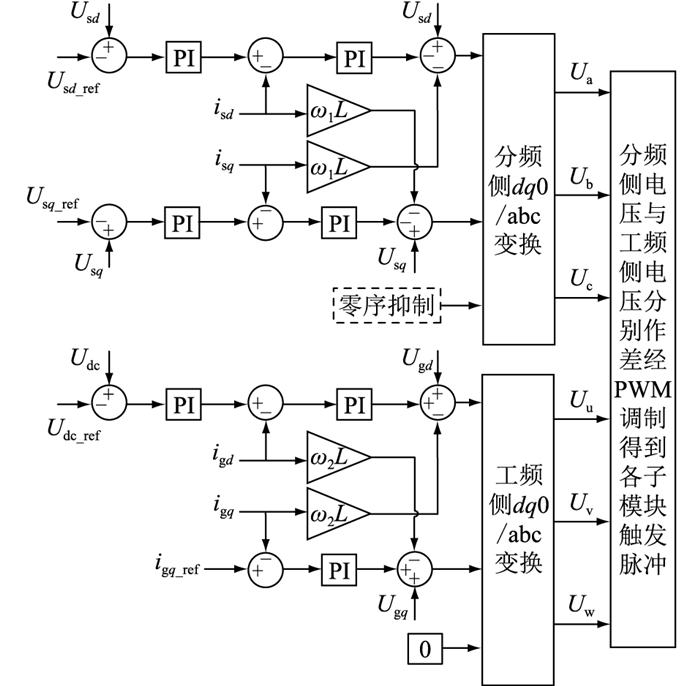
|
图 3 M3C-FFTS控制框图 Fig. 3 Control diagram of M3C-FFTS |
5.1 子模块电容纹波电压验证
桥臂au子模块电容电压Uau的波形如图 4所示,存在多种频率分量。对Uau进行快速傅里叶变换(fast Fourier transform,FFT)分析,其频谱如图 5所示,所含频率成分为10 Hz、30 Hz、40 Hz、60 Hz、70 Hz和100 Hz,幅值与理论计算结果一致,验证了前文理论分析的准确性。
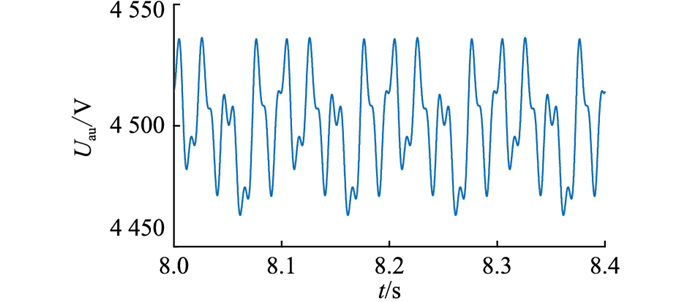
|
图 4 桥臂电容电压 Fig. 4 Arm capacitor voltage |
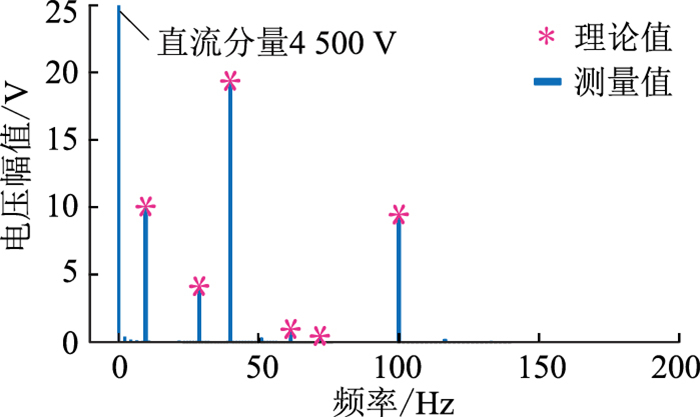
|
图 5 桥臂电容电压频谱 Fig. 5 Frequency spectrum of arm capacitor voltage |
桥臂电流波形如图 6所示,对其进行FFT分析得到其频谱,即图 7。观察可知,桥臂电流由8个频率分量组成,分别为10 Hz、20 Hz、50 Hz、60 Hz、80 Hz、90 Hz、120 Hz和150 Hz。该结果与第3章中分析一致,验证了理论分析的准确性。图 7(a)虚线框内为小于40 A的谐波分量,其细节见图 7(b)。
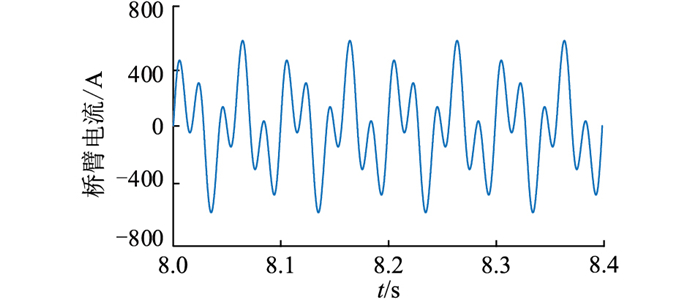
|
图 6 桥臂电流波形 Fig. 6 Arm current waveform |
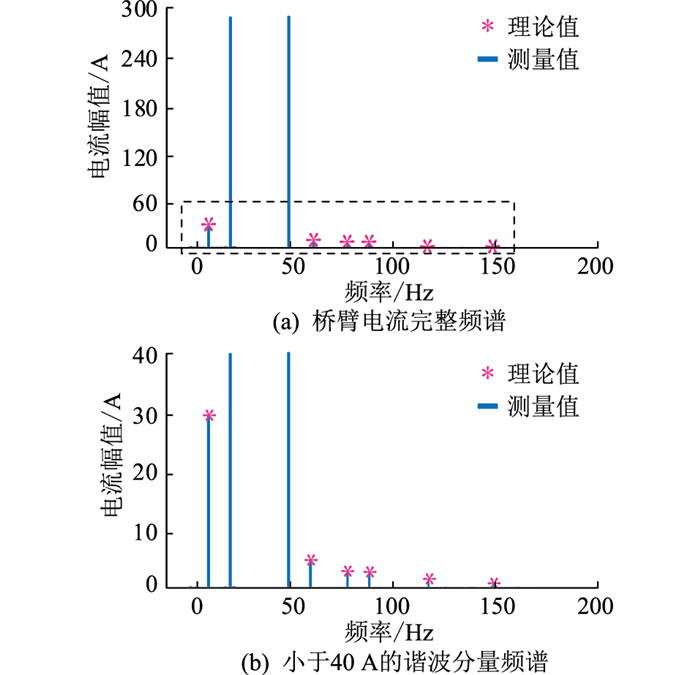
|
图 7 桥臂电流频谱 Fig. 7 Frequency spectrum of arm current |
分频侧三相电流isabc和工频侧三相电流iguvw的波形分别如图 8(a)、图 8(b)所示,二者FFT结果分别如图 9(a)、图 9(b)所示,分频侧基波(20 Hz)幅值和工频侧基波(50 Hz)幅值均为867 A。由图 9可知,分频侧三相电流isabc和工频侧三相电流iguvw除了含有各自基波电流以外,还含有频率为60 Hz和150 Hz的谐波电流,即前文中所述3ω1频率和3ω2频率的零序谐波电流,验证了理论分析的准确性。
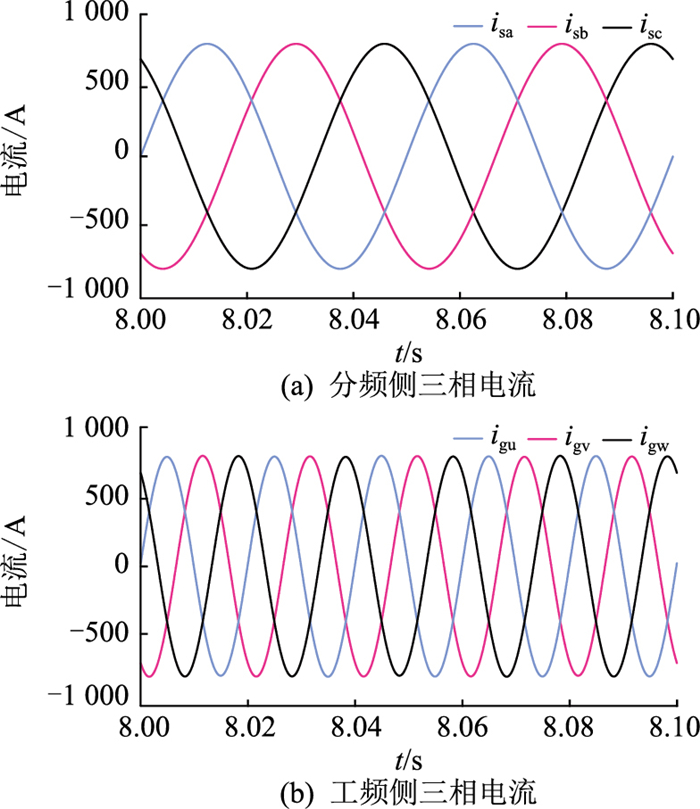
|
图 8 两侧交流系统电流波形 Fig. 8 Current waveforms of AC systems on both sides |
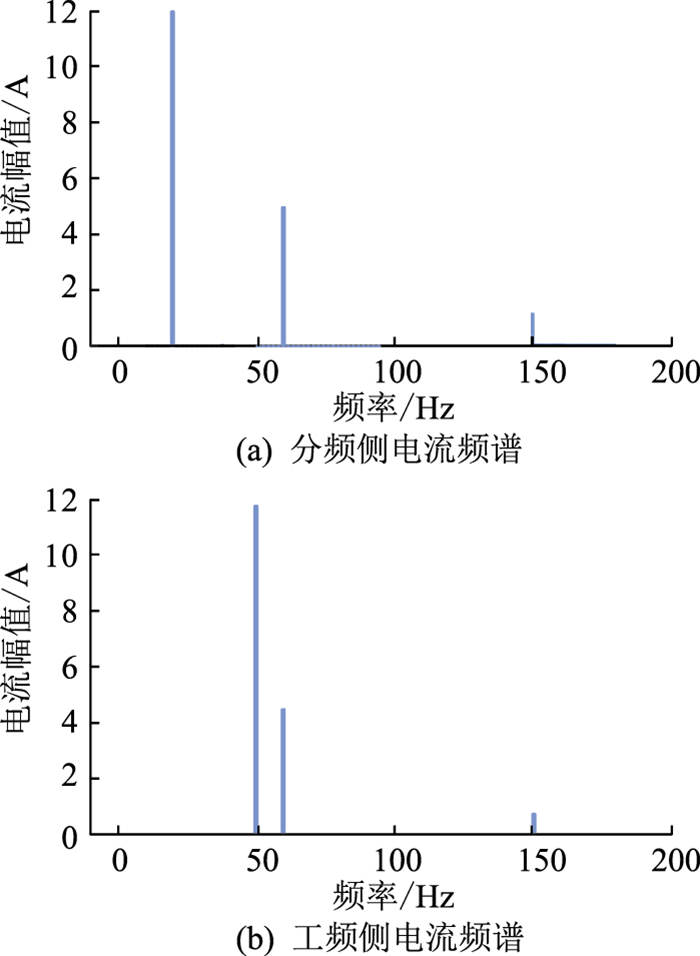
|
图 9 两侧交流系统电流频谱 Fig. 9 Frequency spectrum of currents of AC systems on both sides |
当采用变压器的方式进行零序电流隔离时,以现有模型为基础,在分频侧安装YgD11变压器,中性点不接地,此时系统分频侧线电流频谱如图 10所示。仿真结果显示,投入角接变压器可以有效隔离60 Hz和150 Hz频率的电流,阻止零序电流注入。
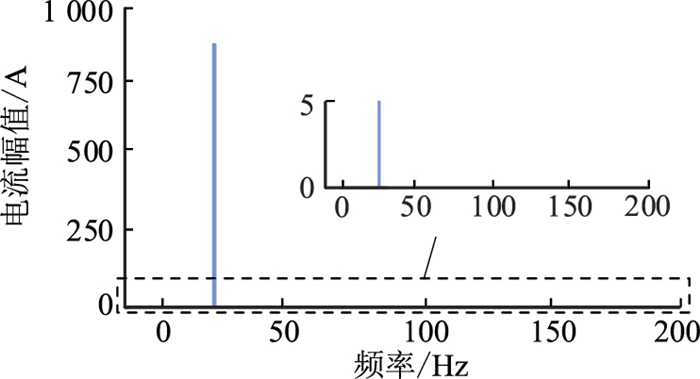
|
图 10 投入角接变压器后分频侧电流频谱 Fig. 10 Current frequency spectrum after connecting to the delta connected transformer on fractional frequency side |
分频侧采用图 2所示零序电流抑制控制策略前后的零序电流波形见图 11。t=0 s启动电路,此时未使用零序电流抑制控制,在t=5 s时投入图 2所示零序电流抑制控制,可以看到零序电流明显减小;采用零序电流抑制控制后分频侧三相电流isabc的频谱和工频侧三相电流iguvw的频谱分别如图 12(a)、12(b)所示。从图中看出,两侧系统零序电流明显减小,验证了所提控制策略的有效性。同时对采用抑制策略后的桥臂电流进一步分析发现,环流频率上的桥臂电流受零序电流抑制控制的影响很小,此时除零序电流频率外的桥臂电流的频谱与图 7几乎一致,故不再重复给出其频谱图。
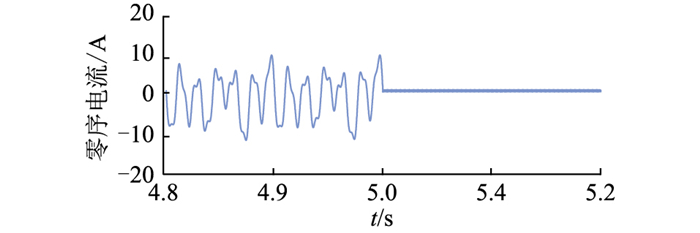
|
图 11 分频侧采用抑制策略前后零序电流 Fig. 11 Zero-sequence currents on the fractional frequency side before and after the zero-sequence current mitigation control |
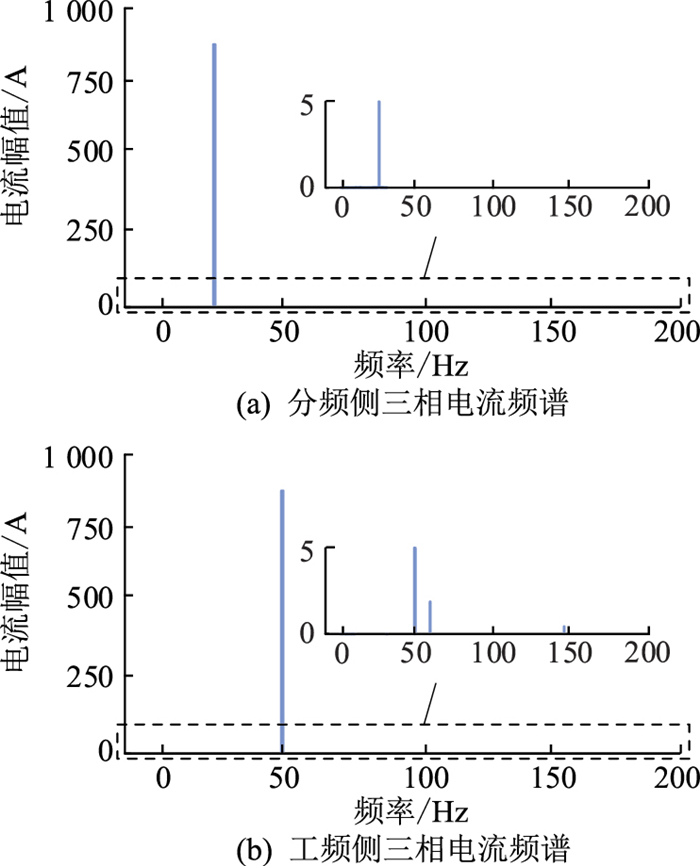
|
图 12 采用抑制策略后交流系统电流频谱 Fig. 12 Current frequency spectrum of AC systems after the zero-sequence current mitigation control |
M3C作为分频输电系统的核心装置,其谐波分布特性对设计网侧滤波器、分析系统阻抗特性和稳定性、提升运行效率具有重要影响。文中针对M3C多频率耦合特性进行一般化推导,得到子模块电容电压纹波和9个桥臂电流谐波的详细表达式,对其谐波分布及影响谐波大小的因素进行分析。得到结论如下:
(1) 子模块电容电压纹波中含有频率为ω2-ω1,2ω1,ω1+ω2,2ω2,3ω1-ω2和2ω2-2ω1的分量,其中,频率为3ω1-ω2和2ω2-2ω1的分量由ω2-2ω1频率的桥臂谐波电流二次耦合产生。电容和工作频率将影响纹波电压幅值,电容电压纹波将进一步耦合影响桥臂电压和电流。
(2) 桥臂电流由8个不同频率的谐波分量组成,可分为3类:ω1和ω2频率的谐波以正序基波分量流入对应系统内;3ω1和3ω2频率的谐波以零序电流的性质流入两侧系统;ω2-2ω1,2ω2-ω1,2ω1+ω2,ω1+2ω2频率的谐波在变换器中性点处相互抵消,成为变换器内部的环流,各频率谐波大小受两侧系统工作频率、电容和电感影响。
(3) 分频侧系统工作频率ω1须满足条件才能确保整个系统稳定运行,即ω1不能过小,且ω1和2ω1都不能过于接近ω2。
(4) 文中所提针对M3C的零序电流抑制控制策略可有效实现对零序电流的抑制。
M3C谐波特性分析是其序阻抗建模的基础工作。在后续M3C阻抗建模过程中,将基于文中研究成果,考虑稳态时子模块电容电压纹波、桥臂电流频率分布及其与系统输出电流谐波传递关系的影响,在保证阻抗模型精度的前提下,合理降低模型阶数,简化建模过程,建立阻抗模型。
本文得到国网浙江省电力有限公司科技项目(2021ZK05)资助,谨此致谢!
| [1] |
姚伟, 熊永新, 姚雅涵, 等. 海上风电柔直并网系统调频控制综述[J]. 高电压技术, 2021, 47(10): 3397-3413. YAO Wei, XIONG Yongxin, YAO Yahan, et al. Review of voltage source converter-based high voltage direct current integrated offshore wind farm on providing frequency support control[J]. High Voltage Engineering, 2021, 47(10): 3397-3413. (  0) 0) |
| [2] |
HE Q, ZHANG F W, LIU D N, et al. Analysis on the development status and problems of China's offshore wind power[C]//2018 2nd IEEE Conference on Energy Internet and Energy System Integration. Beijing, China. IEEE: 1-4.
(  0) 0) |
| [3] |
王邦彦, 王秀丽, 王碧阳, 等.海上风电分频送出系统可靠性评估模型及方法[J/OL]. 电网技术:1-10[2022-04-27]. DOI: 10.13335/j.1000-3673.pst.2021.2448. WANG Yanbang, WANG Xiuli, WANG Biyang, et al. Reliability evaluation model and method of offshore wind power fractional frequency delivery system[J/OL]. Power System Technology:1-10[2022-04-27]. DOI: 10.13335/j.1000-3673.pst.2021.2448. (  0) 0) |
| [4] |
黄伟捷, 江岳文. 远海风电输电和制氢经济可行性分析[J]. 中国电力, 2022, 55(1): 91-100. HUANG Weijie, JIANG Yuewen. Comparison of economic feasibilites between power transmission and hydrogen production from an offshore wind farm[J]. Electric Power, 2022, 55(1): 91-100. (  0) 0) |
| [5] |
迟永宁, 梁伟, 张占奎, 等. 大规模海上风电输电与并网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(14): 3758-3771. CHI Yongning, LIANG Wei, ZHANG Zhankui, et al. An overview on key technologies regarding power transmission and grid integration of large scale offshore wind power[J]. Proceedings of the CSEE, 2016, 36(14): 3758-3771. (  0) 0) |
| [6] |
王锡凡, 邵成成. 助力能源革命的多频率电力系统[J]. 中国电机工程学报, 2018, 38(21): 6195-6204, 6481. WANG Xifan, SHAO Chengcheng. Develop multi-frequency power systems to promote energy revolution[J]. Proceedings of the CSEE, 2018, 38(21): 6195-6204, 6481. (  0) 0) |
| [7] |
黄雨涵, 丁涛, 李雨婷, 等. 碳中和背景下能源低碳化技术综述及对新型电力系统发展的启示[J]. 中国电机工程学报, 2021, 41(S1): 28-51. HUANG Yuhan, DING Tao, LI Yuting, et al. Decarbonization technologies and inspirations for the development of novel power systems in the context of carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(S1): 28-51. (  0) 0) |
| [8] |
黄明煌, 王秀丽, 刘沈全, 等. 分频输电应用于深远海风电并网的技术经济性分析[J]. 电力系统自动化, 2019, 43(5): 167-174. HUANG Minghuang, WANG Xiuli, LIU Shenquan, et al. Technical and economic analysis on fractional frequency transmission system for integration of long-distance offshore wind farm[J]. Automation of Electric Power Systems, 2019, 43(5): 167-174. (  0) 0) |
| [9] |
王鑫, 王海云, 王维庆. 大规模海上风电场电力输送方式研究[J]. 电测与仪表, 2020, 57(22): 55-62. WANG Xin, WANG Haiyun, WANG Weiqing. Research on power transmission mode of large-scale offshore wind farms[J]. Electrical Measurement & Instrumentation, 2020, 57(22): 55-62. (  0) 0) |
| [10] |
吴小丹, 董云龙, 钱敏慧, 等. 面向分频海上风电送出的模块化多电平矩阵变换器改进V/F解耦控制策略[J/OL]. 电网技术:1-15[2022-04-27]. DOI: 10.13335/j.1000-3673.pst.2021.1239. WU Xiaodan, DONG Yunlong, QIAN Minhui, et al. Improved V/F decoupling control strategy of modular multilevel matrix converter for fractional offshore wind power transmission[J/OL]. Power System Technology:1-15[2022-04-27]. DOI: 10.13335/j.1000-3673.pst.2021.1239. (  0) 0) |
| [11] |
MIURA Y, MIZUTANI T, ITO M, et al. Modular multilevel matrix converter for low frequency AC transmission[C]//2013 IEEE 10th International Conference on Power Electronics and Drive Systems. Kitakyushu, Japan. IEEE: 1079-1084.
(  0) 0) |
| [12] |
孟永庆, 王健, 李磊, 等. 基于双dq坐标变换的M3C变换器的数学模型及控制策略研究[J]. 中国电机工程学报, 2016, 36(17): 4702-4712. MENG Yongqing, WANG Jian, LI Lei, et al. Research on modeling and control strategy of modular multilevel matrix converter based on double dq coordinate transformation[J]. Proceedings of the CSEE, 2016, 36(17): 4702-4712. (  0) 0) |
| [13] |
冯双, 韦超凡, 雷家兴, 等. 面向分频海上风电系统的模块化多电平矩阵变换器混合建模与控制[J]. 中国电机工程学报, 2022, 42(4): 1546-1558. FENG Shuang, WEI Chaofan, LEI Jiaxing, et al. Hybrid modeling and control of modular multilevel matrix converter for offshore fractional frequency transmission system[J]. Proceedings of the CSEE, 2022, 42(4): 1546-1558. (  0) 0) |
| [14] |
王文杰, 杨益平, 杭丽君, 等. 应用于交-交变换的M3C矩阵变换器系统控制策略[J]. 电力系统自动化, 2020, 44(12): 186-192. WANG Wenjie, YANG Yiping, HANG Lijun, et al. Control strategy of M3C matrix converter system applied to AC-AC transformation[J]. Automation of Electric Power Systems, 2020, 44(12): 186-192. (  0) 0) |
| [15] |
杨晓峰, 李泽杰, 郑琼林. 基于虚拟阻抗滑模控制的MMC环流抑制策略[J]. 中国电机工程学报, 2018, 38(23): 6893-6904, 7123. YANG Xiaofeng, LI Zejie, ZHENG Trillion Q. A novel MMC circulating current suppressing strategy based on virtual impedance sliding mode control[J]. Proceedings of the CSEE, 2018, 38(23): 6893-6904, 7123. (  0) 0) |
| [16] |
李光辉, 王伟胜, 郭剑波, 等. 风电场经MMC-HVDC送出系统宽频带振荡机理与分析方法[J]. 中国电机工程学报, 2019, 39(18): 5281-5297, 5575. LI Guanghui, WANG Weisheng, GUO Jianbo, et al. Broadband oscillation mechanism and analysis for wind farm integration through MMC-HVDC system[J]. Proceedings of the CSEE, 2019, 39(18): 5281-5297, 5575. (  0) 0) |
| [17] |
谢小荣, 贺静波, 毛航银, 等. "双高"电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475. XIE Xiaorong, HE Jingbo, MAO Hangyin, et al. New issues and classification of power system stability with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2021, 41(2): 461-475. (  0) 0) |
| [18] |
张天翼, 王海风. 风电并入弱交流系统引发次同步振荡的研究方法综述[J]. 电力系统保护与控制, 2021, 49(16): 177-187. ZHANG Tianyi, WANG Haifeng. Research methods for subsynchronous oscillation induced by wind powerunder weak AC system: a review[J]. Power System Protection and Control, 2021, 49(16): 177-187. (  0) 0) |
| [19] |
郑黎明, 贾科, 毕天姝, 等. 海上风电接入柔直系统交流侧故障特征及对保护的影响分析[J]. 电力系统保护与控制, 2021, 49(20): 20-32. ZHENG Liming, JIA Ke, BI Tianshu, et al. AC-side fault analysis of a VSC-HVDC transmission system connected to offshore wind farms and the impact on protection[J]. Power System Protection and Control, 2021, 49(20): 20-32. (  0) 0) |
| [20] |
张旸, 沈梦娇, 陈新, 等. 基于双谐波线性化的级联H桥静止无功发生装置序阻抗建模与分析[J]. 电工技术学报, 2019, 34(20): 4334-4346. ZHANG Yang, SHEN Mengjiao, CHEN Xin, et al. Sequence impedance modeling and analysis of cascaded H-bridge static var generator based on double-harmonic linearization[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4334-4346. (  0) 0) |
| [21] |
SUN J, LIU H C. Sequence impedance modeling of modular multilevel converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1427-1443. (  0) 0) |
| [22] |
KAWAMURA W, AKAGI H. Control of the modular multilevel cascade converter based on triple-star bridge-cells (MMCC-TSBC) for motor drives[C]//2012 IEEE Energy Conversion Congress and Exposition. Raleigh, NC, USA. IEEE: 3506-3513.
(  0) 0) |
| [23] |
李峰, 王广柱. 模块化多电平矩阵变换器电容电压纹波稳态分析[J]. 中国电机工程学报, 2013, 33(24): 52-58, 9. LI Feng, WANG Guangzhu. Steady-state analysis of sub-modular capacitor voltage ripple in modular multilevel matrix converters[J]. Proceedings of the CSEE, 2013, 33(24): 52-58, 9. (  0) 0) |
| [24] |
SUN P W, WANG X F, HU Y S, et al. The harmonic analysis and the arm capacitor parameters selection of module multilevel matrix converter[C]//2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference. Xi'an, China. IEEE: 1617-1621.
(  0) 0) |
| [25] |
LUO J J, ZHANG X P, XUE Y, et al. Harmonic analysis of modular multilevel matrix converter for fractional frequency transmission system[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1209-1219. (  0) 0) |
| [26] |
MA J K, DAHIDAH M, PICKERT V, et al. Modular multilevel matrix converter for offshore low frequency AC transmission system[C]//2017 IEEE 26th International Symposium on Industrial Electronics. Edinburgh, UK. IEEE: 768-774.
(  0) 0) |
2. State Grid Taizhou Power Supply Company of Zhejiang Electric Power Co., Ltd., Taizhou 318000, China;
3. State Grid Zhejiang Electric Power Co., Ltd., Hangzhou 310007, China
 2022, Vol. 41
2022, Vol. 41


 孙玉巍(1987), 女, 博士, 讲师, 研究方向为电力电子变压器控制技术、交直流配网柔性互联装备及控制技术(E-mail:
孙玉巍(1987), 女, 博士, 讲师, 研究方向为电力电子变压器控制技术、交直流配网柔性互联装备及控制技术(E-mail: