文章编号: 2096-3203(2022)05-0103-07 中图分类号: TM615
2. 国网甘肃省电力公司, 甘肃 兰州 730050;
3. 河海大学能源与电气学院, 江苏 南京 211100
光热发电(concentrating solar power, CSP)是一种比较成熟的太阳能发电技术。至今,国内已建成并网光热电站装机容量达520 MW。新能源发电的置信容量旨在研究新能源发电的“容量价值”,尤其是风电与光伏的间歇性与随机性更大,其“电源”价值较难凸显[1—3]。配置储热子系统是CSP区别于其他新能源发电的主要特征,因此光热电站的容量置信度远超光伏、风力发电。但CSP的容量价值是否能达到常规火电机组的水平以及相同置信度下的经济性仍有待研究[4]。
光热电站储热系统的配置对光热电站出力有较大影响,但关于光热发电的储热系统研究更多地在储热系统的储热形式、储热材料等方向,对储热系统的容量优化研究较少。文献[5]研究储热容量对槽式光热电站发电的影响,讨论储热时长和太阳倍数对单位电价的影响。文献[6]利用SAM软件对美国达科特地区建设50 MW的槽式太阳能电站进行模拟,对比研究不同太阳倍数和蓄热时长对系统年净发电量、系统年效率及容量因子的影响,通过对比平准化度电成本,研究选择系统最佳太阳倍数与蓄热时长的方法。文献[7]建立塔式光热电站的能量转换效率模型及经济性评价模型,以平准化度电成本最低为优化目标,分析在一定太阳倍数下,储热系统容量对电站经济效益的影响,并分析储热系统容量对电站年容量因子的影响。文献[8]针对配备分离式吸热器的50 MW直接蒸汽塔式太阳能电站,通过建立塔式电站系统耦合模型和经济性评价模型,探究太阳倍数和储热时长对其运行性能和标准发电成本的影响。对光热电站储热容量的研究大多都是基于经济性,如度电成本、单位电价等,研究集热面积和储热容量对经济性的影响,并没有将光热电站容量价值等性能指标纳入优化范围,但CSP的容量价值是其相比于风电、光伏等新能源发电最大的优势之一。
为此,文中重点研究光热电站的置信容量。置信容量的评价方法主要可分为可靠性评估法和容量因子法,其中可靠性评估法较容量因子法更精确但计算更复杂,文中基于可靠性评估的方法探索光热电站的容量价值。同时,储热系统容量和镜场集热面积对光热电站容量价值的影响至关重要,文中研究太阳倍数和储热时长对光热电站容量置信度和经济性的影响,并将光热电站的容量置信度和度电成本作为优化目标,建立多目标优化模型,探究太阳倍数和储热时长的最优配置及如何在获得较高容量置信度的条件下保证光热电站的经济性。
1 光热电站效率及经济性模型 1.1 塔式光热电站光-热-电转换效率模型光热电站主要有4种类型:槽式、塔式、碟式和线性菲涅尔式[9]。其中槽式和塔式技术比较成熟,已成功商业化运用,且塔式聚光比较大,工作介质温度较高,具有较高的太阳能光电转换效率,有较大的降低造价空间,适宜发展大容量和长时间储热的光热电站,符合未来的发展趋势。文中以熔盐塔式光热电站为例,进行建模分析。
熔盐塔式光热电站发电原理及组成如图 1所示,其大致可分为聚光集热系统、发电系统和储热系统[7]。文中针对3个系统建立简单的光-热-电转换效率模型。

|
图 1 熔盐塔式光热电站运行原理 Fig. 1 Operating principle of molten salt solar tower power station |
(1) 聚光集热系统。定日镜场是聚光集热系统的重要组成部分,由多块定日镜按一定的布置方式组成。定日镜反射太阳光到集热塔上的吸热器,其热功率为:
| $ P_{\text {solar }}(t)=I_{\mathrm{DNI}}(t) A \eta_{\text {solar }} $ | (1) |
式中:IDNI(t)为t时刻法向直射辐照度;A为定日镜场总集热面积;ηsolar为太阳光被定日镜反射到吸热器入口处的折算效率,与太阳到镜场过程中的定日镜场效率、余弦损失、遮挡损失、大气透射损失等有关[10]。吸热器吸收太阳能并传递给熔盐,熔盐吸收的热量为:
| $ P_{\text {HTF }}(t)=P_{\text {solar }}(t) \eta_{\text {receiver }} $ | (2) |
式中:PHTF(t)为t时刻熔盐吸收的热量;ηreceiver为吸热器吸收太阳辐射的总效率,与吸热器的热效率和热量损失(包括反射、辐射、对流和导热损失)有关[11—14]。
由式(1)和式(2)可知,集热面积越大,光热电站吸收的太阳能越多,原则上系统发电量就越高。但当集热面积过大,超出汽轮机组的热能需求上限时,就会造成资源浪费,同时极大地增加建设成本。因此,一个合适的集热面积对于光热电站的效益率十分重要[15]。一般采用太阳倍数表征集热面积的大小,指在设计法向直射辐照度下,聚光集热系统输出的热功率与汽轮机发电机组额定进口热功率之比,如式(3)所示。
| $ S_{\mathrm{M}}=\frac{P_{\mathrm{HTF}}}{P_{\text {power }}}=\frac{I_{\mathrm{DNI}} A \eta_{\text {solar }} \eta_{\text {receiver }}}{G_{\mathrm{CSP}} / \eta_{\text {power }}} $ | (3) |
式中:Ppower为进入汽轮机组的额定热功率;IDNI为设计点法向直射辐照度;GCSP为光热电站设计容量(汽轮机组额定输出功率);ηpower为汽轮机组热电转换效率。
由于设计法向直射辐照度是人为选定的,与大部分时间的直射辐照度并不相同,并且由于储热系统的存在,定日镜场的集热量不能仅满足汽轮机组的发电需求,所以SM的值一般大于1[16—17]。
(2) 储热系统。储热系统是光热电站的特点之一,储热容量的大小对光热电站运行的稳定性和经济性都具有重要影响。储热系统的存在不仅减少了热量的浪费,还能增加光热电站的运行小时数,但是储热系统也会增加光热电站的初始投资和运维费用。
储热系统在充、放热时会有一定的热量损失。储热系统的充、放热功率为:
| $ P_{\mathrm{st}, \mathrm{in}}(t)=P_{\mathrm{HTF}, \mathrm{in}}(t) \eta_{\mathrm{TES}, \text { in }} $ | (4) |
| $ P_{\mathrm{st}, \text { out }}(t)=\frac{P_{\mathrm{HTF}, \text { out }}(t)}{\eta_{\mathrm{TES}, \text { out }}} $ | (5) |
式中:Pst, in(t), Pst, out(t)分别为t时刻储热系统的充、放热量;PHTF, in(t), PHTF, out(t)分别为储热系统在t时刻内储存和释放的熔盐热量;ηTES, in,ηTES, out分别为储热系统充热损失率和放热损失率。
储热系统储存的热量为:
| $ E_{\mathrm{TES}}(t)=\eta_{\mathrm{TES}} E_{\mathrm{TES}}(t-1)+P_{\mathrm{st}, \text { in }}(t)-P_{\mathrm{st}, \text { out }}(t) $ | (6) |
式中:ETES(t)为t时刻储热系统储存的热量;ηTES为储热系统储热效率。
储热系统容量需满足约束为:
| $ \mu_{\mathrm{TES}} Q_{\mathrm{TES}} \leqslant E_{\mathrm{TES}}(t) \leqslant Q_{\mathrm{TES}} $ | (7) |
式中:QTES为储热系统最大储热容量;μTES为储热系统最低储热容量比。
一般采用储热时长TTES来表征储热容量的大小,指储热系统能储存的最大热量可以供汽轮机组在额定功率下运行的最长时间,如式(8)所示。
| $ T_{\mathrm{TES}}=\frac{Q_{\mathrm{TES}} \eta_{\mathrm{TES}, \text { out }}}{G_{\mathrm{CSP}} / \eta_{\text {power }}} $ | (8) |
(3) 发电系统。高温熔盐从熔盐罐出来后进入蒸汽发生器,与凝汽器冷凝水进行换热,产生高温、高压的水蒸气,推动汽轮机旋转做功发电。一般光热电站发电系统的热-电转换效率与负载水平呈非线性关系,但总体呈装机容量越大,转换效率越高的趋势[18]。
发电系统的实际发电功率为:
| $ \begin{gathered} P_{\mathrm{CSP}}(t)=\left(P_{\mathrm{HTF}}(t)+P_{\mathrm{HTF}, \text { out }}(t)-\right. \\ \left.P_{\mathrm{HTF}, \mathrm{in}}(t)-P_{\mathrm{ab}}(t)\right) \eta_{\text {power }} \end{gathered} $ | (9) |
式中:PCSP(t)为t时刻光热电站的实际发电功率;Pab(t)为t时刻舍弃的热量。
实际发电功率应满足约束为:
| $ \alpha_i \eta_{i, \mathrm{CSP}} G_{\mathrm{CSP}} \leqslant P_{\mathrm{CSP}}(t) \leqslant \alpha_i G_{\mathrm{CSP}} $ | (10) |
式中:αi为光热发电机组i的工作状态,αi=0代表停机状态,αi=1代表运行状态;ηi, CSP为光热发电机组i的最低出力比。
1.2 平准化度电成本光热电站的平准化度电成本(levelized cost of energy, LCOE)是光热电站在全寿命周期中满足一定资本金收益率条件下,能够保证收支平衡的最低上网电价,即电站每发1 kW ·h电所需要的投资成本,是投资决策时所需参考的重要数据[19—20],如式(11)所示,以下简称度电成本。
| $ {C_{{\rm{LCOE}}}} = \frac{{{C_{{\rm{con}}, y}} + \sum\limits_{y = 1}^Y {\frac{{{C_{{\rm{m}}, y}} + {C_{{\rm{other}}, {\rm{y}}}}}}{{{{(1 + r)}^{\;y}}}}} }}{{\sum\limits_{y = 1}^Y {\frac{{{E_y}}}{{{{(1 + r)}^{\;y}}}}} }} $ | (11) |
式中:Ccon, y为第y年的光热电站建设成本;Cm, y为第y年的电站运营维护成本;Cother, y为第y年的其他支出费用;Ey为电站第y年的发电量;r为给定贴现率;Y为光热电站全寿命周期时长。
2 计及容量置信度的光热电站储热容量优化方法 2.1 电力系统可靠性计算光热发电置信容量指在保持电力系统可靠性不变的前提下,光热电站接入某地区电网后,可代替该地区常规机组的装机容量。准确评估电力系统可靠性是计算置信容量的前提。
文中选择期望缺供电量(expected energy not supplied, EENS)作为电力系统可靠性指标,EENS是电力系统由于机组强迫停运而引起的电量不足期望值。对某已知停运容量状态,每小时不足电量等于不足的容量乘以此状态的概率,一年中EENS值为:
| $ R_{\mathrm{EENS}}=\sum\limits_{h=1}^n\left[X-\left(G_h-L_h\right)\right] P_h(X) $ | (12) |
式中: n为一年中所有小时数;Gh为第h小时的可用容量;Lh为第h小时的负荷;X为停运容量;Ph(X)为第h小时停运容量大于等于X的概率。
电力系统可靠性计算方法一般有解析法和蒙特卡洛方法[21—22]。文中采用基于状态-持续时间抽样的序贯蒙特卡洛方法计算EENS,该方法保留发电出力的时序状态,对机组的出力进行状态持续时间抽样。机组采用双状态模型(正常运行和故障状态),假设机组的故障率和修复率分别为ω和μ,平均无故障工作时间TMTTF和平均修复时间TMTTR分别为:
| $ T_{\mathrm{MTTF}}=1 / \omega $ | (13) |
| $ T_{\mathrm{MTTR}}=1 / \mu $ | (14) |
机组强迫停运率为:
| $ U=\frac{\omega}{\omega+\mu}=\frac{T_{\mathrm{MTTR}}}{T_{\mathrm{MTTR}}\;+T_{\mathrm{MTTF}}} $ | (15) |
一般工作时间和修复时间符合指数分布,故正常运行持续时间T1和检修时间T2为:
| $ T_1=-T_{\text {MTTF }} \ln \;\gamma $ | (16) |
| $ T_2=-T_{\mathrm{MTTR}} \ln \;\gamma $ | (17) |
式中:γ为服从[0, 1]区间内均匀分布的随机数。
蒙特卡洛方法计算精度的收敛判据一般选择方差系数β,其表达式为:
| $ \beta=\frac{\sqrt{V\left(\hat{R}_{\mathrm{EENS}}\right)}}{\hat{R}_{\mathrm{EENS}}}=\frac{\sqrt{V\left(f\left(\bar{X}_i\right)\right) / N}}{\hat{R}_{\mathrm{EENS}}} $ | (18) |
式中:
以发输电可靠性测试系统IEEE-RTS 79验证文中电力系统可靠性计算模型的准确性。文中使用基于状态-持续时间抽样的序贯蒙特卡洛方法,计算该测试系统的期望缺供电量EENS和缺电时间期望(loss of load expectation, LOLE),对比解析法“真实值”[23],如表 1所示,证实文中电力系统可靠性计算模型的准确性。
|
|
表 1 IEEE-RTS 79发电可靠性指标 Table 1 Generation reliability of IEEE-RTS 79 test system |
光热电站具有储热系统,可在无光照时利用储存的热量进行发电,因此可建造光热电站来代替常规火电机组以满足负荷需求。文中从规划的角度考虑,假定某地区现已有一定容量的常规机组,为满足逐渐增长的负荷需求,现考虑建立光热电站。光热电站的置信容量,即在保持电力系统可靠性不变的前提下,代替一定容量常规火电机组需要的光热电站装机。可靠性指标可表示为:
| $ R=f\left(G_{\text {now }}+G_{\text {con }}, L\right)=f\left(G_{\text {now }}+G_{\mathrm{CSP}}, L\right) $ | (19) |
式中:f(·)为可靠性评估函数;L为电力系统负荷;Gnow为现有常规机组装机容量;Gcon为能满足负荷增长需求的新增常规机组装机容量;GCSP为新增的光热发电装机容量。
光热电站的置信容量Gcc和容量置信度λ分别为:
| $ G_{\mathrm{cc}}=G_{\mathrm{con}} $ | (20) |
| $ \lambda=\frac{G_{\mathrm{con}}}{G_{\mathrm{CSP}}} \times 100 \% $ | (21) |
文中采用粒子群算法计算光热电站置信度,以光热电站的装机容量表示粒子的位置,适应度函数为加入光热电站并减少拟建设常规机组后的电力系统可靠性指标与原始系统的可靠性指标之差,根据适应度函数不断更新粒子位置,以使系统前后可靠性指标相等。
2.3 储热容量优化方法太阳倍数和储热时长决定不同光热电站出力及运行模式,也是影响光热电站置信度和经济性的关键参数。以光热电站置信度最大和度电成本最低为目标函数,建立光热电站储热系统配置双目标优化模型,如式(22)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {\max \;\lambda }\\ {\min \;{C_{{\rm{LCOE}}}}}\\ {{\rm{s}}{\rm{.t}}{\rm{. }}\quad 1.5 \le {S_{\rm{M}}} \le 3}\\ {\;\;\;\;\;\;\;\;\;4 \le {T_{{\rm{TES}}}} \le 12} \end{array}} \right. $ | (22) |
式中:TTES为储热时长。
将太阳倍数和储热时长在取值范围内参数化扫描,生成144组样本点,分别计算这144组样本的置信度和度电成本,基于这144组样本点的数据进行优化。
光热电站置信度和度电成本作为目标,是多目标优化问题,因此文中使用加权理想点法,引入权重函数,将双目标问题转换成单目标问题进行处理。即先计算出各目标在约束条件下的最优值,由这些最优值构成目标点,再根据实际情况与目标点的距离构成目标函数[24—25],目标函数F如式(23)所示。
| $ \begin{gathered} \min F\left(S_{\mathrm{M}}, T_{\mathrm{TES}}\right)= \\ \sqrt{w_1\left(\frac{\lambda\left(S_{\mathrm{M}}, T_{\mathrm{TES}}\right)-\lambda\left(S_{\mathrm{M}}^*, T_{\mathrm{TES}}^*\right)}{\lambda\left(S_{\mathrm{M}}^*, T_{\mathrm{TES}}^*\right)}\right)^2+} \\ \sqrt{w_2\left(\frac{C_{\mathrm{LCOE}}\left(S_{\mathrm{M}}, T_{\mathrm{TES}}\right)-C_{\mathrm{LCOE}}\left(S_{\mathrm{M}}^{* *}, T_{\mathrm{TES}}^{* *}\right)}{C_{\mathrm{LCOE}}\left(S_{\mathrm{M}}^{* *}, T_{\mathrm{TES}}^{* *}\right)}\right)^2} \end{gathered} $ | (23) |
式中:w1,w2分别为置信度和度电成本的权重值;λ(SM, TTES)为(SM, TTES)时的置信度;λ(SM*, TTES*)为光热电站在约束条件下的最大置信度;CLCOE(SM, TTES)为(SM, TTES)时的度电成本;CLCOE (SM**, TTES**)为光热电站在约束条件下的最小度电成本。
因为光热电站的置信度和度电成本这二者优化方向不同、目的不同,权重的确定有较大主观因素,故文中使用熵权法确定二者的权重。熵权法是一种客观赋权法,根据指标变异性的大小来确定客观权重[26]。首先对度电成本和置信度这2个指标的所有样本点数据进行标准化处理,接着计算2个指标的信息熵值,最后确定这2个指标的权重,代入目标函数中。信息熵可表示为:
| $ e_k=-\frac{1}{\ln M} \sum\limits_{m=1}^M \rho_{k m} \ln \rho_{k m} \quad k=1, 2, \cdots, K $ | (24) |
式中:ek为第k项指标的熵值;K为指标数;M为样本点数;rkm为第k项指标下第m个样本值占该指标的比重。
3 模型验证与分析 3.1 算例简介为响应国家“碳达峰”、“碳中和”的方针政策,文中从规划的角度出发,选择西北某地区作为主要的研究对象。基于现有的数据,假设其年最大负荷值为1.338 5×104 MW,初始系统的常规机组装机规模为9 000 MW,为方便计算,机组容量选择1 000 MW,600 MW和300 MW共3个级别,包括16台机组,其中1 000 MW机组3台,600 MW机组7台,300 MW机组6台,所有机组的强迫停运率参考《2020年上半年全国电力可靠性情况通报》。现需要规划装机4 400 MW常规机组,或建设一定容量的光热电站来代替这4 400 MW的常规机组。初始系统可靠性指标EENS为3.208×105 MW ·h。文中采用该地区典型年小时级光照资源数据,光照资源的波动性在其中充分体现。
3.2 光热电站储热容量优化(1) 置信度分析。不同储热时长和太阳倍数条件下,光热电站置信度的变化情况见图 2和图 3。

|
图 2 储热时长对置信度的影响 Fig. 2 Influence of thermal storage time on capacity credibility |
|
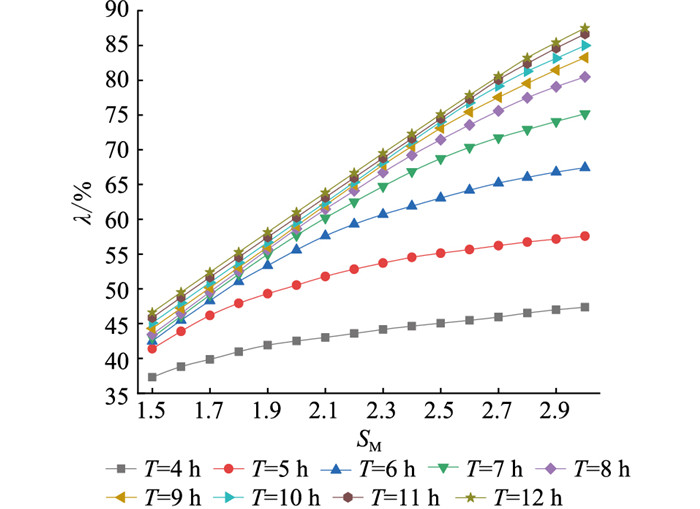
图 3 太阳倍数对置信度的影响 Fig. 3 Influence of solar multiple on capacity credibility |
由图 2和图 3中可知,置信度总体上随储热时长的增加而单调递增,趋势先快后慢,且太阳倍数越大,趋势越明显,这是因为太阳倍数越大,集热场吸收的太阳能越多。当储热容量较小时,不能充分储存这些能量,对光热电站置信度的提升影响较小;但当储热容量逐渐增大,可充分储存集热场吸收的热量,此时太阳倍数越大,对光热电站置信度的影响就越大。当太阳倍数和储热时长足够大,光热电站的置信度最高达88%,表示此时光热电站的容量价值与同等容量的常规火电机组差距不大。
增大太阳倍数(集热面积)和储热时长可以增加光热电站置信度,但以经济性为代价,因此需要结合度电成本对光热电站太阳倍数和储热时长进行优化配置。
(2) 度电成本分析。不同储热时长和太阳倍数条件下,光热电站度电成本的变化情况如图 4和图 5所示。
|
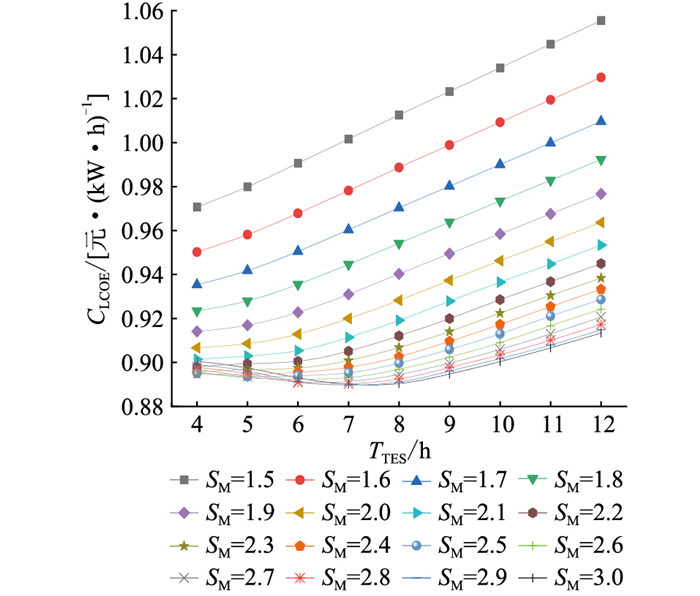
图 4 储热时长对度电成本的影响 Fig. 4 Influence of thermal storage time on LCOE |
|
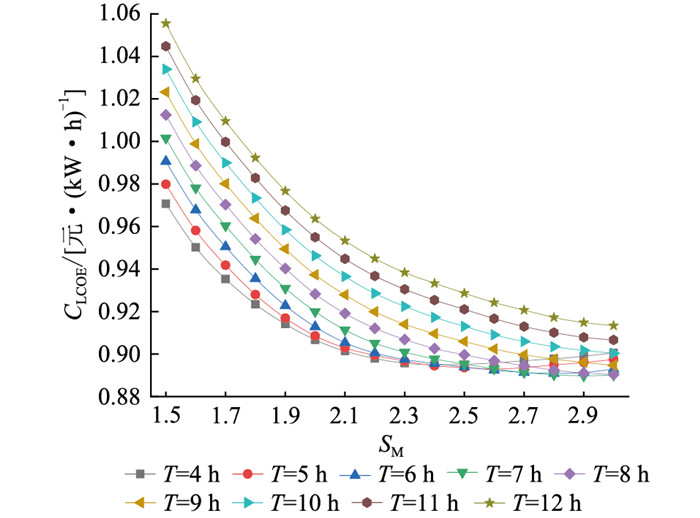
图 5 太阳倍数对度电成本的影响 Fig. 5 Influence of solar multiple on LCOE |
由图 4和图 5可知,当太阳倍数为1.5~2.3时,随着储热时长的增加,光热电站度电成本呈递增趋势;当太阳倍数为2.4~3.0时,度电成本先降低再上升。在储热时长为4~7 h时,度电成本随着太阳倍数的增加呈先降后升的态势;当储热时长在7~12 h时,度电成本随太阳倍数增加呈单调降低的态势。
根据度电成本的计算公式,发电量和投资成本对度电成本有较大影响。度电成本的变化本质上反映的是发电量和投资成本变化率的相对值。当太阳倍数较小时,储热系统带来的发电量增益不大,反而储热带来的成本更大,因此度电成本单调递增。但当太阳倍数足够大时,储热的功能充分发挥,带来的发电量增率更高,因此度电成本有下降的趋势。当储热时间过长时,又会因太阳倍数相对不足,发电量增率不如成本的增率,导致度电成本上升。
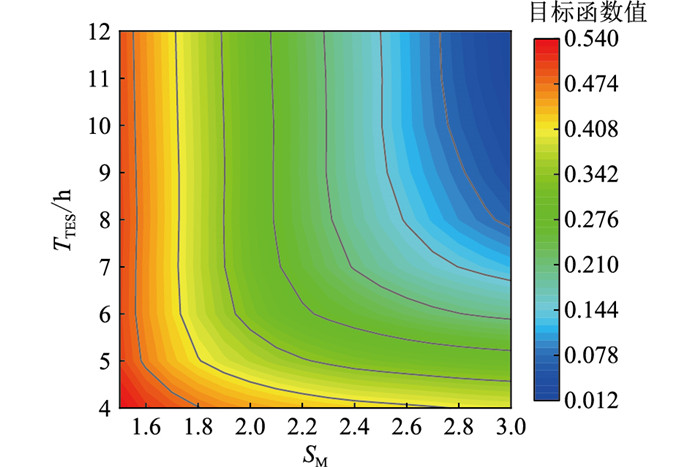
(3) 优化结果。文中使用熵权法确定光热电站置信度的权重为0.736 8,度电成本的权重为0.263 2。计算目标函数可得,当储热时长为12 h、太阳倍数为3.0时,目标函数F(SM, TTES)达到最小值,为0.013 6,即储热时长12 h,太阳倍数3.0为此约束下光热电站的最优配置,此时光热电站置信度为87.5%,度电成本为0.91元/(kW ·h),见图 6。
|
图 6 目标函数F分布 Fig. 6 Distribution of objective function F |
虽然光热电站的成本较风电、光伏高,但其清洁环保、调节性好、稳定性佳的特点是风电、光伏所不具备的,可作为火电的替代能源和调峰电源。随着工程技术的不断发展,光热电站组件成本不断降低,光热电站的经济性也会得到改善。
4 结论文中基于光热电站容量置信度和度电成本,提出一种光热电站太阳倍数和储热容量优化方法。以西北某地区光热电站规划为例,建立光热电站发电效率模型和经济性模型,以容量置信度和度电成本作为优化目标,使用加权理想点法建立目标函数,使用熵权法确定指标权重值,对太阳倍数和储热时长进行优化,结论如下:
(1) 采用熵权法确定光热电站置信度的权重为0.736 8,度电成本的权重为0.263 2,当太阳倍数为3.0,储热时长为12 h,目标函数值最低,为光热电站最优太阳倍数和储热时长,此时光热电站容量置信度为87.5%,度电成本为0.91元/(kW ·h)。相比于当前常见的储热时长7~8 h,更大的储热时长对光热电站的运行稳定性改善较为明显,更加符合未来光热电站的发展趋势。
(2) 光热电站容量置信度随太阳倍数和储热时长呈单调递增,且递增趋势由快变慢。增大太阳倍数可增加吸收的太阳能,但由于光热电站容量有限,故趋势逐渐变缓。增加储热时长,能够有效减少弃光量,然而太阳资源有限,其效果会逐渐降低。
(3) 随着太阳倍数和储热时长的变化,度电成本大体上呈先降后升的趋势,即存在一个最优太阳倍数和储热时长,使得度电成本最低。
在“双碳”目标下,构建以新能源为主体的新型电力系统,光热发电的容量价值等特性愈发重要,后续将对光热发电模型进行完善和细化。此外,文中优化方法中的算法参数和权重确定方法可以进一步改进。
| [1] |
谭笑, 王主丁, 李强, 等. 变电站容量和DG置信容量概率规划[J]. 电网技术, 2019, 43(7): 2267-2275. TAN Xiao, WANG Zhuding, LI Qiang, et al. Probabilistic planning of substation capacity and capacity credit of distribution generators[J]. Power System Technology, 2019, 43(7): 2267-2275. (  0) 0) |
| [2] |
徐志成. 光伏发电容量可信度评估[D]. 合肥: 合肥工业大学, 2017. XU Zhicheng. Capacity credit evaluation of photovoltaic (PV) power generation[D]. Hefei: Hefei University of Technology, 2017. (  0) 0) |
| [3] |
余志强, 王淳, 胡奕涛, 等. 并网光伏发电置信容量评估[J]. 电力系统保护与控制, 2016, 44(7): 122-127. YU Zhiqiang, WANG Chun, HU Yitao, et al. Capacity credit evaluation of grid-connected photovoltaic generation[J]. Power System Protection and Control, 2016, 44(7): 122-127. (  0) 0) |
| [4] |
ZHAO L, YU R Y, WANG Z, et al. Development modes analysis of renewable energy power generation in North Africa[J]. Global Energy Interconnection, 2020, 3(3): 237-246. DOI:10.1016/j.gloei.2020.07.005 (  0) 0) |
| [5] |
高嵩. 储热容量对槽式太阳能热发电的影响研究[J]. 华电技术, 2016, 38(9): 71-73, 80. GAO Song. Study on the influences of thermal storage capacity on solar parabolic trough thermal power generation[J]. Huadian Technology, 2016, 38(9): 71-73, 80. (  0) 0) |
| [6] |
赵明智, 张晓明, 宋士金, 等. 槽式太阳能热发电系统太阳倍数和蓄热时长的选取方法研究[J]. 太阳能, 2015(6): 50-54. ZHAO Mingzhi, ZHANG Xiaoming, SONG Shijin, et al. Study on the selection method of solar multiple and heat storage duration of trough solar thermal power generation system[J]. Solar Energy, 2015(6): 50-54. (  0) 0) |
| [7] |
毛维宙, 陆华军, 单宝奇. 塔式光热电站储热系统容量优化配置[J]. 电气技术, 2018, 19(11): 37-42, 54. MAO Weizhou, LU Huajun, SHAN Baoqi. Optimal allocation of thermal storage system capacity of solar power tower plant[J]. Electrical Engineering, 2018, 19(11): 37-42, 54. (  0) 0) |
| [8] |
罗彦, 杜小泽, 杨立军, 等. 塔式太阳能热发电太阳倍数及储热时长优化研究[J]. 热力发电, 2017, 46(6): 21-27. LUO Yan, DU Xiaoze, YANG Lijun, et al. Optimization design of solar multiple and thermal storage hour for DSG tower power generation[J]. Thermal Power Generation, 2017, 46(6): 21-27. (  0) 0) |
| [9] |
孙希强, 白杨. 太阳能光热发电技术现状极其关键设备存在问题分析[J]. 中国科技信息, 2017(23): 72-75. SUN Xiqiang, BAI Yang. Current status of solar thermal power generation technology and analysis of problems in key equipment[J]. China Science and Technology Information, 2017(23): 72-75. (  0) 0) |
| [10] |
房淼森, 逯静, 姜奕雯. 定日镜能量传输效率建模及镜场排布设计[J]. 太阳能学报, 2021, 42(1): 112-116. FANG Miaosen, LU Jing, JIANG Yiwen. Heliostat energy efficincy modeling and field layout design[J]. Acta Energiae Solaris Sinica, 2021, 42(1): 112-116. (  0) 0) |
| [11] |
李嘉宝, 王沛, 赵亮. 基于分布参数模型的塔式熔盐吸热器换热过程动态特性研究[J]. 可再生能源, 2018, 36(7): 991-996. LI Jiabao, WANG Pei, ZHAO Liang. Study on dynamic characteristics of heat exchange process of a tower type molten salt receiver based on distributed parameter model[J]. Renewable Energy Resources, 2018, 36(7): 991-996. (  0) 0) |
| [12] |
王沛, 李嘉宝, 赵亮, 等. 塔式太阳能熔盐吸热器传热特性及分析[J]. 中国电机工程学报, 2019, 39(12): 3605-3614. WANG Pei, LI Jiabao, ZHAO Liang, et al. Thermal and exergy performance of molten salt external cylindrical receiver of solar power towers[J]. Proceedings of the CSEE, 2019, 39(12): 3605-3614. (  0) 0) |
| [13] |
WANG K, LI M J, ZHANG Z D, et al. Evaluation of alternative eutectic salt as heat transfer fluid for solar power tower coupling a supercritical CO2 Brayton cycle from the viewpoint of system-level analysis[J]. Journal of Cleaner Production, 2021, 279: 123472. DOI:10.1016/j.jclepro.2020.123472 (  0) 0) |
| [14] |
AHMADI M H, GHAZVINI M, SADEGHZADEH M, et al. Solar power technology for electricity generation: a critical review[J]. Energy Science & Engineering, 2018, 6(5): 340-361. (  0) 0) |
| [15] |
MARUGÁN-CRUZ C, SERRANO D, GÓMEZ-HERNÁNDEZ J, et al. Solar multiple optimization of a DSG linear Fresnel power plant[J]. Energy Conversion and Management, 2019, 184: 571-580. DOI:10.1016/j.enconman.2019.01.054 (  0) 0) |
| [16] |
曹传胜. 塔式太阳能热发电站性能的影响因素研究[J]. 太阳能学报, 2020, 41(10): 223-228. CAO Chuansheng. Investigation of influence factors on performance of solar tower power station[J]. Acta Energiae Solaris Sinica, 2020, 41(10): 223-228. (  0) 0) |
| [17] |
李博, 孙即红, 郑韫哲. 塔式太阳能热发电站设计点DNI优化研究[J]. 电力勘测设计, 2019(11): 1-5, 21. LI Bo, SUN Jihong, ZHENG Yunzhe. Optimization of design point DNI of tower CSP plant[J]. Electric Power Survey & Design, 2019(11): 1-5, 21. (  0) 0) |
| [18] |
USAOLA J. Operation of concentrating solar power plants with storage in spot electricity markets[J]. IET Renewable Power Generation, 2012, 6(1): 59. DOI:10.1049/iet-rpg.2011.0178 (  0) 0) |
| [19] |
ZHAO L, WANG W, ZHU L Z, et al. Economic analysis of solar energy development in North Africa[J]. Global Energy Interconnection, 2018, 1(1): 53-62. (  0) 0) |
| [20] |
李心, 赵晓辉, 李江烨, 等. 塔式太阳能热发电全寿命周期成本电价分析[J]. 电力系统自动化, 2015, 39(7): 84-88. LI Xin, ZHAO Xiaohui, LI Jiangye, et al. Analysis of life-cycle levelized cost of electricity for tower solar thermal power[J]. Automation of Electric Power Systems, 2015, 39(7): 84-88. (  0) 0) |
| [21] |
何晔, 潘波, 余梦天, 等. 一种基于重要抽样--序贯蒙特卡洛的运行可靠性评估方法[J]. 电力科学与工程, 2019, 35(1): 24-29. HE Ye, PAN Bo, YU Mengtian, et al. Research on operational reliability evaluation method based on sequential Monte Carlo simulation of importance sampling[J]. Electric Power Science and Engineering, 2019, 35(1): 24-29. (  0) 0) |
| [22] |
耿莲. 大电网可靠性的快速蒙特卡洛仿真及风险分级评估研究[D]. 重庆: 重庆大学, 2019. GENG Lian. Research on fast Monte Carlo simulation methods and risk grade asssessment for composite power system reliability[D]. Chongqing: Chongqing University, 2019. (  0) 0) |
| [23] |
ALI KADHEM A, ABDUL WAHAB N I, ARIS I, et al. Computational techniques for assessing the reliability and sustainability of electrical power systems: a review[J]. Renewable and Sustainable Energy Reviews, 2017, 80: 1175-1186. DOI:10.1016/j.rser.2017.05.276 (  0) 0) |
| [24] |
梅凌骏. 基于理想点多属性决策算法的电力行业碳排放预测[D]. 南昌: 南昌大学, 2018. MEI Lingjun. Based on ideal point multiple attribute decision making algorithm for electric power industry carbon emission prediction[D]. Nanchang: Nanchang University, 2018. (  0) 0) |
| [25] |
杨伍梅, 刘陶文. 基于MATLAB的多目标规划问题的理想点法求解[J]. 湖南城市学院学报(自然科学版), 2017, 26(4): 60-63. YANG Wumei, LIU Taowen. Research on the ideal point method of multi-objective programming based on MATLAB[J]. Journal of Hunan City University (Natural Science), 2017, 26(4): 60-63. (  0) 0) |
| [26] |
赵殿平. 城市配电网运行水平和供电能力综合评价方法研究[D]. 吉林: 东北电力大学, 2018. ZHAO Dianping. Study on comprehensive evaluation method of urban distribution network operating level and power supply capability[D]. Jilin: Northeast Dianli University, 2018. (  0) 0) |
2. State Grid Gansu Electric Power Company, Lanzhou 730050, China;
3. College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, China
 2022, Vol. 41
2022, Vol. 41


 王湘艳(1980),女,博士,高级工程师,从事新能源发电规划工作(E-mail:
王湘艳(1980),女,博士,高级工程师,从事新能源发电规划工作(E-mail: