文章编号: 2096-3203(2022)05-0131-09 中图分类号: TM762
2. 电网安全与节能国家重点实验室(中国电力科学研究院有限公司), 北京 100089
目前可再生能源发电和调控技术逐步成熟,基于分布式发电的微电网技术也随之快速发展[1]。由于可再生能源发电存在不确定性[2],微电网需要配合储能系统消纳可再生能源发电带来的净负荷波动,并设计对应的控制策略,才能使微电网提供频率稳定的电能。而传统分布式电源控制采用的下垂控制技术无法在系统净负载变化的同时维持系统频率恒定,因此常采用分层控制结构的微电网满足频率控制的要求[3—4]。
下垂控制是目前关注度较高的一种对等控制策略[5—12],常作为分层控制中的第一层控制策略使用。在下垂控制中,微源逆变器的频率、电压分别与微电源输出的有功功率、无功功率成线性关系。当微电网净负载过大时,频率或电压的下降会超出微电网的允许范围,此时需要使用第二层控制使微电网的频率和电压快速恢复到允许范围内[13]。比例-积分-微分(proportional integral derivative,PID)控制具有原理简单、可靠性高、便于调整等特点,因此被广泛使用于工程中的频率控制。
文献[5]采用传统比例-积分(proportional integral,PI)控制,输入量为参考量与实际量的差值,通过比例积分计算得到校正量,并叠加到参考量上,但PI控制器参数固定,缺少在线自适应调节的能力,在微电网网络结构或者参数发生改变的情况下控制效果存在进一步优化的空间。为解决PI控制器参数适应性的问题,文献[6]提出了一种自适应PI控制器的直流微电网电压控制策略,根据直流母线电压误差的绝对值调节PI系数,实现最小化电压波动和电网电流谐波,但调节方法主观性较强,无法确保所得参数的最优性。目前不少研究者将智能算法与PI控制器结合,实现PI参数的自适应调节。文献[7]提出了使用模糊控制器和分数阶PID控制结合的方式,将模糊控制器的5个输出作为PID控制器参数的修正量,使PID控制器具有在线自适应调节的能力,且具备更优越的动态特性和鲁棒性能;文献[8—9]在PI控制器的基础上采用模糊推理方法整定PI参数,改善了动态响应,但多个模糊变量涉及更多隶属度函数的设计,且需要制定复杂的模糊规则表,难以产生针对各种微电网场景的通用控制方法。文献[10]提出了一种基于神经元自适应PI算法的微电网改进型主从控制策略,无须设计复杂的参数修正规则即可实现自适应调节,且证明了系统的稳定性。
文中将单神经元自适应PI控制算法作为微电网频率二次控制算法,使用模糊逻辑调整神经元比例系数,在线运行时能根据当前微电网的状态主动调节PI控制器参数,实现频率无偏差控制,并进行在线控制参数自适应优化,达到较好的控制效果。相比于上述已有的基于智能算法的PI控制,文中采用模糊控制自适应调节单一参数,规则设计更简单,计算调节更快,满足毫秒级的微电网频率控制需求,更适合运行于硬件受限的控制器环境中。
1 微电网频率恢复原理 1.1 下垂控制的原理及局限下垂控制[12]是微电网对等控制的一种,主要目的是在微源逆变器之间实现功率的合理分配。下垂控制的表达式为:
| $ \left\{\begin{array}{l} \omega=\omega^*-m_p\left(P^*-P\right) \\ E=E^*-n_q\left(Q^*-Q\right) \end{array}\right. $ | (1) |
式中:ω*为下垂控制器的参考频率;E*为下垂控制器的参考电压;P*为参考有功功率;Q*为参考无功功率;mp, nq分别为下垂控制器的有功-频率下垂系数和无功-电压下垂系数;ω, P, E, Q分别为微电源输出的频率、有功功率、电压和无功功率。
传统下垂控制在没有第二层控制参与的情况下,随着净负载增大频率会逐渐下降,进而偏移标准频率,这对微电网设备的安全和电能质量都会产生影响。为实现系统的频率无差控制,文中使用单神经元自适应PI控制来调节PI参数,并利用模糊逻辑在线调整其神经元比例系数。文中算法不仅具有神经元自适应的特点,还能根据微电网的状态实时调整参数的变动速率,提高系统经历冲击后重新达到稳定点的速度,在一定程度上克服了由微电网的非线性和不确定性带来的缺陷。
1.2 第二层频率恢复控制的原理如式(1)所示,在下垂控制下,输出频率主要与有功功率、所设定的参考功率、参考频率以及下垂系数相关。目前的研究通常从修改参考值ω*,P*[14]和修改下垂系数mp[15]两方面实现频率恢复控制。
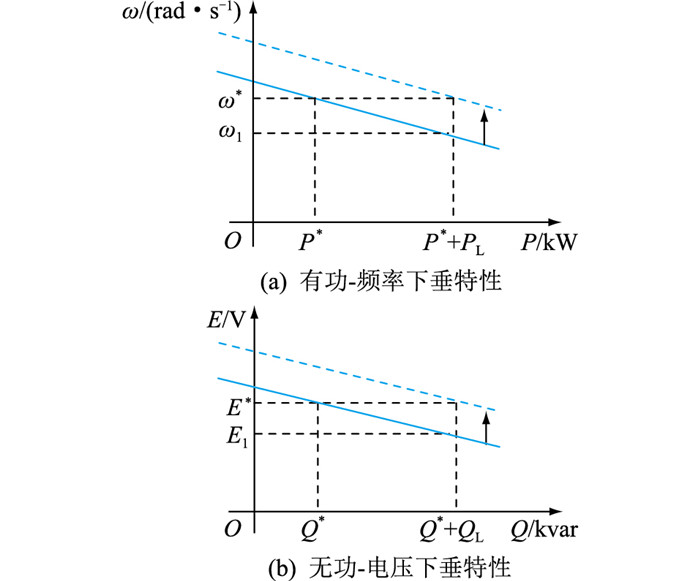
图 1展示了通过修改下垂控制参考值实现微电网二次控制的原理。当接入的负载或可再生能源发电量下降时,系统净负荷上升,逆变器的工作点随着发出功率的升高,在有功-频率下垂特性曲线上向右移动,进而使频率下降。当扰动特别剧烈时,所产生的频率偏差会超出微电网允许范围。文中通过微电网中央控制器(microgrid central controller, MGCC)采集逆变器输出节点的频率值和有功功率,经过MGCC内部的单神经元PI控制得到参考频率的校正量,并将其累加到参考频率上[5],调节下垂特性,使频率恢复到微电网运行时允许的频率范围内。以图 1(a)为例,假设微电网工作时的参考有功功率为P*,此时微电网逆变器输出的电压频率为ω*。当逆变器出力增加PL后,按照下垂特性曲线频率将下降为ω1,这时在下垂控制器的参考值ω*上增加MGCC中由控制算法计算出的校正量Δω,加入校正量之后的下垂特性曲线相比原始特性曲线会上移。在频率恢复控制的过程中不断调整校正量的大小,最终结果如图 1(a)中的蓝色虚线所示,下降后的频率恢复至参考值。当P,Q完全解耦时,无功-电压下垂特性也可以使用这样的方法调节,如图 1(b)所示。
|
图 1 MGCC对逆变器下垂特性的调节 Fig. 1 Modification of invert′s droop characteristic by MGCC |
在工业控制中,由于控制方式直观、鲁棒性好等优点,PID控制是最常见的控制手段[15]。但由于微电网存在难以注入附加扰动等限制,PID控制器的参数可能无法整定达到最优的状态。另外PID控制参数固定,而微电网中往往存在时变性和非线性的负载,随着微电网条件变化,传统PID控制方法可能无法保证控制参数的最优性。
研究者们注意到人工神经网络的自适应特征[16—17]能为PID参数自适应优化提供实现的途径,因此提出了将神经网络和PID控制器结合起来的方法。目前常见的基于多层神经网络控制的计算量较大,且对硬件的计算性能要求较高,难以满足微电网控制的实时性要求,显然不适用于微电网频率控制这种时间尺度短、控制器硬件性能(比如用嵌入式设备作为MGCC)可能受限的场景,因此文中使用单个神经元的控制方式解决上述问题。
传统PID控制的时域表达式为:
| $ u(t)=k_{\mathrm{p}}\left(e(t)+\frac{1}{T_{\mathrm{i}}} \int e(t) \mathrm{d} t+T_{\mathrm{d}} \frac{\mathrm{d} e(t)}{\mathrm{d} t}\right) $ | (2) |
式中:kp为控制器的比例系数;Ti,Td分别为积分时间常数和微分时间常数;e(t)为微电网标准频率(一般设为50 Hz)与逆变器输出频率之差;u(t)为控制器的控制量输出,即下垂控制参考频率的校正量。在数字控制器中,当采样周期Ts较短时,式(2)转变为增量式PID控制器的离散方程:
| $ \begin{gathered} \Delta u(t)=k_{\mathrm{p}}\left(\Delta e(t)+\frac{T_{\mathrm{s}}}{T_{\mathrm{i}}} e(t)+\frac{T_{\mathrm{d}}}{T_{\mathrm{s}}} \Delta^2 e(t)\right)= \\ k_{\mathrm{p}} \Delta e(t)+k_{\mathrm{i}} e(t)+k_{\mathrm{d}} \Delta^2 e(t) \end{gathered} $ | (3) |
式中:ki,kd分别为控制器的积分、微分系数;Δ为差分;Δ2为差分的平方。
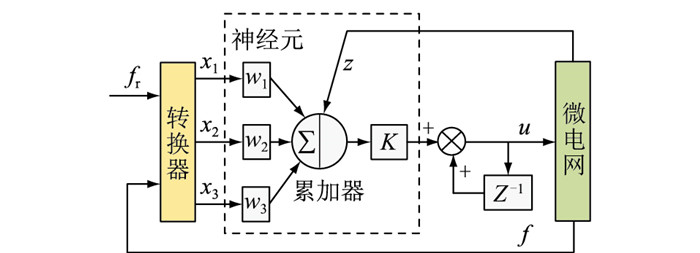
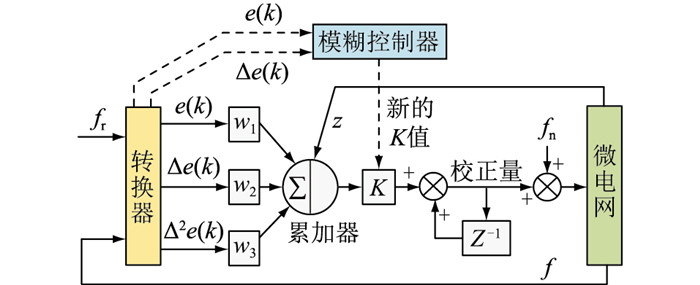
在传统PID控制的基础上,结合单神经元在线调整控制参数的特性,形成具有自适应调节能力的单神经元PID控制器。其系统框图主要包含转换器、神经元和累加器,如图 2所示,Z-1为单位延迟环节。其中转换器的作用是将采集到的实际值转换为需要的差分量,神经元通过权重进行增量式PID控制计算,累加器输出控制量。
|
图 2 单神经元自适应PID控制系统 Fig. 2 Single neuron adaptive PID controller system |
假设微电网设定频率为fr,逆变器输出端频率为f,输入转换器计算后得到控制所需的状态量xi(i=1, 2, 3),其中:
| $ \left\{\begin{array}{l} x_1(t)=e(t)=f_{\mathrm{r}}-f(t) \\ x_2(t)=\Delta e(t)=e(t)-e(t-1) \\ x_3(t)=\Delta^2 e(t)=e(t)-2 e(t-1)+e(t-2) \end{array}\right. $ | (4) |
选取性能指标为z(t)=e(t);wi(t)(i=1, 2, 3)为xi(t)在求和中的权重。在离散控制系统中,根据式(3)控制器最终产生的控制信号为:
| $ u(k)=u(k-1)+K \sum\limits_{i=1}^3 w_i(k) x_i(k) $ | (5) |
式中:K为神经元比例系数,K>0;k为迭代次数。
2.2 权重学习方法文中对权重wi(k)(i=1, 2, 3)的调整采用有监督的Hebb学习规则,即:
| $ \left\{\begin{array}{l} w_i(k+1)=(1-c) w_i(k)+\eta p_i(k) \\ p_i(k)=z(k) u(k) x_i(k) \end{array}\right. $ | (6) |
式中:pi为在控制过程中衰减的变量,当频率与参考值相等时pi=0,被称为递进信号;η为学习速率;c为表示权重惯性的常数;z(k)为性能指标,此处选取z(k)=x1(k)。为保证上述学习算法的收敛性,对权重wi(k)进行规范化处理:
| $ \left\{ {\begin{array}{*{20}{l}} {w_i^\prime (k) = {w_i}(k)/\sum\limits_{j = 1}^3 {\left| {{w_j}(k)} \right|} }\\ {u(k) = u(k - 1) + K\sum\limits_{i = 1}^3 {w_i^\prime } (k){x_i}(k)} \end{array}} \right. $ | (7) |
式中:w′i(k)为规范化处理过后的权重。根据文献[18—19],通常认为wi(k)的在线调节主要与实时频率偏差e(t)和偏差的差分量Δe(t)有关系,离散采样结果分别为e(k)和Δe(k),因此将式(6)递进信号表达式中的xi(k)替换为x1(k)+x2(k),以实现进一步的简化。
| $ \left\{\begin{array}{l} w_1(k+1)=w_1(k)+\eta_{\mathrm{i}} e(k) u(k)\left(x_1(k)+x_2(k)\right) \\ w_2(k+1)=w_2(k)+\eta_{\mathrm{p}} e(k) u(k)\left(x_1(k)+x_2(k)\right) \\ w_3(k+1)=w_3(k)+\eta_{\mathrm{d}} e(k) u(k)\left(x_1(k)+x_2(k)\right) \end{array}\right. $ | (8) |
式中:ηi,ηp,ηd分别为积分、比例和微分系数的学习速率。
在电力系统领域考虑到工业运用的要求,由于存在噪声,通常不使用微分运算,而使用PI控制,文中设计的控制系统中将微分系数的权重和学习速率均设置为0,即消除微分对输出控制量的影响。
3 基于模糊逻辑的神经元比例系数优化 3.1 神经元比例系数的作用从式(5)、式(6)中看出,该神经元PI控制系统中实际的PI参数为:
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{\rm{i}}} = K{w_1}(k)/\sum\limits_{i = 1}^3 {\left| {{w_i}(k)} \right|} }\\ {{k_{\rm{p}}} = K{w_2}(k)/\sum\limits_{i = 1}^3 {\left| {{w_i}(k)} \right|} } \end{array}} \right. $ | (9) |
神经元比例系数K通常被认为是神经元PI控制器中最敏感的参数[20—23]。由式(9)可见,K能直接影响控制器的积分系数和比例系数,从而影响控制器的控制效果。不难发现,K取值过大可能导致超调增大甚至失控;K取值过小会导致被控对象跟随的速率下降。K的不同取值体现了PI控制参数变化的特性,直接影响到控制效果,因此为进一步实现参数优化可从选取合适的K值入手,且根据被控对象的状态实时调节控制速率。
3.2 模糊控制模糊控制策略在一定程度上能克服被控系统的非线性和不确定性[22],文中使用模糊控制器[23]来实现K值的在线调整。模糊控制策略输入为参考频率与逆变器输出端频率的偏差e和偏差的差分量Δe,输出为K值。
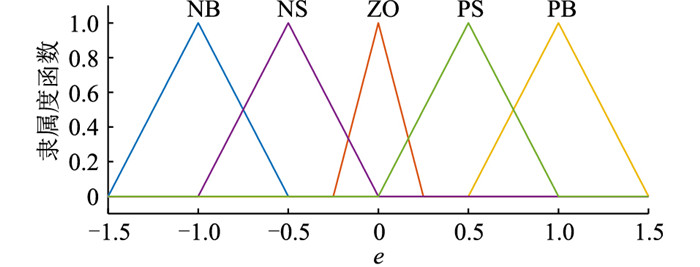
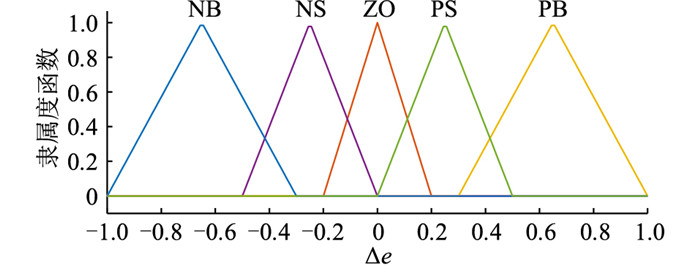
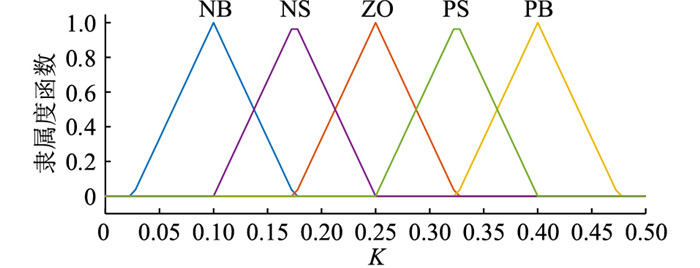
模糊控制器由隶属度函数和模糊规则表构成,隶属度函数用以描述变量对模糊集的隶属关系,模糊规则表则是进行模糊推理和控制的基础。隶属度函数的确定具有一定的主观性,事实上不存在一个统一的用来确定隶属度函数的方法,通常隶属度函数的确定需要把握几个原则:符合实际、单峰性、不存在重合的极大值点、论域内任意一点至多处于2个不为0的模糊子集的隶属度函数中等等。根据微电网正常运行时对频率的要求(±0.5 Hz)以及仿真结果调整隶属度函数,最终确定e,Δe,K的隶属度函数具体形状和参数。文中采用三角形隶属度函数,如图 3—图 5所示。
|
图 3 e的隶属度函数 Fig. 3 Membership function of variable e |
|
图 4 Δe的隶属度函数 Fig. 4 Membership function of variable Δe |
|
图 5 K的隶属度函数 Fig. 5 Membership function of variable K |
当频率出现较大偏差且增量较大时,适当提高神经元比例系数K,能快速达到稳定状态;当频率出现较小偏差且增量较小时,适当降低神经元比例系数K,维持系统稳定。按照此逻辑确定模糊规则表,如表 1所示,其中NB、NS、ZO、PS、PB为模糊集合的标识,用来表征变量的隶属度关系,分别表示负大、负小、零、正小、正大。
|
|
表 1 模糊控制器中采用的模糊规则表 Table 1 Fuzzy control-rule table of the proposed fuzzy controller |
文中使用“最大—最小”的方法进行模糊逻辑推理,解模糊的方法为重心法。
3.3 模糊神经元控制器系统结合模糊逻辑和神经元PID控制形成模糊神经元PID控制器,该控制器能够实现PID参数和神经比例系数的在线调节。控制器实现微电网频率恢复控制的系统流程如图 6所示。
|
图 6 微电网频率恢复控制的系统流程 Fig. 6 Flow chart of microgrid frequency recovery control |
由图 6可知,微电网频率控制流程为:
(1) 控制器采集逆变器输出端频率送入转换器中,转换器计算得到控制所需的状态量e(k),Δe(k)和Δ2e(k)。
(2) 状态量e(k),Δe(k)进入模糊控制器,经过模糊化、模糊推理和解模糊后得到输出量K,将K作为神经元比例系数。
(3) 神经元模型按照权重对状态量加权,并通过累加器求和,得到神经元模型输出,并得到式(5)所计算的控制信号。
(4) 神经元模型按照式(8)修正自身权重。
(5) 将步骤(3)中得到的控制信号作为频率校正量输入下垂控制层,修正频率参考值fn实现频率恢复控制。
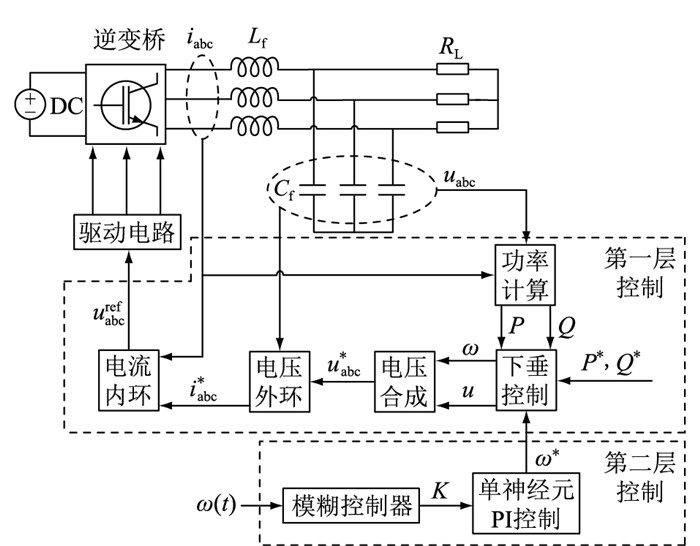
4 仿真实验 4.1 微电网模型在Simulink环境中搭建微电网模型,微电网采用分层控制结构,主控层并网逆变器采用下垂控制策略,下垂控制器中包括PQ计算、dq变换环、参考电压计算环和电压电流双环控制[24—26]。包含第二层控制的总控制流程如图 7所示,其中iabc为逆变器输出电流;uabc为分布式发电输出端电压;uabc*为下垂控制计算后合成的参考电压;i* abc为电压外环输出,作为电流内环的输入参考电流;uabcref为电流内环输出,作为驱动电路调制波输入;Lf,Cf为LC滤波器参数;RL为等效负荷。
|
图 7 下垂控制总流程 Fig. 7 Total flow chart of droop control |
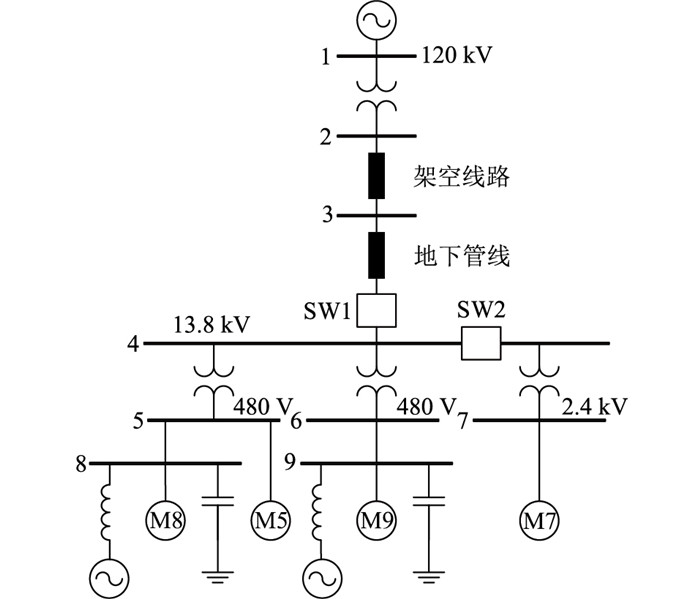
以CERTS推荐的微电网模型为基础进行仿真实验。CERTS给出了一种9节点的微电网模型,如图 8所示。该微电网中120 kV线路通过13.8 kV馈线向负载提供能源,系统包含3条主要馈线:2条为480 V,1条为2.4 kV。
|
图 8 CERTS推荐的微电网模型 Fig. 8 Recommended microgrid system by CERTS |
为便于检验文中所提方法的有效性,只考虑有功负载对频率的影响,将原算例中的电动机负载M5、M7、M8、M9均简化为0.4 MW有功负载,节点8和9分别接入采用传统下垂控制的分布式电源DG1和DG2。DG1、DG2直流电压均为1 500 V;滤波器参数Lf,Cf分别为0.6×10-3 H, 1.5×10-3 C;DG1、DG2本地负载为1 kW。开关SW1断开,微电网孤岛运行。
分层控制结构中第二层控制由MGCC实现,控制层参数如表 2所示。
|
|
表 2 控制层参数 Table 2 Control layer parameters |
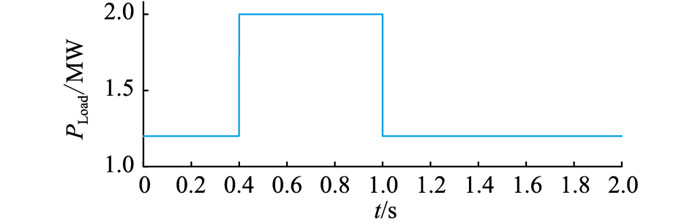
为便于观察下垂控制和频率二次恢复控制的效果,将负载M7设定为0.8 MW有功负载,仿真开始时刻SW2断开,0.4 s时闭合SW2,将负载M7接入微电网;仿真运行1.0 s后将其切除,微电网内总有功负载变化如图 9所示。
|
图 9 微电网总有功负载变化曲线 Fig. 9 Curve of total active load in microgird |
通过多次仿真实验整定PI控制器的参数,发现比例系数设置为0.01、积分系数设置为15时,PI控制器能达到较优的控制效果,传统PI控制器保持该参数不变。固定神经元比例系数的单神经元PI控制将K设定为0.15,超过该值可能导致系统频率无法稳定。
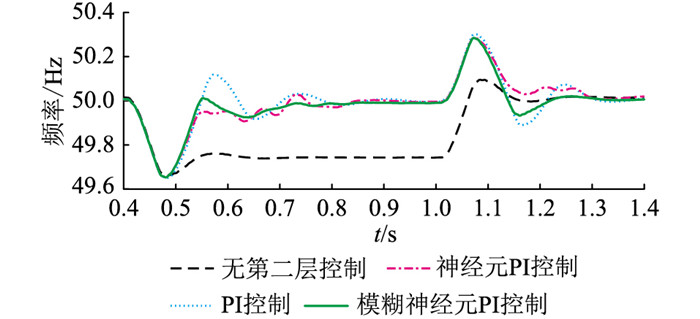
根据下垂控制理论计算,接入负载后将对微电网母线频率造成约0.3 Hz的频率跌落。分别在无二次频率控制、基于PI的二次频率控制、基于神经元PI的二次频率控制(固定K为0.15)和模糊神经元PI控制下进行仿真。仿真结果如图 10—图 13所示。
|
图 10 DG1输出端频率曲线 Fig. 10 Dynamic frequency curves of DG1 |
|
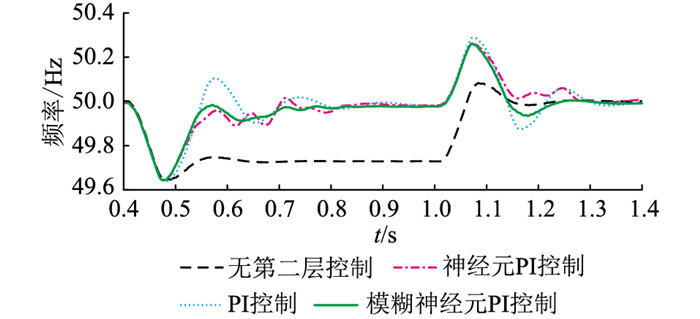
图 11 DG2输出端频率曲线 Fig. 11 Dynamic frequency curves of DG2 |
|
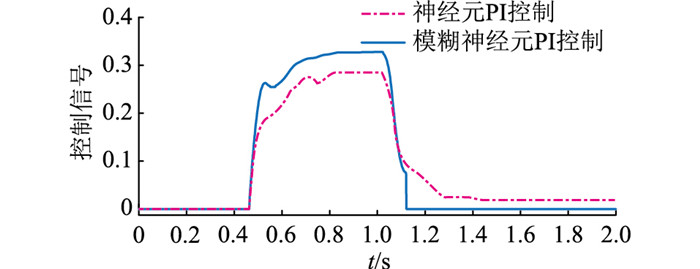
图 12 DG1控制信号变化曲线 Fig. 12 Dynamic control signal curves of DG1 |
|
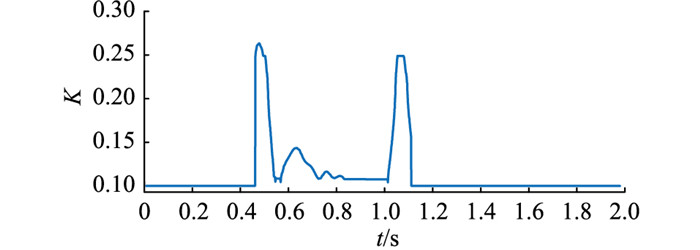
图 13 神经元比例系数K变化曲线 Fig. 13 Neuron proportionality cofficient K values curve |
由图 10、图 11可知,在无第二层控制的情况下,微电网接入负载后频率降低至49.74 Hz左右,此时已经出现了严重的频率偏差。存在第二层控制的情况下,微源控制器对下垂控制参考值进行修正,分布式电源出力增加,进而使输出端频率能够回升到正常水平。以DG1频率变化曲线为例,分析3种频率控制算法在实现频率恢复过程中的性能指标,结果如表 3所示。
|
|
表 3 3种频率恢复算法性能对比 Table 3 Performance comparison of three frequency recovery algorithms |
由表 3可以得出,在文中所设置的仿真环境下,神经元PI控制和PI控制使系统达到稳定所需的调节时间相近,神经元PI控制能有效降低频率的超调量,而模糊神经元PI控制在启动调节时间和超调量上对比前2种算法都有明显的优势。
由图 12、图 13可知,频率控制策略启动后,模糊神经元PI控制输出的控制量迅速增加,在系统逐渐进入稳定状态后,控制量的增量下降,控制量维持平稳。在频率发生波动时,模糊控制器会输出较大的K值,使频率能快速恢复;频率波动降低后,模糊控制器输出的K值下降,提高了系统的稳定性。
从仿真对比结果看出,文中所提控制方法相比于传统PI控制和固定比例系数的单神经元自适应PI控制具有更好的暂态性能,能更快地追踪频率参考信号、抑制频率超调,维持微电网系统的稳定,完成微电网频率的恢复控制。
4.3 2 MW负载扰动仿真测试4.2节仿真结果表明,在一般功率负载接入和切除时,文中所使用的策略能够实现微电网系统频率和电压的快速恢复。为进一步验证微电网系统在遭受大功率扰动下的稳定性,采用2 MW负载投切进行测试。
在4.2节其他条件不变的情况下,将0.8 MW的负载改为2 MW的大有功扰动,接入时间不变,仍为0.4~1.0 s。负载接入后按照下垂控制理论计算,频率将发生约0.9 Hz下降,已经超出系统允许范围。分别在无第二层控制、PI控制、固定K为0.15的神经元PI控制和模糊神经元PI控制下进行仿真,仿真结果如图 14—图 17所示。
|
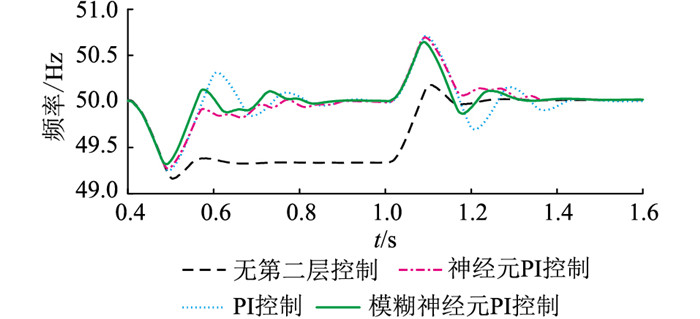
图 14 大负载扰动下DG1输出端频率曲线 Fig. 14 Dynamic frequency curves of DG1 under large load disturbance |
|
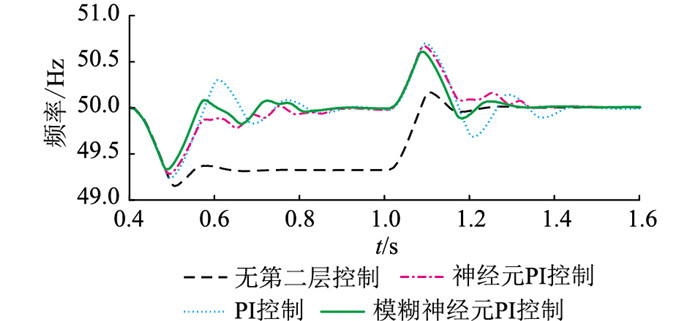
图 15 大负载扰动下DG2输出端频率曲线 Fig. 15 Dynamic frequency curves of DG2 under large load disturbance |
|
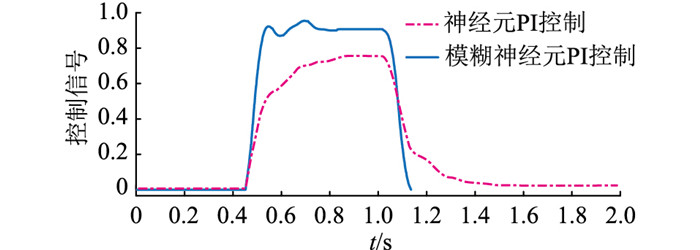
图 16 大负载扰动下DG1控制信号变化曲线 Fig. 16 Dynamic control signal curves of DG1 under large load disturbance |
|
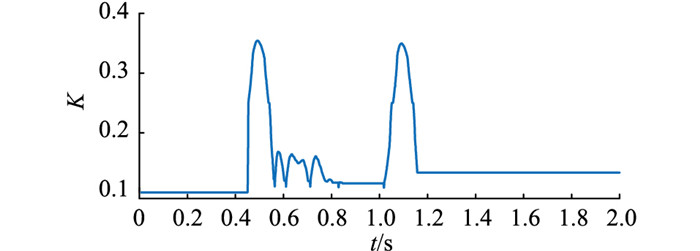
图 17 大负载扰动下神经元比例系数K变化曲线 Fig. 17 Neuron proportionality cofficient K values curve under large load disturbance |
观察图 14、图 15可知,在无第二层控制的情况下,接入2 MW的有功负载会使系统频率下降约0.6 Hz,这是因为仿真中使用的不是恒功率负载,频率下降导致仿真中实际负载低于2 MW,因此与下垂控制计算出的频率偏差不一致。3种频率恢复算法在接入大扰动时性能都有明显下降,体现为调节时间增加,超调量增加。2 MW负载扰动下3种频率控制算法的性能对比如表 4所示。
|
|
表 4 大负载扰动下3种频率恢复算法对比 Table 4 Performance comparison of three frequency recovery algorithms under large load disturbance |
结合表 4和图 16可知,由于神经元PI控制算法的神经元比例系数K固定为0.15,与使用模糊控制器的算法相比控制量增长的速率较慢。图 17展示了使用模糊神经元PI控制算法进行仿真时,神经元比例系数的变化情况。图 13中K的极值为0.26左右,而接入2 MW功率扰动后,K增大为0.35左右,说明模糊控制器能根据扰动大小灵活调整神经元比例系数输出的值,扰动越大,调整时神经元比例系数的值越大;而频率趋于稳定后,模糊控制器将神经元比例系数的值缩小,维持系统稳定。
5 结语在微电网中,电压频率是影响微电网电能质量和负载安全的重要因素,文中建立了基于分层控制结构的微电网仿真模型,在主控层中采用下垂控制策略来实现功率均分。当微电网中的有功负载持续增大时,频率下降有可能超出允许范围,此时MGCC启动基于模糊神经元PI控制算法的二次频率恢复控制,实现频率无差调节。
文中将单神经元自适应PI控制算法作为频率恢复控制的算法,并且使用了模糊控制策略在线优化神经元比例系数K,这一方法相比于固定神经元比例系数的单神经元自适应PI控制具有更好的控制效果,特别是根据频率与标准值的偏差和变化率进行的自适应调节。在扰动影响大时,模糊控制策略给出较大的比例系数用于快速恢复频率;扰动影响减弱时,模糊控制器缩小比例系数的值用于减少频率振荡,缩短系统达到稳定的时间。这一特性对于增强控制系统的鲁棒性有较大帮助,能在一定程度上克服微电网系统的非线性和不确定性,在维持微电网系统稳定的情况下缩短微电网频率恢复的时间。
本文得到电网安全与节能国家重点实验室开放基金(No.YDB51202001923)资助,谨此致谢!
| [1] |
雷艾虎. 低压微电网电压频率分层控制策略研究[D]. 兰州: 兰州理工大学, 2018. LEI Aihu. Research on voltage and frequency hierarchical control strategy of low-voltage microgrid[D]. Lanzhou: Lanzhou University of Technology, 2018. (  0) 0) |
| [2] |
胡迪, 丁明, 毕锐, 等. 光伏和风电互补性对高渗透率可再生能源集群接入规划影响分析[J]. 中国电机工程学报, 2020, 40(3): 821-836. HU Di, DING Ming, BI Rui, et al. Impact analysis of PV and WT complementarity on access planning of high penetrated renewable energy cluster[J]. Proceedings of the CSEE, 2020, 40(3): 821-836. (  0) 0) |
| [3] |
董密, 李力, 粟梅, 等. 微电网经济运行的分布式二次电压-频率恢复控制[J]. 控制理论与应用, 2019, 36(3): 461-472. DONG Mi, LI Li, SU Mei, et al. Distributed secondary voltage-frequency recovery control algorithm for economic operation of microgrid[J]. Control Theory & Applications, 2019, 36(3): 461-472. (  0) 0) |
| [4] |
周烨, 汪可友, 李国杰, 等. 基于多智能体一致性算法的微电网分布式分层控制策略[J]. 电力系统自动化, 2017, 41(11): 142-149. ZHOU Ye, WANG Keyou, LI Guojie, et al. Distributed hierarchical control for microgrid based on multi-agent consensus algorithm[J]. Automation of Electric Power Systems, 2017, 41(11): 142-149. DOI:10.7500/AEPS20160920004 (  0) 0) |
| [5] |
谭清. 基于分层控制微网平滑切换方法研究[D]. 沈阳: 沈阳工业大学, 2018. TAN Qing. Research on smooth switching method based on hierarchical control micro-grid[D]. Shenyang: Shenyang University of Technology, 2018. (  0) 0) |
| [6] |
吴小涛, 谭超, 王国博. 基于自适应PI控制器的直流微电网电压控制策略研究[J]. 华电技术, 2021, 43(9): 14-22. WU Xiaotao, TAN Chao, WANG Guobo. Voltage control strategy for DC microgrid based on adaptive PI controller[J]. Huadian Technology, 2021, 43(9): 14-22. DOI:10.3969/j.issn.1674-1951.2021.09.002 (  0) 0) |
| [7] |
项雷军, 陈昊, 郭新华, 等. 基于模糊分数阶PID的含电动汽车的多能源微电网二次频率控制[J]. 电力自动化设备, 2021, 41(11): 74-80. XIANG Leijun, CHEN Hao, GUO Xinhua, et al. Secondary frequency control of multi-energy microgrid with electric vehicles based on fuzzy fractional-order PID[J]. Electric Power Automation Equipment, 2021, 41(11): 74-80. (  0) 0) |
| [8] |
张梦瑶, 王鑫, 张昕, 等. 基于灵敏度分析的改进微电网下垂控制方法[J]. 电测与仪表, 2019, 56(7): 119-125. ZHANG Mengyao, WANG Xin, ZHANG Xin, et al. The improved droop control method of micro-grid based on sensitivity analysis[J]. Electrical Measurement & Instrumentation, 2019, 56(7): 119-125. (  0) 0) |
| [9] |
吴宇奇, 叶雨晴, 马啸, 等. 下垂控制型微电网孤岛检测盲区通用性求解方法[J]. 电力系统自动化, 2021, 45(10): 106-114. WU Yuqi, YE Yuqing, MA Xiao, et al. General solution method for non-detection zone of droop-controlled islanding detection in microgrid[J]. Automation of Electric Power Systems, 2021, 45(10): 106-114. DOI:10.7500/AEPS20201103008 (  0) 0) |
| [10] |
何浩宇, 赵毅君, 黄美. 孤岛微网模糊PI下垂控制仿真研究[J]. 湖南工程学院学报(自然科学版), 2020, 30(2): 13-19. HE Haoyu, ZHAO Yijun, HUANG Mei. Simulation research on fuzzy PI droop control of island microgrid[J]. Journal of Hunan Institute of Engineering (Natural Science Edition), 2020, 30(2): 13-19. DOI:10.3969/j.issn.1671-119X.2020.02.003 (  0) 0) |
| [11] |
彭明智, 杜鹏, 朱仲贤. 基于神经元自适应PI算法的微电网控制策略研究[J]. 电子测量技术, 2020, 43(1): 80-84. PENG Mingzhi, DU Peng, ZHU Zhongxian. Research on microgrid control strategy based on neuron adaptive PI algorithm[J]. Electronic Measurement Technology, 2020, 43(1): 80-84. (  0) 0) |
| [12] |
张强. 微电网运行模式分析及孤岛检测的研究[D]. 淮南: 安徽理工大学, 2018. ZHANG Qiang. Analysis of operation modes of microgrids and study of islanding detection[D]. Huainan: Anhui University of Science & Technology, 2018. (  0) 0) |
| [13] |
于国星, 侯睿, 汪任潇, 等. 孤岛微网分层分布式频率调节及功率优化控制[J]. 电力系统自动化, 2020, 44(7): 53-60. YU Guoxing, HOU Rui, WANG Renxiao, et al. Hierarchical distributed frequency regulation and power optimization control for islanded microgrid[J]. Automation of Electric Power Systems, 2020, 44(7): 53-60. (  0) 0) |
| [14] |
李燕青, 郭通, 袁燕舞. 基于改进下垂控制的微电网有功与频率控制策略[J]. 电测与仪表, 2017, 54(12): 60-64. LI Yanqing, GUO Tong, YUAN Yanwu. Active and frequency control strategy of micro-grid based on improved droop control[J]. Electrical Measurement & Instrumentation, 2017, 54(12): 60-64. DOI:10.3969/j.issn.1001-1390.2017.12.010 (  0) 0) |
| [15] |
陆善婷, 吉明明, 程军照. 适用于微网的电压频率无偏差下垂控制方法[J]. 电气传动, 2019, 49(3): 78-82. LU Shanting, JI Mingming, CHENG Junzhao. Droop control method without frequency and voltage deviation for microgrid[J]. Electric Drive, 2019, 49(3): 78-82. (  0) 0) |
| [16] |
胡苏南, 施永, 王新颖. 基于数据驱动的孤岛微网自适应调频策略[J]. 电源学报, 2020, 18(6): 5-11. HU Sunan, SHI Yong, WANG Xinying. Adaptive frequency regulation strategy for islanded microgrid based on data driven method[J]. Journal of Power Supply, 2020, 18(6): 5-11. (  0) 0) |
| [17] |
时光远, 王云飞, 姜世公, 等. 基于融合模糊识别和人工神经网络的交直流配电系统发展阶段评估研究[J]. 供用电, 2020, 37(5): 11-17. SHI Guangyuan, WANG Yunfei, JIANG Shigong, et al. Research on developmental stage evaluation of AC/DC distribution system based on fuzzy recognition and artificial neural network[J]. Distribution & Utilization, 2020, 37(5): 11-17. (  0) 0) |
| [18] |
ABDEL GHANY M A, SHAMSELDIN M A, ABDEL GHANY A M. A novel fuzzy self tuning technique of single neuron PID controller for brushless DC motor[J]. International Journal of Power Electronics and Drive Systems (IJPEDS), 2017, 8(4): 1705. DOI:10.11591/ijpeds.v8.i4.pp1705-1713 (  0) 0) |
| [19] |
WANG W, BAI Z M. Performance analysis of an improved single neuron adaptive PID control[C]//2010 Third International Symposium on Intelligent Information Technology and Security Informatics. Jian, China. IEEE, 2010: 22-25.
(  0) 0) |
| [20] |
吴亚平, 姚海滨. 单神经元PID在火花激发光源系统中的应用[J]. 扬州职业大学学报, 2018, 22(3): 30-33. WU Yaping, YAO Haibin. The application of single neuron PID to spark excitation light-source system[J]. Journal of Yangzhou Polytechnic College, 2018, 22(3): 30-33. (  0) 0) |
| [21] |
CHEN X J, QIU H D. Research on single neuron adaptive PID controller[J]. Applied Mechanics and Materials, 2014, 651-653: 826-830. DOI:10.4028/www.scientific.net/AMM.651-653.826 (  0) 0) |
| [22] |
金昊, 白国振, 朱灵康, 等. 磁粉制动器的模糊神经元PID控制[J]. 电子科技, 2017, 30(7): 40-43. JIN Hao, BAI Guozhen, ZHU Lingkang, et al. Fuzzy neural PID control of the magnetic particle brake[J]. Electronic Science and Technology, 2017, 30(7): 40-43. (  0) 0) |
| [23] |
徐娟, 贾志远, 张建军, 等. 基于改进单神经元PID的转子动平衡控制方法[J]. 合肥工业大学学报(自然科学版), 2018, 41(11): 1491-1495. XU Juan, JIA Zhiyuan, ZHANG Jianjun, et al. Rotor dynamic balancing control method based on improved single neuron PID[J]. Journal of Hefei University of Technology (Natural Science), 2018, 41(11): 1491-1495. DOI:10.3969/j.issn.1003-5060.2018.11.010 (  0) 0) |
| [24] |
XIA Y H, PENG Y G, WEI W. Triple droop control method for AC microgrids[J]. IET Power Electronics, 2017, 10(13): 1705-1713. (  0) 0) |
| [25] |
刘自南. 光伏发电系统并网逆变器电压电流双闭环控制仿真研究[J]. 自动化应用, 2021(1): 106-110. LIU Zinan. Simulation research on voltage and current double closed loop control of grid-connected inverter of photovoltaic power generation system[J]. Automation Application, 2021(1): 106-110. (  0) 0) |
| [26] |
余裕璞, 顾煜炯, 和学豪. 逆变器电压电流双闭环控制系统设计[J]. 电力科学与工程, 2019, 35(3): 1-7. YU Yupu, GU Yujiong, HE Xuehao. Design of voltage and current double closed-loop control system for inverter[J]. Electric Power Science and Engineering, 2019, 35(3): 1-7. (  0) 0) |
2. State Key Laboratory of Power Grid Safety and Energy Conservation (China Electric Power Research Institute), Beijing 100089, China
 2022, Vol. 41
2022, Vol. 41


 卢开诚(1996),男,博士,研究方向为微电网控制策略和事件驱动控制(E-mail:
卢开诚(1996),男,博士,研究方向为微电网控制策略和事件驱动控制(E-mail: