文章编号: 2096-3203(2022)05-0140-09 中图分类号: TM727
2. 哈尔滨工业大学电气工程及自动化学院, 黑龙江 哈尔滨 150001;
3. 黑龙江省工业技术研究院, 黑龙江 哈尔滨 150023
我国拥有丰富的可再生能源资源,随着可再生能源的大规模应用,分布式电源成为可再生能源的主要利用形式[1—4]。而分布式电源位置分散,且分布式发电技术不一,因此其大规模接入电力系统时难以直接调度和管理。微电网可以协调调度分布式发电单元、储能单元和负荷,最大限度地利用可再生能源,降低经济成本[5—7]。而如何协调调度,即能量管理方法对微电网的运行至关重要,影响微电网的能源利用率、系统可靠性以及经济性[8]。
随着微电网工程的普及,在一定区域内,微电网之间可能存在并联、串联、嵌套等关系,从而构成复杂的微电网群[9—13]。多个微电网互联构成微电网群系统可以进一步促进微电网间的能量交换,系统内各微电网之间可以进行互联、互供以满足区域供电需求[14]。在多微电网运行时,微电网群不仅需要保证其子微电网的单独控制与稳定运行,还需要实现系统内互联子微电网之间的能量交互,从而实现微电网群系统经济运行[15]。
微电网内风、光资源的随机性和波动性会显著影响微电网的优化运行结果。文献[16]通过模型预测控制实现微电网优化运行,为了应对不可避免的干扰和预测误差,将可再生能源和负荷数据嵌入到模型预测控制框架中,优化微电网的运行经济性。文献[17]构建了风机等不确定集,通过“源、储、荷”协调调度,调动微电网各类可用资源,增强了系统调度的灵活性,针对能量优化鲁棒模型,提出了有效的多阶段求解策略。文献[18]对多时间尺度微电网能量管理模型进行了改进,包括以1 d为尺度的日前计划、以30 min~1 h为尺度的滚动优化、以5~15 min为尺度的短期计划、在5~15 min尺度与实时控制间进一步设置分钟级的调度,提高了微电网能量管理精度。
在微电网群控制架构与能量管理方面,文献[19]针对多个微电网组成的配电系统,提出一种基于代理的分层能量管理模型,基于可再生能源和负载的实现和预测值,简化了微电网群能量管理求解问题。文献[20]构建含配电网层和微电网层的双层日前优化调度模型,在微电网层采用多场景技术描述可再生能源出力随机性,并利用模拟退火算法进行模型求解,考虑了电网友好性和微电网经营自主度。文献[21]提出一种基于动态电价的多微电网两阶段协同优化模型,鼓励私有微电网参与配电网的运行,多微电网与配电网之间的功率共享可以平滑配电网的负载曲线,但未考虑动态随机因素给能量管理带来的误差影响。
针对可再生能源存在随机性、负荷存在波动性的问题,文中提出基于动态随机模型的微电网群能量管理方法。建立光伏单元、风机单元及负荷的动态随机模型,采用微电网群分层控制架构,最终构建微电网间的能量交易模型和能量管理方案。解决了可再生能源随机性带来的净电量计算值偏离实际值、能量管理目标值未达到最优等问题,实现了微电网群的全局经济优化运行。
1 微电网群的组成和控制结构文中采用的微电网群系统主要由分布式发电单元、负荷、储能单元、柴油发电机、微电网间的功率联络线路和控制器间的通讯线组成。分布式发电单元通常是由风机和光伏构成的可再生能源。
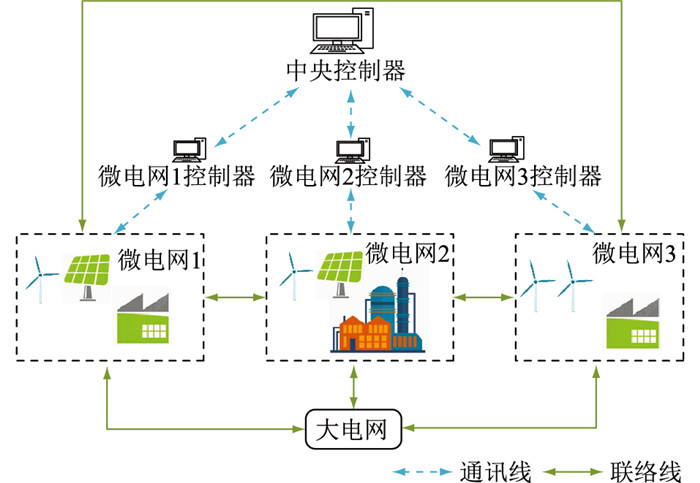
微电网群系统中的子微电网在实现内部功率平衡的同时,还需完成网间的能量交换和微电网与配电网之间的能量交换。微电网群通常采用分层控制,以便于管理,降低逻辑复杂度。图 1为典型的微电网群系统控制结构。
|
图 1 微电网群系统控制结构 Fig. 1 Control structure of multi-microgrids |
微电网群系统可分为2个层面:(1) 微电网群协调控制层,中央控制器收集各微电网发来的信息,根据能量交易方法计算出各微电网之间的交易功率,完成微电网群层面的功率调度;(2) 单微电网内部控制层,微电网控制器收集风力、光伏及负荷的预测信息,以日整体运行费用最低为目标进行调度,得到分布式发电单元出力、储能单元充放电功率、柴油发电机出力及与大电网的交易功率。
2 微电网群的能量交易方法 2.1 微电网间能量交易模型定义在微电网群系统中,包括n个微电网,在一段时间t内,微电网i累计产生的可再生能源功率与负荷功率的差值为功率差额,其表示为:
| $ \Delta P_{i, t}=P_{{\mathrm{pv}i}, t}+P_{{\mathrm{wt}i}, t}-P_{{\mathrm{l}i}, t} $ | (1) |
式中:Ppvi, t为微电网i在时段t内的光伏出力;Pwti, t为微电网i在时段t内的风机出力;Pli, t为微电网i在时段t内负载消耗功率。ΔPi, t>0时,定义为微电网i能量富余;ΔPi, t < 0时,定义为微电网i能量缺省;ΔPi, t=0时,定义为微电网i能量自给自足。
2.2 微电网间的能量交易方法单独运行时,能量富余的微电网需要向大电网售电,能量缺省的微电网需要蓄电池放电或者柴油发电机发电,甚至向大电网购电以保持微电网内部功率平衡。为了减少群内各微电网与大电网的能量交易,制定能量交易方法,使能量在微电网群内部优先消纳。
制定价格激励机制,微电网间能量交易价格低于向大电网购电的价格,高于向大电网售电的价格。激励微电网间优先进行能量交易,提高整体经济效益。微电网间进行能量交易时,应考虑以下因素:
(1) 可再生能源渗透率。微电网j的可再生能源渗透率为:
| $ u_j=\frac{P_{\mathrm{wt} j, t}+P_{\mathrm{pv}j, t}}{P_{\mathrm{l} j, t}} $ | (2) |
(2) 线路损耗。由于微电网间存在一定的距离,在能量交易过程中,电能需要通过输电线路进行传输,能量传输必然会产生能量损耗,微电网间距离不同,线路损耗也不同。微电网i,j之间的线路损耗为:
| $ l_{i, j}=I_{i, j}^2 R_{i, j} $ | (3) |
式中:Ii, j为流经微电网i,j联络线的电流;Ri, j为微电网i,j间线缆阻抗。
将可再生能源渗透率和线路损耗的乘积作为能量交易的参数,能量交易参数与可再生能源渗透率之间为线性比例关系。当2个以上微电网能量富余时,可再生能源渗透率高的微电网优先提供能量。当2个以上微电网能量缺省时,可再生能源渗透率低的微电网优先获得能量。
余电微电网在能量交易中所获得的收益等于向少电微电网售电收益,交易后的日整体经济成本为能量交易后运行维护成本减去收益;少电微电网由从大电网购电转变为从余电微电网购电,购电成本降低,交易后的日整体经济成本为能量交易后运行维护成本加上从余电微电网购电成本。
3 微电网群的能量管理方法可再生能源出力存在很大的随机性,负荷具有很大的波动性,若微电网群的能量调度计划未考虑上述动态随机因素,将会导致调度功率偏差过大,得到的调度计划将偏离最优计划。现有的微电网动态随机处理方法主要分为4类:(1) 采用多场景方法适应风电出力随机性,作为日前调度模型[22];(2) 蒙特卡洛模拟方法[17],利用随机方法产生符合概率分布的微电网具体运行场景与优化调度方案;(3) 机会约束规划技术[23],计算满足约束条件的决策概率,令其不低于所需置信水平并进行求解,从而得到合理方案;(4) 多时间尺度技术[24],在日前计划阶段使用发电单元和负荷预测值制定初步调度方案,在滚动优化、实时调度等阶段基于最新数据对上级遗留偏差进行修正。
上述方法考虑了微电网动态随机因素,不同程度上缓解了动态随机因素带来的波动,但前3种调度方法仍为日前调度,无法实现微电网内部的实时功率平衡,而第四种调度方法基于最新数据对日前调度计划进行修正,调度计划误差变小。因此,需采用基于模型预测的多时间尺度方法对微电网单元进行调度。
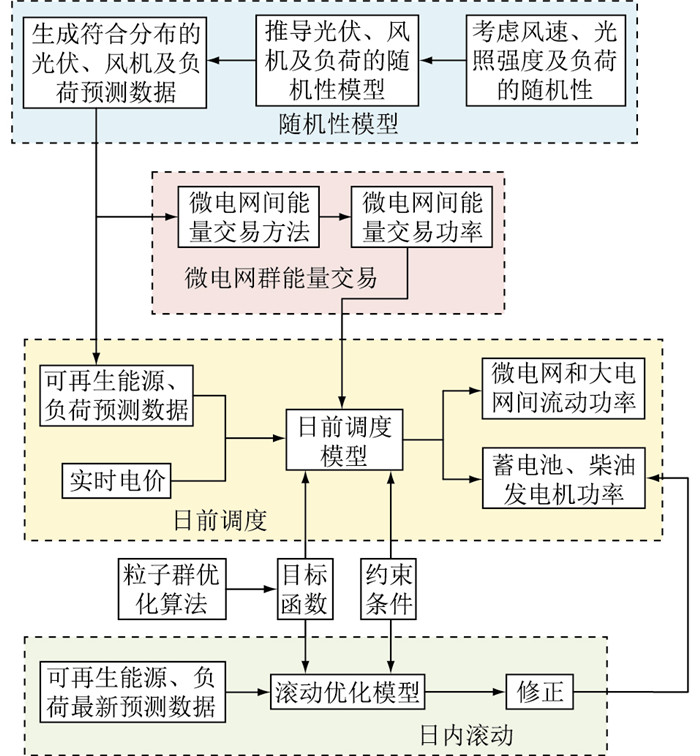
单微电网以日整体经济成本最低为目标,基于模型预测,改进传统多时间尺度,构建多时间尺度能量管理模型框架,包括日前调度计划、日内滚动优化,进行实时调度,所提出的微电网群能量管理框架如图 2所示。
|
图 2 微电网群能量管理框架 Fig. 2 Energy management block of multi-microgrids |
微电网间能量交易模型根据接收的可再生能源预测数据、能量交易指令,利用粒子群优化算法进行数据的优化迭代,生成的优化结果送至日前调度模型。日前调度模型的功能是对接收到的优化数据进行处理,获得微电网内和微电网间能量流动数据,以1 h为尺度,基于光伏、风机及负荷日前预测和分时电价信息,在满足系统约束条件的基础上,以微电网日运行成本最低为目标,优化各单元能量调度。由于日前计划与实时调度时间跨度大,日前调度偏差较大,以15 min为时间尺度,将可再生能源、负荷预测数据代入滚动优化模型,对日前调度模型生成的微电网内和微电网间能量流动数据进行刷新和修正,从而完成微电网能量管理。
3.1 不确定因素的随机模型 3.1.1 风电出力的随机模型风力发电具有间歇性,风电出力预测基于风速预测进行,风速随机性和间歇性反映了风电出力变化特征。通常可用Weibull分布描述风速分布模型,风速分布模型表达式为:
| $ f(v)=\frac{k}{c}\left(\frac{v}{c}\right)^{k-1} \mathrm{e}^{-\left(\frac{v}{c}\right)^k} $ | (4) |
式中:c为Weibull尺度参数,代表某时段风力发电场的平均风速;k为Weibull形状参数;v为风速。
3.1.2 光伏出力的随机模型光伏出力易受云朵、树叶等遮挡而出现波动,即光伏阵列在云朵移动、日照角度变化下因阴影遮蔽、光照强度变化而出现功率波动。固定场合下日照强度符合数学概率分布,可将其视为近似Beta分布的随机变量,对应的概率分布表达式为:
| $ f(r)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)}\left(\frac{r}{r_{\max }}\right)^{\alpha-1}\left(1-\frac{r}{r_{\max }}\right)^{\beta-1} $ | (5) |
式中:r为该时段内太阳的实际光照强度;rmax为该时段内太阳的最大光照强度;α,β为Beta分布的形状参数,由该时段气候地形等因素决定;Γ(·)为Gamma函数。
光伏出力同样服从Beta分布,其概率密度函数为:
| $ f_{\mathrm{PV}}\left(P_{\mathrm{PV}}\right)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)}\left(\frac{P_{\mathrm{PV}}}{P_{\mathrm{PV} \max }}\right)^{\alpha-1}\left(1-\frac{P_{\mathrm{PV}}}{P_{\mathrm{PV}\max }}\right)^{\beta-1} $ | (6) |
其中:
| $ P_{\mathrm{PV} \max }=A \eta r_{\max } $ | (7) |
式中:PPVmax为光伏阵列的最大输出功率;A为光伏阵列面积;η为发电效率。
3.1.3 负荷的随机模型用户负荷的接入具有随时性与不可控性,可利用正态分布函数描述负荷的不确定性。负荷的概率密度函数为:
| $ f\left(P_{\mathrm{L}}\right)=\frac{1}{\sqrt{2 \pi} \sigma_{\mathrm{L}}} \mathrm{e}^{-\frac{\left(P_{\mathrm{L}}-\mu_{\mathrm{L}}\right)^2}{2 \sigma_{\mathrm{L}}^2}} $ | (8) |
式中:PL为负荷值;μL为负荷期望值;σL为负荷的标准差。
3.2 日前和日内调度模型文中设计的微电网群日前调度过程如下:
(1) 基于风速、光照强度和温度等预测信息,提前预测下一日每小时的风机、光伏发电和负荷功率;
(2) 利用上述微电网群的能量交易方法和功率预测值,计算得到微电网之间的流动功率;
(3) 进行多目标处理,考虑分时电价,优化下一日每小时各微电网与大电网的交易功率、各柴油发电机发电功率以及储能设备的充放电功率。
日内调度优化过程如下:
(1) 不改变日前优化结果中各微电网与大电网的交易功率及各微电网与其他微电网的交易功率;
(2) 以15 min为周期,更新风电、光伏和负荷的功率预测值,滚动优化各微电网中柴油发电机的出力和储能设备的充放电功率。
微电网i日内经济优化目标函数为:
| $ \begin{gathered} \min F_{2, i}=\sum\limits_{t=1}^{96}\left(C_{\mathrm{pv}}\left(P_{{\mathrm{pv}i}, t}\right)+C_{\mathrm{wt}}\left(P_{{\mathrm{wt}i}, t}\right)+\right. \\ \left.C_{\mathrm{bat}}\left(P_{{\mathrm{bat}i}, t}\right)+C_{\mathrm{de}}\left(P_{{\mathrm{de}i}, t}\right)+C_{\mathrm{cut}}\left(P_{{\mathrm{cut}i}, t}\right)\right) \end{gathered} $ | (8) |
式中:Cpv(Ppvi, t)为微电网i在时段t内的光伏维护成本;Cwt(Pwti, t)为微电网i在时段t内的风机维护成本;Cbat(Pbati, t)为微电网i在时段t内的蓄电池运行维护成本;Cde(Pdei, t)为微电网i在时段t内的柴油发电机运行成本;Ccut(Pcuti, t)为微电网i在时段t内供电不足时切负荷的成本。可靠性目标和约束条件与日前调度一致。
3.3 系统经济目标函数完成典型日预测后,进一步建立微电网群的目标函数。微电网群的能量管理以日整体运行费用最低为目标,因此在已建成的微电网群上进行能量管理时无须考虑系统的初始建设成本。考虑可再生能源机组运行维护成本、蓄电池运行维修成本、柴油发电机运行成本、向大电网购售电的成本以及供电不足时切负荷的成本,则系统经济目标函数为:
| $ \begin{gathered} \min F_1=\sum\limits_{t=1}^{24} \sum\limits_{i=1}^n\left(C_{\mathrm{pv}}\left(P_{{\mathrm{pv}i}, t}\right)+C_{\mathrm{wt}}\left(P_{\mathrm{wt} i, t}\right)+\right. \\ C_{\mathrm{bat}}\left(P_{\mathrm{bat} i, t}\right)+C_{\mathrm{grid}}\left(P_{\mathrm{grid} i, t}\right)+ \\ \left.C_{\mathrm{de}}\left(P_{\mathrm{de} i, t}\right)+C_{\mathrm{cut}}\left(P_{\mathrm{cut} i, t}\right)\right) \end{gathered} $ | (9) |
式中:F1为日整体运行费用;Cgrid(Pgridi, t)为微电网i在时段t内与大电网交易费用。
3.4 系统运维和交易费用 3.4.1 光伏和风机在时段t内的运行维护成本微电网建设初期可通过优化配置确定初始投入成本[25],在运行过程中则需要考虑系统各单元的运维成本。光伏和风机运行维护费用正比于其产生的电能:
| $ C_{\mathrm{pv}}\left(P_{{\mathrm{pv}i}, t}\right)=P_{\mathrm{PV}, t} K_{\mathrm{PV}} $ | (10) |
| $ C_{\mathrm{wt}}\left(P_{{\mathrm{wt}i}, t}\right)=P_{\mathrm{wT}, t} K_{\mathrm{wT}} $ | (11) |
式中:PPV, t,PWT, t分别为气象数据计算出来的光伏和风机输出功率;KPV,KWT分别为光伏和风机的运行维护系数,代表了不同发电单元出力时单位功率下维护成本和运行成本之和。
3.4.2 蓄电池在时段t内的运行维护成本蓄电池的运行维护成本不是固定的,计算如下:
| $ C_{\text {bat }}\left(P_{{\text {bat}i}, t}\right)=\left|P_{{\text {bat}i}, t} w_t K_{\text {bat }}\right| $ | (12) |
式中:Pbati, t为微电网i在时段t内蓄电池的充放电功率,充电时为负值,放电时为正值;Kbat为蓄电池的运行维护系数;wt为蓄电池时段t内荷电状态(state of charge, SOC)下的权重因子。
3.4.3 与大电网交易费用微电网与大电网并联运行过程中,需要考虑与电网交易费用。采用更接近实际情况的分时计价模式,费用如下:
| $ C_{\text {grid}}\left(P_{\text {grid}i, t}\right)=C_{\text {grid}i, t} P_{\text {grid}i, t} $ | (13) |
式中:Pgridi, t为微电网i在时段t与大电网的交易功率,微电网i从大电网获取电能时为正,售电时为负;Cgridi, t为时段t内的电价。
3.4.4 切负荷费用切负荷是在子微电网无法互济、整个微电网群无法实现能量平衡的情况下进行的,通过切掉部分可中断负荷以保证微电网的稳定运行。切负荷会给用户带来经济损失,因此需要费用,切负荷的成本也考虑分时计价:
| $ C_{\mathrm{cut}}\left(P_{\mathrm{cut} i, t}\right)=C_{\mathrm{cut} i, t} P_{\mathrm{cut}i, t} $ | (14) |
式中:Pcuti, t为时段t内微电网i切负荷的功率;Ccuti, t为时段t内切负荷的补偿电价。
微电网运行也需考虑可靠性,通常以负载失电率作为系统评价指标,其定义如下:
| $ f_1=\sum\limits_{t=1}^{24} P_{\mathrm{s}}(t) / \sum\limits_{t=1}^{24} P_{\text {load }}(t) $ | (15) |
式中:Ps(t)为时段t未能满足系统的缺失功率;Pload(t)为时段t的负荷功率。为保证微电网的稳定运行,负载失电率越低越好。
整体目标函数为:
| $ F=\min F_1+1\;000\;000\left(f_1-0.1\right) $ | (16) |
f1作为惩罚函数加入目标函数,当负载失电率高于0.1时,经济成本会很高以致于优化失效。
3.5 系统约束条件 3.5.1 功率平衡约束| $ \begin{gathered} P_{\mathrm{pv}i, t}+P_{\mathrm{wt} i, t}+P_{\mathrm{bat}i, t}+P_{\mathrm{de} i, t}+P_{\mathrm{grid} i, t}= \\ P_{\text {load}i, t}+\sum\limits_{i \neq j} P_{i, j, t} \end{gathered} $ | (17) |
式中:Pdei, t为微电网i中柴油发电机在时段t内的发电功率;Ploadi, t为微电网i在时段t的负荷功率;Pi, j, t为时段t内微电网i流向微电网j的功率。
3.5.2 系统运行约束系统运行约束为:(1) 微电网与大电网的联络线传输功率限制,不能超过最大传输功率Pgridmax;(2) 考虑到运行成本,柴油发电机出力不能低于最小发电功率Pdemin,也不能超过最大输出功率Pdemax,爬坡功率不能超过最大幅值ΔPdemax;(3) 蓄电池在充放电过程中的SOC不得超过其限值,蓄电池在充放电过程中不能超过最大充放电功率。为了体现微电网优越性,定义微电网群中可再生能源利用率约束,其中LREE, min为设置的可再生能源利用率LREE的下限值; 同时考虑柴油发电机碳排放治理成本约束指标,Fe为柴油发电机产生的环境污染治理成本;a为不同的排放气体(包括二氧化碳,氮氧化物和二氧化硫等);Wdiesel, a为污染气体a的生产系数;Pdiesel, t为时段t内发出功率;Ca为污染气体a的单位重量治理成本;bSOC为蓄电池的荷电状态;PREG(t, j)为微电网中可再生能源j(包括光伏和风机)在t时刻发出的功率。
| $ P_{\text {grid }, t} \leqslant\left|P_{\text {grid }}^{\max }\right| $ | (18) |
| $ P_{\mathrm{demin}} \leqslant P_{\mathrm{de}i, t} \leqslant P_{\mathrm{demax}} $ | (19) |
| $ \left|P_{\mathrm{de}, t}-P_{\mathrm{de}, t-1}\right| \leqslant \Delta P_{\mathrm{de}}^{\max } $ | (20) |
| $ -P_{\text {batmax }} \leqslant P_{\text {bat}i, t} \leqslant P_{\text {batmax }} $ | (22) |
| $ \begin{gathered} L_{\mathrm{REE}}(j)=\int_0^T P_{\mathrm{REG}}(t, j) \mathrm{d} t / \int_0^T P_{\text {load }}(t) \mathrm{d} t \\ L_{\mathrm{REE}}(j) \geqslant L_{\mathrm{REE}, \min } \end{gathered} $ | (23) |
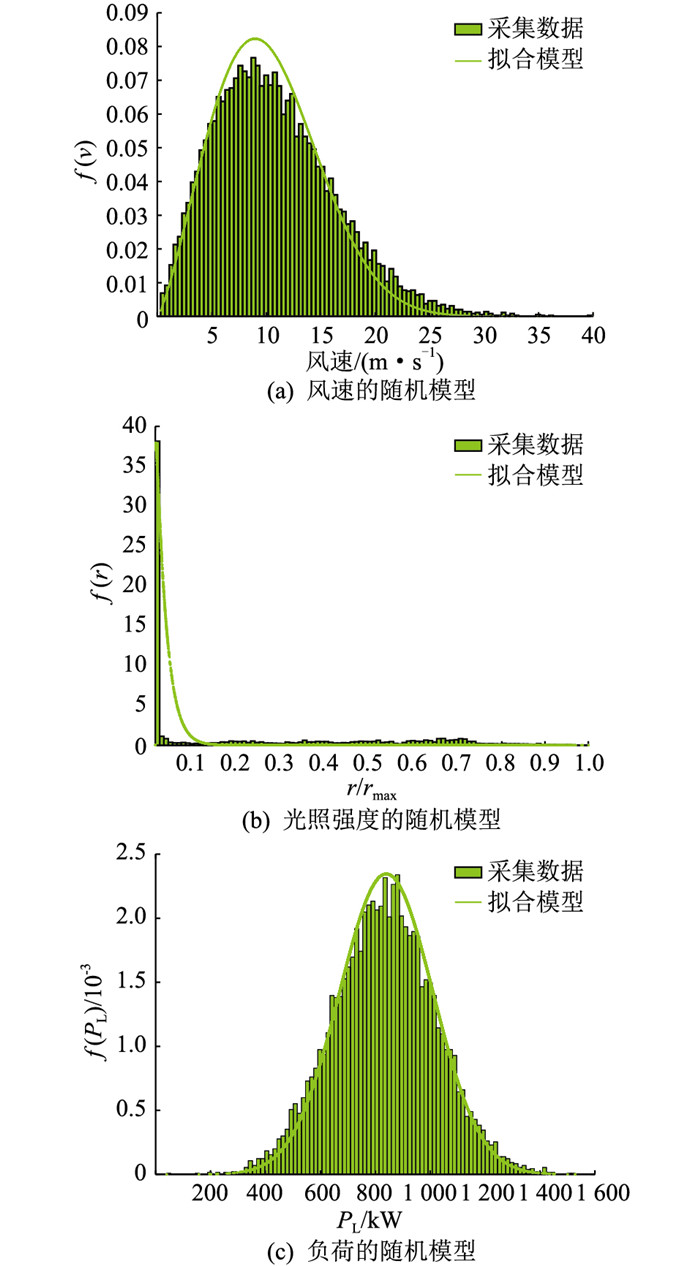
利用采集数据拟合的风速、光照强度和负荷随机性相关模型如图 3所示。可看出所提出的随机模型可较好地模拟可再生能源出力真实值。风速随机模型中形状参数k为2.3,尺度参数c为11.5;光照强度随机模型中,Beta分布的形状参数α和β分别为1.05和45;负荷随机模型中负荷期望值μL为840,负荷的标准差σL为170;粒子群优化算法中种群数量为40,最大迭代次数为200。
|
图 3 系统随机模型 Fig. 3 System stochastic models |
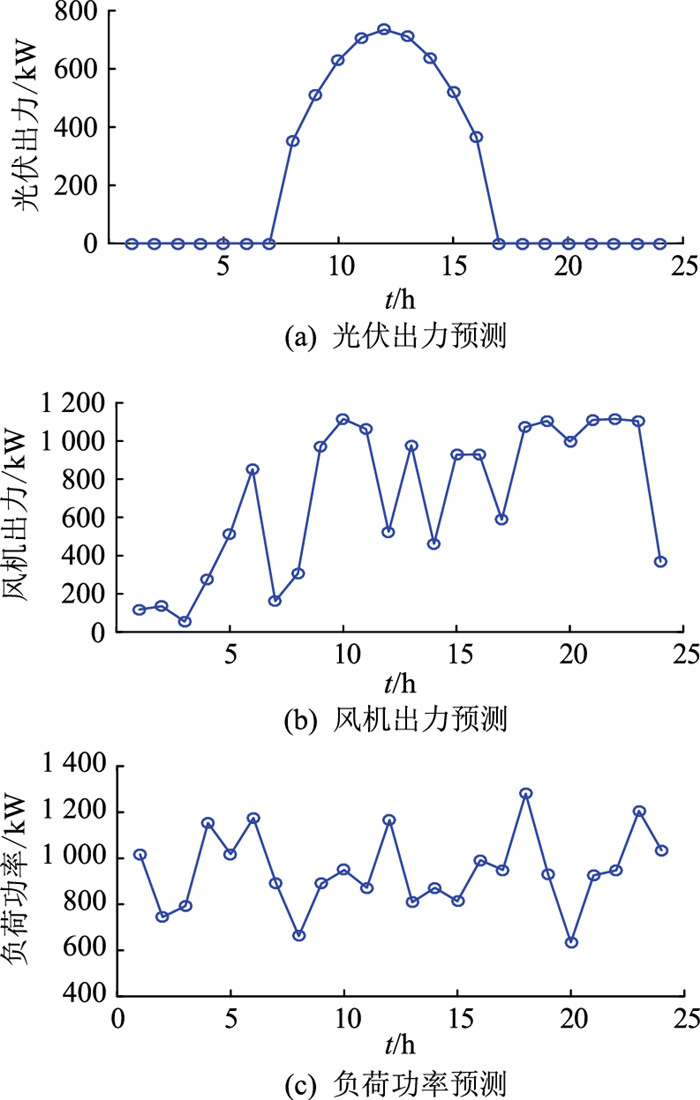
以微电网1为例,光伏出力、风机出力及负荷功率如图 4所示。由图 4(a)可以看出,在01:00—07:00和17:00—24:00,光伏出力为零,符合自然环境中光照的分布情况,且光伏单元出力呈连续的曲线,符合光照强度连续变化的情况。由图 4(b)可以看出,风机单元出力波动很大,整体来看,白天输出功率较大,夜间输出功率较小,白天输出功率在中午时间段内波动明显。由图 4(c)可以看出,虽然负荷功率有波动,但都在1 000 kW附近波动,在中午和晚上用电高峰时间段负荷功率明显变大,在凌晨、下午等用电低谷时间段功率明显变小。
|
图 4 微电网1日前预测数据 Fig. 4 Day-ahead forecast data of microgrid 1 |
日前调度过程中,微电网与大电网进行能量交易时,考虑分时计价,激励用户改变用电时间段,避免出现用电高峰时间段供电不足的情况。
分时计价方案具体见表 1。其中,电价峰时段为10:00—15:00,18:00—21:00;谷时段为23:00—24:00,00:00—07:00;平时段为07:00—10:00,15:00—18:00,21:00—23:00。购售电价格随用电峰谷时段变化,峰时段电价最高,谷时段电价最低,激励用户自主改变用电时间,保证供电可靠性。
|
|
表 1 分时计价方案 Table 1 Time of use pricing scheme |
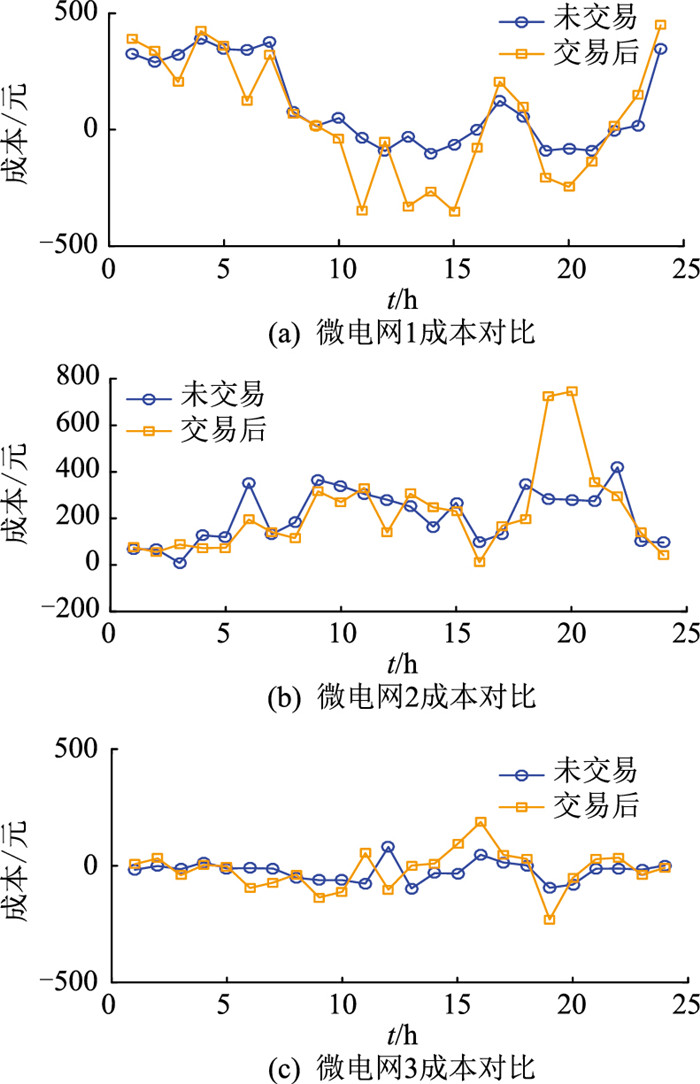
为进一步说明系统内微电网间的能量交易可提高微电网群系统的经济效益,文中基于能量交易的日前调度结果与未进行能量交易的日前调度结果作对比。3个微电网进行微电网间能量交易与未进行能量交易时的整体日经济成本见表 2。可以看出,微电网1的成本明显降低,微电网2的成本变化不大,微电网3的成本小幅度增加,但从微电网群系统来看,相比未进行能量交易,进行能量交易后经济成本降低,计算统计数据,成本降低了22.0%。
|
|
表 2 能量管理前后经济成本对比 Table 2 Comparison of economic cost before and after energy management |
3个微电网交易前后的日经济成本对比见图 5。可以看出,能量交易后微电网1的成本明显降低,几乎每个时间段的成本都低于未进行能量交易时的成本;微电网2的成本几乎不变;微电网3的成本在大多数时间段都稍低于未进行能量交易时的成本。
|
图 5 微电网交易前后成本对比 Fig. 5 Cost comparison of microgrids before and after transaction |
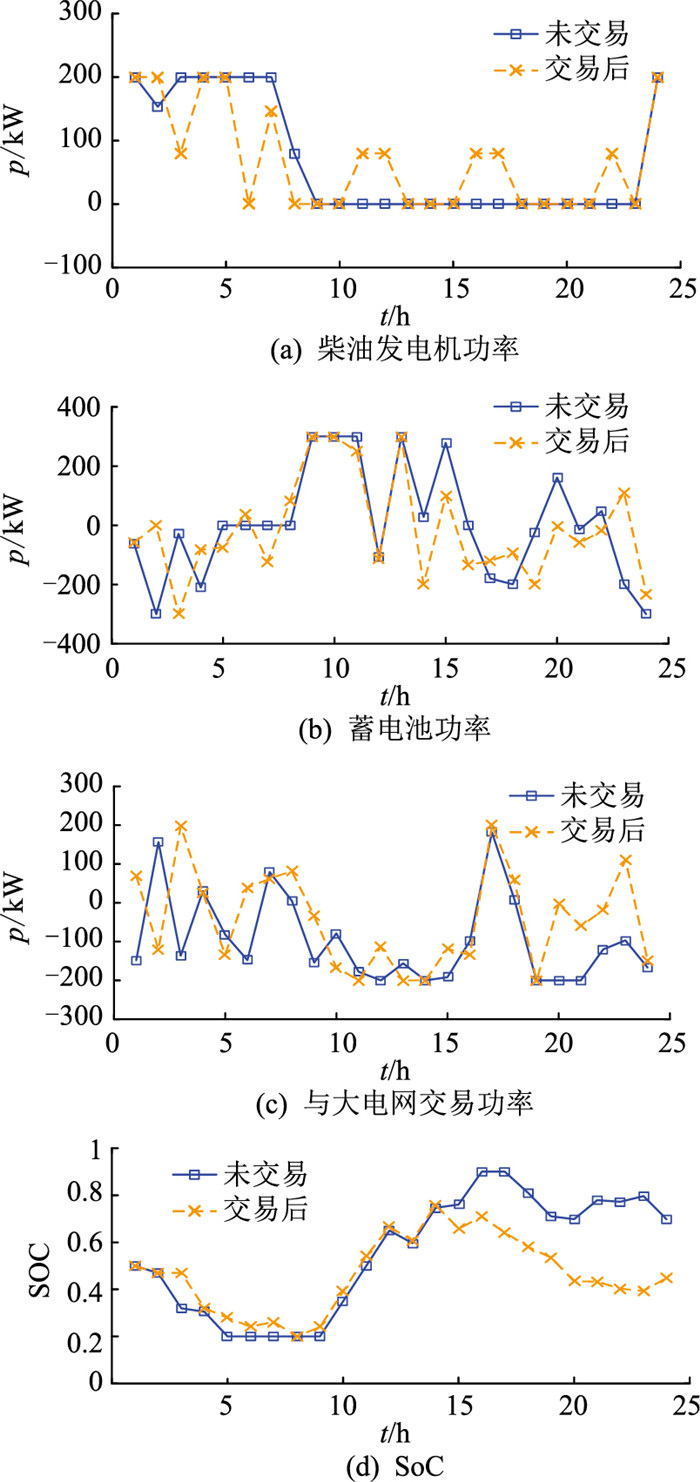
以微电网1为例,日前调度结果如图 6所示。从图 6(a)可以看出,柴油发电机功率明显减少,但某些时间段未进行能量交易,柴油发电机功率为零,而进行能量交易后柴油发电机功率为正,这是由于微电网1售电给其他微电网后,微电网自身某些时间段存在能量不足,需要柴油发电机输出功率,但柴油发电机输出功率有最小输出功率约束,因此能量交易后的曲线存在高于未进行能量交易的情况。从图 6(b)可以看出, 蓄电池功率总体减少。从图 6(c)可以看出, 与大电网交易功率基本不变。从图 6(d)可以看出, 蓄电池的SOC变化更平缓,可有效增加蓄电池的循环次数,有利于系统的经济运行。
|
图 6 日前调度结果 Fig. 6 Day-ahead scheduling results |
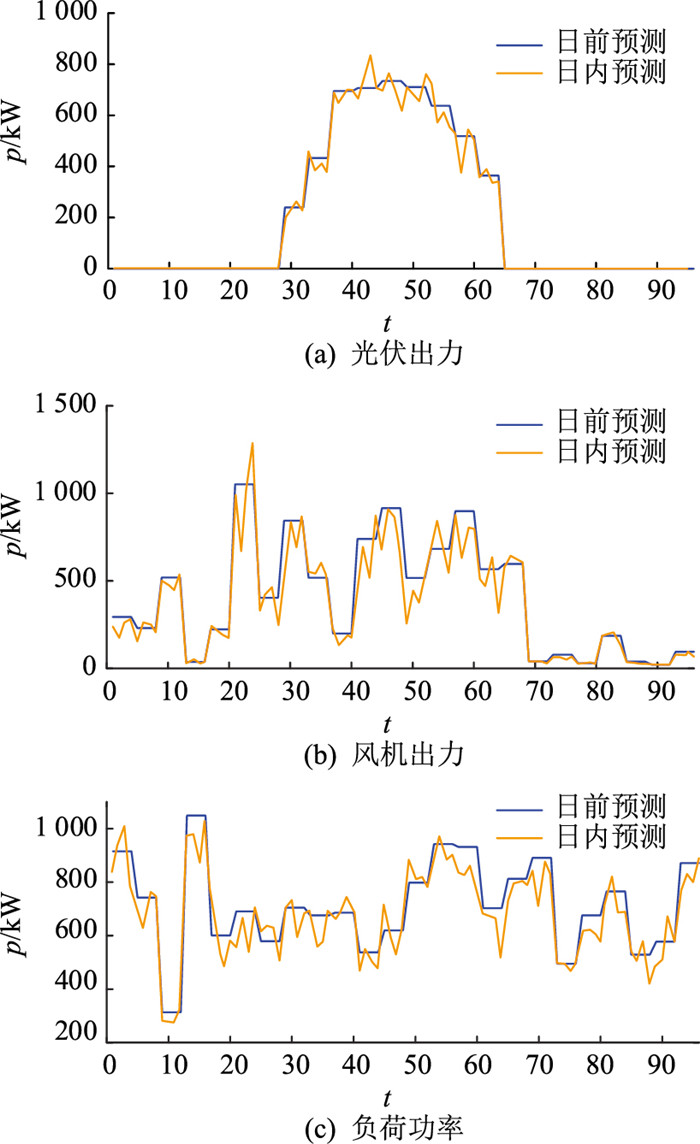
由于对风电、光伏和负荷功率日前预测的时间尺度为1 d,时间尺度较大,预测值不够精确,因此,日前调度结果也会有误差。采用日内滚动修正误差,以15 min为时间尺度,将新的预测值用于日内调度,优化各单元出力。日前预测值误差大多满足正态分布,以微电网1为例,得到图 7所示新预测值。
|
图 7 日内预测值 Fig. 7 Intra-day forecast values |
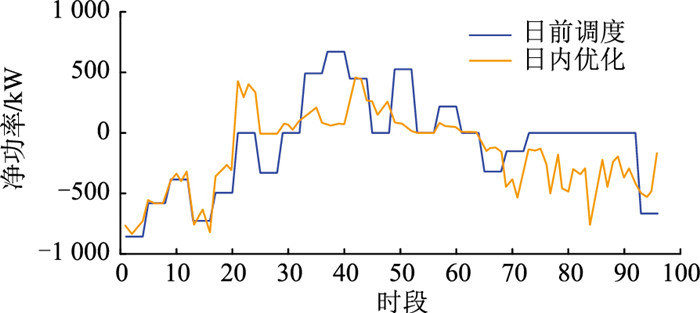
净功率可定义为微电网中可再生能源出力与负荷消耗功率间的差值。微电网1的净功率曲线如图 8所示,可以看出,在时段68—96(17:00— 24:00)内日前和日内数据相差较大。
|
图 8 净功率曲线 Fig. 8 Net power curves |
日内优化的各单元出力与日前出力对比见图 9。
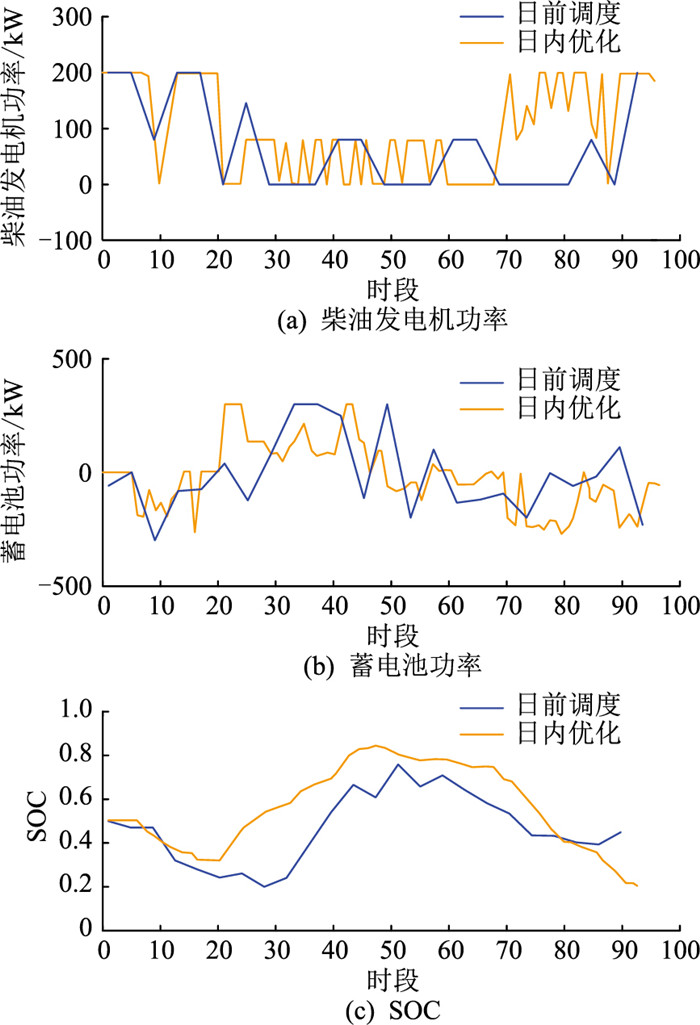
|
图 9 日内调度结果 Fig. 9 Intra-day scheduling results |
由于日内调度的时间尺度更精确,净功率曲线在时段68—96(17:00—24:00)内差别较大,柴油发电机出力弥补误差,因此有较大变化,其余时段基本吻合;蓄电池出力整体上变小;蓄电池的SOC变化相比日前调度更为平缓,没有大的波动。
5 结语文中针对微电网中可再生能源出力存在随机性、负荷存在波动性的问题,提出了单微电网的基于动态随机模型的多时间尺度能量管理方法,建立了能量管理框架。考虑自然条件下风光荷的不确定性,基于Weibull、Beta及正态概率分布函数,建立了光伏、风机出力及负荷的的动态随机模型。微电网群的能量管理模型包括日前调度模型和日内优化模型,确定其目标函数和约束条件,目标函数考虑风机、光伏、蓄电池、柴油发电机、与大电网交易及切负荷等运行维护成本和可靠性目标,约束条件考虑功率上下限等。最后,在理论基础上进行微电网群的算例分析,验证了所提能量管理模型和方法的有效性,系统经济成本在能量交易后显著降低。
在未来的研究工作中,将进一步考虑所提方案在工程应用中面临的实际问题,如考虑微电网群运行模式变化以及微电网通讯中断给能量管理带来的影响等。
本文得到国网黑龙江省电力有限公司科技项目“偏远地区源网荷储交直流混联系统研究及示范工程技术方案设计”(52243720031)资助,谨此致谢!
| [1] |
滕松, 刘毅, 钟睿, 等. 基于高比例可再生能源的废矿抽蓄电站优化配置研究[J]. 电力工程技术, 2020, 39(4): 87-95, 103. TENG Song, LIU Yi, ZHONG Rui, et al. Optimal configuration of abandoned mine pumped storage power station based on high proportion of renewable energy[J]. Electric Power Engineering Technology, 2020, 39(4): 87-95, 103. (  0) 0) |
| [2] |
JIA K, YANG Z, FANG Y, et al. Influence of inverter-interfaced renewable energy generators on directional relay and an improved scheme[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11843-11855. DOI:10.1109/TPEL.2019.2904715 (  0) 0) |
| [3] |
MAI T, HAND M M, BALDWIN S F, et al. Renewable electricity futures for the United States[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 372-378. DOI:10.1109/TSTE.2013.2290472 (  0) 0) |
| [4] |
SUN J, LI M J, ZHANG Z G, et al. Renewable energy transmission by HVDC across the continent: system challenges and opportunities[J]. CSEE Journal of Power and Energy Systems, 2017, 3(4): 353-364. DOI:10.17775/CSEEJPES.2017.01200 (  0) 0) |
| [5] |
史军, 王加澍, 熊峰, 等. 基于智能负载的微电网精准切负荷控制策略[J]. 电力工程技术, 2020, 39(2): 103-109. SHI Jun, WANG Jiashu, XIONG Feng, et al. Load-shedding control strategy of microgrid based on smart loads[J]. Electric Power Engineering Technology, 2020, 39(2): 103-109. (  0) 0) |
| [6] |
LYU C, JIA Y W, XU Z. A novel communication-less approach to economic dispatch for microgrids[J]. IEEE Transactions on Smart Grid, 2021, 12(1): 901-904. DOI:10.1109/TSG.2020.3018622 (  0) 0) |
| [7] |
NETO P J D S, BARROS T A D S, SILVEIRA J P C, et al. Power management strategy based on virtual inertia for DC microgrids[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12472-12485. DOI:10.1109/TPEL.2020.2986283 (  0) 0) |
| [8] |
赵波, 张后谊, 陈民铀, 等. 体系动态架构下的多微电网系统能量管理模型与动态链接行为分析方法[J]. 中国电机工程学报, 2020, 40(20): 6468-6482. ZHAO Bo, ZHANG Houyi, CHEN Minyou, et al. Energy management model and dynamic link behavior analysis method for multi-microgrid systems under dynamic system of systems architecture[J]. Proceedings of the CSEE, 2020, 40(20): 6468-6482. (  0) 0) |
| [9] |
丁明, 潘浩, 张晶晶. 分布式电源接入交直流混合微电网群优化规划研究[J]. 太阳能学报, 2021, 42(6): 54-62. DING Ming, PAN Hao, ZHANG Jingjing. Research on optimal planning of AC/DC hybrid microgrid cluster with distributed generation access[J]. Acta Energiae Solaris Sinica, 2021, 42(6): 54-62. (  0) 0) |
| [10] |
ZAERY M, WANG P B, LU X N, et al. Fully distributed controller for economic load sharing of DC microgrid clusters[C]//2020 IEEE Applied Power Electronics Conference and Exposition. New Orleans, LA, USA. IEEE: 597-602.
(  0) 0) |
| [11] |
WU X Y, XU Y, HE J H, et al. Pinning-based hierarchical and distributed cooperative control for AC microgrid clusters[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9865-9885. DOI:10.1109/TPEL.2020.2972321 (  0) 0) |
| [12] |
PULCHERIO M, ILLINDALA M S, CHOI J, et al. Robust microgrid clustering in a distribution system with inverter-based DERs[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5152-5162. DOI:10.1109/TIA.2018.2853039 (  0) 0) |
| [13] |
HU W Q, WU Z J, LV X X, et al. Robust secondary frequency control for virtual synchronous machine-based microgrid cluster using equivalent modeling[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 2879-2889. DOI:10.1109/TSG.2021.3067317 (  0) 0) |
| [14] |
杨炜晨, 苗世洪, 张世旭, 等. 交直流混合微电网群分布式自治经济控制策略[J]. 中国电机工程学报, 2021, 41(3): 857-868. YANG Weichen, MIAO Shihong, ZHANG Shixu, et al. Distributed autonomous economic control strategy for AC/DC hybrid microgrid cluster[J]. Proceedings of the CSEE, 2021, 41(3): 857-868. (  0) 0) |
| [15] |
桑博, 张涛, 刘亚杰, 等. 多微电网能量管理系统研究综述[J]. 中国电机工程学报, 2020, 40(10): 3077-3093. SANG Bo, ZHANG Tao, LIU Yajie, et al. Energy management system research of multi-microgrid: a review[J]. Proceedings of the CSEE, 2020, 40(10): 3077-3093. (  0) 0) |
| [16] |
PARISIO A, RIKOS E, GLIELMO L. A model predictive control approach to microgrid operation optimization[J]. IEEE Transactions on Control Systems Technology, 2014, 22(5): 1813-1827. DOI:10.1109/TCST.2013.2295737 (  0) 0) |
| [17] |
向月, 刘俊勇, 魏震波, 等. 考虑可再生能源出力不确定性的微电网能量优化鲁棒模型[J]. 中国电机工程学报, 2014, 34(19): 3063-3072. XIANG Yue, LIU Junyong, WEI Zhenbo, et al. Robust model of microgrid energy optimization with uncertain renewable energy sources[J]. Proceedings of the CSEE, 2014, 34(19): 3063-3072. (  0) 0) |
| [18] |
窦晓波, 徐忞慧, 董建达, 等. 微电网改进多时间尺度能量管理模型[J]. 电力系统自动化, 2016, 40(9): 48-55. DOU Xiaobo, XU Minhui, DONG Jianda, et al. Multi-time scale based improved energy management model for microgrid[J]. Automation of Electric Power Systems, 2016, 40(9): 48-55. (  0) 0) |
| [19] |
DEHGHANPOUR K, NEHRIR H. An agent-based hierarchical bargaining framework for power management of multiple cooperative microgrids[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 514-522. DOI:10.1109/TSG.2017.2746014 (  0) 0) |
| [20] |
米师农, 张建成, 郭伟. 一种市场环境下的电网友好型多微网优化调度方法[J]. 电力建设, 2018, 39(6): 117-124. MI Shinong, ZHANG Jiancheng, GUO Wei. Grid-friendly optimal scheduling method for multi-microgrid system in electricity marketing environment[J]. Electric Power Construction, 2018, 39(6): 117-124. DOI:10.3969/j.issn.1000-7229.2018.06.015 (  0) 0) |
| [21] |
HU X T, LIU T Q. Co-optimisation for distribution networks with multi-microgrids based on a two-stage optimisation model with dynamic electricity pricing[J]. IET Generation, Transmission & Distribution, 2017, 11(9): 2251-2259. (  0) 0) |
| [22] |
王守相, 王栋, 韩亮. 考虑不确定性的微网日前经济优化调度区间线性规划方法[J]. 电力系统自动化, 2014, 38(24): 5-11, 47. WANG Shouxiang, WANG Dong, HAN Liang. Interval linear programming method for day-ahead optimal economic dispatching of microgrid considering uncertainty[J]. Automation of Electric Power Systems, 2014, 38(24): 5-11, 47. DOI:10.7500/AEPS20131212010 (  0) 0) |
| [23] |
赵书强, 李志伟. 考虑可再生能源出力不确定性的多能源电力系统日前调度[J]. 华北电力大学学报(自然科学版), 2018, 45(5): 1-10. ZHAO Shuqiang, LI Zhiwei. Day-ahead scheduling of multi-energy power system considering renewable energy uncertain output[J]. Journal of North China Electric Power University (Natural Science Edition), 2018, 45(5): 1-10. DOI:10.3969/j.ISSN.1007-2691.2018.05.01 (  0) 0) |
| [24] |
EBRAHIMI M R, AMJADY N. Adaptive robust optimization framework for day-ahead microgrid scheduling[J]. International Journal of Electrical Power & Energy Systems, 2019, 107: 213-223. (  0) 0) |
| [25] |
WANG P B, WANG W, XU D G. Optimal sizing of distributed generations in DC microgrids with comprehensive consideration of system operation modes and operation targets[J]. IEEE Access, 6: 31129-31140. DOI:10.1109/ACCESS.2018.2842119 (  0) 0) |
2. School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China;
3. Heilongjiang Institute of Industrial Technology, Harbin 150023, China
 2022, Vol. 41
2022, Vol. 41


 徐明宇(1983), 男, 硕士, 研究员级高级工程师, 从事大规模新能源并网控制、运行与优化工作(E-mail:
徐明宇(1983), 男, 硕士, 研究员级高级工程师, 从事大规模新能源并网控制、运行与优化工作(E-mail: