文章编号: 2096-3203(2022)05-0116-08 中图分类号: TM721.3
2. 国网辽宁省电力有限公司经济技术研究院, 辽宁 沈阳 110015
大规模分布式电源(distributed generation, DG)的分散接入给电网带来了接入无序、电能质量差、供电可靠性低等问题[1—2]。传统的交流配电网难以应对配电网飞速发展带来的各种挑战,因此迫切需要新技术来提高配电网的灵活性。直流配电网具有不涉及相位调控、线损小等优点,利用柔性直流技术构建交直流混合配电网将会是未来重要的发展方向[3]。其中,电压源换流器(voltage source converter, VSC)作为典型的柔性互联装置,可以对潮流进行双向控制,从而对网络进行合理的功率分配。
目前,相关文献通过规划DG的接入位置和容量实现交直流混合配电网的优化运行。文献[4]考虑不同类型DG的时序特性,建立了以网络损耗最小为目标函数的选址定容模型,实现了网络的经济运行;文献[5]提出了一种基于区间直觉模糊理论的DG规划方案,可以有效改善网络电压质量,保证安全性;文献[6]提出了一种DG接入点确定后各接入点的容量分配方法,能有效改善潮流分布,降低网络损耗;文献[7]考虑DG的不确定性,提出了一种交直流混合配电网分布式优化模型,从而提高网络运行的经济性。上述研究虽能在一定程度上实现网络的优化运行,但未发挥柔性互联装置在网络运行时能够灵活转移功率的优势。为此,部分国内外学者进一步考虑通过DG与柔性互联装置协调配合以实现交直流网络优化运行。文献[8]在文献[4]的基础上,考虑DG不同的渗透比例,建立了以VSC端口功率为变量的优化数学模型,但未考虑VSC直流侧控制策略的影响;文献[9]提出了一种含智能软开关的柔性配电网DG规划方法,但考虑的运行目标单一;文献[10]通过能量路由器与DG的协调规划,提高了配电网消纳可再生能源的能力和网络运行的经济性,但未考虑网络运行的安全性;文献[11]将柔性互联装置与充电装置相结合,建立了计及DG的多目标优化模型,但未考虑DG接入前的规划;文献[12]提出了一种DG接入含柔性互联装置的交直流混合配电网的优化配置方法,提高了交直流混合配电网对DG的消纳水平,但未考虑DG接入后二者的协调运行。
针对以上问题,文中提出一种基于DG和多端VSC协调控制的交直流混合配电网优化运行方法。首先,针对DG的选址,采用节点网损灵敏度分析的方法,得出交流网络不同位置的负荷节点对网络损耗影响的一般规律,进而定义了一种潮流计算时评估DG接入的指标;然后,建立考虑网络运行经济性、安全性和DG利用率的多目标优化模型,对多端VSC端口功率电压和DG有功出力进行协调控制。仿真计算结果分析证明了所提优化运行方法的有效性。
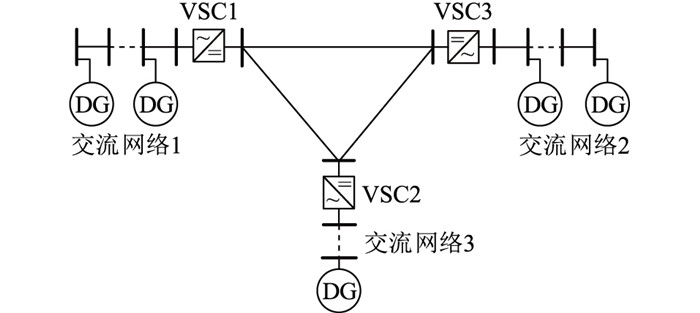
1 交直流混合配电网结构及VSC建模 1.1 交直流混合配电网结构交直流混合配电网有多种构建方式,如文献[13]将部分现有交流线路改造为直流线路,并通过换流器与交流线路连接形成交直流混合配电网;文献[14]将已知配电系统进行扩展,融合电力电子变压器得到交直流混合配电网,其直流侧通过两端并供互联形成了环型结构。考虑到VSC作为交直流配电网耦合连接的典型装置,参考文献[14],构建图 1所示交直流混合配电网。
|
图 1 交直流混合配电网结构 Fig. 1 Structure of AC/DC hybrid distribution network |
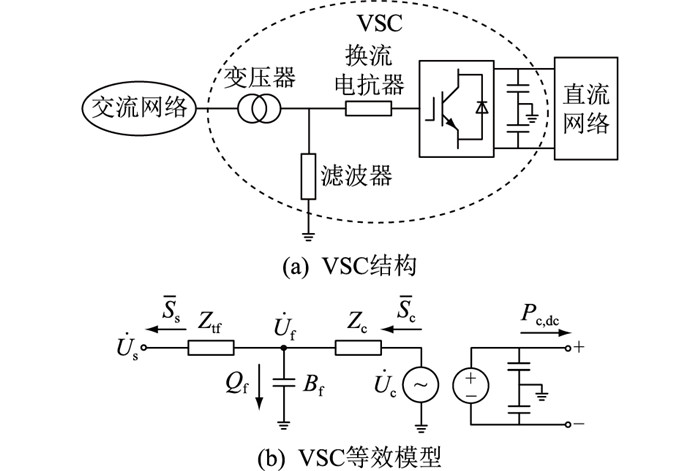
VSC等效模型的建立是交直流混合配电网潮流计算的基础[15—16]。VSC结构及等效模型见图 2。
|
图 2 VSC结构及等效模型 Fig. 2 Structure and equivalent model of VSC |
研究表明,DG并网对配电网的运行有很大影响,包括电压水平、网损等方面,且其影响程度与DG的安装位置密切相关[17]。合理的安装位置可以有效减小有功损耗、改善配电网电压质量。配置不合理将适得其反,甚至会影响电网安全稳定运行。文中通过灵敏度分析提出一种DG选址指标。
2.1.1 节点网损灵敏度分析交流网络中任一节点i的负荷功率为Pi+jQi,假设交流网络中其他节点均没有负荷,则交流网络的损耗为节点i的负荷电流由根节点流至节点i经过所有支路引起的有功损耗。对于整个交流网络的损耗,可先算出每个节点(i=1, 2, …, N)的负荷电流引起的损耗,最后依据叠加定理求和即可。
以图 3所示交流配电系统的任一节点i进行分析,其中r为根节点;Rr, i,Xr, i分别为节点i到根节点的等效电阻、等效电抗;Pi,Qi分别为节点i的负荷有功、无功功率。假设系统中仅有该节点接入负荷,则系统的网络损耗都是由该节点产生的,此时的网损如式(1)所示,Ui为节点i的电压。
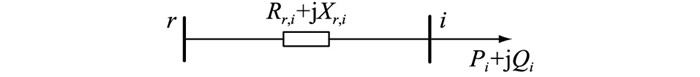
|
图 3 配电网节点i等效图 Fig. 3 Equivalent diagram of node i in the distribution network |
| $ \Delta P=\frac{P_i^2+Q_i^2}{U_i^2} R_{r, i} $ | (1) |
引入根节点r的电压:
| $ U_r=U_i+\frac{P_i R_{r, i}+Q_i X_{r, i}}{U_i} $ | (2) |
配电网的网损还可以近似表示为:
| $ \Delta P=\frac{\left(U_r-U_i\right)^2}{R_{r, i}} $ | (3) |
联立式(1)—式(3),由节点i引起的网损最终可以表示为:
| $ \Delta P=\frac{1}{2}\left[\frac{P_i^2+Q_i^2}{U_i^2} R_{r, i}+\frac{\left(P_i R_{r, i}+Q_i X_{r, i}\right)^2}{U_i^2 R_{r, i}}\right] $ | (4) |
以交流配电网的不同节点作为分析对象,从式(4)可以看出,网络的有功损耗可以看成是关于不同节点到根节点的等效电阻Rr, i和等效电抗Xr, i的函数。考虑到网络的有功损耗是由线路电阻造成的,并且不同节点对应的Rr, i也不同,因此Rr, i可以反映节点在配电网中的位置信息。对式(4)中变量Rr, i求偏导数,即:
| $ \begin{gathered} \partial \Delta P / \partial R_{r, i}=\left(P_i^2+Q_i^2\right) /\left(2 U_i^2\right)+\left[2 P _ { i } R _ { r , i } \left(P_i R_{r, i}+\right.\right. \\ \left.\left.Q_i X_{r, i}\right)-\left(P_i R_{r, i}+Q_i X_{r, i}\right)^2\right] /\left(2 U_i^2 R_{r, i}^2\right) \end{gathered} $ | (5) |
由式(5)可知,若使节点i在系统中引起的网损最小,应该满足:
| $ F_i=\frac{\partial \Delta P}{\partial R_{r, i}}=0 $ | (6) |
文中将Fi定义为节点i的网损灵敏度指标,用来衡量由节点i引起的网络损耗,Fi值越接近0,说明引起的效果越小。因此,式(5)可表示为:
| $ \begin{gathered} \left(P_i^2+Q_i^2\right) / U_i^2+\left[2 P_i R_{r, i}\left(P_i R_{r, i}+Q_i X_{r, i}\right)-\right. \\ \left.\left(P_i R_{r, i}+Q_i X_{r, i}\right)^2\right] /\left(U_i^2 R_{r, i}\right)=0 \end{gathered} $ | (7) |
整理得:
| $ \begin{gathered} R_{r, i}^2\left(P_i^2+Q_i^2\right)=\left(P_i R_{r, i}+Q_i X_{r, i}\right)^2- \\ 2 P_i R_{r, i}\left(P_i R_{r, i}+Q_i X_{r, i}\right) \end{gathered} $ | (8) |
由式(8)可知,等式两边的值越接近,节点i引起的网络损耗就越小,因此潮流计算时可以采用式(9)计算得到Fi为:
| $ \begin{gathered} F_i=\mid\left(P_i^2+Q_i^2\right) R_{r, i}^2+\left(P_i R_{r, i}+Q_i X_{r, i}\right)^2- \\ 2 P_i R_{r, i}\left(P_i R_{r, i}+Q_i X_{r, i}\right) \mid \end{gathered} $ | (9) |
Fi综合考虑了节点的位置和负荷功率,节点i的Fi越大,其引起的网络有功损耗越大。当网络结构确定时,网络损耗较大主要是由节点i负荷大小不合理引起的,应当安装DG以减小该节点的Fi,从而起到降低网络损耗的作用。DG选址时,应按照Fi从大到小的顺序进行安装。
2.2 DG和多端VSC的协调控制网络运行需要考量的不仅是网络损耗,文中在DG选址的基础上,进一步构建综合考虑网络运行经济性、电压质量和DG利用率的多目标优化模型,对多端VSC的端口功率电压变量和DG的有功出力进行协调控制。
2.2.1 多端VSC的协调控制策略VSC的交直流端口具有不同的控制模式,有功功率和无功功率可以实现独立控制。交流端口包含定功率控制和定电压控制2种控制模式;多端VSC的直流端口采取的控制策略包括下垂协调控制和主从协调控制。
以图 1为例,当多端VSC采取下垂协调控制时,VSC1、VSC2、VSC3的直流端口均采用有功-电压下垂控制,共同承担系统功率平衡和电压调节,如图 4所示,Udck, max,Udck, min分别为直流侧电压的最大值和最小值。

|
图 4 下垂协调控制策略 Fig. 4 Droop control strategy |
对应的控制方程为:
| $ U_{\mathrm{dc} k}-U_{\mathrm{dc}, \text { ref }k}-\rho_k\left(P_{\mathrm{dc} k}-P_{\mathrm{dc}, \text { ref }k}\right)=0 \quad k=1, 2, 3 $ | (10) |
式中:ρk为曲线的斜率,即下垂系数;Udck, Pdck分别为直流侧电压和功率;Udc, refk,Pdc, refk为端口设定值;k为多端VSC中各换流器的标号。
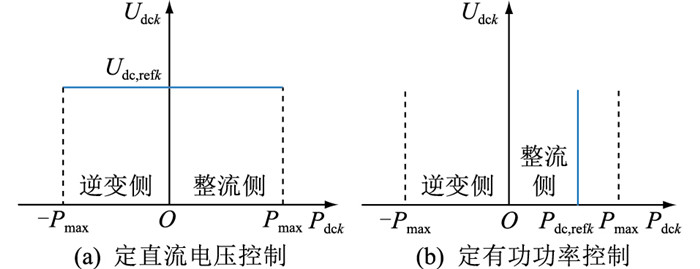
主从协调控制的思想是将网络中的换流器分为主、从两部分。当多端VSC采用主从协调控制时,图 1中VSC1采取定直流电压控制,VSC2、VSC3采用定有功功率控制,如图 5所示,Pmax为换流器端口有功功率最大值。
|
图 5 主从协调控制策略的2种控制模式 Fig. 5 Two control modes of master-slave control strategy |
多目标优化问题定义为:
| $ \left\{ {\begin{array}{*{20}{l}} {\min {f_h}(X) = \left\{ {{f_1}(X), {f_2}(X), \cdots , {f_l}(X)} \right\}}\\ {{\rm{ s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;{g_j}(X) \le 0\quad j = 1, 2, \cdots , p{\rm{ }}}\\ {\;\;\;\;\;\;\;\;\;\;\;X \in D \subset {\mathit{\boldsymbol{R}}^n}} \end{array}} \right. $ | (11) |
式中:fh(X)为多目标函数;I为目标函数的个数;gj(X)为对控制变量及状态量的约束;p为约束条件个数;X为控制变量,文中模型的控制变量为多端VSC端口的功率电压和DG的有功出力;D为定义域;Rn为n维空间向量。文中以最小化网络有功总损耗、节点电压偏移量和DG的盈余量为目标,具体如式(12)、式(15)和式(16)所示。
| $ \begin{gathered} \min f_1=P_{\mathrm{ac-loss}}+P_{\mathrm{dc}-\mathrm{loss}}+P_{\text {FID-loss }}= \\ \sum\limits_{i=1}^n U_i \sum\limits_{j \in i} U_j\left(G_{i j} \cos \delta_{i j}+B_{i j} \sin \delta_{i j}\right)+ \\ \sum\limits_{i=1}^{m-1} \sum\limits_{j=i+1}^m G_{i j}\left(U_i-U_j\right)^2+P_{\mathrm{vsc}-\mathrm{loss}} \end{gathered} $ | (12) |
其中,VSC的内部有功损耗为:
| $ P_{\mathrm{vsc}-\text { loss }}=a+b I_{\mathrm{c}}+c I_{\mathrm{c}}^2 $ | (13) |
| $ I_{\mathrm{c}}=\frac{\sqrt{P_{\mathrm{c}}^2+Q_{\mathrm{c}}^2}}{\sqrt{3} U_{\mathrm{c}}} $ | (14) |
式中:Pac-loss,Pdc-loss,Pvsc-loss分别为交流、直流部分和VSC内部有功损耗;n为交流系统节点个数;Uj为节点j的电压;Gij,Bij,δij分别为节点i,j间的电导、电纳和相角差;m为直流系统的节点个数;a,b,c为VSC的损耗系数;Pc,Qc,Ic分别为换流器的有功功率、无功功率和电流;Uc为可控电压源电压。
| $ \min f_2=\sum\limits_{i=1}^{N_A}\left(\frac{U_i-U_{\mathrm{spec}, i}}{U_{\max , i}-U_{\min , i}}\right)^2 $ | (15) |
式中:NA为所有节点数目;Uspec, i为节点i的电压期望值;Umax, i,Umin, i分别为节点i电压的最大值和最小值。
| $ \min f_3=1-\left(\sum\limits_{q=1}^{N_{\mathrm{G}}} P_{\mathrm{DG}, q} / \sum\limits_{q=1}^{N_{\mathrm{G}}} P_{\mathrm{DG} \max , q}\right) $ | (16) |
式中:NG为DG安装节点数目;PDG, q为安装在节点q的DG有功出力;PDGmax, q为安装在节点q的DG出力最大值。
2.2.3 约束条件文中采用交替迭代法求解交直流混合配电网潮流,求解的思想是将交、直流潮流方程分别进行迭代求解,以VSC为界限通过端口参数进行交互[19—20]。为保证网络稳定运行,要求满足支路功率约束、状态变量约束和控制变量约束。
(1) 交流和直流部分支路功率约束。
| $ \left\{\begin{array}{l} S_{i j, \mathrm{AC}} \leqslant S_{\max , \mathrm{AC}} \\ S_{j i, \mathrm{AC}} \leqslant S_{\max , \mathrm{AC}} \\ S_{i j, \mathrm{DC}} \leqslant S_{\max , \mathrm{DC}} \\ S_{j i, \mathrm{DC}} \leqslant S_{\max , \mathrm{DC}} \end{array}\right. $ | (17) |
式中:Sij, AC,Sji, AC分别为交流支路ij的正向和反向视在功率; Sij, DC,Sji, DC分别为直流支路ij的正向和反向视在功率;Smax, AC,Smax, DC分别为交流和直流支路输送视在功率的极限值。
(2) 节点电压约束。
| $ U_{\min , i} \leqslant U_i \leqslant U_{\max , i} $ | (18) |
(3) 文中模型的控制变量约束。
| $ \left\{\begin{array}{l} \sqrt{P_{\mathrm{vsc}}^2+Q_{\mathrm{vsc}}^2} \leqslant S_{\max , \mathrm{vsc}} \\ P_{\mathrm{DGmin}} \leqslant P_{\mathrm{DG}} \leqslant P_{\mathrm{DGmax}} \\ S_{\mathrm{smin}} \leqslant S_{\mathrm{s}} \leqslant S_{\mathrm{smax}} \\ P_{\mathrm{dcmin}} \leqslant P_{\mathrm{dc}} \leqslant P_{\mathrm{dcmax}} \end{array}\right. $ | (19) |
式中:Pvsc,Qvsc分别为VSC的有功功率和无功功率;Smax, vsc为VSC的最大容量;PDG为DG实际有功出力;PDGmin,PDGmax分别为DG出力的最小值和最大值;Ss为VSC交流侧端口的传输功率;Ssmin,Ssmax分别为交流端口的最小、最大传输容量;Pdc为VSC直流侧端口注入直流配电网的有功功率;Pdcmin,Pdcmax分别为注入功率的上、下限值。
2.2.4 NSGA-II优化算法多目标优化求解通常采用约束法、权重系数等方法将多目标问题转化为单目标问题[21—22],虽然这种方法能在一定程度上降低求解难度,但破坏了多目标优化本身的物理意义,且寻优结果受权重系数等参数影响较大。针对文中交直流混合配电网多目标优化问题,采用非支配排序遗传算法[23—24](nondominated sorting genetic algorithm-Ⅱ, NSGA-Ⅱ),融合精英策略,能够实现高效搜索,且不需要事先对目标函数权重值进行调整取值,可以快速得到一系列Pareto最优解,以供决策者根据不同需求进行取值。
3 优化运行实现流程文中提出的基于DG和多端VSC协调控制的交直流混合配电网运行步骤如下。
步骤1:确定交直流混合配电网。输入系统基准功率、系统节点数、线路数、线路参数、种群数目、迭代次数等网络原始参数。
步骤2:将交流侧网络各个节点的已知参数代入式(9),求出各个节点网损灵敏度指标的数值Fi,按照Fi由大到小确定DG的安装位置。
步骤3:确定控制变量和目标函数。文中协调控制的控制变量为多端VSC的运行功率电压和DG的有功出力。
步骤4:采用NSGA-Ⅱ多目标求解算法[23—24]对多目标函数进行求解, 满足迭代条件则输出Pareto最优解集。
步骤5:根据DG的盈余量确定不同的解集方案,以便为决策人员提供参考。
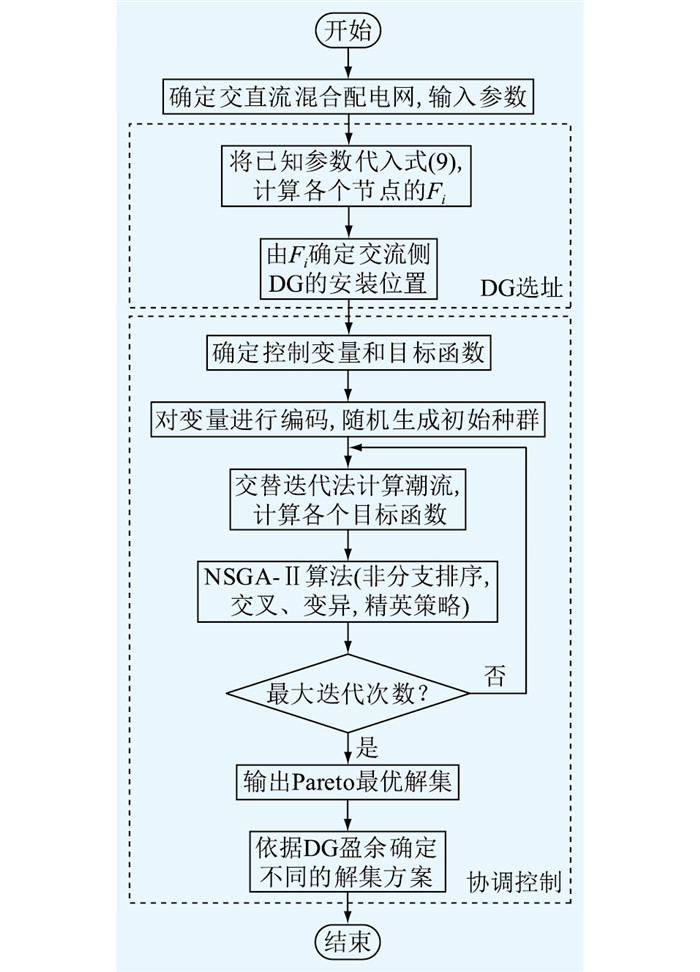
结合上述步骤,基于DG和多端VSC协调控制的交直流混合配电网优化运行流程见图 6。
|
图 6 优化运行实现流程 Fig. 6 Optimized operation implementation process |
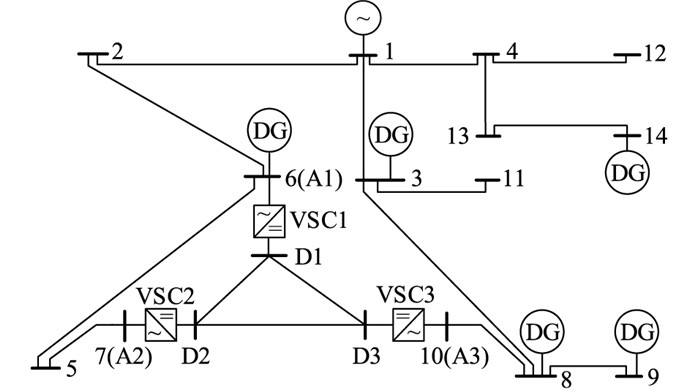
将IEEE 14节点配电系统修改为交直流混合配电网进行验证,如图 7所示,换流器VSC1、VSC2和VSC3的交流端口分别接在14节点配电网的节点6,7和10上,3个直流端口形成多端VSC交直流混合配电网。
|
图 7 基于修改IEEE 14节点系统的交直流混合配电网 Fig. 7 AC/DC hybrid distribution network based on modified IEEE 14-bus system |
潮流计算时选取的基准电压为10 kV,三相基准功率为100 MV ·A。交流线路的阻抗和负荷参数与IEEE 14节点配电网参数相同,直流电缆线路采用ACSR240电缆,电缆线路长度均为10 km。VSC等效变压器阻抗Ztf为0.001 5+j0.112 1 Ω,电纳Bf为0.088 7 S,换流电抗器阻抗Zc为0.000 1+j0.164 3 Ω;损耗系数a=1.103,b=0.887,c=2.885(整流侧),c=4.371(逆变侧);下垂系数取0.005。电压允许的波动范围设置为[0.95, 1.05] p.u.。对于NSGA-Ⅱ算法,设置种群数目为100,迭代次数为200,交叉概率和变异概率分别为0.9和0.01。
VSC1的A1端口采用定电压控制方式,在系统优化运行时通过调节末端电压来影响交流潮流分布;VSC2的A2端口和VSC3的A3端口采用定功率控制方式,优化运行时作为可调负荷来影响交流潮流分布;多端VSC直流端口采用下垂协调控制时,下垂系数在实际运行时不能频繁调整,需要提前设定,因此不作为优化变量。
4.2 仿真结果分析 4.2.1 DG选址仿真分析首先通过各节点的Fi确定DG接入位置。根据式(9)得到交流侧各节点的Fi,如表 1所示。
|
|
表 1 各节点的Fi值 Table 1 Fi of each node |
同一分支上安装DG的数目一般不超过2个[25],虽然节点3,8,9位于同一分支,但考虑到该分支的Fi都很高,故选择节点3,8,9,14,6安装DG,具体安装位置如图 7所示。
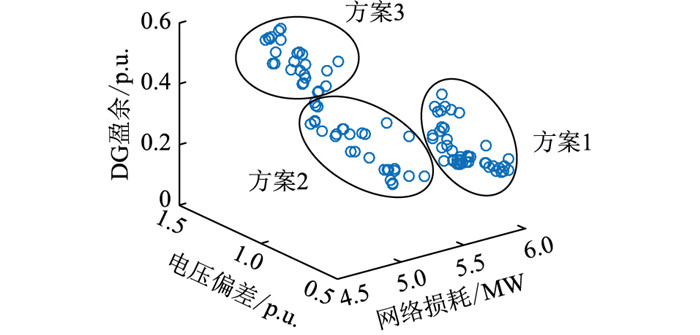
4.2.2 多端VSC采用下垂控制时的优化模型仿真分析当多端VSC采用下垂协调控制时,协调控制DG有功出力和多端VSC获得的Pareto最优解集如图 8所示。
|
图 8 采用下垂协调控制后的Pareto最优解集 Fig. 8 Pareto optimal sets by droop control |
根据DG的盈余量区段[0, 0.2] p.u.,[0.2, 0.4] p.u.和[0.4, 0.6] p.u.,对应DG利用率区段80%~100%, 60%~80%和40%~60%,将得到的Pareto最优解集划分成3个最优解集方案,如表 2所示。
|
|
表 2 下垂控制下3种最优解集方案 Table 2 Three optimal solution set schemes under droop control |
方案1能实现DG的充分消纳,但对比方案2、3,却增大了网络损耗和电压偏差。这是由于以分布式光伏为代表的DG会因高渗透带来功率倒送、节点电压越限等问题,从而增加网络损耗,造成电压偏差增大。方案3可以实现最小的网络损耗,但由于DG的利用率不高,就地补偿的有功功率不能很好地减少线路的功率流动,抑制了调节电压的效果。方案2能实现DG 60%~80%的消纳,对网损和电压偏差的抑制效果也较为明显,若不考虑各个目标的侧重程度,可以考虑将其作为Pareto解集的折衷解集。
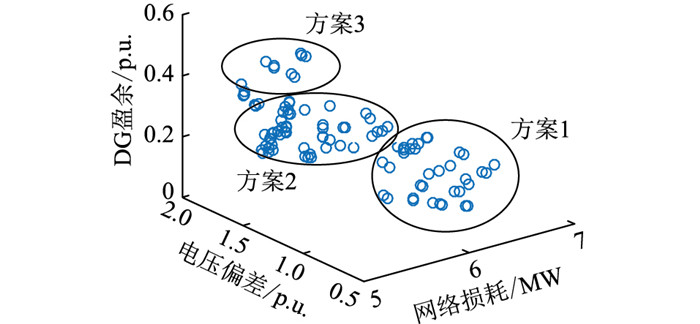
4.2.3 多端VSC采用主从控制时的优化模型仿真分析当多端VSC采取主从协调控制策略时,获得的Pareto最优解集如图 9所示。对比图 8和图 9,可以看出二者整体的收敛趋势是相同的。
|
图 9 采用主从协调控制优化后的Pareto最优解集 Fig. 9 Pareto optimal sets by master-slave control |
与下垂协调控制策略结果分析相同,根据DG盈余将得到的Pareto最优解集划分成3个最优解集方案,如表 3所示。
|
|
表 3 主从控制下3种最优解集方案 Table 3 Three optimal solution set schemesunder master-slave control |
从图 8、图 9中解集的整体分布可以看出,多端VSC采用主从协调控制更有利于DG的消纳,但采用下垂协调控制后网损和电压偏差更小。这是因为下垂协调控制可以通过端口有功功率和电压的斜率关系制约实现各个端口间功率的自动分配,从而有效改善网络中的潮流分布。
5 结论文中综合多端柔性互联装置整体潮流调控能力和DG局部调节的优势,提出一种基于DG和多端VSC协调控制的交直流混合配电网优化运行方法,通过对改进的IEEE 14节点交直流混合配电网进行分析、验证,得到相关结论如下:
(1) DG的优化接入问题实际上是离散非线性整数规划问题,对算法的精度和适用性要求较高。文中所提的DG选址指标能根据网络特征有效地确定DG接入位置,摆脱了算法选择的局限,简化了优化计算,但所提选址指标适用场景有限,仅适用于交直流混合配电网交流侧和传统交流配电网DG选址,而未考虑交直流混合配电网直流的DG接入情况。
(2) 随着配电网DG的渗透率不断提高,多端VSC作为一种高效的调节手段,通过与DG相配合,可提高可再生能源的消纳水平以及配电系统运行的经济性和安全性。
(3) 采用NSGA-Ⅱ多目标优化算法求解多目标优化问题得到均匀分布的Pareto前沿,能为决策人员提供较为完整和准确的信息,实际工程中决策人员可根据不同目标的侧重程度得到具体方案。
本文得到新能源电力系统国家重点实验室(华北电力大学)自主研究课题项目(LAPS202124)资助,谨此致谢!
| [1] |
谢宁, 曾杰, 徐琪, 等. 交直流混合的分布式可再生能源系统综述[J]. 南方电网技术, 2017, 11(9): 30-35. XIE Ning, ZENG Jie, XU Qi, et al. Overview of AC & DC hybrid distributed renewable energy system[J]. Southern Power System Technology, 2017, 11(9): 30-35. (  0) 0) |
| [2] |
BAHRAMI S, THERRIEN F, WONG V W S, et al. Semidefinite relaxation of optimal power flow for AC-DC grids[J]. IEEE Transactions on Power Systems, 2017, 32(1): 289-304. DOI:10.1109/TPWRS.2016.2543726 (  0) 0) |
| [3] |
梁海平, 王岩, 刘英培, 等. 计及源荷不确定性的混合交直流主动配电网分层-分布式优化调度[J]. 电力自动化设备, 2021, 41(12): 62-69, 77. LIANG Haiping, WANG Yan, LIU Yingpei, et al. Hierarchical-distributed optimal scheduling of hybrid AC/DC active distribution network considering source and load uncertainties[J]. Electric Power Automation Equipment, 2021, 41(12): 62-69, 77. (  0) 0) |
| [4] |
芮松华, 刘海璇, 王洪波, 等. 基于遗传-蚁群算法的交直流配电网分布式电源优化配置[J]. 电力建设, 2019, 40(4): 9-17. RUI Songhua, LIU Haixuan, WANG Hongbo, et al. DG planning method for AC/DC distribution network using genetic-ant colony algorithm[J]. Electric Power Construction, 2019, 40(4): 9-17. DOI:10.3969/j.issn.1000-7229.2019.04.002 (  0) 0) |
| [5] |
罗志刚, 韦钢, 袁洪涛, 等. 基于区间直觉模糊理论的直流配网规划方案综合决策[J]. 电工技术学报, 2019, 34(10): 2011-2021. LUO Zhigang, WEI Gang, YUAN Hongtao, et al. Comprehensive decision of DC distribution network planning based on interval intuitionistic fuzzy theory[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2011-2021. (  0) 0) |
| [6] |
王卓. 基于换流器选址的中压交直流混合配电网规划研究[D]. 北京: 中国电力科学研究院, 2019. WANG Zhuo. Research of medium voltage AC-DC hybrid distribution network planning based on converter siting[D]. Beijing: China Electric Power Research Institute, 2019. (  0) 0) |
| [7] |
王家怡, 高红均, 刘友波, 等. 考虑风电不确定性的交直流混合配电网分布式优化运行[J]. 中国电机工程学报, 2020, 40(2): 550-563. WANG Jiayi, GAO Hongjun, LIU Youbo, et al. A distributed operation optimization model for AC/DC hybrid distribution network considering wind power uncertainty[J]. Proceedings of the CSEE, 2020, 40(2): 550-563. (  0) 0) |
| [8] |
刘浩武, 王守相, 刘琪, 等. 考虑DG渗透率的交直流混合配电网运行优化方法[J]. 供用电, 2020, 37(5): 18-23. LIU Haowu, WANG Shouxiang, LIU Qi, et al. Operation optimization method of AC/DC distribution network considering DGpenetration rate[J]. Distribution & Utilization, 2020, 37(5): 18-23. (  0) 0) |
| [9] |
薛飞, 马丽, 朱昊, 等. 柔性配电网中考虑SOP优化的分布式电源双层规划[J]. 电力系统及其自动化学报, 2020, 32(8): 109-115. XUE Fei, MA Li, ZHU Hao, et al. Bi-level programming of distributed generations in flexible distribution network with SOP optimization[J]. Proceedings of the CSU-EPSA, 2020, 32(8): 109-115. (  0) 0) |
| [10] |
盛万兴, 段青, 王良, 等. 基于多代理协调机制的能量路由器群组与配电网综合规划[J]. 高电压技术, 2021, 47(1): 1-13. SHENG Wanxing, DUAN Qing, WANG Liang, et al. Comprehensive planning for energy routers and distribution network based on multi-agent system coordination mechanism[J]. High Voltage Engineering, 2021, 47(1): 1-13. (  0) 0) |
| [11] |
贾善翔, 彭克, 李喜东, 等. 基于智能软开关的柔性互联交直流配电系统分布式优化[J]. 电力系统自动化, 2021, 45(8): 95-103. JIA Shanxiang, PENG Ke, LI Xidong, et al. Distributed optimization of flexible interconnected AC/DC distribution system based on soft open point[J]. Automation of Electric Power Systems, 2021, 45(8): 95-103. (  0) 0) |
| [12] |
王守相, 李琦, 赵倩宇, 等. 计及源荷随机性的交直流配电网电压多目标优化改进粒子群算法[J]. 电力系统及其自动化学报, 2021, 33(12): 10-17. WANG Shouxiang, LI Qi, ZHAO Qianyu, et al. Improved particle swarm optimization algorithm for multi-objective voltage optimization of AC/DC distribution network considering the randomness of source and loads[J]. Proceedings of the CSU-EPSA, 2021, 33(12): 10-17. (  0) 0) |
| [13] |
张璐, 唐巍, 梁军, 等. 基于VSC的交直流混合中压配电网功率-电压协调控制[J]. 中国电机工程学报, 2016, 36(22): 6067-6075. ZHANG Lu, TANG Wei, LIANG Jun, et al. Power-voltage coordinated control in hybrid AC/DC medium voltage distribution networks based on VSC[J]. Proceedings of the CSEE, 2016, 36(22): 6067-6075. (  0) 0) |
| [14] |
耿琪, 胡炎, 何建宗, 等. 含电力电子变压器的交直流混合电网最优潮流[J]. 电网技术, 2019, 43(9): 3288-3298. GENG Qi, HU Yan, HE Jianzong, et al. Optimal power flow for hybrid AC/DC grid with power electronic transformer[J]. Power System Technology, 2019, 43(9): 3288-3298. (  0) 0) |
| [15] |
邓红雷, 张莉彬, 唐崇旺, 等. 一种基于直角坐标注入电流模型的交直流潮流计算方法[J]. 电测与仪表, 2020, 57(24): 29-34. DENG Honglei, ZHANG Libin, TANG Chongwang, et al. Algorithm with AC/DC power flow calculation based on rectangular coordinate current-injecting model[J]. Electrical Measurement & Instrumentation, 2020, 57(24): 29-34. (  0) 0) |
| [16] |
胥威汀, 欧阳雪彤, 苏运掣, 等. 计及VSC的交直流混联电网扩展规划研究[J]. 电力系统保护与控制, 2019, 47(13): 30-36. XU Weiting, OUYANG Xuetong, SU Yunche, et al. Expansion planning of AC/DC power grid with VSC[J]. Power System Protection and Control, 2019, 47(13): 30-36. (  0) 0) |
| [17] |
刘科研, 盛万兴, 马晓晨, 等. 基于多种群遗传算法的分布式光伏接入配电网规划研究[J]. 太阳能学报, 2021, 42(6): 146-155. LIU Keyan, SHENG Wanxing, MA Xiaochen, et al. Planning research of distributed photovoltaic source access distribution network based on multi-population genetic algorithm[J]. Acta Energiae Solaris Sinica, 2021, 42(6): 146-155. (  0) 0) |
| [18] |
林昶咏, 吴桂联, 张林垚, 等. 分布式电源接入配电系统优化规划方案[J]. 现代电力, 2019, 36(6): 82-87. LIN Changyong, WU Guilian, ZHANG Linyao, et al. Planning scheme optimization for distributed generation accessed in distribution system[J]. Modern Electric Power, 2019, 36(6): 82-87. (  0) 0) |
| [19] |
姜涛, 张勇, 李雪, 等. 电力系统交直流潮流的全纯嵌入计算[J]. 电工技术学报, 2021, 36(21): 4429-4443, 4481. JIANG Tao, ZHANG Yong, LI Xue, et al. A holomorphic embedded method for solving power flow in hybrid AC-DC power system[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4429-4443, 4481. (  0) 0) |
| [20] |
彭克, 张新慧, 陈羽. 适用于多端柔性互联的交直流配电网潮流计算方法[J]. 电力自动化设备, 2017, 37(1): 22-27. PENG Ke, ZHANG Xinhui, CHEN Yu. Power flow calculation algorithm for AC-DC hybrid distribution network with multi-terminal flexible interconnection[J]. Electric Power Automation Equipment, 2017, 37(1): 22-27. (  0) 0) |
| [21] |
高崇, 王天霖, 张俊潇, 等. 基于协同进化NSGA-Ⅱ的多目标交直流配电网规划方法[J/OL]. 电测与仪表: 1-7[2021-08-11]. http://kns.cnki.net/kcms/detail/23.1202.TH.20210125.1605.007.html. GAO Chong, WANG Tianlin, ZHANG Junxiao, et al. Multi-objective AC/DC distribution network planning method based on co-evolution NSGA-Ⅱ[J/OL]. Electrical Measurement and Instrumentation: 1-7[2021-08-11]. http://kns.cnki.net/kcms/detail/23.1202.TH.20210125.1605.007.html. (  0) 0) |
| [22] |
刘青, 赵洋, 李宁, 等. 基于分布式神经动力学算法的微电网多目标优化方法[J]. 电力系统保护与控制, 2021, 49(11): 105-114. LIU Qing, ZHAO Yang, LI Ning, et al. Multiple objective optimization of a microgrid based on a distributed neural dynamics algorithm[J]. Power System Protection and Control, 2021, 49(11): 105-114. (  0) 0) |
| [23] |
武晓朦, 王欢. 基于NSGAⅡ的交直流系统无功优化[J]. 西安石油大学学报(自然科学版), 2019, 34(5): 122-126. WU Xiaomeng, WANG Huan. Reactive power optimization of AC-DC system on NSGAⅡ[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2019, 34(5): 122-126. (  0) 0) |
| [24] |
史晨豪, 唐忠, 戴尉阳, 等. 基于多要素改进NSGAⅡ算法的有源配电网多目标优化策略[J]. 供用电, 2021, 38(6): 50-55. SHI Chenhao, TANG Zhong, DAI Weiyang, et al. Multi-ojective optimization strategy of active distribution network based on multi-factor improved NSGA Ⅱ algorithm[J]. Distribution & Utilization, 2021, 38(6): 50-55. (  0) 0) |
| [25] |
MOUSAVIZADEH S, HAGHIFAM M R, SHARIATKHAH M H. A new approach for load flow calculation in AC/DC distribution networks considering the control strategies of different converters[J]. International Transactions on Electrical Energy Systems, 2016, 26(11): 2479-2493. (  0) 0) |
2. State Grid Liaoning Electric Power Co., Ltd. Economic Research Institute, Shenyang 110015, China
 2022, Vol. 41
2022, Vol. 41


 徐永海(1966),男,博士,教授,研究方向为新能源电力系统、电能质量分析等(E-mail:
徐永海(1966),男,博士,教授,研究方向为新能源电力系统、电能质量分析等(E-mail: