文章编号: 2096-3203(2022)04-0183-09 中图分类号: TM74
2. 国网江苏省电力有限公司双创中心, 江苏 南京 210024;
3. 东南大学电气工程学院, 江苏 南京 210096
近年来,电动汽车(electric vehicle, EV)以其低碳、节能的优势被大范围推广应用[1-5]。2030年,我国EV保有量将会达到6 000万辆[6]。大规模EV入网,不仅提高了电力市场资源利用率,还推动了能源清洁低碳变革。虚拟电厂(virtual power plant, VPP)作为电力系统中的一种新型运营主体[7-10],可在聚合管理某区域EV充电行为的同时,有效整合随机性强且分布范围广的分布式能源共同参与电力市场,既可引导EV用户有序充电,还可实现多种新能源间的优势互补。
目前,国内已有针对EV有序充电管理、VPP运营商与EV博弈的相关研究。文献[11]基于主从博弈理论实现小区充电代理商与EV间的利益分配,但接入的EV数量较少,且未协调其他可控资源共同参与电力市场。文献[12]通过动态分时电价实现充电站内EV的有序充电管理,但未考虑EV充电过程的随机性。文献[13]基于多充电站代理商间的非合作博弈关系,建立电力零售市场下充电站的投标策略,实现EV与电网的有序互动, 但未考虑VPP与EV间的利益均衡。文献[14]提出基于博弈论的决策优化模型,避免了大规模EV直接入网带来的优化控制问题,但仿蛛网算法和时间分块法不能准确高效地解决博弈问题中的非线性部分。文献[15]虽解决了多VPP的利益均衡问题,但VPP内针对EV用户的分时电价是固定的,未考虑EV用户的充电成本。
目前,为处理风电出力和常规负荷波动给VPP运行带来的风险[16],常用的方法有方差计量法、风险价值(value at risk, VaR)法及条件风险价值(conditional value at risk, CVaR)法。方差计量法将大于收益均值的部分视为风险,存在不合理性[17]。VaR法在原理和统计估计方法上存在缺陷,并未考虑风险信息的“尾部效应”。而CVaR法考虑了尾部风险,且其凸性使得基于CVaR的组合优化方法更易于实施,故CVaR相比前两者更有优势。文献[17]将CVaR理论引入VPP参与调峰市场的优化模型中,为评估VPP运营商参与调峰市场的风险收益提供了依据。文献[18]基于两阶段随机规划,建立计及CVaR的VPP能量管理模型,在可接受的风险水平下实现VPP收益最大化。文献[19]将CVaR理论运用到综合能源系统优化中, 提高了系统的风险管控能力。通过上述文献可知,CVaR法在规避风险、协助运营商获得稳定收益方面较有优势。
基于上述文献提到的EV有序充电管理方法、博弈论及CVaR理论,文中提出以VPP作为售电运营商,协调燃气轮机组、风电机组、储能、常规负荷和需求响应负荷,参与EV有序充电管理的主从博弈模型。模型中,VPP通过整合内部资源并制定合理的定价策略引导EV有序充电,这不仅解决了VPP运营商与EV用户间的利益分配问题,且完成了内部资源的整合优化。进一步地,考虑风电出力的波动性及常规负荷的不确定性对VPP运营收益的影响,文中将CVaR理论引入VPP运营商与EV用户的主从博弈定价模型中,用于衡量运营商风险收益,为VPP运营商依据自身风险偏好制定运营策略提供了参考。
1 VPP结构及其运营模式文中VPP结构由燃气轮机组、风电机组、储能、常规负荷、需求响应负荷和EV组成[20]。假设VPP运营商作为价格接受者,在整合内部可控资源后参与日前电力市场[21],EV用户按照与VPP运营商议定的购电价格充电,其余分布式资源则统一按照电网电价购售电,VPP的具体运营模式为[22]:
(1) 当日能量市场交易结束前,EV用户向运营商提交次日的充电时段和充电需求电量。VPP运营商则基于EV用户需要,整合协调内部各类可控负荷后,确定次日各时段电量需求,拟定次日的购售电计划。
(2) VPP运营商在日前市场同电网签订购售电合同后,及时向EV用户发布次日各时段电价信息,并安排内部其余可控资源的出力计划。另外,文中规定VPP运营商的零售电价不得高于其在日前市场中的购电价格,且设置电价上限及均值,避免VPP恶意定价,尽可能保证EV用户利益。
(3) EV用户在入网后由智能终端自动控制EV充电,并即时支付充电费用,对未按照约定时段及电量充电的EV用户,予以履约考核。
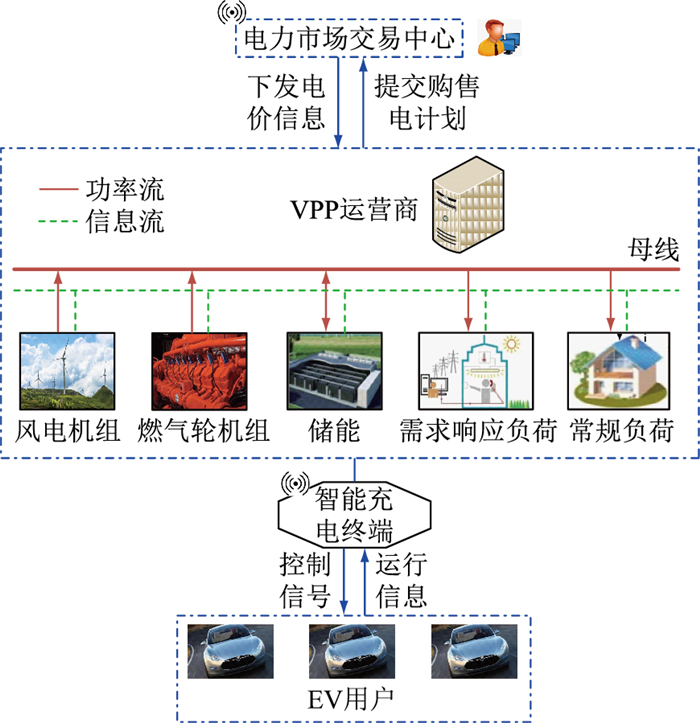
基于上述运营模式,VPP运营商工作的重点是制定次日各时段的充电电价,与传统的定价优化问题不同,运营商的收入取决于EV的充电策略及各类可控资源的运行安排,但EV的充电行为并不受运营商的直接控制,而是受电价的影响。根据电价约定,日均充电价格不变,如果VPP运营商刻意抬升某时段电价,势必有其他时段的电价低于平均值,此时智能终端会自动选择电价较低的时段为EV自动充电。综上,EV用户、VPP运营商与电网的互动架构如图 1所示。
|
图 1 EV用户、VPP运营商与电网的互动架构 Fig. 1 Interactive architecture between EV users, VPP operators and power grid |
主从博弈模型的上层问题为VPP日运营收益最大,其目标函数为式(1),需要满足的约束条件为式(7)—式(23)。
| $ \begin{gathered} \max F= \\ (1-\beta) \sum\limits_{t=1}^{T} \sum\limits_{\omega=1}^{N} \rho_{\omega}\left[\sum\limits_{i=1}^{n} \pi_{t \omega} P_{\mathrm{EV}, i, t \omega} \Delta t-\left(C_{\mathrm{CGT}, t \omega}+\right.\right. \\ \left.\left.C_{\mathrm{ESS}, t\omega }+C_{\mathrm{DR}, t \omega}+C_{\mathrm{DAM}, t \omega}\right)\right]+\beta\left(\delta-\frac{1}{1-\partial} \sum\limits_{\omega=1}^{N} \rho_{\omega} \xi_{\omega}\right) \end{gathered} $ | (1) |
式中:F为VPP运营总收益;T为VPP的一个调度周期,取24 h;N为VPP运行场景总数;ρω为场景ω出现的概率;n为VPP内的EV总数;Δt为调度步长,取1 h;πtω为场景ω下t时段EV的充电价格;PEV, i, tω为场景ω下t时段第i辆EV的充电功率;CCGT, tω为场景ω下t时段可控分布式电源的发电成本;CESS, tω为场景ω下t时段储能设备的运维成本;CDR, tω为场景ω下t时段需求响应负荷的调度成本;CDAM, tω为场景ω下t时段VPP与电网交互的成本;β为风险偏好系数,表示VPP运营商对风险收益的偏好程度,β∈[0, 1],β值越大表示VPP运营商对风险收益越厌恶,其设计的定价策略就越保守;∂为置信水平;δ为置信水平∂下的VaR值;ξω为引入的辅助变量。
CCGT, tω为:
| $ C_{\mathrm{CGT}, t \omega}=\left(a P_{\mathrm{CGT}, t \omega}+b\right) \Delta t $ | (2) |
式中:a,b为成本系数;PCGT, tω为场景ω下t时段燃气轮机组的输出功率。
CESS, tω为[23]:
| $ C_{\mathrm{ESS}, t \omega}=\kappa_{\mathrm{ESS}}\left(\frac{P_{\mathrm{ESS}, t \omega}^{\mathrm{dis}}}{\eta_{\mathrm{ESS}}^{\mathrm{dis}}}+P_{\mathrm{ESS}, t \omega}^{\mathrm{ch}} \eta_{\mathrm{ESS}}^{\mathrm{ch}}\right) \Delta t $ | (3) |
式中:κESS为折算后储能设备的单位充放电成本;PESS, tωch,PESS, tωdis分别为场景ω下t时段储能设备的充、放电功率;ηESSch,ηESSdis分别为储能设备的充、放电效率。
CDR, tω为[24]:
| $C_{\mathrm{DR}, t \omega}=\kappa_{\mathrm{DR}}\left|P_{\mathrm{DR}, t \omega}-\bar{P}_{\mathrm{DR}, t \omega}\right| \Delta t $ | (4) |
式中:κDR为需求响应负荷的单位调度成本;PDR, tω,PDR, tω分别为场景ω下t时段需求响应负荷的实际受调度功率和期望用电功率。式(4)中的绝对值项会导致模型非线性而无法求解,故引入辅助变量PDR, tωa,PDR, tωb,将式(4)转化为:
| $ C_{\mathrm{DR}, t {\omega}}=\kappa_{\mathrm{DR}}\left(P_{\mathrm{DR}, t{\omega}}^{\mathrm{a}}+P_{\mathrm{DR}, t \omega}^{\mathrm{b}}\right) \Delta t $ | (5) |
CDAM, tω为:
| $ C_{\mathrm{DAM}, t \omega}=\left(\lambda_{\mathrm{DAM}, t}^{+} P_{\mathrm{DAM}, t \omega}^{\mathrm{buy}}-\lambda_{\mathrm{DAM}, t}^{-} P_{\mathrm{DAM}, t \omega}^{\mathrm{sell}}\right) \Delta t $ | (6) |
式中:λDAM, t+,λDAM, t-分别为t时段电网下发给VPP的购、售电价格;PDAM, tωbuy,PDAM, tωsell分别为场景ω下t时段VPP在日前市场中的购、售电功率。
2.2 主从博弈模型上层问题的约束条件充电价格的相关约束为:
| $ \pi^{1} \leqslant \pi_{t \omega} \leqslant \pi^{\mathrm{u}} $ | (7) |
| $\sum\limits_{t=1}^{T} \frac{\pi_{t \omega}}{T}=\pi_{\text {aver }} $ | (8) |
式中:πu,πl分别为EV充电价格的上、下限;πaver为EV充电价格的平均值。式(7)表示VPP运营商给EV用户制定的充电价格的上、下限约束。式(8)为均价约束,防止VPP运营商定价不合理。
可控分布式电源的相关约束为:
| $P_{\mathrm{CGT}}^{\min } \leqslant P_{\mathrm{CGT}, t \omega} \leqslant P_{\mathrm{CGT}}^{\max } $ | (9) |
式中:PCGTmin,PCGTmax分别为燃气轮机组的最小、最大输出功率。式(9)表示燃气轮机组的输出功率应在上下限范围内。
储能设备的相关约束为:
| $ 0 \leqslant P_{\mathrm{ESS}, t \omega}^{\mathrm{ch}} \leqslant u_{t \omega} P_{\mathrm{ESS}}^{\max } $ | (10) |
| $0 \leqslant P_{\mathrm{ESS}, t \omega}^{\mathrm{dis}} \leqslant\left(1-u_{t \omega}\right) P_{\mathrm{ESS}}^{\max } $ | (11) |
| $ 0 \leqslant S_{t \omega} \leqslant S_{(t-1) \omega}+\eta_{\mathrm{ESS}}^{\mathrm{ch}} P_{\mathrm{ESS}, t \omega}^{\mathrm{ch}}-\frac{P_{\mathrm{ESS}, t \omega}^{\mathrm{dis}}}{\eta_{\mathrm{ESS}}^{\mathrm{dis}}} \leqslant S_{\mathrm{ESS}}^{\mathrm{max}} $ | (12) |
| $S_{0}=S_{T} $ | (13) |
式中: utω为引入的布尔变量,表示场景ω下t时段储能设备的状态;PESSmax为储能设备充放电功率最大值;Stω为场景ω下t时段储能设备的电量;SESSmax为储能设备的最大容量;S0为储能设备的初始电量;ST为T时段储能设备的电量。式(10)、式(11)限制了储能设备的充放电功率大小,且不能在同一时段同时充放电。式(12)、式(13)为储能设备的电量状态方程,为使储能设备循环利用,储能设备T时段的电量应等于初始电量[25]。
需求响应负荷的相关约束为:
| $ \sum\limits_{t=1}^{T} P_{\mathrm{DR}, t \omega} \Delta t=E_{\mathrm{DR}} $ | (14) |
| $ E_{\mathrm{DR}}^{\min } \leqslant P_{\mathrm{DR}, t \omega} \Delta t \leqslant E_{\mathrm{DR}}^{\max } $ | (15) |
式中:EDR为需求响应负荷一个周期内用电量之和;EDRmin,EDRmax分别为需求响应负荷的最小、最大的用电需求。式(14)表示VPP一个调度周期内需求响应负荷的用电量应为定值。式(15)表示需求响应负荷t时段的用电需求量应在上下限范围内。
另外,由于式(4)转化为式(5)的过程中引入了辅助变量,应增加相应约束条件:
| $ P_{\mathrm{DR}, t \omega}-\bar{P}_{\mathrm{DR}, t \omega}+P_{\mathrm{DR}, t \omega}^{\mathrm{a}}-P_{\mathrm{DR}, t \omega}^{\mathrm{b}}=0 $ | (16) |
| $ P_{\mathrm{DR}, t \omega}^{\mathrm{a}} \geqslant 0 $ | (17) |
| $ P_{\mathrm{DR}, t \omega}^{\mathrm{b}} \geqslant 0 $ | (18) |
VPP与电网交互的相关约束为:
| $ 0 \leqslant P_{\mathrm{DAM}, t \omega}^{\text {buy }} \leqslant M z_{t \omega} $ | (19) |
| $ 0 \leqslant P_{\mathrm{DAM}, t \omega}^{\mathrm{sell}} \leqslant M\left(1-z_{t \omega}\right) $ | (20) |
式中:M为一足够大的正数;ztω为引入的布尔变量,表示VPP在日前市场的购售电状态。式(19)、式(20)表示VPP的购售电量应大于等于0,且不能在t时段同时购售电。
功率平衡约束为:
| $ \begin{gathered} \sum\limits_{i=1}^{n} P_{\mathrm{EV}, i, t \omega}+P_{\mathrm{ESS}, t \omega}^{\mathrm{ch}}-P_{\mathrm{ESS}, t \omega}^{\mathrm{dis}}-P_{\mathrm{CGT}, t \omega}+P_{\mathrm{DR}, t \omega}- \\ P_{\mathrm{W}, t \omega}+P_{\mathrm{L}, t \omega}=P_{\mathrm{DAM}, t \omega}^{\mathrm{buy}}-P_{\mathrm{DAM}, t \omega}^{\mathrm{sell}} \end{gathered} $ | (21) |
式中:PW, tω,PL, tω分别为场景ω下t时段VPP内风电输出功率和常规负荷功率。
CVaR相关约束为[26]:
| $ \begin{aligned} &\delta-\sum\limits_{t=1}^{T}\left[\sum\limits_{i=1}^{n} \pi_{t \omega} P_{\mathrm{EV}, i, t \omega} \Delta t-\left(C_{\mathrm{CGT}, t \omega}+C_{\mathrm{ESS}, t{\omega}}+\right.\right.\\ &\left.\left.C_{\mathrm{DR}, t \omega}+C_{\mathrm{DAM}, t \omega}\right)\right] \leqslant \xi_{\omega} \end{aligned} $ | (22) |
| $ \xi_{\omega} \geqslant 0 $ | (23) |
式(22)、式(23)表示ξω为正值时,δ与场景ω下VPP运营收益的差值应小于等于ξω。
2.3 主从博弈模型下层问题的目标函数及约束条件主从博弈模型下层描述的是EV用户充电策略的优化问题,其优化目标为:
| $ P_{\mathrm{EV}, i, t \omega}=\operatorname{argmin} \sum\limits_{t} \pi_{t \omega} P_{\mathrm{EV}, i, t \omega} $ | (24) |
约束条件为:
| $ \sum\limits_{t \in T_{\mathrm{p}}} P_{\mathrm{EV}, i, t \omega}=\tau_{i} Q_{i, \max }-Q_{i, 0} $ | (25) |
| $ 0 \leqslant P_{\mathrm{EV}, i, t \omega} \leqslant P_{\mathrm{EV}, i}^{\max } \quad \forall t \in T_{\mathrm{p}} $ | (26) |
| $ P_{\mathrm{EV}, i, t \omega}=0 \quad \forall t \notin T_{\mathrm{p}} ; t \in T ; \forall i $ | (27) |
式中:τi为第i辆EV出行需要的最低电量占车载电池最大容量的比例;Qi, max为第i辆EV车载电池的最大容量;Qi, 0为第i辆EV入网时车载电池的初始电量;PEV, imax为第i辆EV的最大充电功率;Tp为EV的充电时段。
目标函数式(24)表示EV用户在VPP运营商给出的电价下,最小化充电成本。约束条件中,式(25)表示EV在并网时充电至离网需求电量;式(26)为EV充电功率约束;式(27)表示EV在离网后的充电功率为0。
综上,VPP运营商定价策略与EV用户充电策略形成了主从博弈关系。式(1)—式(27)中,VPP运营商应考虑EV用户对充电价格的反应,故πtω和PEV, i, tω都是变量,且主从博弈模型既不是线性的也不是凸的。文中后续通过Karush-Kuhn-Tucker (KKT)条件和对偶理论,将式(1)—式(27)所示的双层非线性规划问题转化为可求解的混合整数线性规划问题,并找到主从博弈双方的利益均衡点。
3 主从博弈模型求解方法对于主从博弈模型中的下层问题,因EV用户在决策时,其收到的充电价格由VPP运营商制定,故首先通过KKT条件[27]对式(24)—式(27)进行替代,得到变量PEV, i, tω和πtω的约束关系。设式(25)约束对应的对偶变量为μi, ω;式(26)约束对应的对偶变量为ϑi, tω-,ϑi, tω+;式(27)约束对应的对偶变量为σi, tω。则式(24)—式(27)的KKT条件为:
| $\pi_{t \omega}-\mu_{i, \omega}-\vartheta_{i, t \omega}^{-}-\vartheta_{i, t \omega}^{+}-\sigma_{i, t \omega}=0 \quad \forall i ; \forall t ; \forall \omega $ | (28) |
| $ \sum\limits_{t \in T_{\mathrm{p}}} P_{\mathrm{EV}, i, t \omega}=\tau_{i} Q_{i, \max }-Q_{i, 0} \quad \forall i ; \forall \omega $ | (29) |
| $ \vartheta_{i, t \omega}^{-} P_{\mathrm{EV}, i, t \omega}=0 \quad \vartheta_{i, t \omega}^{-} \geqslant 0 ; \forall t \in T_{\mathrm{p}} ; \forall i ; \forall \omega $ | (30) |
| $ \begin{aligned} &\vartheta_{i, t \omega}^{+}\left(P_{\mathrm{EV}, i, t \omega}-P_{\mathrm{EV}, i}^{\max }\right)=0 \\ &\vartheta_{i, t \omega}^{+} \geqslant 0 ; \forall t \in T_{\mathrm{p}} ; \forall i ; \forall \omega \end{aligned} $ | (31) |
| $ 0 \leqslant P_{\mathrm{EV}, i, t \omega} \leqslant P_{\mathrm{EV}, i}^{\max } \quad \forall t \in T_{\mathrm{p}} ; \forall \omega $ | (32) |
| $\sigma_{i, t \omega}=0 \quad \forall t \in T_{\mathrm{p}} ; \forall i ; \forall \omega $ | (33) |
| $P_{\mathrm{EV}, i, t}=0 \quad \forall t \in T_{\mathrm{p}} ; \forall i ; \forall \omega $ | (34) |
式(30)和式(31)为原约束与其对偶变量的互补松弛性条件,因其是非线性的,故进行线性化后才能求解,进而对互补松弛条件进行线性化处理。参考文献[28]中的Big-M法,通过引入布尔变量φi, tω-和φi, tω+后,约束式(30)和式(31)可转化为线性不等式。
| $0 \leqslant \vartheta_{i, t \omega}^{-} \leqslant M \varphi_{i, t \omega}^{-} \quad \forall t \in T_{\mathrm{p}} ; \forall i ; \forall \omega $ | (35) |
| $ 0 \leqslant P_{\mathrm{EV}, i, t \omega} \leqslant M\left(1-\varphi_{i, t \omega}^{-}\right) \quad \forall t \in T_{\mathrm{p}} ; \forall i ; \forall \omega $ | (36) |
| $0 \leqslant P_{\mathrm{EV}, i}^{\max }-P_{\mathrm{EV}, i, t \omega} \leqslant M \varphi_{i, t \omega}^{+} \quad \forall t \in T_{\mathrm{p}} ; \forall i ; \forall \omega $ | (37) |
| $ -M\left(1-\varphi_{i, t \omega}^{+}\right) \leqslant \vartheta_{i, t \omega}^{+} \leqslant 0 \quad \forall t \in T_{\mathrm{p}} ; \forall i ; \forall \omega $ | (38) |
式中:M为一个较大的正数。经过转化,式(35)—式(38)与式(30)、式(31)等价。
进一步,对目标函数式(1)进行线性化。因式(1)中的πtω,PEV, i, tω均为自变量,故πtωPEV, i, tω是一个非线性的复合变量,无法直接求解。但对偶理论表明,在目标问题有最优解的情况下,最优解处原问题与对偶问题的目标函数值一定相等,故有:
| $ \begin{gathered} \sum\limits_{t=1}^{T} \pi_{t \omega} P_{\mathrm{EV}, i, t \omega}= \\ \mu_{i, \omega}\left(\tau_{i} Q_{i, \max }-Q_{i, 0}\right)+\sum\limits_{t=1}^{T} \vartheta_{i, t \omega}^{+} P_{\mathrm{EV}, i}^{\max } \end{gathered} $ | (39) |
综上所述,VPP运营商与EV用户的主从博弈模型可转化为混合整数线性规划问题。
| $\left\{\begin{array}{l} \max F=(1-\beta)\left\{\sum\limits _ { \omega = 1 } ^ { N } \sum \limits_ { i = 1 } ^ { n } \rho _ { \omega } \left[\mu_{i, \omega}\left(\delta_{i} Q_{i, \max }-Q_{i, 0}\right)+\right.\right. \\ \left.\sum\limits_{t=1}^{T} \vartheta_{i, t}^{+} P_{\mathrm{EV}, i}^{\max }\right]-\sum\limits_{\omega=1}^{N} \sum\limits_{t=1}^{T} \rho_{\omega}\left(C_{\mathrm{CGT}, t \omega}+C_{\mathrm{ESS}, t \omega}+\right. \\ \left.\left.C_{\mathrm{DR}, t \omega}+C_{\mathrm{DAM}, t{\omega}}\right)\right\}+\beta\left(\delta-\frac{1}{1-\partial} \sum\limits_{\omega=1}^{N} \rho_{\omega} \xi_{\omega}\right) \\ \text { s.t. 式(7)—式(23) } \\ \quad \text { 式 (28)、式(29) } \\ \quad \text { 式(32)—式 (38) } \end{array}\right. $ | (40) |
混合整数线性规划式(40)可通过商业求解器Gurobi 9.1.1进行求解。
4 算例分析 4.1 算例参数文中算例将等值聚合后的EV分为3组,即EV1为100辆、EV2为60辆、EV3为40辆,用(100, 60, 40)表示。每组EV的充电时段见表 1,表中1表示EV在该时段充电,0表示EV在该时段不充电。为模拟所有可能的EV充电偏好,根据EV的行驶特性和充电行为[11, 20], 设EV1为“早出晚归型”,EV2为“常规作息型”,EV3为“深夜工作型”。3组EV的基本参数见表 2,电力市场购电的分时电价[29]见表 3。为防止VPP从市场套利,λDAM, t-=λDAM, t+/1.2;πu=1.2λDAM, t+;πl=0.8λDAM, t+;πaver=0.562 9元/(kW ·h)。VPP内其余资源的运行参数见表 4。
|
|
表 1 EV充电时段 Table 1 Charging period of EV |
|
|
表 2 EV基本参数 Table 2 Basic parameters of EV |
|
|
表 3 分时电价 Table 3 Time-of-use tariff |
|
|
表 4 VPP运行参数 Table 4 Operating parameters of VPP |
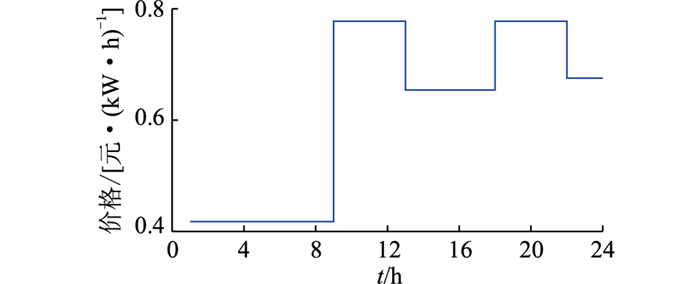
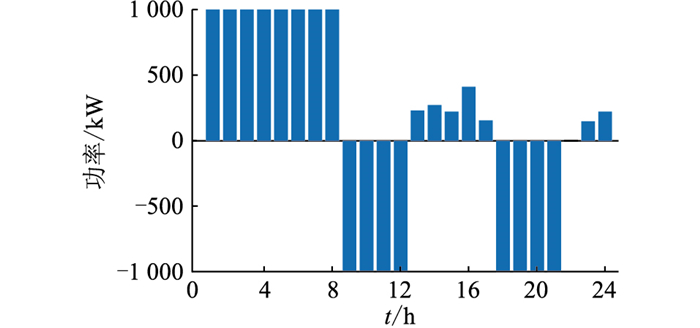
基于4.1节的参数设置,取β=0.5求解得到VPP运营总收益为1 113元。VPP运营商的最优售电定价、EV用户的最优充电方案及VPP运营商的购售电功率、需求响应负荷的实际与期望功率、燃气轮机组的输出功率和储能设备的充放电功率如图 2—图 7所示。图 4中,VPP运营商购电时取值为正,售电时取值为负。图 7中,储能设备充电时取值为正,放电时取值为负。
|
图 2 VPP运营商的最优售电定价 Fig. 2 Optimal electricity sales pricing for VPP operators |
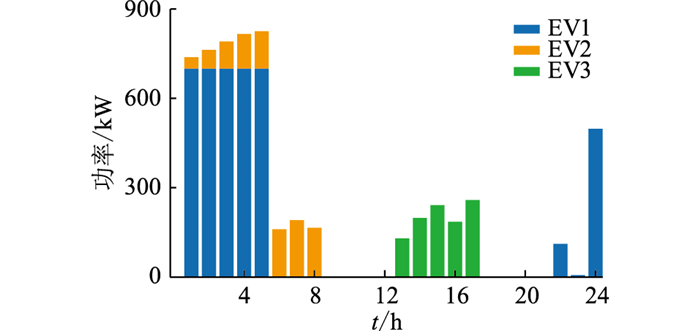
|
图 3 EV用户的最优充电方案 Fig. 3 Optimal charging solution for EV users |
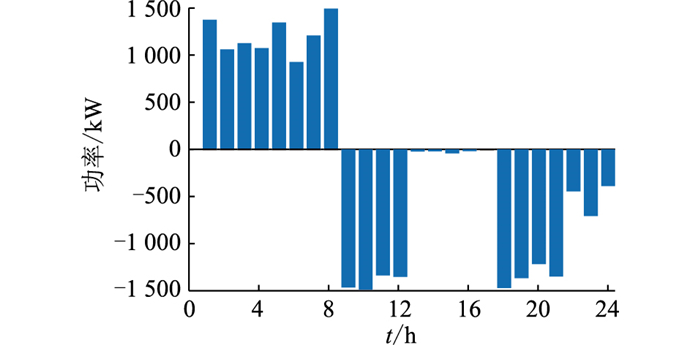
|
图 4 VPP运营商的购售电功率 Fig. 4 Electric power purchased and sold by VPP operators |
|
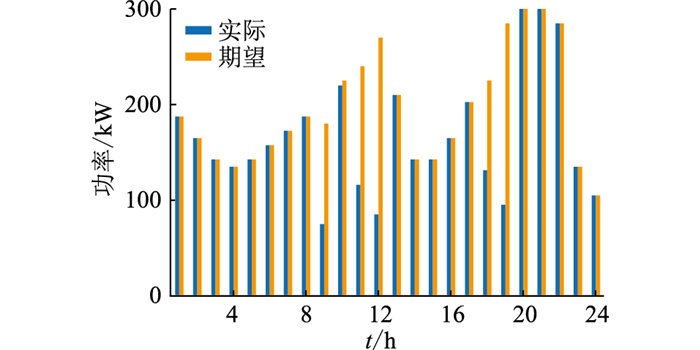
图 5 需求响应负荷的实际与期望功率 Fig. 5 The actual and expected power of demand response load |
|
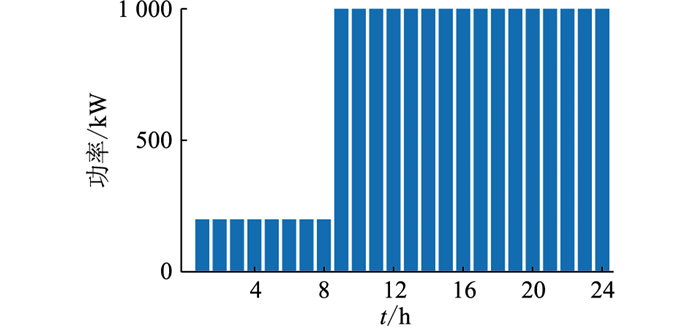
图 6 燃气轮机组的输出功率 Fig. 6 The output power of the gas turbine unit |
|
图 7 储能设备的充放电功率 Fig. 7 The charging and discharging power of the energy storage equipment |
EV1数量明显多于另外2组,由图 2、图 3可知,VPP运营商总是在EV1充电时段将电价设置为该时段电价的上限,而在EV1不充电时段降低电价,以获取更高收益。不仅如此,VPP拟定的定价策略理论上虽不能完全满足EV1的利益需求,但从商业角度来看,这种定价策略既符合了VPP的利益需求,也使EV用户在满足出行电量需求的前提下,充电成本最小。
由图 4—图 7可知,由于1 h—8 h VPP的常规负荷较小且风电机组出力较大,从日前市场直接购电比VPP内燃气轮机组发电更加经济实惠,故这个时段燃气轮机组只需维持最低输出功率。另外,除去售给EV用户的电量,发出的多余电量存储在储能设备中,以便在“峰电价”时段使用或售出。9 h—12 h,随着电网的分时电价提高,VPP运营商在满足EV用户充电需求的前提下,尽可能安排燃气轮机组及储能设备输出电能,以获得额外收益。因13 h—17 h是“平电价”时段,故VPP运营商会将部分“峰电价”时段的需求响应负荷调整到该时段。18 h—21 h是“峰电价”时段,VPP运营商也会设置更高的售电电价引导EV用户合理地选择充电时段,同时会将储能设备中的电能全部释放以获取更多收益。22 h—24 h是“平电价”时段,VPP运营商会优先使用风电机组发出的电能,部分售给EV用户供其充电,部分由储能设备存储,实现供需平衡,避免弃风现象。
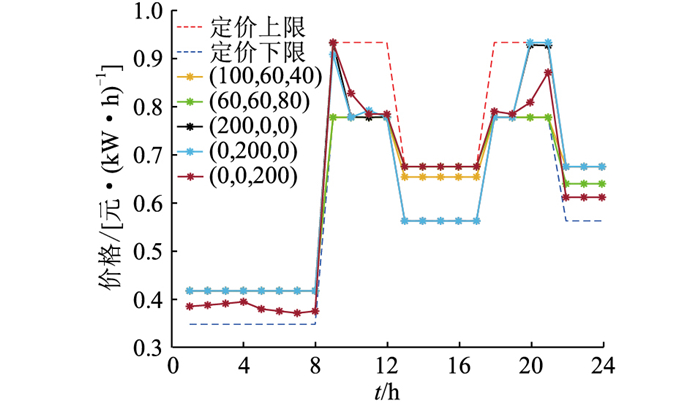
4.3 EV比例对最优解的影响在EV总数不变的前提下,设EV数量分别为(100, 60, 40),(60, 60, 80),(200, 0, 0),(0, 200, 0),(0, 0, 200),得到不同EV比例下VPP运营商的最优定价策略,如图 8所示。不同EV比例下VPP运营收益与EV充电成本对比如图 9所示。
|
图 8 不同EV比例下VPP运营商的定价策略 Fig. 8 Pricing strategies of VPP operators under different EV ratios |
|
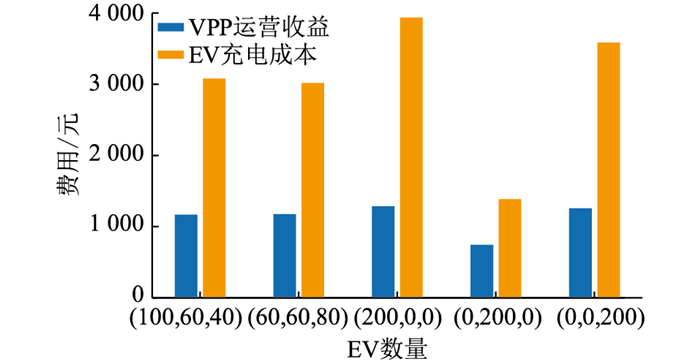
图 9 不同EV比例下VPP运营商收益与EV充电成本对比 Fig. 9 Comparison of VPP operator revenue and EV user charging costs under different EV ratios |
由图 8可知,不同EV比例下VPP运营商的最优定价策略并不相同,EV数量为(100, 60, 40)和(60, 60, 80)的定价策略基本相同,与其他比例下的EV定价策略差异很大。说明VPP运营商只会在EV类型过于集中时灵活改变定价策略,这种行为受充电EV数量的影响不大。
由图 9可知,EV数量为(200, 0, 0)或(0, 0, 200)时,VPP运营收益和EV充电成本都较高,而EV数量为(0, 200, 0)时,VPP运营收益和EV充电成本最低。这主要是由EV用户可接受充电时段决定的,EV2可接受的充电时段多,时间跨度大,故其可选择在“谷电价”时段完成充电。而EV1和EV3的可充电时段仅有8 h,无法灵活选择充电时段,只能按VPP运营商设置的电价充电,导致充电成本高于EV2,但其充电成本仍低于直接从实时市场购电的成本,从这一角度来看,所有的EV用户仍是获利的。
进一步地,当3种类型的EV数量较为均匀时,VPP运营收益会降低。这是因为当VPP中EV充电类型过于单一时,运营商会将该类型EV充电时段的电价调高,不充电时段的电价调低,最大程度获得盈利。而当3类EV的数量较为均衡时,VPP运营商为满足多种充电时段需求,各个时段的充电价格不能设置太高,从而导致总收益减少。
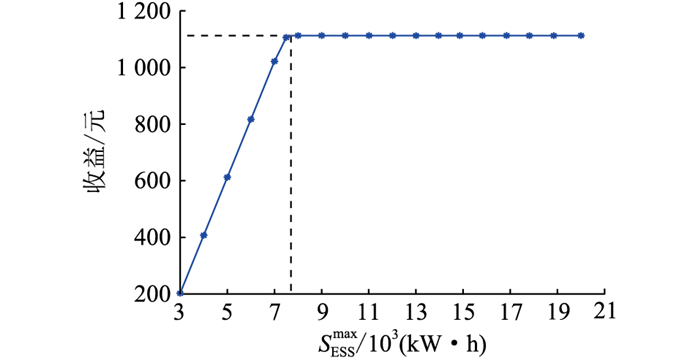
4.4 储能设备容量对VPP运营收益的影响设SESSmax从3 000 kW ·h到20 000 kW ·h变化,其余参数不变,VPP运营收益如图 10所示。
|
图 10 不同SESSmax下的VPP运营收益 Fig. 10 VPP operating income under different SESSmax |
由图 10可知,随着SESSmax的增加,VPP运营收益逐渐增加后趋于稳定,当SESSmax为7 700 kW ·h时,VPP的最大运营收益为1 113.0元。这是因为储能容量越大,VPP在“谷电价”时段可存储更多电能,在“峰电价”时段将存储的电量售出可获取更多额外收益。但SESSmax增大到一定程度后,受储能自身充放电功率限制,可能会出现容量浪费的情况,故VPP运营收益最终会趋于稳定。
4.5 风险偏好系数对VPP运营收益的影响不同β下的VPP运营收益如表 5所示。由表 5可知,随着β减小,VPP运营收益增加。由计算可知,EV用户的充电成本一直为2 936.3元,并不会改变。这说明,当风电机组出力或常规负荷发生波动时,VPP运营商会优先保障EV用户利益,并不会将风险成本转嫁到EV用户的充电成本上,而是靠VPP内储能设备、燃气轮机组的容量调节或从市场中购售电的方式维持系统的稳定运营。
|
|
表 5 不同β下的VPP运营收益 Table 5 VPP operating income under different β |
文中提出了基于主从博弈的VPP运营商与EV用户之间的主从博弈模型,在协调各类可控资源时,既考虑了EV充电策略对VPP售电价格的影响,也考虑了VPP定价策略受EV充电行为的影响,实现了VPP运营商与EV用户的双赢。
文中通过KKT条件和对偶理论,将非线性的主从博弈模型转化成可求解的混合整数线性规划问题进行求解。算例证明了求解方法的有效性,得出在一定范围内增加储能最大容量是VPP运营商提高运营收益的重要途径。VPP运营商在获得高收益的同时也面临着高风险,在低风险时获得的收益也很低,故VPP运营商应根据自身风险偏好程度及VPP内可控资源的出力特点,灵活衡量风险与收益之间的关系。
| [1] |
FANG C, ZHAO X J, XU Q, et al. Aggregator-based demand response mechanism for electric vehicles participating in peak regulation in valleytime of receiving-end power grid[J]. Global Energy Interconnection, 2020, 3(5): 453-463. DOI:10.1016/j.gloei.2020.11.005 (  0) 0) |
| [2] |
陈盛凯, 杨伟, 徐泽, 等. 考虑电动汽车V2G的分布式电源优化配置[J]. 电力电容器与无功补偿, 2021, 42(5): 143-149. CHEN Shengkai, YANG Wei, XU Ze, et al. Optimal allocation for distributed generation considering V2G of electric vehicle[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(5): 143-149. (  0) 0) |
| [3] |
杨书强, 范文奕, 赵阳, 等. 基于充电功率场景模型的电动汽车负荷建模[J]. 全球能源互联网, 2021, 4(6): 575-584. YANG Shuqiang, FAN Wenyi, ZHAO Yang, et al. Electric vehicle load modeling based on charging power scenarios[J]. Journal of Global Energy Interconnection, 2021, 4(6): 575-584. (  0) 0) |
| [4] |
杨书强, 范文奕, 赵阳, 等. 基于充电功率场景模型的电动汽车负荷建模[J]. 全球能源互联网, 2021, 4(6): 575-584. YANG Shuqiang, FAN Wenyi, ZHAO Yang, et al. Electric vehicle load modeling based on charging power scenarios[J]. Journal of Global Energy Interconnection, 2021, 4(6): 575-584. (  0) 0) |
| [5] |
宋莉, 刘敦楠, 庞博, 等. 需求侧资源参与电力市场机制及典型案例实践综述[J]. 全球能源互联网, 2021, 4(4): 401-410. SONG Li, LIU Dunnan, PANG Bo, et al. Mechanism of demand-side resource participation in the electricity market and typical case practice review[J]. Journal of Global Energy Interconnection, 2021, 4(4): 401-410. (  0) 0) |
| [6] |
陈丽丹, 张尧, Antonio FIGUEIREDO. 电动汽车充放电负荷预测研究综述[J]. 电力系统自动化, 2019, 43(10): 177-191. CHEN Lidan, ZHANG Yao, FIGUEIREDO A. Overview of charging and discharging load forcasting for electric vehicles[J]. Automation of Electric Power Systems, 2019, 43(10): 177-191. DOI:10.7500/AEPS20180814001 (  0) 0) |
| [7] |
LIU R Z, LIU Y, JIN Z X. Impact of industrial virtual power plant on renewable energy integration[J]. Global Energy Interconnection, 2020, 3(6): 545-552. DOI:10.1016/j.gloei.2021.01.004 (  0) 0) |
| [8] |
田立亭, 程林, 郭剑波, 等. 虚拟电厂对分布式能源的管理和互动机制研究综述[J]. 电网技术, 2020, 44(6): 2097-2108. TIAN Liting, CHENG Lin, GUO Jianbo, et al. A review on the study of management and interaction mechanism for distributed energy in virtual power plants[J]. Power System Technology, 2020, 44(6): 2097-2108. (  0) 0) |
| [9] |
孔英会, 高会生, 张铁峰, 等. 面向虚拟电厂的5G通信技术应用探讨[J]. 电力信息与通信技术, 2020, 18(8): 80-85. KONG Yinghui, GAO Huisheng, ZHANG Tiefeng, et al. Discussion on application of 5G communication technology forvirtual power plant[J]. Electric Power Information and Communication Technology, 2020, 18(8): 80-85. (  0) 0) |
| [10] |
卫璇, 潘昭光, 王彬, 等. 云管边端架构下虚拟电厂资源集群与协同调控研究综述及展望[J]. 全球能源互联网, 2020, 3(6): 539-551. WEI Xuan, PAN Zhaoguang, WANG Bin, et al. Review on virtual power plant resource aggregation and collaborative regulation using cloud-tube-edge-end architecture[J]. Journal of Global Energy Interconnection, 2020, 3(6): 539-551. (  0) 0) |
| [11] |
魏韡, 陈玥, 刘锋, 等. 基于主从博弈的智能小区代理商定价策略及电动汽车充电管理[J]. 电网技术, 2015, 39(4): 939-945. WEI Wei, CHEN Yue, LIU Feng, et al. Stackelberg game based retailer pricing scheme and EV charging management in smart residential area[J]. Power System Technology, 2015, 39(4): 939-945. (  0) 0) |
| [12] |
徐智威, 胡泽春, 宋永华, 等. 基于动态分时电价的电动汽车充电站有序充电策略[J]. 中国电机工程学报, 2014, 34(22): 3638-3646. XU Zhiwei, HU Zechun, SONG Yonghua, et al. Coordinatedcharging strategy for PEV charging stations based on dynamic time-of-use tariffs[J]. Proceedings of the CSEE, 2014, 34(22): 3638-3646. (  0) 0) |
| [13] |
詹祥澎, 杨军, 韩思宁, 等. 考虑电动汽车可调度潜力的充电站两阶段市场投标策略[J]. 电力系统自动化, 2021, 45(10): 86-96. ZHAN Xiangpeng, YANG Jun, HAN Sining, et al. Two-stagemarket bidding strategy of charging station considering schedulable potential capacity of electric vehicle[J]. Automation of Electric Power Systems, 2021, 45(10): 86-96. DOI:10.7500/AEPS20200414006 (  0) 0) |
| [14] |
李牧青, 宋依群, 严正, 等. 电动汽车代理商的博弈竞争模型和算法研究[J]. 电网技术, 2014, 38(6): 1512-1517. LI Muqing, SONG Yiqun, YAN Zheng, et al. Research on game model and algorithm for electric vehicle aggregations[J]. Power System Technology, 2014, 38(6): 1512-1517. (  0) 0) |
| [15] |
周博, 吕林, 高红均, 等. 多虚拟电厂日前鲁棒交易策略研究[J]. 电网技术, 2018, 42(8): 2694-2703. ZHOU Bo, LYU Lin, GAO Hongjun, et al. Robust day-ahead trading strategy for multiple virtual power plants[J]. Power System Technology, 2018, 42(8): 2694-2703. (  0) 0) |
| [16] |
范松丽, 艾芊, 贺兴. 基于机会约束规划的虚拟电厂调度风险分析[J]. 中国电机工程学报, 2015, 35(16): 4025-4034. FAN Songli, AI Qian, HE Xing. Risk analysis on dispatch of virtual power plant based on chance constrained programming[J]. Proceedings of the CSEE, 2015, 35(16): 4025-4034. (  0) 0) |
| [17] |
李嘉媚, 艾芊. 考虑调峰辅助服务的虚拟电厂运营模式[J]. 电力自动化设备, 2021, 41(6): 1-13. LI Jiamei, AI Qian. Operation mode of virtual power plant considering peak regulation auxiliary service[J]. Electric Power Automation Equipment, 2021, 41(6): 1-13. (  0) 0) |
| [18] |
王海冰, 王简, 王承民, 等. 计及风险约束的虚拟电厂能量管理建模[J]. 中国电机工程学报, 2017, 37(20): 5942-5950. WANG Haibing, WANG Jian, WANG Chengmin, et al. Risk-constrained energy management modeling of virtual power plant[J]. Proceedings of the CSEE, 2017, 37(20): 5942-5950. (  0) 0) |
| [19] |
武赓, 武庆国, 王昊婧, 等. 考虑风险规避的综合能源服务商能源购置策略[J]. 电力自动化设备, 2019, 39(6): 12-20. WU Geng, WU Qingguo, WANG Haojing, et al. Energy purchasing strategy of multi-energy service provider considering risk aversion[J]. Electric Power Automation Equipment, 2019, 39(6): 12-20. (  0) 0) |
| [20] |
张高, 王旭, 蒋传文. 基于主从博弈的含电动汽车虚拟电厂协调调度[J]. 电力系统自动化, 2018, 42(11): 48-55. ZHANG Gao, WANG Xu, JIANG Chuanwen. Stackelberg game based coordinated dispatch of virtual power plant considering electric vehicle management[J]. Automation of Electric Power Systems, 2018, 42(11): 48-55. DOI:10.7500/AEPS20170607005 (  0) 0) |
| [21] |
周亦洲, 孙国强, 黄文进, 等. 计及电动汽车和需求响应的多类电力市场下虚拟电厂竞标模型[J]. 电网技术, 2017, 41(6): 1759-1767. ZHOU Yizhou, SUN Guoqiang, HUANG Wenjin, et al. Strategic bidding model for virtual power plant in different electricity markets considering electric vehicles and demand response[J]. Power System Technology, 2017, 41(6): 1759-1767. (  0) 0) |
| [22] |
郭红霞, 白浩, 刘磊, 等. 统一电能交易市场下的虚拟电厂优化调度模型[J]. 电工技术学报, 2015, 30(23): 136-145. GUO Hongxia, BAI Hao, LIU Lei, et al. Optimal scheduling model of virtual power plant in a unified electricity trading market[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 136-145. DOI:10.3969/j.issn.1000-6753.2015.23.017 (  0) 0) |
| [23] |
孙振新, 刘汉强, 赵喆, 等. 储能经济性研究[J]. 中国电机工程学报, 2013, 33(S1): 54-58. SUN Zhenxin, LIU Hanqiang, ZHAO Zhe, et al. Research on economical efficiency of energy storage[J]. Proceedings of the CSEE, 2013, 33(S1): 54-58. (  0) 0) |
| [24] |
刘一欣, 郭力, 王成山. 微电网两阶段鲁棒优化经济调度方法[J]. 中国电机工程学报, 2018, 38(14): 4013-4022, 4307. LIU Yixin, GUO Li, WANG Chengshan. Economic dispatch of microgrid based on two stage robust optimization[J]. Proceedings of the CSEE, 2018, 38(14): 4013-4022, 4307. (  0) 0) |
| [25] |
蒋向兵, 汤波, 余光正, 等. 面向新能源就地消纳的园区储能与电价协调优化方法[J]. 电力系统自动化, 2022, 46(5): 51-64. JIANG Xiangbing, TANG Bo, YU Guangzheng, et al. Coordination and optimization method of park-level energy storage and electricity price for local accommodation of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(5): 51-64. (  0) 0) |
| [26] |
郭红霞, 高瑞, 杨苹. 基于条件风险价值的微电网现货市场两阶段调度[J]. 电网技术, 2019, 43(8): 2665-2674. GUO Hongxia, GAO Rui, YANG Ping. Two-stage dispatch of microgrid based on CVaR theory under electricity spot market[J]. Power System Technology, 2019, 43(8): 2665-2674. (  0) 0) |
| [27] |
ZHANG B Y, LI Q Q, WANG L H, et al. Robust optimization for energy transactions in multi-microgrids under uncertainty[J]. Applied Energy, 2018, 217: 346-360. DOI:10.1016/j.apenergy.2018.02.121 (  0) 0) |
| [28] |
ZENG B, ZHAO L. Solving two-stage robust optimization problems using a column-and-constraint generation method[J]. Operations Research Letters, 2013, 41(5): 457-461. DOI:10.1016/j.orl.2013.05.003 (  0) 0) |
| [29] |
王宣元, 刘敦楠, 刘蓁, 等. 泛在电力物联网下虚拟电厂运营机制及关键技术[J]. 电网技术, 2019, 43(9): 3175-3183. WANG Xuanyuan, LIU Dunnan, LIU Zhen, et al. Operation mechanism and key technologies of virtual power plant under ubiquitous Internet of Things[J]. Power System Technology, 2019, 43(9): 3175-3183. (  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd. Business Startups and Innovation Center, Nanjing 210024, China;
3. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2022, Vol. 41
2022, Vol. 41


 李强(1981), 男, 博士, 研究员级高级工程师, 从事电力系统分析与控制、电力市场、博弈论等相关工作(E-mail:
李强(1981), 男, 博士, 研究员级高级工程师, 从事电力系统分析与控制、电力市场、博弈论等相关工作(E-mail: