文章编号: 2096-3203(2022)04-0018-07 中图分类号: TM712
2. 东南大学电气工程学院, 江苏 南京 210096;
3. 智能电网保护和运行控制国家重点实验室, 南瑞集团(国网电力科学研究院)有限公司, 江苏 南京, 211106;
4. 江苏方天电力技术有限公司, 江苏 南京 211102
近年来,随着大规模新能源、储能和直流输电工程的大量投入,我国许多电网的电力电子设备数量和容量快速增加,电网正逐渐演变为高比例的电力电子电力系统[1-5]。与传统电力系统相比,新型电力系统的惯量不足,负荷侧的惯量占比逐渐升高[6-8]。异步电机作为电力系统的主要负荷,其惯量不可忽视[9]。因此,研究电力系统中异步电机的惯性响应,评估惯性时间尺度下异步电机的有效惯量和异步电机对系统频率调节的支撑能力,对评估电力系统惯量具有重要意义。
并网异步电机的电磁场中存储的电能和转子中的动能会根据系统频率的变化而变化,从而抑制系统频率改变[10-12]。传统异步电机的惯量研究主要从能量出发,通过大量仿真数据估算异步电机动能,根据惯量的基本定义式得出异步电机的自身惯量[13-14]。然而异步电机本身惯量与对电力系统所表现的惯量有所差异。根据异步电机的转子运动方程,异步电机的惯量等于不平衡有功功率扰动量与转子转速变化率的比。现有研究大多利用实测数据及惯性时空特性辨识来分析负荷侧惯量。文献[15]基于实测数据,针对实际电网仿真应用中的节点负荷和全网负荷进行建模,分析负荷频率特性,但未考虑异步电机的频率时空特性。文献[16-17]基于在线监测得到电力系统总惯量,利用电力系统总惯量减去同步电机惯量以及电源侧的虚拟惯量,最终得到负荷侧异步电机惯量,但此方法未考虑负荷中静态负荷的惯量影响,计算繁杂,无法为实际电力系统提供有效参考。文献[18]在机电时间尺度下建立异步电机内电势相位运动方程,通过内电势相位运动量化异步电机的有效惯量,详细全面地介绍了异步电机有效惯量的时变特性,明确分析了并网设备的频率动态特性,然而未继续对异步电机在惯性响应时间尺度下的频率支撑能力进行评估。
为评估惯性时间尺度下异步电机的等效惯量,文中建立机械暂态下的异步电机模型,推导出其传递函数并分析异步电机对电网呈现惯量的时变特性和影响因素。根据惯量响应阶段频率具备支撑能力这一思路,评估异步电机对系统频率的支撑能力。文中提出异步电机等效惯量评估模型,量化动态负荷的惯性支撑能力,并针对模型的频率支撑能力及异步电机受到频率扰动后的动态特性进行了分析。最后,基于Matlab/Simulink和PSASP平台搭建仿真模型,验证了文中所提异步电机等效惯量评估模型的有效性。
1 异步电机动态频率特性分析 1.1 异步电机模型异步电机的转子运动方程描述了电磁功率Pe和机械功率Pm的关系,是异步电机负荷建模的基本方程[19],具体如下:
| $ 2{H_{{\rm{am}}}}\frac{{d{\omega _{\rm{r}}}}}{{{\rm{d}}t}} = \Delta {P_{\rm{e}}}\Delta {P_{\rm{m}}} $ | (1) |
式中:Ham为异步电机的惯性常数;ωr为异步电机转子角速度;ΔPe为异步电机的偏移电磁功率;ΔPm为异步电机的偏移机械功率。
异步电机机电暂态下,可将转子侧参数折算到定子侧,异步电机的定、转子绕组的机械暂态电路如图 1(a)所示。由于实际应用中定、转子互感抗Xm远远大于转子绕组的漏抗Xr,因此异步电机的机械暂态等效电路如图 1(b)所示。

|
图 1 异步电机机械暂态电路 Fig. 1 Circuit in electromechanical transient state of asynchronous motor |
图 1中Rs,Xs分别为定子绕组的等值电阻和漏抗;Rr为转子绕组的等值电阻;Ut为异步电机机端电压;sslip为滑差率,其计算见式(2)。
| $ {s_{{\rm{slip}}}} = \frac{{\omega - {\omega _{\rm{r}}}}}{\omega } $ | (2) |
式中:ω为系统角速度。
由图 1(b)可知异步电机的电磁功率Pe计算如下:
| $ {P_{\rm{e}}} = \frac{{U_{\rm{t}}^2}}{{{{\left( {{R_{\rm{s}}} + \frac{{{R_{\rm{r}}}}}{{{s_{{\rm{slip}}}}}}} \right)}^2} + {{\left( {{X_{\rm{s}}} + {X_{\rm{r}}}} \right)}^2}}}\left( {\frac{{{R_{\rm{r}}}}}{{{s_{{\rm{slip}}}}}} + {R_{\rm{s}}}} \right) $ | (3) |
机械负载特性对异步电机特性具有极为重要的影响,机械功率Pm计算如下:
| $ {P_{\rm{m}}} = {\omega _{\rm{r}}}k\left[ {\alpha + \left( {1 - \alpha } \right){{\left( {1 - {s_{{\rm{slip}}}}} \right)}^\rho }} \right] $ | (4) |
式中:k为负载系数;α为恒力矩;ρ为异步电机机械负载特性相关指数。在实际应用中,k,ρ均为时变量,文中为研究异步电机惯性响应过程中的频率支撑能力,以k=1.85,ρ=2为例,则机械功率为二次函数形式[20]。
1.2 频率支撑能力分析系统频率受到负荷扰动而发生变化的变化范围较小时,可使用小信号模型求解惯性响应阶段异步电机的频率支撑能力并进行惯量评估[21]。
由式(3)和式(4)可知,异步电机电磁功率、机械功率与ω、ωr呈非线性关系。对异步电机进行小信号建模,在稳态初始工作点下通过线性化推导各参数间关系,求出异步电机对电力系统的有效惯量。
基于式(2),在初始工作点下进行线性化处理,滑差率sslip的变化量可表示如下:
| $ \Delta {s_{{\rm{slip}}}} = \frac{{{\omega _{{\rm{r0}}}}}}{{\omega _0^2}}\Delta \omega + \left( { - \frac{1}{{{\omega _{\rm{0}}}}}} \right)\Delta {\omega _{\rm{r}}} $ | (5) |
式中:ωr0为异步电机转子角速度的初值;ω0为系统角速度的初值;Δω,Δωr分别为系统角速度和异步电机转子角速度的变化量。
同理,基于式(3)和式(4),在初始工作点下,电磁功率pe及机械功率pm的变化量可表示如下:
| $ \Delta {P_{\rm{e}}} = {f_{{\rm{es}}}}\Delta {s_{{\rm{slip}}}} $ | (6) |
| $ \Delta {P_{\rm{m}}} = {f_{{\rm{ms}}}}\Delta {s_{{\rm{slip}}}} + {f_{{\rm{mw}}}}\Delta {\omega _{\rm{r}}} $ | (7) |
其中:
| $ {f_{{\rm{es}}}} = \frac{{\left[ {{{\left( {{X_{\rm{s}}} + {X_{\rm{r}}}} \right)}^2} - {{\left( {{R_{\rm{s}}} + \frac{{{R_{\rm{r}}}}}{{{s_{{\rm{slip0}}}}}}} \right)}^2}} \right]U_{\rm{t}}^2\left( { - \frac{{{R_{\rm{r}}}}}{{s_{{\rm{slip0}}}^2}}} \right)}}{{{{\left[ {{{\left( {{R_{\rm{s}}} + \frac{{{R_{\rm{r}}}}}{{{s_{{\rm{slip0}}}}}}} \right)}^2} + {{\left( {{X_{\rm{s}}} + {X_{\rm{r}}}} \right)}^2}} \right]}^2}}} $ | (8) |
| $ {f_{{\rm{ms}}}} = k{\omega _{{\rm{r0}}}}\rho \left( {1 - \alpha } \right){\left( {1 - {s_{{\rm{slip0}}}}} \right)^{\rho -1}} $ | (9) |
| $ {f_{{\rm{mw}}}} = k\left[ {\alpha + \left( {1 - \alpha } \right){{\left( {1 - {s_{{\rm{slip0}}}}} \right)}^\rho }} \right] $ | (10) |
式中:sslip0为滑差率的初值。
同时对式(1)作线性化处理,可得:
| $ 2{H_{{\rm{am}}}}s\Delta {\omega _{\rm{r}}} = \Delta {P_{\rm{e}}} - \Delta {P_{\rm{m}}} $ | (11) |
式中:s为拉普拉斯算子。
基于式(5)—式(11),得到异步电机的小信号模型框图,如图 2所示。
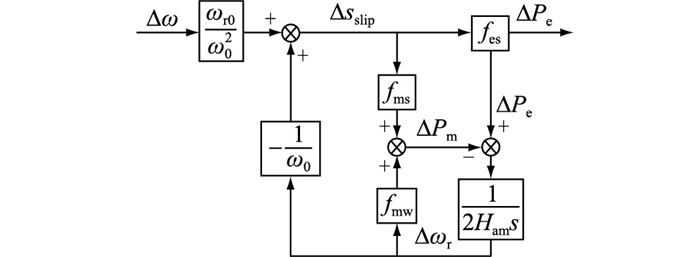
|
图 2 异步电机小信号模型框图 Fig. 2 Block diagram of small signal model of asynchronous motor |
图 2中Δω可以直接观测得到。由梅森增益公式,可直接求解输入量Δω与输出量ΔPe的传递函数G(s),如式(12)所示。
| $ G\left( s \right) = \frac{{\Delta {P_{\rm{e}}}}}{{\Delta \omega }} = \frac{{{K_1}s + {K_2}}}{{2{H_{{\rm{am}}}}s + {K_3}}} $ | (12) |
其中:
| $ {K_1} = 2\frac{{{\omega _{{\rm{r0}}}}}}{{\omega _0^2}}{f_{{\rm{es}}}}{H_{{\rm{am}}}} $ | (13) |
| $ {K_2} = \frac{{{\omega _{{\rm{r0}}}}}}{{\omega _0^2}}{f_{{\rm{es}}}}{f_{{\rm{mw}}}} $ | (14) |
| $ {K_3} = {f_{{\rm{mw}}}} + \left( { - \frac{1}{{{\omega _0}}}} \right)\left( {{f_{{\rm{ms}}}} - {f_{{\rm{es}}}}} \right) $ | (15) |
根据式(12),可得到异步电机对电力系统所表现的有效惯量有如下形式:
| $ H\left( s \right) = \frac{{\Delta {P_{\rm{e}}}}}{{s\Delta \omega }} = \frac{{{K_1}s + {K_2}}}{{\left( {2{H_{{\rm{am}}}}s + {K_3}} \right)s}} $ | (16) |
由式(16)可知,当电力系统存在不平衡功率时,系统的转速扰动量Δω为负数,转子转动惯量响应,异步电机的转差率sslip为负数。受到异步电机转差率瞬时响应,电磁功率扰动量ΔPe为负数,减小系统发电机负载。同时由于电磁功率Pe的变化,导致异步电动机转速ωr变化,进一步影响电磁功率Pe的变化。在负荷扰动发生之初,异步电机的转差率瞬时响应提供频率支撑能力,之后异步电机会逐步释放存储在转子之中的动能,进一步增强对系统的频率支撑能力。由此可知,异步电机有效惯量并不是一个恒定常数,而具有时变特性。同时由式(13)—式(15)所求出的系数可知,异步电机本身参数及其运行工作点都会影响异步电机对系统的有效惯量[22]。
2 异步电机惯性响应阶段等效惯量评估与同步电机相比,异步电机的有效惯量由于受到系统频率的影响,具有时变特性。在实际电力系统中,异步电机作为电力系统负荷的重要组成部分,其惯量不能忽视。合理量化评估异步电机对系统频率的支撑能力,对保证电力系统的频率稳定具有重要意义。基于上述背景,文中采用对系统具有相同频率支撑能力的同步电机替代异步电机。首先,构建异步电机频率响应模型,推导出复频域下负荷的响应模型;然后,利用推导出的结果,通过拉式反变换,求解出时域下的关系式;最后,考虑相同的频率支撑能力,求解异步电机的等效惯量评估模型。
2.1 异步电机频率响应模型将全网所有发电机转子运动方程等值聚合为单机模型,同时针对原动机-调速系统动态环节进行等值拟合处理,利用单机模型表示全系统,得到系统频率响应(system frequency response, SFR)模型。
文中为研究异步电机频率响应过程及其惯量,以SFR模型为基础,增加了异步电机频率响应传递函数,如图 3所示[23]。由于负荷是分散接入系统的,因此单个负荷变化很难引起系统频率变化。实际应用中,如PSASP及BPA仿真算例,通常将某个节点的动态负荷等值为单机模型进行分析,能够有效反映负荷变化对系统频率的影响。
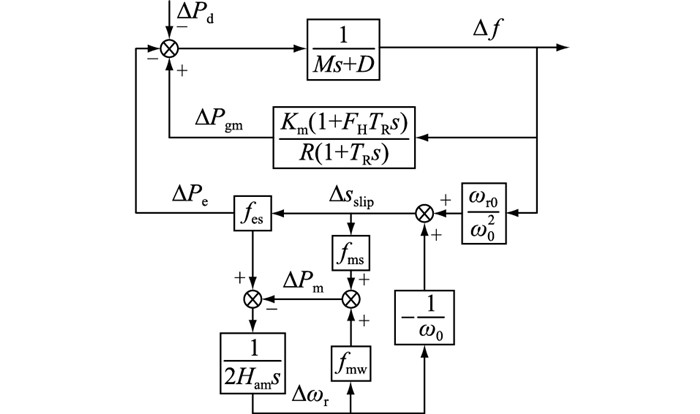
|
图 3 考虑异步电机的SFR模型 Fig. 3 SFR model with asynchronous motor |
图 3中M为发电机惯性时间常数,其求解见式(17);D为系统的阻尼系数;TR为再热时间常数;FH为高压涡轮分数;Km为与发电机功率因数和备用系数相关的系数;R为调速器调速系数;ΔPd为系统的负荷扰动功率;ΔPgm为一次调频增加的出力。等效同步电机的传递函数如式(18)所示。
| $ M = \frac{{\sum\limits_{i = 1}^n {{H_{{\rm{g}},i}}{S_{{\rm{g}},i}}} }}{{\sum\limits_{i = 1}^n {{S_{{\rm{g}},i}}} }} $ | (17) |
| $ {G_2}\left( s \right) = {T_{\rm{m}}}s $ | (18) |
式中:Hg,i,Sg,i分别为第i台发电机的惯性常数和容量;n为系统中发电机的数量;Tm为同步电机等效惯量,其数值应与最终所求的异步电机等效惯量相同。
负荷扰动功率ΔPd为系统输入量,当ΔPd>0时,系统有功负荷增加,系统频率减少,此时异步电机减少出力(ΔPd<0),调速器作用,增加系统发电机出力(ΔPgm>0)。ΔPd和ΔPgm这2个反馈量会削弱系统负荷的扰动,调整系统频率变化[24-25]。
2.2 惯性响应阶段等效惯量当系统负荷发生波动时,产生频率偏差量Δf,Δf经过同步电机以及异步电机,对系统消耗的电磁功率分别如下:
| $ \Delta f = \frac{1}{{s(Ms + D)}} $ | (19) |
| $ {P_{{\rm{ge}}}} = {\rm{ }}\frac{{{T_{\rm{m}}}}}{{Ms + D}} $ | (20) |
| $ {P_{{\rm{ae}}}} = \frac{{{K_1}s + {K_2}s}}{{s\left( {Ms + D} \right)\left( {2{H_{{\rm{am}}}}s + {K_3}} \right)}} $ | (21) |
式中:Δf为阶跃扰动信号经过电力系统传递函数以后的频率变化量;Pge为同步电机所消耗的电磁功率;Pae为异步电机所消耗的电磁功率。
对式(20)和式(21)进行拉式反变换,得到负荷扰动后电机的电磁功率,具体如下:
| $ {P_{{\rm{ge}}}} = \frac{{{T_{\rm{m}}}}}{M}{{\rm{e}}^{ - \frac{D}{M}t}} $ | (22) |
| $ {P_{{\rm{ae}}}}{\rm{ = }}\frac{{{K_2}}}{{{K_3}D}} + \frac{{M{K_2} - D{K_1}}}{{D\left( {2D{H_{{\rm{am}}}} - M{K_3}} \right)}}{{\rm{e}}^{ - \frac{D}{M}t}} + \frac{{2{K_2}{H_{{\rm{am}}}} - {K_1}{K_3}}}{{{K_3}\left( {{K_3}M - 2D{H_{{\rm{am}}}}} \right)}}{{\rm{e}}^{ - \frac{{{K_3}}}{{2{H_{{\rm{am}}}}}}t}} $ | (23) |
传统模式下,频率控制的分析主要关注系统中同步电机的频率特性,认为异步电机的影响集中表现为一个阻尼系数,然而实际上异步电机对系统频率具有支撑作用。且由式(22)和式(23)可知,异步电机和同步电机经过负荷扰动以后,对系统提供的功率均为时变函数,且与电网总惯量、电网频率变化量、电机自身惯量等诸多因素有关[26]。
为了对异步电机惯量的频率支撑能力进行评估,须求出异步电机等效惯量。在惯量响应的时间内,当同步电机与异步电机受到相同系统频率扰动时,对系统表现相同的频率支撑能力的异步电机惯量可由同特性的同步电机惯量等效。基于上述原理,在相同的惯量响应时间下,对式(22)和式(23)进行时域积分。当二者相等时,可求出异步电机等效惯量,具体如下:
| $ \smallint _{_0}^{{t_{\rm{g}}}}{P_{{\rm{ge}}}}{\rm{d}}t = \smallint _{_0}^{{t_{\rm{g}}}}{P_{{\rm{ae}}}}{\rm{d}}t $ | (24) |
| $ {T_{\rm{m}}} = \frac{{\smallint _0^{{t_{\rm{g}}}}\frac{1}{M}{{\rm{e}}^ - }^{\frac{D}{M}t}{\rm{d}}t}}{{\smallint _0^{{t_{\rm{g}}}}{P_{{\rm{ae}}}}{\rm{d}}t}} $ | (25) |
式(25)的展开形式为:
| $ {T_{\rm{m}}} = \frac{D}{{1 - {{\rm{e}}^ - }^{\frac{D}{M}{t_{\rm{g}}}}}}\left[ {\frac{{{K_2}}}{{{K_3}D}}{t_{\rm{g}}} + \frac{{M\left( {M{K_2} - D{K_1}} \right)}}{{{D^2}\left( {2D{H_{{\rm{am}}}}M{K_3}} \right)}} \times \left( {1 - {{\rm{e}}^ - }^{\frac{D}{M}{t_{\rm{g}}}}} \right)} \right]{\rm{ }} + \frac{{2{H_{{\rm{am}}}}\left( {2{K_2}{H_{{\rm{am}}}} - {K_1}{K_3}} \right)}}{{K_3^2\left( {{K_3}M - 2D{H_{{\rm{am}}}}} \right)}}\left( {1 - {{\rm{e}}^{ - \frac{{{K_3}}}{{2{H_{{\rm{am}}}}}}{t_{\rm{g}}}}}} \right) $ | (26) |
式中:tg为惯量响应时间。
当2个具有相同等效惯量的电机受到系统相同大小的负荷扰动时,在惯性时间尺度下,一次调频介入之前,2个电机对系统反馈的能量相同,系统频率的变化量相同。
3 算例验证与异步电机频率响应分析在Matlab/Simulink仿真平台上,搭建如图 3所示的系统频率模型,为验证所提异步电机有效惯量的准确性,分析系统频率扰动后异步电机的变化,须将异步电机接入等效的电力系统中。异步电机参数如下:Ham=0.5 s.,ωr0=0.973 p.u.,Xs=0.11 p.u.,Xr=0.12 p.u.,Rs=0.011 p.u.。为验证文中所提异步电机频率支撑能力评估模型的准确性,文中基于PSASP仿真平台的WSCC9V7模型进行仿真验证。
3.1 惯量验证与分析设置M=6.02 s,D=0.8。为分析异步电机频率响应过程,系统不施加一次调频措施。输出量为系统频率变化量Δf和异步电机电磁功率偏移量ΔPe,稳态情况下应有Δf=0,ΔPe=0。
10 s时向系统施加一个阶跃信号ΔPfh=0.005 p.u.,通过监测Δf和ΔPe的变化来检测异步电机对系统频率的支撑作用,结果如图 4和图 5所示。
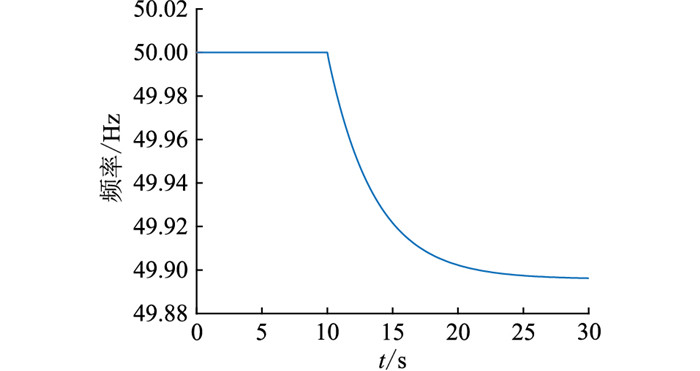
|
图 4 系统频率 Fig. 4 Frequency of system |
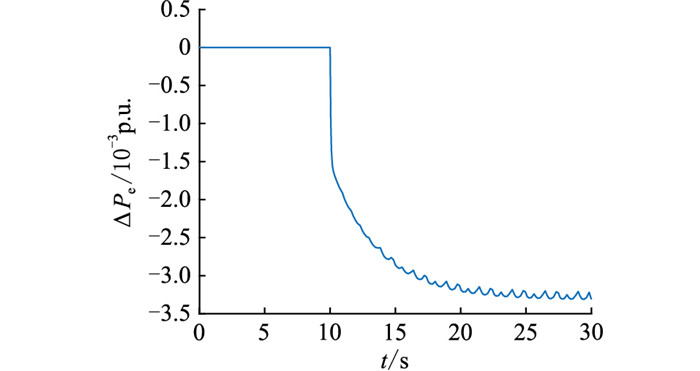
|
图 5 异步电机电磁功率偏移量 Fig. 5 The variation of electromagnetic power of asynchronous motor |
图 4表明当系统负荷增加且无外界新接入电源或电源增加出力的情况下,系统频率降低,最终系统频率稳定在49.89 Hz。由图 5可知,随着系统频率的下降,异步电机电磁功率下降。进而证明系统频率减少时,异步电机电磁功率减小,减少了发电机负载,向系统提供了惯性响应,对系统频率的调节起到了支撑作用。
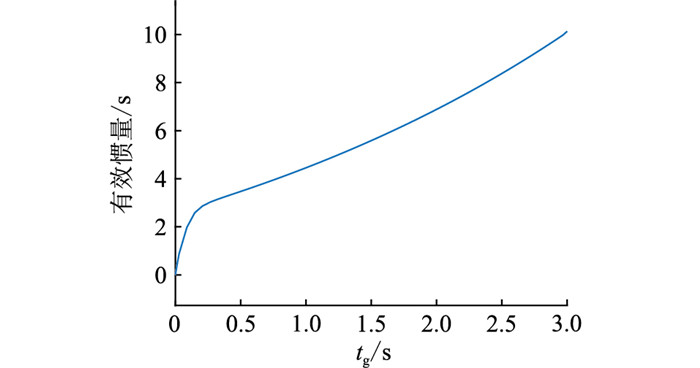
当系统发生有功不平衡扰动后,各发电机组按照惯量大小瞬时分担扰动功率,一般在3 s后一次调频介入[23],文中取惯量响应时间tg为3 s。在惯量响应阶段,异步电机的有效惯量如图 6所示。可见,惯量变化曲线具有如1.2节所述的时变特性。系统频率减小,异步电机的转差率首先响应,有效惯量较小。此后存储在异步电机转子上的动能逐渐释放,异步电机的有效惯量逐渐增大。
|
图 6 惯性响应阶段异步电机有效惯量 Fig. 6 The effective inertia of asynchronous motor in inertial response stage |
基于式(25)可推导求得异步电机的等效惯量Tm为3.620 4 s。经过推导计算,证明了异步电机对系统所表现的惯量与本身惯量具有差异。0 s时,向系统施加一个ΔPfh=0.003 p.u.的扰动量,观察在惯量响应时间tg=3 s内系统频率变化量,见图 7。
|
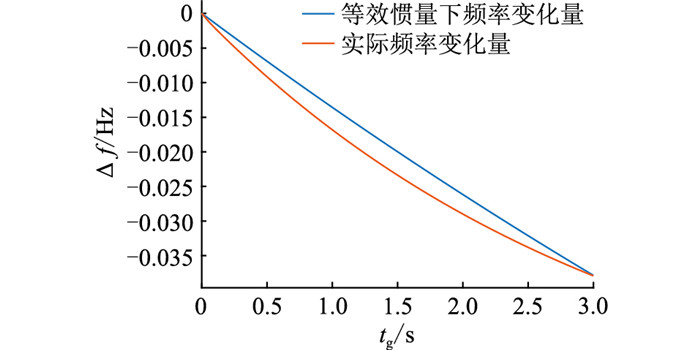
图 7 系统频率变化量 Fig. 7 The variation of system frequency |
由图 7可知,异步电机的实际频率变化量和2.2节提出的拥有异步电机等效惯量的同步电机的频率变化量变化趋势相同。且在相同的惯性时间下,频率变化大小一致,3 s时,Δf均为0.04 Hz。仿真结果验证了等效惯量评估模型的有效性。
3.3 复杂算例验证为验证仿真模型中惯量响应曲线的准确性,文中基于PSASP搭建算例仿真系统,如图 8所示,发电机采用五阶模型。在稳态情况下,Δf和ΔPe均为0。t=0时,在系统负荷节点M1施加一个ΔPe=0.02p.u.的扰动,观测系统负荷节点M2和M3的频率变化。为验证异步电机频率支撑能力,系统不施加一次调频措施。图 8中,G1—G3为同步电机;T1—T3为连接发电机的主变压器。

|
图 8 PSASP三机九节点仿真模型 Fig. 8 Simulation model of PSASP with three machines and nine nodes |
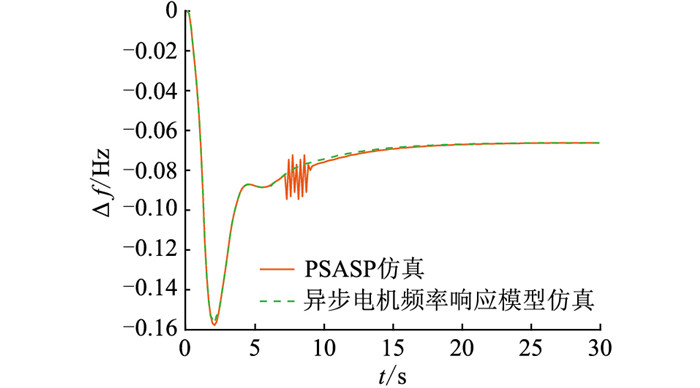
图 9为PSASP系统频率曲线与异步电机频率响应模型所得频率曲线的对比。可以看到2个模型曲线波形和频率稳态偏差基本一致,验证了文中所提模型的准确性。
|
图 9 PSASP仿真与异步电机频率响应模型曲线对比 Fig. 9 The curve comparison between PSASP simulation and asynchronous motor frequency response model |
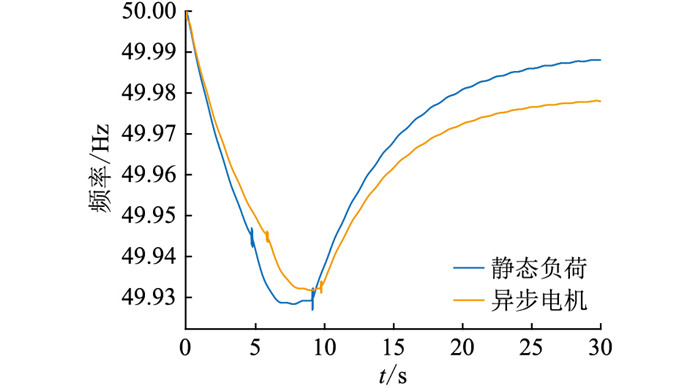
为更加符合实际,在电力系统中增加了调速器、调压器及静态稳定器设备,施加ΔPe=0.05 p.u的扰动。图 10为系统带有相同功率静态负荷和异步电机负荷时的频率曲线,表 1为频率曲线偏差最大点,即nadir点的参数。
由表 1和图 10可知,具有惯量的异步电机能够更有效地阻止频率变化,系统频率变化量明显小于静态负荷,系统频率曲线nadir点时间更靠后,对电力系统频率有支撑能力。同时也由于惯量阻止频率变化的作用,系统频率恢复相较于没有惯量的静态负荷恢复更慢。
|
|
表 1 负荷频率曲线nadir点参数 Table 1 Parameters of nadir point of load frequency curves |
|
图 10 异步电机和静态负荷的频率曲线 Fig. 10 Frequency response curves of asynchronous motor and static load |
文中构建了机电暂态下的异步电机模型,列出了异步电机的电磁功率和机械功率方程;利用小信号模型,评估了异步电机在系统中所表现出的有效惯量及等效模型;提出了可评估电机对系统频率支撑能力的异步电机等效惯量评估模型。结论如下:
(1) 系统发生有功不平衡扰动时,系统频率受其影响发生变化,具有频率响应能力的异步电机能够减小自身的电磁功率,减小对系统有功功率的扰动,有效阻止系统频率发生变化,对系统的频率调节具有支撑作用。
(2) 在异步电机频率响应的初始阶段,异步电机转差率受到系统频率的影响,减小自身的电磁功率,对系统表现较小的有效惯量;随后存储在异步电机转子中的动能释放,对系统表现较大的有效惯量,异步电机的有效惯量呈现时变特性。
(3) 文中算例验证了所提异步电机等效惯量评估模型的准确性,能够有效量化反映异步电机对系统的频率支撑能力。为新能源高占比的低惯量电力系统的频率稳定性分析及调节提供参考。
实际应用中,综合负荷的感应电机参数辨识不仅须辨识单台电机参数,还要辨识采用单机还是多机模型,而电机数量及参数随时间变化。商用仿真软件(PSASP、BPA等)和电网实际应用中,通常将某个节点的动态负荷等值为单机模型进行分析。单个异步电机的等效惯量评估对实际电网的意义不大且不具备可观性,精度较差。后续将开展异步电机等值和参数辨识等方面研究工作,并分析时变参数对惯量评估模型的影响。
本文得到智能电网保护和运行控制国家重点实验室开放课题“双高背景下电网转动惯量评估方法及监测技术研究”(SGNR0000KJJS2200305)资助,谨此致谢!
| [1] |
林晓煌, 文云峰, 杨伟峰. 惯量安全域: 概念、特点及评估方法[J]. 中国电机工程学报, 2021, 41(9): 3065-3079. LIN Xiaohuang, WEN Yunfeng, YANG Weifeng. Inertia security region: concept, characteristics, and assessment method[J]. Proceedings of the CSEE, 2021, 41(9): 3065-3079. (  0) 0) |
| [2] |
葛晓琳, 刘亚, 符杨, 等. 考虑惯量支撑及频率调节全过程的分布鲁棒机组组合[J]. 中国电机工程学报, 2021, 41(12): 4043-4058. GE Xiaolin, LIU Ya, FU Yang, et al. Distributed robust unit commitment considering the whole process of inertia support and frequency regulations[J]. Proceedings of the CSEE, 2021, 41(12): 4043-4058. (  0) 0) |
| [3] |
文云峰, 杨伟峰, 林晓煌. 低惯量电力系统频率稳定分析与控制研究综述及展望[J]. 电力自动化设备, 2020, 40(9): 211-222. WEN Yunfeng, YANG Weifeng, LIN Xiaohuang. Review and prospect of frequency stability analysis and control of low-inertia power systems[J]. Electric Power Automation Equipment, 2020, 40(9): 211-222. (  0) 0) |
| [4] |
CHRISTENSEN P, ANDERSEN G K, SEIDEL M, et al. High penetration of power electronic interfaced power sources and the potential contribution of grid forming converters[R]. Brussels: the European Network of Transmission System Operators for electricity, 2020.
(  0) 0) |
| [5] |
张剑云, 李明节. 新能源高渗透的电力系统频率特性分析[J]. 中国电机工程学报, 2020, 40(11): 3498-3507. ZHANG Jianyun, LI Mingjie. Analysis of the frequency characteristic of the power systems highly penetrated by new energy generation[J]. Proceedings of the CSEE, 2020, 40(11): 3498-3507. (  0) 0) |
| [6] |
孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究[J]. 中国电机工程学报, 2020, 40(16): 5179-5192. SUN Huadong, WANG Baocai, LI Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16): 5179-5192. (  0) 0) |
| [7] |
江涵, 岳程燕, 严兴煜, 等. 高比例可再生能源系统惯量约束对灵活性分析的影响研究[J]. 电力系统保护与控制, 2021, 49(18): 44-51. JIANG Han, YUE Chengyan, YAN Xingyu, et al. Influence of system inertia on flexibility resource analysis for an interconnection system with a high proportion of intermittent renewable energy[J]. Power System Protection and Control, 2021, 49(18): 44-51. (  0) 0) |
| [8] |
刘铖, 赵晓洋, 张宇驰, 等. 面向区域间振荡模式的电力系统小扰动惯量域构建[J]. 电力系统保护与控制, 2021, 49(20): 9-19. LIU Cheng, ZHAO Xiaoyang, ZHANG Yuchi, et al. Construction of a small signal inertia region of a power system for inter-area oscillation mode[J]. Power System Protection and Control, 2021, 49(20): 9-19. (  0) 0) |
| [9] |
张武其, 文云峰, 迟方德, 等. 电力系统惯量评估研究框架与展望[J]. 中国电机工程学报, 2021, 41(20): 6842-6856. ZHANG Wuqi, WEN Yunfeng, CHI Fangde, et al. Research framework and prospect on power system inertia estimation[J]. Proceedings of the CSEE, 2021, 41(20): 6842-6856. (  0) 0) |
| [10] |
李少林, 王伟胜, 张兴, 等. 基于频率响应区间划分的风电机组虚拟惯量模糊自适应控制[J]. 电网技术, 2021, 45(5): 1658-1665. LI Shaolin, WANG Weisheng, ZHANG Xing, et al. Fuzzy adaptive virtual inertia control strategy of wind turbines based on system frequency response interval division[J]. Power System Technology, 2021, 45(5): 1658-1665. (  0) 0) |
| [11] |
KUMAR D S, LAU P, SHARMA A, et al. Improvement of transient response in grid-tied photovoltaic systems using virtual inertia[J]. IET Smart Grid, 2021, 4(1): 1-14. DOI:10.1049/stg2.12001 (  0) 0) |
| [12] |
CHENG Y, AZIZIPANAH-ABARGHOOEE R, AZIZI S, et al. Smart frequency control in low inertia energy systems based on frequency response techniques: a review[J]. Applied Energy, 2020, 279: 115798. DOI:10.1016/j.apenergy.2020.115798 (  0) 0) |
| [13] |
ZHOU T, LIU Z C, YE H, et al. Frequency response modeling and equivalent inertial estimation of induction machine[J]. Energy Reports, 2022, 8: 554-564. (  0) 0) |
| [14] |
WANG D, YUAN X M, ZHANG M Q. Power-balancing based induction machine model for power system dynamic analysis in electromechanical timescale[J]. Energies, 2018, 11(2): 438. DOI:10.3390/en11020438 (  0) 0) |
| [15] |
臧晓明, 陈谦, 闪鑫, 等. 基于实测数据的负荷频率参数辨识及影响分析[J]. 电力系统及其自动化学报, 2019, 31(4): 32-38. ZANG Xiaoming, CHEN Qian, SHAN Xin, et al. Frequency parameter identification and impact analysis of load based on measured data[J]. Proceedings of the CSU-EPSA, 2019, 31(4): 32-38. (  0) 0) |
| [16] |
TAVAKOLI M R B, POWER M, RUTTLEDGE L, et al. Load inertia estimation using white and grey-box estimators for power systems with high wind penetration[J]. IFAC Proceedings Volumes, 2012, 45(21): 399-404. DOI:10.3182/20120902-4-FR-2032.00071 (  0) 0) |
| [17] |
WATANABE K, NANAHARA T. Study on inertial response of fix-speed wind turbine generator[C]//201449th International Universities Power Engineering Conference (UPEC). Cluj-Napoca, Romania. IEEE, 2014: 1-6.
(  0) 0) |
| [18] |
王玎, 袁小明. 异步电机机电时间尺度有效惯量评估及其对可再生能源并网系统频率动态的影响[J]. 中国电机工程学报, 2018, 38(24): 7258-7266, 7452. WANG Ding, YUAN Xiaoming. Available inertia estimation of induction machine in electromechanical timescale and its effects on frequency dynamics of power systems with renewable energy[J]. Proceedings of the CSEE, 2018, 38(24): 7258-7266, 7452. (  0) 0) |
| [19] |
屈星, 李欣然, 李培强, 等. 计及配电网调压的综合负荷建模[J]. 中国电机工程学报, 2018, 38(6): 1695-1705, 1906. QU Xing, LI Xinran, LI Peiqiang, et al. Load modeling considering voltage regulation of the distribution network[J]. Proceedings of the CSEE, 2018, 38(6): 1695-1705, 1906. (  0) 0) |
| [20] |
SIGRIST L, ROUCO L. An induction motor model for system frequency response models[J]. International Transactions on Electrical Energy Systems, 2017, 27(11): e2413. DOI:10.1002/etep.2413 (  0) 0) |
| [21] |
CHEN L, WANG X H, MIN Y, et al. Modelling and investigating the impact of asynchronous inertia of induction motor on power system frequency response[J]. International Journal of Electrical Power & Energy Systems, 2020, 117: 105708. (  0) 0) |
| [22] |
王玎. 基于幅相运动方程的异步电动机机电时间尺度建模及其对电力系统机电动态影响研究[D]. 武汉: 华中科技大学, 2018. WANG Ding. Modeling of electromechanical timescale of induction motor based on internal voltage magnitude-phase motion equation and its impact on power system electromechanical dynamics[D]. Wuhan: Huazhong University of Science andTechnology, 2018. (  0) 0) |
| [23] |
张恒旭, 李常刚, 刘玉田, 等. 电力系统动态频率分析与应用研究综述[J]. 电工技术学报, 2010, 25(11): 169-176. ZHANG Hengxu, LI Changgang, LIU Yutian, et al. Reviews on power system dynamic frequency analysis and its application[J]. Transactions of China Electrotechnical Society, 2010, 25(11): 169-176. (  0) 0) |
| [24] |
SHI Q X, LI F X, CUI H T. Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6355-6367. DOI:10.1109/TPWRS.2018.2824823 (  0) 0) |
| [25] |
HUANG H, LI F X. Sensitivity analysis of load-damping characteristic in power system frequency regulation[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1324-1335. DOI:10.1109/TPWRS.2012.2209901 (  0) 0) |
| [26] |
PRADHAN C, BHENDE C N. Frequency sensitivity analysis of load damping coefficient in wind farm-integrated power system[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1016-1029. (  0) 0) |
its equivalent inertia evaluation
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China;
3. State Key Laboratory of Smart Grid Protection and Control, Nari Group Corporation, Nanjing 211106, China;
4. Jiangsu Frontier Electric Technology Co., Ltd., Nanjing 211102, China
 2022, Vol. 41
2022, Vol. 41


 周涛(1991), 男, 博士, 讲师, 研究方向为电力系统运行与控制(E-mail:
周涛(1991), 男, 博士, 讲师, 研究方向为电力系统运行与控制(E-mail: