文章编号: 2096-3203(2022)04-0033-11 中图分类号: TM74
2. 电力系统及发电设备控制与仿真国家重点实验室(清华大学), 北京 100084;
3. 国网江苏省电力有限公司电力科学研究院, 江苏 南京 211103;
4. 江苏省电力试验研究院有限公司, 江苏 南京 211103;
5. 四川大学电气工程学院, 四川 成都 610065
为应对日益严峻的化石能源紧缺和环境污染问题,以风电和光伏发电为代表的新能源发电技术在全球范围内得到了广泛关注与应用。我国风能蕴藏量丰富,当前探明技术可开发量达6~10亿kW,为大力发展风电事业提供了有利条件。进入21世纪以来,我国风电装机量和发电量迅猛增长,截至2015年,我国风电累计装机容量达到145.1 GW,跃居全球首位[1—2],截至2020年,全国累计装机容量达288.32 GW。
随着风电装机容量的不断增长,风电接入给电力系统带来的影响也逐渐凸显。近年来风电接入引发的电力系统次同步振荡事故屡见报道。例如2009年10月22日,位于美国德州南部的一双馈风电场经串补线路并网系统中,由于输电线路故障,发生了频率在20 Hz左右的次同步振荡事故,造成大量风电机组脱网[3];2012年底至2014年初,我国沽源地区风电机群经串补线路并网系统累计记录发生次同步振荡事件58次,其中较为严重的情况造成了风电机组大面积脱网[4];2015年7月1日,我国新疆哈密地区一直驱风电场并网系统发生了频率在20~40 Hz的次同步振荡事故,且振荡传播至300 km外一火电厂,引发火电机组的次同步扭振,造成机组轴系扭振保护动作而切机[5]。
风电接入引发的振荡给电力系统安全稳定运行带来了巨大挑战,是实现风电友好型并网面临的主要瓶颈之一。与传统火电厂不同,风电机组单机容量较小,一个风电场内通常具有数十台甚至是数百台风电机组,这一特征给风电并网系统次同步振荡研究带来了巨大挑战[6]。一方面,风电并网系统振荡的产生多是源于风电场与交流电网间产生了不利的动态交互作用,由于风电机组数量庞大,风电机组之间以及机组与交流电网之间存在着复杂的动态耦合,造成系统内动态交互特征及影响难以厘清,风电机组自身动态、风电机组数量和风电场网络结构均会对系统振荡特性产生影响[7],目前对于风电并网系统振荡失稳机理仍未形成共识。另一方面,风电场详细模型阶数高,用于次同步振荡分析时计算量大、效率低,难以直接在此基础上进行深入的理论研究,合理有效地对风电场进行等值建模,是研究风电接入引发电力系统振荡的基础。
在风电场动态等值研究的早期,主流的研究方法基本上都沿用了传统电力系统动态等值研究中的基本思路与方法,例如风电场动态等值中常用的容量加权平均法、参数辨识法和基于聚类分析的多机等值法的基本思想,在以往传统多机电力系统动态等值研究中均可见其踪迹[8]。近年来,一种基于一致性控制理论的风电并网系统小干扰稳定性解耦分析方法得到了广泛关注与研究应用[9—13],除此之外,该解耦思想在电力电子多馈入系统[14—18]和多机电力系统[19—20]小干扰稳定性分析中也有广泛的应用。文中结合风电接入对电力系统振荡稳定性影响方面的研究现状,对近年来风电场动态等值领域内的研究成果进行梳理和归类,讨论了各类等值方法用于风电并网系统次同步振荡分析时的优势与不足,最后总结了风电场小干扰等值中仍待解决的关键问题和未来的发展方向,以期为未来针对风电汇集系统小干扰等值与风电并网系统次同步振荡展开进一步研究提供参考和借鉴。
1 风电接入对电力系统振荡稳定性的影响近年来,风电并网系统次同步振荡事故屡见报道,工业界和学术界针对风电接入对电力系统振荡稳定性的影响机理展开了深入研究,普遍认为风电并网后与交流电网间产生的不利动态交互作用是系统振荡的主要诱因。下面将对近年来风电接入对电力系统振荡稳定性影响方面的主要研究成果进行评述和分析,其中重点关注对风电场与串补线路、同步发电机组轴系和弱交流电网间动态交互作用影响的研究,其均具有典型振荡事件为背景。
1.1 风电场与串补线路间动态交互作用的影响2009年美国德州发生的风电并网系统次同步振荡事故和2014年我国沽源地区发生的次同步振荡事故,均是风电场经串联补偿线路并网引发电力系统振荡的典型事件。自此之后,国内外针对风电经串补线路并网系统振荡问题展开了深入研究,大量研究成果表明,风电场与串补线路间的动态交互作用可产生一RLC谐振电路,串补度等系统参数的变化可能造成系统等效电阻在某一谐振频率下为负,从而导致系统振荡失稳。
文献[21]以双馈风机为例,建立了其经串补线路并网系统的等效阻抗模型,分析发现随串补度变化,在某一次同步谐振频率下,等效阻抗模型中的电阻为负,造成系统振荡失稳。文献[22—23]建立了双馈风机经串补线路并网系统的等效RLC电路模型,在此基础上分析发现次同步谐振频率下,双馈风机可能对外呈负电阻特性,且转子侧换流器电流控制内环参数增大会造成负电阻增大,当双馈风机负电阻超过外部交流电网中总的正电阻时,系统便会发生次同步振荡。这一研究结果表明,双馈风机经串补线路并网系统次同步振荡是由双馈风机换流器控制系统参与的感应发电机效应引起的。文献[24—25]分别对双馈风机和串补线路建立其解析阻抗模型,分析了双馈风机经串补线路并网系统次同步振荡的产生机理和影响因素,得到的结论与文献[21—23]一致。在文献[24—25]的基础上,文献[26—27]推导了双馈风机经串补线路并网系统的聚合RLC电路模型,并基于该模型,研究了系统次同步振荡的产生机理,认为振荡源于系统中的动态元件构成了RLC谐振电路,且由于感应发电机效应,双馈风机在次同步振荡频率下呈负电阻特性,若由此造成了聚合RLC电路中总电阻为负,就会引发系统振荡,这也再次说明,系统中的振荡与机械系统扭振无关,为一种纯粹的电气振荡/谐振。另外,文献[22—23,26—27]分析了串补度、双馈风机转子转速、转子侧换流器电流控制内环参数和风电机组数量对系统振荡稳定性的影响,结果表明:串补度提高、转子转速降低,均会造成滑差减小,双馈风机负电阻特性加剧,转子侧换流器电流控制内环比例积分制器比例系数增加,也会造成负电阻绝对值增加,进而导致系统稳定性降低甚至是失稳。文献[28]基于模式分析,通过计算双馈风机经串补线路并网系统主导振荡模式的参与因子,发现对该振荡模式参与度较高的状态变量主要与双馈风机定子磁链和串补线路相关,这也表明系统中的振荡为一种电气振荡/谐振,与基于阻抗模型分析所得结论是一致的;文献[29]采用了类似的分析思路,发现风速、双馈风机转子侧换流器控制参数、交流电网强度和串补度均对会对系统振荡稳定性产生影响。文献[30—32]采用模式分析法,研究了双馈风机经串补线路并网系统振荡稳定性的影响因素,所得结论与文献[22—23,26—27]基于阻抗分析法所得结论一致,即串补度提高、风速降低和双馈风机转子侧换流器电流控制内环比例系数增加均会造成系统稳定性降低。
以上研究均是针对双馈风机经串补线路并网系统展开的,相对而言,直驱风机经串补线路并网系统次同步振荡方面的研究较少。文献[33—34]中基于阻抗分析法研究了直驱风机经串补线路并网系统振荡稳定性的影响因素,均认为锁相环动态和串补度是影响系统振荡稳定性的关键因素,串补度增加和直驱风机有功输出增加均会造成系统稳定性降低。文献[35]通过计算直驱风机经串补线路并网系统的主导振荡模式及其参与因子,发现串补度对振荡频率影响较大,且振荡与机械系统扭振无关,也是一种纯粹的电气振荡/谐振。
1.2 风电场与同步发电机组轴系间动态交互作用的影响2015年发生于我国新疆哈密地区的次同步振荡事件,是风电场与同步机轴系间动态交互引发电力系统大范围振荡的典型代表事件。现有研究中大多将风电接入引发同步机轴系扭振的原因归结为风电机组向同步发电机轴系提供了负的阻尼转矩,造成轴系扭振模式阻尼降低[36—40]。文献[36—37]基于模式分析研究了双馈风机并网对同步机轴系扭振模式的影响,指出双馈风机接入可能会造成轴系扭振模式阻尼降低,且随双馈风机输出有功功率的增加,轴系扭振模式阻尼降低。文献[38]推导了直驱风机输出功率向同步机轴系提供的电磁转矩,并基于复转矩系数法分析了直驱风机向同步机轴系提供负的阻尼转矩的可能性与成立条件。文献[39—40]分析了电压源换流器与同步机轴系间动态交互作用的产生及影响,指出电压源换流器控制外环和锁相环动态会导致换流器呈现负电阻特性,从而向发电机轴系提供负的阻尼转矩,导致系统阻尼恶化,尤其是换流器输出功率较大时,其负电阻特性对系统阻尼的影响加剧,造成系统振荡失稳风险增加。
1.3 风电场与弱交流电网间动态交互作用的影响2015年新疆哈密地区直驱风电场次同步振荡事件同样是风电场与弱交流电网间动态交互引发电力系统振荡的代表事件,其振荡由风电场引发,进而传播至数百公里外的火电厂,引发火电机组轴系扭振。该直驱风电场规模大、且远离交流主电网,经由不含串补装置的长距离高压交流输电线路并网,为典型的风电接入弱交流电网系统。现有研究大多将弱电网条件下风电并网系统振荡失稳归因于电网强度减弱造成风电机组在谐振频率下出现负电阻特性,或电网强度减弱导致系统主导振荡模式在复平面上向右移动。针对并网直驱风电场,文献[41—43]基于阻抗模型分析发现,弱电网条件下,并网直驱风机/风电场会表现出负电阻特性,若由此造成系统在谐振频率下的整体等效电阻为负,则风电场与交流电网间的动态交互会引发系统失稳,且风电机组数量增加或网侧换流器控制系统比例系数减小、电网强度减弱,均会加剧系统的负电阻特性。文献[44]通过计算并网直驱风机阻抗对换流器控制系统参数的灵敏度,分析了网侧换流器电流控制内环参数、直流电压外环参数和锁相环参数对系统次同步振荡稳定性的影响。文献[45]针对复杂风电并网系统振荡稳定性分析,提出了一种阻抗网络模型,并基于该模型分析发现,除交流电网强度和风电机组数量变化会影响系统稳定性之外,网络结构不同,系统稳定性也存在差异。文献[46—47]针对并网直驱风机,基于模式分析发现,随交流电网强度减弱,风电机组锁相环模式和网侧换流器直流电压外环模式会在复平面上向右移动,最终导致系统振荡失稳。针对并网双馈风电场,文献[48]通过在不同电网强度下对系统进行模式分析,发现随电网强度减弱,双馈风机网侧换流器直流电压外环模式阻尼降低;文献[49—51]采用同样的思路,分析了电网强度对并网双馈风机锁相环模式的影响,得到了类似的规律,即随交流电网强度减弱,锁相环模式沿复平面向右移动,造成系统振荡稳定性降低。此外,文献[50—51]中采用复转矩系数法,分析了锁相环参数和交流电网强度对锁相环模式阻尼的影响机理,通过分析锁相环回路的开环相频特性曲线,发现交流电网强度减弱,会造成锁相环回路在谐振频率附近的相角裕度减小,振荡模式阻尼降低,而锁相环控制环节参数增大,会造成振荡回路放大倍数增加,从而振荡模式频率增大,系统阻尼恶化。
2 风电场小干扰等值方法 2.1 传统单机等值与多机等值方法 2.1.1 单机等值目前,风电场单机等值模型的建立方法按照等值风电机组参数的来源,可分为容量加权平均法和参数辨识法。其中,容量加权平均法基于对风电场内部风电机组物理参数的聚合,获得等值风电机组参数;参数辨识法根据风电场并网点动态响应的实测或仿真数据,对等值风电机组参数进行辨识[52]。
(1) 容量加权平均法。根据IEC和WECC制定的风电场建模导则,一个由同型风电机组构成的风电场可等效为一台扩容风电机组[53]。扩容风机容量采用风电场额定容量,参数通过以各风电机组单机容量与风电场总容量的比值为权重,计算所有风电机组参数加权平均值的方法确定[53—56]。因此,这一风电场单机等值模型的建立方法通常称为容量加权平均法。
目前,容量加权平均法主要用于等值风电机组发电机及其轴系参数的计算,以双馈感应风机为例,等值风机参数计算方法如下[53—56]:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_{{\rm{eq}}}} = \sum\limits_{i = 1}^N {{S_i}} ,{P_{{\rm{eq}}}} = \sum\limits_{i = 1}^N {{P_i}} ,{w_i} = \frac{{{S_i}}}{{{S_{{\rm{eq}}}}}}{\rm{ }}}\\ {{x_{{\rm{meq}}}} = \sum\limits_{i = 1}^N {{w_i}{x_{{\rm{m}}i}}} ,{x_{{\rm{seq}}}} = \sum\limits_{i = 1}^N {{w_i}{x_{{\rm{s}}i}}} ,{x_{{\rm{seq}}}} = \sum\limits_{i = 1}^N {{w_i}{x_{{\rm{r}}i}}} }\\ {{r_{{\rm{seq}}}} = \sum\limits_{i = 1}^N {{w_i}{r_{{\rm{s}}i}}} ,{r_{{\rm{seq}}}} = \sum\limits_{i = 1}^N {{w_i}{r_{{\rm{r}}i}}} ,{H_{{\rm{seq}}}} = \sum\limits_{i = 1}^N {{H_{{\rm{t}}i}}} }\\ {{H_{{\rm{geq}}}} = \sum\limits_{i = 1}^N {{H_{{\rm{g}}i}},{K_{{\rm{eq}}}} = \sum\limits_{i = 1}^N {{K_i}} ,{D_{{\rm{eq}}}} = \sum\limits_{i = 1}^N {{D_i}} } } \end{array}} \right. $ | (1) |
式中:S,P分别为感应发电机的容量和有功功率;xm,xs,xr分别为感应发电机激磁电抗、定子绕组电抗和转子绕组电抗;rs,rr分别为感应发电机定、转子绕组电阻;Ht,Hg分别为风力机和发电机轴系的惯性时间常数;K,D分别为轴系刚度系数和阻尼系数;wi为权重;下标i为原风电场内风电机组i的参数;下标eq为等值风电机组的参数;N为风电场内风电机组的数量。
(2) 参数辨识法。参数辨识法将等值风电机组看作一灰箱,即其模型已知(仍为一台扩容风电机组),但是参数部分未知,根据被等值风电场在并网点动态响应的实测数据或仿真数据,对灰箱中的未知参数进行辨识[57—61]。等值风电机组参数辨识的过程本质上可看作对一优化问题的建模与求解。其中优化目标为:在相同工况或相同外部扰动下,等值风机与被等值风电场在并网点的动态响应,如输出功率波动或电压波动等的误差最小[57—61]。待求量为等值风机参数。由于优化过程涉及微分方程组和非线性优化问题的求解,一般采用智能优化算法如遗传算法和粒子群算法[57—59],以及基于其提出的改进算法[60, 62]。
由于风电机组参数众多,包括风力机与发电机部分参数、换流器及其控制系统参数和锁相环参数等,如果在辨识中考虑等值风电机组所有参数,势必耗费大量计算时间[52]。现有基于参数辨识的风电场动态等值研究中,大多通过仿真分析,计算风电场动态响应对风电机组参数的灵敏度,选取对风电场动态响应影响较大的参数作为关键参数进行辨识[57—62]。对于非关键参数,由于其对风电场动态响应的影响较小,且难以根据动态响应数据进行辨识,在等值模型中,控制环节的非关键参数可以取典型值[8],发电机和风力机部分的非关键参数常采用容量加权平均法确定[61]。关键参数的具体确定方法可参考文献[52]和文献[57]。
2.1.2 风电机组机端变压器等值对于风电场内风电机组的机端变压器,一般将其等值为一台位于等值风电机组机端的扩容变压器,扩容变压器容量和阻抗的计算[52—62]如式(2)和式(3)所示。
| $ {S_{{\rm{Teq}}}} = \sum\limits_{i = 1}^N {{S_{{\rm{T}}i}}} $ | (2) |
| $ {Z_{{\rm{Teq}}}} = \frac{{{Z_{{\rm{T}}i}}}}{N} $ | (3) |
式中:STeq,ZTeq分别为扩容变压器的容量和阻抗;STi,ZTi分别为风电场内风电机组i机端变压器的容量和阻抗。
实际上,扩容变压器容量应为原风电场内所有风电机组机端变压器容量之和,扩容变压器阻抗为风电场内所有风电机组机端变压器阻抗的并联[52—62]。但是,现有研究中大多默认风电场内风电机组机端变压器型号相同,从而其阻抗相同,因此,等值变压器阻抗通常写为式(2)和式(3)所示的形式。且式(2)和式(3)中的变量可以为有名值或系统基准容量下的标幺值,若以变压器额定容量为基准容量,则有ZTeq=ZTi(ZTi以STi为基准值,ZTeq以STeq为基准值)[61]。
2.1.3 集电网络等值风电场集电网络等值的常用方法有恒功率损耗法和恒电压降落法。文中将简要介绍这2种方法的基本原理与应用。
(1) 恒功率损耗法。恒功率损耗法是最常用的风电场集电网络等值方法,其以等值前后集电网络上功率损耗基本不变为原则,将风电场集电网络等效为一聚合阻抗[63—70],因此恒功率损耗法也称为等值损耗功率法[63]。以图 1所示的一般结构风电场为例,采用恒功率损耗法计算集电网络聚合阻抗的方法如式(4)所示。

|
图 1 简单示例风电场 Fig. 1 A simple illustration wind farm |
| $ {Z_{{\rm{weq}}}} = \frac{{{S_{{\rm{loss}}}}}}{{I_{\rm{w}}^2}} $ | (4) |
式中:Zweq为集电网络聚合阻抗;Iw为风电场输出电流,
具体计算如式(5)所示。
| $ {S_{{\rm{loss}}}} = I_1^2{Z_1} + {\left( {\sum\limits_{k = 1}^2 {{I_k}} } \right)^2}{\rm{ }}{Z_2} + I_3^2{Z_3} + {\left( {\sum\limits_{k = 3}^4 {{I_k}} } \right)^2}{Z_4} + {\left( {\sum\limits_{k = 1}^5 {{I_k}} } \right)^2}{Z_5}{\left( {\sum\limits_{k = 1}^6 {{I_k}} } \right)^2}{Z_6} $ | (5) |
对于更加复杂的网络结构,可按照式(4)和式(5)所示原理,根据风电场潮流计算结果,计算集电网络的聚合阻抗。现有研究中大多对上述计算过程进行了简化,认为各风电机组输出电流相等[63—68],以图 1所示风电场为例,此时,集电网络聚合阻抗的计算公式为:
| $ {Z_{{\rm{weq}}}} = \frac{{{\rm{ }}{Z_1} + {2^2}{Z_2} + {Z_3} + {2^2}{Z_4} + {5^2}{Z_5} + {6^2}{Z_6}}}{{{6^2}}} $ | (6) |
由式(6)可抽象出当前常用的风电场集电网络聚合阻抗计算公式为[64]:
| $ {Z_{{\rm{weq}}}} = {\rm{ }}\frac{{\sum\limits_{m = 1}^N {n_m^2{Z_m}} }}{{{N^2}}} $ | (7) |
式中:Zm为线路m的阻抗;nm为线路m上游风电机组数量。需要补充说明的是,式(7)主要针对常见的由链式和干线式结构构成的风电场集电网络的等值;若考虑更加复杂的网络结构,如环网,则可根据式(4)所示恒功率损耗法的基本原理与定义计算风电场集电网络的聚合阻抗。
(2) 恒电压降落法。以N机风电场为例,采用恒电压降落法计算风电场集电网络聚合阻抗的基本公式为[66]:
| $ {Z_{{\rm{weq}}}} = \frac{{\sum\limits_{m = 1}^N {{w_k}\left( {{V_k} - {V_{{\rm{pcc}}}}} \right)} }}{{\sum\limits_{m = 1}^N {{I_k}} }} $ | (8) |
式中:Zweq为集电网络聚合阻抗;Vk,Ik分别为风电机组k的端电压和输出电流(k=1, 2, …, N);Vpcc为风电场端口母线电压;wk为风电机组k额定容量与风电场额定容量的比值。
式(8)为恒电压降落法计算风电场集电网络聚合阻抗的基本原理,其中分子项可看作所有风电机组机端变压器端口与风电场端口之间电压降落的加权平均值,分母项为风电场输出电流。电压和电流的具体值可通过潮流计算获得,现有研究中大多对此作了简化,例如在计算风电机组输出电流时认为系统各节点电压相同,均为系统额定电压,并根据所得电流和线路阻抗计算电压降落。
多机等值法中首先根据风电场内各风电机组的运行状态,将风电场划分为若干由型号相同且工况相似的风电机组构成的风电机群,再对各风电机群进行单机等值。对风电机群进行单机等值的方法与风电场单机等值建模方法一致,下文重点介绍风电机群划分方法。
当前一般通过聚类分析对风电场进行分群,聚类指标一般选用能够描述风电机组运行状态的变量,如风速、风电机组输出功率、端电压和转子转速等,常用的聚类方法有K均值聚类、C均值聚类、支持向量机及其改进算法[6, 63—70]。
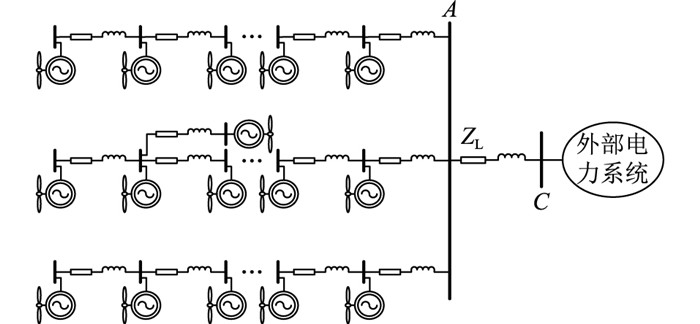
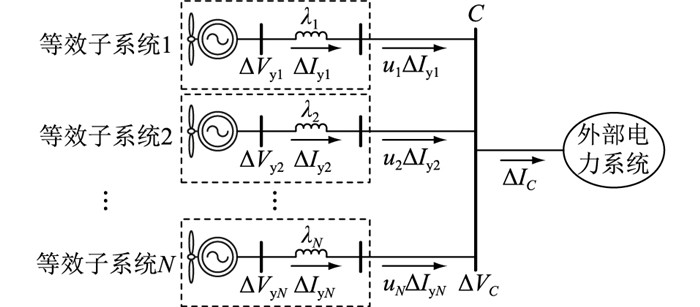
2.2 风电并网系统小干扰稳定性解耦分析方法与动态等值模型文献[9—13]中提出了一种风电并网系统小干扰稳定性的解耦分析方法。对于图 2所示的N机风电场/风电机群(后文以风电场为例进行说明,ZL为风电外送线路阻抗),在风电场内风电机组线性化状态空间模型相同的条件下,通过引入一变量变换,可将该风电场的小信号模型解耦为N个相互独立的等效子系统,具体结构如图 3所示。
|
图 2 并网风电场示意 Fig. 2 Agrid-connected wind farm |
|
图 3 并网风电场等效子系统示意 Fig. 3 Equivalent subsystems of the grid-connected wind farm |
变量变换的具体过程如下:
采用节点阻抗矩阵,图 2所示并网风电场的网络方程通常可表示为式(9)。
| $ \Delta \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{Z}}_{\rm{w}}}\Delta \mathit{\boldsymbol{I}} + \Delta {\mathit{\boldsymbol{V}}_{CN}} $ | (9) |
式中:
若忽略线路电阻,Zw可表示如下:
| $ {\mathit{\boldsymbol{Z}}_{\rm{w}}} = \left[ {\begin{array}{*{20}{l}} {{x_{11}}\mathit{\boldsymbol{E}}\;}&{{x_{12}}\mathit{\boldsymbol{E}}}& \cdots &{{x_{1N}}\mathit{\boldsymbol{E}}}\\ {{x_{21}}\mathit{\boldsymbol{E}}}&{{x_{22}}\mathit{\boldsymbol{E}}}& \cdots &{{x_{2N}}\mathit{\boldsymbol{E}}}\\ \vdots & \vdots &\;& \vdots \\ {{x_{N1}}\mathit{\boldsymbol{E}}}&{{x_{N2}}\mathit{\boldsymbol{E}}}& \cdots &{{x_{NN}}\mathit{\boldsymbol{E}}} \end{array}} \right] = {\mathit{\boldsymbol{X}}_{\rm{w}}} \otimes \mathit{\boldsymbol{E}} $ | (10) |
其中:
| $ {\mathit{\boldsymbol{X}}_{\rm{w}}} = \left[ {\begin{array}{*{20}{l}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1N}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2N}}}\\ \vdots & \vdots &\;& \vdots \\ {{x_{N1}}}&{{x_{N2}}}& \cdots &{{x_{NN}}} \end{array}} \right] $ | (11) |
若线路动态可忽略,则:
| $ \mathit{\boldsymbol{E}}\left[ {\begin{array}{*{20}{c}} 0&{ - 1}\\ 1&0 \end{array}} \right] $ | (12) |
若考虑线路动态,则:
| $ \mathit{\boldsymbol{E}}(s) = \left[ {\begin{array}{*{20}{c}} {s/{w_0}} &{ - 1}\\ 1 &{s/{w_0}} \end{array}} \right] $ | (13) |
式中:Xw为风电场网络电抗矩阵;⊗为克罗内克乘积。
矩阵Xw通常为一实对称矩阵,若对于矩阵Xw有相似对角化变换UTXwU=diag(λi),则所引入变量变换的表示形式如下:
| $ \Delta \mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{U}}_n}\Delta \mathit{\boldsymbol{Y}} $ | (14) |
| $ \Delta \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{U}}_2}\Delta {\mathit{\boldsymbol{V}}_Y} $ | (15) |
| $ \Delta \mathit{\boldsymbol{I}} = {\mathit{\boldsymbol{U}}_2}\Delta {\mathit{\boldsymbol{I}}_Y} $ | (16) |
式中:ΔX为风电场状态变量列向量;Un=U⊗En,En为n阶单位矩阵,n为一台风机线性化模型的阶数;U2=U⊗E2,E2为2阶单位矩阵。
图 3中的λi和ui分别为风电场网络电抗矩阵的特征值和对应的特征向量中的所有元素之和。文献[10]中结合风电汇集电网的特点,进一步分析发现,若有λ1<λ2<…<λN,则ui<<uN,即风电场与外部交流系统间的动态交互作用集中体现在第N个等效子系统中,从而可根据第N个等效子系统建立风电场单机等值模型,具体结构如图 4所示。

|
图 4 并网风电场单机等值模型 Fig. 4 Single-machine equivalent model of the grid-connected wind farm |
其中,风电机组模型和参数与图 2中保持一致,风电机组输入风速可以取风电场内所有风机输入风速的平均值,外部交流系统的模型和参数也与图 2中保持一致,但是风电机组与外部交流系统接口间的潮流关系发生了变化,具体如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{I_C} = {I_{yN}} = N{I_{yN0}} + {u_N}\Delta {I_{yN}}}\\ {{V_{yN}} = {V_{yN0}} + \Delta {V_{yN}} = {V_{yN0}} + j{\lambda _N}\Delta {I_{yN}} + {u_N}\Delta {V_C}} \end{array}} \right. $ | (17) |
针对不同类型问题分析所提出的风电场等值建模方法也存在差异。针对小干扰稳定性分析的风电场等值建模方法以能有效反映风电场在扰动作用下的动态响应特性或风电场的主导振荡模式为目标。由于风电机组具有多时间尺度特性,考虑不同时间尺度下的小干扰稳定性分析时,所用的风电场等值建模方法也存在差异。若考虑暂态稳定性分析,则需考虑风机非线性特性,基于线性化模型提出的风电场等值建模方法不再适用。
3 各类风电场小干扰等值模型用于风电并网系统次同步振荡分析的有效性第2章对现有风电场小干扰等值方法进行了分类介绍和分析,结合第1章对风电接入对电力系统振荡稳定性影响研究现状的分析,可以看出:
(1) 风电接入引发的电力系统振荡多是源自风电场与外部交流系统之间产生了不利的动态交互作用,且这一动态交互中通常有风电机组换流器控制环节动态的参与。因此,适用于风电并网系统次同步振荡研究的风电场动态等值模型应能有效反映原风电场内大规模换流器整体的动态输入-输出特性。此外,由于当前风电并网系统次同步振荡研究多是基于小型号(线性化)模型展开,考虑次同步振荡研究的风电场等值模型应能有效反映原风电场在次同步频率范围内的振荡模式。
(2) 容量加权平均法通过对风电场内风电机组物理参数的直接聚合,建立风电场单机等值模型,计算量小,原理简单。但是,由于容量加权平均法主要针对等值风电机组发电机部分参数的计算,所建立的单机等值模型主要反映了风电机组发电机及其传统系统部分时间尺度下的风电场动态特性。风电机组换流器及其控制系统动态是风电并网系统中动态交互作用引发振荡的关键所在,然而,对于等值风电机组换流器控制系统参数,目前未见有文献给出明确的直接聚合方法和有效性验证。因此,基于容量加权平均法建立的风电场单机等值模型用于风电并网系统振荡稳定性分析时,所得结果可能存在较大误差[57]。
(3) 基于参数辨识法建立的风电场等值模型准确度较高,但是,等值风电机组参数的辨识需要风电场并网点动态响应数据的支持,若实测数据不足,则需通过仿真获取风电场的响应数据。而且,在对等值风电机组参数进行优化求解的过程中,每一次迭代中均需要通过非线性仿真获取等值风机并网运行的动态响应数据。因此,参数辨识法在提高等值模型准确度的同时,也增加了等值模型参数求解的计算量,尤其是对于含多风电场/风电机群并网的大规模电力系统,待求变量较多,且系统复杂,采用参数辨识法建立各风电场/风电机群的单机等值模型,可能需要耗费大量计算时间[9—10, 52]。此外,风电并网系统振荡稳定性受风电场稳态运行点变化的影响,风电场内风电机组数量变化或风电机组出力变化均会造成系统稳定性的变化;若在每一种可能的运行状态下,均对等值风电机组参数进行辨识,也会面临巨大的计算量[9—10]。最后,基于参数辨识法获得的等值风电机组参数与原风电场内风电机组参数、运行点和机组数量之间的映射关系湮没在了对优化问题进行迭代求解的过程中,因此,所建立的风电场单机等值模型可用于对具体风电场振荡特性的仿真分析,而难以用于对原风电场内风电机组数量、出力和参数变化引发风电并网系统振荡失稳机理的研究[52]。
(4) 风电并网系统小干扰稳定性的解耦分析与等值方法中,等值模型表示形式与原风电场网络结构、场内风电机组数量和风电机组参数之间的直接映射关系清晰,且其有效性具有基于数学模型的理论推导为依据。因此,该等值模型可有效反映风电机组大规模接入对电力系统振荡稳定性的影响,相对于容量加权平均模型和参数辨识模型而言,更加适用于风电并网系统振荡稳定性分析。但是解耦分析方法与相关等值模型是在风电场内风电机组线性化模型(近似)相同的条件下得到的,实际中,由于风电机组型号差异或稳态工况的分散性,同一风电场内风电机组的线性化模型通常是不同的。对于解耦分析思想应如何应用于风电机组线性化模型存在差异的情况下,还有待深入研究与探讨。
(5) 现有风电并网系统次同步振荡研究中,多是研究风机接入引发电力系统次同步振荡的原因,或是认为风电场内风机型号相同,从而采用一台扩容风机代表一个风电场或风电机群,而并未对如此等值的有效性进行验证。因此,在基于一致性控制理论的风电并网系统小干扰稳定性解耦分析方法出现之前,风电并网系统次同步振荡和风电场等值是电力系统领域中2个独立的研究课题,次同步振荡研究中所采用的风电场等值模型可在一定程度上揭示风电接入引发电力系统次同步振荡的机理,但是由于其等值过程中的简化,如忽略集电网络等,导致其无法有效揭示风机数量和集电网络结构等的变化对系统次同步振荡的影响,仅分析了风机控制系统参数等的影响。当基于一致性控制理论的解耦分析方法被用于并网风电场次同步振荡研究后,才开始揭示风电场网络结构和风机数量变化对系统次同步振荡的影响,同时得到了一种能准确反映风电场在扰动作用的动态响应特性的风电场等值模型。
4 结论与展望文中考虑风电并网系统振荡稳定性分析,对现有主要风电场小干扰等值建模方法的优势和不足进行了分析。结论如下:
(1) 容量加权平均法计算量小、原理简单,但是由于其中未考虑对风电机组换流器控制环节动态的等值,所建立的等值模型用于风电并网系统振荡稳定性分析时,通常存在较大误差;
(2) 参数辨识法可提高等值模型的准确度,但是等值模型的建立可能需耗费大量计算时间,且等值模型与原风电场网络结构、场内风电机组数量和风电机组参数之间的映射关系湮没在参数辨识的优化迭代过程中,所建立的等值模型难以用于风电接入引发电力系统振荡的机理分析;
(3) 解耦分析方法和相关等值模型可有效反映原风电场内风电机组参数、机组数量和网络结构对风电并网系统振荡稳定性的影响,但是仅适用于风电场内风电机组模型(近似)相同的情况。
综上,考虑振荡稳定性分析,风电场动态等值建模研究中还存在如下问题亟待解决:
(1) 应如何考虑风电机组型号和工况差异的影响。风电场动态等值中,针对风电机组型号和工况差异,当前普遍采用的解决方案是,根据风电机组型号和运行状态,对风电机组进行聚类分群,从而将风电场划分为几个由型号相同且工况相似的风电机组构成的风电机群,再对各风电机群进行单机等值。但是,风电场网络结构和风电机组空间分布复杂,同一风电机群内的风电机组可能位于不同支路上,与其他风电机群内的风电机组之间存在着复杂的动态耦合,这一特征为基于参数辨识法或解耦分析法建立风电场动态等值模型带来巨大挑战。
(2) 风电机组动态特性的相似程度应如何衡量。风电机组参数和运行点差异均会造成其动态特性的差异,这些差异最终将体现在动态过程中风电机组可测量状态变量,例如输出功率、电流、端电压和转子转速等的差异上。但是实际中,这些量测量大多应为稳态数据,对于应如何基于稳态数据分析风电机组动态特性的相似程度,还需进一步研究与明确。
(3) 解耦分析方法应如何拓展应用于风电机组模型存在较大差异的情况。解耦分析法为分析大规模风电汇集系统振荡稳定性奠定了基础,且可以很好的反映风电机组数量和风电场网络解耦对风电场稳定性的影响。但是这一方法局限于风电机组线性化模型(近似)相同的情况。若可将这一研究思想扩展至风电场内风电机组线性化模型不同的情况,则会为风电并网系统振荡问题分析与研究带来巨大便利,对此,国内已有一些研究团队进行了大量有益尝试。
本文得到国网江苏省电力有限公司科技项目“多电力电子变流器接入江苏电网引发宽频振荡风险评估及优化控制策略研究”(J2020129),电网安全与节能国家重点实验室开放基金(FX80-21-001)资助,谨此致谢!
| [1] |
鲁宗相, 李昊, 乔颖. 从灵活性平衡视角的高比例可再生能源电力系统形态演化分析[J]. 全球能源互联网, 2021, 4(1): 12-18. LU Zongxiang, LI Hao, QIAO Ying. Morphological evolution of power systems with high share of renewable energy generations from the perspective of flexibility balance[J]. Journal of Global Energy Interconnection, 2021, 4(1): 12-18. (  0) 0) |
| [2] |
王清. 双馈风电接入对电力系统稳定性影响机理研究[D]. 北京: 华北电力大学, 2016. WANG Qing. Mechanism of the impact of DFIGs on power system stability[D]. Beijing: North China Electric Power University, 2016. (  0) 0) |
| [3] |
ADAMS J, CARTER C, HUANG S H. ERCOT experience with Sub-synchronous Control Interaction and proposed remediation[C]//PES T & D 2012. Orlando, FL, USA. IEEE, 2012: 1-5.
(  0) 0) |
| [4] |
董晓亮, 田旭, 张勇, 等. 沽源风电场串补输电系统次同步谐振典型事件及影响因素分析[J]. 高电压技术, 2017, 43(1): 321-328. DONG Xiaoliang, TIAN Xu, ZHANG Yong, et al. Practical SSR incidence and influencing factor analysis of DFIG-based series-compensated transmission system in Guyuan farms[J]. High Voltage Engineering, 2017, 43(1): 321-328. (  0) 0) |
| [5] |
LIU H, BI T S, CHANG X Q, et al. Impacts of subsynchronous and supersynchronous frequency components on synchrophasor measurements[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(3): 362-369. DOI:10.1007/s40565-016-0225-4 (  0) 0) |
| [6] |
ZOU J X, PENG C, XU H B, et al. A fuzzy clustering algorithm-based dynamic equivalent modeling method for wind farm with DFIG[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1329-1337. DOI:10.1109/TEC.2015.2431258 (  0) 0) |
| [7] |
DU W J, WANG Y, WANG H F, et al. Collective impact of multiple doubly fed induction generators with similar dynamics on the oscillation stability of a grid-connected wind farm[J]. IEEE Transactions on Power Delivery, 2021, 36(5): 2942-2954. DOI:10.1109/TPWRD.2020.3030645 (  0) 0) |
| [8] |
CHOW J H. Power System Coherency and Model Reduction[M]. New York, NY: Springer New York, 2013.
(  0) 0) |
| [9] |
董文凯, 杜文娟, 王海风. 用于风电场小干扰稳定性检验的降阶模式计算方法[J]. 电工技术学报, 2021, 36(7): 1468-1479. DONG Wenkai, DU Wenjuan, WANG Haifeng. Reduced-order modal computation method for small-signal stability examination of a wind farm[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1468-1479. (  0) 0) |
| [10] |
董文凯, 杜文娟, 王海风. 用于振荡稳定性分析的并网风电场动态等效模型[J]. 中国电机工程学报, 2021, 41(1): 75-87, 399. DONG Wenkai, DU Wenjuan, WANG Haifeng. Dynamic equivalent model of a grid-connected wind farm for oscillation stability analysis[J]. Proceedings of the CSEE, 2021, 41(1): 75-87, 399. (  0) 0) |
| [11] |
FU Q, DU W J, WANG H F, et al. Small-signal stability analysis of a VSC-MTDC system for investigating DC voltage oscillation[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5081-5091. DOI:10.1109/TPWRS.2021.3072399 (  0) 0) |
| [12] |
DU W J, DONG W K, WANG H F. Small-signal stability limit of a grid-connected PMSG wind farm dominated by the dynamics of PLLs[J]. IEEE Transactions on Power Systems, 2020, 35(3): 2093-2107. DOI:10.1109/TPWRS.2019.2946647 (  0) 0) |
| [13] |
HUANG L B, XIN H H, LI Z Y, et al. Identification of generalized short-circuit ratio for on-line stability monitoring of wind farms[J]. IEEE Transactions on Power Systems, 2020, 35(4): 3282-3285. DOI:10.1109/TPWRS.2020.2975413 (  0) 0) |
| [14] |
DONG W, XIN H H, WU D, et al. Small signal stability analysis of multi-infeed power electronic systems based on grid strength assessment[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1393-1403. DOI:10.1109/TPWRS.2018.2875305 (  0) 0) |
| [15] |
辛焕海, 董炜, 袁小明, 等. 电力电子多馈入电力系统的广义短路比[J]. 中国电机工程学报, 2016, 36(22): 6013-6027. XIN Huanhai, DONG Wei, YUAN Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027. (  0) 0) |
| [16] |
章枫, 辛焕海, 徐谦, 等. 直流多馈入系统的广义短路比: 影响因素分析[J]. 中国电机工程学报, 2017, 37(18): 5303-5312, 5529. ZHANG Feng, XIN Huanhai, XU Qian, et al. Generalized short circuit ratio for multi-infeed DC systems: influence factors[J]. Proceedings of the CSEE, 2017, 37(18): 5303-5312, 5529. (  0) 0) |
| [17] |
辛焕海, 章枫, 于洋, 等. 多馈入直流系统广义短路比: 定义与理论分析[J]. 中国电机工程学报, 2016, 36(3): 633-647. XIN Huanhai, ZHANG Feng, YU Yang, et al. Generalized short circuit ratio for multi-infeed DC systems: definition and theoretical analysis[J]. Proceedings of the CSEE, 2016, 36(3): 633-647. (  0) 0) |
| [18] |
ZHANG F, XIN H H, WANG Z, et al. Generalized short circuit ratio for multi-infeed LCC-HVDC systems[C]//2017 IEEE Power & Energy Society General Meeting. Chicago, IL, USA. IEEE, 2017: 1-5.
(  0) 0) |
| [19] |
FAN L L. Interarea oscillations revisited[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1585-1586. (  0) 0) |
| [20] |
DU W J, DONG W K, WANG Y, et al. A method to design power system stabilizers in a multi-machine power system based on single-machine infinite-bus system model[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3475-3486. DOI:10.1109/TPWRS.2020.3041037 (  0) 0) |
| [21] |
VARMA R K, MOHARANA A. SSR in double-cage induction generator-based wind farm connected to series-compensated transmission line[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2573-2583. DOI:10.1109/TPWRS.2013.2246841 (  0) 0) |
| [22] |
王亮, 谢小荣, 姜齐荣, 等. 大规模双馈风电场次同步谐振的分析与抑制[J]. 电力系统自动化, 2014, 38(22): 26-31. WANG Liang, XIE Xiaorong, JIANG Qirong, et al. Analysis and mitigation of SSR problems in large-scale wind farms with doubly-fed wind turbines[J]. Automation of Electric Power Systems, 2014, 38(22): 26-31. DOI:10.7500/AEPS20131010016 (  0) 0) |
| [23] |
WANG L, XIE X R, JIANG Q R, et al. Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2772-2779. DOI:10.1109/TPWRS.2014.2365197 (  0) 0) |
| [24] |
FAN L L, MIAO Z X. Nyquist-stability-criterion-based SSR explanation for type-3 wind generators[J]. IEEE Transactions on Energy Conversion, 2012, 27(3): 807-809. DOI:10.1109/TEC.2012.2193491 (  0) 0) |
| [25] |
MIAO Z X. Impedance-model-based SSR analysis for type 3 wind generator and series-compensated network[J]. IEEE Transactions on Energy Conversion, 2012, 27(4): 984-991. DOI:10.1109/TEC.2012.2211019 (  0) 0) |
| [26] |
XIE X R, ZHANG X, LIU H K, et al. Characteristic analysis of subsynchronous resonance in practical wind farms connected to series-compensated transmissions[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1117-1126. DOI:10.1109/TEC.2017.2676024 (  0) 0) |
| [27] |
LIU H K, XIE X R, HE J B, et al. Damping DFIG-associated SSR by adding subsynchronous suppression filters to DFIG converter controllers[C]//2016 IEEE Power and Energy Society General Meeting. Boston, MA. IEEE, 2016: 1-5.
(  0) 0) |
| [28] |
SURIYAARACHCHI D H R, ANNAKKAGE U D, KARAWITA C, et al. A procedure to study sub-synchronous interactions in wind integrated power systems[J]. IEEE Transactions on Power Systems, 2013, 28(1): 377-384. DOI:10.1109/TPWRS.2012.2204283 (  0) 0) |
| [29] |
OSTADI A, YAZDANI A, VARMA R K. Modeling and stability analysis of a DFIG-based wind-power generator interfaced with a series-compensated line[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1504-1514. DOI:10.1109/TPWRD.2009.2013667 (  0) 0) |
| [30] |
FAN L L, KAVASSERI R, MIAO Z L, et al. Modeling of DFIG-based wind farms for SSR analysis[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2073-2082. DOI:10.1109/TPWRD.2010.2050912 (  0) 0) |
| [31] |
FAN L L, ZHU C X, MIAO Z X, et al. Modal analysis of a DFIG-based wind farm interfaced with a series compensated network[J]. IEEE Transactions on Energy Conversion, 2011, 26(4): 1010-1020. DOI:10.1109/TEC.2011.2160995 (  0) 0) |
| [32] |
FAN L L, MIAO Z X. Mitigating SSR using DFIG-based wind generation[J]. IEEE Transactions on Sustainable Energy, 2012, 3(3): 349-358. DOI:10.1109/TSTE.2012.2185962 (  0) 0) |
| [33] |
BEZA M, BONGIORNO M. On the risk for subsynchronous control interaction in type 4 based wind farms[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 1410-1418. DOI:10.1109/TSTE.2018.2889181 (  0) 0) |
| [34] |
XU Y K, ZHANG M, FAN L L, et al. Small-signal stability analysis of type-4 wind in series-compensated networks[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 529-538. DOI:10.1109/TEC.2019.2943578 (  0) 0) |
| [35] |
ZHAO S Q, LI R, GAO B F, et al. Sub and super synchronous oscillations between type 4 wind turbines and series compensated AC transmission systems[C]//2018 IEEE Power & Energy Society General Meeting. Portland, OR, USA. IEEE, 2018: 1-5.
(  0) 0) |
| [36] |
LEON A E. Integration of DFIG-based wind farms into series-compensated transmission systems[J]. IEEE Transactions on Sustainable Energy, 2016, 7(2): 451-460. DOI:10.1109/TSTE.2015.2498312 (  0) 0) |
| [37] |
李辉, 陈耀君, 李洋, 等. 双馈风电场并网对汽轮发电机次同步振荡的影响[J]. 电机与控制学报, 2015, 19(6): 47-54. LI Hui, CHEN Yaojun, LI Yang, et al. Impact of DFIG-based wind farms interconnected to power grid on subsynchronous oscillation of turbogenerator[J]. Electric Machines and Control, 2015, 19(6): 47-54. (  0) 0) |
| [38] |
吴杨, 肖湘宁, 罗超, 等. 直驱风机对火电机组次同步振荡的影响及抑制方法[J]. 现代电力, 2019, 36(5): 31-38. WU Yang, XIAO Xiangning, LUO Chao, et al. Impact of PMSG to thermal power units on sub-synchronous oscillation characteristics and suppression strategy[J]. Modern Electric Power, 2019, 36(5): 31-38. DOI:10.3969/j.issn.1007-2322.2019.05.005 (  0) 0) |
| [39] |
ALAWASA K M, MOHAMED Y A R I, XU W. Modeling, analysis, and suppression of the impact of full-scale wind-power converters on subsynchronous damping[J]. IEEE Systems Journal, 2013, 7(4): 700-712. DOI:10.1109/JSYST.2012.2226615 (  0) 0) |
| [40] |
ALAWASA K M, MOHAMED Y A R I, XU W. Active mitigation of subsynchronous interactions between PWM voltage-source converters and power networks[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 121-134. DOI:10.1109/TPEL.2013.2251904 (  0) 0) |
| [41] |
LIU H K, XIE X R, HE J B, et al. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708-4720. DOI:10.1109/TPWRS.2017.2682197 (  0) 0) |
| [42] |
谢小荣, 刘华坤, 贺静波, 等. 直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J]. 中国电机工程学报, 2016, 36(9): 2366-2372. XIE Xiaorong, LIU Huakun, HE Jingbo, et al. Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems[J]. Proceedings of the CSEE, 2016, 36(9): 2366-2372. (  0) 0) |
| [43] |
宋瑞华, 郭剑波, 李柏青, 等. 基于输入导纳的直驱风电次同步振荡机理与特性分析[J]. 中国电机工程学报, 2017, 37(16): 4662-4670, 4891. SONG Ruihua, GUO Jianbo, LI Baiqing, et al. Mechanism and characteristics of subsynchronous oscillation in direct-drive wind power generation system based on input-admittance analysis[J]. Proceedings of the CSEE, 2017, 37(16): 4662-4670, 4891. (  0) 0) |
| [44] |
张明远, 肖仕武, 田恬, 等. 基于阻抗灵敏度的直驱风电场并网次同步振荡影响因素及参数调整分析[J]. 电网技术, 2018, 42(9): 2768-2777. ZHANG Mingyuan, XIAO Shiwu, TIAN Tian, et al. Analysis of SSO influencing factors and parameter adjustment for grid-connected full-converter wind farm based on impedance sensitivity[J]. Power System Technology, 2018, 42(9): 2768-2777. (  0) 0) |
| [45] |
LIU H K, XIE X R. Impedance network modeling and quantitative stability analysis of sub-/super-synchronous oscillations for large-scale wind power systems[J]. IEEE Access, 2018, 6: 34431-34438. DOI:10.1109/ACCESS.2018.2849830 (  0) 0) |
| [46] |
FAN L L, MIAO Z X. Wind in weak grids: 4 Hz or 30 Hz oscillations?[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5803-5804. DOI:10.1109/TPWRS.2018.2852947 (  0) 0) |
| [47] |
FAN L L, MIAO Z X. An explanation of oscillations due to wind power plants weak grid interconnection[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 488-490. DOI:10.1109/TSTE.2017.2713980 (  0) 0) |
| [48] |
HU J B, HUANG Y H, WANG D, et al. Modeling of grid-connected DFIG-based wind turbines for DC-link voltage stability analysis[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1325-1336. DOI:10.1109/TSTE.2015.2432062 (  0) 0) |
| [49] |
WANG D, HOU Y H, HU J B. Stability of DC-link voltage control for paralleled DFIG-based wind turbines connected to Weak AC grids[C]//2016 IEEE Power and Energy Society General Meeting. Boston, MA, USA. IEEE, 2016: 1-5.
(  0) 0) |
| [50] |
LIU J, YAO W, WEN J Y, et al. Impact of power grid strength and PLL parameters on stability of grid-connected DFIG wind farm[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 545-557. DOI:10.1109/TSTE.2019.2897596 (  0) 0) |
| [51] |
刘巨, 姚伟, 文劲宇. 考虑PLL和接入电网强度影响的双馈风机小干扰稳定性分析与控制[J]. 中国电机工程学报, 2017, 37(11): 3162-3173, 3371. LIU Ju, YAO Wei, WEN Jinyu. Small signal stability analysis and control of double-fed induction generator considering influence of PLL and power grid strength[J]. Proceedings of the CSEE, 2017, 37(11): 3162-3173, 3371. (  0) 0) |
| [52] |
张剑, 何怡刚. 基于轨迹灵敏度分析的永磁直驱风电场等值模型参数辨识[J]. 电工技术学报, 2020, 35(15): 3303-3313. ZHANG Jian, HE Yigang. Parameters identification of equivalent model of permanent magnet synchronous generator wind farm based on analysis of trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3303-3313. (  0) 0) |
| [53] |
HUANG P H, EL MOURSI M S, XIAO W D, et al. Subsynchronous resonance mitigation for series-compensated DFIG-based wind farm by using two-degree-of-freedom control strategy[J]. IEEE Transactions on Power Systems, 2015, 30(3): 1442-1454. DOI:10.1109/TPWRS.2014.2348175 (  0) 0) |
| [54] |
LI W X, CHAO P P, LIANG X D, et al. An improved single-machine equivalent method of wind power plants by calibrating power recovery behaviors[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4371-4381. DOI:10.1109/TPWRS.2017.2771323 (  0) 0) |
| [55] |
FANG R M, SHANG R Y, WU M L, et al. Application of gray relational analysis to k-means clustering for dynamic equivalent modeling of wind farm[J]. International Journal of Hydrogen Energy, 2017, 42(31): 20154-20163. DOI:10.1016/j.ijhydene.2017.06.023 (  0) 0) |
| [56] |
吴红斌, 何叶, 赵波, 等. 基于改进K-means聚类算法的风电场动态等值[J]. 太阳能学报, 2018, 39(11): 3232-3238. WU Hongbin, HE Ye, ZHAO Bo, et al. Research on dynamic equivalent of wind farm based on improved K-means clustering algorithm[J]. Acta Energiae Solaris Sinica, 2018, 39(11): 3232-3238. (  0) 0) |
| [57] |
WANG Y F, LU C, ZHU L P, et al. Comprehensive modeling and parameter identification of wind farms based on wide-area measurement systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(3): 383-393. DOI:10.1007/s40565-016-0208-5 (  0) 0) |
| [58] |
LI H, YANG C, ZHAO B, et al. Aggregated models and transient performances of a mixed wind farm with different wind turbine generator systems[J]. Electric Power Systems Research, 2012, 92: 1-10. DOI:10.1016/j.epsr.2012.04.019 (  0) 0) |
| [59] |
EL-SHARKAWI M A. Dynamic equivalent models for wind power plants[C]//2011 IEEE Power and Energy Society General Meeting. Detroit, MI, USA. IEEE, 2011: 1-5.
(  0) 0) |
| [60] |
CHENG X Y, LEE W J, SAHNI M, et al. Dynamic equivalent model development to improve the operation efficiency of wind farm[C]//2015 IEEE/IAS 51st Industrial & Commercial Power Systems Technical Conference (I & CPS). Calgary, AB, Canada. IEEE, 2015: 1-9.
(  0) 0) |
| [61] |
ZHOU Y H, ZHAO L, LEE W J. Robustness analysis of dynamic equivalent model of DFIG wind farm for stability study[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5682-5690. DOI:10.1109/TIA.2018.2858738 (  0) 0) |
| [62] |
ERLICH I, SHEWAREGA F, FELTES C, et al. Determination of dynamic wind farm equivalents using heuristic optimization[C]//2012 IEEE Power and Energy Society General Meeting. San Diego, CA, USA. IEEE, 2012: 1-8.
(  0) 0) |
| [63] |
朱乾龙, 韩平平, 丁明, 等. 基于聚类-判别分析的风电场概率等值建模研究[J]. 中国电机工程学报, 2014, 34(28): 4770-4780. ZHU Qianlong, HAN Pingping, DING Ming, et al. Probabilistic equivalent model for wind farms based on clustering-discriminant analysis[J]. Proceedings of the CSEE, 2014, 34(28): 4770-4780. (  0) 0) |
| [64] |
BROCHU J, LAROSE C, GAGNON R. Generic equivalent collector system parameters for large wind power plants[J]. IEEE Transactions on Energy Conversion, 2011, 26(2): 542-549. DOI:10.1109/TEC.2010.2087022 (  0) 0) |
| [65] |
陈树勇, 王聪, 申洪, 等. 基于聚类算法的风电场动态等值[J]. 中国电机工程学报, 2012, 32(4): 11-19, 24. CHEN Shuyong, WANG Cong, SHEN Hong, et al. Dynamic equivalence for wind farms based on clustering algorithm[J]. Proceedings of the CSEE, 2012, 32(4): 11-19, 24. (  0) 0) |
| [66] |
周明, 葛江北, 李庚银. 基于云模型的DFIG型风电场动态电压等值方法[J]. 中国电机工程学报, 2015, 35(5): 1097-1105. ZHOU Ming, GE Jiangbei, LI Gengyin. Cloud model based DFIG wind farm dynamic voltage equivalence method[J]. Proceedings of the CSEE, 2015, 35(5): 1097-1105. (  0) 0) |
| [67] |
胡庆林, 付盼. 考虑电网故障后转子转速的风电场等值建模[J]. 高压电器, 2018, 54(6): 216-222. HU Qinglin, FU Pan. Equivalent model of wind farm considering the rotor speed after grid fault[J]. High Voltage Apparatus, 2018, 54(6): 216-222. (  0) 0) |
| [68] |
孙元存, 刘三明, 王致杰, 等. 基于IGWO-K-means的风电场动态等值建模[J]. 现代电力, 2018, 35(5): 49-55. SUN Yuancun, LIU Sanming, WANG Zhijie, et al. Dynamic equivalent modeling of wind farm based on IGWO-K-means method[J]. Modern Electric Power, 2018, 35(5): 49-55. DOI:10.3969/j.issn.1007-2322.2018.05.007 (  0) 0) |
| [69] |
杜晓岩, 尹华杰, 叶超, 等. 基于改进模糊C均值聚类和MPSO的风电场等值研究[J]. 广东电力, 2016, 29(8): 38-44. DU Xiaoyan, YIN Huajie, YE Chao, et al. Equivalent model of wind power farm based on improved fuzzy C means clusteringand MPSO[J]. Guangdong Electric Power, 2016, 29(8): 38-44. DOI:10.3969/j.issn.1007-290X.2016.08.008 (  0) 0) |
| [70] |
吴琴, 钟庆, 王钢, 等. 基于模糊C均值聚类的风电场多机等值方法[J]. 现代电力, 2016, 33(6): 27-32. WU Qin, ZHONG Qing, WANG Gang, et al. Multi-machine equivalent approach of wind farm based on fuzzy C-means clustering[J]. Modern Electric Power, 2016, 33(6): 27-32. DOI:10.3969/j.issn.1007-2322.2016.06.005 (  0) 0) |
2. State Key Lab of Control and Simulation of Power Systems and Generation Equipment (Tsinghua University), Beijing 100084, China;
3. State Grid Jiangsu Electric Power Co., Ltd. Research Institute, Nanjing 211103, China;
4. Jiangsu Electric Power Test Research Institute Co., Ltd., Nanjing 211103, China;
5. College of Electric Engineering, Sichuan University, Chengdu 610065, China
 2022, Vol. 41
2022, Vol. 41


 董文凯(1992), 男, 博士, 助理研究员, 研究方向为电力系统振荡的分析与控制(E-mail:
董文凯(1992), 男, 博士, 助理研究员, 研究方向为电力系统振荡的分析与控制(E-mail: