文章编号: 2096-3203(2022)04-0051-07 中图分类号: TM73
2. 北京市能源发展研究基地, 北京 102206;
3. 新能源电力与低碳发展研究北京市重点实验室, 北京 102206
在新能源场站配置储能可以平抑风电、光伏功率波动,转移弃风、弃光电量,提升可再生能源利用率[1-5]。储能规模与其在电力系统中发挥的作用直接相关,然而现阶段储能投资运行成本高,难以支撑大规模的储能应用。因此,科学合理地配置储能,对提升储能经济性以及促进其可持续发展具有重要意义[6-10]。
在进行储能配置时通常需要考虑两方面。一是优化储能投资运维模式,降低成本;二是与可再生能源联合运营,提高收入。在优化成本方面,文献[11-14]结合储能投资时的容量成本、功率成本以及运维成本,根据经济学理论,从全生命周期角度核算储能总成本。而在联合运营方面,文献[15-17]基于可再生能源的出力特性,量化储能消纳弃风、弃光的效益,从经济和环保角度进行储能配置。上述研究在储能配置方面已取得较好的成果,但仅单独考虑了容量配置或功率配置,忽略了储能容量和功率间的相关性。此外,在进行算例分析时,通常仅选取单一季节下的典型日进行储能配置,忽略了其他季节下储能容量可能出现过剩或不足的情况,不能较好地适应可再生能源出力和负荷需求的季节性波动。
基于上述分析,文中提出考虑可再生能源出力季节性波动的储能优化配置方法。将储能长期规划与短期运行相结合,兼顾储能容量和功率配置,同时对4个季节下可再生能源利用率进行优化,保障储能经济性,并进一步提升可再生能源利用率。
1 储能全生命周期成本分析 1.1 储能年化成本储能成本主要包括建设初期用于设备购买及安装的投资成本以及使用过程中补偿电池损耗的运维成本。储能投资成本主要与储能容量和功率相关,运维成本可按投资成本的一定比例近似估算。
| $ \begin{gathered} C_{\mathrm{in}}=c_{\mathrm{p}} P_{\mathrm{ess}}+c_{\mathrm{e}} E_{\mathrm{ess}} \end{gathered} $ | (1) |
| $ C_{\mathrm{op}}=c_{\mathrm{o}} C_{\mathrm{in}} $ | (2) |
式中:Cin,Cop分别为储能投资成本和年运维成本;Pess,Eess分别为储能规划功率和规划容量;cp,ce分别为储能单位功率成本和单位容量成本;co为储能年运维成本系数。
考虑资金的时间价值,以储能等效寿命折算成年化投资成本。根据微观经济学理论,等额系列资金回收系数为:
| $\eta=\frac{r(1+r)^{n_{\mathrm{ess}}}}{(1+r)^{n_{\mathrm{ess}}}-1} $ | (3) |
式中:r为折现率;ness为储能等效寿命。
则储能年化总成本为:
| $ C_{\mathrm{ess}}=\eta C_{\mathrm{in}} C_{\mathrm{op}} $ | (4) |
储能系统的寿命主要受环境温度、充放电速率、放电深度及充放电循环次数等因素影响。以锂电池为例,通常以充放电循环次数衡量储能寿命,当达到最大循环次数时,即可认为该电池损耗达到极限。由于储能系统并不总是以最大放电深度进
行工作,因此应按照实际充放电行为对循环次数进行折算[18-19]。文中采用4个季节下的典型日进行储能日等效循环次数计算,进而根据储能生命周期额定循环次数折算储能的等效寿命。
| $ n_{\mathrm{eq}}=\frac{1}{4} \sum\limits_{i=1}^{4} \sum\limits_{t=1}^{24} \frac{Q_{i, t}^{\mathrm{d}}}{E_{\mathrm{ess}}} $ | (5) |
| $ n_{\mathrm{ess}}=\frac{n_{0}}{365 n_{\mathrm{eq}}} $ | (6) |
式中:neq为储能日等效循环次数;Qi, td为季节i时段t的储能实际放电量,i=1,2, 3,4分别表示春、夏、秋、冬4个季节,t=1,2,…,24分别表示一天的24个时段;n0为储能生命周期额定循环次数,即放电深度为100%时的最大循环次数。
2 储能容量规划模型 2.1 目标函数 2.1.1 储能总收益最大电网对可再生能源消纳能力不足时,储能可以储存电量,在可再生能源消纳能力充裕时进行释放,从而缓解弃风、弃光问题。因此可将安装储能后增加的风电、光伏并网收益作为储能的收益。
| $ \begin{gathered} \max S_{\mathrm{ess}}=\frac{1}{4} S_{\text {new }}-\frac{1}{365} C_{\mathrm{ess}} \end{gathered} $ | (7) |
| $S_{\text {new }}=\sum\limits_{i=1}^{4} \sum\limits_{t=1}^{24}\left(p^{\mathrm{w}} \Delta Q_{i, t}^{\mathrm{w}}+p^{\mathrm{pv}} \Delta Q_{i, t}^{\mathrm{pv}}\right) $ | (8) |
式中:Sess为储能总收益;Snew为新增可再生能源并网收益;ΔQi, tw,ΔQi, tpv分别为季节i时段t的风电、光伏新增发电量;pw,ppv分别为风电、光伏上网电价。
2.1.2 风光综合利用率最大为进一步提升储能对可再生能源消纳的促进作用,对风光综合利用率进行优化。现有研究大多选取单一季节下的典型日进行优化,而文中同时对4个季节下的典型日进行优化。对日利用率的简单求和或算数平均意义不大,且不能更好地显示不同季节下的可再生能源出力及负荷特性。因此,以4个季节的最小风光综合利用率最大化为优化目标,则配置后的储能规模能够实现全年风电、光伏利用率均处于较高水平。
| $\max R=\min _{i} \sum\limits_{i=1}^{24} \frac{Q_{i, t}^{\mathrm{w}}+Q_{i, t}^{\mathrm{pv}}}{Q_{i, t}^{\mathrm{w}-\max }+Q_{i, t}^{\mathrm{pv}-\max }} $ | (9) |
式中:R为风光综合利用率;Qi, tw,Qi, tpv分别为季节i时段t的风电、光伏出力;Qi, tw-max,Qi, tpv-max分别为季节i时段t的风电、光伏出力上限。
2.2 约束条件 2.2.1 发电机组运行约束(1) 燃气轮机运行约束。燃气轮机在运行时不能随意变更出力大小及启停状态,因此需要对其出力上下限、启停时间和爬坡速率进行约束。
| $ \left\{\begin{array}{l} Q^{\text {gas-min }} \leqslant Q_{i, t}^{\text {gas }} \leqslant Q^{\text {gas-max }} \\ \left(T_{i, t}^{\text {on }}-M^{\text {on }}\right)\left(u_{i, t}-u_{i, t+1}\right) \geqslant 0 \\ \left(T_{i, t}^{\text {off }}-M^{\text {off }}\right)\left(u_{i, t+1}-u_{i, t}\right) \geqslant 0 \\ \left|Q_{i, t+1}^{\text {th }}-Q_{i, t}^{\text {th }}\right| \leqslant Q^{\text {th-v }} \end{array}\right. $ | (10) |
式中:Qi, tgas为季节i时段t的燃气轮机出力;Qgas-max,Qgas-min分别为燃气轮机出力上、下限;T i, ton,T i, toff分别为季节i时段t的燃气轮机持续运行、停机时间;Mon,Moff分别为燃气轮机最小持续运行、停机时间;ui, t为季节i时段t的燃气轮机启停0-1变量,0,1分别表示停机、运行状态;Qi, tth为季节i时段t的燃气轮机爬坡速率;Qth-v为燃气轮机爬坡速率上限。
(2) 可再生能源运行约束。受自然环境影响,风电和光伏在实际运行中存在出力上、下限。
| $ \left\{\begin{array}{l} Q_{i, t}^{\mathrm{w}-\mathrm{min}} \leqslant Q_{i, t}^{\mathrm{w}} \leqslant Q_{i, t}^{\mathrm{w}-\max } \\ Q_{i, t}^{\mathrm{pv}-\min } \leqslant Q_{i, t}^{\mathrm{pv}} \leqslant Q_{i, t}^{\mathrm{pv}-\max } \end{array}\right. $ | (11) |
式中:Qi, tw-min,Qi, tpv-min分别为季节i时段t的风电、光伏出力下限。
2.2.2 储能系统约束(1) 储能运行约束。通常用荷电状态表示储能系统的运行情况,为保障储能系统的稳定运行,将荷电状态限制在一定范围内,且一个调度周期内开始和结束时的荷电状态应相等,保障储能在下个周期的调节能力。
| $ \left\{\begin{array}{l} E_{i, t+1}^{\mathrm{soc}}=E_{i, t}^{\mathrm{soc}}+\frac{\zeta_{\mathrm{c}} Q_{i, t+1}^{\mathrm{c}}}{E_{\mathrm{ess}}}-\frac{Q_{i, t+1}^{\mathrm{d}}}{\zeta_{\mathrm{d}} E_{\mathrm{ess}}} \\ E^{\mathrm{soc}-\min } \leqslant E_{i, t}^{\mathrm{soc}} \leqslant E^{\mathrm{soc}-\max } \\ E_{i, 1}^{\mathrm{soc}}=E_{i, 24}^{\mathrm{soc}} \end{array}\right. $ | (12) |
式中:Ei, tsoc为季节i时段t的储能荷电状态;Esoc-max,Esoc-min分别为储能荷电状态上、下限;Ei, 1soc,Ei, 24soc分别为季节i调度周期开始、结束时的荷电状态;ζc,ζd分别为储能的充、放电效率。
(2) 储能功率约束。储能系统不能同时处于充电和放电的状态,且最大充、放电功率不能超过规划时的额定功率。
| $\left\{\begin{array}{l} Q_{i, t}^{\mathrm{c}} Q_{i, t}^{\mathrm{d}}=0 \\ 0 \leqslant Q_{i, t}^{\mathrm{c}} \leqslant P_{\mathrm{ess}} \\ 0 \leqslant Q_{i, t}^{\mathrm{d}} \leqslant P_{\mathrm{ess}} \end{array}\right. $ | (13) |
式中:Qi, tc为季节i时段t的储能实际充电量。
(3) 持续放电时间约束。在进行储能容量配置时,容量选择太小对调度系统的调节作用有限,容量选择过大则会显著增加投资及运维成本。储能持续放电时间是指储能以额定功率连续工作的时间,与储能的容量和功率直接相关,因此对期望持续放电时间进行约束,从而进一步控制储能成本。
| $ \left\{\begin{array}{l} H=\frac{E_{\text {ess }}}{P_{\text {ess }}} \\ H_{\min } \leqslant H \leqslant H_{\max } \end{array}\right. $ | (14) |
式中:H为储能期望持续放电时间;Hmax,Hmin分别为储能最大、最小持续放电时间,可根据不同的储能配置需求选择合理的H。
2.2.3 电力系统约束电力系统约束包括电力平衡约束、备用容量约束和可再生能源渗透率约束。电力平衡约束和备用容量约束分别如式(15)、式(16)所示。
| $ \begin{gathered} Q_{i, t}^{\mathrm{gas}}+Q_{i, t}^{\mathrm{w}}+Q_{i, t}^{\mathrm{pv}}+Q_{i, t}^{\mathrm{d}}=G_{i, t}+Q_{i, t}^{\mathrm{c}} \end{gathered} $ | (15) |
| $ Q^{\mathrm{gas}-\max }-Q_{i, t}^{\mathrm{gas}} \geqslant \alpha G_{i, t} $ | (16) |
式中:Gi, t为季节i时段t的负荷需求;α为燃气轮机备用容量系数。
可再生能源的功率波动性和随机性会给电网带来冲击,在保证持续稳定供电的前提下,应对可再生能源的最大并网比例进行约束。
| $Q_{i, t}^{\mathrm{w}}+Q_{i, t}^{\mathrm{pv}} \leqslant \beta G_{i, t} $ | (17) |
式中:β为可再生能源最大渗透率。
2.3 模型转化常用的多目标求解方法主要有智能算法和线性加权法,这些方法在转化前须对目标进行归一化处理,而归一化处理会掩盖不同季节可再生能源的变化特性。因此,文中采用主要目标法对模型进行转化并求解[20],将风光综合利用率最大设置为主要目标,然后引入目标缩放系数,将储能总收益最大转化为约束条件,研究不同盈利状态下风光综合利用率的变化情况。转化后的优化模型为:
| $\left\{\begin{array}{l} \text { 式 }(9) \\ \text { s.t. } S_{\mathrm{ess}} \geqslant \varphi S_{\mathrm{ess}}^{*} \\ ~~~\text { 式 }(10)-\text { 式 }(17) \end{array}\right. $ | (18) |
式中:Sess*为以储能总收益最大为单目标进行求解的最优值;φ∈[0, 1]为目标缩放系数,φ为0表示只要储能系统不亏损即可接受,φ为1表示能够实现最大收益。
式(18)属于混合整数非线性规划模型,可以用Lingo软件直接进行求解, 求解流程如图 1所示。
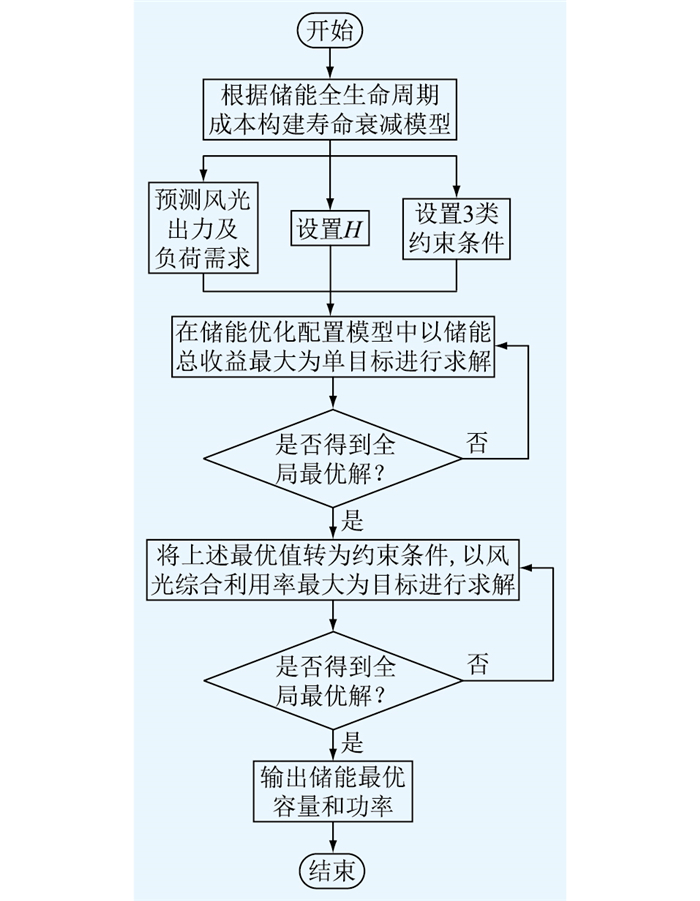
|
图 1 储能优化配置求解流程 Fig. 1 Solution process of energy storage optimization configuration |
为验证文中所提储能优化配置模型的有效性,以配置800 kW风电机组、500 kW光伏机组和1 000 kW燃气轮机组的微电网为例进行仿真分析[21]。根据气象划分法,选取1月、4月、7月、10月作为冬、春、夏、秋的典型月。利用2019年新疆某地区典型月每天各时段的风速、温度和日照强度历史数据,预测得到风电、光伏4个季节典型日的出力曲线见图 2[22]。风电、光伏上网电价分别为0.54元/(kW ·h)和0.6元/(kW ·h),4个季节相应典型日的负荷预测曲线见图 3。
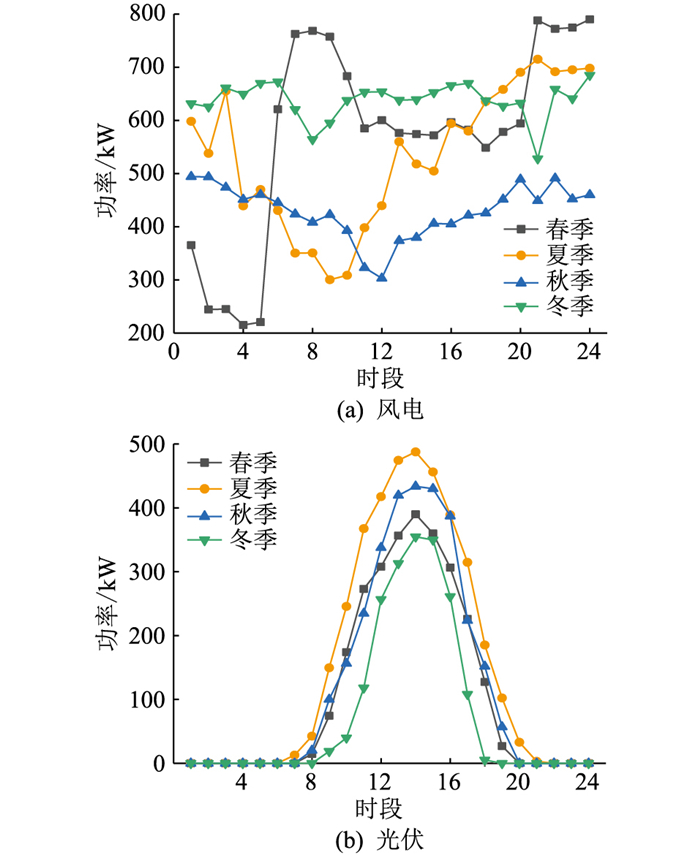
|
图 2 4个季节典型日的风电和光伏出力预测 Fig. 2 Output forecast of wind power and photovoltaic on typical day in four seasons |
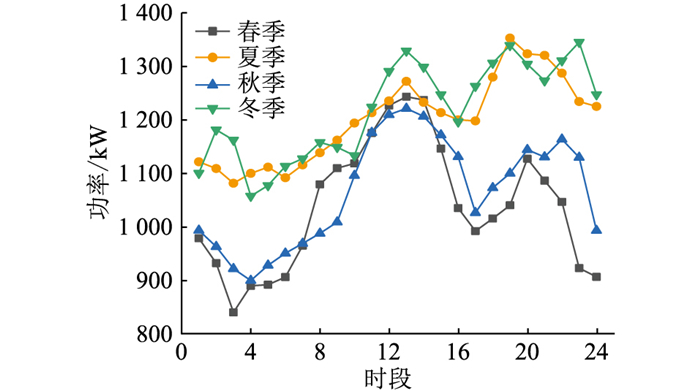
|
图 3 4个季节典型日的负荷预测 Fig. 3 Load forecast on typical day in four seasons |
储能通过能量时移实现用电负荷的削峰填谷以及可再生能源的高效利用,因此需要较长的放电时间。文中采用锂电池在发电侧对储能系统进行配置。设置H为3~6 h;cp为1 000元/kW;ce为1 600元/(kW ·h)[23];co为5%;r为4.9%;n0为1 500;ζc,ζd均为90%;Ei, 1soc为0.5;Esoc-max,Esoc-min分别为0.9, 0.1。由于储能的调节作用,α降至10%,β提升至80%。
3.2 结果分析文中分3种情景对储能的配置规模和电力系统运行效果进行分析。情景一:以储能系统总收益最大为单目标进行储能配置;情景二:以情景一为基础,采用主要目标法以风光综合利用率最大为目标进行储能配置;情景三:选取单一典型日,以春季为例进行储能配置,并分析该储能规模对其他季节电力系统运行效果的影响。3种情景下的储能配置结果及电力系统运行效果如表 1所示。
|
|
表 1 3种情景下的储能配置及电力系统运行效果 Table 1 Energy storage configuration and power system operation effect under three scenarios |
目前储能成本较高,当以储能总收益最大为单目标进行优化配置时,可在保证电力系统安全运行的情况下尽可能降低储能的容量和功率,并减少储能的放电量,延长储能寿命,降低储能成本。安装储能后可再生能源4个季节下典型日的最低风光综合利用率由93.01%提升至95.34%,4个季节风光综合利用率平均提升2.05%。为了应对可再生能源高渗透率对电力系统的冲击,可大幅增加储能规模,在可再生能源发电量大时将原弃电量储存下来,并通过延长持续放电时间,更好地发挥储能系统的能量时移作用。当牺牲部分储能收益,追求更高的可再生能源利用率时,最低风光综合利用率进一步提升至96.55%,4个季节风光综合利用率平均提升3.05%。然而,大规模消纳可再生能源使储能只能通过频繁充放电维持电力系统稳定,这对储能寿命造成了巨大冲击。但风电、光伏新增发电量带来的可再生能源并网收益,可抵消储能建设及运维的部分成本,对储能总收益的影响并不显著。情景三更是如此,当只选择春季典型日进行储能配置时,由于春季风光综合利用率较低,需要较大的储能容量和功率实现可再生能源的高效消纳,造成储能规模在其他季节过剩的情况。此类情况虽然将最低风光综合利用率提升至98.58%,风光综合利用率平均提升4.67%,并获得了较高的新增可再生能源并网收益,但在储能配置规模增加和等效寿命减少的双重作用下,储能年化总成本相较于情景一增加了近2倍,导致出现了负收益。
3种情景下的储能荷电状态如图 4所示。情景一为追求利润最大,储能系统偏向运行于较高荷电状态水平,放电深度小,对储能寿命较为友好。而情景二中,储能呈现截然不同的运行方式且季节性效应明显。在风电、光伏发电量较多的夏季和冬季,储能主要以充电为主。在风电、光伏发电量较少的春季和秋季,储能则主要以放电为主,同时增加了放电深度,整体提升可再生能源利用率。情景三中,春季储能的运行能够较好地贴近风电、光伏出力特性,但过剩的储能容量即使在风电、光伏发电量较多的夏季和冬季,也无法被完全利用。
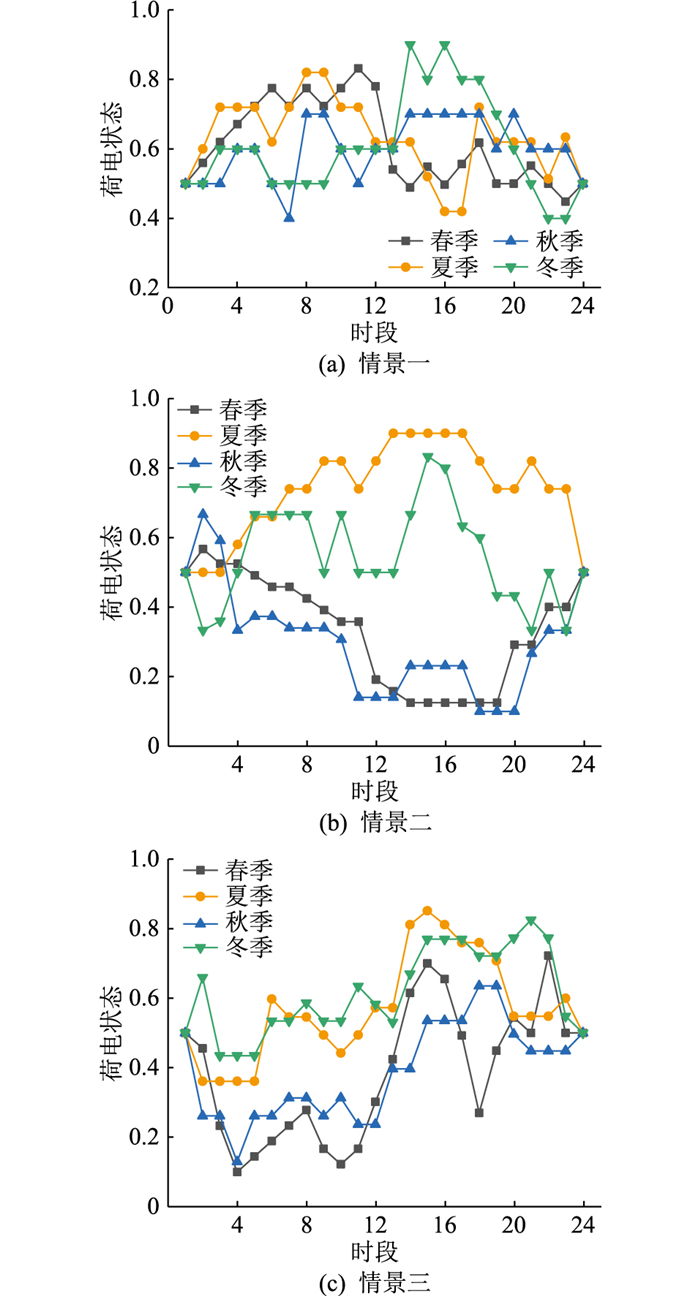
|
图 4 3种情景下的储能荷电状态 Fig. 4 Energy storage state of charge under three scenarios |
3种情景下各季节的可再生能源利用率如表 2所示。随着储能规模的增加,风电、光伏利用率均有一定提升,情景三实现了光伏100%消纳。除了储能规模,风电、光伏实际出力和负荷需求也是影响可再生能源利用率的2个重要因素。分季节来看,夏季和冬季的负荷需求显著高于春季和秋季。风电出力主要集中在冬季,故3种情景下均是冬季风电利用率最高。而春季同样具有较好的风力资源,但负荷较低,风电的消纳效果并不理想。夏季光伏的高出力和高负荷需求使得光伏在夏季的利用率最高。受温度和辐射强度影响,光伏在冬季的发电资源最差,但由于冬季的负荷需求高,光伏仍然具有较好的消纳效果。此外,由于光伏装机规模小,其整体利用率均高于风电。
|
|
表 2 3种情景下各季节的可再生能源利用率 Table 2 Renewable energy utilization rate in each season under three scenarios |
4个季节下典型日的最低风光综合利用率均发生在春季。一方面是风电在春季的出力波动性最大且春季负荷需求较低,给风电消纳带来了一定困难;另一方面风电规模大,使得其对风光综合利用率的影响要高于光伏。但是,低利用率给予了储能发挥作用的空间,安装储能对春季风光综合利用率提升的效果最明显,相较于不含储能,情景一提升了2.33%,情景二提升了3.54%,情景三提升了5.57%,但这需要付出巨大的成本。从电源类型看,储能配置提升光伏消纳的效果要好于风电,这是由于光伏上网电价高,优先消纳光伏能够提升储能总收益。
4 结论在当前储能成本较高的背景下,为保障储能运行的经济性,提升其在不同季节下的适应性,文中基于风电、光伏出力和负荷需求的季节性波动,对储能的功率和容量进行配置。结合3种情景下的储能配置和电力系统运行情况得出以下结论。
(1) 单纯追求收益最大时,储能放电深度小,对寿命较为友好,但降低了可再生能源利用率。
(2) 通过增加储能规模和延长持续放电时间可以提升可再生能源利用率,虽然储能收益有所降低,但幅度不大。
(3) 当选取的单一典型日风光综合利用率较低时,配置的储能会出现规模过剩的现象。相反,当仅按照风光综合利用率较高的季节进行储能配置时,其规模可能不足以在其他季节根据风电、光伏出力进行调节,造成大量可再生能源的浪费。
因此,在进行储能规划时,应统筹考虑可再生能源全年变化情况,并适当增加储能规模及持续放电时间,从而兼顾储能收益和可再生能源利用率。此外,可以选取混合储能配置或将储能系统引入辅助服务市场,通过储能“低储高发”套利,提供调频、调压、黑启动服务等,进一步提升储能经济效益。关于不同类型储能间的协调运行以及储能容量对不同辅助服务应用的兼容性等问题,将在后续工作中进行研究。
| [1] |
张文建, 崔青汝, 李志强, 等. 电化学储能在发电侧的应用[J]. 储能科学与技术, 2020, 9(1): 287-295. ZHANG Wenjian, CUI Qingru, LI Zhiqiang, et al. Application of electrochemical energy storage in power generation[J]. Energy Storage Science and Technology, 2020, 9(1): 287-295. (  0) 0) |
| [2] |
姜海洋, 杜尔顺, 朱桂萍, 等. 面向高比例可再生能源电力系统的季节性储能综述与展望[J]. 电力系统自动化, 2020, 44(19): 194-207. JIANG Haiyang, DU Ershun, ZHU Guiping, et al. Review and prospect of seasonal energy storage for power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2020, 44(19): 194-207. (  0) 0) |
| [3] |
刘畅, 卓建坤, 赵东明, 等. 利用储能系统实现可再生能源微电网灵活安全运行的研究综述[J]. 中国电机工程学报, 2020, 40(1): 1-18, 369. LIU Chang, ZHUO Jiankun, ZHAO Dongming, et al. A review on the utilization of energy storage system for the flexible and safe operation of renewable energy microgrids[J]. Proceedings of the CSEE, 2020, 40(1): 1-18, 369. (  0) 0) |
| [4] |
贺鸿杰, 张宁, 杜尔顺, 等. 电网侧大规模电化学储能运行效率及寿命衰减建模方法综述[J]. 电力系统自动化, 2020, 44(12): 193-207. HE Hongjie, ZHANG Ning, DU Ershun, et al. Review on modeling method for operation efficiency and lifespan decay of large-scale electrochemical energy storage on power grid side[J]. Automation of Electric Power Systems, 2020, 44(12): 193-207. (  0) 0) |
| [5] |
赵永凯, 王靖韬, 赵维, 等. 计及多目标的园区级综合能源系统协同优化模型研究[J]. 电力信息与通信技术, 2021, 19(11): 123-130. ZHAO Yongkai, WANG Jingtao, ZHAO Wei, et al. Multi-objective optimization of park-level integrated energy system: model and analysis[J]. Electric Power Information and Communication Technology, 2021, 19(11): 123-130. (  0) 0) |
| [6] |
阮绵晖, 郑建平, 刘尧, 等. 离网直流微网群混合储能容量优化配置方法[J]. 电力工程技术, 2021, 40(3): 99-105. RUAN Mianhui, ZHENG Jianping, LIU Yao, et al. Optimization configuration method for hybrid energy storage capacity of independent DC microgrid cluster[J]. Electric Power Engineering Technology, 2021, 40(3): 99-105. (  0) 0) |
| [7] |
叶季蕾, 李斌, 张宇, 等. 基于全球能源互联网典型特征的储能需求及配置分析[J]. 发电技术, 2021, 42(1): 20-30. YE Jilei, LI Bin, ZHANG Yu, et al. Energy storage requirements and configuration analysis based on typical characteristics of global energy Internet[J]. Power Generation Technology, 2021, 42(1): 20-30. (  0) 0) |
| [8] |
夏川淋, 史林军, 史江峰, 等. 基于改进粒子群算法的电池储能系统多控制器参数优化[J]. 电力信息与通信技术, 2021, 19(6): 57-63. XIA Chuanlin, SHI Linjun, SHI Jiangfeng, et al. Improved PSO-based parameters optimization of ESS's multi-controllers[J]. Electric Power Information and Communication Technology, 2021, 19(6): 57-63. (  0) 0) |
| [9] |
HOU H, XU T, WU X X, et al. Optimal capacity configuration of the wind-photovoltaic-storage hybrid power system based on gravity energy storage system[J]. Applied Energy, 2020, 271: 115052. DOI:10.1016/j.apenergy.2020.115052 (  0) 0) |
| [10] |
任浩, 孟仁杰, 窦仁晖, 等. 基于5G网络的"源-网-荷-储"优化调控系统设计[J]. 电力信息与通信技术, 2020, 18(12): 23-28. REN Hao, MENG Renjie, DOU Renhui, et al. Design of optimal control system of 'source-grid-load-storage' based on 5G network[J]. Electric Power Information and Communication Technology, 2020, 18(12): 23-28. (  0) 0) |
| [11] |
傅旭, 李富春, 杨欣, 等. 基于全寿命周期成本的储能成本分析[J]. 分布式能源, 2020, 5(3): 34-38. FU Xu, LI Fuchun, YANG Xin, et al. Cost analysis of energy storage based on life cycle cost[J]. Distributed Energy, 2020, 5(3): 34-38. (  0) 0) |
| [12] |
陈海生, 刘畅, 齐智平. 分布式储能的发展现状与趋势[J]. 中国科学院院刊, 2016, 31(2): 224-231. CHEN Haisheng, LIU Chang, QI Zhiping. Developing trend and present status of distributed energy storage[J]. Bulletin of Chinese Academy of Sciences, 2016, 31(2): 224-231. (  0) 0) |
| [13] |
宾洋, 于静美, 朱英凯, 等. 实时雨流计数法及其在钴酸锂电池健康状态建模中的应用[J]. 中国电机工程学报, 2017, 37(12): 3627-3635, 3692. BIN Yang, YU Jingmei, ZHU Yingkai, et al. A real-time rain flow algorithm and its application to state of health modeling for LiCoO2 lithium-ion batteries[J]. Proceedings of the CSEE, 2017, 37(12): 3627-3635, 3692. (  0) 0) |
| [14] |
葛玉友, 尚策. 寿命约束的储能规划[J]. 中国电机工程学报, 2020, 40(19): 6150-6161. GE Yuyou, SHANG Ce. Energy storage planning constrained by its life[J]. Proceedings of the CSEE, 2020, 40(19): 6150-6161. (  0) 0) |
| [15] |
刘永前, 梁超, 阎洁, 等. 风-光电站中储能系统混合最优配置及其经济性研究[J]. 中国电力, 2020, 53(12): 143-150. LIU Yongqian, LIANG Chao, YAN Jie, et al. Optimal configuration and economic study of hybrid energy storage system in wind and solar power plants[J]. Electric Power, 2020, 53(12): 143-150. (  0) 0) |
| [16] |
张悦, 刘文泽. 考虑功率波动及储能寿命的微电网储能容量优化配置[J]. 电测与仪表, 2021, 58(10): 59-66. ZHANG Yue, LIU Wenze. Optimal allocation of micro-grid energy storage capacity considering power fluctuation and energy storage life[J]. Electrical Measurement & Instrumentation, 2021, 58(10): 59-66. (  0) 0) |
| [17] |
LIU W P, LIU Y T. Enabling wind farm to be black-start source by energy storage[J]. The Journal of Engineering, 2019(18): 5138-5141. (  0) 0) |
| [18] |
WEE K W, CHOI S S, VILATHGAMUWA D M. Design of a least-cost battery-supercapacitor energy storage system for realizing dispatchable wind power[J]. IEEE Transactions on Sustainable Energy, 2013, 4(3): 786-796. DOI:10.1109/TSTE.2013.2248029 (  0) 0) |
| [19] |
HE G, CHEN Q, MOUTIS P, et al. An intertemporal decision framework for electrochemical energy storage management[J]. Nature Energy, 2018, 3(5): 404-412. (  0) 0) |
| [20] |
梁吉, 左艺, 张玉琢, 等. 基于可再生能源配额制的风电并网节能经济调度[J]. 电网技术, 2019, 43(7): 2528-2534. LIANG Ji, ZUO Yi, ZHANG Yuzhuo, et al. Energy-saving and economic dispatch of power system containing wind power integration under renewable portfolio standard[J]. Power System Technology, 2019, 43(7): 2528-2534. (  0) 0) |
| [21] |
刘思夷, 赵波, 汪湘晋, 等. 基于Benders分解的独立型微电网鲁棒优化容量配置模型[J]. 电力系统自动化, 2017, 41(21): 119-126, 146. LIU Siyi, ZHAO Bo, WANG Xiangjin, et al. Capacity configuration model for robust optimization of stand-alone microgrid based on Benders decomposition[J]. Automation of Electric Power Systems, 2017, 41(21): 119-126, 146. (  0) 0) |
| [22] |
TAN Q L, MEI S F, YE Q, et al. Optimization model of a combined wind-PV-thermal dispatching system under carbon emissions trading in China[J]. Journal of Cleaner Production, 2019, 225: 391-404. (  0) 0) |
| [23] |
王磊, 冯斌, 王昭, 等. 计及电池储能寿命损耗的风光储电站储能优化配置[J]. 电力科学与工程, 2019, 35(5): 1-6. WANG Lei, FENG Bin, WANG Zhao, et al. Optimal configuration of energy-storage capacity for wind/photovoltaic/energy-storage station considering energy-storage life loss[J]. Electric Power Science and Engineering, 2019, 35(5): 1-6. (  0) 0) |
2. Research Center for Beijing Energy Development, Beijing 102206, China;
3. Beijing Key Laboratory of Renewable Electric Power and Low Carbon Development, Beijing 102206, China
 2022, Vol. 41
2022, Vol. 41


 梅书凡(1995), 男, 博士在读, 研究方向为能源环境建模与优化(E-mail:
梅书凡(1995), 男, 博士在读, 研究方向为能源环境建模与优化(E-mail: