文章编号: 2096-3203(2022)04-0220-09 中图分类号: TM732
2. 西安交通大学电气工程学院, 陕西 西安 710049
近年来随着电力系统新技术的发展以及风电、光伏、氢能等新能源的快速应用,电网格局逐渐强化[1-3]。电力用户从传统的消费者向产消者转变,电力系统在发电、输配电、用电等层面都经历着深刻变革[4-5]。从用户角度来看,在新的生产、生活、消费方式的影响下,在愈加完善的需求侧响应的实施背景下,用户行为习惯与用电特性也在逐步发生改变[6-7]。随着先进电力测量技术和测量仪器的推广应用,电力企业可以获取大量的电力用户用电行为信息。如何有效地认识并利用海量的电力用户数据,进一步对用户的用电特性、行为偏好进行挖掘分析是目前亟待解决的实际问题。
电力用户行为画像是建立在真实用电数据基础上的用户特征抓取和刻画,其可将用户特征转化为直观易读的特征标签。该技术可以实现对用户的精准分类和特征把握,进而为电力系统整体经济运行及相关政策制定提供依据。目前电力用户行为画像研究主要分为3个层面:场景层面[8-9]、指标层面[10-11]和方法层面[12-13]。文献[8]将大数据分析技术与画像技术融合应用于电力系统资产全寿命周期管理,运用标签手段构建资产运行管理工作的画像体系。文献[9-12]利用聚类算法对用户数据进行聚类分析,但没有考虑初始聚类数的选择问题。文献[13]通过改进k均值算法实现了对家庭电力用户的多维度特性分析,但计算过程依赖计算机强大的数据存储及并行计算能力。文献[14]考虑了智能仪器采集及处理过程中的用户隐私保护问题,提出了能够保护用户隐私的多阶段聚类方法,兼顾分析精准度与隐私保护性,但须人为选定聚类中心,可靠性较差。
电力用户行为画像中,用户用电特征选择的恰当与否直接影响到电力用户行为刻画的准确程度,目前已有许多学者针对电力用户负荷的特征选择进行了研究[15-18]。综合来看,特征选择可以理解为寻找一个能够有效识别研究对象关键特征的最优特征子集,其主要流程为:原始特征集生成、特征子集评价、最优特征子集选择及验证。在原始特征集基础上进行特征子集的有效挑选,需要一定的搜索策略[19]。此外,还须使用评价指标来度量特征子集选择的有效程度[20]。在针对特征选择方法的研究中,基于信息熵的特征选择方法在文本分类[21]、多标签分类[22]中广泛应用,但文献[21-22]均未考虑不同特征之间相关性的影响。文献[23]将信息增益与Pearson相关系数相结合,构建了基于特征重要性指标的基因数据特征选择方法。但Pearson相关系数要求变量数据连续且符合正态分布,受数据异常值的影响较大。而Spearman相关系数对变量数据的分布没有要求且对错误数据和极端值不敏感,因此能够较好地解决当前电力用户用电数据测量收集存在异常值的问题。
文中提出一种基于信息增益与Spearman相关系数的电力用户行为画像方法。首先利用间隔统计量法确定k-means算法的最优聚类数,在此基础上对电力用户用电数据进行聚类分析;然后构造考虑特征引入后信息增益与特征间相关系数的特征集适应性评价系数,用于选择最优特征集;最后通过遗传算法(genetic algorithm, GA)进行最优特征集的高效快速求解,并以最优特征集为基础对电力用户用电特征进行刻画。
1 电力用户用电数据聚类分析分析与处理电力用户用电数据是构建其行为画像的第一步,区分用电偏好不同的用户有助于对其行为特征进行准确刻画。常用的聚类分析方法为k-means聚类算法,其原理为利用样本数据间的距离差异来区分出不同的类别并作出相应划分,但其类别数须提前给定,而实际应用中最优聚类数并不是显而易见的,因此常用肘部法则[23]、轮廓系数法[24]、Canopy法[25]等来解决此问题。肘部法则简单易行,但会存在肘点位置不明显的情形;轮廓系数法计算量大,算法复杂;Canopy法引入了新的参数,但新参数赋值困难。
文献[26]提出间隔统计量法,可以很好地解决最佳聚类数的选择问题。其基本思想是通过蒙特卡洛模拟法引入参考测度值,对比随机生成的对照样本集与实际样本集的类内偏离量的差异,评判当前聚类数目的合理性,选取统计量达到最大值时的聚类数作为最佳聚类数目,具体方法如下。
假设对含有n个数据的样本集进行聚类,聚类数为k。聚类结果中每个聚类所包含的样本子集称为一个簇,簇内所有样本子集取值的平均值称为该簇的中心。样本集类内偏移量Dk定义如下:
| $ D_{k}=\sum\limits_{i=1}^{k} \sum\limits_{x \in C_{i}}\left|x-m_{i}\right|^{2} $ | (1) |
式中:Ci为聚类形成的第i个簇;x为Ci的样本点;mi为第i个簇的中心。
间隔统计量定义如下:
| $ G_{k}=E\left(\log _{2} D_{k}^{*}\right)-\log _{2} D_{k} $ | (2) |
式中:Dk*为对照样本集的类内偏移量;E(·)为期望函数。
其中,对照样本集的类内偏移量期望值通过蒙特卡洛模拟产生。在样本数据取值范围内按照均匀分布随机地产生和原始样本集数量相同的随机样本,并对其进行聚类,得到类内偏移量,重复多次并求取平均值,得到对照样本集类内偏移量期望值的近似值,计算公式如下:
| $ E\left(\log _{2} D_{k}^{*}\right)=\frac{1}{N} \sum\limits_{b=1}^{N} \log _{2} D_{k b}^{*} $ | (3) |
式中:N为蒙特卡洛模拟次数,文中取20;Dkb*为第b次模拟产生的随机样本集的类内偏移量。
为了修正蒙特卡洛模拟采样带来的误差,还须计算标准差来矫正间隔统计量,标准差sk的计算公式如下:
| $s_{k}=\sqrt{\frac{N+1}{N}} \sqrt{\frac{1}{N} \sum\limits_{b=1}^{N}\left(\log _{2} D_{k b}^{*}-E\left(\log _{2} D_{k}^{*}\right)\right)^{2}} $ | (4) |
指标Jk可以评价聚类个数选择的优劣情况,其定义如下:
| $ J_{k}=G_{k}-G_{k+1}+s_{k+1} $ | (5) |
根据间隔统计量的思想,最终选择满足Jk≥0的最小的k作为最优聚类个数。确定k值后,采用k-means算法对电力用户用电数据进行聚类分析,得到电力用户用电数据分类结果。
2 电力用户用电特征选择与量化特征选择是电力用户行为画像中的重要环节,获得能够准确刻画用户关键特性且数量合理的特征集是电力用户行为画像的理想目标。电力用户负荷数据蕴含的特性可以通过不同方面的特征指标进行刻画,但是不同特征对于用户特性的刻画可能是重复的,即不同特征之间存在相关性。因此在特征选择时,应考虑特征的有效性及特征之间的冗余度,且为了增强用户特征的可理解性,应对用户特征进行量化分析。
文中采用的电力用户用电特征选择与量化方法如下:首先构建多维度的电力用户原始特征集,在此基础上度量各个特征的加入对电力用户整体信息增益的程度;然后引入Spearman相关系数度量不同特征间的相似程度;最后计及特征引入之后的信息增益以及特征间的相似程度,得到特征集适应性评价系数,选择评价系数最高的特征集作为最优的电力用户用电特征集。
2.1 原始特征集电力用户用电特征体现在用户负荷曲线特性上,针对负荷特性的分析指标主要有:(1) 数值型,即用电量t1、最大负荷t2、最小负荷t3、平均负荷t4、峰谷差t5;(2) 比率型,即负荷率t6、峰谷差率t7、峰时耗电率t8、谷时耗电率t9、平时耗电率t10[27]。上述特征指标构成电力用户原始特征集,即原始特征集为T={t1, t2, …, t10}。
2.2 特征信息增益特征的信息增益可以有效度量不同特征对电力用户行为刻画的有效程度。为了更好地理解这一指标,须引入信息熵的概念。信息熵可以衡量系统的不确定性程度,其值越大,表示系统内部越混乱,信息量越大。信息量可以度量某一事件是否发生,信息量越大,发生概率越小,不确定性越大。
对于随机变量X,假设其所有可能取值为{x1, x2, …, xk},相应的发生概率为{p(x1), p(x2), …, p(xk)},则随机变量X的信息熵定义如式(6)所示。
| $ A(X)=-\sum\limits_{i=1}^{k} p\left(x_{i}\right) \log _{2} p\left(x_{i}\right) $ | (6) |
在电力用户用电特征分析中,随机变量X的所有可能取值为聚类形成的所有簇,相应的概率为各个簇所包含的样本个数占样本总数的比例。
引入特征Y会改变随机变量X的信息熵。假设特征Y的所有可能取值为{y1, y2, …, yn},相应的发生概率为{p(y1), p(y2), …, p(yn)},即落在各个特征取值内的样本个数占样本总数的比例。对于某一特征取值yj,其内部包含样本分属各个簇的概率为{p(yj1), p(yj2), …, p(yjk)}。则特征Y加入后随机变量X的信息熵计算公式如下:
| $ A(X \mid Y)=-\sum\limits_{j=1}^{n} p\left(y_{j}\right)\left(-\sum\limits_{i=1}^{k} p\left(y_{j i}\right) \log _{2} p\left(y_{j i}\right)\right) $ | (7) |
对于某一特征Y,其信息增益可以衡量Y的引入对随机变量X的不确定性降低的有效程度。信息增益在数值上定义为特征Y引入前后随机变量X信息熵的差值,用H(Y)表示,计算公式为式(8)。特征的信息增益数值越大,其对变量的区分能力越强。
| $H(Y)=A(X)-A(X \mid Y) $ | (8) |
电力用户特征集中特征个体之间并不是相互独立的,不同特征之间存在一定的相关性,因此仅用信息增益表征不同指标的性能优劣存在不足。为了衡量不同特征间的相关性,从而降低电力用户特征集的冗余性,引入Spearman相关系数[28-30]。Spearman相关系数属于非参数统计方法,可用于衡量不同变量之间的相关性。其中,变量间的相关性是用单调函数描述的,即不同变量间的变化趋势越相近,相关系数数值越大,相关性越强。且Spearman相关系数对数据分布的要求并不像Pearson相关系数等方法那样严格。只要变量的观测值成对出现,不论变量的分布形态、样本容量如何,都可以用Spearman相关系数进行度量。
对于任意2个特征Y1和Y2,Spearman相关系数的定义如下:
| $B_{Y_{1}, Y_{2}}=1-6 \sum\limits_{l=1}^{N_{\mathrm{r}}} d_{l}^{2} /\left[N_{\mathrm{r}}\left(N_{\mathrm{r}}^{2}-1\right)\right] $ | (9) |
式中:Nr为特征Y1,Y2的样本个数;dl为特征Y1与Y2的第l个取值在各自样本中所处的秩次(排列顺序)差值。
2.4 特征集适应性评价系数对于某一特征集S⊆T,综合特征信息增益的有效性及特征间相关系数所度量的冗余性,构建特征集适应性评价系数,其定义如下:
| $ P(S)=H(S)-B(S) $ | (10) |
其中:
| $ H(S)=\frac{1}{N_{S}} \sum\limits_{p=1}^{N_{S}} H\left(Y_{p}\right) $ | (11) |
| $ B(S)=\frac{1}{N_{S}^{2}} \sum\limits_{Y_{p}, Y_{q} \in S} B_{Y_{p}, Y_{q}} $ | (12) |
式中:H(S)为特征集S中所有特征的信息增益指标;B(S)为特征集S中所有特征的冗余性指标;NS为特征集S所包含特征的个数;Yp,Yq为属于特征集S的2个不同特征。
2.5 特征值量化为提高用户特征标签的易读性,对特征进行量化分析。采用打分制,以0~1分为基准,衡量不同电力用户在每类特征维度下的用电特性,计算方法如下:
| $M_{i, j}=\frac{\chi_{i, j}-\chi_{j \min }}{\chi_{j \max }-\chi_{j \min }} $ | (13) |
式中:Mi, j为第i类用户第j个标签的量化值;χi, j为第i类用户第j个标签量化平均值;χjmin为所有用户第j个标签的最小值;χjmax为所有用户第j个标签的最大值。
3 最优特征求解算法在初始特征集确定的基础上选择最优特征集,理论上需要遍历所有可能的特征子集,然而这样做计算量大、耗时长。电力用户特征集中单个特征的取值为0-1变量,整个问题的可行域由离散点组成,须采用高效的求解算法。GA将所研究的特征集组合抽象成一群包含染色体的种群组合,借鉴自然界动物进化中的选择、交叉、变异等过程,通过概率数学化,在代际传递过程中不断更新种群染色体,使得适应度高的个体的染色体信息得以保留,最终筛选出最具适应性的个体,即最优特征子集。GA具有天然的离散决策变量特性,且具有简单、通用、高效的特点,适用于处理最优集的选取问题。
为避免求解过程中陷入局部最优解,在算法中灵活地加入随机性以改善算法特性,随机性主要体现在随机产生初始种群和对遗传算子的操作上。选择算子方面,采用“轮盘赌选择法”选择较优个体,同时添加可选择的精英保留策略以便捕捉更多的全局最优细节;交叉算子方面,通过一定的概率交换父本和母本的部分基因;变异算子方面,按照一定概率对种群个体进行变异操作,增强算法的全局寻优能力。算法的主要构成如下:
(1) 编码。采用二进制编码格式,为保证原始特征集中的所有待选特征都被编码,根据特征集中的特征个数,选取编码长度为10,染色体为C={c1, c2, …, c10}。当特征被选中时相应编码为1,否则为0。其中,每一个二进制位编码都对应特征集中的一个特征决策变量。
(2) 适应度函数。适应度函数可以评判不同特征子集(种群个体染色体)之间的性能差异,选择P(S)作为适应度函数。适应度越高的个体遗传的可能性更高,即个体所代表的特征集中的特征对电力用户的信息增益越大且相互之间冗余度越低。
(3) 遗传算子。在GA中,代表特征集合的种群进化过程可分为3种:选择、交叉和变异。在种群代际更新过程中,3种进化过程按照发生概率作用于种群,通过“物竞天择、适者生存”的原则,种群朝着适应度提高的方向进化发展。
依照评判标准,适应度越高的个体存活的概率越高,更有可能将自身的遗传信息传递下去。通常采用“轮盘赌选择法”进行较优个体的选择,个体被选中的概率与其适应度数值相匹配。将经过选择的个体按照一定的概率(文中取值为0.6)进行交叉操作,形成后代个体。同时为了保持种群的生物多样性,增强GA的全局最优能力,避免陷入局部次优的境地,须按照一定的概率(文中取值为0.01)对种群个体进行变异操作。变异是指染色体上的单个基因(编码中的某一个二进制码)发生突变,相应基因值变成了其等位基因,从而产生了一个全新的个体。
基于GA的最优特征集求解流程如图 1所示。
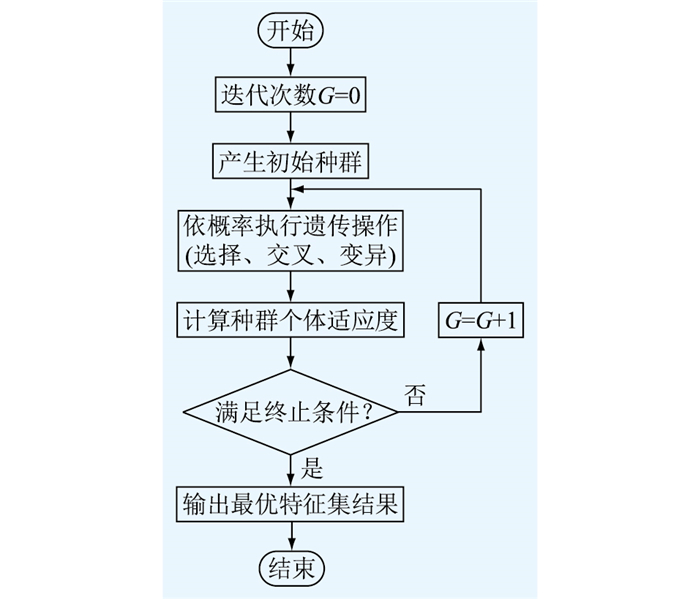
|
图 1 基于GA的最优特征集求解流程 Fig. 1 Solving process of optimal feature set based on GA |
电力用户行为画像过程示意如图 2所示,大致可以分为用户数据聚类分析、最优特征子集选取、电力用户行为特征量化3个步骤。首先基于间隔统计量法确定最佳聚类数,然后对电力用户原始用电数据进行聚类分析;在原始特征集基础上,综合考虑特征有效性和冗余度构建特征集适应性评价系数,并利用GA求解得到最优特征子集;针对不同的用户类别以及不同的特征指标,对电力用户行为特征进行量化分析。
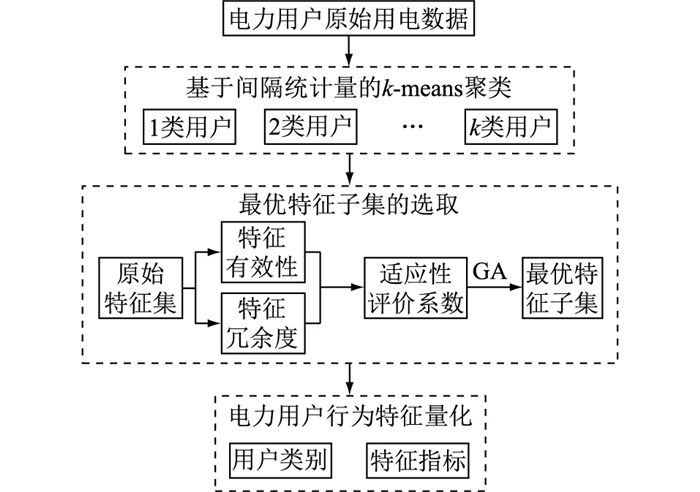
|
图 2 电力用户行为画像过程示意 Fig. 2 The schematic diagram of power users′ behavior portrait process |
算例采用2018年1月份河南省18个地市的日负荷数据,数据间隔时间1 h,以这些负荷数据作为电力用户原始数据样本。与特征有关的峰、谷、平时段依据河南省实际情况作如下划分:峰时段为09:00—12:00、17:00—22:00;谷时段为01:00—08:00;平时段为13:00—16:00、23:00—24:00。
5.2 电力用户聚类分析根据电力用户用电数据计算得出的间隔统计量如图 3所示。可以看到,当k取值为1~6时,Jk为负值,此时增大k值能够提高用户分类准确度;当k增大到7时,Jk首次出现正值,故k=7是满足Jk≥0的最小k值,因此,电力用户最佳聚类数为7。
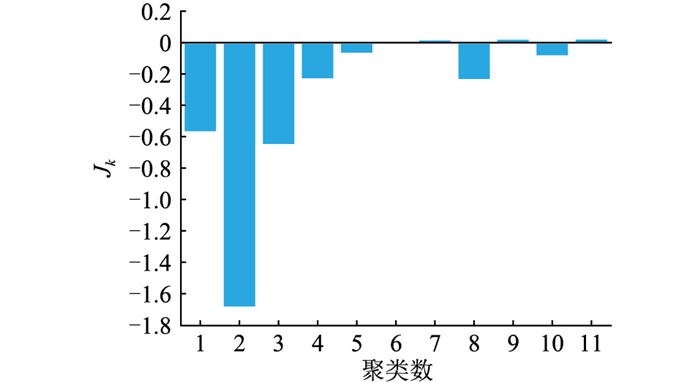
|
图 3 电力用户用电数据间隔统计量计算结果 Fig. 3 Numerical results of gap statistic for power users′ electricity consumption data |
得到最佳聚类数基础后,对电力用户进行聚类分析。电力用户原始用电数据及聚类结果如图 4、图 5所示。
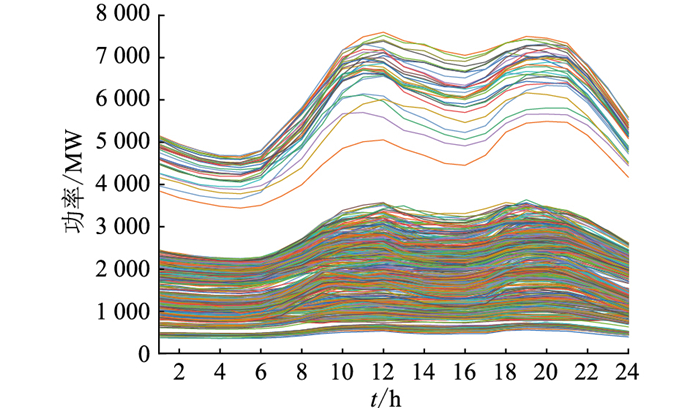
|
图 4 电力用户原始用电数据 Fig. 4 Power users′ raw electricity consumption data |
|
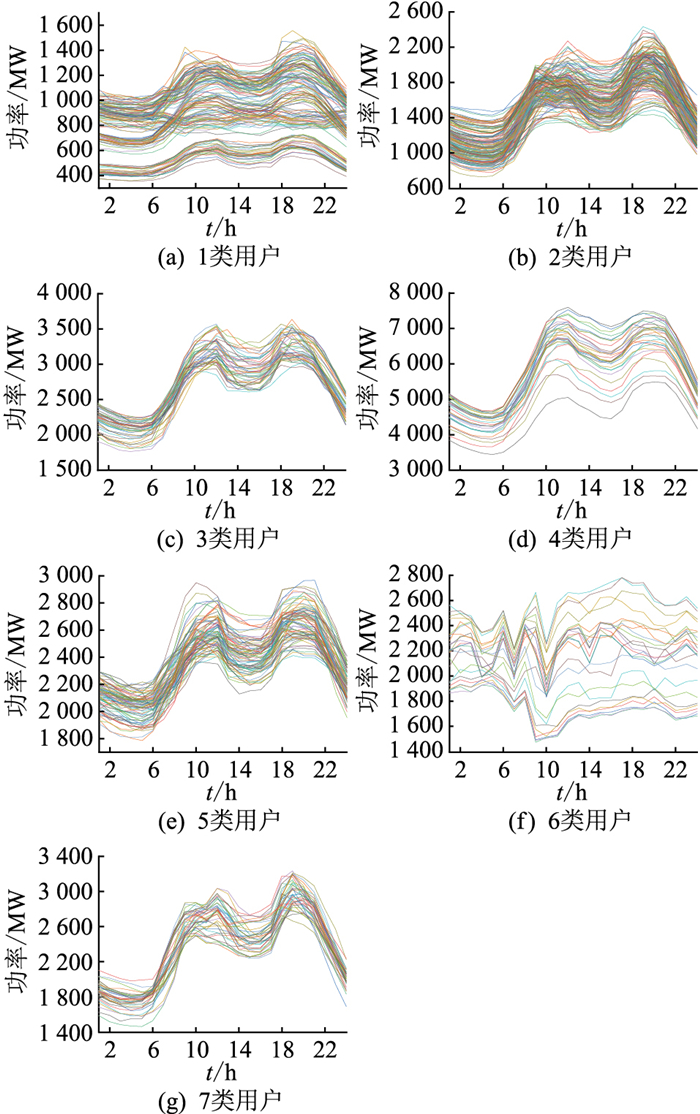
图 5 电力用户用电数据聚类结果 Fig. 5 Clustering results of power users′ electricity consumption data |
从聚类结果图的负荷曲线形态和相应纵坐标范围来看,间隔统计量法能够很好地区分原始负荷数据。由图 5可见,1类用户负荷分布在400~1 400 MW之间且峰谷差较小;2类用户负荷分布在800~2 400 MW之间,相应午高峰和晚高峰差值比较明显;3类用户、5类用户、7类用户负荷分布在大致相同的范围内,但这3类用户负荷的峰值、谷值、峰谷值时段存在差异;4类用户负荷值较大,分布在3 500~7 500 MW之间;6类用户的负荷曲线在具体形态方面与其他类别用户差异较大。
5.3 不同特征信息增益与相关性不同特征的加入对电力用户信息增益效果如图 6所示。用电量t1、最大负荷t2、最小负荷t3、平均负荷t4、峰谷差t5的信息增益值较大,均大于0.8;负荷率t6、峰谷差率t7、峰时耗电率t8和谷时耗电率t9的信息增益值居中,为0.6左右;平时耗电率t10的信息增益较小,仅为0.15。

|
图 6 不同特征对电力用户的信息增益值 Fig. 6 Information gain value of different features to power users |
不同特征之间的Spearman相关系数计算结果见表 1。
|
|
表 1 不同特征之间的相关系数计算结果 Table 1 Numerical results of correlation coefficients between different features |
分析其中相关性较强的几个特征指标可以发现,用电量t1、最大负荷t2、最小负荷t3、平均负荷t4这4个指标之间的正相关性较强。负荷率t6与谷时耗电率t9具有较强的正相关性,峰谷差率t7与峰时耗电率t8具有较强的正相关性,且负荷率t6、谷时耗电率t9与峰谷差率t7、峰时耗电率t8之间具有明显的负相关性。可以看到,基于Spearman相关系数的分析方法可以有效识别不同特征之间存在的相关关系。
5.4 基于GA的最优特征集选择首先通过随机方式产生若干数量的初始种群(种群数量大小取100),然后采用GA进行迭代求解。在迭代过程中,通过适应度函数对种群内的较优个体进行选择,适应度数值越大,被选择的概率越大。而后按照一定概率对选择出来的个体进行交叉、变异等操作,最终形成新一代种群。设置一定的停止准则(文中设置为迭代次数上限200),算法按照上述规则重复进行种群迭代更新,直到满足停止准则。
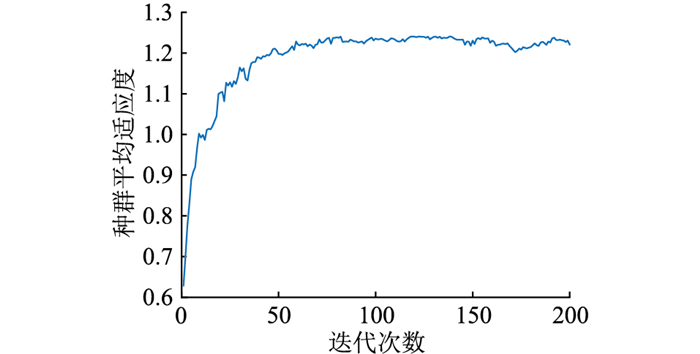
基于上述算法求得的适应度值最高的种群个体为T={0, 0, 0, 0, 1, 1, 1, 0, 1, 0},即最优特征集求解结果为T={t5,t6,t7,t9}。GA迭代求解最优特征集的过程见图 7。由图 7可知,求得最优个体的迭代次数为12,相应个体的适应度值为1.240 5,表明了GA用于求解最优特征集的高效性,但此时种群平均适应度为0.9左右,而GA最终求得的种群平均适应度为1.2左右。这一结果说明在求得最优个体时,种群个体之间的差异性仍然较大,算法在全局范围内仍有较大搜索空间,即算法对全局最优解的搜索能力较强。
|
图 7 GA迭代求解最优特征集过程 Fig. 7 Iterative process of GA in solving optimal feature set |
通过以上得到的最优特征集,对不同类型的电力用户进行行为画像,具体如图 8所示。最优特征指标下电力用户用电特性如图 9所示。
|
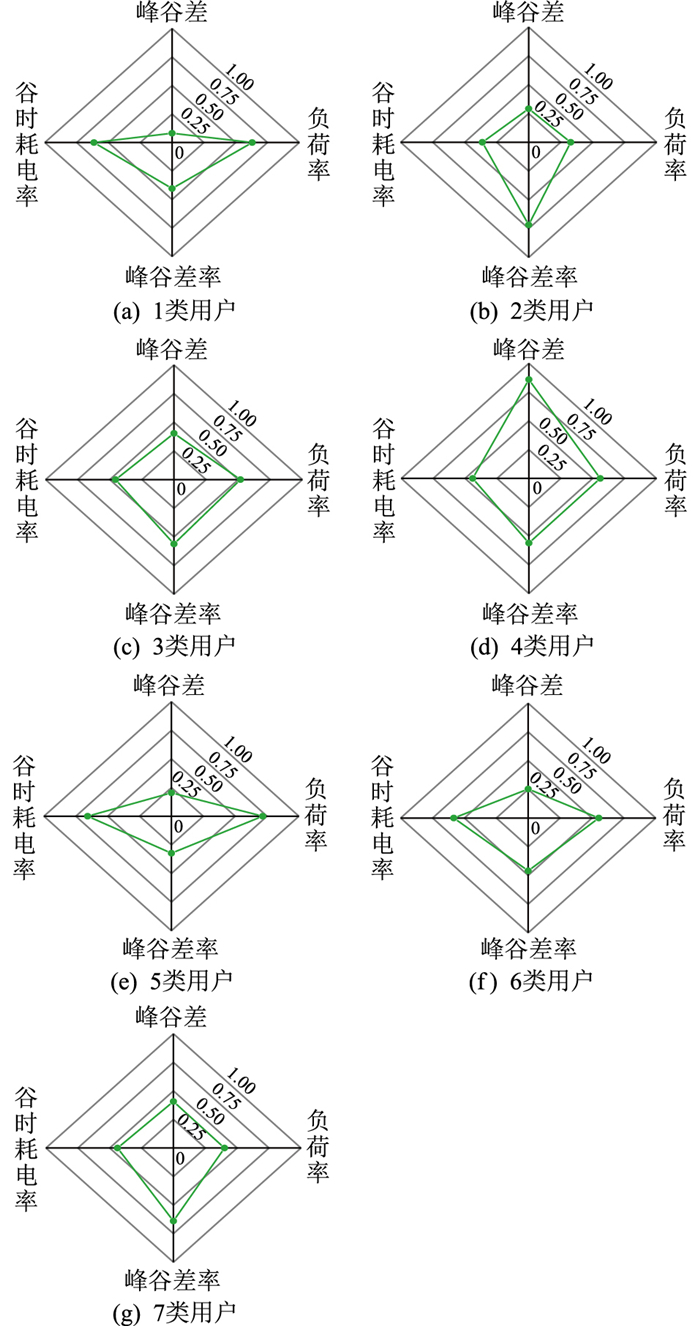
图 8 电力用户用电行为画像 Fig. 8 Behavior portrait of power users |
|
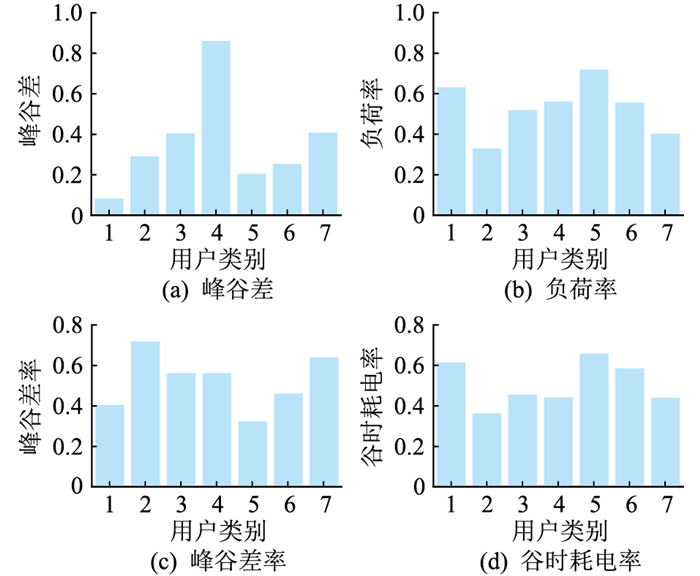
图 9 最优特征指标下电力用户用电特征 Fig. 9 Electricity consumption features of power users under the optimal characteristic index |
综合来看,不同用户在不同特征维度下的偏好有所差异。1类用户峰谷差值较小,结合用户负荷聚类结果图来看,表明其负荷数值较小且曲线较平滑。2类用户峰谷差率较大但峰谷差不大,说明其整体负荷水平不高但在一天当中波动较大。3类用户和7类用户各项特征指标均适中,说明其负荷特性较为均衡。4类用户峰谷差最大且峰谷差率较大,表明其负荷水平较高,且负荷在一天中波动幅值和相对幅度均较大。5类用户和6类用户峰谷差和峰谷差率均较小,但负荷率和谷时耗电率均较大,表明其负荷曲线较为平缓。
6 结语文中提出一种基于信息增益与Spearman相关系数的电力用户行为画像方法。利用间隔统计量法高效地确定了最优聚类数,采用k-means算法对电力用户用电数据进行了聚类分析;计及特征的信息增益及特征间冗余性,构造了特征集适应性评价系数,用于选择最优特征集;通过GA进行最优特征集的高效快速求解,并在最优特征集基础上对电力用户用电特性进行了刻画。为便于工程人员对用户特征的理解,采用打分制对特征加以量化分析,清晰地展现出不同电力用户在不同特征下的用电特性。算例分析结果表明该方法可以对电力用户用电数据进行高效聚类分析并选择出兼具较高有效性和较低冗余性的最优特征集,同时能够有效构建电力用户行为画像。
| [1] |
ZHANG S X, SHI C, JIANG X, et al. Analysis of the trend of global power sources based on comment emotion mining[J]. Global Energy Interconnection, 2020, 3(3): 283-291. DOI:10.1016/j.gloei.2020.07.009 (  0) 0) |
| [2] |
LIU Z, ZHANG Y, WANG Y, et al. Development of the interconnected power grid in Europe and suggestions for the energy internet in China[J]. Global Energy Interconnection, 2020, 3(2): 111-119. DOI:10.1016/j.gloei.2020.05.003 (  0) 0) |
| [3] |
申洪, 周勤勇, 刘耀, 等. 碳中和背景下全球能源互联网构建的关键技术及展望[J]. 发电技术, 2021, 42(1): 8-19. SHEN Hong, ZHOU Qinyong, LIU Yao, et al. Key technologies and prospects for the construction of global energy internet under the background of carbon neutral[J]. Power Generation Technology, 2021, 42(1): 8-19. (  0) 0) |
| [4] |
孙宏斌, 郭庆来, 潘昭光. 能源互联网: 理念、架构与前沿展望[J]. 电力系统自动化, 2015, 39(19): 1-8. SUN Hongbin, GUO Qinglai, PAN Zhaoguang. Energy Internet: concept, architecture and frontier outlook[J]. Automation of Electric Power Systems, 2015, 39(19): 1-8. DOI:10.7500/AEPS20150701007 (  0) 0) |
| [5] |
鞠平, 周孝信, 陈维江, 等. "智能电网+"研究综述[J]. 电力自动化设备, 2018, 38(5): 2-11. JU Ping, ZHOU Xiaoxin, CHEN Weijiang, et al. "Smart Grid Plus" research overview[J]. Electric Power Automation Equipment, 2018, 38(5): 2-11. (  0) 0) |
| [6] |
张铁峰, 顾明迪. 电力用户负荷模式提取技术及应用综述[J]. 电网技术, 2016, 40(3): 804-811. ZHANG Tiefeng, GU Mingdi. Overview of electricity customer load pattern extraction technology and its application[J]. Power System Technology, 2016, 40(3): 804-811. (  0) 0) |
| [7] |
苏适, 李康平, 严玉廷, 等. 基于密度空间聚类和引力搜索算法的居民负荷用电模式分类模型[J]. 电力自动化设备, 2018, 38(1): 129-136. SU Shi, LI Kangping, YAN Yuting, et al. Classification model of residential power consumption mode based on DBSCAN and gravitational search algorithm[J]. Electric Power Automation Equipment, 2018, 38(1): 129-136. (  0) 0) |
| [8] |
赵永柱, 马霁讴, 张可心. 基于电力资产全寿命周期的标签画像技术研究[J]. 电网与清洁能源, 2018, 34(1): 51-58. ZHAO Yongzhu, MA Jiou, ZHANG Kexin. Research on the label portrait technology based on life cycle of electricity assets[J]. Power System and Clean Energy, 2018, 34(1): 51-58. DOI:10.3969/j.issn.1674-3814.2018.01.009 (  0) 0) |
| [9] |
罗滇生, 杜乾, 别少勇, 等. 基于负荷分解的居民差异化用电行为特性分析[J]. 电力系统保护与控制, 2016, 44(21): 29-33. LUO Diansheng, DU Qian, BIE Shaoyong, et al. Analysis of differentiation residential electricity consumption characteristic based on power load decomposition[J]. Power System Protection and Control, 2016, 44(21): 29-33. DOI:10.7667/PSPC151908 (  0) 0) |
| [10] |
王成亮, 郑海雁. 基于模糊聚类的电力客户用电行为模式画像[J]. 电测与仪表, 2018, 55(18): 77-81. WANG Chengliang, ZHENG Haiyan. A portrait of electricity consumption behavior mode of power users based on fuzzy clustering[J]. Electrical Measurement & Instrumentation, 2018, 55(18): 77-81. DOI:10.3969/j.issn.1001-1390.2018.18.013 (  0) 0) |
| [11] |
陆晓, 徐春雷, 冷钊莹, 等. 基于数据驱动方法的疫情阶段电力用户负荷特性画像模型[J]. 电力建设, 2021, 42(2): 93-106. LU Xiao, XU Chunlei, LENG Zhaoying, et al. Load characteristic portrait model of power users in epidemic stage applying data-driven method[J]. Electric Power Construction, 2021, 42(2): 93-106. (  0) 0) |
| [12] |
王利利, 张琳娟, 许长清, 等. 能源互联网背景下园区用户画像及成熟度评价模型研究[J]. 中国电力, 2020, 53(8): 19-28. WANG Lili, ZHANG Linjuan, XU Changqing, et al. Research on park users portrait and maturity evaluation model under the background of energy Internet[J]. Electric Power, 2020, 53(8): 19-28. (  0) 0) |
| [13] |
赵莉, 候兴哲, 胡君, 等. 基于改进k-means算法的海量智能用电数据分析[J]. 电网技术, 2014, 38(10): 2715-2720. ZHAO Li, HOU Xingzhe, HU Jun, et al. Improved k-means algorithm based analysis on massive data of intelligent power utilization[J]. Power System Technology, 2014, 38(10): 2715-2720. (  0) 0) |
| [14] |
王保义, 胡恒, 张少敏. 差分隐私保护下面向海量用户的用电数据聚类分析[J]. 电力系统自动化, 2018, 42(2): 121-127. WANG Baoyi, HU Heng, ZHANG Shaomin. Differential privacy protection based clustering analysis of electricity consumption data for massive consumers[J]. Automation of Electric Power Systems, 2018, 42(2): 121-127. (  0) 0) |
| [15] |
陆俊, 朱炎平, 彭文昊, 等. 智能用电用户行为分析特征优选策略[J]. 电力系统自动化, 2017, 41(5): 58-63, 83. LU Jun, ZHU Yanping, PENG Wenhao, et al. Feature selection strategy for electricity consumption behavior analysis in smart grid[J]. Automation of Electric Power Systems, 2017, 41(5): 58-63, 83. (  0) 0) |
| [16] |
冯志颖, 唐文虎, 吴青华, 等. 考虑负荷纵向随机性的用户用电行为聚类方法[J]. 电力自动化设备, 2018, 38(9): 39-44, 53. FENG Zhiying, TANG Wenhu, WU Qinghua, et al. Users' consumption behavior clustering method considering longitudinal randomness of load[J]. Electric Power Automation Equipment, 2018, 38(9): 39-44, 53. (  0) 0) |
| [17] |
杨卫红, 赖清平, 兰宇, 等. 基于调节潜力指标的用户用电行为聚类分析算法研究[J]. 电力建设, 2018, 39(6): 96-104. YANG Weihong, LAI Qingping, LAN Yu, et al. Research on clustering analysis algorithm based on adjustable potential index for user power consumption behavior[J]. Electric Power Construction, 2018, 39(6): 96-104. DOI:10.3969/j.issn.1000-7229.2018.06.013 (  0) 0) |
| [18] |
刘洋, 刘洋, 许立雄, 等. 计及数据类别不平衡的海量用户负荷典型特征高性能提取方法[J]. 中国电机工程学报, 2019, 39(14): 4093-4104. LIU Yang, LIU Yang, XU Lixiong, et al. A high performance extraction method for massive user load typical characteristics considering data class imbalance[J]. Proceedings of the CSEE, 2019, 39(14): 4093-4104. (  0) 0) |
| [19] |
李郅琴, 杜建强, 聂斌, 等. 特征选择方法综述[J]. 计算机工程与应用, 2019, 55(24): 10-19. LI Zhiqin, DU Jianqiang, NIE Bin, et al. Summary of feature selection methods[J]. Computer Engineering and Applications, 2019, 55(24): 10-19. DOI:10.3778/j.issn.1002-8331.1909-0066 (  0) 0) |
| [20] |
严雪颖, 秦川, 鞠平, 等. 负荷功率模型的最优特征选择研究[J]. 电力工程技术, 2021, 40(3): 84-91. YAN Xueying, QIN Chuan, JU Ping, et al. Optimal feature selection of load power models[J]. Electric Power Engineering Technology, 2021, 40(3): 84-91. (  0) 0) |
| [21] |
刘庆和, 梁正友. 一种基于信息增益的特征优化选择方法[J]. 计算机工程与应用, 2011, 47(12): 130-132, 136. LIU Qinghe, LIANG Zhengyou. Optimized approach of feature selection based on information gain[J]. Computer Engineering and Applications, 2011, 47(12): 130-132, 136. DOI:10.3778/j.issn.1002-8331.2011.12.037 (  0) 0) |
| [22] |
张振海, 李士宁, 李志刚, 等. 一类基于信息熵的多标签特征选择算法[J]. 计算机研究与发展, 2013, 50(6): 1177-1184. ZHANG Zhenhai, LI Shining, LI Zhigang, et al. Multi-label feature selection algorithm based on information entropy[J]. Journal of Computer Research and Development, 2013, 50(6): 1177-1184. (  0) 0) |
| [23] |
谢娟英, 吴肇中, 郑清泉. 基于信息增益与皮尔森相关系数的2D自适应特征选择算法[J]. 陕西师范大学学报(自然科学版), 2020, 48(6): 69-81. XIE Juanying, WU Zhaozhong, ZHENG Qingquan. An adaptive 2D feature selection algorithm based on information gain and Pearson correlation coefficient[J]. Journal of Shaanxi Normal University (Natural Science Edition), 2020, 48(6): 69-81. (  0) 0) |
| [24] |
闫泓序, 余顺坤, 林依青. 我国工业电力用户价值画像模型构建与应用研究[J]. 中国管理科学, 2021, 29(10): 224-235. YAN Hongxu, YU Shunkun, LIN Yiqing. Research on the construction and application of the customer value portrait model of industrial power enterprise in China[J]. Chinese Journal of Management Science, 2021, 29(10): 224-235. (  0) 0) |
| [25] |
许元斌, 李国辉, 郭昆, 等. 基于改进的并行K-Means算法的电力负荷聚类研究[J]. 计算机工程与应用, 2017, 53(17): 260-265. XU Yuanbin, LI Guohui, GUO Kun, et al. Research on parallel clustering of power load based on improved K-Means algorithm[J]. Computer Engineering and Applications, 2017, 53(17): 260-265. DOI:10.3778/j.issn.1002-8331.1603-0110 (  0) 0) |
| [26] |
TIBSHIRANI R, WALTHER G, HASTIE T. Estimating the num-ber of clusters in a data set via the gap statistic[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2001, 63(2): 411-423. DOI:10.1111/1467-9868.00293 (  0) 0) |
| [27] |
张承畅, 张华誉, 罗建昌, 等. 基于云计算和改进K-means算法的海量用电数据分析方法[J]. 计算机应用, 2018, 38(1): 159-164. ZHANG Chengchang, ZHANG Huayu, LUO Jianchang, et al. Massive data analysis of power utilization based on improved K-means algorithm and cloud computing[J]. Journal of Computer Applications, 2018, 38(1): 159-164. (  0) 0) |
| [28] |
田剑刚, 张沛, 彭春华, 等. 基于分时长短期记忆神经网络的光伏发电超短期功率预测[J]. 现代电力, 2020, 37(6): 629-638. TIAN Jiangang, ZHANG Pei, PENG Chunhua, et al. Ultra short-term forecast of photovoltaic generation based on time-division long short-term memory neural networks[J]. Modern Electric Power, 2020, 37(6): 629-638. (  0) 0) |
| [29] |
张大海, 杨宇辰, 刘艳梅, 等. 基于EMD与Spearman相关系数的混合直流线路纵联保护方法[J]. 电力系统保护与控制, 2021, 49(9): 1-11. ZHANG Dahai, YANG Yuchen, LIU Yanmei, et al. Hybrid HVDC line pilot protection method based on EMD and Spearman correlation coefficient[J]. Power System Protection and Control, 2021, 49(9): 1-11. (  0) 0) |
| [30] |
赵铁成, 谢丽蓉, 叶家豪. 基于误差修正的NNA-ILSTM短期风电功率预测[J]. 智慧电力, 2022, 50(1): 29-36. ZHAO Tiecheng, XIE Lirong, YE Jiahao. NNA-ILSTM short term wind power prediction based on error correction[J]. Smart Power, 2022, 50(1): 29-36. (  0) 0) |
2. School of Electrical Engineering, Xi'an Jiaotong University, Xi'an 710049, China
 2022, Vol. 41
2022, Vol. 41


 王圆圆(1988), 女, 博士, 高级工程师, 从事能源经济研究相关工作(E-mail:
王圆圆(1988), 女, 博士, 高级工程师, 从事能源经济研究相关工作(E-mail: