文章编号: 2096-3203(2022)04-0205-08 中图分类号: TM72
2. 南瑞集团(国网电力科学研究院)有限公司, 江苏 南京 211106
混合直流输电技术综合了电网换相换流器高压直流(line commutated converter-high voltage direct current, LCC-HVDC)技术成熟、成本低廉、损耗小和电压源型换流器高压直流(voltage source converter-high voltage direct current, VSC-HVDC)可控性能好、占地面积小、不存在换相失败故障的优势,近年来得到了快速发展,先后已有多个工程开工建设或投入运行[1-4]。模块化多电平换流器(modular multilevel converter, MMC)是混合直流输电工程的重要组成部分,目前针对MMC的研究多集中在对称单极结构方面,包括换流器的仿真建模[5-6]、控制保护策略[7-8]、故障特性分析[9]和故障穿越[10-12]等。而基于MMC的混合直流输电系统大多采用常规直流的双极结构,相对于对称单极结构具有更高的可靠性和更大的输送容量。
对称单极结构与双极结构接线方式不同,2种结构在故障特性方面存在较大差异[13]。文献[14]分析了双极MMC联结变压器阀侧接地故障引起严重过电压的机理,并给出了相应解决方法;文献[15]分析了双极MMC多端直流输电系统站内交流三相接地故障的故障机理;文献[16]分析了双极MMC输电系统直流故障的故障特性,并与对称单极输电系统进行了对比分析。然而,以上研究并未涉及MMC中核心部件桥臂电抗器及其穿墙套管的故障特性。桥臂电抗器作为换流器与交流电网的连接桥梁,不仅能够抑制桥臂间环流,还能在换流器内部故障和直流侧故障时抑制流过功率器件的故障电流上升率,因此有必要对其进行深入分析。
现有文献对桥臂电抗器的研究主要集中在参数设计[17]和试验方法[18-19]上,对双极结构中如何合理布置桥臂电抗器并对其进行有效保护的报道较少。针对目前工程实践中双极柔性直流输电系统MMC桥臂电抗器布置方案存在的故障过流问题,文中详细对比分析了桥臂电抗器布置在靠近交流连接点和靠近直流连接点2个不同位置对换流器故障电流的影响,指出桥臂电抗器布置在靠近直流连接点能够有效降低MMC桥臂故障过电流水平,但当桥臂电抗器穿墙套管发生相间短路故障时,现有保护策略不能及时发现,给MMC的安全运行带来隐患。因此文中提出一种基于桥臂环流谐波分量识别的桥臂电抗器穿墙套管相间短路故障保护策略,能够有效识别桥臂电抗器穿墙套管相间短路故障,并通过PSCAD/EMTDC进行仿真,验证了该保护策略的有效性。
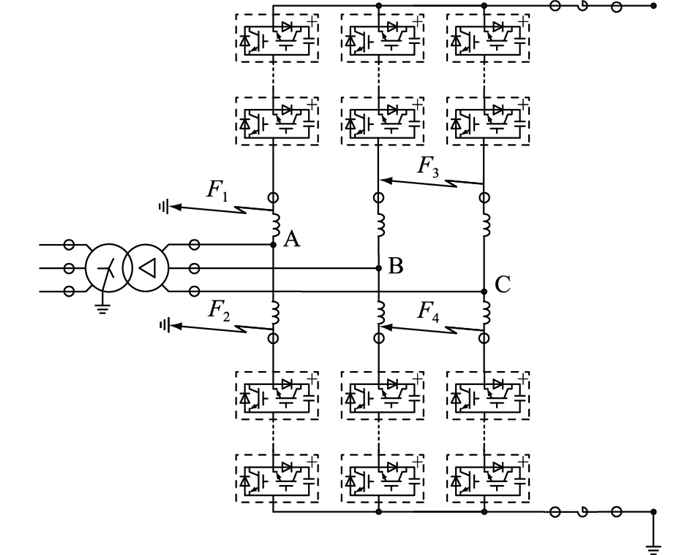
1 桥臂电抗器布置 1.1 桥臂电抗器靠近交流连接点目前工程中MMC桥臂电抗器一般安装在交流连接点与桥臂换流阀之间,如图 1所示。桥臂电抗器一般紧靠阀厅安装,与换流阀通过穿墙套管相连,也有小容量工程为了避免穿墙套管故障而将桥臂电抗器安装于阀厅内。
|
图 1 桥臂电抗器靠近交流连接点示意 Fig. 1 The schematic diagram of bridge arm reactor near the AC connection point |
工程中因穿墙套管的质量或安装问题而导致其绝缘降低被击穿的故障时有发生[20-24],桥臂电抗器穿墙套管的击穿故障在双极结构的工程中会引起严重的过电流[10]。当桥臂电抗器穿墙套管发生击穿接地故障,即图 1中A相上桥臂阀底与桥臂电抗器穿墙套管之间金属性接地故障F1时,A相上桥臂的故障回路中无桥臂电抗器,若故障时恰好投入的子模块个数较少,将引起过大的故障电流,可能导致子模块无法有效闭锁,进而损坏功率器件。若发生图 1中下桥臂阀顶与桥臂电抗器穿墙套管之间金属性接地故障F2,同样可能产生较大的故障电流,导致功率器件无法正常关断而损坏。而对于图 1中B相上桥臂阀底、C相上桥臂阀底与桥臂电抗器穿墙套管之间金属性短路故障F3或者B相下桥臂阀顶、C相下桥臂阀顶与桥臂电抗器穿墙套管之间金属性短路故障F4出现的情况,此时B、C两相的上桥臂换流阀将不经桥臂电抗器而直接短路, 相当于2个不同的电压源直接并联,这将引起巨大的故障电流,直接损坏换流阀。为了避免上述故障带来的严重后果,工程设计中往往采取额外措施,如增大直流电抗器来避免设备损坏。
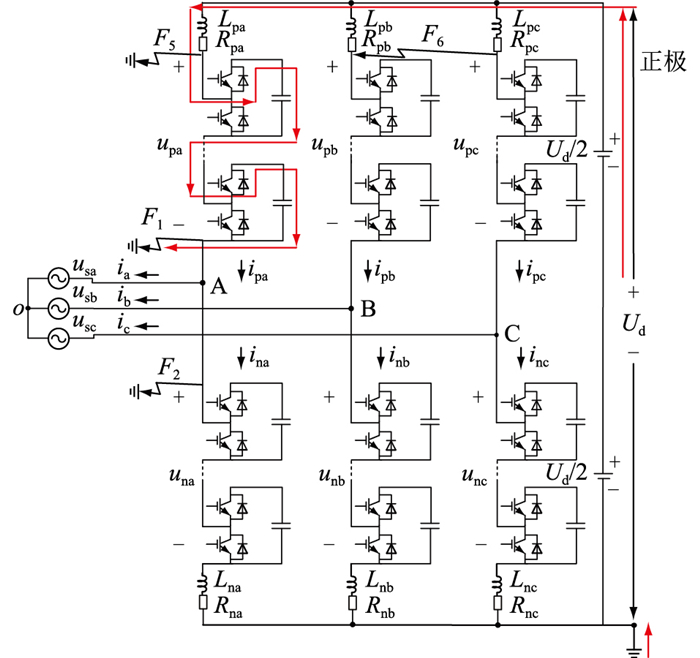
1.2 桥臂电抗器靠近直流连接点为解决上述问题,文中提出将桥臂电抗器的安装位置由原来的交流连接点与桥臂换流阀之间调整至直流正极公共点或负极公共点与桥臂换流阀之间,如图 2所示。当发生故障F1、F2、A相上桥臂阀顶与桥臂电抗器穿墙套管之间金属性接地故障F5时,故障回路中均有桥臂电抗器,可以有效抑制故障电流上升率。当桥臂电抗器穿墙套管发生两相短路,如图 2中B相上桥臂阀顶、C相上桥臂阀顶与桥臂电抗器穿墙套管之间发生相间金属性短路故障F6时,仅会引起B、C两相的桥臂电抗器参数发生改变,导致相单元间的环流变大,对换流阀的稳态运行并不会造成太大影响。因不会引起较大的故障电流,现有的基于差动或过流原理的直流保护策略并不能及时识别这种故障,虽然这种故障对系统的正常运行影响不大,但若长期未能发现并解决,最终也会给换流阀以及桥臂电抗器等设备带来危害。
|
图 2 桥臂电抗器靠近直流连接点示意 Fig. 2 The schematic diagram of bridge arm reactor near the DC connection point |
图 2为桥臂电抗器安装在靠近直流侧的三相MMC拓扑结构,定义桥臂电流的正方向为流入电容的方向,交流电气量的正方向按逆变运行的方式定义。
依据环流的定义,MMC上、下桥臂电流可以表示为:
| $i_{\mathrm{p} j}=i_{\mathrm{z}j}+\frac{i_{j}}{2}=i_{\mathrm{z}j\text{ac}}+i_{\text{z} j \mathrm{dc}}+\frac{i_{j}}{2} $ | (1) |
| $ i_{\mathrm{n} j}=i_{\text{z} j}-\frac{i_{j}}{2}=i_{\text{z}j\text{ac}}+i_{\text{z}j\text{dc}}-\frac{i_{j}}{2} $ | (2) |
式中:ipj,inj分别为各相上、下桥臂电流,j=a, b, c;izj为各相桥臂环流;izjac为各相交流环流;izjdc为各相直流环流;ij为各相阀侧交流电流;
MMC拓扑中各相上、下桥臂实际可等效为一个受控电压源,因此由基尔霍夫电压定律(Kirchhoff′s voltage law,KVL)可得:
| $ u_{\mathrm{p} j}=\frac{U_{\mathrm{d}}}{2}-u_{\mathrm{on}}-L_{\mathrm{p} j} \frac{\mathrm{d} i_{\mathrm{p} j}}{\mathrm{~d} t}-R_{\mathrm{p} j} i_{\mathrm{p} j}-u_{\mathrm{s} j} $ | (3) |
| $ u_{\mathrm{n} j}=\frac{U_{\mathrm{d}}}{2}+u_{\mathrm{on}}-L_{\mathrm{n} j} \frac{\mathrm{d} i_{\mathrm{n} j}}{\mathrm{~d} t}-R_{\mathrm{n} j} i_{\mathrm{n} j}+u_{\mathrm{s} j} $ | (4) |
式中:upj,unj分别为各相上、下桥臂等效受控电压源电压;Lpj,Lnj分别为各相上、下桥臂电感;Rpj,Rnj分别为各相上、下桥臂等效电阻;uon为中性点共模电压;usj为各相阀侧交流电压;Ud为直流电压。
式(1)—式(4)构成了MMC拓扑的整个数学分析基础, 对于对称单极接线方式和双极接线方式均适用。
2.2 桥臂电抗器穿墙套管故障特性分析 2.2.1 桥臂电抗器穿墙套管接地故障在双极接线方式中,当MMC换流器阀侧连接线发生接地故障,如图 2中A相上桥臂阀底与桥臂电抗器穿墙套管之间金属性接地故障F1时,故障接地点与换流器的直流侧接地点G将形成短路电流通路,如图 2中红色线路所示。
对A相上桥臂列KVL方程有:
| $L_{\mathrm{pa}} \frac{\mathrm{d} i_{\mathrm{pa}}}{\mathrm{d} t}+R_{\mathrm{pa}} i_{\mathrm{pa}}=U_{\mathrm{d}}-u_{\mathrm{pa}} $ | (5) |
因upa为A相上桥臂受控电压源的输出电压,结合上、下桥臂的开关函数,有:
| $u_{\mathrm{pa}}=U_{\mathrm{c}}(1-m \cos \omega t) $ | (6) |
| $m=\frac{2 U_{\mathrm{s}}}{U_{\mathrm{d}}} $ | (7) |
式中:Uc为控制电压,0≤Uc≤Ud/2;m为调制比,0≤m≤1;Us为阀侧交流相电压幅值。
将式(6)代入式(5),有:
| $L_{\mathrm{pa}} \frac{\mathrm{d} i_{\mathrm{pa}}}{\mathrm{d} t}+R_{\mathrm{pa}} i_{\mathrm{pa}}=U_{\mathrm{d}}-U_{\mathrm{c}}(1-m \cos \omega t) $ | (8) |
其解为:
| $ \begin{gathered} i_{\mathrm{pa}}=\frac{U_{\mathrm{d}}-U_{\mathrm{c}}}{R_{\mathrm{pa}}}+\frac{m U_{\mathrm{c}}}{\sqrt{R_{\mathrm{pa}}^{2}+\left(\omega L_{\mathrm{pa}}\right)^{2}}}+\left[i_{\mathrm{pa}}\left(0^{+}\right)-\right. \\ \left.\frac{U_{\mathrm{d}}-U_{\mathrm{c}}}{R_{\mathrm{pa}}}-\frac{m U_{\mathrm{c}}}{\sqrt{R_{\mathrm{pa}}^{2}+\left(\omega L_{\mathrm{pa}}\right)^{2}}}\right] \mathrm{e}^{-\frac{R_{\mathrm{pa}^t}}{L_{\mathrm{pa}}}} \end{gathered} $ | (9) |
其中ipa(0+) 为故障瞬间A相上桥臂电流值,当m=1,Uc=Ud/2,ωt =0时刻发生此接地故障时,桥臂故障电流将达到最大,考虑到实际中Rpa非常小,为毫欧级别,因此若不采取限制措施,桥臂故障电流将达到数十千安,换流阀将损坏。此外,考虑到整流侧的直流电流方向与故障电流方向相反,而逆变侧的直流电流方向与故障电流方向相同,因此在逆变侧发生此故障时后果更为严重,故下文主要针对逆变侧开展研究。
发生故障F1时,相比于桥臂电抗器布置在靠近直流连接点,桥臂电抗器布置在靠近交流连接点时其故障回路中电抗器较小,故障电流更大,一旦发生此故障,换流阀损坏概率较大。因此,工程中一般通过增大直流电抗器来限制故障电流上升率,进而达到限制故障电流的目的。这种方式实质上是将电压源的内阻增大甚至改造为电流源,从而有效降低故障电流,达到保护设备的目的,但该方法一方面增加了占地和成本,另一方面直流系统的动态调节性能也大为降低。
对于故障F2或故障F5采用上述方法进行分析后同样可以发现当桥臂电抗器布置在靠近直流连接点时,其故障回路中将包含桥臂电抗器,故障电流上升率将得到有效抑制,从而可以不用额外增加直流电抗器而达到限制故障电流水平的目的,避免设备损坏。
对于接地故障,因其故障电流较大,特征明显,工程中大多采用基于差动原理的快速差动保护作为主保护,当故障电流达到保护定值后其动作延时一般不超过1 ms即出口闭锁换流器并跳开相关断路器,隔离故障保护设备。
2.2.2 桥臂电抗器穿墙套管相间短路故障在双极接线方式中,当MMC换流阀与桥臂电抗器穿墙套管之间发生相间金属性短路故障时,由于并不会形成差流,因此基于差动原理的保护往往会失效,此时一般采用过流速断保护作为此故障的主保护。
当桥臂电抗器布置在靠近交流连接点,发生桥臂电抗器相间金属性短路故障F3或F4时,将导致换流器阀侧交流相间短路,或者换流器的桥臂间短路,此时阀侧交流电流或桥臂电流将急剧增大,过流速断保护能迅速识别故障,出口闭锁换流器并跳开相关断路器,隔离故障,保护相关设备的安全。
而当桥臂电抗器布置在靠近直流侧连接点,发生桥臂电抗器相间短路故障F6时,仅会引起B相和C相的等效桥臂电抗器发生改变,并不会导致桥臂电流或阀侧交流电流或直流电流急剧变化,现有的差动保护或过流速断保护均无法有效识别该故障。因此,须对此故障进行进一步分析。
将式(1)、式(2)分别代入式(3)、式(4)中,分别相加和相减可得式(10)、式(11)。
| $ L_{\mathrm{c} j} \frac{\mathrm{d} i_{\text{z} j}}{\mathrm{~d} t}+R_{\mathrm{c} j} i_{\text{z} j}=U_{\mathrm{d}}-u_{\mathrm{c} j}-\frac{1}{2}\left(L_{\mathrm{d} j} \frac{\mathrm{d} i_{j}}{\mathrm{~d} t}+R_{\mathrm{d} j} i_{j}\right) $ | (10) |
| $ \begin{gathered} \frac{1}{4}\left(L_{\mathrm{c} j} \frac{\mathrm{d} i_{j}}{\mathrm{~d} t}+R_{\mathrm{c} j} i_{j}\right)=-\frac{1}{2} u_{\mathrm{d} j}-u_{\mathrm{s} j}- \\ u_{\mathrm{on}}-\frac{1}{2}\left(L_{\mathrm{d}j} \frac{\mathrm{d} i_{\mathrm{z}j}}{\mathrm{d} t}+R_{\mathrm{d} j} i_{\mathrm{z}j}\right) \end{gathered} $ | (11) |
式中:Lcj,Ldj分别为各相上、下桥臂电感之和与之差;Rcj,Rdj分别为各相上、下桥臂等效电阻之和与之差;ucj,udj分别为各相上、下桥臂等效电压之和与之差。
对于图 2所示故障F6,假设MMC上、下桥臂电路参数完全相同,即桥臂电感均为L,等效电阻均为R,令ipbc=ipb+ipc则有:
| $ u_{\mathrm{pb}}=\frac{U_{\mathrm{d}}}{2}-u_{\mathrm{on}}-\frac{L}{2} \frac{\mathrm{d} i_{\mathrm{pbc}}}{\mathrm{d} t}-\frac{R}{2} i_{\mathrm{pbc}}-u_{\mathrm{sb}} $ | (12) |
| $ u_{\mathrm{pc}}=\frac{U_{\mathrm{d}}}{2}-u_{\mathrm{on}}-\frac{L}{2} \frac{\mathrm{d} i_{\mathrm{pbc}}}{\mathrm{d} t}-\frac{R}{2} i_{\mathrm{pbc}}-u_{\mathrm{sc}} $ | (13) |
结合式(10)—式(13)可以得到:
| $ 2\left(L \frac{\mathrm{d} i_{\mathrm{za}}}{\mathrm{d} t}+R i_{\mathrm{za}}\right)=U_{\mathrm{d}}-u_{\mathrm{ca}} $ | (14) |
| $ \begin{aligned} &L \frac{\mathrm{d} i_{\mathrm{zb}}}{\mathrm{d} t}+R i_{\mathrm{zb}}=\frac{U_{\mathrm{d}}}{2}-\frac{3}{4} u_{\mathrm{cb}}+\frac{1}{4} u_{\mathrm{cc}}+ \\ &\frac{1}{4}\left[L \frac{\mathrm{d}\left(i_{\mathrm{b}}-i_{\mathrm{c}}\right)}{\mathrm{d} t}+R\left(i_{\mathrm{b}}-i_{\mathrm{c}}\right)\right] \end{aligned} $ | (15) |
| $\begin{gathered} L \frac{\mathrm{d} i_{\mathrm{zc}}}{\mathrm{d} t}+R i_{\mathrm{zc}}=\frac{U_{\mathrm{d}}}{2}-\frac{3}{4} u_{\mathrm{cc}}+\frac{1}{4} u_{\mathrm{cb}}- \\ \frac{1}{4}\left[L \frac{\mathrm{d}\left(i_{\mathrm{b}}-i_{\mathrm{c}}\right)}{\mathrm{d} t}+R\left(i_{\mathrm{b}}-i_{\mathrm{c}}\right)\right] \end{gathered} $ | (16) |
通过式(14)—式(16)可以发现,故障F6发生后,即使MMC各桥臂电路参数完全相同,B相和C相的交流电流之差与B相或C相的桥臂环流间仍存在较强耦合,而非故障相A相交流电流与桥臂环流间并无耦合。B相和C相的交流电流之差与B相或C相的桥臂环流间的耦合主要体现在故障相B相和C相的交流电流之差(主要为基频分量)将会在B相和C相的桥臂环流(主要为二倍频分量和直流量)中引入基频分量。考虑到实际工程中交流电流数值较大,因此故障相B相和C相的交流电流之差将会在B相和C相的桥臂环流中引入较大的基频分量。
结合式(10)—式(13)同时还可以得到:
| $ \frac{1}{4}\left(L \frac{\mathrm{d} i_{\mathrm{a}}}{\mathrm{d} t}+R i_{\mathrm{a}}\right)=-\frac{u_{\mathrm{da}}}{2}-u_{\mathrm{sa}}-u_{\mathrm{on}} $ | (17) |
| $ \begin{gathered} \frac{1}{4}\left(L \frac{\mathrm{d} i_{\mathrm{b}}}{\mathrm{d} t}+R i_{\mathrm{b}}\right)=-\frac{3 u_{\mathrm{db}}}{8}+\frac{u_{\mathrm{dc}}}{8}-\frac{3}{4} u_{\mathrm{sb}}+\frac{1}{4} u_{\mathrm{sc}}- \\ \frac{1}{2} u_{\mathrm{on}}+\frac{1}{4}\left[L \frac{\mathrm{d}\left(i_{\mathrm{zb}}-i_{\mathrm{zc}}\right)}{\mathrm{d} t}+R\left(i_{\mathrm{zb}}-i_{\mathrm{zc}}\right)\right] \end{gathered} $ | (18) |
| $ \begin{gathered} \frac{1}{4}\left(L \frac{\mathrm{d} i_{\mathrm{c}}}{\mathrm{d} t}+R i_{\mathrm{c}}\right)=-\frac{3}{8} u_{\mathrm{dc}}+\frac{1}{8} u_{\mathrm{db}}-\frac{3}{4} u_{\mathrm{sc}}+\frac{1}{4} u_{\mathrm{sb}}- \\ \frac{1}{2} u_{\mathrm{on}}-\frac{1}{4}\left[L \frac{\mathrm{d}\left(i_{\mathrm{zb}}-i_{\mathrm{zc}}\right)}{\mathrm{d} t}+R\left(i_{\mathrm{zb}}-i_{\mathrm{zc}}\right)\right] \end{gathered} $ | (19) |
从式(17)—式(19)可知,故障F6发生后,即使MMC各桥臂电路参数完全相同,B相和C相的桥臂环流电流之差与B相或C相的交流电流之间仍存在耦合,而非故障相A相中桥臂环流与交流电流之间并无耦合。B相和C相的桥臂环流电流之差与B相或C相的交流电流之间存在耦合主要体现在故障相B相和C相的桥臂环流电流之差(主要为二倍频分量和直流量)将会在B相或C相的交流电流中引入直流分量及二倍频分量。考虑到实际工程中环流抑制控制器的作用及桥臂电抗器的平滑滤波作用,故障相B相和C相的桥臂环流电流之差将非常小,且桥臂等效电阻R较小, 为毫欧级,故障引起的直流分量及二倍频分量在故障相的交流电流中占比将非常小,其值可能与上、下桥臂电抗器的制造误差所引起的直流分量及二倍频分量相当,不利于故障的识别。
由以上分析可知,通过提取并检测桥臂环流中基频分量的大小可以识别桥臂电抗器是否发生相间短路故障。当检测到桥臂环流中的基频分量超过故障定值并持续一定时间时,可认为此时发生了桥臂电抗器相间短路故障,直流控制保护系统将发出闭锁本站MMC信号并跳开相应开关隔离故障,同时通知对端换流站执行闭锁逻辑,停运直流。在设计故障保护定值时须考虑因MMC上、下桥臂电抗器的制造误差所引起的桥臂环流基频分量,因此可以将定值整定为0.05~0.1倍的桥臂电流峰值或桥臂电流有效值。此外,桥臂电抗器相间短路故障将导致MMC失去三相对称性,此时直流电流中将含有基频及二倍频分量,考虑到三相之间的部分抵消,最终的检测精度可能达不到保护识别的要求,但可作为辅助判据,提高保护的可靠性。
综上所述,将MMC桥臂电抗器的安装位置由目前的靠近交流连接点改至靠近直流连接点,能够有效降低因交流穿墙套管故障而引起的故障电流,避免换流阀的损坏。桥臂电抗器安装位置的改变也会导致穿墙套管个数的改变,桥臂电抗器安装在靠近直流连接点后所需的交流穿墙套管数由6根降至3根,降低了交流套管故障概率。虽然直流穿墙套管的根数由2根增加至6根,增加了成本,同时也增大了直流侧故障概率,但双极结构中主要矛盾已由直流侧故障转变为阀侧接地故障[9-10],阀侧接地故障更易损坏换流阀。从降低MMC阀侧接地故障概率以保护换流阀来看,建议后续采用双极结构的直流工程将桥臂电抗器的安装位置由靠近交流连接点改至靠近直流连接点。
3 仿真验证在PSCAD/EMTDC中搭建双极MMC直流输电系统仿真模型。仿真系统参数如下:系统额定直流电压Ude为400 kV;额定直流电流Ide为3 000 A;MMC所连交流系统额定电压Uac为525 kV;阀侧额定电压Uv为182.6 kV;直流电抗器电感为50 mH;桥臂电抗器电感L为50 mH(对应于图 2中Lpj与Lnj均相等的情况,即Lpj=Lnj=L);桥臂等效电阻R为0.013 24 Ω(对应于图 2中Rpj与Rnj均相等的情况,即Rpj=Rnj=R);子模块电容Cd为18 mF;子模块额定电压Uc为1.905 kV;桥臂子模块数量为210个,绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)/二极管导通电阻为0.085 mΩ。
3.1 桥臂电抗器穿墙套管接地故障仿真分析当单极直流系统稳定输送功率667 MW时,在逆变侧的MMC A相上桥臂阀底施加金属性接地故障,即图 2中故障F1。
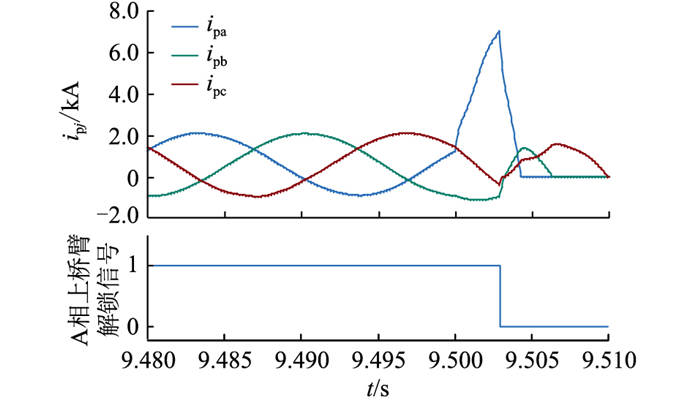
图 3为桥臂电抗器靠近交流连接点,在A相上桥臂阀底于9.500 s施加金属性接地故障时的仿真波形, 故障发生2.8 ms后桥臂电抗器差动保护动作,闭锁换流器。由图 3可以看到A相上桥臂的电流ipa在闭锁前最高达到了7.02 kA,而目前的IGBT器件最大额定电流仅为3 kA, 其最大关断电流为6 kA, 超过6 kA IGBT器件将无法可靠关断。因此,一旦发生此种故障,换流器将因无法可靠闭锁而损坏,故工程中一般通过增大直流电抗器来限制故障电流。
|
图 3 桥臂电抗器靠近交流连接点发生A相接地故障时波形 Fig. 3 The waveforms when phase A occurs ground fault for the bridge arm reactor near the AC connection point |
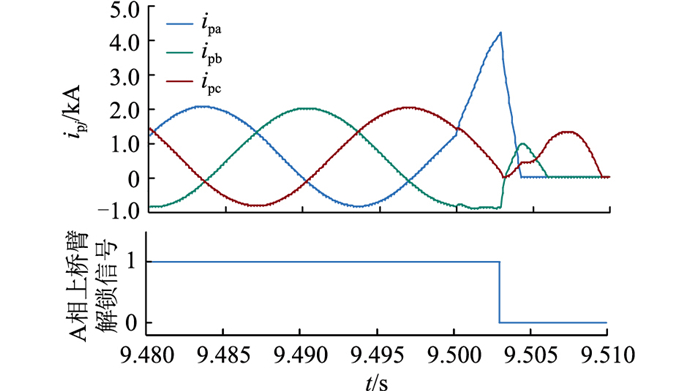
图 4为桥臂电抗器靠近直流连接点,在A相上桥臂阀底于9.500 s施加金属性接地故障时的仿真波形, 故障发生2.9 ms后交流穿墙套管差动保护动作,闭锁换流器。由图 4可见,A相上桥臂的电流ipa在闭锁前最高达到了4.22 kA,相比于桥臂电抗器靠近交流连接点时,故障电流减小了2.8 kA,且不超过现有IGBT器件的关断能力,因而不需要增大直流电抗器即可保证换流器的安全。
|
图 4 桥臂电抗器靠近直流连接点发生A相接地故障时波形 Fig. 4 The waveforms when phase A occurs ground fault for the bridge arm reactor near the DC connection point |
图 5—图 7为桥臂电抗器靠近直流连接点,在B、C相上桥臂电抗器阀侧于9.500 s施加金属性短路故障(即图 2中故障F6)时的仿真波形。
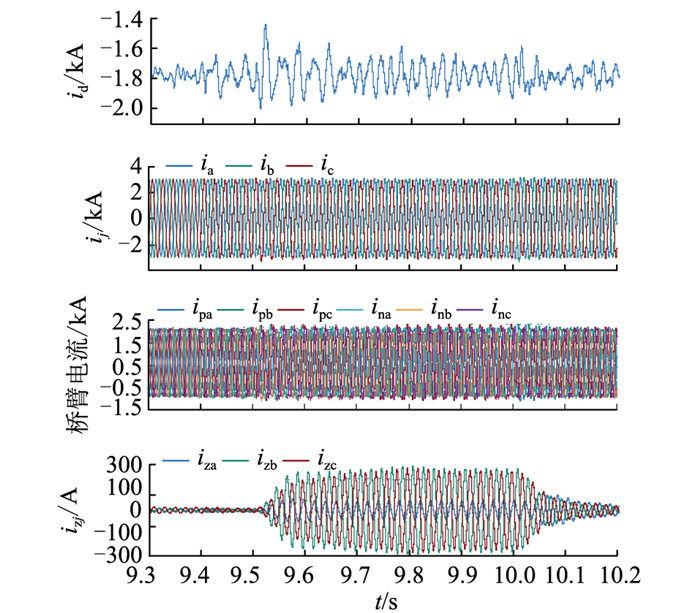
|
图 5 桥臂电抗器靠近直流连接点发生BC相间短路故障时电流波形 Fig. 5 The current waveforms when the BC phase short- circuit fault occurs for the bridge arm reactor near the DC connection point |
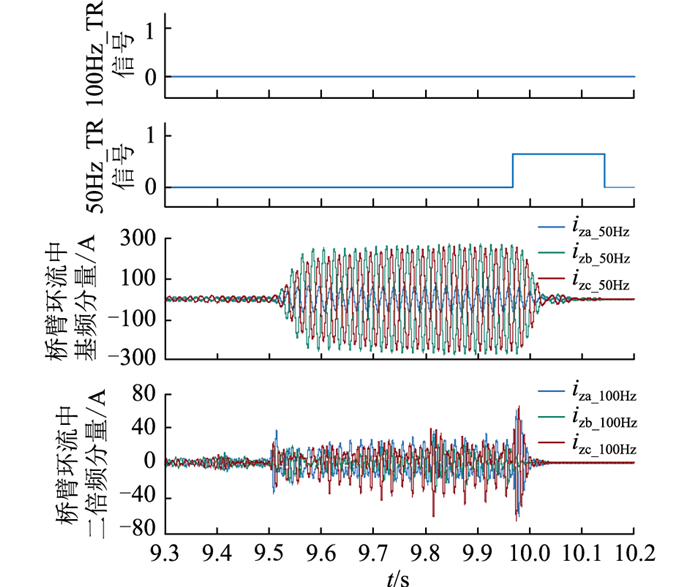
|
图 6 桥臂电抗器靠近直流连接点发生BC相间短路故障时环流电流波形 Fig. 6 The circulation current waveforms when the BC phase short-circuit fault occurs for the bridge arm reactor near the DC connection point |
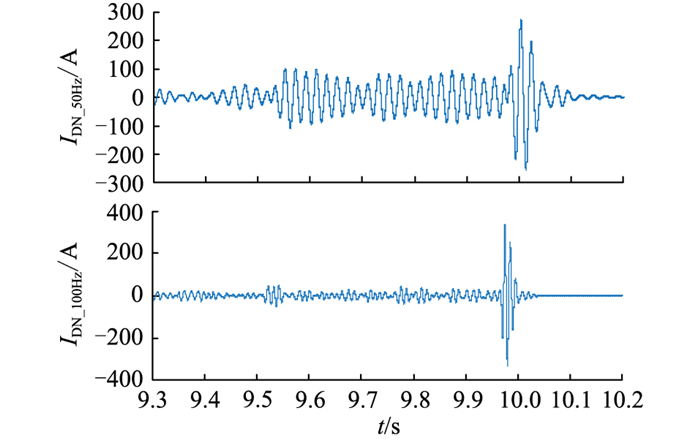
|
图 7 桥臂电抗器靠近直流连接点发生BC相间短路故障时直流电流谐波分量 Fig. 7 The harmonic currents of DC current when the BC phase short-circuit fault occurs for the bridge arm reactor near the DC connection point |
由图 5可见,在BC相间短路故障发生后,换流器桥臂电流ipj, inj,阀侧交流电流ij和直流电流id均没有较大变化,阀侧交流电流中的直流分量及二倍频分量非常小,与稳态运行时基本一致,而桥臂环流izj中的50 Hz分量在故障发生后增加较大,具有明显的故障特征,与前文理论分析一致。
由图 6可见,在桥臂电抗器BC相间短路故障发生后,B相桥臂环流izb, C相桥臂环流izc中的50 Hz分量izb_50Hz与izc_50Hz开始增大,其有效值由稳态运行时接近0 A增大到故障时的275 A,而非故障相A相的桥臂环流iza中50 Hz分量iza_50Hz只稍微增加,这与前文理论分析一致。即可以通过检测桥臂环流中的50 Hz分量来识别桥臂电抗器两相短路故障,且具有足够的识别精度。图 6中50Hz_TR信号由0变为1表示桥臂环流中的50 Hz分量在超过保护定值250 A并达到延迟时间后的动作信号,其动作后将出口闭锁换流器。此外,从图 6中还可以看到BC相间短路故障发生后,B相桥臂环流izb, C相桥臂环流izc中的100 Hz分量izb_100Hz与izc_100Hz并没有明显增加,最多只增加了40 A,因而100Hz_TR信号并未变1,与前述理论分析一致,即桥臂电抗器相间短路故障并不会改变环流的主要成分二倍频分量的大小。
由图 7可见,在桥臂电抗器BC相间短路故障发生后,直流电流中的50 Hz分量IDN_50Hz开始增大,但增加的不是太显著,最大值只达到100 A,而100 Hz分量IDN_100Hz则变化很小基本没有太大改变,与前文理论分析一致,直流电流中的50 Hz及100 Hz分量的故障检测精度不高,可能引起误动,不能有效识别故障位置,只适合作为辅助判据。
4 结语文中针对双极MMC,分析了桥臂电抗器布置在靠近交流连接点和靠近直流连接点2个不同位置对换流器阀侧接地故障电流的影响,研究表明桥臂电抗器布置在靠近直流连接点时能够有效限制故障电流上升率,降低桥臂子模块过电流水平。桥臂电抗器布置在靠近直流连接点后,其穿墙套管发生相间短路故障时现有保护策略并不能及时发现,因此提出一种基于桥臂环流谐波分量识别的桥臂电抗器穿墙套管相间短路故障保护策略,从而有效识别桥臂电抗器穿墙套管相间短路故障,PSCAD/EMTDC仿真结果验证了相关分析的准确性。文中对桥臂电抗器的安装位置及故障特性进行了深入分析,给采用MMC的直流工程提供了参考, 后续可以对MMC主回路参数设计进行更全面深入的研究。
本文得到国网电力科学研究院有限公司科技项目“±800 kV混合级联多端直流输电系统控制保护关键技术及应用研究”(JS1900544)资助,谨此致谢!
| [1] |
赵文强, 宣佳卓, 陆翌, 等. 适用于常规直流改造的混合直流输电系统主电路拓扑研究[J]. 电力自动化设备, 2018, 38(12): 186-193. ZHAO Wenqiang, XUAN Jiazhuo, LU Yi, et al. Research on circuit topology of hybrid HVDC system suitable for refurbishing existing LCC-HVDC[J]. Electric Power Automation Equipment, 2018, 38(12): 186-193. (  0) 0) |
| [2] |
赵成勇, 郭春义, 刘文静. 混合直流输电[M]. 北京: 科学出版社, 2014. ZHAO Chengyong, GUO Chunyi, LIU Wenjing. Hybrid high voltage direct current transmission system[M]. Beijing: Science Press, 2014. (  0) 0) |
| [3] |
赵文强, 高得力, 马云龙, 等. 基于混合式MMC的混合高压直流输电系统启动策略[J]. 电力系统自动化, 2018, 42(7): 62-70. ZHAO Wenqiang, GAO Deli, MA Yunlong, et al. Startup strategy of hybrid HVDC transmission system based on hybrid MMC[J]. Automation of Electric Power Systems, 2018, 42(7): 62-70. (  0) 0) |
| [4] |
王永平, 赵文强, 杨建明, 等. 混合直流输电技术及发展分析[J]. 电力系统自动化, 2017, 41(7): 156-167. WANG Yongping, ZHAO Wenqiang, YANG Jianming, et al. Hybrid high-voltage direct current transmission technology and its development analysis[J]. Automation of Electric Power Systems, 2017, 41(7): 156-167. (  0) 0) |
| [5] |
杨洁, 刘开培, 饶雪, 等. 多端柔性直流输电系统小信号建模[J]. 中国电机工程学报, 2015, 35(16): 4015-4024. YANG Jie, LIU Kaipei, RAO Xue, et al. Small signal modeling for VSC-MTDC[J]. Proceedings of the CSEE, 2015, 35(16): 4015-4024. (  0) 0) |
| [6] |
贺之渊, 刘栋, 庞辉. 柔性直流与直流电网仿真技术研究[J]. 电网技术, 2018, 42(1): 1-12. HE Zhiyuan, LIU Dong, PANG Hui. Research of simulation technologies of VSC-HVDC and DC grids[J]. Power System Technology, 2018, 42(1): 1-12. (  0) 0) |
| [7] |
阳岳希, 杨杰, 贺之渊, 等. 基于MMC的背靠背柔性直流输电系统控制策略[J]. 电力系统自动化, 2017, 41(4): 120-124, 157. YANG Yuexi, YANG Jie, HE Zhiyuan, et al. Control strategy of MMC based back-to-back HVDC transmission system[J]. Automation of Electric Power Systems, 2017, 41(4): 120-124, 157. (  0) 0) |
| [8] |
屠卿瑞, 陈桥平, 李一泉, 等. 柔性直流输电系统桥臂过流保护定值配合方法[J]. 电力系统自动化, 2018, 42(22): 172-177. TU Qingrui, CHEN Qiaoping, LI Yiquan, et al. Coordination method of arm overcurrent protection settings in flexible HVDC transmission system[J]. Automation of Electric Power Systems, 2018, 42(22): 172-177. DOI:10.7500/AEPS20180312001 (  0) 0) |
| [9] |
潘荣贞, 廖其艳, 王健. 闭锁状态下MMC子模块电容充电升压机理及对策[J]. 南方电网技术, 2018, 12(1): 7-13. PAN Rongzhen, LIAO Qiyan, WANG Jian. Boosting mechanism and counter measures of MMC sub-module capacitor charging in blocking state[J]. Southern Power System Technology, 2018, 12(1): 7-13. (  0) 0) |
| [10] |
董旭, 张峻榤, 王枫, 等. 风电经架空柔性直流输电线路并网的交直流故障穿越技术[J]. 电力系统自动化, 2016, 40(18): 48-55. DONG Xu, ZHANG Junjie, WANG Feng, et al. AC and DC fault ride-through technology for wind power integration via VSC-HVDC overhead lines[J]. Automation of Electric Power Systems, 2016, 40(18): 48-55. DOI:10.7500/AEPS20151201001 (  0) 0) |
| [11] |
曹帅, 向往, 姚良忠, 等. 风电经混合型MMC-HVDC并网的交直流故障穿越策略[J]. 电力系统自动化, 2018, 42(7): 37-43, 49. CAO Shuai, XIANG Wang, YAO Liangzhong, et al. AC and DC fault ride-through strategies for wind power integration via hybrid MMC-HVDC[J]. Automation of Electric Power Systems, 2018, 42(7): 37-43, 49. (  0) 0) |
| [12] |
郭贤珊, 李探, 李高望, 等. 张北柔性直流电网换流阀故障穿越策略与保护定值优化[J]. 电力系统自动化, 2018, 42(24): 196-202. GUO Xianshan, LI Tan, LI Gaowang, et al. Fault ride-through strategy and protection setting optimization of converter valve for Zhangbei VSC-HVDC grid[J]. Automation of Electric Power Systems, 2018, 42(24): 196-202. DOI:10.7500/AEPS20180506004 (  0) 0) |
| [13] |
李振动, 安海清, 樊小伟, 等. 双极MMC-HVDC系统站内接地故障特性及保护策略[J]. 电力系统自动化, 2020, 44(5): 77-83. LI Zhendong, AN Haiqing, FAN Xiaowei, et al. Converter ground-ing fault characteristics and protection strategy in bipolar MMC-HVDC system[J]. Automation of Electric Power Systems, 2020, 44(5): 77-83. (  0) 0) |
| [14] |
LI G, LIU W, JOSEPH T, et al. Double-thyristor-based protection for valve-side single-phase-to-ground faults in HB-MMC-based bipolar HVDC systems[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5810-5815. DOI:10.1109/TIE.2019.2931502 (  0) 0) |
| [15] |
薛士敏, 范勃旸, 刘冲, 等. 双极柔性直流输电系统换流站交流三相接地故障分析及保护[J]. 高电压技术, 2019, 45(1): 21-30. XUE Shimin, FAN Boyang, LIU Chong, et al. Fault analysis and protection scheme for converter AC three-phase grounding of bipolar HVDC systems[J]. High Voltage Engineering, 2019, 45(1): 21-30. (  0) 0) |
| [16] |
陈继开, 孙川, 李国庆, 等. 双极MMC-HVDC系统直流故障特性研究[J]. 电工技术学报, 2017, 32(10): 53-60, 68. CHEN Jikai, SUN Chuan, LI Guoqing, et al. Study on characteristics of DC fault in bipolar MMC-HVDC system[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 53-60, 68. (  0) 0) |
| [17] |
徐政, 肖晃庆, 张哲任. 模块化多电平换流器主回路参数设计[J]. 高电压技术, 2015, 41(8): 2514-2527. XU Zheng, XIAO Huangqing, ZHANG Zheren. Design of main circuit parameters of modular multilevel converters[J]. High Voltage Engineering, 2015, 41(8): 2514-2527. (  0) 0) |
| [18] |
朱俊霖, 赵林杰, 杨柳, 等. ±350 kV柔性直流输电用桥臂电抗器温升试验[J]. 南方电网技术, 2016, 10(7): 57-61. ZHU Junlin, ZHAO Linjie, YANG Liu, et al. Temperature rise test of valve bridge arm reactor for ±350 kV VSC-HVDC system[J]. Southern Power System Technology, 2016, 10(7): 57-61. (  0) 0) |
| [19] |
李泓志, 贺之渊, 杨杰, 等. 模块化多电平换流器操作过电压分析[J]. 高电压技术, 2017, 43(4): 1144-1151. LI Hongzhi, HE Zhiyuan, YANG Jie, et al. Switching overvoltage analysis for modular multilevel converters[J]. High Voltage Engineering, 2017, 43(4): 1144-1151. (  0) 0) |
| [20] |
刘杉, 宋胜利, 卢理成, 等. ±800 kV特高压直流穿墙套管故障分析及设计改进[J]. 高电压技术, 2019, 45(9): 2928-2935. LIU Shan, SONG Shengli, LU Licheng, et al. Failure analysis and design improvement of ±800 kV UHVDC wall bushings[J]. High Voltage Engineering, 2019, 45(9): 2928-2935. (  0) 0) |
| [21] |
张施令. ±800 kV"U"型SF6气体绝缘穿墙套管绝缘性能分析[J]. 电瓷避雷器, 2018(3): 134-138. ZHANG Shiling. Analysis on dielectric characteristics of ±800 kV "U" type wall bushing with SF6 gas insulation[J]. Insulators and Surge Arresters, 2018(3): 134-138. (  0) 0) |
| [22] |
张晋寅, 韦晓星, 夏谷林, 等. 南方电网直流穿墙套管运行特性分析[J]. 电瓷避雷器, 2019(4): 230-237. ZHANG Jinyin, WEI Xiaoxing, XIA Gulin, et al. Operating characteristic analysis of DC wall bushings in CSG[J]. Insulators and Surge Arresters, 2019(4): 230-237. (  0) 0) |
| [23] |
宋友, 徐卓林, 兰贞波, 等. 1200 kV特高压交流胶浸纤维穿墙套管技术应用研究[J]. 电瓷避雷器, 2021(2): 41-46. SONG You, XU Zhuolin, LAN Zhenbo, et al. Application of 1200 kV UHV AC resin impregnated fiber wall bushing technology[J]. Insulators and Surge Arresters, 2021(2): 41-46. (  0) 0) |
| [24] |
柴影辉, 钟建英, 谭盛武, 等. 基于有限元分析的特高压直流穿墙套管结构优化设计[J]. 电瓷避雷器, 2021(2): 47-52. CHAI Yinghui, ZHONG Jianying, TAN Shengwu, et al. Structural optimization design of UHVDC wall bushing based on finite element analysis[J]. Insulators and Surge Arresters, 2021(2): 47-52. (  0) 0) |
2. NARI Group (State Grid Electric Power Research Institute) Co., Ltd., Nanjing 211106, China
 2022, Vol. 41
2022, Vol. 41


 赵文强(1985), 男, 硕士, 高级工程师, 从事直流输电控制保护技术及电力电子技术应用相关工作(E-mail:
赵文强(1985), 男, 硕士, 高级工程师, 从事直流输电控制保护技术及电力电子技术应用相关工作(E-mail: