文章编号: 2096-3203(2022)03-0032-07 中图分类号: TM73;TM712
2. 南瑞集团(国网电力科学研究院)有限公司,江苏 南京 211106;
3. 国网河南省电力公司电力科学研究院,河南 郑州 450052
安全稳定控制系统(security and stability control system, SSCS)由通信通道和控制站点组成,主要用于维护电网频率和功角稳定[1-4]。通信通道一般采用光纤通信,长度可达几十、几百甚至上千公里; 控制站点包括多层站点,其中底层站点连接不同类型的控制资源,如水电[5]、抽蓄、可切负荷[6]、储能、高压直流换流站等[7],通过切泵、减载、直流调制等维持电网有功平衡。
SSCS可基于动态数据参数,也可由严重事件直接驱动。低频减载属于前者,启动须等待几个摇摆周期,时间长达数秒。在此过程中可能发生机组停运和大面积停电,恶化电网暂态过程。因此,在电网发生重大事件(如特高压直流受端单极或双极闭锁)时,可立即启动SCCS,快速增加有功出力或减少有功缺额,加快频率恢复过程。
我国能源基地和负荷中心不重叠,有必要采取大容量、远距离交/直流输电[8-10],例如西南到华东、青海到华中、西北到华中直流工程等。这些跨区线路实现分区电网互联,便于共享稳定控制资源,但是需要增加对各分区SSCS的控制层,增加了SSCS结构复杂程度,降低了SSCS通信网络可靠性。
SSCS一般采用树状结构[11-12],一个上层站点控制一个或多个下层站点。其优点是层级清晰,同级站点间相互独立,易于设计和实现控制策略。但若站点或其上游通道故障,下游所有站点和通道将失效。层级越多,上述缺点越明显。为增加可靠性,可在协控总站增加异地备用,但是备用越多,建设和维护成本越高,控制越复杂,误动可能性越大,因此须改进树状SSCS结构以提高其可靠性。
SSCS结构设计需要考虑经济成本、控制复杂性、可靠性等因素。对于SSCS可靠性,现有研究方法包括状态空间[13-15]、故障树[16-17]、蒙特卡洛抽样[18]、复杂网络方法[19-21]等。文献[22]提出互联系统SSCS扁平化概念。扁平化SSCS可靠性评估中,站点间存在双向/环状通道,因此不易确定所有控制路径。SSCS扁平化改造效果可由控制能力量化,控制能力不仅取决于通道可用与否,还取决于底层站点可控容量。同时,扁平化的SSCS中站点、路径间关系更加复杂,不易识别薄弱环节、判断关键元件对SSCS控制能力的影响。
文中在树状SSCS中增加双向/环状通信通道,实现扁平化设计。搜索顶层至底层站点间有向路径,计及元件可用率和可控容量,量化SSCS的控制能力; 定义站点平均控制能力指标和站点平均关联路径数指标,量化扁平化设计效果; 提出SSCS控制能力对站点和通道可用率的灵敏度的解析表达,以确定扁平化SSCS薄弱环节; 通过算例分析验证了所提算法的正确性。
1 SSCS扁平化设计方式 1.1 传统SSCS结构图 1(a)为传统电网SSCS树状结构,其中S,R分别为站点和控制资源。顶层站点S1通过通道连接中间站点,控制6个底层站点站及其资源。当有站点或通道故障时,系统将失去对部分资源的控制。为提升系统控制能力,可适当增加站点或通道。例如,为避免S8和S11故障时失去对R1和R4的控制,增加热备用站点S14和S15,实现对R1和R4的控制以保全系统功能,见图 1(b)。但若S2故障,无论S10是否有备用,R2和R3都将失去控制。图 1(c)增加中间站点备用,可以提高系统控制能力,但是将增加成本、控制复杂程度和误动可能性。

|
图 1 SSCS A的结构 Fig. 1 Configuration of SSCS A |
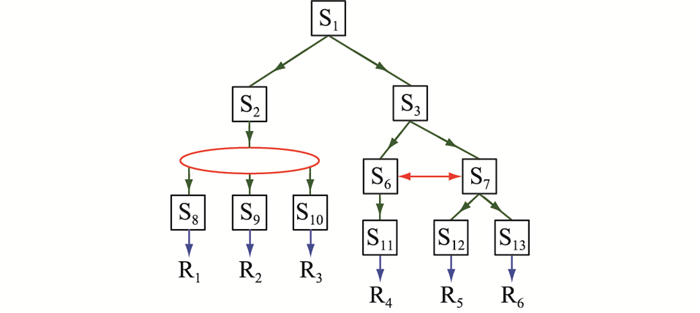
对于图 1(a),图 2给出扁平化设计思路。在中间站点S6和S7间增加横向联系,实现两者相互备用。然后在S2以下,以环网代替第三层站点,此时S2通过环网直接控制S8-S10。扁平化后,站点间路径不唯一,例如S3可直达S6,也可经S7到达S6,从而提升了系统的控制能力。
|
图 2 SSCS A扁平化设计 Fig. 2 Flat design of SSCS A |
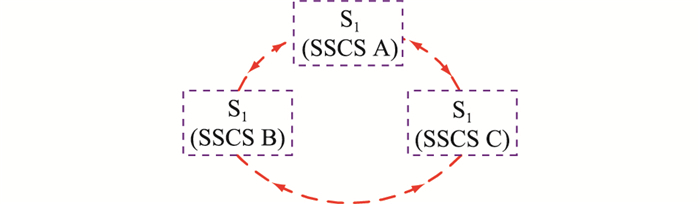
从分区电网互联角度出发,图 3通过环形通信通道将3个SSCS顶层站点联系起来。若一个电网有功需求得不到满足,可以从其他电网获得支援。
|
图 3 3个分区电网SSCS互联 Fig. 3 Integration of SSCS of three regional systems |
实际跨区电网SSCS扁平化设计,还须考虑以下因素:
(1) 跨区电网SSCS设计主要针对有功平衡和频率稳定,很少考虑无功/电压,因为无功很少进行大容量、远距离传输。
(2) 扁平化设计须兼顾站点功能和重要性、通道建设和维护成本等。有些站点位于枢纽变电站、大机组、负荷中心附近,扁平化设计过程中这些站点必须保留。
(3) 扁平化淡化了站点间层级关系,可能会增加控制复杂程度,实际系统不可能也没必要全部采用环网,只要对部分薄弱站点或通道扁平化,因此薄弱环节辨识对扁平化设计非常重要。薄弱环节辨识取决于控制路径可用率和控制容量。
2 SSCS控制路径搜索定义从顶层站点到底层站点的任意通路为控制路径。对树状系统,通过观察可以确定所有路径,如图 1(a)中从S1出发有6条控制路径,分别控制R1-R6; 图 1(b)中有2个底层备用子站,增加2条路径; 而图 1(c)、图 2和图 3中考虑中间站点备用、站点局部扁平化及多个SSCS互联,路径数大幅增加,手动查找容易遗漏,因此建立以下SSCS路径算法。
2.1 邻接矩阵计算从拓扑结构来说,可以视站点为顶点,通道为边,用邻接矩阵D中的元素dij来描述SSCS的连通特性。若站点i有路径指向j,定义dij =1;否则dij =0。将图 2站点重新排序并标记各通道得到图 4,根据图 4结构可得出11阶D矩阵,如式(1)所示。树状结构SSCS的D矩阵只有上三角有非零元素,而扁平化SSCS的D矩阵在下三角也有非零元素。
| $ \boldsymbol{D}=\left[\begin{array}{lllllllllll} 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] $ | (1) |

|
图 4 站点重新编号后的SSCS A Fig. 4 SSCS A with renumbering to stations |
以D矩阵为基础,从每个顶层站点出发,沿着有向路径逐步搜索到底层站点,可得所有控制路径:
(1) 从D矩阵第1行至第11行,依次展开。如果第i行对应顶层站点,记录站点i,从第1列到第11列依次展开; 否则转下一行。
(2) 对第i行第j列,如果dij=0,站点i和j间没有通信通道,分析下一列。如果dij=1且j不是底层站点,记录通道ij和站点j。对第j行从第1列到第11列类似分析djk。如果djk=1且k是底层站点,记录站点k,路径数加1,终止该路径搜索。
(3) 为避免在双向或环状通道中循环,在记录站点和通道时,需要避免搜索路径的重复。
按照上述原则,S1指向S2和S3。S2指向底层站点S6、S7、S8,因此得到3条控制路径,如图 5所示。S3指向S4和S5,S4指向底层站点S9,路径数加1;S4还指向S5,S5指向底层站点S10和S11,路径数加2。由此可得所有控制路径。

|
图 5 控制路径的拓扑搜索 Fig. 5 Topology search to control path |
增加横向联系后,SSCS可能出现环路,这在变电站通信和电网稳定控制系统中都可能存在。文中在建立连接矩阵时,已经避免环路重复搜索。和树状网络一样,环路控制也须明确上下级关系,只是前者上下级关系静态不变而后者动态变化。
3 SSCS控制能力定义和薄弱环节辨识 3.1 SSCS对各控制资源的可控概率控制路径所关联元件成串联关系,因此第n条路径可用率an是各关联元件可用率ak的乘积,如式(2)所示。与树状系统相比,扁平化后同一元件关联不同路径的场景大大增加。
| $ a_{n}=\prod\limits_{k \in n} a_{k} $ | (2) |
路径中关联元件包括站点和通道。假设站点k的可用率为akstation,由式(3)可得路径m可用率ampath。通道可用率akcable与长度呈负相关,其表达式见式(4)。
| $ a_{m}^{\text {path }}=\prod\limits_{k_{1} \in m} a_{k_{1}}^{\text {station }} \prod\limits_{k_{2} \in m}\left(1-l_{k_{2}} u_{0}^{\text {cable }}\right) $ | (3) |
| $ a_{k}^{\text {cable }}=1-l_{k} u_{0}^{\text {cable }} $ | (4) |
式中:k1,k2分别为站点和通道编号; lk为通道k的长度; u0cable为单位长度通道的故障概率; lk2为路径m中通道k2的长度; astationk1为路径m中k1站点的可用率。
实际通道如专用光纤复合架空地线(optical fiber composite overhead ground wire, OPGW)的可靠性包括电气、机械、光学等方面,任一方面性能下降都可能导致通信功能失效。文献[23]采用Weibull函数描述光纤失效概率,但实际光纤可用率受设备材料完好程度、接地方式、沿线地理气候条件(雷击等)、人为因素等影响[24],须结合运行方式和故障类型具体分析,然后代入文中所提模型计算分析。
各控制路径间为并联关系,资源n可控概率An见式(5),其中m为SSCS控制资源n路径的总数。
| $ A_{n}=1-\prod\limits_{i=1}^{m}\left(1-a_{i}^{\text {path }}\right) $ | (5) |
路径可用率越高、可调容量越大,SSCS控制能力越强。因此定义系统对资源n的控制能力Cn为顶层站点对底层站点的可控概率An与其底层站点可控容量Pn的乘积:
| $ C_{n}=A_{n} P_{n} $ | (6) |
Pn与当前运行方式有关。对于高压直流系统,当前载荷越大,可上调出力越小; 对于储能系统,抽蓄电站中抽水机组越少,允许切泵量越少。
SSCS的控制能力为对各资源控制能力之和CSSCS,见式(7),其中M为控制资源总数。
| $ C_{\mathrm{SSCS}}=\sum\limits_{n=1}^{M} C_{n}=\sum\limits_{n}^{M} A_{n} P_{n} $ | (7) |
联立式(4)、式(5)和式(7)可得CSSCS为:
| $ \begin{gathered} C_{\mathrm{SSCS}}=\sum\limits_{n=1}^{M}\left\{1-\prod\limits_{i=1, i \in n}^{m}[1-\right. \\ \left.\left.\prod\limits_{k_{1} \in i} a_{k_{1}}^{\text {station }} \prod\limits_{k_{2} \in i}\left(1-l_{k_{2}} u_{0}^{\text {cable }}\right)\right]\right\} P_{n} \end{gathered} $ | (8) |
扁平化对SSCS的影响是增加了光纤成本和控制路径,提升了控制能力,减少了站点和层级数。为量化扁平化正面效果,定义站点平均控制能力αSSCS为控制能力与站点数量Nstation的比值:
| $ \alpha_{\mathrm{SSCS}}=\frac{C_{\mathrm{SSCS}}}{N_{\text {station }}} $ | (9) |
定义SSCS站点平均关联路径数为βSSCS,表达式见式(10)。路径起止于站点,因此关联元件数Mn必为奇数。
| $ \beta_{\mathrm{SSCS}}=\frac{\sum\limits_{n=1}^{M} \frac{M_{n}+1}{2}}{N_{\text {station }}} $ | (10) |
扁平化增加了确定薄弱环节的难度,可以每次断开一条通道或一个站点,比较断开前、后的CSSCS和αSSCS,但计算量太大。以下提出薄弱站点辨识解析算法。以站点k为例,联立式(4)和式(8),计算CSSCS关于akstation的灵敏度,见式(11)。灵敏度越大,说明该站点停运对系统影响越大,可对其增加检修频率或设备异地备用,或加强扁平化设计。
| $ \begin{gathered} \frac{\partial C_{\mathrm{SSCS}}}{\partial a_{k}^{\text {station }}}=\frac{\partial\left\{\sum\limits_{n=1}^{M}\left[1-\prod\limits_{i=1}^{m}\left(1-a_{i}^{\text {path }}\right)\right] P_{n}\right\}}{\partial a_{k}^{\text {station }}} \\ -\sum\limits_{n=1}^{M} P_{n} \frac{\partial \prod\limits_{k \in N_{i}}\left(1-a_{i}^{\text {path }}\right)}{\partial a_{k}^{\text {station }}} \prod\limits_{k \notin N_{i}}\left(1-a_{i}^{\text {path }}\right)= \\ -\sum\limits_{n=1}^{M} P_{n}\left[\sum\limits_{k \notin N_{i}, i=1}^{x} \frac{-a_{i}^{\text {path }}}{a_{k}^{\text {station }}} \prod\limits_{j \neq i}\left(1-a_{j}^{\text {path }}\right)\right] \times \\ \prod\limits_{k \in N_{i}, i=x+1}^{m}\left(1-a_{i}^{\text {path }}\right) \end{gathered} $ | (11) |
式中:Ni为控制路径i中站点序号集合。
类似可推导系统控制能力对通道可用率的灵敏度。对灵敏度较大的通道,需要降低故障率、减少修复时间,或者加强扁平化设计。
4 算例分析SSCS站点可靠性参数参考文献[25],光纤通道可靠性参数参考文献[26]。分区电网A中,R1可控容量为300 MW,R2可控容量为200 MW,R3可控容量为100 MW,R4可控容量为100 MW,R5可控容量为50 MW,R6可控容量为100 MW。
4.1 不同结构SSCS控制能力计算计算树状结构、底层备用、中间备用和扁平化结构下SSCS对各控制资源的控制能力,见表 1。与传统树状结构和增加站点备用设计方案相比,增加横向通信通道/环状结构实现扁平化可显著提高SSCS控制能力。
|
|
表 1 树状SSCS控制能力 Table 1 Controllability of SSCS with tree structure |
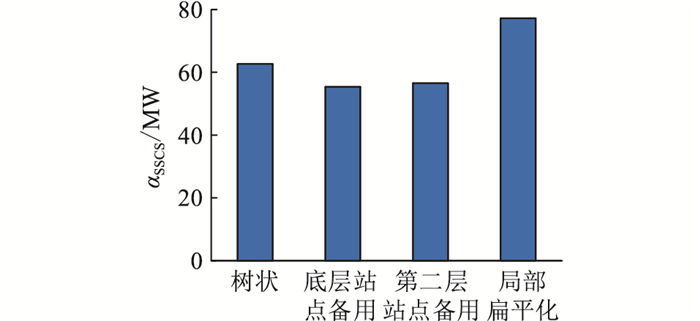
针对电网A,图 6给出不同SSCS结构的平均控制能力。相比于树状结构,增加站点备用会降低系统对站点的平均控制能力。相比于增加底层站点备用,增加第二层站点备用,系统平均控制能力指标提高更加明显。局部扁平化增加了通道,减少了站点层级,从而加强了SSCS控制能力。图 7给出站点平均关联路径数。可以看出,增加备用或局部扁平化都可提高βSSCS以及系统对站点的利用率。
|
图 6 不同结构下分区SSCS的αSSCS Fig. 6 αSSCS of SSCS with different structures |

|
图 7 不同结构下SSCS的βSSCS Fig. 7 βSSCS of SSCS with different structures |
SSCS控制能力对站点可用率的灵敏度见图 8。站点1层级最高,灵敏度也最大。分别分析站点3、5、10,对于同一支路的树状结构,站点层级越高,控制路径越多,故障后果越严重。

|
图 8 CSSCS对akstation的灵敏度 Fig. 8 Sensitivity of CSSCS to akstation |
SSCS控制能力对通道可用率的灵敏度见图 9。通道2控制R4、R5、R6的所有路径且不可替代,因此对SSCS影响最大。通道1和3均控制R1、R2、R3控制资源的所有路径,故两者灵敏度相同。通道4、5、7、9对SSCS控制能力的灵敏度相同,因此重新量化通道4、5、7、9对各控制资源控制能力Ci的灵敏度,见表 3。系统对R4和R6控制能力分别受通道7和9的影响较大。

|
图 9 CSSCS对akcable的灵敏度 Fig. 9 Sensitivity of CSSCS to akcable |
|
|
表 3 Ci对akcable的灵敏度 Table 3 Sensitivity of Ci to akcable |
文中针对电网SSCS扁平化需求,搜索顶层/底层站点间所有路径,量化扁平化SSCS控制能力及评估指标,提出灵敏度模型以确定薄弱环节,得到以下结论:
(1) SSCS控制能力与控制路径的可用率和可控容量有关。路径可用率越高,可控容量越大,系统控制能力越好。可以通过增加可用率或路径以提高系统控制能力。
(2) 增加备用或采用扁平化结构能增加SSCS的控制路径。优先增加层级较高站点备用。相比于增加备用,扁平化设计对提高SSCS控制能力的效果更明显。
(3) 站点或通道所关联的路径越多,路径控制容量越大,站点或通道越薄弱,故障影响越大。在SSCS设计中,应优先考虑这些薄弱元件。
文中SSCS扁平化设计考虑了系统可靠性和控制能力。实际扁平化设计还须考虑控制难度和光纤成本等因素,有待进一步研究。
| [1] |
董希建, 罗剑波, 崔晓丹, 等. 安全稳定控制系统全程控制时间及其构成[J]. 电力系统自动化, 2018, 42(5): 163-168. DONG Xijian, LUO Jianbo, CUI Xiaodan, et al. Whole control time and its constitution of security and stability control system[J]. Automation of Electric Power Systems, 2018, 42(5): 163-168. (  0) 0) |
| [2] |
丁卫东, 张丽全, 许剑冰, 等. 电网安全稳定控制系统标准体系研究评述[J]. 电力工程技术, 2021, 40(1): 58-64. DING Weidong, ZHANG Liquan, XU Jianbing, et al. Review of standard system of power grid security and stability control system[J]. Electric Power Engineering Technology, 2021, 40(1): 58-64. (  0) 0) |
| [3] |
顾卓远, 汤涌, 孙华东, 等. 基于响应的电力系统安全稳定综合防御技术[J]. 中国电机工程学报, 2019, 39(4): 943-953. GU Zhuoyuan, TANG Yong, SUN Huadong, et al. Study on framework of comprehensive defense architecture for power system security and stability[J]. Proceedings of the CSEE, 2019, 39(4): 943-953. (  0) 0) |
| [4] |
王胜明, 徐泰山, 陈刚, 等. 电网安全稳定控制系统当值策略可实施评估方法[J]. 电力系统自动化, 2019, 43(24): 126-133. WANG Shengming, XU Taishan, CHEN Gang, et al. Practicability assessment method of duty strategy for security and stability control system in power grid[J]. Automation of Electric Power Systems, 2019, 43(24): 126-133. DOI:10.7500/AEPS20181122002 (  0) 0) |
| [5] |
周野, 刘福锁, 常海军, 等. 用于频率紧急控制的水电群精准控制策略[J]. 电力系统自动化, 2020, 44(11): 121-126. ZHOU Ye, LIU Fusuo, CHANG Haijun, et al. Accurate control strategies of hydropower group for frequency emergency control[J]. Automation of Electric Power Systems, 2020, 44(11): 121-126. (  0) 0) |
| [6] |
陆崎, 任祖怡, 徐柯, 等. 基于隐枚举法的稳定控制优化切机方法[J]. 电力系统自动化, 2016, 40(5): 139-144. LU Qi, REN Zuyi, XU Ke, et al. Optimal generator tripping scheme based onimplicit enumeration method[J]. Automation of Electric Power Systems, 2016, 40(5): 139-144. (  0) 0) |
| [7] |
李德胜, 罗剑波. 特高压直流配套安全稳定控制系统的典型设计[J]. 电力系统自动化, 2016, 40(14): 151-157. LI Desheng, LUO Jianbo. Typical design of security and stability control system for UHVDC transmission[J]. Automation of Electric Power Systems, 2016, 40(14): 151-157. DOI:10.7500/AEPS20160120010 (  0) 0) |
| [8] |
朱泽翔, 李诗旸, 张建新, 等. 南方电网多直流协调稳定控制系统实现与验证[J]. 南方电网技术, 2020, 14(12): 10-16. ZHU Zexiang, LI Shiyang, ZHANG Jianxin, et al. Implementation and verification of multi-DC coordinated stability control system in China southern powergrid[J]. Southern Power System Technology, 2020, 14(12): 10-16. (  0) 0) |
| [9] |
DONG X J, SING H C, JIA H P, et al. Reliability analysis of security and stability control system with typical structure in power grids[C]//2019 IEEE Power & Energy Society General Meeting. Atlanta, GA, USA. IEEE, 2019: 1-5.
(  0) 0) |
| [10] |
YU W J, XUE Y S, LUO J B, et al. An UHV grid security and stability defense system: considering the risk of power system communication[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 491-500. DOI:10.1109/TSG.2015.2392100 (  0) 0) |
| [11] |
沈凤杰, 张伟, 张浩, 等. 适应调控一体化模式的安控装置管理系统方案设计与实践[J]. 电力系统自动化, 2017, 41(23): 143-149. SHEN Fengjie, ZHANG Wei, ZHANG Hao, et al. Design and practice of management system for safety and stability control devices adapted to integrated mode of power grid dispatching and control[J]. Automation of Electric Power Systems, 2017, 41(23): 143-149. (  0) 0) |
| [12] |
黄天聪, 邓礼力, 薛武, 等. 输变电设备物联网通信网络结构及拓扑分析[J]. 高电压技术, 2015, 41(12): 3922-3928. HUANG Tiancong, DENG Lili, XUE Wu, et al. Communication network structure and topology analysis of Internet of Things for power transmission and transformation equipment[J]. High Voltage Engineering, 2015, 41(12): 3922-3928. (  0) 0) |
| [13] |
郄朝辉, 李威, 崔晓丹, 等. 基于分层马尔可夫的可修复稳定控制系统可靠性分析[J]. 中国电力, 2020, 53(3): 101-109. QIE Zhaohui, LI Wei, CUI Xiaodan, et al. Reliability analysis of repairable stability control system based on hierarchical Markov[J]. Electric Power, 2020, 53(3): 101-109. (  0) 0) |
| [14] |
HE R W, XIE H J, DENG J H, et al. Reliability modeling and assessment of cyber space in cyber-physical power systems[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 3763-3773. (  0) 0) |
| [15] |
BAI G H, LIU T, ZHANG Y N, et al. An improved method for reliability evaluation of two-terminal multistate networks based on state space decomposition[J]. IEEE Transactions on Reliability, 2021, 70(3): 1084-1095. (  0) 0) |
| [16] |
李辉, 邓吉利, 姚然, 等. 计及运行工况的MMC换流阀可靠性建模与分析[J]. 电力自动化设备, 2018, 38(10): 108-114. LI Hui, DENG Jili, YAO Ran, et al. Reliability modeling and analysis of MMC converter valve considering operation conditions[J]. Electric Power Automation Equipment, 2018, 38(10): 108-114. (  0) 0) |
| [17] |
GJORGIEV B, ANTENUCCI A, VOLKANOVSKI A, et al. An FTA method for the unavailability of supply in gas networks supported by physical models[J]. IEEE Transactions on Reliability, 2020, 69(2): 740-753. (  0) 0) |
| [18] |
朱介北, 邱威, 孙宁, 等. 基于序贯蒙特卡洛法的安全稳定控制系统架构可靠性分析[J]. 电力系统自动化, 2021, 45(15): 21-27. ZHU Jiebei, QIU Wei, SUN Ning, et al. Reliability analysis of security and stability control system architecture based on sequential Monte Carlo method[J]. Automation of Electric Power Systems, 2021, 45(15): 21-27. (  0) 0) |
| [19] |
刘涤尘, 冀星沛, 王波, 等. 基于复杂网络理论的电力通信网拓扑脆弱性分析及对策[J]. 电网技术, 2015, 39(12): 3615-3621. LIU Dichen, JI Xingpei, WANG Bo, et al. Topological vulnerability analysis and countermeasures of electrical communication network based on complex network theory[J]. Power System Technology, 2015, 39(12): 3615-3621. (  0) 0) |
| [20] |
刘威, 张东霞, 丁玉成, 等. 基于随机矩阵理论与熵理论的电网薄弱环节辨识方法[J]. 中国电机工程学报, 2017, 37(20): 5893-5901. LIU Wei, ZHANG Dongxia, DING Yucheng, et al. Power grid vulnerability identification methods based on random matrix theory and entropy theory[J]. Proceedings of the CSEE, 2017, 37(20): 5893-5901. (  0) 0) |
| [21] |
刘鑫蕊, 李欣, 孙秋野, 等. 考虑冰灾环境的配电网态势感知和薄弱环节辨识方法[J]. 电网技术, 2019, 43(7): 2243-2252. LIU Xinrui, LI Xin, SUN Qiuye, et al. A new method for situation awareness and weakness identification of distribution network considering ice disaster[J]. Power System Technology, 2019, 43(7): 2243-2252. (  0) 0) |
| [22] |
辛培哲, 闫培丽, 肖智宏, 等. 新一代智能变电站通信网络技术应用研究[J]. 电力建设, 2013, 34(7): 17-23. XIN Peizhe, YAN Peili, XIAO Zhihong, et al. Application of communication network technology in new generation smart substation[J]. Electric Power Construction, 2013, 34(7): 17-23. (  0) 0) |
| [23] |
郭思嘉, 赵振东, 张倩宜. 基于Weibull函数分布的电力通信网光缆失效率模型[J]. 电力系统保护与控制, 2017, 45(17): 92-99. GUO Sijia, ZHAO Zhendong, ZHANG Qianyi. Failure rate model for optical fiber cable in electric power communication network based on Weibull distribution function[J]. Power System Protection and Control, 2017, 45(17): 92-99. (  0) 0) |
| [24] |
王倩, 吴田, 施荣, 等. 750 kV输电线路光纤复合架空地线的接地方式[J]. 高电压技术, 2011, 37(5): 1274-1280. WANG Qian, WU Tian, SHI Rong, et al. Grounding mode of optical fiber composite overhead ground wire of 750 kV[J]. High Voltage Engineering, 2011, 37(5): 1274-1280. (  0) 0) |
| [25] |
颜云松, 孙宁, 张楠, 等. 基于预防检修周期优化的电网稳定控制系统失效风险评估[J]. 电力系统保护与控制, 2021, 49(17): 139-146. YAN Yunsong, SUN Ning, ZHANG Nan, et al. Evaluation of unavailability risk of the security and stability control system of power systems based on optimization of the preventive maintenance period[J]. Power System Protection and Control, 2021, 49(17): 139-146. (  0) 0) |
| [26] |
赵丽莉, 王梦璕, 倪明, 等. 安全稳定控制装置硬件系统可靠性分析[J]. 电力系统保护与控制, 2016, 44(13): 67-73. ZHAO Lili, WANG Mengxun, NI Ming, et al. Analysis of hardware system's reliability of security and stability control device[J]. Power System Protection and Control, 2016, 44(13): 67-73. (  0) 0) |
2. NARI Group (State Grid Electric Power Research Institute) Co., Ltd., Nanjing 211106, China;
3. State Grid Henan Electric Power Company Research Institute, Zhengzhou 450052, China
 2022, Vol. 41
2022, Vol. 41


 李生虎(1974),男,博士,教授,博士生导师,研究方向为电力系统建模与可靠性分析、风电并网电力系统分析与控制、特高压直流和柔性交流输电(E-mail:
李生虎(1974),男,博士,教授,博士生导师,研究方向为电力系统建模与可靠性分析、风电并网电力系统分析与控制、特高压直流和柔性交流输电(E-mail: