文章编号: 2096-3203(2022)03-0194-08 中图分类号: TM715
2. 三峡大学电气与新能源学院,湖北 宜昌 443002
发展清洁能源已成为必然趋势,我国明确提出“十四五”时期将推动能源清洁低碳、安全高效利用。目前,新能源产业正进入加速发展的新阶段,电动汽车(electric vehicle,EV)既为经济增长注入强劲新动能,又有助于实现“碳达峰,碳中和”目标[1-2]。但大规模EV充电负荷接入给电网运行安全性和稳定性带来巨大冲击[3-5],因此降低此负面影响、促进EV与电网互利共赢需要研究大规模EV的分布特性和充电负荷的有效预测[6-7]。
现阶段,国内外学者针对EV在出行链和其充电负荷时空分布预测模型建立上已有一定研究。文献[8]通过对EV自身条件、充电设施和用户习惯的研究,建立EV充电负荷影响因素模型,但未考虑EV在道路中的时空转移对充电负荷的影响。文献[9]基于出行链与原点-终点(origin-destinatin, OD)矩阵确定EV起讫点,并采用跟驰模型对EV在路网中的行程进行微观分析,但忽略了EV行程中的随机性。文献[10]则基于EV出行途中的动态交通信息建立了路段和节点阻抗模型,对其出行行为进行预测,并利用OD矩阵和最短路径算法确定EV出行行程。文献[11]考虑动态EV行驶过程,建立了速度与车流量关系模型和动态路况模型。文献[12]不设定起讫点,通过EV历史出行特点拟合出行概率函数,利用马尔可夫决策过程(Markov decision process,MDP)理论和轮盘赌算法模拟EV出行链,但未考虑动态交通信息对出行链的影响。
EV时空分布预测通常分为2类:一是基于历史真实数据预测未来短期内的EV出行规律[13-14];二是建立EV空间转移模型模拟EV出行路径的选择[15-16]。第二类方法中车主出行选择是影响预测精度的一个重要因素,现有研究大多把重点放在最优出行链中,忽视了车主出行时面临抉择的主观性和随机性[17-18]。此外,EV作为通行工具和负荷载体,其充电行为不仅受汽车性能、电池损耗程度等自身车况因素的影响,还受到天气、温度、交通路况、日期类型[19-22]等出行环境的影响。综上所述,EV时空负荷预测主要存在以下2点问题:一是上述文献对EV时空分布进行建模求解时,缺少对车主出行行为方式及空间动态路况的考虑;二是现有的路况环境模型多是单向对出行链信息输入,而未考虑路段内EV数量变化对交通信息的影响。建立动态出行信息模型有助于提高对EV时空分布位置、到站信息和充电需求的预测精度。
针对上述问题,文中建立一种计及耦合因素的EV充电负荷时空分布预测模型。根据居民出行需求和EV的不同类别构建私家车、出租车和公交车出行模型,并考虑温度、道路等级、拥堵情况,建立EV单位里程能耗模型。为模拟车主在当前动态更新交通信息下的决策行为,将出行模型与动态更新的能耗模型结合,以单次出行时长为依据构建MDP出行链,进而实现对EV出行路径的动态规划、空间位置分布预测和实时电量计算。根据EV时空分布与充电条件获取EV充电负荷接入充电站时刻。以某典型区域为例,对比分析EV及其充电负荷在不同策略、职能区域和出行日情况下的时空分布,验证了所提方法具有一定现实意义与参考价值。
1 EV时空转移模型将EV的出行起讫点根据车主的出行意愿分为5种:回家(H)、工作(W)、购物用餐(SE)、社交休闲(SR)和其他事务(O)。在不同类别节点均设有EV充电站,节点间的空间转移即为EV行驶过程。
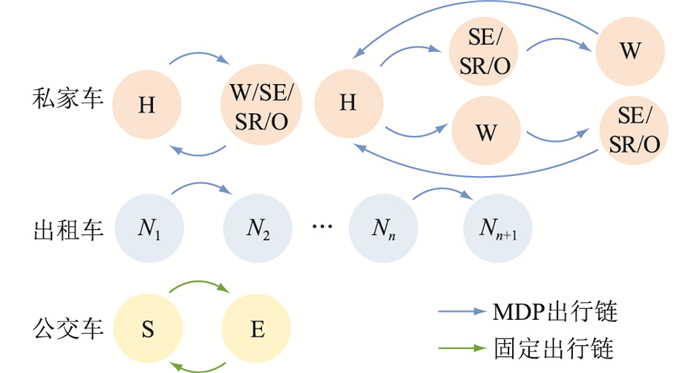
1.1 不同EV出行模型考虑区域内居民日常出行需求,根据EV出行时间、行为方式和充电需求不同,将EV分为私家车、出租车和公交车。针对其不同特点建立3种出行链,如图 1所示,Nn为随机网络节点;S为公交车起始站;E为公交车终点站。
|
图 1 EV出行模型划分 Fig. 1 EV travel model division |
公交车出行模型往返于起讫点之间,如图 1中公交车出行链所示,一般根据当地居民需求规划出行路线并固定出行时间,此处不在赘述。
1.1.1 私家车出行模型私家车出行具有较强的目的性,依据MDP理论考虑车主的出行体验,建立私家车出行模型。
文中采用“H-W”(表示EV从家前往工作地)方式来描述出行链。私家车出行分2类:第一类为单一目标出行链,即图 1中私家车出行链左侧所示的H-W/SE/SR/O-H;第二类为多目标出行链,即图 1私家车出行链右侧所示的H-SE/SR/O-W-H或H-W-SE/SR/O-H。EV出行时刻ts与停留时长tp符合正态分布,其概率密度函数为:
| $ f(t)=\frac{1}{\sqrt{2 \pi} \sigma} \mathrm{e}^{-\frac{(t-\mu)^{2}}{2 \sigma^{2}}} $ | (1) |
式中:μ,σ分别为t时刻的均值和方差。通过调整μ和σ确定不同出行链的ts与tp。
1.1.2 出租车出行模型出租车出行具有极高的随机性,采用轮盘赌算法随机生成其终点,利用MDP理论决定出行路径,如图 1出租车出行链所示。出租车的平均载客时长[23]和平均接客等待时间μtaxi表达式分别为:
| $ T_{\mathrm{taxi}, t}=\sum\limits_{x=1}^{5} q_{x} t^{6-x} $ | (2) |
| $ \mu_{\mathrm{taxi}}=T_{1}-T_{\mathrm{taxi}, t} $ | (3) |
式中:Ttaxi,t为t时刻出租车的平均载客时长;qx为拟合参数;x为自然数;T1为60 min。
假设出租车的停车等待时间与私家车tp一样服从正态分布,可根据式(1)利用蒙特卡洛法抽取EV出租车的接客等待时间。
1.2 基于MDP理论的路径模拟及抉择 1.2.1 EV出行阶段划分采用MDP理论模拟车主对EV出行路径的决策。如图 2所示,将EV出行链分为4个阶段:

|
图 2 EV行驶阶段划分 Fig. 2 EV driving stage division |
(1) 出行准备阶段。根据出行需求获取EV出行目的地。
(2) 行驶阶段。根据温度、道路等级和拥堵情况计算EV耗能。
(3) 决策阶段。根据EV荷电状态(state of charge,SOC)判断是否满足下一段路径行驶的电量需求。若满足需求,则根据剩余行程信息采用MDP理论确定下一段行驶路径;若不满足,则在此站点进行充电。
(4) 目的地。若EV转移至终点,记录自身行驶信息。利用EV历史信息(仅与前一天的行程有关)和SOC阈值判断EV是否有充电需求,如有,则驶入充电站内。
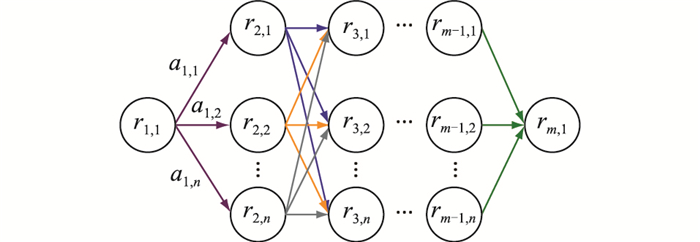
1.2.2 EV出行路径决策EV行驶过程中节点转移如图 3所示,其中rm, n为第m次抉择时选择第n个相邻节点;a为EV可选择出行路径。假设EV从r1, 1出发,在行驶途中每次可转移节点有n个,经过m-2次抉择到达目的地rm, 1。将EV在行驶过程中可能经过的所有路段视为状态集S;EV到达各节点的所有时刻视为决策时刻集T;EV在所有决策时刻做出的路径决策所组成的集合视为行动集A;EV在行驶过程中每段路径的行驶时间视为报酬R。
|
图 3 节点转移示意 Fig. 3 Schematic diagram of node transfer |
EV出行具有马尔可夫性,基于EV行驶过程中车主对剩余行程最短时间与路网拥堵信息的考虑,EV从当前节点rcur转移到下一节点rnex节点的节点间转移概率为P(a|rcur, rnex),如式(4)所示。
| $ P\left(a \mid r^{\text {cur }}, r^{\text {nex }}\right)=\left\{\begin{array}{l} 1 \quad m=n \\ \sum\limits_{m=1}^{M} \sum\limits_{k=1}^{K} \frac{S_{m, k}^{\text {pass }}}{V_{m, k}^{\text {pass }}} / \sum\limits_{n=1}^{N} \sum\limits_{k=1}^{K} \frac{S_{n, k}^{\text {total }}}{V_{n, k}^{\text {total }}} \quad m<n \end{array}\right. $ | (4) |
式中:N为节点rcur转移至终点所有可行方案数目;M为所有可行路径中下一次转移经过节点rnex方案数目;K为当前方案中节点转移经过的节点数目;Sn, ktotal,Sm, kpass分别为在N和M下第k段路径长度;Vn, ktotal,Vm, kpass分别为在N和M下第k段路径EV行驶速度。
由式(4)可得EV在当前节点向所有相邻节点转移的概率,即以剩余行程出行时长为目标,形成一个总概率密度为1的EV节点转移密度函数,然后依据蒙特卡洛法选取EV转移节点。完成转移后,重复上述过程直至EV转移至终点,据此形成MDP出行链。
2 EV充电负荷时空分布预测 2.1 动态路况信息模型EV时空转移过程中,高温和拥堵等外因制约着EV的单位里程能耗和出行速度,间接影响出行时长和车主对出行路径的选择,从而改变EV充电负荷的时空分布。
2.1.1 拥堵模型区域道路会因某时刻车辆数量变化出现不同程度拥堵,而区域EV渗透率不足会使EV数量不能反映道路内车辆实际拥堵情况。为此,文中首先基于基础数据,通过多次模拟确定路段在单位时间内的车流量分布规律,获得历史道路内EV数量,采用蒙特卡洛法随机抽取每一个调度周期内道路j的EV数量Pt, j;其次,假设一定数量阈值内EV速度相同,通过单位距离内的EV数量Nt, jEV确定t时刻道路j的EV出行速度v。在每个调度周期开始时更新各路段EV数量,EV在每次节点转移结束时对出行速度v进行修正,即动态更新v。
| $ N_{t, j}^{\mathrm{EV}}=\left(N_{t, j}^{\mathrm{raa}}+b_{j} P_{t, j}\right) /\left(2 S_{\mathrm{cur}}\right) $ | (5) |
式中:Scur为当前道路长度;Nt, jEV,Nt, jroa分别为在调度周期开始时t时刻的道路单位距离内和道路内的EV数量;bj为修正参数。
调整修正参数bj可以改变仿真中各路段内的交通流量,在实际应用中可根据真实路况进行取值以模拟由于EV渗透率不足所致的汽车拥堵,文中仿真的所有路段bj取值相同。
2.1.2 EV单位里程能耗模型EV单位里程能耗、道路等级和v之间的关系可表示为[24]:
| $ \left\{\begin{array}{l} E_{\mathrm{fas}}^{\mathrm{raa}}=-0.004 v+0.247+1.520 / v \\ E_{\mathrm{tru}}^{\mathrm{raa}}=0.004 v-0.179+5.492 / v \\ E_{\mathrm{sbaa}}^{\mathrm{raa}}=-0.001 v+0.210+1.531 / v \\ E_{\mathrm{bra}}^{\mathrm{raa}}=-0.002 v+0.208+1.553 / v \end{array}\right. $ | (6) |
式中:Efasroa,Etruroa,Esbraroa,Ebraroa分别为快速路、主干路、次干路和支路的单位里程能耗。
EV能耗会随温度变化而产生非线性的变化,温度单位里程能耗Ectem模拟与温度的关系为[25]:
| $ E_{c}^{\mathrm{tem}}=\sum\limits_{y=1}^{6} p_{y} c^{y-1} $ | (7) |
式中:py为拟合参数;y为自然数;c为当前环境温度。
根据式(7),拟合曲线EV在20 ℃时的单位里程能耗E20tem最小。结合式(6)、式(7),以20 ℃为标准温度,获得EV在温度c下行驶在r等级道路下的单位里程能耗Er, cEV为:
| $ E_{r, c}^{\mathrm{EV}}=E_{r}^{\mathrm{roa}} E_{c}^{\mathrm{tem}} / E_{20}^{\mathrm{tem}} $ | (8) |
式中:Erroa为EV在r等级道路下的单位里程能耗。
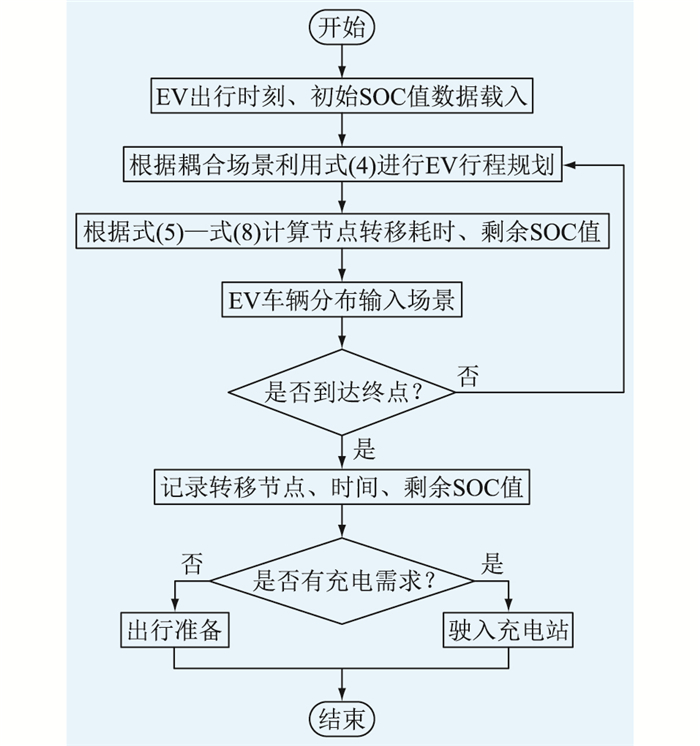
2.2 EV充电负荷预测基于1.1节的EV出行模型和2.1节的路况信息模型,对EV充电负荷时空分布进行计算,其流程如图 4所示。
|
图 4 EV充电负荷计算流程 Fig. 4 Flow chart of EV charging load calculation |
为提高初始信息如历史SOC值、拥堵情况等信息的可靠性,采用经验值进行预仿真,记录所得EV时空分布数据、SOC值并修正经验值。道路内车辆数量随时间不断变化,在EV单次行程中,每次节点转移后的末端时刻更新道路车辆数量,并重新计算下一次节点转移时EV的行驶速度;场景模型中的拥堵情况和温度则在调度周期ΔT开始时刻进行更新。
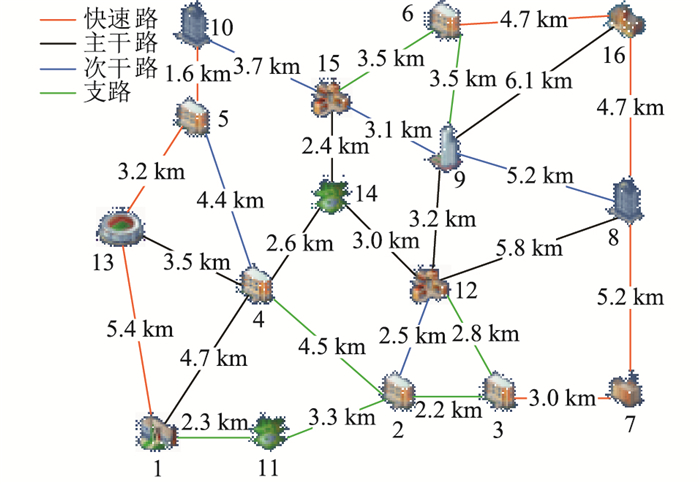
3 算例仿真及分析 3.1 交通网络和EV参数某典型区域的交通拓扑结构如图 5所示。根据区域内生活需求的不同类型对区域进行划分。节点1~6为居民区;节点7~10为工作区;节点11~15提供购物用餐、社交休闲服务,定义为休闲区;节点16为其他,仿真时将其纳入休闲区。各交通节点处均配备充电站,城市道路为双行路。
|
图 5 仿真区域拓扑 Fig. 5 Simulation area topology |
区域内私家车、出租车和公交车分别有2 280辆、500辆和50辆。公交车出行时间、路径较为固定,其充电行为也较为规律,但充电负荷较大,所以文中只对其接入电网负荷进行分析。车主在工作日和非工作日出行需求不同,采用经验值设置起始时各节点内私家车出行目的地,进行预仿真作为历史数据,采用灰度预测累加生成的方式生成区域内不同出行目的地的私家车数量。
配置2种类型的EV,参数见表 1:EV1为小型轿车,用于私家车和出租车出行;EV2为大型公交车。其中,CEV为EV电池容量;PEV为EV在站内的充电功率;Rch为充电效率;Sexp为充电期望SOC值;Smin为最低SOC阈值。仿真调度时段为24 h,拟合参数与调度周期如表 2所示。
|
|
表 1 EV配置参数 Table 1 EV configuration parameters |
|
|
表 2 拟合参数与调度周期 Table 2 Fitting parameters and scheduling time |
假设EV满足如下条件之一时即在当前站点充电:
(1) 完成整个行程时SOC值小于充电阈值0.2;
(2) 行驶中SOC值低于Smin或不足以使其转移至下一节点;
(3) EV到达终点时剩余SOC值小于该EV单次行程所消耗的SOC值。
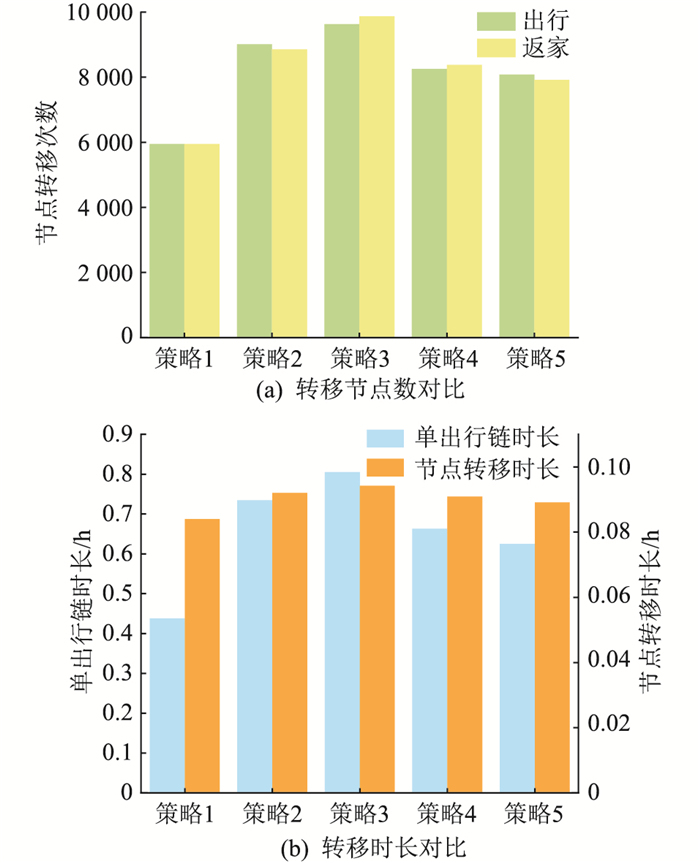
3.2 出行策略对比为体现采用动态信息的MDP出行链的优势性,另设3种典型传统策略和一种无EV与交通信息交互的策略进行对比。策略1:采用最短路径法;策略2:采用蒙特卡洛法的出行链[26];策略3:采用文献[6]的MDP出行链;策略4:采用文中MDP出行链但无动态交通信息;策略5:文中MDP出行链含动态交通信息输入。图 6为不同出行策略的对比结果。
|
图 6 不同出行策略对比 Fig. 6 Comparison of different travel strategies |
将图 6中的策略1、2、3与策略4,策略5与策略4分别进行对比,可以看出:
策略1采用的最短路径法没有考虑到自身车辆聚集会导致道路拥堵,因此EV在行程规划中只会作出同一种抉择。策略1的单出行链出行时长较策略4低33.87%,但其出行路径抉择方式不符合EV出行具有随机性的特点。
策略2考虑了出行时长,采用蒙特卡洛法抽取出行行程,其所预测出的单出行链时长较策略4高9.80%。策略2获取出行行程的方式是根据已有行程信息确定整个出行链,因此其概率密度函数的准确性取决于历史数据的可靠性。EV的出行具有马尔可夫性,策略4利用MDP理论在每个节点根据当前位置、目的地、路网信息重新规划下一行程,能更有效地获取EV出行链。
策略3的节点转移次数、单出行链时长较策略4分别要高17.23%和21.53%,这是由于策略3所采用的出行链与文中MDP出行链计算报酬R的方式不同,与文中通过式(4)计算所得相邻节点的转移概率函数也不同。策略3转移概率侧重于体现车主根据当前位置对相邻最短路径的选择;而策略4转移概率侧重于体现车主对总出行时长最短的需求,更符合车主的一般出行需求,能得到更有效的数据,实现对EV时空分布的预测。
策略5相较策略4节点转移次数降低3.80%,单出行链时长和节点转移时长分别降低了5.65%和1.98%。这是由于建立动态信息可以不断更新2.1.1节的拥堵模型,使EV在路网中的分布能通过式(5)影响EV在道路内行驶的速度,进而改变出行链中各节点转移概率,有助于车主根据当前时刻前行道路的拥堵情况抉择出下一行驶路径,验证了动态交通信息能带给车主更短出行时长的行驶体验。
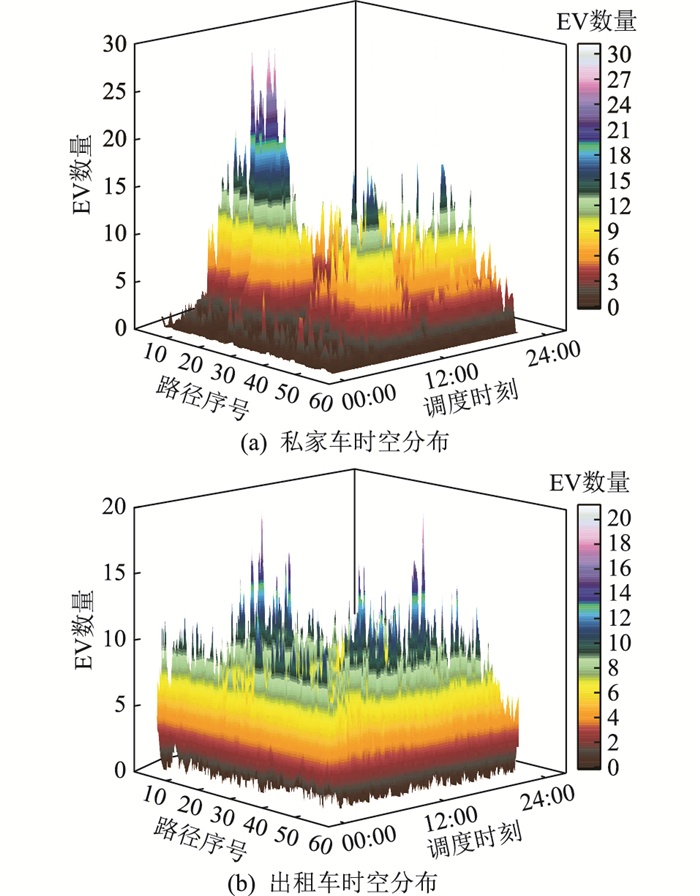
3.3 EV数量的时空分布以典型工作日为例,道路内EV时空分布如图 7所示。
|
图 7 EV时空分布 Fig. 7 Temporal and spatial distribution of EV |
对于私家车,早高峰和晚高峰分别出现在时段07:30-08:30和18:00-19:00;在路径序号9(节点3-节点7)、15(节点4-节点14)、46(节点14-节点12)和路径序号22(节点7-节点3)、33(节点10-节点5)、45(节点14-节点4)道路分别出现明显的早高峰和晚高峰。由于私家车早上出行的时间较为密集,其停留时间分布较为分散,造成早高峰和晚高峰的时刻中前者峰值较为明显,后者则高峰持续时间较长。部分道路由于处于区域中心位置,会同时出现早高峰与晚高峰,如路径序号41(节点12-节点14)和路径序号46。对于出租车,其出行地点与等待时间随机性较大,整体会呈现均匀分布。但在路径序号15和46等区域中心道路,出租车日分布数量略高于其他道路。这是由于EV进行路径抉择时依据总行程时长进行行程规划转移,导致EV在快速路与区域中心路径易出现集群现象,造成交通拥堵。
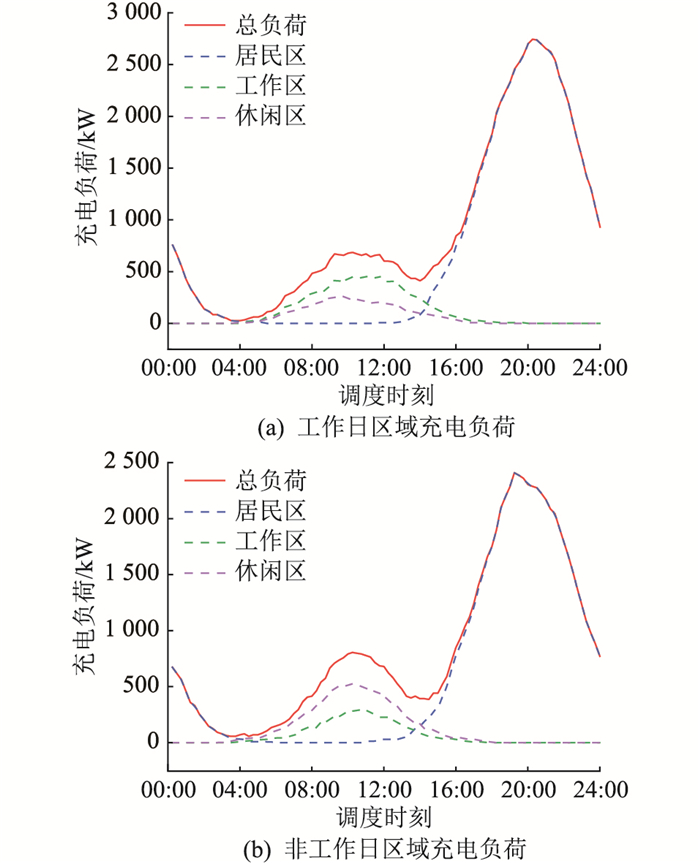
3.4 充电负荷时空分布 3.4.1 工作日与非工作日私家车充电负荷对比图 8为工作日与非工作日的私家车充电负荷曲线。对比可见,在工作日工作区的私家车充电负荷大于休闲区,非工作日则相反。由于车主在工作日与非工作日具有不同的出行需求,造成了分布上的差异,同时表明上述模型具有适用性,能根据区域内车主出行习惯计算得到在不同出行日下的EV充电负荷曲线。另外,私家车的充电行为多集中在返回居民区,且晚高峰EV充电需求较大,这是由于车主下班时间较为固定且集中。根据3.1节中充电条件(1),车主在完成一天行程返家后,SOC值低于0.2时,EV有充电需求,因此在居民区充电的EV数量大于其他区域。由图 8可知,工作日居民区充电负荷峰值比非工作日高13.95%,峰值时刻滞后至20:00。
|
图 8 充电负荷分析 Fig. 8 Charging load analysis |
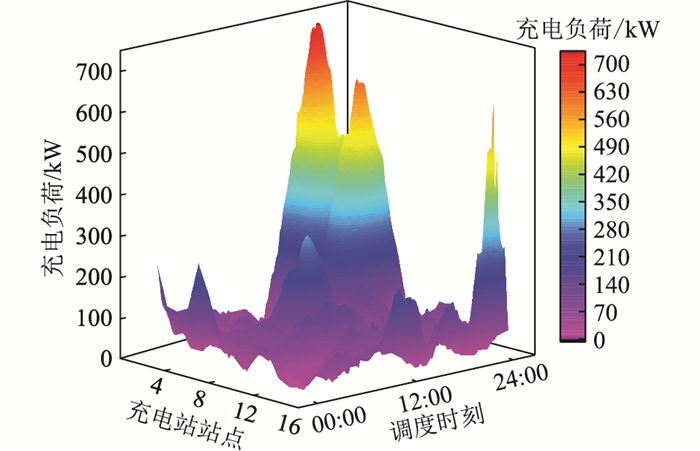
充电站依据EV到站时间作为优先级评判标准,对EV进行充电服务。图 9为工作日总充电负荷的时空分布图。结合图 8,由于私家车返程使充电负荷分布集中在节点1~6(居民区)和18:00-22:00时段,峰值735 kW出现在21:00时刻。根据1.1节中的公交车出行链设置节点16为公交车起始点和返程终点,并使公交车充电聚集在节点16。由于其往返时间相差不大,该节点充电负荷集中在20:00-24:00时段,峰值出现在22:00时刻,达到642 kW。充电负荷符合现实生活中EV充电负荷分布的规律。
|
图 9 区域总充电负荷时空分布 Fig. 9 Temporal and spatial distribution of regional total charging load |
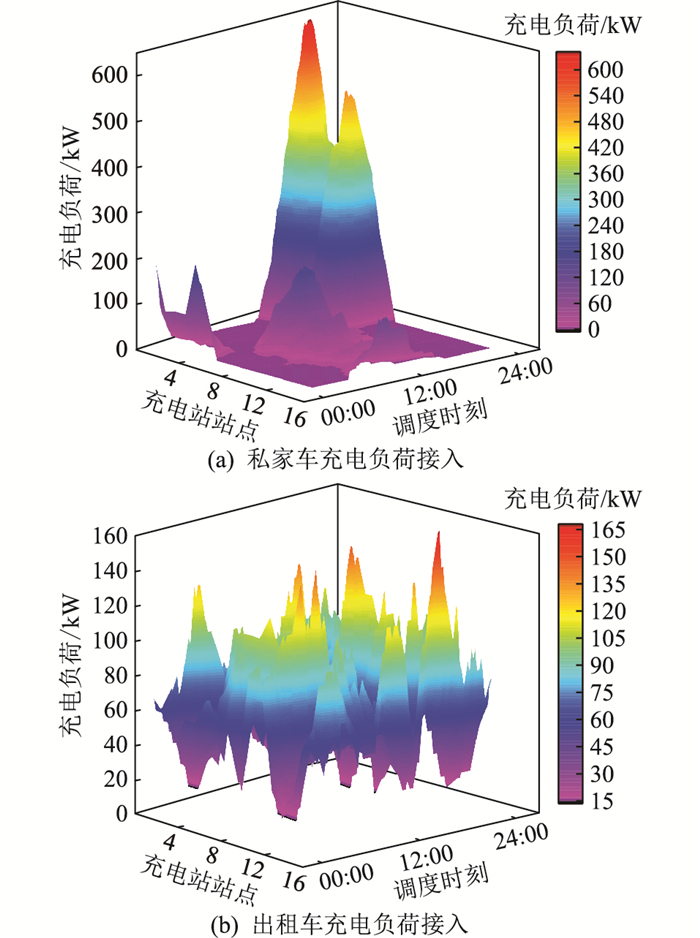
由于公交车的充电负荷集中在公交站点,文中只对私家车和出租车的充电行为进行分析。图 10为私家车和出租车的充电负荷时空分布。
|
图 10 EV充电负荷时空分布 Fig. 10 Temporal and spatial distribution of EV charging load |
由图 10中可以看出私家车充电行为多选择在上班时的工作区与返家后的居民区,最大负荷峰值高达644 kW,如不进行有序充、放电会给电网带来巨大压力。而出租车的充电行为则根据车主有充电需求时所处位置,具有很大的随机性。出租车在区域中心道路和快速路的两端节点如节点9、11、16进行充电行为的概率大于偏远节点,这是由于出租车以出行总时长为依据进行路径规划转移,经过位于仿真区域中心位置道路的概率较大,易在道路两端就近充电。
4 结论EV充电负荷时空分布受其自身转移随机性影响,难以准确获取每一辆EV进站充电信息。文中根据出行特性与车辆类别建立私家车、出租车和公交车3种出行模型。考虑对EV充电负荷分布影响较大的因素,即温度、行驶路况、拥堵情况,建立EV单位里程能耗模型,并引入MDP理论动态规划EV出行路径,从而更准确有效地得到区域内EV时空分布和充电负荷接入充电站数据。通过仿真对比得出以下结论:
(1) 计及多耦合因素的动态规划出行路径相比其他随机策略能减少单出行链时长,能真实反映车主在面临实时交通情况时调整自身出行的策略。
(2) 相比传统方法的出行链,文中出行链基于总出行时长确定节点间转移概率,能更合理地得到车主在每个道路节点的抉择概率。
(3) 不同出行日下不同区域充电负荷预测结果与实际情况相符,验证了文中所提出的方法可以满足不同场景下的负荷预测,具有普适性。
文中计及耦合因素的EV充电负荷时空分布预测能为后续研究中的充电站选址定容与EV有序充放电提供数据支撑,以便充分利用EV闲置资源缓解电网负荷压力,实现削峰填谷。
| [1] |
蔡黎, 张权文, 代妮娜, 等. 规模化电动汽车接入主动配电网研究进展综述[J]. 智慧电力, 2021, 49(6): 75-82. CAI Li, ZHANG Quanwen, DAI Nina, et al. Review on research progress of large-scale electric vehicle access to active distribution network[J]. Smart Power, 2021, 49(6): 75-82. DOI:10.3969/j.issn.1673-7598.2021.06.012 (  0) 0) |
| [2] |
CHENG S, WEI Z B, ZHAO Z K. Decentralized scheduling optimization for charging-storage station considering multiple spatial-temporal transfer factors of electric vehicles[J]. International Journal of Energy Research, 2021, 45(5): 6800-6815. DOI:10.1002/er.6272 (  0) 0) |
| [3] |
FOTOUHI Z, HASHEMI M R, NARIMANI H, et al. A general model for EV drivers' charging behavior[J]. IEEE Transactions on Vehicular Technology, 2019, 68(8): 7368-7382. DOI:10.1109/TVT.2019.2923260 (  0) 0) |
| [4] |
程杉, 陈梓铭, 徐康仪, 等. 基于合作博弈与动态分时电价的电动汽车有序充放电方法[J]. 电力系统保护与控制, 2020, 48(21): 15-21. CHENG Shan, CHEN Ziming, XU Kangyi, et al. An orderly charging and discharging method for electric vehicles based on a cooperative game and dynamic time-of-use price[J]. Power System Protection and Control, 2020, 48(21): 15-21. (  0) 0) |
| [5] |
贺瑜环, 杨秀媛, 陈麒宇, 等. 电动汽车智能充放电控制与应用综述[J]. 发电技术, 2021, 42(2): 180-192. HE Yuhuan, YANG Xiuyuan, CHEN Qiyu, et al. Review of intelligent charging and discharging control and application of electric vehicles[J]. Power Generation Technology, 2021, 42(2): 180-192. (  0) 0) |
| [6] |
程杉, 魏昭彬, 赵子凯, 等. 考虑电动汽车时空接入随机性的充储电站有序充放电分散式优化[J]. 电力自动化设备, 2021, 41(6): 28-35, 44, 36. CHENG Shan, WEI Zhaobin, ZHAO Zikai, et al. Decentralized optimization of ordered charging and discharging for charging-storage station considering spatial-temporal access randomness of electric vehicles[J]. Electric Power Automation Equipment, 2021, 41(6): 28-35, 44, 36. (  0) 0) |
| [7] |
严雪颖, 秦川, 鞠平, 等. 负荷功率模型的最优特征选择研究[J]. 电力工程技术, 2021, 40(3): 84-91. YAN Xueying, QIN Chuan, JU Ping, et al. Optimal feature selection of load power models[J]. Electric Power Engineering Technology, 2021, 40(3): 84-91. (  0) 0) |
| [8] |
王浩林, 张勇军, 毛海鹏. 基于时刻充电概率的电动汽车充电负荷预测方法[J]. 电力自动化设备, 2019, 39(3): 207-213. WANG Haolin, ZHANG Yongjun, MAO Haipeng. Charging load forecasting method based on instantaneous charging probability for electric vehicles[J]. Electric Power Automation Equipment, 2019, 39(3): 207-213. (  0) 0) |
| [9] |
龙雪梅, 杨军, 吴赋章, 等. 考虑路网-电网交互和用户心理的电动汽车充电负荷预测[J]. 电力系统自动化, 2020, 44(14): 86-93. LONG Xuemei, YANG Jun, WU Fuzhang, et al. Prediction of electric vehicle charging load considering interaction between road network and power grid and user's psychology[J]. Automation of Electric Power Systems, 2020, 44(14): 86-93. (  0) 0) |
| [10] |
李晓辉, 李磊, 刘伟东, 等. 基于动态交通信息的电动汽车充电负荷时空分布预测[J]. 电力系统保护与控制, 2020, 48(1): 117-125. LI Xiaohui, LI Lei, LIU Weidong, et al. Spatial-temporal distribution prediction of charging load for electric vehicles based on dynamic traffic information[J]. Power System Protection and Control, 2020, 48(1): 117-125. (  0) 0) |
| [11] |
宋雨浓, 林舜江, 唐智强, 等. 基于动态车流的电动汽车充电负荷时空分布概率建模[J]. 电力系统自动化, 2020, 44(23): 47-56. SONG Yunong, LIN Shunjiang, TANG Zhiqiang, et al. Spatial-temporal distribution probabilistic modeling of electric vehicle charging load based on dynamic traffic flow[J]. Automation of Electric Power Systems, 2020, 44(23): 47-56. (  0) 0) |
| [12] |
田梦瑶, 汤波, 杨秀, 等. 综合考虑充电需求和配电网接纳能力的电动汽车充电站规划[J]. 电网技术, 2021, 45(2): 498-509. TIAN Mengyao, TANG Bo, YANG Xiu, et al. Planning of electric vehicle charging stations considering charging demands and acceptance capacity of distribution network[J]. Power System Technology, 2021, 45(2): 498-509. (  0) 0) |
| [13] |
郭创新, 刘洞宇, 朱承治, 等. 电动汽车居民区充电负荷建模分析[J]. 电力自动化设备, 2020, 40(1): 1-9. GUO Chuangxin, LIU Dongyu, ZHU Chengzhi, et al. Modeling and analysis of electric vehicle charging load in residential area[J]. Electric Power Automation Equipment, 2020, 40(1): 1-9. (  0) 0) |
| [14] |
席乐, 张琳娟, 秦楠, 等. 峰平谷电价下动态修正充电目标的EV充电负荷预测[J]. 电力系统及其自动化学报, 2020, 32(8): 62-69. XI Le, ZHANG Linjuan, QIN Nan, et al. EV charging load prediction with dynamically modified charging target under peak-flat-valley electricity price[J]. Proceedings of the CSU-EPSA, 2020, 32(8): 62-69. (  0) 0) |
| [15] |
杨洪明, 李明, 文福拴, 等. 利用实时交通信息感知的电动汽车路径选择和充电导航策略[J]. 电力系统自动化, 2017, 41(11): 106-113. YANG Hongming, LI Ming, WEN Fushuan, et al. Route selection and charging navigation strategy for electric vehicles employing real-time traffic information perception[J]. Automation of Electric Power Systems, 2017, 41(11): 106-113. DOI:10.7500/AEPS20160821005 (  0) 0) |
| [16] |
陈丽丹, 张尧, Antonio Figueiredo. 融合多源信息的电动汽车充电负荷预测及其对配电网的影响[J]. 电力自动化设备, 2018, 38(12): 1-10. CHEN Lidan, ZHANG Yao, FIGUEIREDO A. Charging load forecasting of electric vehicles based on multi-source information fusion and its influence on distribution network[J]. Electric Power Automation Equipment, 2018, 38(12): 1-10. (  0) 0) |
| [17] |
UL-HAQ A, AZHAR M, MAHMOUD Y, et al. Probabilistic modeling of electric vehicle charging pattern associated with residential load for voltage unbalance assessment[J]. Energies, 2017, 10(9): 1351. DOI:10.3390/en10091351 (  0) 0) |
| [18] |
CAO Y, WANG T, KAIWARTYA O, et al. An EV charging management system concerning drivers' trip duration and mobility uncertainty[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(4): 596-607. DOI:10.1109/TSMC.2016.2613600 (  0) 0) |
| [19] |
SCHÄUBLE J, KASCHUB T, ENSSLEN A, et al. Generating electric vehicle load profiles from empirical data of three EV fleets in southwest Germany[J]. Journal of Cleaner Production, 2017, 150: 253-266. DOI:10.1016/j.jclepro.2017.02.150 (  0) 0) |
| [20] |
王海玲, 张美霞, 杨秀. 基于气温影响的电动汽车充电需求预测[J]. 电测与仪表, 2017, 54(23): 123-128. WANG Hailing, ZHANG Meixia, YANG Xiu. Electric vehicle charging demand forecasting based on influence of weather and temperature[J]. Electrical Measurement & Instrumentation, 2017, 54(23): 123-128. DOI:10.3969/j.issn.1001-1390.2017.23.020 (  0) 0) |
| [21] |
于海洋, 张路, 任毅龙. 基于出行链的电动汽车充电行为影响因素分析[J]. 北京航空航天大学学报, 2019, 45(9): 1732-1740. YU Haiyang, ZHANG Lu, REN Yilong. Influential factors analysis of electric vehicle charging behavior based on trip chain[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(9): 1732-1740. (  0) 0) |
| [22] |
张琳娟, 许长清, 王利利, 等. 基于OD矩阵的电动汽车充电负荷时空分布预测[J]. 电力系统保护与控制, 2021, 49(20): 82-91. ZHANG Linjuan, XU Changqing, WANG Lili, et al. OD matrix based spatiotemporal distribution of EV charging load prediction[J]. Power System Protection and Control, 2021, 49(20): 82-91. (  0) 0) |
| [23] |
李艳红, 袁振洲, 谢海红, 等. 基于出租车OD数据的出租车出行特征分析[J]. 交通运输系统工程与信息, 2007, 7(5): 85-89. LI Yanhong, YUAN Zhenzhou, XIE Haihong, et al. Analysis on trips characteristics of taxi in Suzhou based on OD data[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(5): 85-89. DOI:10.3969/j.issn.1009-6744.2007.05.015 (  0) 0) |
| [24] |
XING Q, CHEN Z, ZHANG Z Q, et al. Charging demand forecasting model for electric vehicles based on online ride-hailing trip data[J]. IEEE Access, 2019, 7: 137390-137409. DOI:10.1109/ACCESS.2019.2940597 (  0) 0) |
| [25] |
YUKSEL T, MICHALEK J J. Effects of regional temperature on electric vehicle efficiency, range, and emissions in the United States[J]. Environmental Science & Technology, 2015, 49(6): 3974-3980. (  0) 0) |
| [26] |
温剑锋, 陶顺, 肖湘宁, 等. 基于出行链随机模拟的电动汽车充电需求分析[J]. 电网技术, 2015, 39(6): 1477-1484. WEN Jianfeng, TAO Shun, XIAO Xiangning, et al. Analysis on charging demand of EV based on stochastic simulation of trip chain[J]. Power System Technology, 2015, 39(6): 1477-1484. (  0) 0) |
2. College of Electrical Engineering and New Energy, China Three Gorges University, Yichang 443002, China
 2022, Vol. 41
2022, Vol. 41


 程杉(1981), 男, 博士,教授,博士生导师, 研究方向为分布式能源与微电网、综合能源系统、智能配用电等(E-mail:
程杉(1981), 男, 博士,教授,博士生导师, 研究方向为分布式能源与微电网、综合能源系统、智能配用电等(E-mail: