文章编号: 2096-3203(2022)03-0178-08 中图分类号: TM855
2. 国网上海市电力公司, 上海 200437
高压套管作为输变电工程的核心部件,在高压输电稳定运行过程中扮演重要角色,一旦发生绝缘故障,将造成巨大的直接和间接经济损失。高压套管的主要绝缘结构可分为油浸纸电容式结构和胶浸纸(resin impregnated paper,RIP)电容式结构2种。油浸纸电容式套管结构相对成熟,但近年来因其自身材料导致的绝缘事故频频发生,漏油、爆炸和燃烧的风险不可避免[1]。因此由皱纹纸和铝箔交替卷制,在真空条件下干燥再经环氧树脂浇注、固化后形成的干式套管,即RIP套管逐渐成为换流变阀侧套管和穿墙套管的主流绝缘结构[2-5]。尽管套管在安装前会进行干燥,但在长期运行过程中,芯体吸收的潮气难以除去,而水分会危害绝缘结构稳定运行,对RIP套管的运行安全和使用寿命造成严重影响[6]。
如何有效评估高压套管绝缘状况长期以来备受关注。以介电响应理论为基础的诊断方法,作为一种新型的绝缘状态无损诊断方法,近年来被广泛应用于高压套管绝缘性能检测,其测试方法主要有3种,包括时域的回复电压测量(recovery voltage measurement,RVM)[7]、极化/去极化电流(polarization and depolarization current,PDC)测量[8]以及频域介电谱(frequency-domain dielectric spectroscopy,FDS)测量[9]。由于RVM法受现场的干扰较大,已逐渐被淘汰。FDS测量法携带信息丰富、测量频带宽、抗干扰能力强,但相比于PDC法,其测量时间较长,且当含水量较低时评估误差较大[10-11]。目前国外已开发出商用的PDC测量设备,如奥地利OMICRON公司生产的介电响应分析仪DIRANA、ALF Engineering公司生产的PDC-Analyser-1MOD,因此文中尝试将PDC测量技术应用于RIP绝缘含水量的定量评估。
为解释受潮PDC测试结果,目前主要技术路线有:(1) 不同含水量的PDC曲线之间相互对比,获得变化趋势,定性得到受潮状态;(2) 根据实际情况建立绝缘等效模型,如经典德拜弛豫模型,通过模型参数变化分析绝缘状态;(3) 提取PDC曲线特征参数,构建特征参数与受潮特征量之间的拟合关系,从而实现绝缘状态评估。
文中研究了基于PDC法的RIP绝缘受潮状态评估方法,在实验室条件下搭建了PDC测试平台,测量不同含水量的RIP绝缘样片PDC曲线,分析PDC图谱的变化规律;建立扩展德拜模型,利用Matlab仿真拟合获得了扩展德拜模型各分支参数及拟合曲线,并提取用于含水量定量评估的特征参量。该研究成果为RIP绝缘的受潮状态评估提供了数据参考和技术支撑。
1 试验方法及理论基础 1.1 试验方法文中主要从理论角度探索受潮状态对RIP绝缘性能的影响,为排除受潮均匀度对结果的干扰,仅考虑均匀受潮的情况。文中试验采用的试品是从工程用RIP套管电容芯体上切割打磨加工成的7 cm×8 cm×1 mm样片。为制备不同含水量的RIP绝缘样片,试验开始前须对样片进行干燥处理,将样片放入水分测定仪内,在100 ℃环境下干燥至重量不再减少,获得样片初始重量m0。该水分测定仪同时具备加热和称重功能,其加热源为高效卤素灯,可使样片均匀受热,加热温度范围为50~180 ℃,重量测量的分辨率为0.001 g。之后将样片浸没水中2 h,取出自然晾干并称重,重量为m,再进行不同程度的干燥处理得到不同含水量的样品。样片的含水量为:
| $ w_{\mathrm{mc}}=\frac{m-m_{0}}{m_{0}} \times 100 \% $ | (1) |
一般认为含水量小于0.5%为完全干燥[12-13],文中试验制备的样片含水量为0.88%~2.03%,该范围可囊括工程中的范围。在实验室中搭建如图 1所示的PDC测试平台,将样片放入三电极测量系统中并夹紧,保护电极可有效消除边缘效应以及沿面泄漏电流对PDC测量结果的影响,该三电极结构则放置于金属容器内。PDC测量采用奥地利OMICRON公司开发的DIRANA介电响应分析仪,该设备可提供最高200 V的直流电压,电流测量范围为±20 mA,测量精度为0.5%测量值±1 pA。

|
图 1 PDC测试平台 Fig. 1 PDC test platform |
PDC测量需持续很长时间才能使所有的极化物质达到松弛状态[14],DIRANA用户指南中指出5 000~7 000 s的极化持续时间足以评估电力设备的绝缘状态,同样的时间也建议用于去极化持续时间。因此试验设置200 V的恒定激励电压源,极化和去极化时间均设置为5 000 s。较长时间暴露在空气中的RIP绝缘样片很容易二次受潮而影响介电性能,为保证试验过程中样片状态的稳定性,试验中将测试所用的三电极结构连同金属容器放置于温湿度控制箱内,测量引线引至温湿度控制箱外部与PDC测量设备相连。为减小环境温湿度对试验结果的影响,对RIP绝缘样片进行的所有测试均保持温度为20 ℃、湿度为30%。PDC测量前后各测一次质量,取平均值作为样片的m值。为防止样片内部杂散电流和残存电荷对测试结果产生影响,每次PDC测量前都将其静置24 h保证充分放电。
1.2 PDC测量原理PDC测量简化图如图 2(a)所示,图 2(b)为阶跃充电电压U0作用下的典型波形图,其中Tp为极化持续时间,即极化电流测量的最大时间;Td为去极化持续时间。PDC测量法通过在样片两端施加和撤去直流电压,测量阶跃电压作用下的充电电流和松弛状态下的放电电流来诊断样片的绝缘状态。

|
图 2 PDC测量原理 Fig. 2 Principle of PDC measurement |
在Tp时间段内,由于样片的导电性和各种极化过程将产生极化电流ipol,当t=t1时撤掉激励电压,并将样片两端短暂短接,去除表面电荷的干扰,此时样片内部会产生去极化现象,产生去极化电流idepol,可表示为[15]:
| $ i_{\mathrm{pol}}(t)=C_{0} U_{0}\left(\sigma_{0} / \varepsilon_{0}+f(t)\right) $ | (2) |
| $ i_{\text {depol }}(t)=-C_{0} U_{0}\left(f(t)-f\left(t+T_{\mathrm{P}}\right)\right) $ | (3) |
式中:C0为几何电容;ε0为真空介电常数,为8.852×10-12 F/m;σ0为样片直流电导率;f(t)为介电响应函数。若充电时间足够长,f(t+TP)≈0,去极化电流可简化为:
| $ i_{\text {depol }}(t)=-C_{0} U_{0} f(t) $ | (4) |
文献[16]指出可根据测量时间最大时的极化电流和去极化电流,利用式(2)-式(4)计算直流电导率σ0。
| $ \sigma_{0}=\frac{\varepsilon_{0}}{C_{0} U_{0}}\left(i_{\mathrm{pol}}\left(T_{\mathrm{p}}\right)-i_{\text {depol }}\left(T_{\mathrm{p}}\right)\right) $ | (5) |
通过对绝缘系统建模解谱分析,可以更好地理解RIP绝缘的介电响应。去极化电流包括出现在RIP绝缘内不同位置的各种弛豫机制的总和。RIP绝缘样片中,每个极性基团的构型都不同,在施加电场后的响应时间也不同,极化过程可用一个耗能元件R和一个储能元件C串联的支路模拟[17]。因此RIP绝缘结构可用一系列电阻和电容串、并联的R-C电路模型表示,即扩展德拜模型,如图 3所示,其满足τi=RiCi的时间常数规律。除极化电流外,在电场作用下绝缘层还流动传导电流,其由图 3中的绝缘电阻R0引起。

|
图 3 扩展德拜模型 Fig. 3 Extended Debye model |
根据PDC法的实际测量值求解模型参数,C0可由传统的工频电容测量技术确定,R0由最大时间Tp的极化电流和去极化电流之差计算得出。其他参数可通过拟合去极化电流确定,见式(6)-式(8)。
| $ i_{\mathrm{depol}}(t)=\sum\limits_{i=1}^{n} A_{i} \mathrm{e}^{-t / \tau_{i}} $ | (6) |
| $ i_{\mathrm{pol}}(t)=\frac{U_{0}}{R_{0}}+\sum\limits_{i=1}^{n} U_{0} \frac{\mathrm{e}^{-t / \tau_{i}}}{R_{i}} $ | (7) |
| $ A_{i}=U_{0} \frac{1-\mathrm{e}^{-T_{\mathrm{p}} / \tau_{i}}}{R_{i}} $ | (8) |
式中:Ri,Ci,Ai,τi分别为第i条支路的电阻、电容、弛豫贡献系数、时间常数。推导可得Ri,Ci分别为:
| $ R_{i}=\left(1-\mathrm{e}^{-T_{\mathrm{p}} / \tau_{i}}\right) U_{0} / A_{i} $ | (9) |
| $ C_{i}=\tau_{i} / R_{i} $ | (10) |
对于电路模型的求解,微分解析法[18-20]虽然避免了计算模型参数不唯一的问题,但微分过程的物理意义难以解释,且数学计算的工作量和误差均较大;末端点解析法[21-22]虽然避免了大量的数学计算,但由于去极化电流噪声较大,取某一点计算会对求解结果的误差影响过大。因此文中注重拟合优度,选择智能优化算法[23-24]进行解谱分析。
由于文中构建的等效模型是非线性非凸问题,传统的数学优化算法,如最小二乘法拟合精度不够、拟合效果较差,将不再适用。遗传算法(genetic alogrithm, GA)属于进化类算法[25],对初值依赖性较低,可以在全局范围内进行搜索,具有一定的跳出局部最优的能力,但求解结果具有一定的随机性。内点法求解速度快,得到的优化结果稳定性高,但对初值依赖较高,在求解非线性非凸问题时,不同的初值对求解结果影响较大,容易陷入局部最优。考虑到目标函数,即式(11)中只包含较少的优化变量,因此提出GA与内点法相结合的方式进行求解。利用GA的初值不敏感性和较强的全局搜索能力,先计算一个局部次优解,然后将其作为内点法的初值,执行进一步的迭代优化,得到最终的拟合结果。
| $ \min \sum\limits_{i=1}^{n}\left|i_{\text {depol }}^{\text {measure }}(t)-i_{\text {depol }}^{\text {fitting }}(t)\right| $ | (11) |
式中:idepolmeasure(t),idepolfitting(t)分别为去极化电流的实测值和拟合值。
最后引入拟合优度R2对整体拟合效果进行评价,其定义为:
| $ R^{2}=1-\sum\limits_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2} / \sum\limits_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2} $ | (12) |
式中:yi为实测数据;
由于RIP绝缘的高电阻性,去极化电流通常在非常小的范围内还会受到感应交流电流、电磁干扰和附近高压静电装置静电感应的影响。采用德拜模型可以对现场测量的PDC噪声进行去噪,拟合得出光滑的电流曲线,这也是后期相关参数准确计算的基础。
2 受潮时域试验结果及分析 2.1 受潮状态对PDC的影响样片不同含水量的PDC实测结果见图 4,为便于比较,试验将去极化电流值的极性改为正值。显而易见,RIP绝缘样片受潮状态对PDC曲线有较大影响。

|
图 4 RIP绝缘样片不同含水量的PDC Fig. 4 PDC of RIP insulation samples with different moisture contents |
由图 4(a)可知,极化初期,由于电荷的注入及较快的迁移速率,极化电流值较大,该部分为吸收电流;随极化时间增加,极化电流波形逐渐趋于平稳,此阶段为介质极化弛豫过程。整体来看,随着RIP绝缘样片含水量的增加,极化电流ipol逐渐增大,随时间衰减的幅度也发生显著变化。绝缘样片中的水分迁移会对其电导率产生较大影响,含水量增加提高了RIP绝缘的直流电导率,增加了极化强度,导致极化电流曲线上升。
由图 4(b)可知,去极化电流idepol随含水量的增加逐渐增大,去极化曲线的衰减时间常数也增大。去极化电流与绝缘样片内部带电粒子的极化密切相关[14]。水作为一种强极性分子,其相对介电常数较高,含水量增加将促使RIP绝缘样片在外加极化电压下产生的束缚电荷越多,样片内部的电荷密度增大,因此去极化电流增大。在去极化过程中去极化电流衰减越来越慢,导致其衰减到0的时间也越久。同时水分子能与RIP绝缘样片中的一些亲水性的离子或基团结合,使其更容易偏离平衡位置,极化强度和响应速度增加,因此去极化电流增大。
文献[14]指出当极化时间足够长(一般大于3 000 s)时,对于线性电介质材料,其电导电流等于极化电流与去极化电流之差。图 5为RIP绝缘样片不同含水量的电导电流。可以看出,随着含水量的增加,电导电流变大,样片的电导率明显增大。电导电流曲线与极化电流曲线几乎一致,尤其在曲线后期,其主要原因为测试后期大部分极化过程已经衰减完,极化电流主要由电导电流组成[18]。

|
图 5 RIP绝缘样片不同含水量的电导电流 Fig. 5 Conductivity currents of RIP insulation samples with different moisture contents |
由图 4(a)可知,极化电流的衰减快慢同RIP绝缘样片含水量具有较为一致的对应关系,此即电流吸收现象。绝缘电阻和吸收比均为反映绝缘性能的基本指标,工程上主要通过测量这2个指标来判断受潮情况。绝缘电阻定义为加压60 s后测得的电阻值,即:
| $ R_{60}=U_{0} / i_{\mathrm{pol}}(60) $ | (13) |
吸收比Ka定义为绝缘电阻与加压15 s的电阻值之比,即:
| $ K_{\mathrm{a}}=\frac{R_{60}}{R_{15}}=\frac{i_{\mathrm{pol}}(15)}{i_{\mathrm{pol}}(60)} $ | (14) |
极化指数Pi定义为加压600 s的电阻值与60 s的电阻值之比,即:
| $ P_{\mathrm{i}}=\frac{R_{600}}{R_{60}}=\frac{i_{\mathrm{pol}}(60)}{i_{\mathrm{pol}}(600)} $ | (15) |
式中:ipol(15),ipol(60),ipol(600)分别为加压15 s、60 s和600 s的极化电流值。
不同含水量的直流电导率可由式(5)计算得到,对于文中的试验样片,式(5)可等效为:
| $ \sigma_{0}=\frac{d}{S U_{0}}\left(i_{\mathrm{pol}}\left(T_{\mathrm{p}}\right)-i_{\mathrm{depol}}\left(T_{\mathrm{p}}\right)\right) $ | (16) |
式中:d为试验样片厚度;S为高压电极与测量电极间样片面积,即0.0252π m2;U0=200 V;Tp=5 000 s。
表 1给出了上述时域特征参数的计算值,可以看出随着含水量增加,绝缘电阻R60、吸收比Ka、极化指数Pi均逐渐减小,而直流电导率σ0逐渐增加。其原因为当绝缘性能变差时,电流吸收现象不明显,电流随时间下降缓慢。一般认为Ka>1.3表示绝缘合格,Ka < 1.3表示绝缘受潮或存在局部缺陷,可见,当含水量大于1.38%时不再符合RIP套管安全运行标准。该时域特征参数作为反应绝缘性能的基本指标,在一定程度上反映了RIP绝缘样片受潮状态。但与PDC曲线结果相比,其提供的绝缘状态信息较少,尤其在RIP套管内部绝缘结构较复杂时,不能提供全面丰富的绝缘状态信息。
|
|
表 1 RIP绝缘样片不同含水量的时域特征参数 Table 1 Time domain characteristic parameters of RIP insulation samples with different moisture contents |
澳大利亚学者[18]在进行德拜模型参数辨识研究中指出,模型的极化支路数应在6~10条,理论上无法确定通用最优支路数。但考虑到拟合结果的优劣直接反应了与真实微观过程的吻合程度,文中以拟合优度R2作为主要指标确定最优支路数,分别在支路数n∈[6, 10]时对含水量1.78%进行拟合,得到的拟合优度R2与支路数n的关系如图 6所示。当n<9时,拟合优度随支路数的增加而显著增大;n=9或n=10时,拟合优度几乎不变,因此兼顾拟合效果和算法求解复杂度,文中取n=9。

|
图 6 拟合优度与支路数的关系 Fig. 6 Relationship between goodness of fit and the number of branches |
图 7给出了含水量为0.88%时拟合方法解析的结果,拟合参量数值见表 2。对其他含水量的RIP绝缘样片,因篇幅限制,扩展德拜模型拟合参数部分结果见表 3、表 4,不同含水量的去极化电流拟合优度均高于0.99。因此,通过扩展德拜模型拟合可以对实测PDC进行去噪,拟合得出光滑的电流曲线。整体来看,随着时间常数的增加,极化电容Ci逐渐增加,而极化电阻Ri和极化电流弛豫贡献系数Ai没有明显变化规律。最大时间常数分支的Ai(即A9)随含水量增加而变大,Ai的变大反映了去极化电流尾部电流值上升情况。

|
图 7 含水量为0.88%时去极化电流及各分支拟合结果 Fig. 7 Depolarization currents and fitting results of each branch with the moisture content of 0.88% |
|
|
表 2 wmc为0.88%时的扩展德拜模型等效电路参数 Table 2 Equivalent circuit parameters of the extended Debye model when wmc is 0.88% |
|
|
表 3 wmc为1.38%时的扩展德拜模型等效电路参数 Table 3 Equivalent circuit parameters of the extended Debye model when wmc is 1.38% |
|
|
表 4 wmc为1.78%时的扩展德拜模型等效电路参数 Table 4 Equivalent circuit parameters of the extended Debye model when wmc is 1.78% |
最大时间常数分支的Ai与含水量之间的变化规律如图 8所示。由图 8可见,A9与含水量wmc存在拟合效果较好的线性函数关系,函数表达式见式(17),拟合优度为0.967,因此A9可以作为评估受潮状态的特征参量。

|
图 8 最大时间常数分支的Ai与含水量的关系 Fig. 8 Relationship between Ai of maximum time constant branch and moisture contents |
| $ A_{9}=2.318 \times 10^{-11} w_{\mathrm{mc}}-1.756 \times 10^{-11} $ | (17) |
由图 4(b)可以看出,5 000 s去极化电流的幅值对RIP绝缘样片的受潮状态非常敏感,含水量越高,RIP绝缘样片的去极化电流幅值越大。然而,直接利用去极化电流值难以定量分析RIP绝缘的受潮状态,因此文中提出了一种通过计算RIP绝缘去极化电量Qdepol(t)的方法将受潮状态与PDC测量结果联系起来,将其定义为去极化电流idepol(t)对测量时间的积分。
| $ Q_{\text {depol }}(t)=\int_{1}^{t} \sum\limits_{i=1}^{n}\left(A_{i} \mathrm{e}^{-t / \tau_{i}}\right) \mathrm{d} t \quad 1<t \leqslant 5\ 000 $ | (18) |
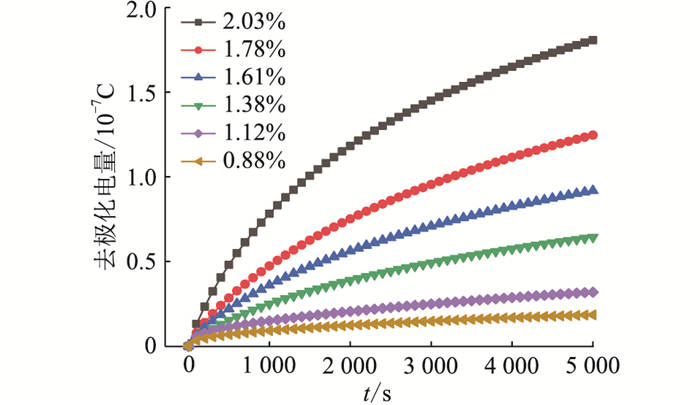
图 9给出了不同含水量下RIP绝缘样片的Qdepol(t)随测试时间的变化,去极化电量与时间呈二次多项式拟合关系,即Qdepol(t)=at2+bt+c,不同含水量的a,b,c参量如表 5所示。
|
图 9 RIP绝缘样片不同含水量的去极化电量 Fig. 9 Depolarization charge quantity of RIP insulation samples with different moisture contents |
|
|
表 5 RIP绝缘样片不同含水量的拟合参数 Table 5 Fitting parameters of RIP insulation samples with different moisture contents |
显而易见,去极化电量随样片含水量的增加而显著增大。文中将极化时间为5 000 s时的Qdepol(t)定义为稳定去极化电量,记为Qd-5000, ,并拟合研究Qd-5000与RIP绝缘样片含水量之间的关系,如图 10所示,得到的拟合方程见式(19)。稳定去极化电量与含水量wmc呈指数函数关系,拟合优度为0.997。因此,Qd-5000可以作为评估RIP绝缘样片受潮状态的特征参量。

|
图 10 稳定去极化电量和含水量的关系 Fig. 10 Relationship between stable depolarization charge quantity and moisture contents |
| $ Q_{\mathrm{d}-5000}=2.755 \times 10^{-8} \times w_{\mathrm{mc}}^{2.625} $ | (19) |
文中通过对不同含水量的RIP绝缘样片进行PDC测量,分析受潮状态对扩展德拜模型的影响,并提取特征参量对RIP绝缘样片的受潮状态进行定量分析,得出以下结论:
(1) 随着含水量的增加,PDC曲线整体向上移动;计算得到的多个时域特征参数(R60, Ka, Pi和σ0)均对含水量变化反应灵敏。绝缘电阻R60、吸收比Ka、极化指数Pi均逐渐减小,而直流电导率σ0逐渐增加。
(2) 构建RIP绝缘等效电路模型是其绝缘状态评估的关键,等效电路参数辨识是该研究的难点。针对原有PDC测量等效模型参数辨识方法的不足,文中创新性地提出了GA与内点法相结合的拟合方法,建立的9支路扩展德拜模型可以较好地拟合RIP绝缘不同松弛极化过程。
(3) 提取了2个受潮状态特征参量,即最大时间常数分支的弛豫贡献系数A9和稳定去极化电量Qd-5000。RIP绝缘的含水量越高,去极化电量越大;A9与含水量同线性函数具有0.967的拟合优度;Qd-5000与含水量同指数函数具有0.997的拟合优度,均可作为评估RIP绝缘样片受潮状态的特征参量。
现场运行过程中,环境温度、介质损耗发热、不均匀受潮和老化等都将对RIP套管的绝缘状态产生很大影响,因此若将PDC测量技术用于RIP套管绝缘的状态评估,还须进一步深入研究。
| [1] |
孔灿, 张大宁, 田杰, 等. 110 kV变压器油纸绝缘套管不均匀绝缘受潮劣化分析[J]. 智慧电力, 2020, 48(4): 119-124. KONG Can, ZHANG Daning, TIAN Jie, et al. Non-uniform moisture degradation analysis of 110 kV transformer oil-paper insulation bushing[J]. Smart Power, 2020, 48(4): 119-124. DOI:10.3969/j.issn.1673-7598.2020.04.018 (  0) 0) |
| [2] |
杜林, 冉鹂蔓, 蔚超, 等. 基于扩展德拜模型的油纸绝缘受潮频域特征量研究[J]. 电工技术学报, 2018, 33(13): 3051-3058. DU Lin, RAN Liman, WEI Chao, et al. Study on frequency domain characteristics of moisture in oil-paper insulation based on extended Debye model[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3051-3058. (  0) 0) |
| [3] |
WANG Y Q, LUO Y, GUAN J, et al. Dielectric properties of epoxy resin impregnated paper insulation in different stages of partial discharge development[J]. Polymer Composites, 2020, 41(1): 360-368. DOI:10.1002/pc.25375 (  0) 0) |
| [4] |
宋友, 徐卓林, 兰贞波, 等. 1 200 kV特高压交流胶浸纤维穿墙套管技术应用研究[J]. 电瓷避雷器, 2021(2): 41-46. SONG You, XU Zhuolin, LAN Zhenbo, et al. Application of 1 200 kV UHV AC resin impregnated fiber wall bushing technology[J]. Insulators and Surge Arresters, 2021(2): 41-46. (  0) 0) |
| [5] |
王黎明, 聂章翔, 赵晨龙, 等. 水分在环氧树脂复合绝缘子护套中的渗透特性[J]. 高电压技术, 2019, 45(1): 173-180. WANG Liming, NIE Zhangxiang, ZHAO Chenlong, et al. Water permeation characteristic in cycloaliphatic epoxy resin composite insulator sheath[J]. High Voltage Engineering, 2019, 45(1): 173-180. (  0) 0) |
| [6] |
ZHANG H L, LIU P, ZHANG X Y, et al. Dielectric spectra of epoxy resin impregnated crepe paper composites in different humidity[C]//2016 IEEE International Conference on High Vol tage Engineering and Application. Chengdu, China. IEEE, 2016: 1-4.
(  0) 0) |
| [7] |
SAHA T K, YAO Z T. Experience with return voltage measurements for assessing insulation conditions in service-aged transformers[J]. IEEE Transactions on Power Delivery, 2003, 18(1): 128-135. DOI:10.1109/TPWRD.2002.803722 (  0) 0) |
| [8] |
GU C, ZHU M Z, ZHU W B, et al. Thermal ageing condition assessment for transformer using natural ester-paper insulation based on polarization and depolarization current[C]//2018 International Conference on Diagnostics in Electrical Engineering (Diagnostika). Pilsen, Czech Republic. IEEE, 2018: 1-4.
(  0) 0) |
| [9] |
VERMA H C, BARAL A, PRADHAN A K, et al. A method to estimate activation energy of power transformer insulation using time domain spectroscopy data[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(5): 3245-3253. DOI:10.1109/TDEI.2017.006640 (  0) 0) |
| [10] |
刘伟, 李洋, 张璐, 等. 不均匀受潮油纸绝缘套管频域介电谱仿真研究[J]. 电力工程技术, 2020, 39(6): 143-150. LIU Wei, LI Yang, ZHANG Lu, et al. Simulation of frequency domain spectroscopy characteristics of oil-paper insulated bush ing under non-uniform moisture content[J]. Electric Power Engineering Technology, 2020, 39(6): 143-150. (  0) 0) |
| [11] |
周凯, 李明志, 饶显杰, 等. 基于极化-去极化电流法的变压器油纸绝缘低频介质损耗特性分析[J]. 高电压技术, 2020, 46(8): 2830-2838. ZHOU Kai, LI Mingzhi, RAO Xianjie, et al. Analysis of low-frequency dielectric loss characteristics of oil-paper insulation based on polarization and depolarization current method[J]. High Voltage Engineering, 2020, 46(8): 2830-2838. (  0) 0) |
| [12] |
MORSALIN S, PHUNG B T. Dielectric response study of service-aged XLPE cable based on polarisation and depolarisation current method[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(1): 58-66. DOI:10.1109/TDEI.2019.008306 (  0) 0) |
| [13] |
吴广宁, 宋臻杰, 杨飞豹, 等. 基于时域介电谱和去极化电量的变压器油纸绝缘老化特征量研究[J]. 高电压技术, 2017, 43(1): 195-202. WU Guangning, SONG Zhenjie, YANG Feibao, et al. Study on aging characteristics of transformer oil-paper insulation based on the time domain dielectric spectroscopy and depolarization charge quantity[J]. High Voltage Engineering, 2017, 43(1): 195-202. (  0) 0) |
| [14] |
SAHA T K, PRADHAN M K, YEW J H. Optimal time selection for the polarisation and depolarisation current measurement for power transformer insulation diagnosis[C]//2007 IEEE Power Engineering Society General Meeting. Tampa, FL, USA. IEEE, 2007: 1-7.
(  0) 0) |
| [15] |
饶显杰, 周凯, 李明志, 等. 基于电力电缆绝缘去极化电流的扩展Debye等效电路参数辨识[J]. 高电压技术, 2020, 46(3): 1037-1043. RAO Xianjie, ZHOU Kai, LI Mingzhi, et al. Parameter identification for extended Debye equivalent circuit based on depolarization current of power cable insulation[J]. High Voltage Engineering, 2020, 46(3): 1037-1043. (  0) 0) |
| [16] |
YANG L J, CHEN J R, WANG S H, et al. Dielectric response measurement of oil-paper insulation based on system identification and its time-frequency-domain conversion method[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(5): 1688-1698. DOI:10.1109/TDEI.2018.007033 (  0) 0) |
| [17] |
MISHRA D, HAQUE N, BARAL A, et al. Assessment of interfacial charge accumulation in oil-paper interface in transformer insulation from polarization-depolarization current measurements[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(3): 1665-1673. DOI:10.1109/TDEI.2017.006525 (  0) 0) |
| [18] |
SAHA T K, PURKAIT P, MULLER F. Deriving an equivalent circuit of transformers insulation for understanding the dielectric response measurements[J]. IEEE Transactions on Power Delivery, 2005, 20(1): 149-157. DOI:10.1109/TPWRD.2004.835436 (  0) 0) |
| [19] |
吴广宁, 夏国强, 宋臻杰, 等. 基于小波分析和时域介电谱的变压器油纸绝缘老化状态评估[J]. 高电压技术, 2018, 44(1): 226-233. WU Guangning, XIA Guoqiang, SONG Zhenjie, et al. Status assessment of aging condition of transformer oil-paper insulation based on time domain dielectric spectroscopy and wavelet analysis[J]. High Voltage Engineering, 2018, 44(1): 226-233. (  0) 0) |
| [20] |
蔡金锭, 祝顺才. 基于灰色聚类-集合赋权法的变压器油纸绝缘状态评估[J]. 高电压技术, 2018, 44(3): 765-771. CAI Jinding, ZHU Shuncai. Evaluation of transformer oil-paper insulation statement based on gray clustering and set weighting methods[J]. High Voltage Engineering, 2018, 44(3): 765-771. (  0) 0) |
| [21] |
张晓燕, 刘庆珍, 蔡金锭. 基于末端双点解析法的变压器油纸绝缘新特征量提取及老化诊断[J]. 高电压技术, 2019, 45(10): 3317-3326. ZHANG Xiaoyan, LIU Qingzhen, CAI Jinding. Extraction of new characteristic parameters and aging diagnosis for transformer oil-paper insulation based on terminal two-point analytical method[J]. High Voltage Engineering, 2019, 45(10): 3317-3326. (  0) 0) |
| [22] |
高竣, 廖瑞金, 王有元, 等. 基于扩展Debye模型的变压器油纸绝缘老化特征量研究[J]. 电工技术学报, 2016, 31(4): 211-217. GAO Jun, LIAO Ruijin, WANG Youyuan, et al. Ageing characteristic quantities of oil-paper insulation for transformers based on extended Debye model[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 211-217. DOI:10.3969/j.issn.1000-6753.2016.04.028 (  0) 0) |
| [23] |
高浩, 刘庆珍, 蔡金锭. 基于去极化电流Prony拟合的油纸绝缘德拜参数辨识方法[J]. 高压电器, 2020, 56(11): 210-218. GAO Hao, LIU Qingzhen, CAI Jinding. Debye parameter identification method of oil-paper insulation based on depolarization current Prony algorithm fitting[J]. High Voltage Apparatus, 2020, 56(11): 210-218. (  0) 0) |
| [24] |
蔡金锭, 曾静岚, 李安娜. 采用I-APSO算法的弛豫响应等效电路参数辨识[J]. 电机与控制学报, 2015, 19(11): 78-83, 97. CAI Jinding, ZENG Jinglan, LI Anna. Parameter identification for equivalent circuit of relaxation response based on interval-active particle swarm optimization algorithm[J]. Electric Machines and Control, 2015, 19(11): 78-83, 97. (  0) 0) |
| [25] |
郑嘉龙. 基于非线性规划遗传算法的并网逆变器LCL滤波器参数优化研究[J]. 电力电容器与无功补偿, 2019, 40(5): 146-150. ZHENG Jialong. Study on parametric optimization of LCL filter of grid-connected inverter based on nonlinear programming genetic algorithm[J]. Power Capacitors & Reactive Power Compensation, 2019, 40(5): 146-150. (  0) 0) |
2. State Grid Shanghai Electric Power Company, Shanghai 200437, China
 2022, Vol. 41
2022, Vol. 41


 张寒(1997), 女, 硕士在读, 研究方向为高压套管在线监测与绝缘诊断技术(E-mail:
张寒(1997), 女, 硕士在读, 研究方向为高压套管在线监测与绝缘诊断技术(E-mail: