文章编号: 2096-3203(2022)03-0055-09 中图分类号: TM464
当电网发生低电压故障时,光伏并网系统的并网逆变器输出能力下降,无法将光伏输出功率完全输送到网侧,由此产生的不平衡功率将对直流母线电容充电,严重时将损坏设备[1-2]。因此,研究和应用低电压穿越(low voltage ride through, LVRT)技术对光伏并网系统的稳定运行具有重要意义[3-5]。
目前国内外学者针对光伏LVRT技术已开展大量研究。文献[6-8]借鉴风电机组的LVRT控制策略[9],在光伏并网系统的直流侧接入卸荷电路,消耗故障期间的不平衡功率,从而实现故障穿越。虽然该方案能有效稳定直流母线电压,但需要额外安装硬件电路以消耗不平衡功率,因此存在功率损失和结构复杂的问题。为最大程度利用电网故障期间的不平衡功率、避免光伏功率损失,文献[10-11]在并网系统接入储能设备以实现电网故障期间系统的功率平衡,稳定直流母线电压。储能设备虽然能储存电网故障期间的不平衡功率,但是其高昂的成本是该方案面临的主要问题。
除接入额外硬件设备实现并网系统LVRT外,针对光伏工作点控制的低成本LVRT控制策略也受到广泛关注。文献[12]通过改进扰动观察法实现直流母线的功率平衡,但其调节时间较长,可能导致母线电压上升。文献[13]为实现更迅速的工作点调整,故障期间根据电压跌落程度线性调节光伏输出电流,以避免逆变器输出过电流。但该方案忽视了光伏工作电流与光伏输出功率间的非线性关系,因此故障穿越过程中仍存在部分不平衡功率,导致故障前后母线电压波动。文献[14]针对系统功率不平衡问题,提出一种基于光伏系统下垂特性的LVRT控制策略,通过引入扰动参数较为准确地估算了低电压故障期间光伏工作点的位置。但实际应用过程中控制参数的选取对估算精度的影响较大,且该策略未考虑不对称故障情况。此外,目前基于光伏工作点控制的LVRT控制策略对于功率削减后光伏输出功率恢复的研究较少,通常采用常规扰动观察法追踪最大功率点,因此故障后光伏输出功率恢复较慢。
文中在上述研究的基础上,提出基于柔性工作点追踪(flexible power point tracking, FPPT)的LVRT控制策略。所提控制策略针对故障期间并网系统的光伏工作点调节问题,分别提出基于FPPT的光伏故障快速减载控制和光伏故障快速恢复控制。为证明所提控制策略的有效性,文中基于Matlab仿真平台和硬件在环(hardware in the loop, HIL)测试系统,针对多种故障类型,将文中所提控制策略与多种并网控制系统进行了对比验证。
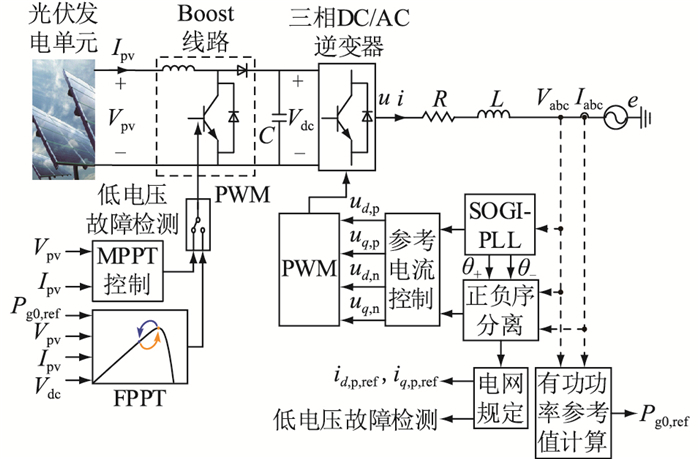
1 基于FPPT的LVRT控制FPPT是一种根据系统运行情况和电网要求将光伏工作点调节到某个参考位置以改善因高比例光伏电源接入电网引起的电压、频率波动问题的控制策略[15]。基于FPPT的LVRT控制策略采用两级式光伏并网系统以实现光伏工作点的灵活调节,如图 1所示。两级式光伏并网系统中,光伏阵列通过Boost电路连接直流母线电容,阵列产生的功率通过并网逆变器输入电网。
|
图 1 两级式光伏并网系统示意 Fig. 1 Schematic diagram of the two-stage photovolatic grid-connected system |
图 1中,MPPT控制为光伏最大功率点追踪控制; PWM为脉冲宽度调制; SOGI-PLL为基于二阶广义积分器的锁相环; Vpv,Ipv分别为光伏工作点电压和电流; C为直流母线电容; Vdc为直流母线电压; e为系统并网点电压; u为逆变器交流侧电压; i为逆变器输出电流; R,L分别为逆变器等值电阻和电感; θ+,θ-分别为并网点电压正序和负序分量相位角; Vabc,Iabc分别为光伏逆变器交流侧电压和电流; Pg0, ref为逆变器输出有功功率平均值的参考值; ud, p,uq, p,ud, n,uq, n分别为逆变器输出电压的正序有功、正序无功、负序有功和负序无功分量; id, p, ref,iq, p, ref分别为逆变器输出电流的正序有功和无功分量参考值。
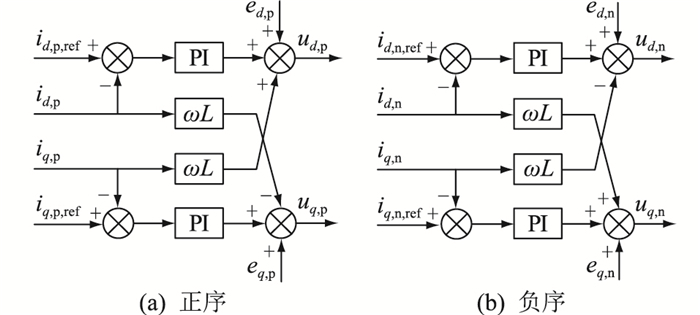
1.1 并网逆变器控制考虑到电网电压不平衡情况,文中并网逆变器采用基于正负序分离的参考电流控制,控制框图如图 2所示。其中,ω为电网电压角频率; PI为比例积分控制; id, p,iq, p,id, n,iq, n分别为逆变器输出电流的正序有功、正序无功、负序有功和负序无功分量; ed, p,eq, p,ed, n,eq, n分别为并网点电压的正序有功、正序无功、负序有功和负序无功分量。
|
图 2 基于正负序分离的逆变器参考电流控制 Fig. 2 Schematic diagram of reference current control of inverter based on separating positive and negative sequence components |
并网系统正常工作情况下,id, p, ref由电压外环控制给出。为保证逆变器以单位功率因数运行,逆变器输出电流的正序无功分量参考值iq, p, ref设定为0。电网低电压故障期间,为满足国家电网公司的LVRT标准[16],最大程度利用逆变器无功输出能力,并网逆变器放弃电压外环控制,根据电网电压跌落程度直接调节逆变器输出电流的正序有功、无功分量参考值id, p, ref,iq, p, ref。其中,逆变器输出电流正序无功分量参考值iq, p, ref根据电网电压跌落程度调节满足:
| $ i_{q, \mathrm{p}, \mathrm{ref}}=\left\{\begin{array}{l} 0 \quad e_{d, \mathrm{p}}>0.9 e_{\mathrm{N}} \\ \frac{K_{1}\left(0.9 e_{\mathrm{N}}-e_{d, \mathrm{p}}\right) I_{\mathrm{N}}}{e_{\mathrm{N}}} \quad 0.2 e_{\mathrm{N}} \leqslant e_{d, \mathrm{p}} \leqslant 0.9 e_{\mathrm{N}} \\ K_{2} I_{\mathrm{N}} \quad e_{d, \mathrm{p}}<0.2 e_{\mathrm{N}} \end{array}\right. $ | (1) |
式中:eN为并网点额定电压; IN为逆变器额定输出电流; K1,K2为常量[16],分别为1.5和1.1。
同时,为防止逆变器电流保护控制[17]断开电网,逆变器输出电流的正序有功分量参考值id, p, ref为:
| $ i_{d, \mathrm{p}, \mathrm{ref}}=\sqrt{\left(K_{2} I_{\mathrm{N}}\right)^{2}-i_{q, \mathrm{p}, \text { ref }}^{2}} $ | (2) |
为抑制电网不平衡故障期间光伏并网逆变器可能输出的负序电流,尽可能减少负序电流对输电线路的危害[18],文中将逆变器输出电流的负序分量参考值id, n, ref和iq, n, ref设定为0。
1.2 故障快速减载控制由于电网低电压故障持续时间很短,暂时忽略光伏发电单元的光照变化和温度变化。在外部环境不变的情况下,光伏发电单元的功率-电压曲线为一个单峰曲线,如图 3所示。其中,Ppv为光伏发电单元输出功率; MPP为光伏最大功率点。

|
图 3 传统光伏减载控制 Fig. 3 Traditional active power curtailment control of photovoltaic |
电网低电压故障期间,光伏系统可以通过将自身出力减载至光伏理想输出功率Pfault,实现并网系统功率平衡。此时存在2个可能的工作点,即A点和B点。虽然工作点向B点调节可以实现更快的响应,但光伏工作点控制在B点可能会因为突然的光照变化而影响系统的稳定运行[19],因此文中选择A点进行减载控制。
传统光伏减载控制通过扰动观察法实现低电压故障期间光伏并网系统的功率平衡,控制原理如图 3中蓝色箭头所示。经过一定时间的工作点扰动,控制策略能够实现光伏减载,但其较长的调节时间仍会导致母线电压上升。
为保证低电压故障期间光伏并网系统的功率平衡,快速稳定直流母线电压,文中提出故障快速减载控制,通过图形近似的方法快速估算近似的减载点工作电压,以此整定故障期间的光伏工作点,实现光伏输出功率快速减载。该策略主要分为2个步骤:(1) 调节光伏工作点至次优工作点,快速减载光伏输出功率,实现并网系统功率的基本平衡; (2) 根据直流母线电压再次调节光伏工作点,稳定直流母线电压。控制过程如图 4所示。

|
图 4 快速减载控制策略 Fig. 4 Rapid active power curtailment control |
并网系统中,逆变器输出瞬时有功功率Pg和瞬时无功功率Qg可分别表示为:
| $ \left\{\begin{array}{l} P_{\mathrm{g}}=P_{\mathrm{g} 0}+P_{\mathrm{c} 2} \cos 2 \omega t+P_{\mathrm{s} 2} \sin 2 \omega t \\ Q_{\mathrm{g}}=Q_{\mathrm{g} 0}+Q_{\mathrm{c} 2} \cos 2 \omega t+Q_{\mathrm{s} 2} \sin 2 \omega t \end{array}\right. $ | (3) |
式中:Pg0,Qg0分别为光伏并网逆变器输出有功功率和无功功率的平均值; Pc2,Ps2,Qc2,Qs2分别为并网逆变器输出功率二倍频分量的有功余弦项、有功正弦项、无功余弦项和无功正弦项的幅值。
其中:
| $ P_{\mathrm{g} 0}=e_{d, \mathrm{p}} i_{d, \mathrm{p}}+e_{q, \mathrm{p}} i_{q, \mathrm{p}}+e_{d, \mathrm{n}} i_{d, \mathrm{n}}+e_{q, \mathrm{n}} i_{q, \mathrm{n}} $ | (4) |
根据式(4),电网低电压故障期间,逆变器输出有功功率平均值的参考值Pg0, ref可以表示为:
| $ P_{\mathrm{g} 0, \mathrm{ref}}=e_{d, \mathrm{p}} i_{d, \mathrm{p}, \mathrm{ref}}+e_{q, \mathrm{p}} i_{q, \mathrm{p}, \mathrm{ref}}+e_{d, \mathrm{n}} i_{d, \mathrm{n}, \mathrm{ref}}+e_{q, \mathrm{n}} i_{q, \mathrm{n}, \mathrm{ref}} $ | (5) |
在忽略逆变器功率损耗等因素的前提下,文中将Pg0, ref作为低电压故障期间光伏输出功率的参考值,即Ppv, ref。
如图 4所示,最大功率点MPP左侧的功率-电压曲线可以近似视为斜率一定的直线L。D点为光伏输出功率参考值Ppv, ref与直线L的交点,C点为D点在光伏功率-电压曲线上的水平投影。将C点设定为低电压故障期间光伏次优工作点,以此实现低电压故障发生后光伏输出功率快速减载。此时,C点的工作电压Vc通过比例关系可以表示为:
| $ V_{\mathrm{c}}=\frac{P_{\mathrm{pv}, \mathrm{ref}}}{P_{\mathrm{mpp}}} V_{\mathrm{mpp}} $ | (6) |
式中:Vmpp为故障发生前光伏最大功率点电压; Pmpp为故障发生前光伏最大功率点功率。
C点为估算得到的光伏次优工作点,为消除相关误差,此时可以根据光伏并网系统直流母线电压的实际值对光伏工作点再次作出调节,以此稳定直流母线电压。此时,光伏工作电压参考值Vref可以表示为:
| $ V_{\mathrm{ref}}= \begin{cases}V_{\mathrm{pv}}+\Delta V \quad V_{\mathrm{dc}}<V_{\mathrm{dc}, \min } \\ V_{\mathrm{pv}}-\Delta V \quad V_{\mathrm{dc}}>V_{\mathrm{dc}, \max } \\ V_{\mathrm{pv}} \quad V_{\mathrm{dc}, \min } \leqslant V_{\mathrm{dc}} \leqslant V_{\mathrm{dc}, \max }\end{cases} $ | (7) |
式中:ΔV为工作电压调节步长; Vdc, max,Vdc, min分别为直流母线电压上、下限参考值。
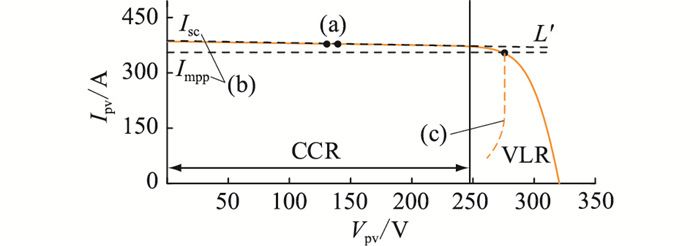
1.3 故障快速恢复控制电网电压恢复后,常规控制系统通过扰动观察法将光伏工作点由减载工作点扰动至最大功率点需一定的调节时间,见图 3中黄色箭头。为减少光伏工作点调节时间,文中提出故障快速恢复控制。该控制采样减载工作点电压电流参数,通过拟合出的曲线估算光伏短路电流,再通过Lambert-W函数推算最大功率点电压。所提方法能实现电压故障恢复后光伏输出功率快速恢复,控制过程见图 5。
|
图 5 故障快速恢复控制 Fig. 5 Fast recovery control for faults |
故障期间文中减载控制将光伏工作点调节至最大功率点左侧,而在光伏电流-电压曲线中,减载控制光伏工作点所在区域为线性恒流区(constant current region, CCR)[20],如图 5所示。由图知,恒流区光伏电流-电压曲线的工作点都可近似拟合为一条斜率一定的直线L′。故障恢复前,采样CCR中一对光伏工作点,如图 5中(a)所示,则直线L′的斜率m可以表示为:
| $ m=\frac{I_{\mathrm{pv}}(k)-I_{\mathrm{pv}}(k-1)}{V_{\mathrm{pv}}(k)-V_{\mathrm{pv}}(k-1)} $ | (8) |
式中:Ipv(k),Vpv(k)分别为当前采样的光伏工作电流、电压值; Ipv(k-1),Vpv(k-1)分别为前一采样周期采样的光伏工作电流、电压值。
直线L′的纵截距(短路电流Isc),如图 5中(b)所示,可以表示为:
| $ I_{\mathrm{sc}}=I_{\mathrm{pv}}(k)-m V_{\mathrm{pv}}(k) $ | (9) |
由于光伏最大功率点MPP处电流Impp与Isc间有近似的线性关系[21],因此Impp可表示为:
| $ I_{\mathrm{mpp}} \approx K_{I_{\mathrm{sc}}} I_{\mathrm{sc}} $ | (10) |
式中:KIsc=0.92。不同太阳辐照度下光伏最大功率点MPP大致位于电压参考线(voltage linear reference, VLR)[22]上,如图 5中(c)所示。由于电网电压恢复速度很快,此时可以忽略电压恢复期间光伏阵列的光照变化。因此,故障恢复后光伏最大功率点电压Vmpp, rcvy可以通过Lambert-W函数估算[23]:
| $ \begin{gathered} R_{\mathrm{mpp}, \text { rcvy }}\\ \eta W\left(I_{\mathrm{mpp}}\left(1+\frac{R_{\mathrm{s}}+\sqrt{R_{\mathrm{p}} R_{\mathrm{s}}+R_{\mathrm{s}}^{2}}}{R_{\mathrm{p}}}\right) / I_{\mathrm{s}}\right)-R_{\mathrm{s}} I_{\mathrm{mpp}} \end{gathered} $ | (11) |
式中:Is为反向饱和电流; Rs,Rp分别为光伏串联电阻和并联电阻; W(·)为Lambert-W函数。
| $ \eta=N_{\mathrm{s}} A K T / q $ | (12) |
式中:Ns为组件串联数; A为光伏二极管理想因子; K为波尔兹曼常数; T为光伏温度; q为基本电荷。
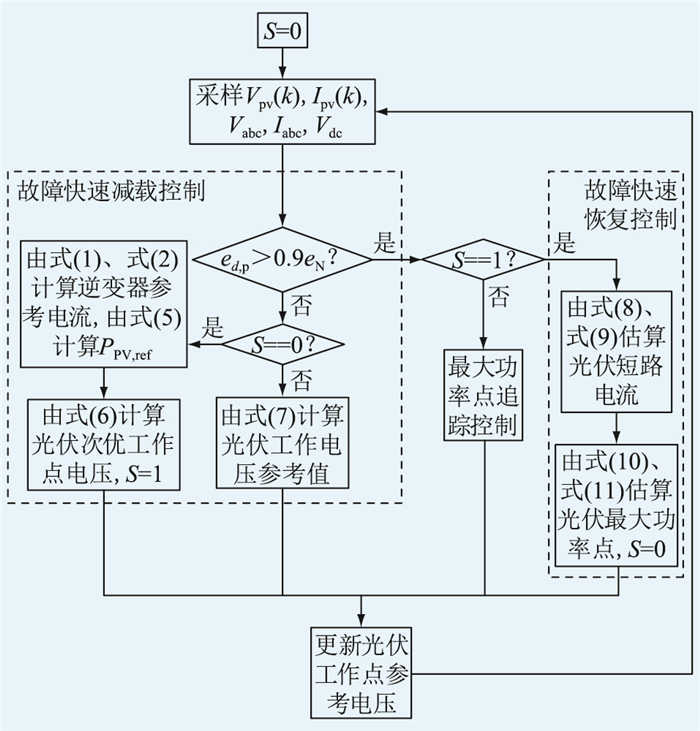
综上,文中提出的基于FPPT的LVRT控制流程如图 6所示。S为信号量,为常数0或1,无实际物理意义。
|
图 6 基于FPPT的LVRT控制策略 Fig. 6 Flow chat of LVRT control strategy based on FPPT |
文中基于Matlab/Simulink仿真平台对光伏并网点三相对称故障、两相相间短路故障和单相短路故障进行仿真研究,验证所提LVRT控制策略的可行性。并网系统容量为100 kW,光伏阵列最大功率点电压为273 V,直流母线电容为35 mF,通过0.38 kV/10 kV变压器并入10 kV电网。并网系统直流母线电压额定值为650 V,母线电压最大值和最小值分别设为750 V和550 V。控制系统中,直流母线上、下限参考值分别设为700 V和650 V。
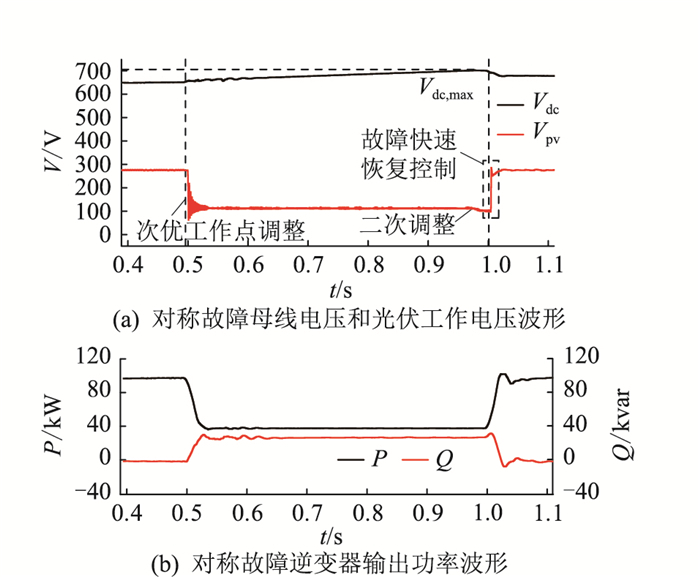
2.1 三相对称故障仿真分析0.5 s时刻,10 kV母线发生三相对称短路故障,光伏并网点电压跌至0.5 p.u.,故障持续时间0.5 s,1 s时刻故障切除,系统恢复正常运行。图 7为基于Matlab的三相对称故障的仿真波形。
|
图 7 基于Matlab的三相对称故障的仿真波形 Fig. 7 Simulation waveforms of three-phase symmetrical fault based on Matlab |
0.5 s时刻控制策略检测到故障后,通过快速减载控制迅速调整光伏工作点至次优工作点,以平衡系统有功功率。当直流母线电压超过控制系统的上限参考值(700 V)时,控制系统对光伏工作点作二次调整。由图 7(a)可知,所提控制策略能较好地通过故障快速减载控制平衡系统有功功率,稳定直流母线电压。1 s时刻故障结束后,控制策略通过故障快速恢复控制迅速将光伏工作电压调整至最大功率点电压。
图 7(b)为故障期间并网逆变器输出有功功率和无功功率曲线,P,Q分别为逆变器输出的有功功率和无功功率。故障期间逆变器输出有功功率下降,但逆变器控制仍能利用逆变器的无功输出能力输出无功功率支持电网恢复。
2.2 三相不对称故障仿真分析电网不对称故障期间,注入电网的电流会出现负序分量。为此,文中逆变器采用基于正负序分离的参考电流控制策略消除负序分量,同时使逆变器输出电流在故障期间保持平衡。
图 8为基于Matlab的三相不对称故障仿真波形。图 8(a)和图 8(b)的并网系统发生两相相间短路故障,光伏并网点b、c相电压在0.5 s时刻从1.0 p.u.跌落到0.5 p.u.,故障持续0.5 s; 图 8(c)和图 8(d)的并网系统发生单相接地故障,光伏并网点c相电压在0.5 s时刻从1.0 p.u.跌落到0.5 p.u.,故障持续0.5 s。其中,Ia,Ib,Ic分别为逆变器a相、b相和c相的输出电流。

|
图 8 基于Matlab的三相不对称故障的仿真波形 Fig. 8 Simulation waveforms of three-phase asymmetric fault based on Matlab |
由图 8(a)和图 8(c)可知,所提控制策略在2种故障期间较好地稳定了并网系统的直流母线电压; 同时,所采用的逆变器控制故障期间输出电流波形保持三相平衡,电流幅值控制较好。逆变器输出电流的正负序分离波形如图 8(b)和图 8(d)所示。故障期间所采用的逆变器控制能够根据电网电压跌落程度不同调节逆变器输出电流的正序无功分量iq, p,从而达到根据电网电压跌落程度输出无功功率的控制目标,同时也能较好地将不对称故障期间的负序电流控制为0。
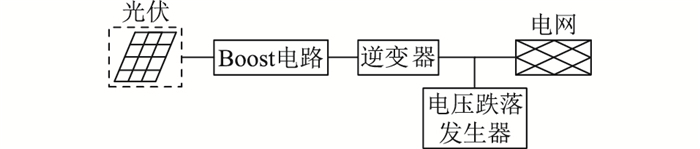
3 实验分析为验证所提光伏并网系统LVRT控制策略的有效性,文中基于HIL测试平台进行验证,如图 9所示。光伏并网系统的主电路模型是在StarSim电力模型实时仿真软件中开发的,在HIL测试系统中运行。信号转接板负责传递仿真器与控制器间的信号,实现仿真器与控制器之间的通信。示波器可对并网系统并网点电压、光伏工作电压、直流母线电压等参数进行观测。主控计算机实现整个平台的操控工作,系统结构如图 10所示。

|
图 9 HIL测试平台示意 Fig. 9 Step of HIL test system |
|
图 10 光伏并网实验系统结构 Fig. 10 Structure of photovoltaic grid-connected experimental system |
假定环境温度和辐照度分别为25 ℃和1 000 W/m2。电网发生故障时,对称故障和不对称故障对并网系统的影响不同,因此文中分别对三相对称故障、两相相间短路故障以及单相接地故障进行实验分析,实验参数如表 1所示。
|
|
表 1 两级式光伏并网系统参数 Table 1 Two-stage photovoatic grid- connected system parameters |
为比较验证LVRT控制策略的有效性和优越性,文中考虑以下4种控制方案。
方案一:常规并网系统无LVRT控制。故障期间光伏发电单元采用MPPT控制,逆变器采用传统比例积分控制。
方案二:基于直流卸荷电路的LVRT控制。光伏发电单元采用MPPT控制,逆变器直流侧并联直流卸荷电路以消耗低电压故障期间的不平衡功率,将直流母线电压稳定在额定值。并网逆变器采用传统比例积分控制。
方案三:基于扰动观察法的LVRT控制。光伏发电单元采用基于扰动观察法的LVRT控制策略以调节故障期间光伏输出功率,并网逆变器采用基于正负序分离的参考电流控制。
方案四:基于FPPT的LVRT控制。光伏发电单元采用文中所提策略,逆变器采用基于正负序分离的参考电流控制。
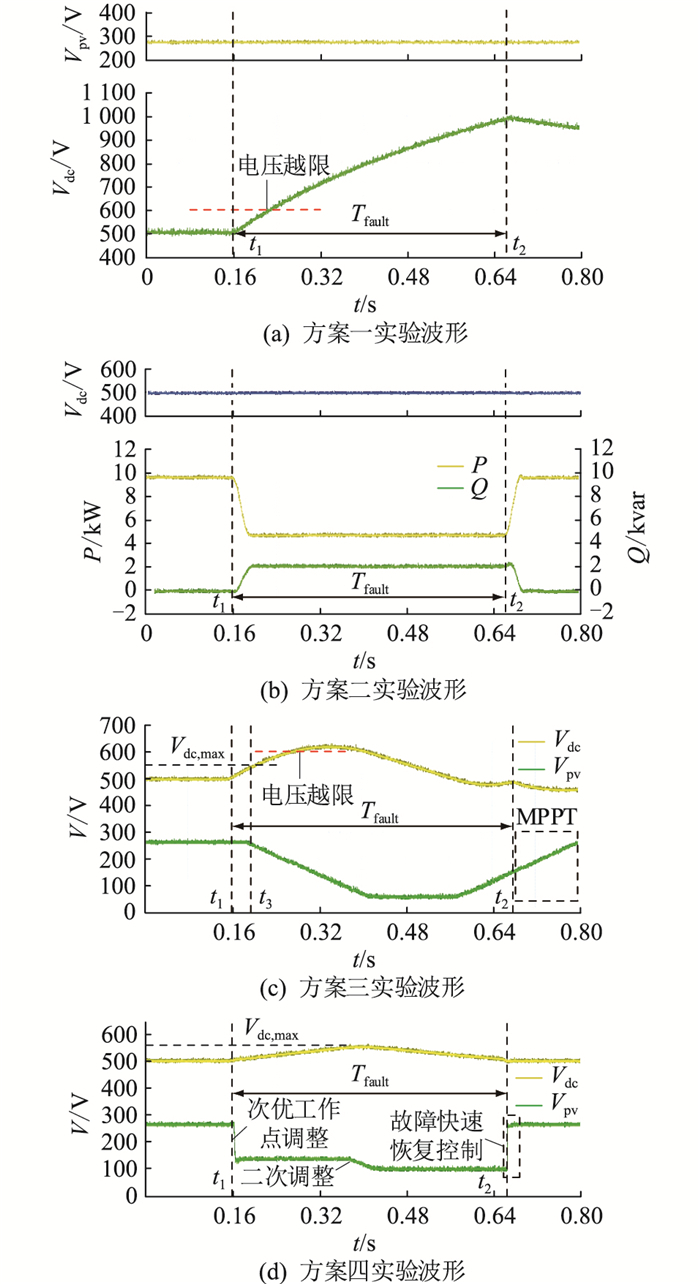
3.1 三相对称故障实验分析三相对称故障时4种控制方案的对比实验波形如图 11所示。故障期间光伏并网点电压在t1时刻跌落到0.5 p.u.,低电压故障持续0.5 s。
|
图 11 三相对称故障对比实验波形 Fig. 11 Waveforms of comparative experiment of symmetrical fault |
电网三相对称故障发生后,方案一由于无LVRT控制,光伏单元仍保持MPPT控制,光伏工作电压保持在263 V附近,如图 11(a)中黄色曲线所示。由于并网点发生低电压故障,逆变器的输出能力下降,并网系统的不平衡功率将对母线电容充电。由图 11(a)中绿色曲线可知,t1时刻故障发生后,直流母线电压Vdc不断上升,由500 V额定值跃升至600 V以上,超过系统的直流母线电压最大值,容易造成设备损坏。t2时刻电网故障恢复后,母线电压才缓慢下降。
由图 11(b)可知,方案二能通过直流卸荷电路消耗低电压故障产生的不平衡功率,将直流母线电压稳定在500 V的额定值; 同时能在故障期间利用逆变器无功输出能力输出无功功率支持电网恢复,实现故障穿越。但由于需要引入额外硬件设备以平衡故障期间的不平衡功率,因此方案二的控制结构复杂且成本较高。
由图 11(c)可知,t3时刻母线电压上升至Vdc, max时,方案三通过扰动观察法降低光伏工作点电压以实现光伏输出功率的减载控制。由于工作点调节时间较长,直流母线电压最终仍超过600 V的电压限值,容易造成设备损坏。t2时刻电网恢复后,控制策略为恢复光伏输出功率,通过扰动观察法追踪光伏最大功率点。截至0.8 s,光伏阵列工作电压还未能稳定控制在Vmpp,因此方案三故障恢复后光伏输出功率恢复较慢。
由图 11(d)可知,t1时刻控制策略检测到低电压故障发生后,通过快速减载控制迅速调整光伏工作点至次优工作点。由于光伏工作点的迅速调整,光伏阵列的输出功率得以快速减载,故障后并网系统功率基本平衡。因此方案四的直流母线电压与方案一、三相比变化平稳。当检测到母线电压Vdc超过Vdc, max时,控制策略通过二次微调光伏工作点进一步稳定电压,防止电压越限。与方案二相比,方案四的直流母线电压在t1~t2故障期间虽稍有波动,但通过所提控制策略能够稳定在系统限定范围内,且由于方案四基于FPPT平衡系统有功功率,不必外接额外硬件设备,故经济性更优。t2时刻电网恢复后,方案四能通过故障快速恢复控制迅速将光伏阵列工作电压调整至最大功率点电压,以此恢复光伏阵列输出功率至故障前水平。与方案三在故障恢复后通过扰动观察法追踪光伏最大功率点相比,方案四能更迅速估算并追踪光伏最大功率点电压,因此光伏输出功率恢复更快。
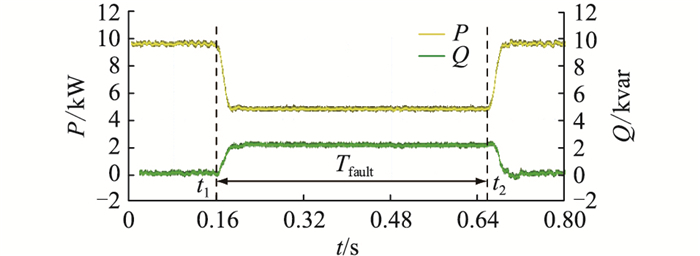
图 12为方案四逆变器输出功率波形。低电压故障期间,逆变器输出的有功功率下降,但控制策略能够利用逆变器无功输出能力输出无功功率,以支撑系统电压。
|
图 12 方案四逆变器输出功率波形 Fig. 12 Output power waveforms of the inverter of scheme 4 |
电网不对称故障期间,负序分量的存在影响并网系统的稳定运行。为证明LVRT控制的性能,分别通过两相相间短路故障和单相接地故障进行验证,其实验波形如图 13所示。两相相间短路故障发生在t1时刻,光伏并网点b、c相电压从1.0 p.u.跌落到0.5 p.u.,故障持续0.5 s。单相接地故障中,并网点c相电压在t1时刻跌落50%,故障持续0.5 s。

|
图 13 三相不对称故障实验波形 Fig. 13 Experimental waveforms of three-phase asymmetrical faults |
图 13(a)和图 13(b)分别为并网系统在2种故障期间直流母线电压和逆变器输出电流波形。由图知,所提控制系统的直流母线电压均被稳定在电压限值内,逆变器的输出电流幅值平稳,波形较好。
图 13(c)和图 13(d)分别为2种故障期间逆变器输出电流正负序分离波形。由图知,所提控制策略能根据不同的电压跌落程度调节逆变器输出电流的正序无功分量iq, p,从而控制并网逆变器根据并网点电压跌落程度输出无功功率,支持电压恢复; 同时也能较好地控制逆变器输出电流的负序分量id, n和iq, n为0。
4 结语文中针对光伏并网系统低电压故障穿越问题,提出一种基于FPPT的LVRT控制策略。仿真和实验结果表明,低电压故障期间,文中提出的控制策略能通过灵活调节光伏工作点位置实现故障期间系统功率平衡,迅速稳定直流母线电压。电网低电压故障恢复后,控制策略能估算光伏最大功率点电压以快速恢复光伏最大输出功率。该控制策略能够通过故障快速减载控制克服MPPT控制时系统功率不平衡的问题,并通过故障快速恢复控制实现光伏输出功率的快速恢复,合理地减少了光伏工作点调节时间,提高了光伏并网系统LVRT控制的可靠性,不必接入额外硬件设备,有较好的经济性。后续的研究计划包括多峰值光伏电站的故障检测、LVRT控制以及参数优化等,进而促进光伏并网发电技术的推广应用。
本文得到江苏省高校自然科学研究面上项目(20KJB470020)资助,谨此致谢!
| [1] |
YANG Y H, ENJETI P, BLAABJERG F, et al. Wide-scale adoption of photovoltaic energy: grid code modifications are explored in the distribution grid[J]. IEEE Industry Applications Magazine, 2015, 21(5): 21-31. DOI:10.1109/MIAS.2014.2345837 (  0) 0) |
| [2] |
解吉蔷, 杨秀, 王巨波. 基于MPPT运行模式的光伏发电系统低电压穿越无功控制策略[J]. 太阳能学报, 2019, 40(12): 3426-3434. XIE Jiqiang, YANG Xiu, WANG Jubo. A reactive power control strategy in low-voltage ride-through of photovoltaic generation system based on mppt mode[J]. Acta Energiae Solaris Sinica, 2019, 40(12): 3426-3434. (  0) 0) |
| [3] |
易洋, 骆雅姿, 张子瑜, 等. 集中式光伏电站汇集系统故障分析与保护方案[J]. 电力工程技术, 2021, 40(2): 2-10. YI Yang, LUO Yazi, ZHANG Ziyu, et al. Failure analysis and protection scheme of centralized photovoltaic power station convergence system[J]. Electric Power Engineering Technology, 2021, 40(2): 2-10. (  0) 0) |
| [4] |
JOSHI J, SWAMI A K, JATELY V, et al. A comprehensive review of control strategies to overcome challenges during LVRT in PV systems[J]. IEEE Access, 2021, 9: 121804-121834. DOI:10.1109/ACCESS.2021.3109050 (  0) 0) |
| [5] |
纪竹童, 周娜娜, 赵品, 等. 光伏逆变器低电压穿越控制策略研究[J]. 电力电容器与无功补偿, 2017, 38(5): 176-180. JI Zhutong, ZHOU Nana, ZHAO Pin, et al. Study on low voltage-ride-through control strategy of photovoltaic inverter[J]. Power Capacitors & Reactive Power Compensation, 2017, 38(5): 176-180. (  0) 0) |
| [6] |
魏承志, 刘幸蔚, 陈晓龙, 等. 具有低电压穿越能力的光伏发电系统仿真建模[J]. 电力系统及其自动化学报, 2016, 28(10): 67-73. WEI Chengzhi, LIU Xingwei, CHEN Xiaolong, et al. Modeling and simulation of photovoltaic power system with low voltage ride through capability[J]. Proceedings of the CSU-EPSA, 2016, 28(10): 67-73. (  0) 0) |
| [7] |
HAIDAR A M A, JULAI N. An improved scheme for enhancing the ride-through capability of grid-connected photovoltaic systems towards meeting the recent grid codes requirements[J]. Energy for Sustainable Development, 2019, 50: 38-49. DOI:10.1016/j.esd.2019.02.007 (  0) 0) |
| [8] |
党克, 郑玉浩, 杨富磊, 等. 利用串联制动电阻提高光伏并网系统故障穿越能力的研究[J]. 太阳能学报, 2017, 38(2): 302-308. DANG Ke, ZHENG Yuhao, YANG Fulei, et al. Study of improving fault ride-through ability of grid-connected PV generation system using series braking resistor[J]. Acta Energiae Solaris Sinica, 2017, 38(2): 302-308. (  0) 0) |
| [9] |
姜惠兰, 范中林, 陈娟. 动态调整转子撬棒阻值的双馈风电机组低电压穿越方法[J]. 电力系统自动化, 2018, 42(1): 125-131. JIANG Huilan, FAN Zhonglin, CHEN Juan. Low voltage ride-through method of DFIG based wind turbines by dynamically adjusting crowbar resistance of rotor[J]. Automation of Electric Power Systems, 2018, 42(1): 125-131. (  0) 0) |
| [10] |
MANIKANTA B V V N, KESAVARAO G, TALATI S. LVRT of grid connected PV system with energy storage[J]. International Journal of Control Theory and Applications, 2017, 10(5): 75-86. (  0) 0) |
| [11] |
林岩, 张建成. 含虚拟同步发电机的光/柴/储独立微网控制策略[J]. 电网技术, 2017, 41(4): 1277-1284. LIN Yan, ZHANG Jiancheng. Control strategy of islanded photovoltaic-diesel-storage microgrid with virtual synchronous generator[J]. Power System Technology, 2017, 41(4): 1277-1284. (  0) 0) |
| [12] |
付文雯, 曾成碧, 苗虹, 等. 基于改进最大功率跟踪的光伏低电压穿越[J]. 电源技术, 2016, 40(5): 1052-1055. FU Wenwen, ZENG Chengbi, MIAO Hong, et al. Low-voltage ride through of photovoltaic system based on improved maximum power point tracking control[J]. Chinese Journal of Power Sources, 2016, 40(5): 1052-1055. (  0) 0) |
| [13] |
TANG C Y, CHEN Y T, CHEN Y M. PV power system with multi-mode operation and low-voltage ride-through capability[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7524-7533. DOI:10.1109/TIE.2015.2449777 (  0) 0) |
| [14] |
YANG Y H, SANGWONGWANICH A, LIU H P, et al. Low voltage ride-through of two-stage grid-connected photovoltaic systems through the inherent linear power-voltage characteristic[C]//2017 IEEE Applied Power Electronics Conference and Exposition. Tampa, FL, USA. IEEE, 2017: 3582-3588.
(  0) 0) |
| [15] |
SANGWONGWANICH A, YANG Y H, BLAABJERG F. Development of flexible active power control strategies for grid-connected photovoltaic inverters by modifying MPPT algorithms[C]//2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia. Kaohsiung, Taiwan, China. IEEE, 2017: 87-92.
(  0) 0) |
| [16] |
国家质量监督检验检疫总局, 中国国家标准化管理委员会. 光伏发电站接入电力系统技术规定: GB/T 19964-2012[S]. 北京: 中国标准出版社, 2013. Standardization Administration of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine. Technical requirements for connecting photovoltaic power station to power system: GB/T 19964-2012[S]. Beijing: Standards Press of China, 2013. (  0) 0) |
| [17] |
房志学, 苏建徽, 王华锋, 等. 微网逆变器低电压穿越控制策略[J]. 电力系统自动化, 2019, 43(2): 143-149, 161. FANG Zhixue, SU Jianhui, WANG Huafeng, et al. Low voltage ride-through control strategy of microgrid inverter[J]. Automation of Electric Power Systems, 2019, 43(2): 143-149, 161. (  0) 0) |
| [18] |
周柯, 葛钦, 葛平娟, 等. 不平衡负荷下输出并联型电力电子变压器的优化控制策略[J]. 电工技术学报, 2018, 33(S1): 149-156. ZHOU Ke, GE Qin, GE Pingjuan, et al. The research on the control strategy of PET under unbalanced load[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 149-156. (  0) 0) |
| [19] |
SANGWONGWANICH A, YANG Y H, BLAABJERG F, et al. Delta power control strategy for multistring grid-connected PV inverters[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3862-3870. DOI:10.1109/TIA.2017.2681044 (  0) 0) |
| [20] |
ALI A N, PREMKUMAR K, VISHNUPRIYA M, et al. Design and development of realistic PV emulator adaptable to the maximum power point tracking algorithm and battery charging controller[J]. Solar Energy, 2021, 220: 473-490. DOI:10.1016/j.solener.2021.03.077 (  0) 0) |
| [21] |
BOLLIPO R B, MIKKILI S, BONTHAGORLA P K. Critical review on PV MPPT techniques: classical, intelligent and optimisation[J]. IET Renewable Power Generation, 2020, 14(9): 1433-1452. DOI:10.1049/iet-rpg.2019.1163 (  0) 0) |
| [22] |
SCARPA V V R, BUSO S, SPIAZZI G. Low-complexity MPPT technique exploiting the PV module MPP locus characterization[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1531-1538. DOI:10.1109/TIE.2008.2009618 (  0) 0) |
| [23] |
ALASAN M, ABDEL ALEEM S H E, ZOBAA A F. On the root mean square error (RMSE) calculation for parameter estimation of photovoltaic models: a novel exact analytical solution based on Lambert W function[J]. Energy Conversion and Management, 2020, 210: 112716. DOI:10.1016/j.enconman.2020.112716 (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 王琦(1975),女,博士,教授,研究方向为新能源发电及并网、综合能源建模及优化控制(E-mail:
王琦(1975),女,博士,教授,研究方向为新能源发电及并网、综合能源建模及优化控制(E-mail: