文章编号: 2096-3203(2022)03-0083-09 中图分类号: TM732
2. 华南理工大学电力学院,广东 广州 510640
经过多年开发,我国西南地区大规模梯级水电站陆续竣工投产,梯级水电对电网调度安全稳定和经济效益的影响日益显著[1]。发电机组检修计划[2]和机组组合[3]是电网调度运行的2个基本业务,关系着电网的安全稳定运行。由于我国大多数河流年内丰水期和枯水期的流量相差悬殊,属于同一梯级的水电站之间也存在复杂的耦合关系[4],这给制定水火电系统检修计划和机组组合方案带来了挑战。在传统模式下,电力调度中心先制定检修计划,再以确定的检修计划为边界条件安排机组组合。在制定检修计划时,一般由调度中心根据各发电企业上报的检修计划,在考虑相关约束后进行调整,统一确定最终的计划。检修计划的制定主要以经济性最优[5-6]、最大化备用指标或等备用率为目标[7-8],也有学者关注发电企业的满意度,如文献[9]提出以发电企业上报的检修计划被调整数最少为目标优化模型,在满足可靠性要求的同时,尽可能地维持发电企业期望的检修计划。而水火电系统机组组合方案的制定主要以经济性最优为目标[10-11]。但传统模式下,确定的检修计划会在一定程度限制机组组合的优化空间,不合理的检修计划也可能导致无法找到可行的机组组合方案,造成不必要的削减负荷运行。即使找到可行的机组组合方案,也可能因为没有充分协调好梯级水电的上下游耦合关系及丰枯水期特性,使总体的经济性降低。
为了解决检修计划和机组组合之间的冲突,有学者提出了对机组组合和机组检修进行协同优化的思路。文献[12]分析了传统模式的不足,以系统运行总成本最小为目标建立了月度机组组合与检修协同优化模型,并进行N-1安全校核;文献[13]在建立协同优化模型时同时考虑了机组和线路的检修,并采用拉格朗日松弛和Benders分解的组合算法求解模型;文献[14]针对含新能源的电力系统,建立了月度机组组合和检修计划协同优化随机模型。综合来看,对机组组合和检修计划进行协同优化,主要具有以下方面的优点:第一,协同优化能够提高系统运行的安全性,通过协同优化的检修计划和机组组合方案互相匹配,满足可靠性的要求;第二,当以经济性为目标时,优化得到的机组组合和检修计划是两项业务总成本最低的方案,与传统模式相比具有更好的经济性;第三,可提高电网消纳清洁能源的能力。
目前对检修计划与机组组合协同优化的研究主要集中于火电系统,也有学者对水火电系统的检修计划和发电计划联合优化进行研究。文献[15]根据梯级水电的特性进行建模,提出了水火电系统的检修计划和中长期调度优化方法;文献[16]以系统总能耗最小为目标,建立了水火电发电计划和检修计划的协调优化模型。但文献[15]和[16]中的发电计划采用经济调度模型,未考虑机组的启停,还不是完整的水火电检修计划和机组组合协同优化。水火电检修计划和机组组合协同优化问题在数学上可描述为一个复杂的混合整数规划模型,需要采用高效算法实现快速求解。在检修计划或者检修计划与机组组合协同优化的相关研究中,通常采用拉格朗日松弛[17]、Benders分解[18-19],或者将两者结合[20]来求解问题,也有一些学者采用启发式的方法[21-22]来加速问题的求解。
文中以最小化系统总成本和检修计划调整成本为目标,考虑梯级水电耦合特性,建立水火电检修计划和机组组合的协同优化模型,并将其转换为混合整数线性规划(mixed-inetger linear programming, MILP)模型。文中提出采用目标标度集合方法(objective scaling ensemble approach, OSEA)[23]加速求解,分2个阶段对该模型进行求解,并通过6机水火电系统和某省级实际电力系统测试进行验证。
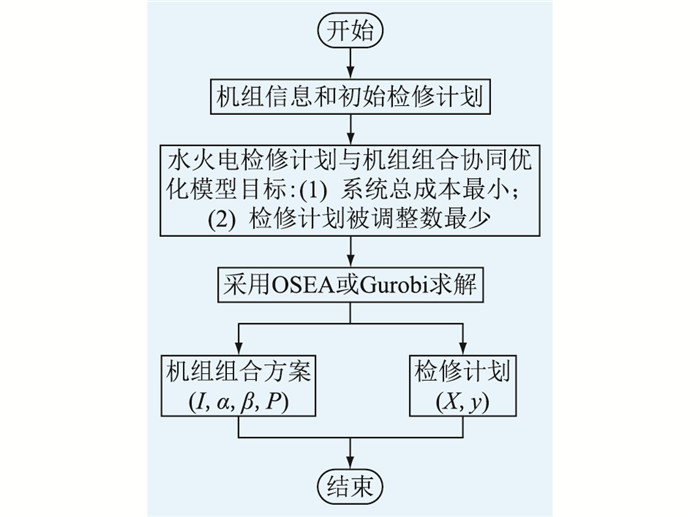
1 水火电检修计划与机组组合协同优化模式文中提出的水火电检修计划与机组组合协同优化模式如图 1所示。
|
图 1 水火电检修计划与机组组合协同优化模式 Fig. 1 Collaborative optimization mode of maintenance scheduling and unit commitment for hydropower and thermal power systems |
图 1中,I为机组启停状态;α,β分别为机组开机和停机动作;P为机组有功出力;X为机组检修状态;y为机组检修计划是否被调整。在该模式下,发电企业将期望的检修计划上报给电力调度中心,调度中心以最小化系统总成本和检修计划调整成本为目标建立协同优化模型,采用OSEA或调用Gurobi求解器求解模型,同时得到检修计划和机组组合方案。
2 水火电检修计划与机组组合协同优化模型 2.1 目标协同优化的目标是最小化系统总成本(包括火电机组的运行成本、火电机组的启停成本以及水火电机组的检修成本)和检修计划调整成本,如式(1)所示。
| $ \begin{array}{c} \min \left(\sum\limits_{t=1}^{T} \sum\limits_{i=1}^{N_{\mathrm{th}, \mathrm{G}}}\left(C_{\mathrm{th}, \mathrm{P}, i, t}+C_{\mathrm{th}, \mathrm{up}, i, t}+C_{\mathrm{th}, \mathrm{d}, i, t}+C_{\mathrm{th}, \mathrm{M}, i, t}\right)+\right. \\ \left.\sum\limits_{t=1}^{T} \sum\limits_{j=1}^{N_{\mathrm{hy}, \mathrm{G}}} C_{\mathrm{hy}, \mathrm{M}, j, t}+\sum\limits_{i=1}^{N_{\mathrm{th}, \mathrm{G}}} C_{\mathrm{th}, \mathrm{ad}, i}+\sum\limits_{j=1}^{N_{\mathrm{hy}, \mathrm{G}}} C_{\mathrm{hy}, \mathrm{ad}, j}\right) \end{array} $ | (1) |
式中:T为调度周期内总时段数;t为调度时段;i,j分别为火电和水电机组的编号;Nth, G,Nhy, G分别为火电和水电机组数目;Cth, P, i, t为火电机组i在t时段的运行成本;Cth, up, i, t ,Cth, dn, i, t分别为火电机组i在t时段的开机和停机成本;Cth, M, i, t,Chy, M, j, t分别为火电机组i和水电机组j在t时段的检修成本;Cth, ad, i,Chy, ad, j分别为火电机组i和水电机组j上报的检修计划被调整时的惩罚费用。
火电机组运行成本如式(2)所示。
| $ C_{\mathrm{th}, \mathrm{P}, i, t}=a_{i} P_{\mathrm{th}, i, t}^{2}+b_{i} P_{\mathrm{th}, i, t}+c_{i} I_{\mathrm{th}, i, t} $ | (2) |
式中:ai, bi, ci分别为火电机组i的运行成本的二次项、一次项和常数项系数;Pth, i, t为火电机组i在t时段的有功出力;Ith, i, t为火电机组i在t时段的启停状态,是0/1变量,1表示开机,0表示停机。
由于水电机组运行时不会消耗燃料,所以水电机组的运行成本为0。
对式(2)进行分段线性化[24],得到线性化后的运行成本表达式如式(3)所示。
| $ \left\{\begin{array}{l} C_{\mathrm{th}, \mathrm{P}, i, t}=\sum\limits_{m=1}^{M_{\max }} k_{i, m} p_{i, t, m}+ \\ \ \ \ \ \ \ \ \ \left(a_{i} P_{\mathrm{th}, i, \min }^{2}+b_{i} P_{\mathrm{th}, i, \min }+c_{i}\right) I_{\mathrm{th}, i, t} \\ P_{\mathrm{th}, i, t}=\sum\limits_{m=1}^{M_{\max }} p_{i, t, m}+P_{\mathrm{th}, i, \min } I_{\mathrm{th}, i, t} \\ \ \ \ \ \ \ \ \ \ \ \ \ 0 \leqslant p_{i, t, m} \leqslant \Delta P_{i, m} \end{array}\right. $ | (3) |
式中:m为分段编号;Mmax为总分段数;ki, m为火电机组i运行成本曲线第m个分段的斜率;pi, t, m为火电机组i在t时段在第m个分段上的出力;ΔPi, m为火电机组i最大和最小出力之差均分到每一段的功率; Pth, i, min为火电机组i的最小有功出力。
火电开机和停机成本如式(4)和式(5)所示。
| $ C_{\text {th,up}, i, t}=\lambda_{\text {th, up}, i} \boldsymbol{\alpha}_{\mathrm{th}, i, t} $ | (4) |
| $ C_{\mathrm{th}, \mathrm{dn}, i, t}=\lambda_{\mathrm{th}, \mathrm{dn}, i} \boldsymbol{\beta}_{\mathrm{th}, i, t} $ | (5) |
式中:λth, up, i,λth, dn, i分别为火电机组i单次开机和停机成本;αth, i, t,βth, i, t分别为火电机组i在t时段的开机和停机动作,是0/1变量,1表示动作,0表示不动作。
水火电检修成本如式(6)和式(7)所示。
| $ C_{\mathrm{th}, \mathrm{M}, i, t} =\lambda_{\mathrm{th}, \mathrm{M}, i, t} X_{\mathrm{th}, i, t} $ | (6) |
| $ C_{\mathrm{hy}, \mathrm{M}, j, t} =\lambda_{\mathrm{hy}, \mathrm{M}, j, t} X_{\mathrm{hy}, j, t} $ | (7) |
式中:λth, M, i, t,λhy, M, j, t分别为火电机组i和水电机组j在t时段的检修成本;Xth, i, t,Xhy, j, t分别为火电机组i和水电机组j在t时段的检修状态,是0/1变量,1表示检修,0表示不检修。
水火电检修调整成本如式(8)和式(9)所示。
| $ C_{\mathrm{th}, \mathrm{ad}, i}=w y_{\mathrm{th}, i} $ | (8) |
| $ C_{\mathrm{hy}, \mathrm{ad}, j}=w y_{\mathrm{hy}, j} $ | (9) |
式中:w为机组检修计划被调整的惩罚成本;yth, i,yhy, j分别为火电机组i和水电机组j的检修计划是否与上报的时段相同,是0/1变量,1表示被调整,0表示未被调整。
2.2 约束条件(1) 水火电机组出力上下限约束。
| $ P_{\mathrm{th}, i, \text { min }} I_{\mathrm{th}, i, t} \leqslant P_{\mathrm{th}, i, t} \leqslant P_{\mathrm{th}, i, \text { max }} I_{\mathrm{th}, i, t} $ | (10) |
| $ P_{\mathrm{hy}, j, \min } I_{\mathrm{hy}, j, t} \leqslant P_{\mathrm{hy}, j, t} \leqslant P_{\mathrm{hy}, j, \max } I_{\mathrm{hy}, j, t} $ | (11) |
式中:Pth, i, min,Phy, j, min分别为火电机组i和水电机组j的最小有功出力;Pth, i, max,Phy, j, max分别为火电机组i和水电机组j的最大有功出力。Ihy, j, t为水电机组j在t时段的启停状态,是0/1变量,1表示开机,0表示停机。
(2) 火电机组最小开停机时间约束。
最小开机时间约束如式(12)所示。
| $ \left\{\begin{array}{l} I_{\mathrm{th}, i, t}=1 \quad t \in\left[1, U_{i}\right] \\ U_{i}=\left(T_{\mathrm{on}, i}-T_{\mathrm{on}, i, 0}\right) I_{\mathrm{th}, i, 0}\\ \sum\limits_{\tau=t}^{\min \left(T,t+T_{\text {on}, i},-1\right)} I_{\mathrm{th}, i, \tau} \geqslant\left(I_{\mathrm{th}, i, t}-I_{\mathrm{th}, i, t-1}\right) \times\\ \ \ \ \ \ \ \min \left(T_{\text {on}, i}, T-t+1\right) \quad t \in\left[U_{i}+1, T\right] \end{array}\right. $ | (12) |
最小停机时间约束如式(13)所示。
| $ \left\{\begin{array}{l} I_{\mathrm{th}, i, t}=0 \quad t \in\left[1, D_{i}\right] \\ D_{i}=\left(T_{\text {off }, i}-T_{\text {off }, i, 0}\right)\left(1-I_{\mathrm{th}, i, 0}\right)\\ \sum\limits_{\tau=t}^{\min \left(T, t+T_{\text {off }, i}-1\right)}\left(1-I_{\mathrm{th}, i, \tau}\right) \geqslant\left(I_{\mathrm{th}, i, t-1}-I_{\mathrm{th}, i, t}\right) \times\\ \ \ \ \ \ \ \min \left(T_{\text {off }, i}, T-t+1\right) \quad t \in\left[D_{i}+1, T\right] \end{array}\right. $ | (13) |
式中:τ为调度时段;Ui, Di分别为机组i在调度开始后需要保持开机和停机的时段数;Ton, i , Toff, i分别为机组i的最小开机时间和最小停机时间;Ton, i, 0, Toff, i, 0分别为机组i在调度开始时已经开机和停机的时间。
(3) 系统功率平衡方程。
| $ \sum\limits_{i=1}^{N_{\mathrm{th}, \mathrm{G}}} P_{\mathrm{th}, i, t}+\sum\limits_{j=1}^{N_{\mathrm{hy}, \mathrm{G}}} P_{\mathrm{hy}, j, t}=P_{\mathrm{L}, t} $ | (14) |
式中:PL, t为t时段系统的总负荷。
(4) 系统备用约束。
通过预留足够的系统旋转备用容量以应对负荷预测误差带来的影响,主要考虑系统的正旋转备用容量,用以补偿因低估系统负荷所带来的影响。
| $ \begin{gathered} \sum\limits_{i=1}^{N_{\mathrm{th} . \mathrm{G}}}\left(P_{\mathrm{th}, i, \max } I_{\mathrm{th}, i, t}-P_{\mathrm{th}, i, t}\right)+ \\ \sum\limits_{j=1}^{N_{\mathrm{hy}, \mathrm{G}}}\left(P_{\mathrm{hy}, j, \max } I_{\mathrm{hy}, j, t}-P_{\mathrm{hy}, j, t}\right) \geqslant \rho P_{\mathrm{L}, t} \end{gathered} $ | (15) |
式中:ρ为备用系数。
(5) 火电机组启停状态与启停动作的关系。
| $ \alpha_{\mathrm{th}, i, t}-\beta_{\mathrm{th}, i, t}=I_{\mathrm{th}, i, t}-I_{\mathrm{th}, i, t-1} $ | (16) |
(6) 水火电机组检修时长约束。
机组实际检修的总时段数应等于上报的检修时长。
| $ \sum\limits_{t=1}^{T} X_{\mathrm{th}, i, t}=T_{\mathrm{th}, \mathrm{M}, i} $ | (17) |
| $ \sum\limits_{t=1}^{T} X_{\mathrm{hy}, j, t}=T_{\mathrm{hy}, \mathrm{M}, j} $ | (18) |
式中:Tth, M, i,Thy, M, j分别为火电机组i和水电机组j上报的检修时长。
(7) 水火电机组检修持续性约束。
检修一旦开始,就不能中断,应该持续到整个检修过程结束。
| $ X_{\mathrm{th}, i, t}-X_{\mathrm{th}, i, t-1} \leqslant X_{\mathrm{th}, i, t+T_{\mathrm{th}, \mathrm{M}, i}-1} $ | (19) |
| $ X_{\mathrm{hy}, j, t}-X_{\mathrm{hy}, j, t-1} \leqslant X_{\mathrm{hy}, j, t+T_{\mathrm{hy}, \mathrm{M}, j}-1} $ | (20) |
(8) 水火电机组检修调整约束。
以yth, i,yhy, j分别表示火电机组i和水电机组j的检修计划是否被调整,应满足的约束关系如式(21)和式(22)所示。
| $ X_{\mathrm{th}, i, t}-X_{\mathrm{th}, i, t-1} \geqslant 1-2 y_{\mathrm{th}, i} \quad t=T_{\mathrm{th}, \mathrm{st}, i} $ | (21) |
| $ X_{\mathrm{hy}, j, t}-X_{\mathrm{hy}, j, t-1} \geqslant 1-2 y_{\mathrm{hy}, j} \quad t=T_{\mathrm{hy}, \mathrm{st}, j} $ | (22) |
式中:Tth, st, i,Thy, st, j分别为火电机组i和水电机组j上报的检修开始时段。
以火电为例,当t =Tth, st, i时,若Xth, i, t和Xth, i, t-1的取值为“0-0”,“0-1”,“1-1”,yth, i只能取值为1,即上报的检修计划被调整;若Xth, i, t和Xth, i, t-1的取值为“1-0”,由于优化目标为最小化成本,yth, i将取值为0,即上报的检修计划未被调整。水电机组同理。
(9) 检修变量与启停状态变量的耦合约束。
当机组进行检修的时候,必须停机;当机组不检修的时候,有开机和停机2种状态。
| $ I_{\mathrm{th}, i, t} \leqslant 1-X_{\mathrm{th}, i, t} $ | (23) |
| $ I_{\mathrm{hy}, j, t} \leqslant 1-X_{\mathrm{hy}, j, t} $ | (24) |
(10) 水电站出力方程。
水电站的总出力等于水电站中每台机组出力的总和。
| $ P_{\mathrm{hs}, k, t}=\sum\limits_{j \in J_{k}} P_{\mathrm{hy}, j, t} $ | (25) |
式中:k为水电站编号;Phs, k, t为水电站k在t时段的总出力;Jk为水电站k中水电机组编号的集合。
(11) 水电站库容上下限约束。
| $ v_{k, \min } \leqslant v_{k, t} \leqslant v_{k, \max } $ | (26) |
式中:vk, max,vk, min分别为水电站k水库容量的上限和下限;vk, t为水电站k在t时段的水库容量。
(12) 水电站库容平衡方程。
| $ v_{k, t}-v_{k, t-1}=q_{k-1, t}+s_{k-1, t}+n_{k, t}-q_{k, t}-s_{k, t} $ | (27) |
式中:qk, t为水电站k在t时段的发电流量;qk-1, t为上一个水电站在t时段的发电流量,近似等于上一个水电站的出库流量;sk, t,sk-1, t分别为水电站k和上一个水电站在t时段的弃水量;nk, t为水电站k在t时段的天然降水量。
(13) 水电站的发电流量方程。
| $ P_{\mathrm{hs}, k, t}=\eta_{k} q_{k, t} $ | (28) |
式中:ηk为水电站k的发电流量和出力的转换系数。
3 求解算法水火电检修计划与机组组合协同优化模型属于MILP问题,包含多组0/1整数变量,这些整数变量之间存在复杂的耦合关系,当问题规模较大时,难以直接高效求解。
OSEA是一种求解大规模混合整数规划问题的有效方法。对于实际工程中出现的大规模MILP问题,最优解中整数变量取值为0的数量比例非常高[25]。如果能够探测出大概率取值为0的整数变量,将其固定后求解降维的MILP模型,将使得问题大大简化,使快速求解成为可能。为了便于讨论,将水火电检修计划与机组组合协同优化MILP模型写成如式(29)的紧凑形式。
| $ \left\{\begin{array}{l} (\mathrm{MILP}) \min z(x)=\sum\limits_{s \in C} c_{s} x_{s}+\sum\limits_{s \in B} c_{s} x_{s} \\ \text {s.t. } \boldsymbol{A x} \geqslant \boldsymbol{b} \\ \ \ \ \ \ \ \ x_{s} \in\{0,1\} \quad \forall s \in B \\ \ \ \ \ \ \ \ x_{s} \geqslant 0 \quad \forall s \in C \end{array}\right. $ | (29) |
式中:s为模型中变量的编号;cs为变量的成本系数;xs为模型中出现的变量;A为约束方程的系数矩阵;x为变量的向量;b为约束方程右端常数的向量;B为0/1整数变量的集合;C为连续变量的集合。
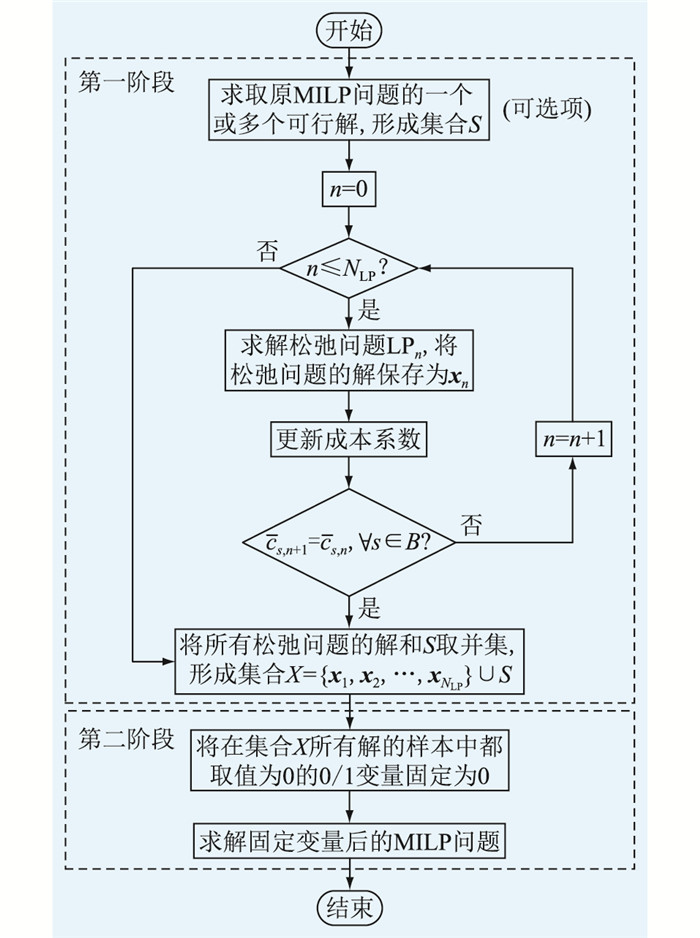
OSEA的实现流程如图 2所示。
|
图 2 采用OSEA求解水火电检修计划与机组组合协同优化模型的流程 Fig. 2 Flow chart of solving collaborative optimization model of maintenance scheduling and unit commitment for hydropower and thermal power systems using OSEA |
采用OSEA求解水火电检修计划与机组组合协同优化模型的具体步骤如下:
第一阶段,对MILP问题目标函数中整数变量的系数进行标度,将原问题松弛为线性规划(linear programming, LP)问题,并按照一定的规则更新系数,可以得到不同的松弛问题集合,求解这些松弛问题,得到多组解的样本。
(1) 该步骤为可选项。在求解松弛问题的同时,求取原MILP问题的一个或多个可行解,形成集合S。
(2) 将原问题中的0/1整数变量松弛为定义域为[0, 1]的连续变量,则原问题转化为LP问题。第n次迭代对应的LP问题如式(30)所示。
| $ \left\{\begin{array}{l} \left(\mathrm{LP}_{n}\right) \min z_{n}^{\mathrm{LP}}(x)=\sum\limits_{s \in C} c_{s} x_{s}+\sum\limits_{s \in B} \bar{c}_{s, n} x_{s} \\ \text {s.t. } \boldsymbol{A} \boldsymbol{x} \geqslant \boldsymbol{b} \\ \quad\ \ \ 0 \leqslant x_{s} \leqslant 1 \quad \forall s \in B \\ \quad\ \ \ x_{s} \geqslant 0 \quad \forall s \in C \end{array}\right. $ | (30) |
式中:cs, n为原0/1变量在第n次迭代松弛问题中的系数;0/1变量包括Ith, i, t, Ihy, j, t, αth, i, t, βth, i, t, Xth, i, t, Xhy, j, t, yth, i, t, yhy, j, t。
(3) 求解松弛后的LP问题,将松弛问题的解记为xn。
(4) 根据式(31)更新各松弛变量的成本系数,若满足式(32)的收敛判据或n达到最大迭代次数NLP,则跳转到步骤5;若不满足,则令n=n+1,并跳转到步骤3。
| $ \bar{c}_{s, n+1}=\left\{\begin{array}{l} \frac{\bar{c}_{s, 0}}{1+x_{s, n}} \quad x_{s, n}>0 \\ \bar{c}_{s, n} \quad x_{s, n}=0 \end{array} \quad \forall s \in B\right. $ | (31) |
式中:xs, n为松弛问题,即式(32)中变量的取值。
| $ \bar{c}_{s, n+1}=\bar{c}_{s, n} \quad \forall s \in B $ | (32) |
(5) 将每个松弛问题的迭代次数解的集合与原问题可行解的集合取并集,即令X= {x1, x2, …, xNLP} ∪S。
第二阶段,若松弛变量在每个松弛问题的解和原问题可行解中都保持为0,则将其固定,然后求解固定变量后的MILP问题,得到最终结果。
(1) 若0/1变量xs在集合X每个解的样本中都取值为0,则将变量xs固定为0,否则不固定。
(2) 求取固定0变量后的MILP问题,得到最终的结果。
4 算例分析假设检修周期为1 a,以天为时间单位。选择6机水火电系统和某实际省级86机水火电系统为测试系统,验证OSEA对模型的适用性和有效性。
所有计算均在Dell计算机上完成,其配置为:Intel Xeon E3处理器,3.30 GHz,内存16 GB。计算软件为GAMS24.3.3,选择Gurobi作为MILP问题的求解器,Cplex作为线性规划问题的求解器。
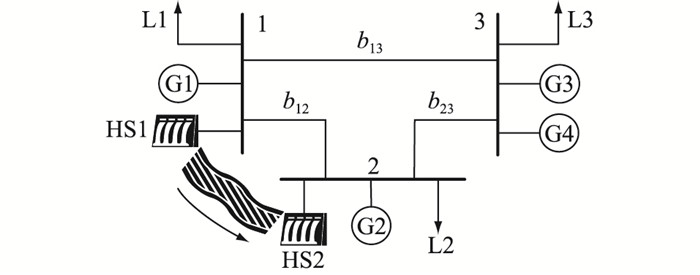
4.1 6机水火电系统结果分析6机水火电系统的接线如图 3所示。该系统包含3个节点、4台火电机组和2台水电机组,b12, b13和b23表示节点间的传输线路。火电机组G1和G2分别接在节点1和2上,火电机组G3和G4接在节点3上;2台水电机组分别属于水电站(hydropower station, HS),表示为HS1和HS2,分别接在节点1和2上,2个水电站属于同一个梯级。
|
图 3 含2个梯级水电站的6机系统 Fig. 3 6-unit system with 2 cascade hydropower stations |
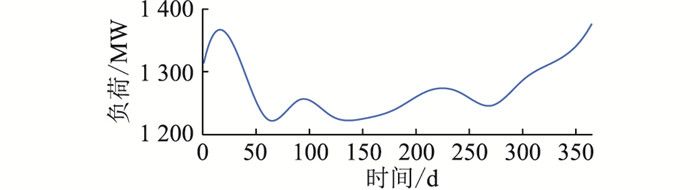
火电机组G1—G4的装机容量均为600 MW,水电站HS1的机组容量为200 MW,水电站HS2的机组容量为190 MW。整个系统的年负荷曲线如图 4所示,备用系数ρ设置为5%。
|
图 4 6机系统年负荷曲线 Fig. 4 Annual load curve of 6-unit system |
该问题含有8 400个0/1变量、9 851个连续变量和19 343个约束。采用2种算法求解该6机系统,即采用Gurobi直接求解原始MILP问题,采用OSEA分2个阶段计算可行解、松弛解及简化MILP问题的解,目标值和求解时间的对比如表 1所示。在OSEA的第一阶段,求解原始MILP问题的可行解和LP问题可以并行计算,选用求解LP问题所用时间内最优的可行解,与LP问题的解取交集。由表 1可见,OSEA最终求得的解对应的目标值比Gurobi所求最优解对应的目标值只增加了0.051%,而OSEA的总求解时间为30.56 s,比Gurobi直接求解减少了36.786%。说明在小规模系统中,与Gurobi相比,OSEA能够在更短时间内求解得到较优的可行解。
|
|
表 1 2种算法求解6机系统的结果对比 Table 1 Comparison of results in 6-unit system by two algorithms |
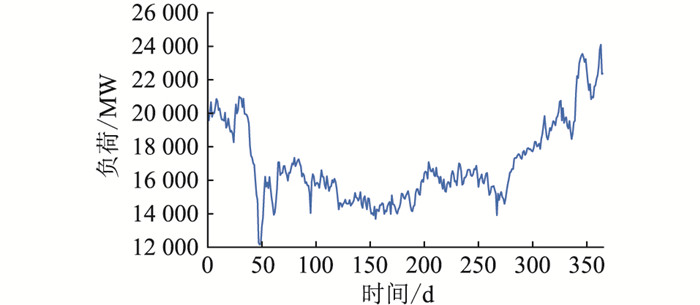
为了进一步验证OSEA对大规模系统的适应性和有效性,文中对某实际省级水火电系统进行计算分析。该系统包括41台火电机组、45台水电机组、202个负荷节点和621条线路。有一条较大的梯级水电接入该系统,7个水电站HS1—HS7依次坐落于该梯级径流上。该省级系统还含有20个风电厂和3个光伏电厂,风电和光伏根据历史的出力数据,作为负的负荷参与系统的功率平衡。系统的年负荷曲线如图 5所示。
|
图 5 86机系统年负荷曲线 Fig. 5 Annual load curve of 86-unit system |
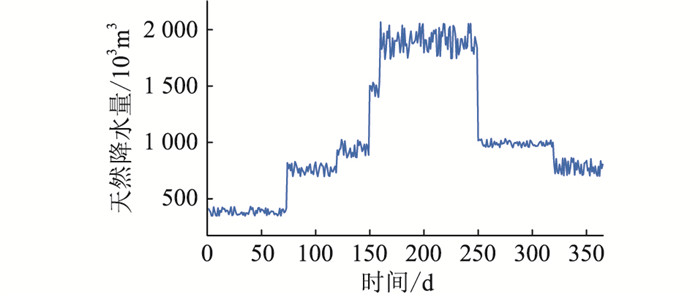
该省份的丰水期为5至10月,枯水期为11月至次年4月,天然降水量反映了这一自然特性。图 6给出了该梯级龙头水电站的年降水情况。
|
图 6 龙头水电站(HS1)的年天然降水曲线 Fig. 6 Annual natural precipitation curve at head hydropower station (HS1) |
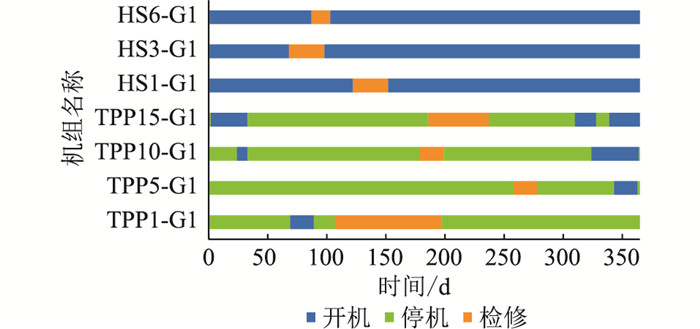
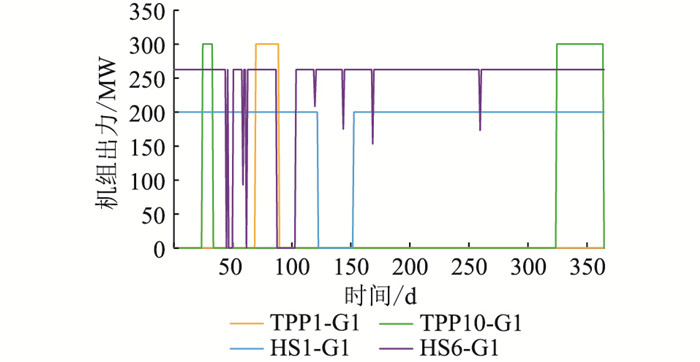
采用OSEA求解水火电检修计划和机组组合协同优化模型,能够同时得到各机组在一年中每个时段的启停状态和检修状态,如图 7所示,其中热电厂(thermal power plant, TPP)中G1表示热电厂内第一台机组。部分机组的年出力曲线如图 8所示。对比图 7和图 8可知,机组检修时必须停机,不检修时可以开机也可以停机。水电机组的检修主要安排在枯水期进行,不检修的时段基本都处于满发的状态。水电优先出力,能够充分利用水资源,减少火电机组的煤耗成本,有利于水火电系统的经济运行。
|
图 7 协同优化模式下部分机组的启停状态和检修状态 Fig. 7 On/off state and maintenance state of some units in the collaborative optimization model |
|
图 8 协同优化模式下部分机组的年出力曲线 Fig. 8 Annual output curve of some units in the collaborative optimization model |
如果仅以经济性最优进行优化,目标函数中不添加检修计划被调整的惩罚项,则优化结果中一共有33台火电机组、38台水电机组上报的检修计划被调整。如果添加检修计划调整的惩罚项,使机组上报的检修计划被调整数最少,则优化结果中只有4台火电机组、15台水电机组的检修计划被调整,能够有效保障发电企业的意愿。该协同优化问题含有87 306个0/1变量,11 4175个连续变量,201 481个约束。采用2种算法求解86机系统模型,目标值和求解时间的对比如表 2所示。
|
|
表 2 2种算法求解86机系统的结果对比 Table 2 Comparison of results in 86-unit system by two algorithms |
由表 2可见,OSEA最终求得的解对应的目标值较Gurobi减少了0.002%,OSEA的总求解时间为1 027 s,比Gurobi直接求解减少了63.454%,验证了该方法对于大规模系统的适用性和优越性。
4.3 非协同优化与协同优化的对比为了验证文中所采用的协同优化模式的有效性,文中在非协同优化模式下对86机水火电系统进行计算分析,并与协同优化的结果进行对比。
在非协同优化模式下,先以最小化运行成本、检修成本和检修计划调整成本为目标编制机组检修计划,再在确定的检修计划下,以最小化运行成本和启停成本为目标安排机组组合,最终得到各机组在一年中每个时段的启停状态和检修状态,如图 9所示,部分机组的年出力曲线如图 10所示。
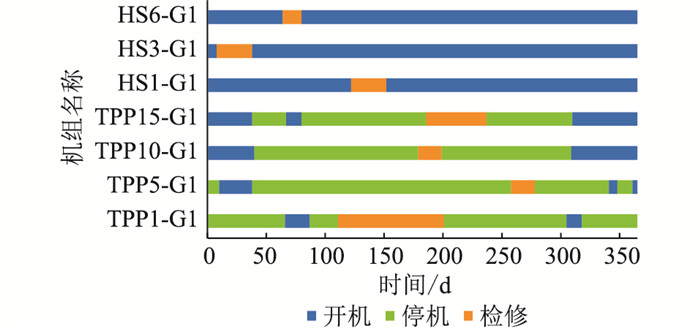
|
图 9 非协同优化模式下部分机组的启停状态和检修状态 Fig. 9 On/off state and maintenance state of some units in the non-collaborative optimization model |
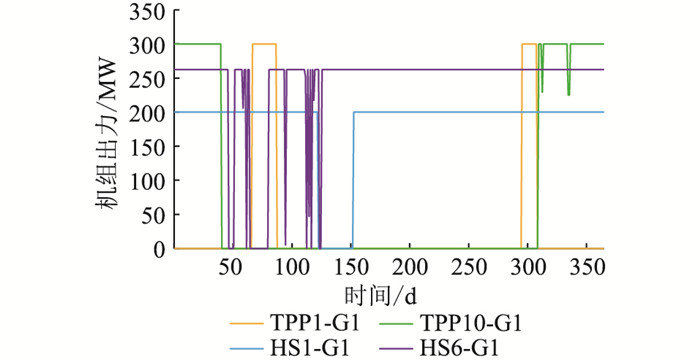
|
图 10 非协同优化模式下部分机组的年出力曲线 Fig. 10 Annual output curve of some units in the non-collaborative optimization model |
对比图 7—图 10可知,与非协同优化相比,协同优化不在确定的检修计划下安排机组组合,能够在更大的求解空间中得到火电机组出力较少的方案,从而减少系统的运行成本。非协同优化和协同优化的各项成本如表 3所示。
|
|
表 3 非协同优化与协同优化的经济性对比 Table 3 Economic comparison between non-colla-borative optimization and collaborative optimization |
由表 3可知,协同优化时除了检修计划调整成本高于非协同优化,运行成本、启停成本和检修成本都比非协同优化低,总成本比非协同优化减少了7.989%,反映出对检修计划和机组组合进行协同优化在经济性上的优势。检修计划调整成本提高是因为协同优化时,能够更充分地协调梯级水电的上下游关系和丰枯水期特性,灵活调整水电的检修计划,进而改变机组组合方案,使总体效益达到最高。
5 结语文中建立的水火电检修计划与机组组合协同优化模型,考虑了梯级水电的耦合特性以及水火电之间的配合,能够有效协调梯级水电站之间的流量关系,以及水火电之间的出力情况。保证水电优先出力,将检修计划被调整的机组安排在枯水期检修,有利于系统经济运行。在追求经济性的同时,尽可能地维持发电企业期望的检修计划,提高发电企业的满意度。
此外,采用OSEA求解MILP问题,能够有效简化原问题,在保证解的质量的同时,大大提高求解速度。随着问题规模的增大,采用OSEA求解混合整数规划问题的效果会更加突显。
本文得到贵州电网有限责任公司科技项目“基于电力现货交易的各类机组最优发电组合与检修安排的决策方法研究及应用”(066500KK52190008)资助,谨此致谢!
| [1] |
刘方. 梯级水电站优化调度与交易策略研究[D]. 北京: 华北电力大学, 2019. LIU Fang. Study on optimal dispatch and market trading strategy of cascade hydropower stations[D]. Beijing: North China Electric Power University, 2019. (  0) 0) |
| [2] |
冯长有, 王锡凡. 电力市场环境下发电机组检修规划研究综述[J]. 电力系统保护与控制, 2011, 39(13): 138-147. FENG Changyou, WANG Xifan. Review of unit maintenance scheduling in market environment[J]. Power System Protection and Control, 2011, 39(13): 138-147. (  0) 0) |
| [3] |
陈鸿琳, 刘明波. 交流潮流约束机组组合的部分代理割方法[J]. 中国电机工程学报, 2018, 38(9): 2540-2550, 2822. CHEN Honglin, LIU Mingbo. Partial surrogate cuts approach for alternating current power flow constrained unit commitment[J]. Proceedings of the CSEE, 2018, 38(9): 2540-2550, 2822. (  0) 0) |
| [4] |
刘方, 张粒子, 蒋燕, 等. 电力市场环境下梯级水电站中长期调度与检修计划双层优化模型[J]. 电网技术, 2018, 42(5): 1541-1549. LIU Fang, ZHANG Lizi, JIANG Yan, et al. Bi-level optimal model of mid-long term scheduling and maintenance planning for cascade hydropower stations in electricity market environment[J]. Power System Technology, 2018, 42(5): 1541-1549. (  0) 0) |
| [5] |
JI G Q, WU W C, ZHANG B M. Robust generation maintenance scheduling considering wind power and forced outages[J]. IET Renewable Power Generation, 2016, 10(5): 634-641. DOI:10.1049/iet-rpg.2015.0198 (  0) 0) |
| [6] |
KAMALI R, KHAZAEI P, BANIZAMANI P, et al. Stochastic unit generation maintenance scheduling considering renewable energy and network constraints[C]//2018 World Automation Congress (WAC). Stevenson, WA, USA. IEEE, 2018: 1-6.
(  0) 0) |
| [7] |
李秋文, 谢冰, 林洁, 等. 水火电机组年度检修计划安排的实用优化模型[J]. 广东电力, 2017, 30(6): 90-93, 119. LI Qiuwen, XIE Bing, LIN Jie, et al. Practical optimization model for annual maintenance scheduling for hydro-thermal unit[J]. Guangdong Electric Power, 2017, 30(6): 90-93, 119. DOI:10.3969/j.issn.1007-290X.2017.06.018 (  0) 0) |
| [8] |
俞晨玺, 孔维禄, 俞柏红, 等. 考虑需求响应的多目标机组检修调度优化[J]. 电力系统保护与控制, 2020, 48(11): 110-118. YU Chenxi, KONG Weilu, YU Bohong, et al. Multi-objective optimization of generation maintenance scheduling considering demand response[J]. Power System Protection and Control, 2020, 48(11): 110-118. (  0) 0) |
| [9] |
谢冰. 机组检修计划及发电计划优化问题研究[D]. 杭州: 浙江大学, 2018. XIE Bing. Research on unit maintenance scheduling and power generation scheduling optimization[D]. Hangzhou: Zhejiang University, 2018. (  0) 0) |
| [10] |
汪超群, 韦化, 吴思缘. 计及潮流约束的水火电力系统机组组合问题的分解-协调算法[J]. 中国电机工程学报, 2017, 37(11): 3148-3161, 3370. WANG Chaoqun, WEI Hua, WU Siyuan. A decomposition-coordination algorithm applied to hydro-thermal unit commitment problems with power flow constraints[J]. Proceedings of the CSEE, 2017, 37(11): 3148-3161, 3370. (  0) 0) |
| [11] |
马留洋. 基于纵横交叉算法的水火电联合调度机组组合问题[D]. 广州: 广东工业大学, 2018. MA Liuyang. A crisscross optimization algorithm for hydro-thermal unit commitment problem[D]. Guangzhou: Guangdong University of Technology, 2018. (  0) 0) |
| [12] |
汪洋, 钟海旺, 夏清, 等. 机组检修与运行组合的协同优化[J]. 电力系统自动化, 2014, 38(21): 26-31, 76. WANG Yang, ZHONG Haiwang, XIA Qing, et al. Collaborative optimization of unit maintenance and security-constrained unit commitment[J]. Automation of Electric Power Systems, 2014, 38(21): 26-31, 76. DOI:10.7500/AEPS20140403002 (  0) 0) |
| [13] |
LOU X S, FENG C Y, CHEN W, et al. Risk-based coordination of maintenance scheduling and unit commitment in power systems[J]. IEEE Access, 2020, 8: 58788-58799. DOI:10.1109/ACCESS.2020.2982183 (  0) 0) |
| [14] |
周明, 夏澍, 李琰, 等. 含风电的电力系统月度机组组合和检修计划联合优化调度[J]. 中国电机工程学报, 2015, 35(7): 1586-1595. ZHOU Ming, XIA Shu, LI Yan, et al. A joint optimization approach on monthly unit commitment and maintenance scheduling for wind power integrated power systems[J]. Proceedings of the CSEE, 2015, 35(7): 1586-1595. (  0) 0) |
| [15] |
MARTÍNEZ M V R, ZULUAGA A H E, GUIMARÃES F G. A MILP model for generation maintenance scheduling coordinated with hydrothermal dispatch[J]. Energy Systems, 2020, 11(4): 839-857. DOI:10.1007/s12667-019-00342-2 (  0) 0) |
| [16] |
葛晓琳, 舒隽, 张粒子. 考虑检修计划的中长期水火电联合优化调度方法[J]. 中国电机工程学报, 2012, 32(13): 36-43, 189. GE Xiaolin, SHU Jun, ZHANG Lizi. Mid-long term optimal dispatching method of hydro-thermal power system considering scheduled maintenance[J]. Proceedings of the CSEE, 2012, 32(13): 36-43, 189. (  0) 0) |
| [17] |
WU L, SHAHIDEHPOUR M, LI T. GENCO's risk-based main- tenance outage scheduling[J]. IEEE Transactions on Power Systems, 2008, 23(1): 127-136. DOI:10.1109/TPWRS.2007.913295 (  0) 0) |
| [18] |
李本新, 韩学山. 发输电检修与机组组合联合决策的Benders分解方法[J]. 电工技术学报, 2015, 30(3): 224-231. LI Benxin, HAN Xueshan. Benders decomposition algorithm to coordination of generation and transmission maintenance scheduling with unit commitment[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 224-231. DOI:10.3969/j.issn.1000-6753.2015.03.028 (  0) 0) |
| [19] |
WANG Y, ZHONG H W, XIA Q, et al. An approach for integrated generation and transmission maintenance scheduling considering N-1 contingencies[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2225-2233. DOI:10.1109/TPWRS.2015.2453115 (  0) 0) |
| [20] |
许奕斌, 章禹, 何宇斌, 等. 计及灵活性的检修-运行协同优化模型及算法[J]. 电力系统自动化, 2018, 42(11): 32-40. XU Yibin, ZHANG Yu, HE Yubin, et al. Collaborative optimization model and algorithm of maintenance and operation considering flexibility[J]. Automation of Electric Power Systems, 2018, 42(11): 32-40. DOI:10.7500/AEPS20170622010 (  0) 0) |
| [21] |
WANG Y, KIRSCHEN D S, ZHONG H W, et al. Coordination of generation maintenance scheduling in electricity markets[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4565-4574. DOI:10.1109/TPWRS.2016.2514527 (  0) 0) |
| [22] |
RODRÍGUEZ J A, ANJOS M F, CÔTÉ P, et al. MILP formulations for generator maintenance scheduling in hydropower systems[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6171-6180. DOI:10.1109/TPWRS.2018.2833061 (  0) 0) |
| [23] |
ZHANG W L, NICHOLSON C D. Objective scaling ensemble approach for integer linear programming[J]. Journal of Heuristics, 2020, 26(1): 1-19. DOI:10.1007/s10732-019-09418-9 (  0) 0) |
| [24] |
陈颖毅, 王丽萍, 赵亚威, 等. 考虑弃水电量机会损失的水火电短期联合优化调度[J]. 水电能源科学, 2020, 38(7): 65-68, 15. CHEN Yingyi, WANG Liping, ZHAO Yawei, et al. Short-term coordination optimal of hydrothermal scheduling considering opportunity loss of surplus hydropower[J]. Water Resources and Power, 2020, 38(7): 65-68, 15. (  0) 0) |
| [25] |
KOCH T, ACHTERBERG T, ANDERSEN E, et al. Miplib 2010[J]. Mathematical Programming Computation, 2011, 3(2): 103-163. DOI:10.1007/s12532-011-0025-9 (  0) 0) |
2. School of Electric Power Engineering, South China University of Technology, Guangzhou 510640, China
 2022, Vol. 41
2022, Vol. 41


 代江(1985),男,硕士,高级工程师, 从事发电调度管理与电力市场工作(E-mail:
代江(1985),男,硕士,高级工程师, 从事发电调度管理与电力市场工作(E-mail: