文章编号: 2096-3203(2022)03-0224-07 中图分类号: TM615
2. 国网浙江省电力有限公司新昌县供电公司,浙江 绍兴 312099;
3. 中国电力科学研究院有限公司,江苏 南京 210003
随着可再生能源被大量应用,加之配电网所接入负荷种类较多、波动性较大,导致配电网存在多种电能质量问题,严重影响电网的稳定运行[1-3]。
现有的电能质量治理装置如静止无功发生器、有源电力滤波器等,都能对电能质量问题进行有效治理。由于其结构及控制方法与逆变器相似[4-5],有专家学者提出多功能逆变器的概念,将电能质量治理与逆变器并网逆变这2种功能复合到1台逆变器中[6-8],不需要额外增加治理装置,该方式可降低成本,提高经济效益[9-10]。文献[11]研究了一种改进重复控制策略下的多功能逆变器,给出了改进重复控制器的设计过程,但该过程较为复杂。文献[12]介绍了一种重复控制器的简便设计方法,设计出H∞重复控制器作为电流内环控制器,但只讨论了单台逆变器用于电能质量治理。文献[13]利用多台多功能逆变器治理配电网中的电能质量问题,但仅考虑理想电网情况。在弱电网环境下,由于电网存在阻抗,会进一步放大电网中的谐波,同时也会引起逆变器谐振,导致逆变器失稳[14-17]。
针对上述问题,考虑电网阻抗对系统的影响,在以H∞重复控制结合电压前馈控制作为并网逆变器内环控制策略的基础上,通过阻抗分析法分析系统稳定性。在前馈通道及前向通道分别引入复数滤波器和超前校正环节来增加系统的相位裕度,扩大了多并联逆变器接入弱电网时的稳定范围,提高了系统对电网阻抗的适应能力。采用基于二阶广义积分的瞬时无功电流检离算法分离负载电流中的不平衡、非线性及无功分量,并对其进行相应的治理与补偿。
1 多功能逆变器系统 1.1 系统结构多功能逆变器(或称分布式发电机(distributed generation,DG))系统整体结构如图 1所示。Udc为直流侧电压;L1为逆变侧电感;L2为网侧电感;C为滤波电容;Rd为阻尼电阻;Lg为电网电感;upcc为公共连接点(point of common coupling,PCC)电压;ug为电网电压;i1为逆变侧电流;i2为并网电流;iref为参考电流;iL为负载电流;θ为锁相环(phase locked loop,PLL)测得的电压相位;DG1,DG2为2台并联的多功能逆变器。

|
图 1 多功能逆变器系统整体结构框图 Fig. 1 Overall structure block diagram of multifunctional inverter system |
理想电网下多功能逆变器内环控制器框图如图 2所示。Gh(s)为控制系统电压前馈环节;G(s)为系统控制器;kc为电容电流反馈系数;kpwm为调制波到逆变侧电压的传递函数。

|
图 2 多功能逆变器内环控制框图 Fig. 2 Inner loop control block diagram of multifunctional inverter |

|
图 3 等效控制框图 Fig. 3 Equivalent control block diagram |
由图 3可以推导出式(1):
| $ \begin{gathered} i_{2}=\frac{G(s) H_{1}(s) H_{2}(s)}{1+G(s) H_{1}(s) H_{2}(s)} i_{\text {ref }}- \\ \frac{H_{2}(s)\left(1-G_{\mathrm{h}}(s) H_{1}(s)\right)}{1+G(s) H_{1}(s) H_{2}(s)} u_{\mathrm{g}} \end{gathered} $ | (1) |
其中:
| $ H_{1}(s)=\frac{k_{\mathrm{pwm}}\left(R_{\mathrm{d}} C s+1\right)}{L_{1} C s^{2}+\left(k_{\mathrm{c}} k_{\mathrm{pwm}}+R_{\mathrm{d}}\right) C s+1} $ | (2) |
| $ \begin{gathered} H_{2}(s)= \\ \frac{L_{1} C s^{2}+\left(k_{\mathrm{c}} k_{\mathrm{pwm}}+R_{\mathrm{d}}\right) C s+1}{L_{1} L_{2} C s^{3}+k_{\mathrm{c}} k_{\mathrm{pwm}} L_{2} C s^{2}+\left(L_{1}+L_{2}\right) C R_{\mathrm{d}} s^{2}+\left(L_{1}+L_{2}\right) s} \end{gathered} $ | (3) |
系统参数以及2台逆变器LCL滤波器参数分别如表 1和表 2所示。
|
|
表 1 系统参数 Table 1 System parameters |
|
|
表 2 2台逆变器LCL滤波器参数 Table 2 LCL filter parameters of two inventers |
依据表 1和表 2完成2台逆变器的H∞控制器G(s)设计[18-19],具体如下。
DG1控制器的表达式如式(4)所示。
| $ G_{1}(s)=\frac{9.285(s+780)}{s+2\ 500-2\ 500 \mathrm{e}^{-0.019\ 6 s}} $ | (4) |
DG2控制器的表达式如式(5)所示。
| $ G_{2}(s)=\frac{7.224(s+706.8)}{s+2\ 500-2\ 500 \mathrm{e}^{-0.019\ 6 s}} $ | (5) |
电压前馈控制Gh(s)的表达式[20]为:
| $ G_{\mathrm{h}}(s)=\frac{1}{k_{\mathrm{pwm}}\left(R_{\mathrm{d}} C s+1\right)} $ | (6) |
文中采用了瞬时无功电流检测算法与二阶广义积分相结合的电流分离算法[21-22],以此分离负载中的不平衡、谐波及无功电流,算法如图 4所示,采用低通滤波器(low-pass filter, LPF)滤波。

|
图 4 电流检测算法 Fig. 4 Current detection algorithm |
图 4中,iLa,iLb,iLc为三相负载电流;iLa+,iLb+,iLc+为三相正序负载电流;id,iq分别为三相正序负载电流在d、q轴上的分量;id,iq分别为基波电流在d,q轴上的分量;iLah,iLbh,iLch为三相负序及谐波电流;iqref为q轴指令电流。将iLah,iLbh,iLch加入逆变器d轴电流指令中,进行跟踪补偿,最终实现对不平衡、谐波及无功电流的治理。
2 弱电网下系统稳定性分析 2.1 单台逆变器稳定性分析为了分析弱电网下单台逆变器的稳定性,建立诺顿等效电路,如图 5所示。
|
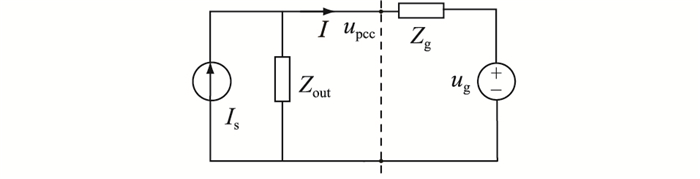
图 5 诺顿等效电路 Fig. 5 Norton equivalent circuit |
将逆变器等效成一个恒流源Is及一个与之并联的等效输出阻抗Zout,电网等效成一个理想电压源ug及一个与之串联的电网阻抗Zg,I为逆变器输出电流。
依据图 5,得到逆变器输出电流I(s)表达式如式(7)所示。
| $ \begin{array}{c} I(s)=\frac{Z_{\text {out }}(s)}{Z_{\text {out }}(s)+Z_{\mathrm{g}}(s)} I_{\mathrm{s}}(s)-\frac{u_{\mathrm{g}}(s)}{Z_{\text {out }}(s)+Z_{\mathrm{g}}(s)}= \\ \left(I_{\mathrm{s}}(s)-\frac{u_{\mathrm{g}}(s)}{Z_{\text {out }}(s)}\right) \times \frac{1}{1+Z_{\mathrm{g}}(s) / Z_{\text {out }}(s)} \end{array} $ | (7) |
由阻抗稳定判据可得:当Zg和Zout幅频特性曲线不相交或其交截处对应频率fs的相角裕度满足式(8)时,逆变器稳定,其中相角裕度用P表示。
| $ P=180^{\circ}-\left(\angle Z_{\mathrm{g}}\left(\mathrm{j} 2 {\rm{ \mathsf{ π} }} f_{\mathrm{s}}\right)-\angle Z_{\text {out }}\left(\mathrm{j} 2 {\rm{ \mathsf{ π} }} f_{\mathrm{s}}\right)\right)>0^{\circ} $ | (8) |
由于电网阻抗中电阻有利于逆变器稳定,而电感不利于逆变器稳定,因此Zg取感性部分,则电网阻抗的相位为90°,由式(8)得到阻抗稳定时Zout的相位关系式,如式(9)所示。
| $ \angle Z_{\mathrm{out}}\left(\mathrm{j} 2 {\rm{ \mathsf{ π} }} f_{\mathrm{s}}\right)>-90^{\circ} $ | (9) |
由式(1)和式(7)可得Zout表达式,即:
| $ Z_{\text {out }}(s)=\frac{1+G(s) H_{1}(s) H_{2}(s)}{H_{2}(s)\left(1-G_{\mathrm{h}}(s) H_{1}(s)\right)} $ | (10) |
依据式(10)绘制DG1和DG2引入补偿策略前等效输出阻抗Bode图,如图 6所示。由图 6可知,补偿前电网电感Lg部分取值下逆变器不稳定,因此采用电压前馈引入复数滤波器[23-24]Gf(s)及系统前向通道引入超前校正环节Gp(s)相结合的方式提高逆变器稳定性,对应公式为式(11)-式(14)。

|
图 6 引入补偿策略前后逆变器等效输出阻抗Bode图 Fig. 6 Bode diagram of equivalent output impedance of inverter before and after introducing compensation strategy |
DG1:
| $ G_{\mathrm{f} 1}(s)=\frac{314(s+\mathrm{j} 314)}{s^{2}+628 s+314^{2}} $ | (11) |
| $ G_{\mathrm{p} 1}(s)=\frac{0.952\ 1 \times 10^{-4} s+0.414\ 5}{0.394 \times 10^{-4} s+1} $ | (12) |
DG2:
| $ G_{\mathrm{f} 2}(s)=\frac{314(s+\mathrm{j} 314)}{s^{2}+628 s+314^{2}} $ | (13) |
| $ G_{\mathrm{p} 2}(s)=1 $ | (14) |
图 6中,Lg取1 mH,DG1和DG2引入复合补偿策略前,Zg与Zout幅值交截处相位均小于-90°,2台逆变器均不稳定;引入复合补偿策略后,2台逆变器等效输出阻抗Zout中频段相位增加,此时交截处相位大于-90°,满足阻抗稳定判据,2台逆变器均稳定,逆变器稳定范围扩大。
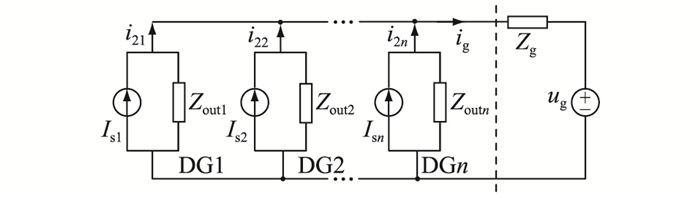
2.2 多台逆变器稳定性分析依据单台逆变器等效模型建立的多逆变器并联等效模型如图 7所示。可以看出,DG1输出电流主要有3类激励源:自身电流源Is1、n-1台逆变器的电流源(包括Is2,…,Isn)以及电网电压源ug。i21,i22,i2n分别为第1台逆变器DG1、第2台逆变器DG2及第n台逆变器DGn的输出电流;Zout1,Zout2,Zoutn分别为DG1、DG2、DGn的等效输出阻抗。
|
图 7 多逆变器并联等效模型 Fig. 7 Parallel equivalent model of multiple inverters |
依据上述分析,以并联的DG1和DG2作为研究对象,根据叠加定理可以得到DG1输出电流i21、DG2输出电流i22的表达式分别如式(15)和式(16)所示。
| $ \begin{gathered} i_{21}(s)=\frac{Z_{\text {op }}(s)}{Z_{\text {op }}(s)+Z_{\mathrm{g}}(s)}\left(G_{1}(s) I_{\mathrm{s} 1}(s)-\frac{u_{\mathrm{g}}(s)}{Z_{\text {out1 }}(s)}\right)+ \\ \frac{Z_{\mathrm{g}}(s)}{Z_{\text {op }}(s)+Z_{\mathrm{g}}(s)} \times\left(\frac{Z_{\text {out1 }}(s)}{Z_{\text {out1 }}(s)+Z_{\text {out2 }}(s)} G_{1}(s) I_{\mathrm{s} 1}(s)-\right. \\ \left.\frac{Z_{\text {out2 }}(s)}{Z_{\text {out1 }}(s)+Z_{\text {out2 }}(s)} G_{2}(s) I_{\mathrm{s} 2}(s)\right) \end{gathered} $ | (15) |
| $ \begin{gathered} i_{22}(s)=\frac{Z_{\mathrm{op}}(s)}{Z_{\mathrm{op}}(s)+Z_{\mathrm{g}}(s)}\left(G_{2}(s) I_{\mathrm{s} 2}(s)-\frac{u_{\mathrm{g}}(s)}{Z_{\mathrm{out} 2}(s)}\right)+ \\ \frac{Z_{\mathrm{g}}(s)}{Z_{\mathrm{op}}(s)+Z_{\mathrm{g}}(s)} \times\left(\frac{Z_{\text {out2 }}(s)}{Z_{\text {out1 }}(s)+Z_{\text {out2 }}(s)} G_{2}(s) I_{\mathrm{s} 2}(s)-\right. \\ \left.\frac{Z_{\text {out1 } }(s)}{Z_{\text {out1 } }(s)+Z_{\text {out2 }}(s)} G_{1}(s) I_{\mathrm{s} 1}(s)\right) \end{gathered} $ | (16) |
总的并网电流ig如式(17)所示。
| $ \begin{gathered} i_{\mathrm{g}}(s)=\frac{Z_{\mathrm{op}}(s)}{Z_{\mathrm{op}}(s)+Z_{\mathrm{g}}(s)} \times \\ \left(G_{1}(s) I_{\mathrm{s} 1}(s)+G_{2}(s) I_{\mathrm{s} 2}(s)-\frac{u_{\mathrm{g}}(s)}{Z_{\text {out1 }}(s)}-\frac{u_{\mathrm{g}}(s)}{Z_{\text {out2 }}(s)}\right) \end{gathered} $ | (17) |
式中:Zop为2台逆变器并联后的总输出阻抗。
由式(17)可知,多逆变器并联系统稳定的条件为:(1) 单个逆变器稳定;(2) Zop与Zg满足奈奎斯特稳定判据。
分析式(15)-式(17)可知,逆变器之间存在谐振电流,然而只在逆变器之间运动,没有流入电网。并网电流与每个逆变器的电流源及电网电压源有关,谐振电流与每个逆变器的等效输出阻抗、电网阻抗、总等效输出阻抗有关。
针对逆变器之间的谐振电流,文献[25]从单逆变器并网谐波产生的机理出发,分析多逆变器并联谐振电流产生机理:当一个逆变器的等效输出阻抗与其他逆变器等效输出阻抗幅值交截处相角接近180°时,该频率处的谐波电流被放大,逆变器之间存在谐振电流。
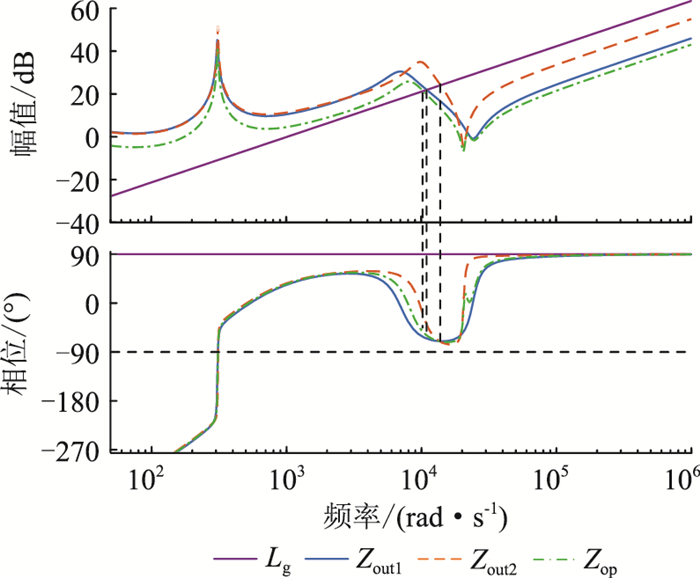
依据表 1和表 2参数,绘制出引入复合补偿策略后DG1等效输出阻抗Zout1、DG2等效输出阻抗Zout2、总等效输出阻抗Zop及电网电感Lg的Bode图,如图 8所示,图中Lg取1 mH。
|
图 8 并联逆变器等效输出阻抗Bode图 Fig. 8 Equivalent output impedance Bode diagram of parallel inverter |
由图 8可知,Zout1,Zout2,Zop均与电网阻抗满足阻抗稳定判据,并联逆变器系统稳定;DG1和DG2的等效输出阻抗交截处相角远小于180°,无谐振电流产生。
3 仿真分析为了验证弱电网下多逆变器并联电能质量的治理效果,在Simulink中构建了弱电网下2台逆变器并联的系统仿真模型进行仿真实验,其结构如图 1所示,实验中仿真参数如表 1和表 2所示。
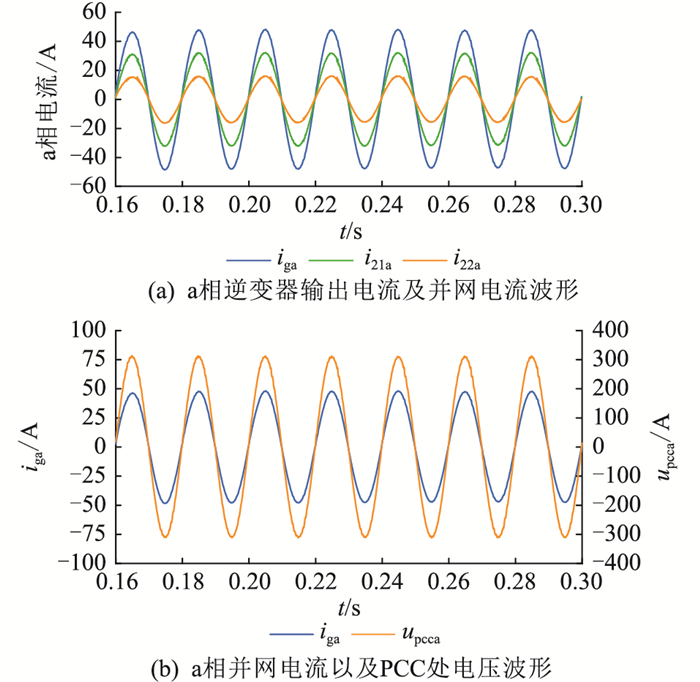
在弱电网条件下,给定DG1有功功率P1为10 kW(即iref1=32.24 A),DG2有功功率P2为5 kW(即iref2=16.12 A),二者无功功率均为0。图 9为并联逆变器中电流及PCC处电压波形,DG1输出电流i21、DG2输出电流i22、总并网电流ig及upcc电压的基波幅值和总谐波失真(total harmonic distortion,THD)值如表 3所示。
|
图 9 并联逆变器中电流及PCC处电压波形 Fig. 9 The waveforms of current and voltage at PCC in parallel inverter |
|
|
表 3 并联逆变器中电流及PCC处电压的基波幅值和THD值 Table 3 The fundamental amplitude and THD of current and voltage at PCC in parallel inverter |
由图 9及表 3可知,并网电流波形及2台逆变器输出电流波形畸变较小,并联逆变器系统稳定,仿真结果与第2章逆变器稳定性分析结果一致。逆变器之间无谐振电流产生,即2台逆变器等效输出阻抗交截处相角小于180°,与图 8的Bode图分析结果一致。
在并联逆变器系统的PCC处分别接入非线性负载(含5次及7次谐波)、不平衡阻性负载(RA=RC=40 Ω,RB=10 Ω)及不平衡感性负载(LA=LC=12 mH,LB=8 mH),采用1.3节介绍的基于二阶广义积分的瞬时无功电流检测算法在并联逆变器系统中进行仿真分析。
情景1:本地接入非线性及不平衡阻性负载,利用单台逆变器的剩余容量实现对负载的电能质量问题进行治理(另一台正常逆变)。在0.2 s时,DG1投入治理,治理前后并网电流及逆变器输出电流波形如图 10所示。

|
图 10 情景1治理前后并网电流及逆变器输出电流波形 Fig. 10 Grid current and inverter output current wave- forms of scenario 1 before and after governance |
由图 10可知,投入治理前并网电流三相不平衡且畸变严重,2台逆变器正常逆变,此时并网电流THD值为6.57%;投入治理后,DG1对负载中的电能质量问题进行治理,并网电流正弦度变好,电流THD值为2.25%,且并网电流三相平衡,DG2仍正常逆变。
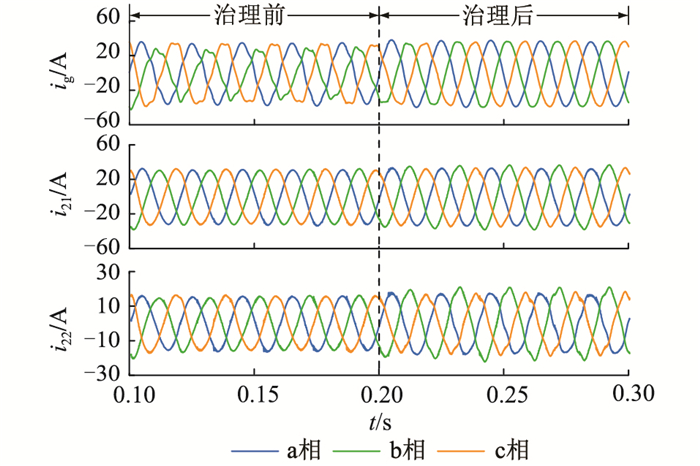
情景2:本地接入非线性及不平衡阻性负载,利用2台逆变器的剩余容量实现对负载的电能质量问题进行治理。在0.2 s时,DG1和DG2同时投入治理(将不平衡、谐波问题分摊至2台逆变器中治理),治理前后并网电流及逆变器输出电流如图 11所示。
|
图 11 情景2治理前后并网电流及逆变器输出电流波形 Fig. 11 Grid current and inverter output current wave- forms of scenario 2 before and after governance |
由图 11可知,投入治理前,并网电流畸变严重且三相不平衡,2台逆变器均正常逆变;投入治理后,DG1和DG2对负载中的电能质量问题进行分摊治理,并网电流正弦度变好,电流THD值为2.29%,并网电流三相平衡。
情景3:本地负载接入非线性及不平衡感性负载,利用2台逆变器进行治理。在0.2 s时,2台逆变器同时投入治理,治理前后并网电流、逆变器输出电流及PCC处电压波形如图 12所示。

|
图 12 情景3治理前后电流及PCC处电压波形 Fig. 12 Current and voltage waveforms at PCC of scenario 3 before and after governance |
由图 12可知,治理前并网电流不平衡且存在畸变,b相电流滞后b相电压一定角度,2台逆变器正常逆变;投入治理后,经过2个周期的调整,并网电流波形正弦度变好,三相电流平衡,b相电流和b相电压同相位。
4 结语系统稳定运行、优质供电是新能源发电的基本要求。文中通过分析弱电网下并联逆变器的稳定性,在此基础上利用并联逆变器治理非线性、不平衡及无功等多种负载引起的电能质量问题。研究表明,在前向通道引入超前校正环节及前馈通道引入复数滤波器可以使并联逆变器工作在更宽的稳定范围;其次并联逆变器可以对负载中多种电能质量问题进行灵活治理,在治理电能质量的同时也保证了系统的稳定运行,为多逆变器并联稳定运行及改善电能质量、解决负载中不平衡、谐波及无功问题提供了有效的解决方案。
本文得到江苏省研究生科研与实践创新项目(SJCX20_0717)资助,谨此致谢!
| [1] |
曾正, 邵伟华, 赵伟芳, 等. 多功能并网逆变器与并网微电网电能质量的分摊控制[J]. 中国电机工程学报, 2015, 35(19): 4947-4955. ZENG Zheng, SHAO Weihua, ZHAO Weifang, et al. Coordination control of multiple multi-functional grid-tied inverters to share power quality issues for grid-connected micro-grid[J]. Proceedings of the CSEE, 2015, 35(19): 4947-4955. (  0) 0) |
| [2] |
USTUN T S, OZANSOY C, ZAYEGH A. Recent developments in microgrids and example cases around the world-A review[J]. Renewable and Sustainable Energy Reviews, 2011, 15(8): 4030-4041. DOI:10.1016/j.rser.2011.07.033 (  0) 0) |
| [3] |
周京华, 闫天乐, 郭磊轩, 等. 微电网背景下电能质量分析与治理[J/OL]. 电气传动: 1-8[2022-01-26]. https://kns.cnki.net/kcms/detail/12.1067.TP.20211227.1418.001.html. ZHOU Jinghua, YAN Tianle, GUO Leixuan, et al. Power quality analysis and governance in the context of microgrid[J/OL]. Electric Drive: 1-8[2022-01-26]. https://kns.cnki.net/kcms/detail/12.1067.TP.20211227.1418.001.html. (  0) 0) |
| [4] |
倪福银, 李正明. 统一电能质量调节器的研究发展综述[J]. 电力系统保护与控制, 2020, 48(20): 177-187. NI Fuyin, LI Zhengming. Overview of unified power quality conditioner research development[J]. Power System Protection and Control, 2020, 48(20): 177-187. (  0) 0) |
| [5] |
宋振浩, 吕志鹏, 刘志涵, 等. 多功能并网逆变器电能质量优化控制策略[J]. 中国科技论文, 2022, 17(3): 339-347. SONG Zhenhao, LYU Zhipeng, LIU Zhihan, et al. Power quality optimization control strategy of multi-function grid-connected inverter[J]. China Sciencepaper, 2022, 17(3): 339-347. DOI:10.3969/j.issn.2095-2783.2022.03.016 (  0) 0) |
| [6] |
宋新甫, 于国康, 孟高军, 等. 基于改进重复控制和模糊PI自整定的并网逆变器设计[J]. 可再生能源, 2020, 38(2): 245-251. SONG Xinfu, YU Guokang, MENG Gaojun, et al. Design of grid-connected inverter based on improved repetitive control and fuzzy PI self-tuning[J]. Renewable Energy Resources, 2020, 38(2): 245-251. DOI:10.3969/j.issn.1671-5292.2020.02.017 (  0) 0) |
| [7] |
LI Y W, HE J W. Distribution system harmonic compensation methods: an overview of DG-interfacing inverters[J]. IEEE Industrial Electronics Magazine, 2014, 8(4): 18-31. DOI:10.1109/MIE.2013.2295421 (  0) 0) |
| [8] |
黄鹏, 戴威, 张莹, 等. 兼具有源电力滤波器功能的多功能并网逆变器控制[J]. 电力工程技术, 2021, 40(1): 107-114. HUANG Peng, DAI Wei, ZHANG Ying, et al. Multi-function grid-connected inverter control with APF function[J]. Electric Power Engineering Technology, 2021, 40(1): 107-114. (  0) 0) |
| [9] |
朱非白, 江道灼, 梁一桥. 基于T型三电平拓扑的新型电能质量补偿器[J]. 电力自动化设备, 2020, 40(6): 149-156. ZHU Feibai, JIANG Daozhuo, LIANG Yiqiao. Novel power quality compensator based on T-type three-level topology[J]. Electric Power Automation Equipment, 2020, 40(6): 149-156. (  0) 0) |
| [10] |
靳伟, 李永丽, 孙广宇. 基于有源阻尼的并网逆变器电流内环H∞重复控制[J]. 中国电机工程学报, 2016, 36(17): 4685-4694. JIN Wei, LI Yongli, SUN Guangyu. H∞ repetitive current controllers for grid-connected inverters based on active damping[J]. Proceedings of the CSEE, 2016, 36(17): 4685-4694. (  0) 0) |
| [11] |
卜立之, 李永丽, 孙广宇, 等. 基于改进型重复控制算法的多功能并网逆变器设计[J]. 电力系统自动化, 2017, 41(12): 48-55, 69. BU Lizhi, LI Yongli, SUN Guangyu, et al. Design ofmulti-functional grid-connected inverter based on modified repetitive con trol algorithm[J]. Automation of Electric Power Systems, 2017, 41(12): 48-55, 69. (  0) 0) |
| [12] |
胡子珩, 张华赢, 李艳, 等. 基于H∞鲁棒控制的多功能光伏逆变器[J]. 电测与仪表, 2020, 57(11): 146-152. HU Ziheng, ZHANG Huaying, LI Yan, et al. Multifunctional photovoltaic inverter based on H∞ robust control[J]. Electrical Measurement & Instrumentation, 2020, 57(11): 146-152. (  0) 0) |
| [13] |
孙广宇, 李永丽, 靳伟, 等. 基于三相多功能逆变器的微电网电能质量综合治理策略[J]. 电网技术, 2019, 43(4): 1211-1221. SUN Guangyu, LI Yongli, JIN Wei, et al. A comprehensive power quality control strategy for microgrid based on three-phase multi-function inverters[J]. Power System Technology, 2019, 43(4): 1211-1221. (  0) 0) |
| [14] |
邹鹏辉, 张治, 张显立. 高渗透率分布式光伏系统谐波与电压控制[J]. 智慧电力, 2020, 48(12): 40-45. ZOU Penghui, ZHANG Zhi, ZHANG Xianli. Harmonic and voltage control of distributed photovoltaic system with high permeability[J]. Smart Power, 2020, 48(12): 40-45. (  0) 0) |
| [15] |
杨雅菲. 弱电网下考虑SOGI-PLL影响的并网逆变器控制策略研究[D]. 北京: 华北电力大学, 2021. YANG Yafei. Research on grid-connected inverter control strategy considering the influence of SOGI-PLL in weak grid case[D]. Beijing: North China Electric Power University, 2021. (  0) 0) |
| [16] |
杨兴武, 王涛, 徐依明, 等. 基于虚拟电感的LCL型并网逆变器电网电压前馈控制策略[J]. 太阳能学报, 2020, 41(11): 56-63. YANG Xingwu, WANG Tao, XU Yiming, et al. Voltage feedforward control of LCL grid-connected inverter based on virtual inductor[J]. Acta Energiae Solaris Sinica, 2020, 41(11): 56-63. (  0) 0) |
| [17] |
SUN J. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078. (  0) 0) |
| [18] |
张俊, 刘文泽. 基于H∞重复控制的微网逆变器控制策略[J]. 电测与仪表, 2020, 57(20): 114-120. ZHANG Jun, LIU Wenze. Control strategy of micro-grid inverter based on H∞ repetitive control[J]. Electrical Measurement & Instrumentation, 2020, 57(20): 114-120. (  0) 0) |
| [19] |
李志军, 张鸿鹏, 王亚楠, 等. 基于LCL型单相APF的重复-H∞控制[J]. 电力电容器与无功补偿, 2019, 40(5): 90-96, 104. LI Zhijun, ZHANG Hongpeng, WANG Yanan, et al. Repetitive-H∞ control of single phase APF based on LCL[J]. Power Capacitor and Reactive Power Compensation, 2019, 40(5): 90-96, 104. (  0) 0) |
| [20] |
黄旭. 弱电网下光伏并网逆变器稳定性分析及其控制策略研究[D]. 焦作: 河南理工大学, 2019. HUANG Xu. Research on stability analysis and control strategy of photovoltaic grid-connected inverter under weak grid[D]. Jiaozuo: Henan Polytechnic University, 2019. (  0) 0) |
| [21] |
万晓凤, 郗瑞霞, 胡海林, 等. 基于果蝇算法的电网不平衡时并网逆变器多目标优化控制研究[J]. 电网技术, 2018, 42(5): 1628-1635. WAN Xiaofeng, XI Ruixia, HU Hailin, et al. Research on multi-objective optimization control of grid-connected inverter under unbalanced grid voltage based on fruit fly algorithm[J]. Power System Technology, 2018, 42(5): 1628-1635. (  0) 0) |
| [22] |
王国玲, 何富桥, 刘旭, 等. 基于二阶广义积分器新能源船舶电网锁相技术[J]. 电机与控制学报, 2020, 24(7): 147-155. WANG Guoling, HE Fuqiao, LIU Xu, et al. Phase-locked loop technique in new energy shipboard grid based on second-order generalized integrators[J]. Electric Machines and Control, 2020, 24(7): 147-155. (  0) 0) |
| [23] |
郑征, 黄旭, 杨明, 等. 弱电网下基于复数滤波器的并网电压前馈控制策略[J]. 电力系统保护与控制, 2018, 46(24): 70-75. ZHENG Zheng, HUANG Xu, YANG Ming, et al. Grid voltage feedforward control strategy forweak grid based on complex filter[J]. Power System Protection and Control, 2018, 46(24): 70-75. (  0) 0) |
| [24] |
涂春鸣, 高家元, 李庆, 等. 具有复数滤波器结构锁相环的并网逆变器对弱电网的适应性研究[J]. 电工技术学报, 2020, 35(12): 2632-2642. TU Chunming, GAO Jiayuan, LI Qing, et al. Research on adaptability of grid-connected inverter with complex coefficient-filter structure phase locked loop to weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2632-2642. (  0) 0) |
| [25] |
王杰. 多并网逆变器的交互影响分析与控制[D]. 重庆: 重庆大学, 2019. WANG Jie. Interaction analysis and control of the multipe grid-connected inverters[D]. Chongqing: Chongqing University, 2019. (  0) 0) |
2. State Grid Zhejiang Electric Power Co., Ltd. Xinchang Power Supply Company, Shaoxing 312099, China;
3. China Electric Power Research Institute Company, Nanjing 210003, China
 2022, Vol. 41
2022, Vol. 41


 张成(1996),男,硕士在读,研究方向为新能源并网技术及电能质量(E-mail:
张成(1996),男,硕士在读,研究方向为新能源并网技术及电能质量(E-mail: