文章编号: 2096-3203(2022)03-0102-08 中图分类号: TM721.1
特高压直流输电线路保护一般都配置行波保护、电压突变量保护作为主保护,线路低电压保护、线路纵差保护作为后备保护[1-3]。近几年来,特高压直流输电工程的直流输电线路长度不断创造新的记录,例如吉泉±1 100 kV特高压直流输电工程的直流线路长度已超出3 000 km。直流输电线路越长,两极直流输电线路之间的耦合越紧密。在特高压直流工程的试验过程中,经常发现当某一极的2个阀组处于运行状态,而另外一极只有1个阀组处于运行状态时,2个阀组运行的一极发生线路故障会导致只有1个阀组运行的一极的电压突变量保护发生误动。特高压直流工程在两极线路相继发生故障时会直接双极闭锁而不进行直流线路故障再重启逻辑,极大地增加了特高压直流工程的双极闭锁风险。
但是,目前对直流输电线路保护的研究主要集中在行波保护和纵差保护,研究方向主要集中于行波在线路终端的反射和折射过程分析[4-6]、行波保护的影响因素及改进[7-10]、新型原理的行波保护[11-14]、行波保护的整定[15]以及线路纵差保护的优化[16-19],很少涉及电压突变量保护的策略优化和直流输电线路长度对保护的影响。文献[20-22]虽然研究了特高压直流输电线路间的电磁耦合对电压突变量保护影响,但是其将两极的架空线路等效为RL串联的集总参数电路,分析结果误差较大。
文中基于分布参数模型分析了特高压直流输电线路长度对电压突变量保护的影响,并根据分析结果提出了电压突变量保护优化策略。仿真计算结果验证了优化后的电压突变量保护的可靠性。
1 故障特征量的时模变换及传输速率 1.1 时模变换相对于线路的电抗、电容来说,因为其电导、电阻很小,所以文中忽略2条直流输电线路的电导和电阻,并且定义特高压直流输电系统额定电压为+800 kV的极为正极,额定电压为-800 kV的极为负极。直流输电线路故障发生以后,故障特征量以波的形式从故障点向线路的两端传播,两极直流输电线路任意一处的电压和电流间的关系如式(1)所示[23-25]:
| $ \left\{\begin{array}{l} {\left[\begin{array}{c} -\frac{\partial U_{1}}{\partial x} \\ -\frac{\partial U_{2}}{\partial x} \end{array}\right]=\left[\begin{array}{cc} L & M_{L} \\ M_{L} & L \end{array}\right]\left[\begin{array}{c} \frac{\partial I_{1}}{\partial t} \\ \frac{\partial I_{2}}{\partial t} \end{array}\right]} \\ {\left[\begin{array}{c} -\frac{\partial I_{1}}{\partial x} \\ -\frac{\partial I_{2}}{\partial x} \end{array}\right]=\left[\begin{array}{cc} C & -M_{C} \\ -M_{C} & C \end{array}\right]\left[\begin{array}{l} \frac{\partial U_{1}}{\partial t} \\ \frac{\partial U_{2}}{\partial t} \end{array}\right]} \end{array}\right. $ | (1) |
式中:U1,U2分别为正极、负极的电压;I1,I2分别为为正极、负极的电流;x为线路的某一处距坐标点的长度;L为单位长度线路的自感;C为单位长度线路的自容;ML,MC分别为单位长度线路的互感和互容;t为时间。
式(2)给定矩阵J左乘式(1)并进行优化得到式(3)。
| $ \boldsymbol{J}=\left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right] $ | (2) |
| $ \left\{\begin{array}{l} {\left[\begin{array}{c} -\frac{\partial\left(U_{1}+U_{2}\right)}{\partial x} \\ -\frac{\partial\left(U_{1}-U_{2}\right)}{\partial x} \end{array}\right]=\left[\begin{array}{cc} L+M_{L} & 0 \\ 0 & L-M_{L} \end{array}\right]\left[\begin{array}{l} \frac{\partial\left(I_{1}+I_{2}\right)}{\partial t} \\ \frac{\partial\left(I_{1}-I_{2}\right)}{\partial t} \end{array}\right]} \\ {\left[\begin{array}{c} -\frac{\partial\left(I_{1}+I_{2}\right)}{\partial x} \\ -\frac{\partial\left(I_{1}-I_{2}\right)}{\partial x} \end{array}\right]=\left[\begin{array}{cc} C-M_{C} & 0 \\ 0 & C+M_{C} \end{array}\right]\left[\begin{array}{l} \frac{\partial\left(U_{1}+U_{2}\right)}{\partial t} \\ \frac{\partial\left(U_{1}-U_{2}\right)}{\partial t} \end{array}\right]} \end{array}\right. $ | (3) |
式中:U1+U2,U1-U2分别为电压共模分量和差模分量;I1+I2,I1-I2分别为电流共模分量和差模分量;L+ML,C-MC分别为单位长度线路的共模分量自感和自容;L-ML,C+MC分别为单位长度线路的差模分量自感和自容。
时模变换后共模分量和差模分量是完全解耦的,并且都是以波的形式独立传输。
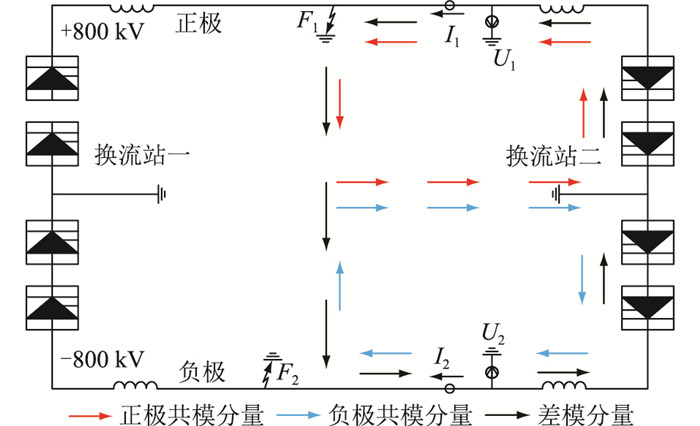
1.2 传输速率分析定义电流流出换流站的方向为电流的正方向。当图 1所示的正极直流输电线路故障F1发生时,正极和负极的共模分量从直流线路流出,接地极线路返回,正极和负极的差模分量从正极直流线路流出,负极直流线路返回。
|
图 1 共模及差模的传输路径 Fig. 1 The transmission path of common mode and differential mode traveling waves |
根据传输线的等相位面运动方程[26],得到共模分量的速率Vcom为:
| $ \left\{\begin{aligned} &V_{\mathrm{com}}= \frac{\omega}{\beta_{\omega \mathrm{a}}} \\ &\beta_{\omega \mathrm{a}}= {\left[\left(\omega^{2} L_{\mathrm{a}} C_{a}-R_{\mathrm{a}} G_{\mathrm{a}}\right) / 2+\right.} \\ &\ \ \ \ \ \ \ \ \ \ \left.\sqrt{\left(R_{\mathrm{a}}^{2}+\omega^{2} L_{\mathrm{a}}^{2}\right)\left(G_{\mathrm{a}}^{2}+\omega^{2} C_{\mathrm{a}}^{2}\right)}\right]^{\frac{1}{2}} \end{aligned}\right. $ | (4) |
式中:ω为角频率;Ra为共模分量自阻;Ga为共模分量自导;La为共模分量自感;Ca为共模分量自容。
差模分量的速率Vdif为:
| $ \left\{\begin{aligned} V_{\mathrm{dif}}=& \frac{\omega}{\beta_{\omega \mathrm{b}}} \\ \beta_{\omega \mathrm{b}}=& {\left[\left(\omega^{2} L_{\mathrm{b}} C_{\mathrm{b}}-R_{\mathrm{b}} G_{\mathrm{b}}\right) / 2+\right.} \\ &\left.\sqrt{\left(R_{\mathrm{b}}^{2}+\omega^{2} L_{\mathrm{b}}^{2}\right)\left(G_{\mathrm{b}}^{2}+\omega^{2} C_{\mathrm{b}}^{2}\right)}\right]^{\frac{1}{2}} \end{aligned}\right. $ | (5) |
式中:Rb为差模分量自阻;Gb为差模分量自导;Lb为差共模分量自感;Cb为差模分量自容。
| $ V_{\mathrm{dif}}-V_{\mathrm{com}}=\frac{\omega\left(\beta_{\omega \mathrm{a}}-\beta_{\omega \mathrm{b}}\right)}{\beta_{\omega \mathrm{b}} \beta_{\omega \mathrm{a}}}=\frac{1}{L_{\mathrm{b}} C_{\mathrm{b}}}-\frac{1}{L_{\mathrm{a}} C_{\mathrm{a}}} $ | (6) |
根据2条线路之间电感的耦合系数要大于电容的耦合系数可知:
| $ V_{\mathrm{dif}}-V_{\mathrm{com}}>0 $ | (7) |
即,差模分量比共模分量传输的快。
2 线路长度对电压突变量保护的影响分析 2.1 保护测点的电压与共模分量、差模分量的关系定义直流输电线路接地故障发生在0时刻,共模分量和差模分量到达保护测点处的时间可通过式(8)计算。
| $ \left\{\begin{array}{l} t_{\mathrm{com}}=\frac{S}{V_{\mathrm{com}}} \\ t_{\mathrm{dif}}=\frac{S}{V_{\mathrm{dif}}} \end{array}\right. $ | (8) |
式中:S为故障点与保护测点之间的线路长度;tcom,tdif分别为共模、差模分量到达保护测点的时间。
共模分量滞后差模分量的时间tΔ为:
| $ t_{\Delta}=t_{\mathrm{com}}-t_{\mathrm{dif}}=S\left(\frac{1}{V_{\mathrm{com}}}-\frac{1}{V_{\mathrm{dif}}}\right) $ | (9) |
根据式(3),正极和负极的电压共模分量、差模分量分别按式(10)和式(11)计算。
正极:
| $ \left\{\begin{array}{l} U_{\mathrm{com} 1}=U_{1}+U_{2} \\ U_{\mathrm{dif} 1}=U_{1}-U_{2} \end{array}\right. $ | (10) |
负极:
| $ \left\{\begin{array}{l} U_{\mathrm{com} 2}=U_{2}+U_{1} \\ U_{\mathrm{dif} 2}=U_{2}-U_{1} \end{array}\right. $ | (11) |
因此,直流电压变化量有:
| $ \left\{\begin{array}{l} \Delta U_{1}=\left(\Delta U_{\mathrm{com} 1}+\Delta U_{\mathrm{dif} 1}\right) / 2 \\ \Delta U_{2}=\left(\Delta U_{\mathrm{com} 2}+\Delta U_{\mathrm{dif} 2}\right) / 2 \end{array}\right. $ | (12) |
式中:ΔU1,ΔU2分别为正极、负极的电压变化量、ΔUcom1,ΔUcom2分别为正极、负极的电压共模分量变化量;ΔUdif1,ΔUdif2分别为正极、负极的电压差模分量变化量。
图 1所示的正极线路F1故障发生后,ΔU1与ΔUcom1,ΔUdif1,tΔ之间的关系和ΔU2与ΔUcom2,ΔUdif2,tΔ之间的关系如图 2所示。

|
图 2 共模分量和差模分量对电压变化量的影响 Fig. 2 Influence of common and differential modes on voltage variation |
根据图 2,可以得出以下结论:
(1) 故障初始的0时刻,差模分量到达保护测点处,电压发生第一次突变,正极和负极的电压变化量大小相等,极性相反。负极的电压变化量极性与负极线路接地故障发生时的电压变化量极性一致,符合负极线路接地故障的特征;正极的电压变化量极性符合正极线路接地故障的特征。此时,根据两极电压的变化不能区分故障极和非故障极。
(2) 共模分量到达保护测点处(时刻tΔ)后,直流电压发生第二次突变。正极电压的第一次突变和第二次突变极性相同,负极电压的第一次突变和第二次突变极性相反。
2.2 传统电压突变量保护逻辑正极:
| $ \left\{\begin{array}{l} \frac{\mathrm{d} U_{1}}{\mathrm{~d} t}<U_{\text {set1 }} \\ U_{1}<U_{\text {set2 }} \\ t>t_{\text {set }} \end{array}\right. $ | (13) |
负极:
| $ \left\{\begin{array}{l} \frac{\mathrm{d} U_{2}}{\mathrm{~d} t}>-U_{\text {set1 }} \\ U_{2}>-U_{\text {set2 }} \\ t>t_{\text {set }} \end{array}\right. $ | (14) |
式中:Uset1,-Uset1分别为正极、负极在双阀组运行(电压±800 kV)时的电压变化速率定值;Uset2,-Uset2分别为正极、负极在双阀组运行(电压±800 kV)时的电压定值;tset为时间定值。当正极或负极处于单阀组运行(电压±400 kV)时,电压变化速率定值、电压定值分别为Uset1/2,-Uset1/2和Uset2/2,-Uset2/2。
2.3 故障点与保护测点之间的距离对传统电压突变量保护的影响根据2.2节可知,传统电压突变量保护是通过检测直流电压的下降幅值和变化速率识别故障的。图 3给出了正极和负极直流输电线路发生故障后,传统电压突变量保护的动作过程。保护测点处电压变化最剧烈的2个时刻是故障波差模分量和故障波共模分量到达保护测点处的时间点,即时间0和时间tΔ处,这2个时间点的电压变化速率都能满足电压变化速率定值。保护测点处的电压变化量是差模分量变化量和共模分量变化量叠加而成,两者任意一个变化量所引起的电压变化量都不足以使电压瞬时值低于电压定值,即只有差模分量变化量和共模分量变化量同极性叠加才能使电压瞬时值低于定值。

|
图 3 传统电压突变量保护的动作过程 Fig. 3 Action process of traditional voltage differential protection |
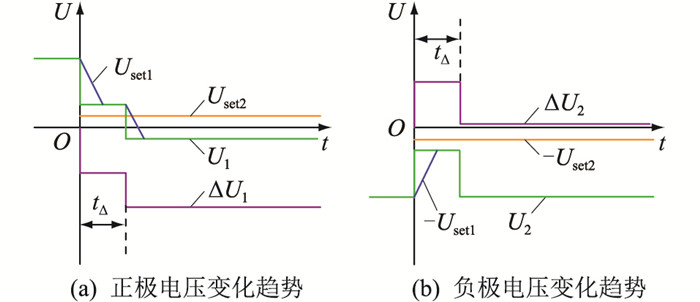
在两极运行阀组数目相等的情况下,两极的运行电压相等,两极的电压突变量保护定值完全相等。因为仅由差模分量变化量或共模分量变化量所引起的电压下降幅度都不足以使电压瞬时值低于电压定值Uset2,另一极电压突变量保护不会误动。图 4给出了正极直流输电线路发生故障时两极电压的变化趋势。
|
图 4 两极运行阀组数目相等时直流电压变化情况 Fig. 4 DC voltage variation at bipolar operation mode with equal number valves |
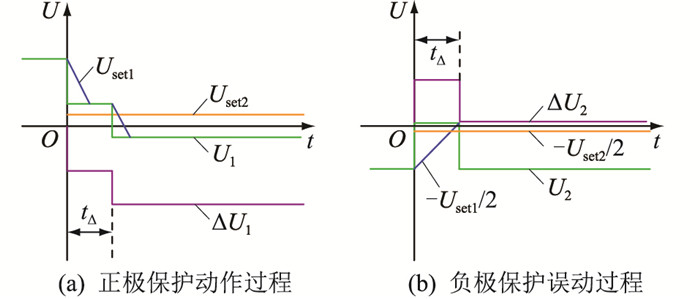
在正极双阀组运行、负极单阀组运行时,正极运行电压是负极运行电压的2倍,正极线路故障产生的故障波幅值也是负极线路故障产生的故障波幅值的2倍。因为负极单阀组运行,所以负极电压突变量保护的电压变化速率定值、电压定值分别为- Uset1/2,- Uset2/2。即,正极直流线路故障时,差模分量就能导致负极电压瞬时值满足电压突变量保护的定值。在差模分量到达保护测点后,如果共模分量在电压突变量保护的时间定值tset内没到达保护测点,那么负极电压突变量保护就会误动。图 5给出了这一过程中两极电压的变化趋势。
|
图 5 负极电压突变量保护的误动过程 Fig. 5 False tripped process of voltage differential protection at negative pole |
根据图 1,正极和负极共模分量的传输回路都包含大地,而且极性相同,而差模分量只在由两极线路、阀组所构成的回路上传输。接地故障发生后,故障电流的回路包含了大地,所以接地故障必定产生故障波共模分量变化量。
当正极发生接地故障时,共模分量的变化量小于零(地电压减正极初始电压),如式(15)所示。
| $ \frac{\mathrm{d} U_{\mathrm{com}}}{\mathrm{d} t}=\frac{\mathrm{d}\left(U_{1}+U_{2}\right)}{\mathrm{d} t}<0 $ | (15) |
当负极发生接地故障时,共模分量的变化量大于零(地电压减负极初始电压),如式(16)所示。
| $ \frac{\mathrm{d} U_{\text {com }}}{\mathrm{d} t}=\frac{\mathrm{d}\left(U_{1}+U_{2}\right)}{\mathrm{d} t}>0 $ | (16) |
当没有接地故障时,共模分量的变化量等于0。
综上,将共模分量变化量的极性作为电压突变量保护的判据能解决差模分量引起的非故障极电压突变量保护误动问题。改进后的判据如式(17)和式(18)所示。
正极:
| $ \left\{\begin{array}{l} \mathrm{d} U_{1} / \mathrm{d} t<U_{\text {set1 }} \\ U_{1}<U_{\text {set2 }} \\ \mathrm{d}\left(U_{1}+U_{2}\right) / \mathrm{d} t<U_{\text {set3 }} \\ t>t_{\text {set }} \end{array}\right. $ | (17) |
负极:
| $ \left\{\begin{array}{l} \mathrm{d} U_{1} / \mathrm{d} t<U_{\text {set1 }} \\ U_{1}<U_{\text {set2 }} \\ \mathrm{d}\left(U_{1}+U_{2}\right) / \mathrm{d} t<U_{\text {set3 }} \\ t>t_{\text {set }} \end{array}\right. $ | (18) |
式中:Uset3,- Uset3分别为正、负极电压的共模分量变化量定值。
3.2 定值整定改进后的电压突变量保护的整定方法与传统的电压突变量保护的整定方法相同。增加的共模分量变化量的极性判据类似于一个方向性判据,因此Uset3(-Uset3)的取值不应太大。文中推荐的整定方法如下:
(1) 定值应大于电压测量误差产生的共模分量变化量。假设单个电压测点的误差为5%,则共模分量的最大误差为10%,其除以相应的时间得到电压测量误差可能产生的最大共模分量变化量。
(2) 在本极发生区外故障时,比如换流阀与平波电抗器之间的极母线上发生金属性接地故障,线路另一端的共模分量变化量能满足Uset3(-Uset3)。
3.3 性能分析区内故障时,在差模分量到达保护测点时刻,传统的电压突变量保护不满足电压定值不会动作,必须要等到共模分量也到达保护测点处才能满足定值。式(17)和式(18)给出的改进算法增加了共模分量的极性判别,也是要等到共模分量到达保护测点处保护才动作,两者在快速性上并无差别。
根据2.2节推荐的整定方法,在本极发生区外故障时,增加的共模变化量极性判据仍然可以满足。因此,在本极线路发生区外接地故障时,改进后的电压突变量保护的可靠性、灵敏性和耐过渡电阻的特性取决于Uset1 (或-Uset1)和Uset2 (或-Uset2),与改进前相比并无差异。在另外一极线路发生接地故障时,增加的共模分量变化量的极性判据避免了双极线路的耦合导致保护误动,提高了可靠性。
另外,因为改进算法的核心理论是基于共模分量和差模分量传播速率的差异,而共模分量和差模分量传播速率只取决于线路的参数,与接地故障电阻大小无关,所以改进算法既适用于金属性接地故障,又适用于非金属性接地故障。
4 试验仿真及分析 4.1 仿真系统为了验证文中所提改进的电压突变量保护逻辑的可行性,根据图 1所示的拓扑结构搭建了双12脉动阀组构成的±800 kV特高压直流实时数字仿真系统(real time digital simulation system,RTDS),其中线路总长1 960 km,导线6分裂,子导线外径36.2 mm,分裂间距450 mm,水平距离22 m,塔高28 m,弧垂20 m。
将改进前、后的电压突变量保护时间定值tset整定为2 ms,故障点与保护测点之间的距离分150 km、1 800 km 2种情况,对图 1所示的正极直流线路金属接地故障F1进行仿真。
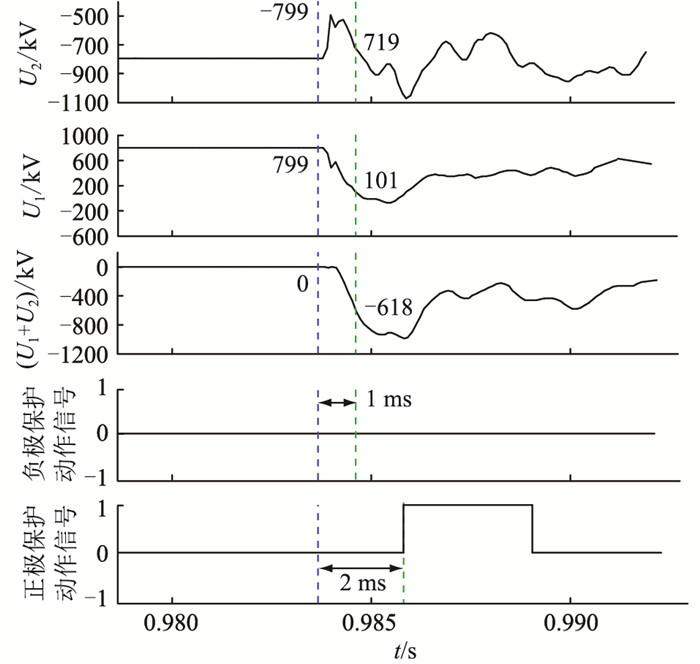
4.2 结果分析采用传统的电压突变量保护逻辑,特高压直流输电系统在双极四阀组工况下,正极F1故障点与保护测点之间的距离等于150 km时的波形如图 6所示。在正极故障瞬间,负极的电压从-799 kV变化至-500 kV之后在1 ms以内恢复。负极无论是电压下降的幅度,还是电压下降后持续的时间都没有达到电压突变量保护的定值,所以负极的电压突变量保护没有动作,符合2.3节的分析。
|
图 6 改进前的双极四阀组仿真波形 Fig. 6 The simulated waves under bipolar four-valve condition before improvement |
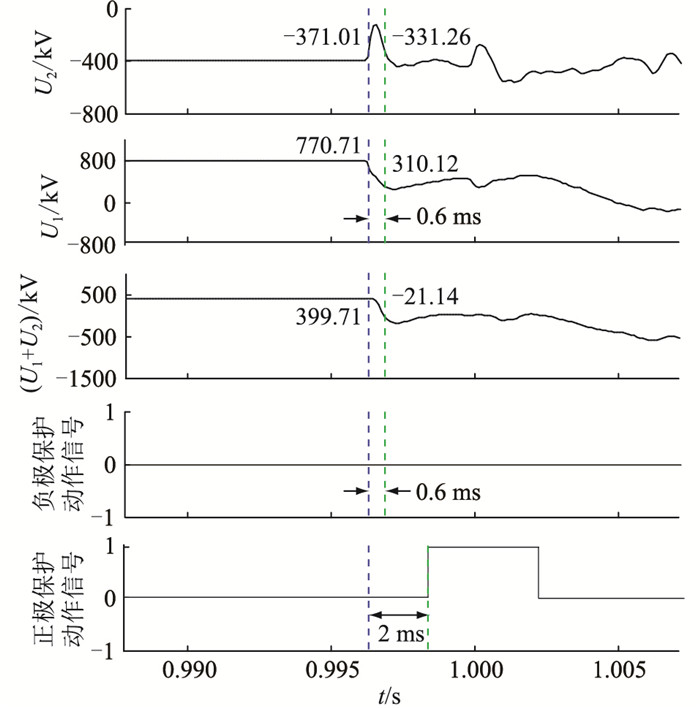
采用传统的电压突变量保护逻辑,特高压直流输电系统在正极双阀组负极单阀组运行工况下,正极F1故障点与保护测点之间的距离等于150 km时的波形如图 7所示。
|
图 7 改进前的负极单阀组仿真波形(tΔ < tset) Fig. 7 The simulated waves under single valve of ne-gative pole condition before improvement(tΔ < tset) |
在正极故障瞬间,负极的电压从-371.01 kV开始变化,在0.6 ms以内恢复。负极电压下降的幅度虽然满足定值Uset2,但是电压下降后持续的时间没有达到电压突变量保护的时间定值tset,所以负极的电压突变量保护没有动作。
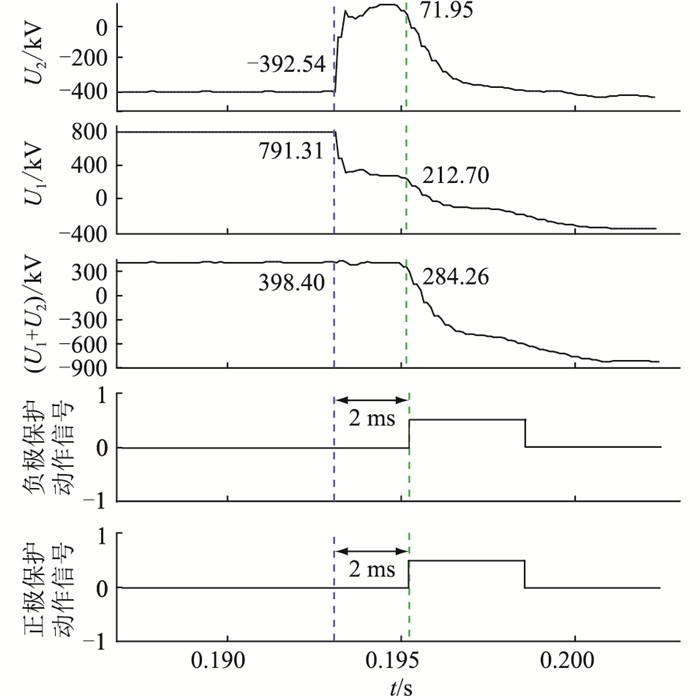
采用传统的电压突变量保护逻辑,特高压直流输电系统在正极双阀组负极单阀组运行工况,正极F1故障点与保护测点之间的距离等于1 800 km时的波形如图 8所示。为了便于观察负极电压的走势,没有投入负极的线路重启功能。正极故障后,负极的电压从-392.54 kV变化至100 kV附近,并且在保护的时间定值tset内都没有恢复,所以负极的电压突变量保护发生误动。
|
图 8 改进前的负极单阀组仿真波形(tΔ> tset) Fig. 8 The simulated waves under single valve of ne-gative pole condition before improvement(tΔ> tset) |
采用改进的电压突变量保护后,特高压直流输电系统在正极双阀组负极单阀组运行工况下,正极F1故障点与保护测点之间的距离等于1 800 km时的波形如图 9所示。差模分量在蓝色虚线处到达保护测点处,在蓝色虚线与绿色虚线之间,正极电压变化幅度535.8 kV,负极电压变化幅度516.2 kV,但是蓝色虚线与绿色虚线之间的共模电压变化量几乎等于0,没有达到定值Uset3,改进后的电压突变量保护没有因为差模分量引起的电压变化而误动。在共模分量到达保护测点后(绿色虚线),正极的电压突变量保护的3个判据全部满足,保护动作。
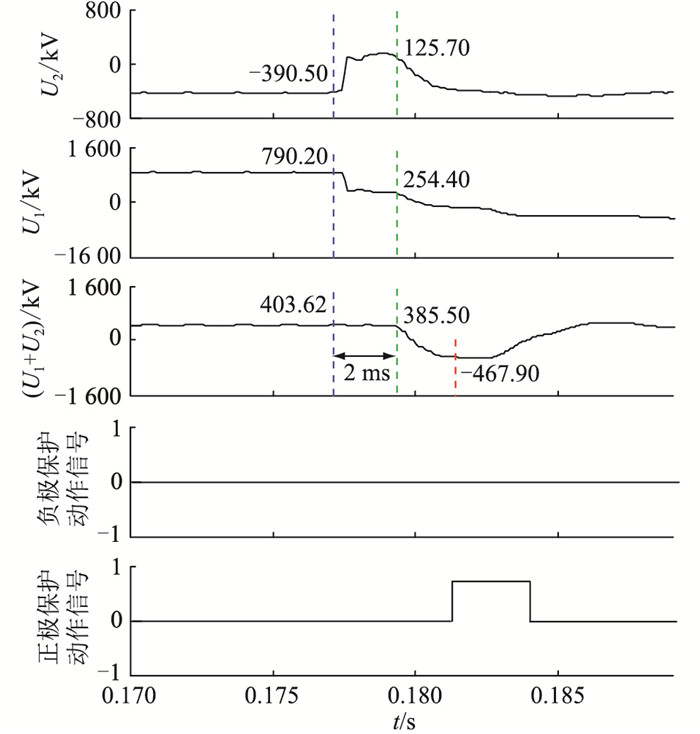
|
图 9 改进后的负极单阀组仿真波形(tΔ>tset) Fig. 9 The improved simulated waves under single valve of negative pole condition (tΔ> tset) |
文中首先通过时模变换解耦了高度耦合的正极电压和负极电压。其次,指出在特高压双极运行阀组数目不一致时引起电压突变量保护误动的原因是在差模分量到达保护测点后,共模分量在电压突变量保护的时间定值tset内没到达保护测点。再次,提出将电压共模分量变化量的极性作为识别故障极的主要判据,并将此判据与传统电压突变量保护的判据融合成改进的电压突变量保护。最后,通过仿真计算验证了改进的电压突变量保护的可靠性。
特高压直流输电系统在两极运行阀组数目不一致时,传统的电压突变量保护存在误动风险,如果误动,两极线路相继故障会导致特高压直流双极闭锁。文中提出的改进的电压突变量保护在区内故障时,其灵敏性、可靠性、快速性、选择性与传统的电压突变量保护无本质区别,但是在区外故障时,其可靠性和选择性优于传统的电压突变量保护,降低了特高压直流工程双极闭锁风险。
| [1] |
刘云. 同塔并架高压直流输电线路故障及保护特性研究[J]. 电力工程技术, 2019, 38(3): 163-169. LIU Yun. Characteristics of fault and protection of the multi HVDC transmission lines on the same tower[J]. Electric Power Engineering Technology, 2019, 38(3): 163-169. (  0) 0) |
| [2] |
戴熙杰. 直流输电基础[M]. 北京: 水利电力出版社, 1990. DAI Xijie. Foundation of HVDC transmission[M]. Beijing: Water Resources and Electric Power Press, 1990. (  0) 0) |
| [3] |
赵畹君. 高压直流输电工程技术[M]. 北京: 中国电力出版社, 2004. ZHAO Wanjun. HVDC transmission engineering technology[M]. Beijing: China Electric Power Press, 2004. (  0) 0) |
| [4] |
薛士敏, 贺家李, 李永丽, 等. 输电线路统一行波理论分析[J]. 电力系统自动化, 2007, 31(20): 32-35, 93. XUE Shimin, HE Jiali, LI Yongli, et al. Analysis of unified traveling wave theory for transmission lines[J]. Automation of Electric Power Systems, 2007, 31(20): 32-35, 93. DOI:10.3321/j.issn:1000-1026.2007.20.007 (  0) 0) |
| [5] |
李爱民, 蔡泽祥, 李晓华. 直流线路行波传播特性的解析[J]. 中国电机工程学报, 2010, 30(25): 94-100. LI Aimin, CAI Zexiang, LI Xiaohua. Study on the propagation characteristics of traveling waves in HVDC transmission lines on the basis of analytical method[J]. Proceedings of the CSEE, 2010, 30(25): 94-100. (  0) 0) |
| [6] |
SHU H C, ZHU Z Z, ZHANG G B, et al. Study on traveling wave propagation characteristics of ±800 UHVDC transmission lines[C]//2010 Asia-Pacific Power and Energy Engineering Conference. Chengdu, China. IEEE, 2010: 1-4.
(  0) 0) |
| [7] |
陈福锋, 杨阳, 宋国兵, 等. 单端量行波保护在中压柔性直流配电网的适应性分析[J]. 电力系统保护与控制, 2016, 44(22): 50-55. CHEN Fufeng, YANG Yang, SONG Guobing, et al. Adaptability analysis of single terminal traveling wave protection in mid-voltage DC distribution based on VSC[J]. Power System Protection and Control, 2016, 44(22): 50-55. DOI:10.7667/PSPC160216 (  0) 0) |
| [8] |
丁津津, 汤汉松, 高博, 等. 基于特征选择与TCED的UHVDC输电线路故障判定方法[J]. 电力工程技术, 2020, 39(3): 92-98. DING Jinjin, TANG Hansong, GAO Bo, et al. Fault diagnosis method of UHVDC transmission line based on feature selection and TCED[J]. Electric Power Engineering Technology, 2020, 39(3): 92-98. (  0) 0) |
| [9] |
李爱民, 蔡泽祥, 李晓华, 等. 高压直流输电线路行波保护影响因素分析及改进[J]. 电力系统自动化, 2010, 34(10): 76-80, 96. LI Aimin, CAI Zexiang, LI Xiaohua, et al. Analysis of influence factors and improvement of traveling wave protections for HVDC line[J]. Automation of Electric Power Systems, 2010, 34(10): 76-80, 96. (  0) 0) |
| [10] |
田得良, 蔡泽祥, 梁益, 等. 特高压直流输电线路行波保护电流判据优化[J]. 电网技术, 2016, 40(8): 2548-2554. TIAN Deliang, CAI Zexiang, LIANG Yi, et al. Optimization strategy on current criterion of travelling wave protection for UHVDC transmission system[J]. Power System Technology, 2016, 40(8): 2548-2554. (  0) 0) |
| [11] |
LI B, LI Y, HE J W, et al. A novel single-ended transient-voltage-based protection strategy for flexible DC grid[J]. IEEE Transactions on Power Delivery, 2019, 34(5): 1925-1937. DOI:10.1109/TPWRD.2019.2910390 (  0) 0) |
| [12] |
郑伟, 武霁阳, 李海锋, 等. 特高压直流线路自适应行波保护[J]. 电网技术, 2015, 39(7): 1995-2001. ZHENG Wei, WU Jiyang, LI Haifeng, et al. Research on adaptive travelling wave based protection for UHVDC transmission line[J]. Power System Technology, 2015, 39(7): 1995-2001. (  0) 0) |
| [13] |
李岩, 龚雁峰, 姜斌. 一种基于方向行波的多端VSC-HVDC系统保护策略[J]. 电力工程技术, 2017, 36(1): 70-73, 83. LI Yan, GONG Yanfeng, JIANG Bin. A protection scheme for multiterminal VSC-HVDC system based on direction traveling waves[J]. Electric Power Engineering Technology, 2017, 36(1): 70-73, 83. DOI:10.3969/j.issn.1009-0665.2017.01.015 (  0) 0) |
| [14] |
张武军, 王慧芳, 何奔腾. T接线路行波差动保护[J]. 电力系统自动化, 2007, 31(3): 61-66. ZHANG Wujun, WANG Huifang, HE Benteng. Traveling-wave differential protection on teed transmission lines[J]. Automation of Electric Power Systems, 2007, 31(3): 61-66. DOI:10.3321/j.issn:1000-1026.2007.03.013 (  0) 0) |
| [15] |
梁益, 蔡泽祥, 田得良, 等. 直流线路行波保护解析整定方法[J]. 电网技术, 2017, 41(1): 298-304. LIANG Yi, CAI Zexiang, TIAN Deliang, et al. Analytical method for travelling wave protection setting of HVDC transmission line[J]. Power System Technology, 2017, 41(1): 298-304. (  0) 0) |
| [16] |
孔飞, 张保会, 王艳婷. 基于行波波形相关性分析的直流输电线路纵联保护方案[J]. 电力系统自动化, 2014, 38(20): 108-114. KONG Fei, ZHANG Baohui, WANG Yanting. A novel pilot protection scheme for HVDC transmission lines based on waveform correlation analysis of traveling wave[J]. Automation of Electric Power Systems, 2014, 38(20): 108-114. DOI:10.7500/AEPS20130922015 (  0) 0) |
| [17] |
李小鹏, 汤涌, 滕予非, 等. 基于反行波幅值比较的高压直流输电线路纵联保护方法[J]. 电网技术, 2016, 40(10): 3095-3101. LI Xiaopeng, TANG Yong, TENG Yufei, et al. Pilot protection method based on amplitude comparison of backward traveling wave for HVDC transmission lines[J]. Power System Technology, 2016, 40(10): 3095-3101. (  0) 0) |
| [18] |
戴志辉, 张程, 刘宁宁, 等. 基于反行波差值的特高压直流线路纵联保护方案[J]. 电力系统保护与控制, 2019, 47(21): 1-10. DAI Zhihui, ZHANG Cheng, LIU Ningning, et al. A pilot protection scheme for UHVDC lines based on backward traveling-wave difference[J]. Power System Protection and Control, 2019, 47(21): 1-10. (  0) 0) |
| [19] |
杨亚宇, 邰能灵, 刘剑, 等. 利用边界能量的高压直流线路纵联保护方案[J]. 中国电机工程学报, 2015, 35(22): 5757-5767. YANG Yayu, TAI Nengling, LIU Jian, et al. A pilot protection scheme for HVDC transmission lines based on boundary energy[J]. Proceedings of the CSEE, 2015, 35(22): 5757-5767. (  0) 0) |
| [20] |
郭宏光, 吴庆范, 黄金海, 等. 特高压直流输电线路间电磁耦合对电压突变量保护影响的研究[J]. 电力系统保护与控制, 2015, 43(18): 114-119. GUO Hongguang, WU Qingfan, HUANG Jinhai, et al. Study on the influence of electromagnetic coupling of UHVDC power transmission lines on the voltage derivative protection[J]. Power System Protection and Control, 2015, 43(18): 114-119. DOI:10.7667/j.issn.1674-3415.2015.18.019 (  0) 0) |
| [21] |
武家辉, 王维庆, 王海云, 等. 哈郑特高压直流送端电网静态电压薄弱点研究与无功补偿[J]. 电力电容器与无功补偿, 2018, 39(3): 134-139. WU Jiahui, WANG Weiqing, WANG Haiyun, et al. Study on the weak point of static voltage of transmission end in Hazheng UHVDC transmission system and reactive power compensation[J]. Power Capacitors & Reactive Power Compensation, 2018, 39(3): 134-139. (  0) 0) |
| [22] |
任军辉, 张帆, 杨晓平. 滇西北至广东特高压直流输电工程直流回路的谐振研究[J]. 电力电容器与无功补偿, 2018, 39(6): 29-32. REN Junhui, ZHANG Fan, YANG Xiaoping. Study on resonance of DC circuit for Dianxibei to Guangdong UHVDC project[J]. Power Capacitors & Reactive Power Compensation, 2018, 39(6): 29-32. (  0) 0) |
| [23] |
葛耀中. 新型继电保护和故障测距的原理与技术[M]. 2版. 西安: 西安交通大学出版社, 2007. GE Yaozhong. Principle and technology of new relay protection and fault location[M]. 2nd ed. Xi'an: Xi'an Jiaotong University Press, 2007. (  0) 0) |
| [24] |
邵庆祝, 赵晓东, 赵创业, 等. 基于高压直流输电线路分布参数模型的模态电流差动保护算法[J]. 电力系统保护与控制, 2021, 49(22): 171-179. SHAO Qingzhu, ZHAO Xiaodong, ZHAO Chuangye, et al. Modal current differential protection method based on distributed parameter model of an HVDC transmission line[J]. Power System Protection and Control, 2021, 49(22): 171-179. (  0) 0) |
| [25] |
王永进, 樊艳芳, 唐勇, 等. 考虑强非线性和波速变化特性的特高压直流输电线路故障测距方法[J]. 电力系统保护与控制, 2020, 48(5): 17-25. WANG Yongjin, FAN Yanfang, TANG Yong, et al. Fault location method for UHVDC transmission lines considering strong nonlinearity and wave velocity variation characteristics[J]. Power System Protection and Control, 2020, 48(5): 17-25. (  0) 0) |
| [26] |
韩昆仑, 蔡泽祥, 贺智, 等. 高压直流输电线路故障行波传播特性及其对行波保护的影响[J]. 电力系统保护与控制, 2013, 41(21): 20-25. HAN Kunlun, CAI Zexiang, HE Zhi, et al. Propagation characteristic of fault traveling wave on HVDC line and its influence on HVDC line traveling wave protection[J]. Power System Protection and Control, 2013, 41(21): 20-25. (  0) 0) |
| [27] |
高本锋, 董沛毅, 刘辛晔, 等. 高压直流输电线路微分欠压保护特性与定值整定[J]. 电网技术, 2015, 39(8): 2303-2311. GAO Benfeng, DONG Peiyi, LIU Xinye, et al. Research of HVDC transmission line differential under-voltage protection characteristics and value setting[J]. Power System Technology, 2015, 39(8): 2303-2311. (  0) 0) |
| [28] |
吴庆范, 黄金海, 张爱玲, 等. 团林换流站电压突变量保护研究[J]. 南方电网技术, 2014, 8(4): 37-41. WU Qingfan, HUANG Jinhai, ZHANG Ailing, et al. Research of undervoltage sensing protection at Tuanlin converter station[J]. Southern Power System Technology, 2014, 8(4): 37-41. (  0) 0) |
| [29] |
付华, 刘公权, 邢亮. 基于同步挤压小波变换的故障行波测距方法[J]. 电力系统保护与控制, 2020, 48(2): 18-24. FU Hua, LIU Gongquan, XING Liang. Fault traveling wave ranging method based on synchrosqueezing wavelet transform[J]. Power System Protection and Control, 2020, 48(2): 18-24. (  0) 0) |
| [30] |
刘涛, 李明, 李婧靓, 等. 贵广Ⅰ回直流线路电压突变量保护逻辑的优化[J]. 南方电网技术, 2014, 8(3): 33-36. LIU Tao, LI Ming, LI Jingjing, et al. Optimization of undervoltage sensing protection logic in Guizhou-Guangdong HVDC line Ⅰ[J]. Southern Power System Technology, 2014, 8(3): 33-36. (  0) 0) |
 2022, Vol. 41
2022, Vol. 41


 杨建明(1984),男,硕士,高级工程师,从事高压直流输电系统控制保护相关工作(E-mail:
杨建明(1984),男,硕士,高级工程师,从事高压直流输电系统控制保护相关工作(E-mail: