文章编号: 2096-3203(2021)06-0009-09 中图分类号: TM715
2. 浙江大学电气工程学院, 浙江 杭州 310058
准确的负荷预测不仅能为电力调度提供依据,而且对电网的规划和稳定运行具有重要意义[1-3]。传统的负荷预测可分为点预测和区间预测[4-7]。点预测是用来预测某一时刻具体的数值[8],通常以预测值和实际值的误差最小为目标;而区间预测是预测某一时刻出力区间,通常以低区间带宽和高区间覆盖率为目标[9]。传统的负荷预测大多是确定性点预测,但由于电力系统受不确定性因素影响,负荷功率也具有不确定性。单纯的点预测无法应对负荷的不确定性。区间预测以概率的形式有效地应对出力的不确定性,通过预测负荷功率上下界,为决策者提供更多信息。因此提高电力负荷的区间预测精度成为目前研究的热门方向。
国内外人员对区间预测进行了广泛的研究。区间预测主要有统计方法[10-11]、上下区间估计[12-13]以及组合预测方法[14]等。文献[9]采用长短期记忆(long short-term memory, LSTM)网络进行点预测并且构建误差的核密度估计,构造不同置信区间下的负荷区间。文献[15]利用分位数回归(quantile regression, QR)构建不同模型从而得到概率预测结果。单纯利用QR很难以非线性拟合的方式去拟合复杂的函数。因此,为了提高区间预测效果,常将神经网络模型和QR一起构建概率预测模型。文献[16]将分位数回归和随机森林(random forest,RF)结合在一起以预测负荷的概率密度,效果远高于传统QR。除了随机森林与分位数相结合,还有支持向量机(support vector machine, SVM)[17]以及径向基函数(radial basis function,RBF)[18]等常见负荷预测方法。
为提高负荷预测的精度,常采用数据分解从数据本身出发对数据分解得到子数据,然后对子数据进行预测重构得到最终的预测结果。对数据进行分解的常见方法有小波分解(wavelet decomposition, WD)[19]、经验模态分解(empirical mode decomposition, EMD)[20-22]等。文献[23]采用经验模态分解将负荷分解为多个模态,然后分别进行预测, 但EMD易受模态混叠的影响。
传统分解、求和预测的方法大多运用在点预测上,较少运用在区间预测上。同时,传统的分解方法由于存在模态混叠的现象,导致预测精度较低。为进一步提高预测精度以及模型分解的泛化能力,文中利用变分模态分解(variational mode decomposition, VMD)提升分解效果,采用深度学习网络长短期记忆神经网络分位数回归(long short-term memory neural network quantile regression, LSTMQR)提升预测精度,提出一种基于VMD-LSTMQR的滚动母线负荷区间预测。首先,采用中心频率法确定VMD母线负荷的最佳分解数量,并将原始的母线负荷分解成一系列不同频率特征的子序列;其次,采用区间预测指标确定不同子序列的最佳滚动步长;然后,分别对各子序列进行LSTMQR区间预测,得到不同子序列的预测结果;最后,将各子序列的区间预测重构,得到原始负荷序列的区间预测。
1 负荷区间预测核心模型 1.1 VMD的基本原理VMD能够自适应地对信号进行分解[24]。不同于传统EMD的递归方式求解模型,VMD通过采用非递归的方式将信号分解成若干层,有效消除欠包络和过包络问题,对噪声具有更好的自适应性。对于一段时间序列x(t),通过迭代搜寻变分模型将时间序列分解成有限带宽的模态分量。设第i个模态分量为ui(t),对应的中心频率为ωi,具体的实现步骤如下。
(1) 各模态的带宽计算。对于每一个分解得到的模态分量ui(t),采用Hilbert变换得到单侧谱。
(2) 将每一个模态函数的中心频率ωi的指数项进行混叠,将模态函数的频谱调制到基频带。
(3) 利用高斯平滑法对已经解调的信号估计其带宽,即计算解调信号的L2范数。转化为求解带约束的变分问题,目标函数为:
| $ \left\{\begin{array}{l} \min \left\{\sum\limits_{i=1}^{K}\left\|\partial_{t}\left[\left(\delta(t)+\frac{\mathrm{j}}{{\rm{ \mathit{ π} }} t}\right) \otimes u_{i}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{i} t}\right\|_{2}^{2}\right\} \\ \text { s.t. } \sum\limits_{i=1}^{K} u_{i}(t)=x(t) \end{array}\right. $ | (1) |
式中:∂t为t的偏导;δ(t)为Dirac分布函数;K为分量个数;ⓧ为卷积运算。为了实现上述目标函数求解,引入二次惩罚项α和拉格朗日乘子λ将极值约束问题转换为无约束问题,如式(2)所示。
| $ \begin{gathered} L\left(u_{i}, \omega_{i}, \lambda\right)= \\ \alpha \sum\limits_{i=1}^{K}\left\|\partial_{t}\left[\left(\delta(t)+\frac{\mathrm{j}}{{\rm{ \mathit{ π} }} t}\right) \otimes u_{i}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{i} t}\right\|_{2}^{2}+ \\ \left\|x(t)-\sum\limits_{i=1}^{K} u_{i}(t)\right\|_{2}^{2}+ \\ \left\langle\lambda(t), x(t)-\sum\limits_{i=1}^{K} u_{i}(t)\right\rangle \end{gathered} $ | (2) |
对式(2)采用交替方向乘子法更新各模态量以及中心频率,如式(3)所示。
| $ \left\{\begin{array}{l} \hat{u}_{i, n+1}(\omega)=\frac{\hat{f}(\omega)-\sum\limits_{p \neq i}^{K} \hat{u}_{p, n}(\omega)+\frac{\hat{\lambda}_{n}(\omega)}{2}}{1+2 \alpha\left(\omega-\omega_{i, n}\right)^{2}} \\ \omega_{i, n+1}=\frac{\int_{0}^{\infty} \omega\left|\hat{u}_{i, n+1}(\omega)\right|^{2} \mathrm{~d} \omega}{\int_{0}^{\infty}\left|\hat{u}_{i, n+1}(\omega)\right|^{2} \mathrm{~d} \omega} \end{array}\right. $ | (3) |
式中:
基于QR的LSTM将QR作为LSTM中的一层。通过改变LSTM不同分位点下的损失函数,构建LSTM的不同条件分位数函数模型,其结构见图 1。
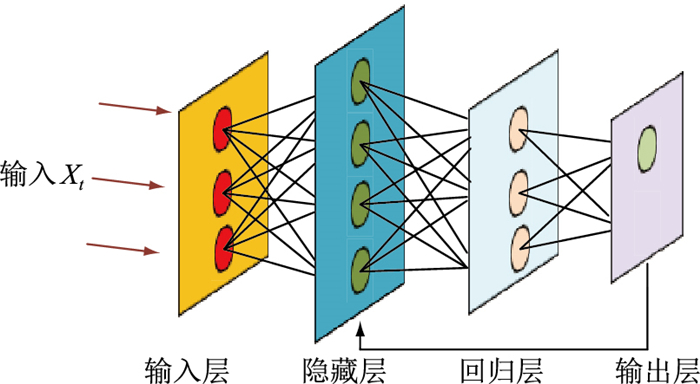
|
图 1 LSTMQR模型 Fig. 1 The model of LSTMQR |
在不同分位点τi下的LSTM的损失函数,即:
| $ \begin{gathered} L\left(\tau_{i}\right)=\min \left[\sum\limits_{t=1}^{N} \rho_{\tau_{i}}\left(Y_{t}-g\left(X_{t}, W\left(\tau_{i}\right), b\left(\tau_{i}\right)\right)\right)+\right. \\ \left.\gamma \sum W^{2}\left(\tau_{i}\right)\right] \end{gathered} $ | (4) |
式中:W(τi),b(τi)分别为LSTM的权重和偏置在分位点τi的集合;γ为正则项惩罚系数;Xt,Yt分别为LSTM的输入和输出;g(·)为映射函数;ρτi(a)为检验函数,如式(5)所示。
| $ \rho_{\tau_{i}}(a)=\left\{\begin{array}{l} a \tau_{i} \quad \tau_{i} \geqslant 0 \\ a\left(\tau_{i}-1\right) \quad \tau_{i} \leqslant 0 \end{array}\right. $ | (5) |
式中:a为整体性变量。
为获得不同分位点τi下的最优W(τi),b(τi),采用梯度下降法进行求解[25]。
2 基于VMD-LSTMQR的滚动负荷区间预测模型 2.1 滚动预测模式文中采用滚动模式对不同子序列区间预测。对于N维的负荷序列,采用VMD分解之后,各子序列的长度也为N维。
滚动模式的步骤为:已知第i个子序列的前n时刻真实数据序列为yi, 1, yi, 2, …, yi, n,根据已知的子序列前n时刻数据去预测n+1时刻的子序列数据出力区间;当达到n+1时刻,将该时刻的数据加入真实数据中并剔除离数据点最远的那个数据,此时时间序列为yi, 2, yi, 3, …, yi, n+1;之后采用该时刻的时间序列去预测n+2时刻子序列的出力区间,按照这种滚动预测模式,完成子序列区间预测。
假设第i个子序列的滚动步长为Ni,采用LSTMQR方法进行区间预测,那么训练集的输入与输出如式(6)所示。
| $ \boldsymbol{X}_{\mathrm{TR}, i}=\left[\begin{array}{cccc} x_{1} & x_{2} & \cdots & x_{N_{i}} \\ x_{2} & x_{3} & \cdots & x_{N_{i}+1} \\ \vdots & \vdots & & \vdots \\ x_{m} & x_{m+1} & \cdots & x_{m+N_{i}-1} \end{array}\right], \boldsymbol{Y}_{\mathrm{TR}, i}=\left[\begin{array}{c} x_{N_{i}+1} \\ x_{N_{i}+2} \\ \vdots \\ x_{m+N_{i}} \end{array}\right] $ | (6) |
式中:XTR, i为第i个子序列的训练输入样本,训练维度为m×Ni;YTR, i为第i个子序列的训练输出样本,训练维度为m维。
在进行LSTMQR区间预测时,根据所设置的分位数预测区间与输入、输出训练集,得到不同分位数下的结果。在进行模型测试的过程中,根据不同的分位数得到所预测数值的区间。测试模型的90%置信区间含义为测试集区间输出由0.05至0.95的分位数预测结果,如式(7)所示。
| $ \begin{gathered} \boldsymbol{X}_{\mathrm{TE}, i} =\left[\begin{array}{cccc} x_{m+1} & x_{m+2} & \cdots & x_{N_{i}+m} \\ x_{m+2} & x_{m+3} & \cdots & x_{N_{i}+m+1} \\ \vdots & \vdots & & \vdots \\ x_{N-N_{i}} & x_{N-N_{i}+1} & \cdots & x_{N-1} \end{array}\right], \\ \boldsymbol{Y}_{\mathrm{TE}, i} =\left[\begin{array}{ccc} x_{N_{i}+m+1}\left(\tau_{i}\right) & x_{N_{i}+m+1}\left(1-\tau_{i}\right) \\ x_{N_{i}+m+2}\left(\tau_{i}\right) & x_{N_{i}+m+2}\left(1-\tau_{i}\right) \\ \vdots & \vdots \\ x_{N}\left(\tau_{i}\right) & x_{N}\left(1-\tau_{i}\right) \end{array}\right] \end{gathered} $ | (7) |
式中:XTE, i为第i个子序列的测试输入样本,训练维度为(N-Ni-m)×Ni;YTE, i为第i个子序列的测试输出样本,训练维度为(N-Ni-m)×2。
2.2 基于VMD-LSTMQR负荷区间预测流程基于VMD-LSTMQR负荷区间预测是先将负荷时间序列分解成K个子序列,然后分别对K个子序列进行LSTMQR的滚动区间预测,根据各子序列区间预测结果进行子序列重构,得到最终的预测结果。基于VMD-LSTMQR负荷滚动预测的流程图如图 2所示,具体的步骤如下:
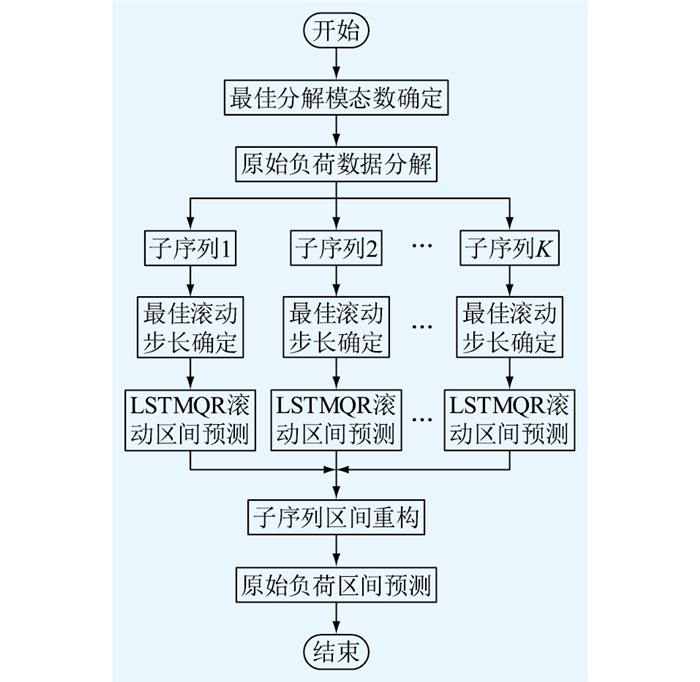
|
图 2 基于VMD-LSTMQR滚动负荷区间预测流程 Fig. 2 The process of rolling interval load prediction based on VMD-LSTMQR |
(1) 对历史的母线负荷数据进行VMD。采用中心频率法确定最佳的分解数量K,并将原始负荷序列分解成K个不同频率特征的子序列。
(2) 根据区间预测指标分别确定不同子序列最优的滚动预测步长。
(3) 采用滚动预测模式对分解的K个子序列分别进行LSTMQR区间预测。
(4) 对预测完成的子序列进行子序列重构,得到原始的负荷区间预测。
2.3 评价指标文中用3个区间指标评价区间预测性能[13]。
(1) 预测区间覆盖率(prediction interval cover ̄age probability,PICP)用于评估预测区间的可靠性。PICP越大表示越多的实际值落入区间概率中,预测效果越好,其表达如式(8)所示。
| $ e_{\mathrm{PICP}}=\frac{1}{N} \sum\limits_{i=1}^{N} \eta_{i} \times 100 \% $ | (8) |
式中:N为预测样本数量;ηi为布尔值,当所预测的区间包含实际功率数值时,记为1,否则记为0。
(2) 预测区间平均带宽(prediction interval normalized average width,PINAW)用于反映预测区间的清晰度。结合预测区间覆盖率指标,PINAW越窄,区间覆盖率预测越高,预测效果越好, 其表达如式(9)所示。
| $ e_{\mathrm{PINAW}}=\frac{1}{N} \sum\limits_{i=1}^{N}\left[\left(U_{i}-L_{i}\right) / y_{\max }\right] $ | (9) |
式中:ymax为预测样本中的最大值;Li为第i个样本下边界值;Ui为第i个样本上边界值。
(3) 归一平均偏差(normalized average deviation,NAD)用于评估实际功率远离预测区间带的程度。NAD越小表示未落入点离预测区间带越近, 其表达如式(10)所示。
| $ e_{\mathrm{NAD}}=\frac{1}{N} \sum\limits_{i=1}^{N} \theta_{i} $ | (10) |
其中:
| $ \theta_{i}= \begin{cases}\left(L_{i}-y_{i}\right) /\left[\frac{1}{N} \sum\limits_{i=1}^{N}\left(U_{i}-L_{i}\right)\right] & y_{i}<L_{i} \\ 0 \quad y_{i} \in\left[L_{i}, U_{i}\right] & \\ \left(y_{i}-U_{i}\right) /\left[\frac{1}{N} \sum\limits_{i=1}^{N}\left(U_{i}-L_{i}\right)\right] & y_{i}>U_{i}\end{cases} $ | (11) |
式中:yi为第i个样本的实测值。
3 算例仿真文中以220 kV与10 kV的母线负荷数据分别验证文中所提方法的有效性。所选取的220 kV母线数据时间是从2017年5月1日到2017年5月31日,采样间隔为5 min。10 kV母线负荷数据时间从2017年1月1日到2018年1月1日,采样间隔为1 h。220 kV和10 kV母线负荷时间序列如图 3所示。文中将220 kV母线负荷前25 d作为训练数据,后6 d作为测试数据;10 kV母线负荷前300 d作为训练数据,后65 d作为测试数据。文中所设置的分位数区间为[0.05, 0.95],间隔为0.05。
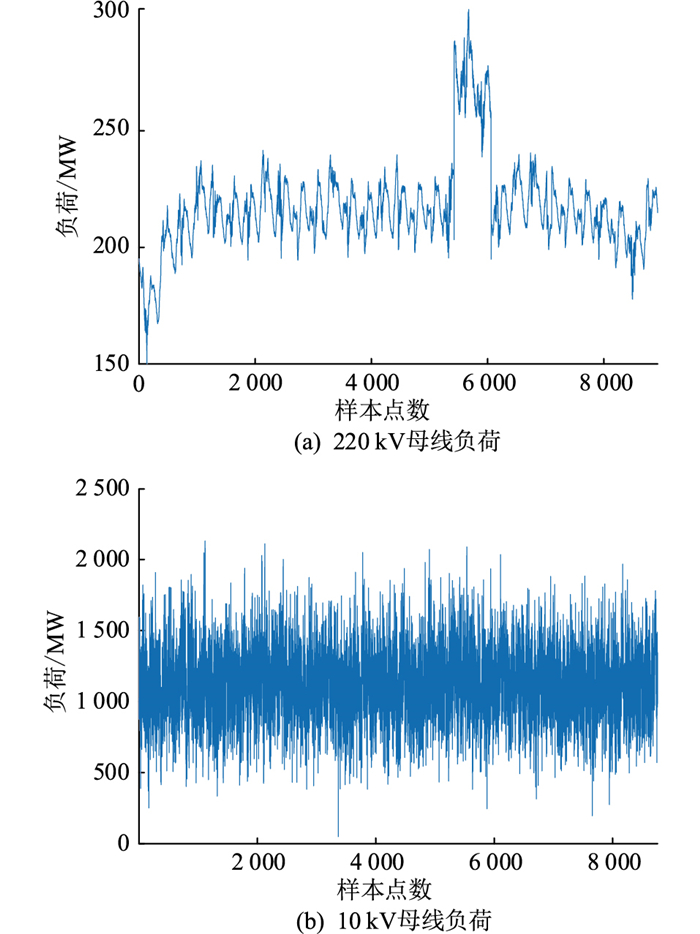
|
图 3 220 kV和10 kV母线负荷 Fig. 3 Bus load power of 220 kV and 10 kV |
从图 3可知,10 kV母线和220 kV母线的整体波动性比较大,具有非平稳性。因此,采用VMD将负荷序列进行分解得到K个不同频率特征的子序列,以提高整体的预测效果。在分解前,采用中心频率法确定最佳分解数量K,模态过多将导致模态重复,模态过少将导致模态分解不够。为确定最佳分解数量K,文中将设定K的取值范围,按照分解的模态数计算其中心频率。若分解到K+1时,有2个模态的中心频率比较相近,则说明出现了多模态的情况,最佳的分解个数为K。文中以220 kV母线负荷为例进行分析。不同分解数量下220 kV母线负荷中心频率结果如表 1所示。
|
|
表 1 220 kV母线负荷不同分解个数下的中心频率 Table 1 The center frequency of different decom- position numbers of 220 kV bus load powe |
由表 1可知,当分解到模态数为7的时候,模态2的中心频率为61 Hz,模态3的中心频率为92 Hz,2个模态的中心频率比较接近。而分解到模态数为6的时候,6个模态之间的中心频率相差比较大。因此,220 kV母线负荷的最佳分解模态数为6。并且,模态的中心频率按照模态高低进行排序,模态1的频率最低,模态6的频率最高。图 4是经过VMD之后的模态1和模态6子序列能量。
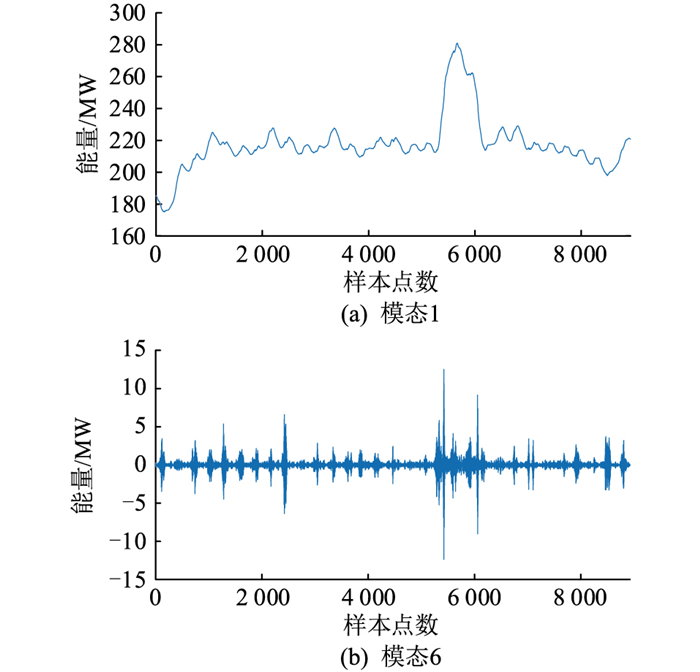
|
图 4 经过VMD之后的模态1和模态6子序列结果 Fig. 4 The subsequence results of mode 1 and mode 6 after VMD |
由图 4可见,模态1的子序列比较平稳,与原负荷序列的趋势走向一致。并且分解之后的数值功率比较大,与原负荷功率的数值比较接近。而模态6的分解频率最高,波动性比较大,分解之后的数值也比较小。因此,模态1的预测结果对最终原始负荷序列的影响最大,而其他模态影响相对较小。
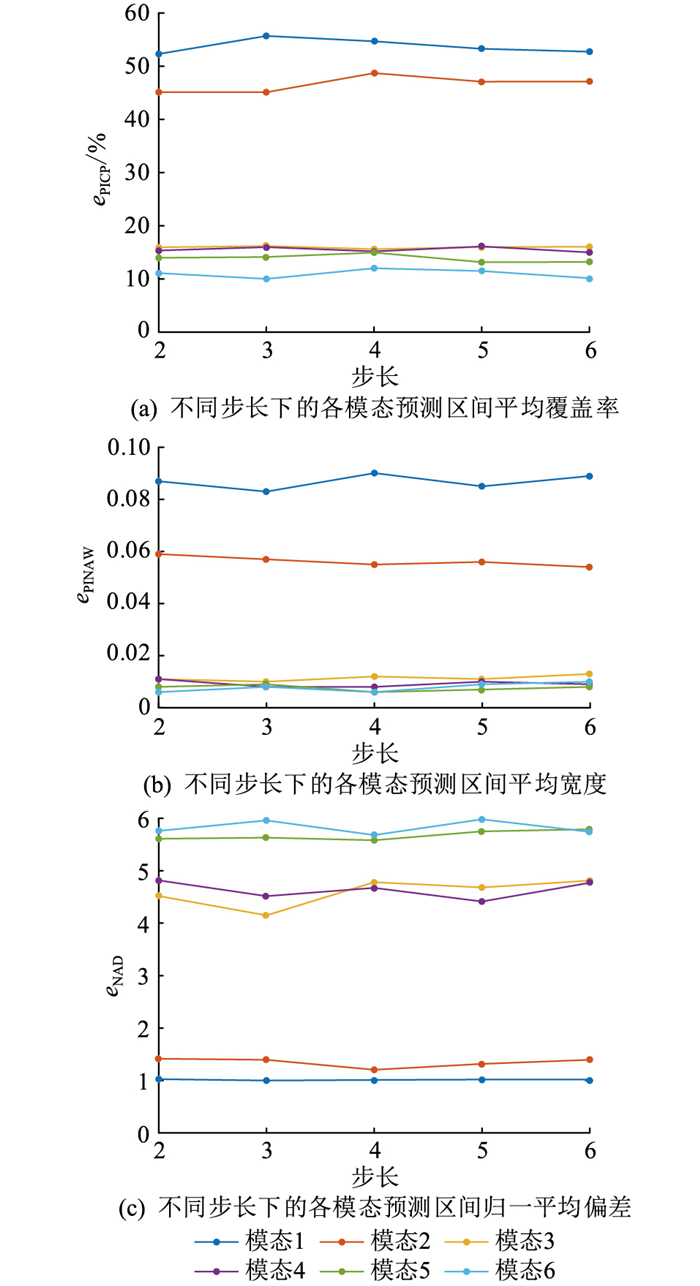
在对不同的分解序列进行预测时,需找到合适的滚动步长。滚动步长过大,数据冗余;滚动步长偏小,无法体现数据的特征。合理的数据长度不仅能包含数据的特征,而且能够避免无效信息。因此,文中设定不同的步长范围,根据最优指标选取最后的滚动步长。不同子分解序列所设定的步长范围为2~6。不同子序列的各步长指标见图 5。
|
图 5 不同步长下各模态区间数值指标 Fig. 5 Index values of each mode under different steps |
图 5反映的是不同步长下不同模态的3个评价指标数值。由于模态1和模态2比较平稳,所以预测区间覆盖率比较高,而模态3至模态6波动比较大,整体预测区间效果不佳。
根据3个指标选取最为合适的步长。在模态1中步长3在最窄的区间带宽下有着更高的区间覆盖率,偏离程度也最低。在模态2中,步长4的区间宽度略低于步长6,但预测区间覆盖率以及偏离程度优于步长6,因此,模态2的最佳步长为4。
在模态3中,步长3的3个指标最佳。在模态4中,虽然步长5的覆盖率比步长3的覆盖率略高,但区间的宽度以及偏离程度比步长3小,故模态4的最佳步长为3。步长4在模态5和模态6中的3个指标最优。由于模态3到模态6的波动比较大,且数值也比较小,其预测效果不佳,可选取任一步长,文中仅挑选不佳结果中最好的步长。综上,模态1到模态6的最佳滚动步长分别为3,4,3,3,4,4。
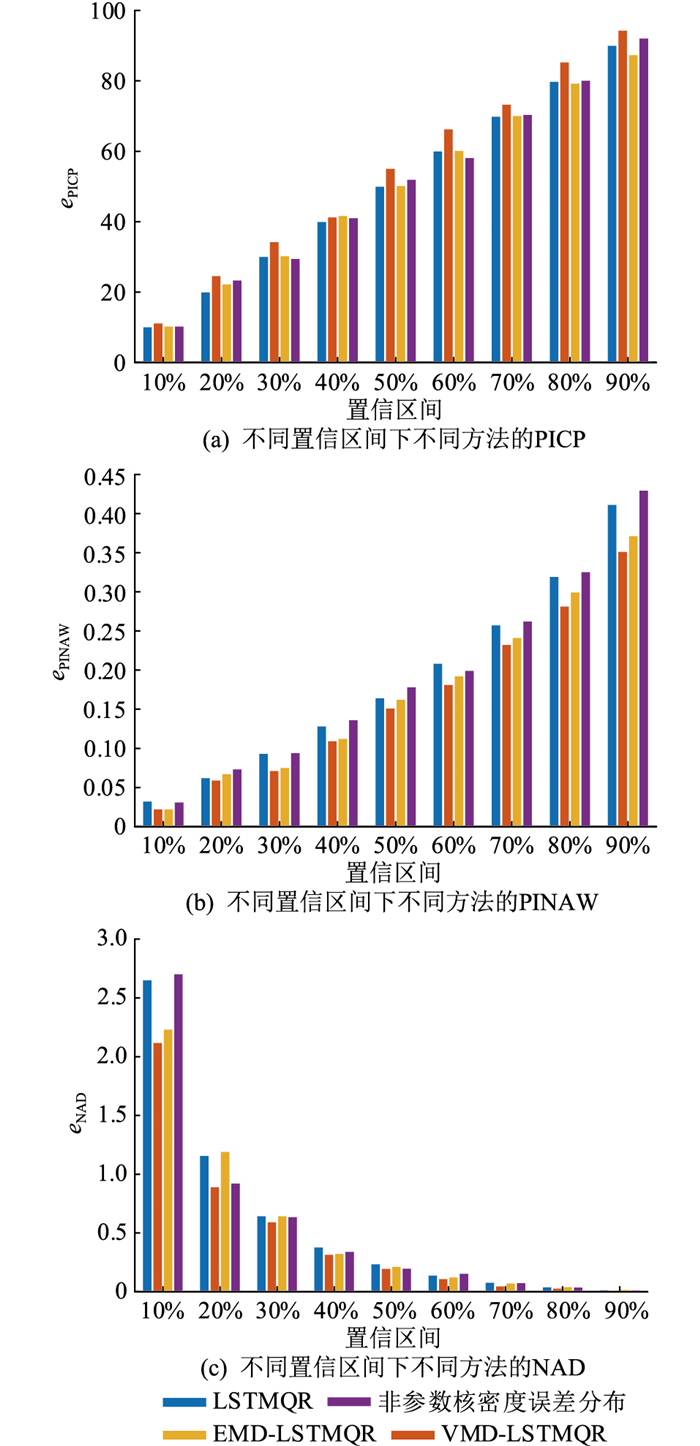
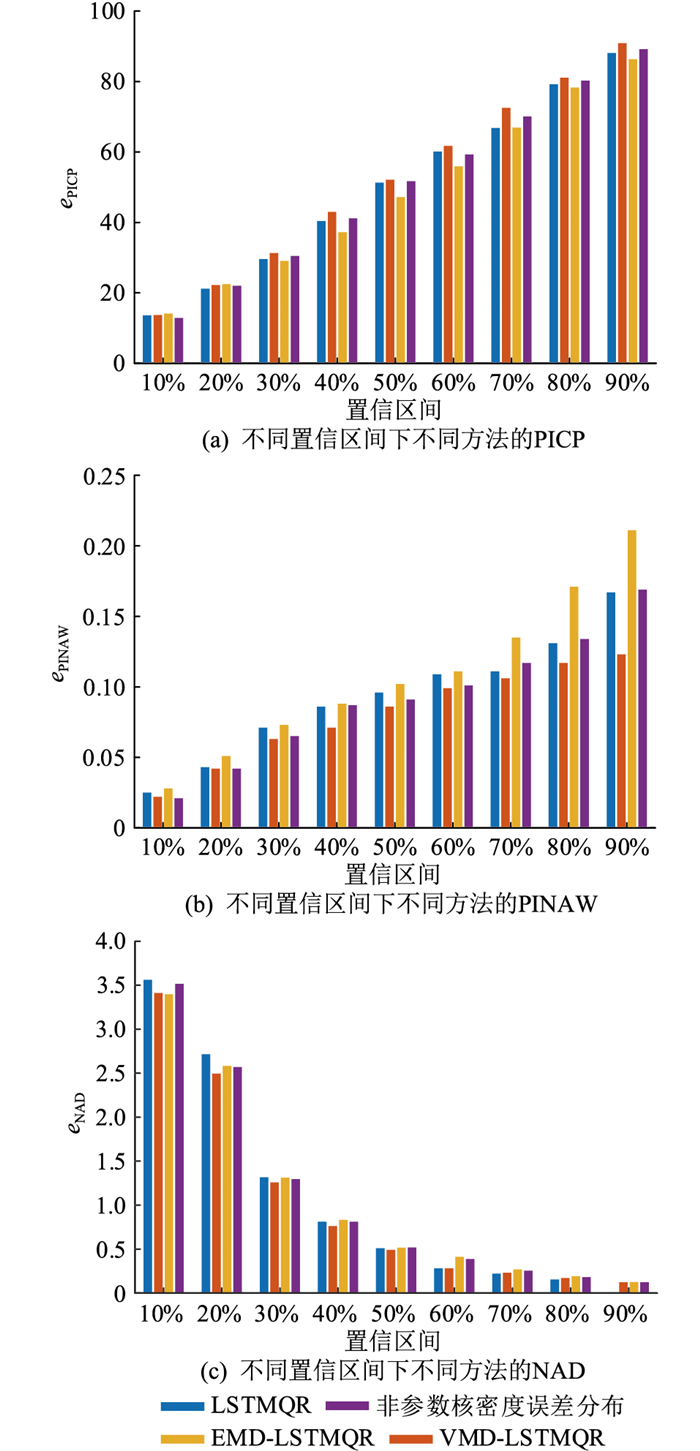
根据各模态的最佳滚动步长分别对各模态序列进行区间预测,根据区间预测结果进行重构,得到原始负荷序列的区间预测结果。为了验证所提方法的有效性,文中将选取另外3种区间预测方法进行对比。3种区间预测方法分别采用LSTMQR直接对原始负荷序列进行区间预测、采用LSTMQR对EMD分解的负荷序列进行预测、采用非参数核密度误差分布的概率区间进行预测。采用4种方法分别对10 kV和220 kV的母线负荷进行预测,不同置信区间3个指标数值如图 6、图 7所示,不同方法下置信区间的平均值如表 2所示。
|
图 6 10 kV母线负荷下不同预测模型精确性比较 Fig. 6 Accuracy comparison of different prediction models for 10 kV bus load power |
|
图 7 220 kV母线负荷下不同预测模型精确性比较 Fig. 7 Accuracy comparison of different prediction models for 220 kV bus load power |
|
|
表 2 220 kV和10 kV母线平均预测结果 Table 2 Average prediction results of 220 kV and 10 kV bus load |
结合图 6和图 7可知,随着置信区间变大,4种方法的区间宽度都在增大,越来越多的功率点落入区间带内,区间覆盖率增加,偏离区间带的程度在不断减小。对比图 6的4种方法可见,无论在哪一个置信区间,采用VMD-LSTMQR区间预测的区间宽度最窄,但区间的偏离程度最低。除了40%置信区间略低于EMD-LSTMQR外,余下任意置信区间下的区间覆盖率均高于其他方法。
从表 2的10 kV平均预测结果可知,采用VMD-LSTMQR方法的平均区间宽度相较其余3种预测方法低0.01~0.03的同时,平均预测区间覆盖率要高出3%~4%,平均偏离区间带降低了0.1左右。而基于非参数核密度误差分布的概率区间预测方法,虽然平均区间宽度最宽,但平均预测精度相比于VMD-LSTMQR要低3%左右。虽然LSTMQR的平均区间宽度要高于VMD-LSTMQR和EMD-LSTMQR,但平均预测精度最低,整体的平均偏离程度也最高。
对比图 7的4种方法,除了在10%置信区间,VMD-LSTMQR的区间宽度要略大于非参数核密度误差区间预测的区间宽度,其余无论在哪一个置信区间,VMD-LSTMQR区间预测的区间宽度均要小于其余3种方法。由表 2的220 kV平均预测结果可知,文中方法在平均区间宽度低于其他3种方法0.01~0.03的同时,平均的预测精度整体上提高了2%~4%。而采用EMD-LSTMQR虽然平均区间宽度最宽,但预测精度最差。
综上,采用VMD-LSTMQR的区间预测方法无论对10 kV母线负荷进行预测,还是对220 kV母线负荷进行预测,都能保证在最低的平均区间宽度下有着更高的区间覆盖率及更低的偏离程度。相对于传统的区间预测方法,预测效果有明显的改善。
图 8为90%置信区间下220 kV母线负荷某一天区间预测结果。

|
图 8 90%置信区间下的负荷预测 Fig. 8 Load prediction of 90% confidence level |
由图 8可知,90%置信区间下实际的负荷功率大部分能很好地落入4种方法所预测的区间带内。90%置信区间下的4种方法整体预测效果均较好,但对比图 8(a)、(b)、(c)、(d)可以发现,该天实际功率与所预测的区间带下边界更接近,而采用VMD-LSTMQR区间预测方法在样本点50~100以及200~288的区间段内所预测的下边界相比于其他3种方法低了5~10 MW,使得所预测的下边界更偏离实际功率。其余3种方法的下边界围绕着实际功率上下波动。对比4种方法预测的上边界可以看出,VMD-LSTMQR上边界预测功率在240~260 MW,而其余方法上边界预测在250~280 MW,下边界预测4种方法预测均在210~220 MW,这也就意味着,采用VMD-LSTMQR预测的区间宽度更小,整体的预测效果更好。
4 结论负荷区间预测能够更加全面地反映负荷变化的趋势,为电网规划和调度提供参考和依据。文中提出一种VMD-LSTMQR的区间负荷预测方法,在选取最合适分解模态的同时进行最优化的区间预测,以实际的案例证明文中所提方法的有效性。结论如下:
(1) 相对于传统的EMD分解,文中采用VMD分解克服模态重叠的现象,并根据中心频率法确定最合适分解模态。
(2) 采用滚动预测的模式进行区间预测,并根据不同模态以3个指标最优为条件找出最为合适的不同模态预测步长。
(3) 对不同模态采用LSTMQR进行区间预测,以分位数和LSTM结合的方法相对于传统的QR预测效果更佳。
综上所述,文中所提出的滚动区间预测方法不仅相对于传统的区间预测方法有更窄的区间、更高的区间精度以及更低的偏离程度,而且所采用的滚动模式更加符合预测模式,能更好地实际作用于电力系统。
| [1] |
钱甜甜, 王珂, 徐立中, 等. 基于双向长短时记忆网络的母线负荷分解方法[J]. 电力工程技术, 2020, 39(6): 104-109. QIAN Tiantian, WANG Ke, XU Lizhong, et al. The bus load decomposition method based on bi-directional long short-term memory model[J]. Electric Power Engineering Technology, 2020, 39(6): 104-109. (  0) 0) |
| [2] |
李冬辉, 尹海燕, 郑博文. 基于MFOA-GRNN模型的年电力负荷预测[J]. 电网技术, 2018, 42(2): 585-590. LI Donghui, YIN Haiyan, ZHENG Bowen. An annual load forecasting model based on generalized regression neural network with multi-swarm fruit fly optimization algorithm[J]. Power System Technology, 2018, 42(2): 585-590. (  0) 0) |
| [3] |
王德文, 孙志伟. 电力用户侧大数据分析与并行负荷预测[J]. 中国电机工程学报, 2015, 35(3): 527-537. WANG Dewen, SUN Zhiwei. Big data analysis and parallel load forecasting of electric power user side[J]. Proceedings of the CSEE, 2015, 35(3): 527-537. (  0) 0) |
| [4] |
彭文, 王金睿, 尹山青. 电力市场中基于Attention-LSTM的短期负荷预测模型[J]. 电网技术, 2019, 43(5): 1745-1751. PENG Wen, WANG Jinrui, YIN Shanqing. Short-term load forecasting model based on Attention-LSTM in electricity market[J]. Power System Technology, 2019, 43(5): 1745-1751. (  0) 0) |
| [5] |
沈兆轩, 袁三男. 利用卷积神经网络支持向量回归机的地区负荷聚类集成预测[J]. 电网技术, 2020, 44(6): 2237-2244. SHEN Zhaoxuan, YUAN Sannan. Regional load clustering integration forecasting based on convolutional neural network support vector regression machine[J]. Power System Technology, 2020, 44(6): 2237-2244. (  0) 0) |
| [6] |
YANG Y D, LI S F, LI W Q, et al. Power load probability density forecasting using Gaussian process quantile regression[J]. Applied Energy, 2018, 213: 499-509. DOI:10.1016/j.apenergy.2017.11.035 (  0) 0) |
| [7] |
彭显刚, 王洪森. 基于竞争ISPO双胞支持向量回归短期负荷预测[J]. 电力系统及其自动化学报, 2014, 26(10): 46-50, 68. PENG Xiangang, WANG Hongsen. Short-term load forecasting based on competitive ISPO and twin support vector regression[J]. Proceedings of the CSU-EPSA, 2014, 26(10): 46-50, 68. DOI:10.3969/j.issn.1003-8930.2014.10.009 (  0) 0) |
| [8] |
方八零, 李龙, 赵家铸, 等. 动态相似与静态相似相结合的短期负荷预测方法[J]. 电力系统保护与控制, 2018, 46(15): 29-35. FANG Baling, LI Long, ZHAO Jiazhu, et al. Short-term load forecasting based on the combination of dynamic similarity and static similarity[J]. Power System Protection and Control, 2018, 46(15): 29-35. DOI:10.7667/PSPC171112 (  0) 0) |
| [9] |
李彬, 彭曙蓉, 彭君哲, 等. 基于深度学习分位数回归模型的风电功率概率密度预测[J]. 电力自动化设备, 2018, 38(9): 15-20. LI Bin, PENG Shurong, PENG Junzhe, et al. Wind power probability density forecasting based on deep learning quantile regression model[J]. Electric Power Automation Equipment, 2018, 38(9): 15-20. (  0) 0) |
| [10] |
QUAN H, SRINIVASAN D, KHOSRAVI A. Uncertainty handling using neural network-based prediction intervals for electrical load forecasting[J]. Energy, 2014, 73: 916-925. DOI:10.1016/j.energy.2014.06.104 (  0) 0) |
| [11] |
何耀耀, 许启发, 杨善林, 等. 基于RBF神经网络分位数回归的电力负荷概率密度预测方法[J]. 中国电机工程学报, 2013, 33(1): 93-98. HE Yaoyao, XU Qifa, YANG Shanlin, et al. A power load probability density forecasting method based on RBF neural network quantile regression[J]. Proceedings of the CSEE, 2013, 33(1): 93-98. (  0) 0) |
| [12] |
HABEN S, GIASEMIDIS G. A hybrid model of kernel density estimation and quantile regression for GEFCom2014 probabilistic load forecasting[J]. International Journal of Forecasting, 2016, 32(3): 1017-1022. DOI:10.1016/j.ijforecast.2015.11.004 (  0) 0) |
| [13] |
杨锡运, 关文渊, 刘玉奇, 等. 基于粒子群优化的核极限学习机模型的风电功率区间预测方法[J]. 中国电机工程学报, 2015, 35(S1): 146-153. YANG Xiyun, GUAN Wenyuan, LIU Yuqi, et al. Prediction intervals forecasts of wind power based on PSO-KELM[J]. Proceedings of the CSEE, 2015, 35(S1): 146-153. (  0) 0) |
| [14] |
XIE J R, HONG T. Temperature scenario generation for probabilistic load forecasting[J]. IEEE Transactions on Smart Grid, 2018, 9(3): 1680-1687. (  0) 0) |
| [15] |
LIU B D, NOWOTARSKI J, HONG T, et al. Probabilistic load forecasting via quantile regression averaging on sister forecasts[J]. IEEE Transactions on Smart Grid, 2017, 8(2): 730-737. (  0) 0) |
| [16] |
ZHANG W J, QUAN H, SRINIVASAN D. Parallel and reliable probabilistic load forecasting via quantile regression forest and quantile determination[J]. Energy, 2018, 160: 810-819. DOI:10.1016/j.energy.2018.07.019 (  0) 0) |
| [17] |
HE Y Y, LIU R, LI H Y, et al. Short-term power load probability density forecasting method using kernel-based support vector quantile regression and Copula theory[J]. Applied Energy, 2017, 185: 254-266. DOI:10.1016/j.apenergy.2016.10.079 (  0) 0) |
| [18] |
ZHANG W J, QUAN H, SRINIVASAN D. An improved quantile regression neural network for probabilistic load forecasting[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4425-4434. DOI:10.1109/TSG.2018.2859749 (  0) 0) |
| [19] |
LI B W, ZHANG J, HE Y, et al. Short-term load-forecasting method based on wavelet decomposition with second-order gray neural network model combined with ADF test[J]. IEEE Access, 2017, 5: 16324-16331. DOI:10.1109/ACCESS.2017.2738029 (  0) 0) |
| [20] |
LIU H, CHEN C, TIAN H Q, et al. A hybrid model for wind speed prediction using empirical mode decomposition and artificial neural networks[J]. Renewable Energy, 2012, 48: 545-556. DOI:10.1016/j.renene.2012.06.012 (  0) 0) |
| [21] |
赵倩, 黄景涛. 基于EMD-SA-SVR的超短期风电功率预测研究[J]. 电力系统保护与控制, 2020, 48(4): 89-96. ZHAO Qian, HUANG Jingtao. On ultra-short-term wind power prediction based on EMD-SA-SVR[J]. Power System Protection and Control, 2020, 48(4): 89-96. (  0) 0) |
| [22] |
方娜, 余俊杰, 李俊晓, 等. 注意力机制下的EMD-GRU短期电力负荷预测[J]. 华侨大学学报(自然科学版), 2021, 42(6): 817-824. FANG Na, YU Junjie, LI Junxiao, et al. Short-term power load forecasting under EMD-GRU attention mechanism[J]. Journal of Huaqiao University (Natural Science), 2021, 42(6): 817-824. (  0) 0) |
| [23] |
汤庆峰, 刘念, 张建华, 等. 基于EMD-KELM-EKF与参数优选的用户侧微电网短期负荷预测方法[J]. 电网技术, 2014, 38(10): 2691-2699. TANG Qingfeng, LIU Nian, ZHANG Jianhua, et al. A short-term load forecasting method for micro-grid based on EMD-KELM-EKF and parameter optimization[J]. Power System Technology, 2014, 38(10): 2691-2699. (  0) 0) |
| [24] |
杨晶显, 张帅, 刘继春, 等. 基于VMD和双重注意力机制LSTM的短期光伏功率预测[J]. 电力系统自动化, 2021, 45(3): 174-182. YANG Jingxian, ZHANG Shuai, LIU Jichun, et al. Short-term photovoltaic power prediction based on variational mode decomposition and long shortterm memory with dual-stage attention mechanism[J]. Automation of Electric Power Systems, 2021, 45(3): 174-182. (  0) 0) |
| [25] |
李丹, 张远航, 杨保华, 等. 基于约束并行LSTM分位数回归的短期电力负荷概率预测方法[J]. 电网技术, 2021, 45(4): 1356-1364. LI Dan, ZHANG Yuanhang, YANG Baohua, et al. Short time power load probabilistic forecasting based on constrained paral-lel-LSTM neural network quantile regression mode[J]. Power System Technology, 2021, 45(4): 1356-1364. (  0) 0) |
2. College of Electrical Engineering, Zhejiang University, Hangzhou 310058, China
 2021, Vol. 40
2021, Vol. 40


 董新伟(1971), 男, 博士, 副教授, 研究方向为电能质量、负荷预测(E-mail:
董新伟(1971), 男, 博士, 副教授, 研究方向为电能质量、负荷预测(E-mail: