文章编号: 2096-3203(2021)06-0043-09 中图分类号: TM73
2. 中国电力科学研究院有限公司, 江苏 南京 210003
随着电网规模日益增加,电力系统的网络结构与动态特性也日趋复杂。局部故障引发连锁反应,从而导致大范围停电的事故时有发生[1-3]。大停电事故严重影响了社会生活与生产,造成了巨大的政治、经济损失。因此,为了减少停电损失,必须提前制定电网恢复预案,其主要目标是尽快恢复尽可能多的重要负荷供电。
在负荷恢复优化的研究中,通常考虑频率、电压、发电机出力、潮流等约束,以负荷恢复量最大为目标,建立负荷恢复模型[4-7]。传统负荷恢复以水电机组或燃气轮机为黑启动电源,但其数量和出力受限于地理和资源分布。随着可再生能源的发展,越来越多的研究利用其功率支撑作用,提高负荷恢复效率[8-10]。但由于可再生能源的不确定性,其波动可能会造成频率越限,影响系统安全。随着大规模电网侧储能电站建成并投运[11],储能可提供更充足的出力,并在一定程度上控制频率[12-14]。利用储能的功率支撑和频率调节能力,可以在保证系统安全的同时,提高系统恢复效率。
针对储能参与停电后系统恢复问题,已有学者展开了大量研究。通过调节储能充放电功率,可以减少电压或潮流越限对系统安全的威胁[15]。储能可作为可再生能源的启动电源或辅助电源,平抑可再生能源出力波动[16-17];也可作为黑启动电源,通过优化机组启动顺序和恢复路径,达到发电能力最大化[18]、断路器操作次数和停电持续时间最小化等目标[19]。由此可见,合理利用储能,可提高系统恢复的效率。但上述研究并未充分考虑储能调频对负荷恢复过程中系统安全性的影响,储能调频作用可以提高系统承受冲击的能力,增加单次负荷的最大有功恢复量,从而提高负荷恢复效率。
储能电站对频率有一定的调节作用,但负荷投入引起的频率偏移仍需在可调范围内。因此,在负荷恢复中必须考虑到负荷不确定性。目前一般采用鲁棒优化[20]、随机优化[21]和模糊方法处理负荷不确定性。鲁棒方法可在负荷巨大波动时仍保证系统安全,但其求解结果较为保守。随机优化通过概率抽样将不确定量转换为确定性量,但准确的负荷概率分布难以获取。模糊机会约束只需少量分布参数,且能权衡目标和风险,已广泛应用于含不确定量的电力系统规划,如机组组合[22]、经济调度[23]及网架重构[24]。
为了充分利用储能的功率支撑和频率调节能力,更大程度地提高负荷恢复效率,文中提出了考虑电网侧储能调频能力的电力系统负荷恢复策略。以最大化负荷恢复量加权总和为目标,考虑负荷不确定性和系统安全约束,建立负荷恢复的模糊机会约束模型。然后引入模糊风险价值实现负荷恢复量与过载风险的权衡,通过清晰等价类将模糊机会约束问题转化为确定的0-1规划问题,并利用人工蜂群算法进行求解。最后通过IEEE 39节点系统的仿真算例对文中策略的有效性进行验证。
1 考虑储能调频能力的负荷恢复策略框架 1.1 储能调频能力在负荷恢复过程中,由于已恢复系统较为脆弱,投入有功负荷可能引起较大的频率偏移。因此,在研究负荷恢复策略时,必须要保证负荷投入过程中的频率安全。传统发电机组可利用自身调速器控制系统频率的偏移,含调速器发电机的功率-频率特性为:
| $ \Delta P_{\mathrm{G}}=-K_{\mathrm{G}} \Delta f $ | (1) |
式中:ΔPG为发电机调整的有功功率,其值为正表示增加出力,为负表示减少出力;KG为传统发电机的单位调节功率;Δf为频率变化量。
在含大规模电网侧储能的系统中,通过调节储能充放电功率,也可调整系统频率。负荷恢复过程中,储能一般采用虚拟惯性或虚拟下垂控制。虚拟惯性控制可以快速响应变化,改善系统频率偏差。但在此方式下,储能有功出力与系统频率的变化率呈比例,当系统偏差稳定时,储能无法出力。虚拟下垂控制方式下,储能可以快速响应频率变化,调整出力,抑制频率偏移,且在频率趋于稳定时,储能依然能够出力。因此,为了充分利用储能功率,加速系统恢复,文中采用虚拟下垂控制。在此方式下,储能有功功率输出与频率偏差的关系为:
| $ \Delta P_{\mathrm{B}}(s)=-K_{\mathrm{B}} G_{\mathrm{B}}(s) \Delta f(s) $ | (2) |
式中:ΔPB(s)为储能系统的输出有功功率;KB为储能的单位调节功率;GB(s)为储能输出有功功率的传递函数;Δf(s)为系统频率偏移量。
为保证储能在负荷恢复过程中能够正常发挥其调频作用,储能系统需留有一定裕量,且储能可调节的最大频率偏差应满足电力系统运行的频率要求。因此,储能系统的单位调节功率KB由储能最大输出功率、额定容量以及系统允许的最大频率偏移共同决定。
1.2 负荷恢复策略框架考虑到负荷不确定性和储能调频能力对系统的影响,文中提出了一种考虑储能调频能力的含电网侧储能电力系统负荷恢复策略,通过优化发电机出力、储能电站出力及负荷出线投切状态,最大化重要负荷的恢复量,具体决策框架如图 1所示。
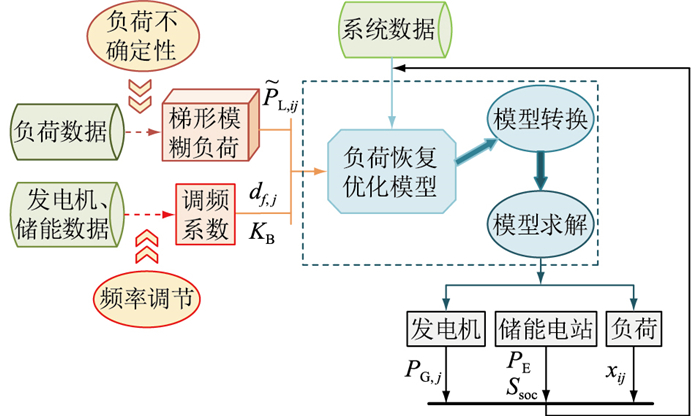
|
图 1 基于模糊机会约束的负荷恢复策略 Fig. 1 Load restoration strategy based on fuzzy chance constriants |
图 1中,决策所需的基础数据包括系统数据、负荷数据、发电机数据和储能数据。考虑到负荷不确定性,基于负荷数据集将不确定性负荷描述为梯形模糊负荷
将上述已知信息输入到文中提出的负荷恢复优化模型中,然后通过模型转换与模型求解,即可得到符合安全约束的发电机、储能电站和负荷的决策结果,调度人员可据此结果给发电机组、储能电站和负荷投切开关下达调度指令。并且,各发电机组出力PG, j,储能电站有功出力PE,荷电状态Ssoc,负荷出线的恢复情况xij将输入模型中,作为下一时步负荷恢复方案决策的基础信息。
2 考虑储能频率响应的模糊机会约束模型在负荷恢复阶段,系统中已有部分发电机组并网运行,系统恢复的主要目标是恢复尽可能多的重要负荷。考虑到储能和已恢复机组的调频能力以及负荷不确定性,文中建立了考虑储能频率响应的负荷恢复模糊机会约束模型。
2.1 模糊机会约束规划 2.1.1 机会约束规划机会约束规划考虑到所做决策在不利情况发生时可能不满足约束条件,允许所做决策在一定程度上不满足约束条件,但约束条件成立的概率不小于某一个置信水平。机会约束的常见形式为:
| $ {Cr}\{g(x, \xi) \leqslant 0\} \geqslant \alpha $ | (3) |
式中:Cr{·}为{·}中事件的可信性;x为决策变量;ξ为模糊变量;g为约束集;α为置信水平。
2.1.2 负荷的模糊建模在利用模糊机会约束处理负荷的不确性定问题时,首先应该将负荷的模糊量以隶属度函数的形式建模。目前,大多数研究采取梯形隶属度函数描述负荷的不确定性[25]。将一个负荷节点上的负荷分为若干条出线,每一条出线对应一个预测的负荷恢复量和波动区间,则负荷隶属函数的数学表达式为:
| $ \mu_{\mathrm{w}}\left(\tilde{P}_{\mathrm{L}, i j}\right)=\left\{\begin{array}{l} 0 \quad \tilde{P}_{\mathrm{L}, i j} \leqslant P_{\mathrm{L} 1, i j} \\ \frac{\tilde{P}_{\mathrm{L}, i j}-P_{\mathrm{L} 1, i j} }{P_{\mathrm{L} 2, i j}-P_{\mathrm{L} 1, i j}}\quad P_{\mathrm{L}, i j}<\tilde{P}_{\mathrm{L}, i j} \leqslant P_{\mathrm{L}2, i j}\\ 1 \quad P_{\mathrm{L} 2, i j}<\tilde{P}_{\mathrm{L}, i j} \leqslant P_{\mathrm{L3}, i j} \\ \frac{P_{\mathrm{L4}, i j}-\tilde{P}_{\mathrm{L}, i j}}{P_{\mathrm{L4}, i j}-P_{\mathrm{L} 3, i j} }\quad P_{\mathrm{L} 3, i j}<\tilde{P}_{\mathrm{L}, i j} \leqslant P_{\mathrm{L4}, i j}\\ 0 \quad \tilde{P}_{\mathrm{L}, i j}>P_{\mathrm{L} 4, i j} \end{array} \quad \right. $ | (4) |
| $ P_{\mathrm{L}k, i j}=\mu P_{\mathrm{av}, i j} $ | (5) |
式中:
为了减少停电损失,系统需尽快为重要负荷恢复供电。根据负荷重要程度,可以将负荷分为3级。其中,中断供电会对政治、经济造成重大损失的负荷设定为一级负荷,在负荷恢复中应该优先恢复;中断供电将造成较大的政治影响和较大的经济损失,且重要用户需要很长时间才能恢复生产的负荷设定为二级负荷,在负荷恢复中应该次优先恢复;其他负荷为三级负荷。
因此,可将最大化负荷恢复量的加权和作为模型的目标函数:
| $ \max f_{\mathrm{Load}}=\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m_{i}}\left(x_{i j} w_{i j} \tilde{P}_{\mathrm{L}, i j}\right) $ | (6) |
式中:fLoad为点负荷恢复量;n为负荷节点的总数;mi为节点i处负荷出线的总数;xij为一个0-1决策变量,表示负荷节点i处第j条出线的负荷是否接入电网,为0表示负荷未接入电网,为1表示负荷接入电网;wij为负荷节点i处第j条出线的权重,根据出线中各级负荷的比例设置相应权重,一级负荷比例最高的出线权重设为5,二级负荷和三级负荷比例最高的出线权重分别设为2和1。
由于负荷的恢复量是不确定的,在系统恢复过程中,可能出现实际恢复量超过系统所能提供的最大恢复量的情况,为保证系统的安全,应该尽可能减少负荷的过载风险。因此,文中引入适用于模糊变量的模糊风险价值函数[26],描述系统恢复过程中由于负荷恢复量过大引起的过载风险,在一定置信水平下量化过载风险。在文中提出的模型中,负荷过载的模糊风险值为:
| $ f_{\mathrm{FV} \mathrm{aR}}=\sup \left\{\gamma \mid {Cr}\left\{\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m_{i}}\left(x_{i j} \tilde{P}_{\mathrm{L}, i j}\right)-\Delta P_{\Sigma} \leqslant \gamma\right\} \leqslant \beta_{1}\right\} $ | (7) |
式中:sup{ }表示“上确界”,即最小上界;γ为一个实数;ΔPΣ为可供给负荷恢复的总有功出力,与储能和系统已恢复的机组有关;β1为模糊风险价值的置信水平。
由上述得到最终的目标函数为:
| $ \max f=f_{\mathrm{Load}}-\lambda f_{\mathrm{FVaR}} $ | (8) |
式中:λ为风险参与系数。
2.3 约束条件 2.3.1 储能运行特性约束假设每一时步内,储能输出功率不变,根据储能输出功率特性,该时步储能的输出功率为:
| $ P_{\mathrm{E}}(t)=\frac{\eta\left(S_{\mathrm{soc}}(t-\Delta t)-S_{\mathrm{soc}}(t)\right) C_{\mathrm{N}}}{\Delta t} $ | (9) |
式中:PE(t)为储能系统在t时步的输出功率,充电时为负,放电时为正;η为储能变流器的效率;Ssoc(t)为储能系统在t时步的荷电状态;Δt为时间间隔;CN为储能系统的额定容量。
由于储能变流器的电力电子特性,其效率会受到储能的输出功率影响,输出功率过大或过小都会严重影响变流器效率。所以,储能系统的输出功率需要限制在合适的范围内:
| $ P_{\mathrm{E} \min } \leqslant P_{\mathrm{E}}(t) \leqslant P_{\mathrm{E} \max } $ | (10) |
式中:PEmin,PEmax分别为储能系统的最小和最大允许输出功率。
为了防止储能系统的过度充电或放电影响储能的可持续运行,通常会对荷电状态加以限制:
| $ S_{\mathrm{soc}, \min } \leqslant S_{\mathrm{soc}}(t) \leqslant S_{\mathrm{soc}, \max } $ | (11) |
式中:Ssoc, min,Ssoc, max分别为最小和最大允许荷电水平。为了保证储能的调频能力和灵活充放电,文中设最小允许荷电水平为20%,最大允许荷电水平为80%。
2.3.2 负荷恢复最大总功率约束负荷恢复阶段,负荷的恢复由已启动机组和储能共同提供功率。因此,负荷恢复的最大有功功率不能超过已恢复机组最大可提供的有功功率和储能系统当前时刻所能输出的最大功率之和。
已恢复机组的最大爬坡量可以表示为:
| $ \Delta P_{\mathrm{G}}=\sum\limits_{j=1}^{N_{\mathrm{G}}} \min \left\{r_{j} \Delta t,\left(P_{\mathrm{GN}, j}-P_{\mathrm{G}, j}\right)\right\} $ | (12) |
式中:ΔPG为已恢复机组的最大爬坡量的总和;NG为已恢复的发电机数量;rj为已恢复发电机组j的爬坡率;PGN, j为已恢复发电机组j的额定有功功率;PG, j为发电机组j前一时步输出的有功功率。
因此,总的负荷恢复的最大有功功率约束可表示为:
| $ {Cr}\left\{\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m_{i}}\left(x_{i j} \tilde{P}_{\mathrm{L}, i j}\right)-P_{\mathrm{E}}(t)-\Delta P_{\mathrm{G}} \leqslant 0\right\} \geqslant \beta_{2} $ | (13) |
式中:β2为负荷恢复最大总功率约束的置信水平。
2.3.3 单次最大可投入负荷有功约束在系统恢复过程中,由于系统的容量相较于正常运行情况还较小,单次负荷恢复量过大可能会引起较大的频率偏移,严重时更会使已恢复系统再次崩溃。因此,要限制单次投入的负荷。
单次最大恢复的有功负荷由已恢复系统的频率响应确定。在已启动机组并网后,系统频率可以由发电机组和储能系统共同进行调节,而且具有快速响应能力的大规模储能系统的调频能力是传统调频的2~3倍。因此,在储能参与的系统恢复中,考虑储能对系统调频能力的提升可以增加单次允许恢复的最大负荷量。
根据典型发电机组的频率响应,可以得到最大频率偏差下传统发电机组可以承受的最大负荷波动,可表示为:
| $ P_{\mathrm{L} \max 1}=\Delta f_{\max } \sum\limits_{j=1}^{N_{\mathrm{G}}} \frac{P_{\mathrm{GN}, j}}{d_{f, j}} $ | (14) |
式中:PLmax1为传统机组可承受的最大单次负荷有功投入量;Δfmax为允许的最大频率偏移量,文中设定为0.5 Hz;df, j为发电机组j的频率响应系数。不同类型的发电机组在不同负荷情况下的频率相应系数不同,其具体数值参考文献[27]。
文中模型的储能系统通过虚拟下垂控制进行频率调节。综合考虑系统的运行情况以及储能的容量和功率限制,可得调节系数的估值;更为准确地,可以在系统参数一定的情况下,利用测量试验得到的响应系数替代虚拟下垂控制的复杂传递函数。储能在最大频率偏差下最大的调节能力为:
| $ P_{\mathrm{L} \max 2}=K_{\mathrm{B}} \Delta f_{\max } $ | (15) |
式中:PLmax2为储能系统提供的最大单次负荷有功投入量。
因此,储能系统与已恢复机组联合运行时,单次最大负荷有功投入量的约束为:
| $ C r\left\{\sum\limits_{j=1}^{m_{i}}\left(x_{i j} \tilde{P}_{\mathrm{L}, i j}\right)-\Delta f_{\max } \sum\limits_{k=1}^{N_{\mathrm{G}}} \frac{P_{\mathrm{GN}, k}}{d_{f, k}}-K_{\mathrm{B}} \Delta f_{\max } \leqslant 0\right\} \geqslant \beta_{3} $ | (16) |
式中:β3为单次最大可投入负荷有功约束的置信水平。
2.3.4 稳态潮流约束稳态潮流约束是电力系统稳定运行的基本要求,在系统恢复的每个时步都必须通过潮流校验,确保潮流收敛。
| $ \left\{\begin{array}{l} P_{\mathrm{d} i}=V_{i} \sum\limits_{j=1}^{N}\left[V_{j}\left(G_{i j} \cos \delta_{i j}+B_{i j} \sin \delta_{i j}\right)\right] \\ Q_{\mathrm{d} i}=V_{i} \sum\limits_{j=1}^{N}\left[V_{j}\left(G_{i j} \sin \delta_{i j}-B_{i j} \cos \delta_{i j}\right)\right] \end{array}\right. $ | (17) |
式中:Pdi,Qdi分别为节点i处注入的有功和无功功率;Vi,Vj分别为节点i,j的电压;Gij,Bij分别为节点i和j之间的电导和电纳;δij为Vi和Vj之间的相角差;N为节点数目。
2.3.5 机组功率和系统电压约束常规发电机组的输出功率必须在其允许的限度内才能正常工作,所以其输出功率应该满足以下条件。为了保证系统运行的安全,必须确保每个节点的电压满足系统的安全限制。
| $ \left\{\begin{array}{l} P_{\mathrm{Gmin}, i} \leqslant P_{\mathrm{G}, i} \leqslant P_{\mathrm{Gmax}, i} \\ Q_{\mathrm{Gmin}, i} \leqslant Q_{\mathrm{G}, i} \leqslant Q_{\mathrm{G} \max , i} \\ U_{\min , i} \leqslant U_{i} \leqslant U_{\max , i} \end{array}\right. $ | (18) |
式中:PG, i,QG, i分别为传统发电机组的有功和无功功率;PGmin, i,PGmax, i分别为最小和最大有功功率;QGmin, i,QGmax, i分别为最小和最大无功功率;Ui为节点i的电压;Umin, i,Umax, i分别为节点i的最小和最大电压。
3 模型求解由于文中的负荷量为梯形模糊变量,首先通过清晰等价类将模糊机会规划问题变成确定的0-1规划问题,然后采用人工蜂群算法进行求解。
3.1 模糊机会约束模型的清晰等价类梯形模糊变量ξ={ a, b, c, d }的模糊期望为:
| $ E_{\mathrm{fuz}}(\xi)=\frac{1}{4}(a+b+c+d) $ | (19) |
则总的负荷恢复量的模糊期望可以表示为:
| $ \begin{gathered} f_{\mathrm{Load}}=E_{\mathrm{fuz}}\left(\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m_{i}}\left(x_{i j} w_{i j} \tilde{P}_{\mathrm{L}, i j}\right)\right)= \\ \frac{1}{4} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m_{i}}\left(x_{i j} w_{i j}\right) \sum\limits_{k=1}^{4} P_{\mathrm{L} k, i j} \end{gathered} $ | (20) |
根据文献[28]给出的梯形模糊参数下模糊风险价值清晰等价类,当β1>0.5时,式(7)可以转化为:
| $ \begin{gathered} f_{\mathrm{FVaR}}=\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m_{i}}\left\{x _ { i j } \left[\left(2-2 \beta_{1}\right) P_{\mathrm{L} 3, i j}+\right.\right. \\ \left.\left.\left(2 \beta_{1}-1\right) P_{\mathrm{L} 4, i j}\right]\right\}-P_{\mathrm{E}}(t)-\Delta P_{\mathrm{G}} \end{gathered} $ | (21) |
当置信水平β2, β3>0.5时,最大负荷恢复量约束和单次最大可投负荷有功约束的清晰等价类可分别表示为:
| $ \begin{gathered} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m_{i}}\left\{x _ { i j } \left[\left(2-2 \beta_{2}\right) P_{\mathrm{L} 3, i j}+\right.\right. \\ \left.\left.\left(2 \beta_{2}-1\right) P_{\mathrm{L4}, i j}\right]\right\} \leqslant P_{\mathrm{E}}(t)+\Delta P_{\mathrm{G}} \end{gathered} $ | (22) |
| $ \begin{gathered} \sum\limits_{j=1}^{m_{i}}\left\{x_{i j}\left[\left(2-2 \beta_{3}\right) P_{\mathrm{L} 3, i j}+\left(2 \beta_{3}-1\right) P_{\mathrm{L} 4, i j}\right]\right\} \leqslant \\ \Delta f_{\max } \sum\limits_{j=1}^{N_{\mathrm{G}}} \frac{P_{\mathrm{G}, j}}{d_{f, j}}+K_{\mathrm{B}} \Delta f_{\max } \end{gathered} $ | (23) |
电力系统负荷恢复优化问题是一个复杂的非线性规划问题,无法直接采用数学方法进行求解,但可以采用智能算法进行求解。常用于求解非线性最优问题的算法有遗传算法、粒子群算法和人工蜂群算法。遗传算法操作复杂,参数较多;粒子群算法易陷入局部最优,收敛速度慢;人工蜂群算法通过模拟蜂群的采蜜行动进行全局寻优,操作简单,收敛速度快,搜索能力强,搜索精度高,有限步数内可收敛到全局最优解。因此,采用人工蜂群算法对文中模型进行求解,具体求解步骤见图 2。

|
图 2 人工蜂群算法流程 Fig. 2 Flow chart of artificial bee colony algorithm |
图 2中,NP为种群数量;LMT为最大蜜源开采次数;LIT为最大迭代次数;约束条件是指:储能特性约束式(10)和式(11),潮流和电压约束式(17)和式(18)以及负荷投入量约束式(22)和式(23)。
4 仿真分析 4.1 仿真场景对IEEE 39节点系统进行仿真,以验证模型的有效性。电网的拓扑结构如图 3所示,传统发电机组位于节点31~39处,储能为容量200 MW ·h,最大输出功率100 MW,储能类型为磷酸铁锂型。考虑到负荷恢复的安全性与效率,将储能置于节点30处,其初始荷电状态设为0.8。综合考虑仿真系统的运行情况以及储能的容量和功率限制,文中储能的单位调节功率系数设为50。

|
图 3 IEEE 39节点拓扑 Fig. 3 IEEE 39 node topology |
系统大停电后,由储能电站启动附近的发电机组,然后按操作人员指定的恢复路径顺序进行负荷恢复。文中将恢复每一个发电机组的时间设为1个时步,对恢复节点39处机组到恢复节点33处机组的过程进行仿真。蓝色实线代表已恢复的系统,节点37处的发电机已并网,其输出有功为51.2 MW。节点25,26,29,39处的负荷恢复量分别为36 MW,40 MW,3 MW,106 MW。红色实线代表待恢复的系统,节点33处发电机的启动功率为67.5 MW。
待恢复节点处的负荷需求的预测值及其权重如表 1所示。假设负荷的波动在10%以内,则隶属度参数μ可以设定为[0.9 0.95 1.05 1.1]。
|
|
表 1 负荷恢复量数据 Table 1 Load recovery data |
文中采用人工蜂群算法求解模糊机会约束优化模型。相关参数设置为:种群数量NP=10;最大蜜源开采次数LMT=5;最大迭代次数LIT=100;置信度水平β1,β2,β3均为0.8;风险参与系数λ=0.2。
4.2 结果分析以IEEE 39节点系统从黑启动节点30到恢复节点33处发电机组的过程为例,进行仿真。设人工蜂群算法的最大迭代次数为100,则这100次迭代过程中目标函数max f的变化如图 4所示。
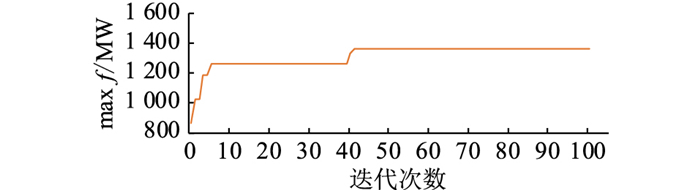
|
图 4 求解迭代过程中的目标函数值变化 Fig. 4 Change of objective function value during solution iteration |
由图 4可以看出,目标函数值初始迭代时为861.84,在迭代的过程中目标函数值逐渐增加,经过4次迭代后逐渐逼近最优解,最后经过40次迭代后达到最优解收敛,并趋于稳定。说明文中利用人工蜂群算法求解模型的过程是收敛的,最终能实现收敛,得到最优解。
为了说明文中模型考虑储能的调频能力对提高负荷恢复效率的作用,对系统恢复过程中,从节点39处机组到节点33处机组的负荷恢复进行仿真。通过求解模糊机会约束模型,在考虑储能的调频能力和不考虑储能调频能力时分别求得负荷恢复结果,如图 5所示。
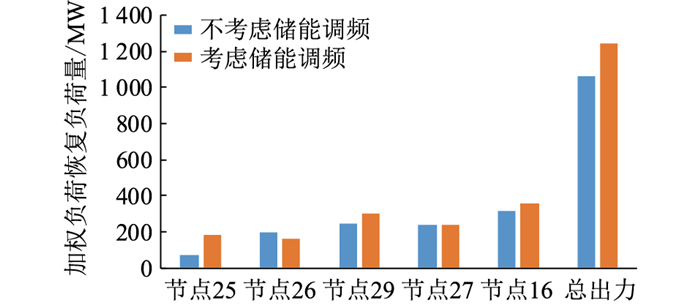
|
图 5 考虑和不考虑储能调频时负荷恢复量 Fig. 5 Load pick-up with/without energy storage system frequency regulation |
由图 5可以看出,在考虑储能调频作用的情况下,可以恢复更多的重要负荷。若不考虑储能的调频作用,由于系统中只有已经并网的37号机组和后续并网的38、39号机组可以调节系统的频率,所能调节的频率范围有限,因此限制了负荷的单次恢复量。若将储能的调频也考虑进来,其快速响应带来的频率调节效果对于该阶段系统的稳定是十分明显的,可以增加系统的调频能力,增大负荷的单次恢复量,从而提高负荷恢复的效率。
为了说明文中模型考虑储能的调频能力能够更好地保证系统的频率安全,通过Simulink搭建系统模型,在有无储能调频作用下,分别对恢复节点33处机组过程中,投入节点16处的负荷出线进行仿真,得到系统频率的变化曲线如图 6所示。
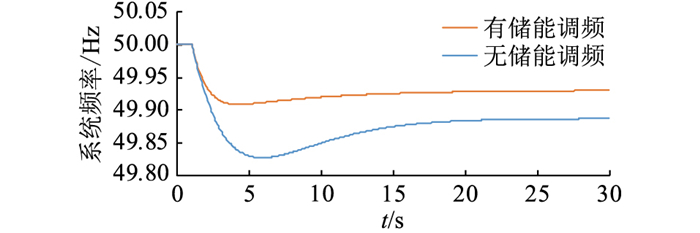
|
图 6 储能有无调频的频率曲线 Fig. 6 Frequency curves with/without energy storage system |
由图 6可以看出,线路投入,储能有调频作用时,系统频率下降到49.909 Hz,最后稳定在49.930 Hz;储能没有调频时,系统频率下降到49.828 Hz,最后稳定在49.887 Hz。综上,储能参与调频可以减少由于负荷投入的冲击导致的暂态频率下降。在负荷恢复过程中,考虑储能的调频能力可以更好地保证系统的安全性。
为了验证储能的容量对于负荷恢复的影响,在恢复节点33处机组的仿真中,分别将储能的容量设为100 MW,150 MW,200 MW,200 MW,然后求解文中提出的模型,得到不同储能容量下的考虑储能调频与不考虑储能调频作用的负荷恢复结果,见图 7。
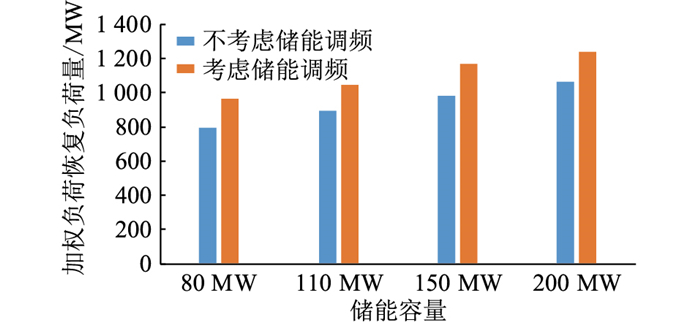
|
图 7 不同储能容量的负荷恢复量 Fig. 7 Load pick-up with different energy storage system capacity |
由图 7可以看出,随着储能容量的增加,负荷的恢复量也在增加。相同容量下,考虑储能调频能力恢复的负荷更多;储能容量越大,可以为负荷恢复提供的功率越多,恢复的总负荷量会增加;储能的频率调节能力越强,系统承受频率波动的能力越强,单次最大可恢复的有功负荷也增加。
为了验证所提模型可以兼顾负荷恢复的风险与收益,在保证系统安全性的同时提高负荷的恢复量,对不同模型的负荷恢复量进行对比。以恢复33号机组为仿真场景,在考虑储能调频的情况下,分别使用模糊机会约束模型、确定性模型和鲁棒模型来优化恢复过程的出力。求解这3种模型得到的负荷恢复结果如表 2所示。
|
|
表 2 3种模型求解结果 Table 2 Solution results of three models |
由表 2可以看出,确定性模型得到的负荷恢复量最大,鲁棒模型得到的负荷恢复量最小,模糊机会约束模型得到的负荷恢复量加权和虽然比确定性模型小,但与鲁棒模型相比较大。鲁棒模型不能有效地利用储能系统和已恢复的发电机组的功率,而确定性模型和模糊机会约束模型可以尽可能多地恢复重要负荷。
为了说明不同模型求解得到的方案的安全性,随机设定负荷波动范围,重复实验20次。每个测试由3个模型求解,得到的总负荷恢复如图 8所示。当实际负荷波动时,如果负荷恢复操作不能满足安全约束,则总负荷恢复量记录为0。
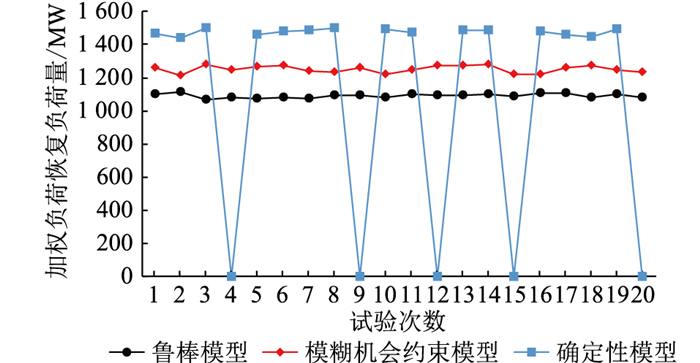
|
图 8 3种模型在随机波动下的结果 Fig. 8 Results of three models in random fluctuation test |
由图 8可以看出,在20个对比实验中,确定性模型超过频率限制5次,但在鲁棒和模糊机会约束模型中没有越限。
从上述仿真结果可以看出,模糊机会约束模型可以保证系统的安全性,并获得更多的重要负荷恢复量。
5 结语针对电力系统负荷恢复过程中,由于电源较少以及系统调频性能弱导致负荷恢复效率低的问题,文中提出了考虑储能调频能力的含电网侧储能电力系统负荷恢复策略。将储能的功率支撑和频率调节作用与已恢复发电机组相结合,提高负荷恢复效率。考虑到负荷不确定性对系统的影响,引入模糊机会约束建立负荷恢复优化模型。仿真结果表明:(1) 在负荷恢复过程中考虑储能的调频能力,可以增加重要负荷的有功恢复量;(2) 考虑储能的调频能力,可以减小系统频率偏移,更好地保证负荷恢复的安全;(3) 采用模糊机会约束模型求解,可以兼顾负荷恢复的风险与收益。
总的来说,文中所提方法可以充分利用储能的功率支撑和频率调节能力,在保证系统安全的同时恢复更多的负荷,提高了系统负荷恢复效率。
本文得到国网江苏省电力有限公司科技项目“基于储能和新能源电站的火电机组黑启动关键技术研究”(J2020127)资助,谨此致谢!
| [1] |
曾辉, 孙峰, 李铁, 等. 澳大利亚"9·28"大停电事故分析及对中国启示[J]. 电力系统自动化, 2017, 41(13): 1-6. ZENG Hui, SUN Feng, LI Tie, et al. Analysis of '9·28' blackout in south Australia and its enlightenment to China[J]. Automation of Electric Power Systems, 2017, 41(13): 1-6. DOI:10.7500/AEPS20170120002 (  0) 0) |
| [2] |
易俊, 卜广全, 郭强, 等. 巴西"3·21"大停电事故分析及对中国电网的启示[J]. 电力系统自动化, 2019, 43(2): 1-6. YI Jun, BU Guangquan, GUO Qiang, et al. Analysis on blackout in Brazilian power grid on March 21, 2018 and its enlightenment to power grid in China[J]. Automation of Electric Power Systems, 2019, 43(2): 1-6. (  0) 0) |
| [3] |
孙华东, 许涛, 郭强, 等. 英国"8·9"大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192. SUN Huadong, XU Tao, GUO Qiang, et al. Analysis on blackout ingreat Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192. (  0) 0) |
| [4] |
李亚男, 顾雪平, 钟慧荣. 考虑负荷类型及停电损失的负荷恢复策略优化[J]. 华北电力大学学报(自然科学版), 2012, 39(3): 6-12. LI Ya'nan, GU Xueping, ZHONG Huirong. Optimization of load recovery plans considering different load types and outage cost[J]. Journal of North China Electric Power University (Natural Science Edition), 2012, 39(3): 6-12. DOI:10.3969/j.issn.1007-2691.2012.03.002 (  0) 0) |
| [5] |
瞿寒冰, 刘玉田. 计及暂态电压约束的负荷恢复能力快速计算[J]. 电力系统自动化, 2009, 33(15): 8-12. QU Hanbing, LIU Yutian. Fast calculation of load restoration capability considering transient voltage constraint[J]. Automation of Electric Power Systems, 2009, 33(15): 8-12. (  0) 0) |
| [6] |
COFFRIN C, VAN HENTENRYCK P. Transmission system restoration with co-optimization of repairs, load pickups, and generation dispatch[J]. International Journal of Electrical Power & Energy Systems, 2015, 72: 144-154. (  0) 0) |
| [7] |
LIAO S W, YAO W, HAN X N, et al. An improved two-stage optimization for network and load recovery during power system restoration[J]. Applied Energy, 2019, 249: 265-275. DOI:10.1016/j.apenergy.2019.04.176 (  0) 0) |
| [8] |
曹曦, 王洪涛. 大规模电网源荷协调恢复决策与控制方法[J]. 中国电机工程学报, 2017, 37(6): 1666-1676. CAO Xi, WANG Hongtao. Source-load coordinated restoration decision-making and control method for large scale power system[J]. Proceedings of the CSEE, 2017, 37(6): 1666-1676. (  0) 0) |
| [9] |
GOLSHANI A, SUN W, SUN K. Real-time optimized load recovery considering frequency constraints[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4204-4215. DOI:10.1109/TPWRS.2019.2922653 (  0) 0) |
| [10] |
ZHAO J, WANG HT, WU Q W, et al. Distributed risk-limiting load restoration for wind power penetrated bulk system[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3516-3528. DOI:10.1109/TPWRS.2020.2973429 (  0) 0) |
| [11] |
李建林, 王上行, 袁晓冬, 等. 江苏电网侧电池储能电站建设运行的启示[J]. 电力系统自动化, 2018, 42(21): 1-9, 103. LI Jianlin, WANG Shangxing, YUAN Xiaodong, et al. Enlightenment from construction and operation of battery energy storage station on grid side in Jiangsu power grid[J]. Automation of Electric PowerSystems, 2018, 42(21): 1-9, 103. DOI:10.7500/AEPS20180809001 (  0) 0) |
| [12] |
张波, 张晓磊, 贾焦心, 等. 基于惯量支撑和一次调频需求的VSG储能单元配置方法[J]. 电力系统自动化, 2019, 43(23): 202-209. ZHANG Bo, ZHANG Xiaolei, JIA Jiaoxin, et al. Configuration method for energy storage unit of virtual synchronous generator based on requirements of inertia support and primary frequency regulation[J]. Automation of Electric Power Systems, 2019, 43(23): 202-209. DOI:10.7500/AEPS20190405002 (  0) 0) |
| [13] |
YOO Y, JUNG S, JANG G. Dynamic inertia response support by energy storage system with renewable energy integration substation[J]. Journal of Modern Power Systems and Clean Energy, 2020, 8(2): 260-266. DOI:10.35833/MPCE.2018.000760 (  0) 0) |
| [14] |
杨丘帆, 王琛淇, 魏俊红, 等. 提升电网惯性与一次调频性能的储能容量配置方法[J]. 电力建设, 2020, 41(10): 116-124. YANG Qiufan, WANG Chenqi, WEI Junhong, et al. Capacity allocation of energy storage system for improving grid inertia and primary frequency regulation[J]. Electric Power Construction, 2020, 41(10): 116-124. (  0) 0) |
| [15] |
刘伟佳, 林振智, 文福拴, 等. 考虑电动汽车支持的电力系统恢复多目标最优策略[J]. 电力系统自动化, 2015, 39(20): 32-40. LIU Weijia, LIN Zhenzhi, WEN Fushuan, et al. Multi-objective optimal strategies for power system restoration with support from electric vehicles[J]. Automation of Electric Power Systems, 2015, 39(20): 32-40. DOI:10.7500/AEPS20150415002 (  0) 0) |
| [16] |
刘英培, 侯亚欣, 梁海平, 等. 一种适用于黑启动的光储联合发电系统协调控制策略[J]. 电网技术, 2017, 41(9): 2979-2986. LIU Yingpei, HOU Yaxin, LIANG Haiping, et al. A coordinated control strategy of PV battery-energy storage hybrid power system for black start[J]. Power System Technology, 2017, 41(9): 2979-2986. (  0) 0) |
| [17] |
杜康, 刘艳, 叶茂, 等. 辅助风电场参与初期黑启动时储能电站容量配置策略[J]. 电力系统保护与控制, 2017, 45(18): 62-68. DU Kang, LIU Yan, YE Mao, et al. Capacity configuration strategy of energy storage power station when assisting the wind farm in integrating into the preliminary black start[J]. Power System Protection and Control, 2017, 45(18): 62-68. (  0) 0) |
| [18] |
SUN L, LIU W, CHUNG C Y, et al. Improving the restorability of bulk power systems with the implementation of a WF-BESS system[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2366-2377. DOI:10.1109/TPWRS.2018.2889990 (  0) 0) |
| [19] |
LIU W J, SUN L, LIN Z Z, et al. Multi-objective restoration optimisation of power systems with battery energy storage systems[J]. IET Generation, Transmission & Distribution, 2016, 10(7): 1749-1757. (  0) 0) |
| [20] |
宋坤隆, 谢云云, 陈晞, 等. 基于信息间隙决策理论的电网负荷恢复鲁棒优化[J]. 电力系统自动化, 2017, 41(15): 113-120, 175. SONG Kunlong, XIE Yunyun, CHEN Xi, et al. Robust restoration method for power system load based on information gap decision theory[J]. Automation of Electric Power Systems, 2017, 41(15): 113-120, 175. (  0) 0) |
| [21] |
YANG Y D, LI S F, LI W Q, et al. Power load probability density forecasting using Gaussian process quantile regression[J]. Applied Energy, 2018, 213: 499-509. DOI:10.1016/j.apenergy.2017.11.035 (  0) 0) |
| [22] |
熊虎, 向铁元, 陈红坤, 等. 含大规模间歇式电源的模糊机会约束机组组合研究[J]. 中国电机工程学报, 2013, 33(13): 36-44. XIONG Hu, XIANG Tieyuan, CHEN Hongkun, et al. Research of fuzzy chance constrained unit commitment containing large-scale intermittent power[J]. Proceedings of the CSEE, 2013, 33(13): 36-44. (  0) 0) |
| [23] |
翟俊义, 任建文, 周明, 等. 含风电电力系统的多时间尺度模糊机会约束动态经济调度模型[J]. 电网技术, 2016, 40(4): 1094-1099. ZHAI Junyi, REN Jianwen, ZHOU Ming, et al. Multi-time scale fuzzy chance constrained dynamic economic dispatch model for power system with wind power[J]. Power System Technology, 2016, 40(4): 1094-1099. (  0) 0) |
| [24] |
张雪丽, 梁海平, 朱涛, 等. 基于模糊机会约束规划的电力系统网架重构优化[J]. 电力系统自动化, 2015, 39(14): 68-74. ZHANG Xueli, LIANG Haiping, ZHU Tao, et al. Optimization of power network reconfiguration based on fuzzy chance constrained programming[J]. Automation of Electric Power Systems, 2015, 39(14): 68-74. (  0) 0) |
| [25] |
陈彬, 王洪涛, 曹曦. 计及负荷模糊不确定性的网架重构后期负荷恢复优化[J]. 电力系统自动化, 2016, 40(20): 6-12. CHEN Bin, WANG Hongtao, CAO Xi. Load restoration optimization during the last stage of network reconfiguration considering load fuzzy uncertainty[J]. Automation of Electric Power Systems, 2016, 40(20): 6-12. (  0) 0) |
| [26] |
WANG B, WANG S M, WATADA J. Fuzzy-portfolio-selection models with value-at-risk[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(4): 758-769. (  0) 0) |
| [27] |
ADIBI M M, BORKOSKI J N, KAFKA R J, et al. Frequency response of prime movers during restoration[J]. IEEE Transactions on Power Systems, 1999, 14(2): 751-756. (  0) 0) |
| [28] |
刘宝碇, 彭锦. 不确定理论教程[M]. 北京: 清华大学出版社, 2005. LIU Baoding, PENG Jin. A course in uncertainty theory course in uncertainty theory[M]. Beijing: Tsinghua University Press, 2005. (  0) 0) |
2. China Electric Power Research Institute (Nanjing), Nanjing 210003, China
 2021, Vol. 40
2021, Vol. 40


 谢云云(1985), 男, 博士, 副教授, 研究方向为极端条件下电力系统运行与控制(E-mail:
谢云云(1985), 男, 博士, 副教授, 研究方向为极端条件下电力系统运行与控制(E-mail: