文章编号: 2096-3203(2021)06-0193-06 中图分类号: TM21
2. 江苏苏电产业管理有限公司, 江苏 南京 210024
国内的输电杆塔以钢材作为主要材料,钢材存在易生锈、单位质量重以及施工运输、运行维护困难等问题,全塔采用钢材的输电线路易发生污秽闪络、风偏放电等事故。为了提高电网的安全性和创新性,寻求新型材料部分或完全替代钢材已成为必然选择[1-3]。
高性能纤维增强复合材料具有轻质高强、耐腐蚀、抗疲劳等优异性能,由其制成的复合绝缘横担在抗拉强度、弯曲强度、抗老化性能和耐腐蚀性能等方面都明显优于金属横担。目前国内主要将复合材料用于220 kV及以下电压等级较低的输电线路中,对于500 kV及以上的超高压输电线路,应用较少。此外,采用复合横担杆塔能够提高结构强度,延长结构使用寿命,缩短杆塔输电的更换周期,因此采用复合横担杆塔代替全钢杆塔成为近年来研究的一个热点[4-6]。在国外,欧美等发达国家从上世纪90年代开始研究复合材料杆塔,并逐步应用到实际输电线路中。在国内,文献[7]对某750 kV输电线路复合横担塔在实际工程中的结构方案进行了对比分析,并给出了推荐的结构形式;文献[8]针对复合横担应用于特高压交流输电线路给出了其设计方案。
我国作为受极端天气灾害影响较严重的国家之一,覆冰灾害的频繁发生给经济社会造成了巨大的损失[9-11]。据不完全统计,我国发生千余次由于覆冰引起的输电线路灾变事故,导线覆冰灾变已成为影响输电设施安全的重要因素之一。因此,结合我国输电线路覆冰灾变的实际,开展输电线路覆冰断线的研究工作具有重要意义[12-13]。目前关于复合横担的设计还未形成统一规范,其主要还是基于静力学设计,未考虑复杂运营荷载下的动力效应和长期使用的耐久性,所以考虑动力效应的复合横担设计显得尤为重要。
文中针对10 kV复合绝缘横担在覆冰断线工况下的力学性能展开研究。首先,在充分掌握线路、杆塔以及横担特性的基础上,采用ANSYS进行动力分析,在确定断线点位置的基础上,对断一根及多根导线的工况组合进行模拟计算,讨论复合横担在覆冰断线工况下的动态应力响应特征,并和覆冰静载情况下的应力水平进行比较;其次,观察复合横担上危险位置是否发生变化,从而对薄弱位置进行强度设计;最后,分别研究方管水平型、方管上字型以及方棒上字型横担在覆冰断线工况下的力学特性,比较3种不同结构形式的复合横担在断线工况下的动力响应。
1 理论分析 1.1 瞬态动力分析简介在进行结构设计和内力分析计算时,所依据的理论一般都是建立在线弹性力学基础上的。而瞬态动力分析是用来求解结构在一定初始和边界条件下的动力响应问题,实质上就是通过求解离散方程得到结构在外加荷载作用下的位移、速度和加速度。所谓的离散就是用许多个离散的节点来对结构进行描述。结构运动的通用方程可表示为:
| $ \mathit{\boldsymbol{M}}\ddot u(t) + \mathit{\boldsymbol{C}}\dot u(t) + \mathit{\boldsymbol{K}}u(t) = \mathit{\boldsymbol{F}}(t) $ | (1) |
式中:ü(t),
对于线性动力学问题,其动力行为完全由线弹性结构行为和结构所受的外部动荷载这2个独立特性来决定,通常采用振型迭加法和直接积分法进行求解。还有一些动力问题会由于材料塑形、结构大转动、大位移和接触等引起非线性,非线性动力问题复杂而又多样,通常无法给出成功分析的简单原则,一般进行求解运算时采用直接积分法成功率较高[14-16]。文中采用直接积分法对复合横担的断线效应进行数值计算。
直接积分法是对全耦合的有限元离散运动方程直接进行积分,该方法一般有2个前提:一个是用满足离散时间点上的方程来代替在求解时间域内的任何时刻都应得到满足的运动方程;另一个是在离散时间点之间的Δt区域内对结构的位移、速度和加速度进行人为的假设。
直接积分法的时间离散化方程有显式和隐式两类。显式方法是由t时刻的运动方程求t+Δt时刻的位移,每步的求解计算量较小,但要求有足够小的时间步长,当时间步长大于结构最小周期的一定比例时,该方法计算得到的结构位移和速度将会发散或出现较大的误差;隐式方法是从与t+Δt时刻运动方程相关联的表达式中求t+Δt时刻的位移,该方法可以允许较大的时间步长(步长取决于精度要求),但每步的求解计算量较大。大多数显式方法都是条件稳定的,而隐式方法则是无条件稳定的,比较典型的显式法和隐式法分别是中心差分法和Newmark法。
1.2 有限元分析理论有限单元法属于数值分析方法[17]中的一大类,它的出现是数值分析方法研究领域的重大突破,是工程领域中应用最为广泛的数值模拟方法。有限单元法的基本思想是将连续的求解区域离散为一组有限个、且按一定方式相互连接的单元的组合体,利用在每一个单元内假设的近似函数来分片地表示全求解域上待求的未知场函数,从而使一个连续的无限自由度问题变成离散的有限自由度问题。
有限元分析的基本概念是用较简单的问题代替复杂问题后再求解。其将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的较简单的近似解,然后推导求解这个域总的满足条件,如结构的平衡条件,从而得到问题的解。这个解不是准确解,而是近似解。由于大多数实际问题难以得到准确解,而有限元不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。
对于不同物理性质和数学模型的问题,有限元求解法的基本步骤是相同的,只是具体公式推导和运算求解不同。有限元求解问题的基本步骤通常如下:
(1) 问题及求解域定义;
(2) 求解域离散化;
(3) 确定状态变量及控制方法;
(4) 单元推导;
(5) 总装求解;
(6) 联立方程组求解和结果解释。
求解结构动力学问题所依据的基本力学变量和方程与静力问题类似,但所有变量都是时间函数,主要包括基本变量ui(ζ, t),εij(ζ, t),σij(ζ, t)。3个变量均是坐标位置ζ(x, y, z)和时间t的函数,一般将其记为ui(t),εij(t),σij(t)。利用达朗贝尔原理将惯性力和阻尼力等效到静力平衡方程中,得到如式(2)所示的平衡方程,再根据位移条件即可求解动力学控制方程。
| $ {\sigma _{ij, j}}\left( t \right) + {\bar b_i}\left( t \right) - \rho {\ddot u_i}\left( t \right) - v{\dot u_i}\left( t \right) = 0 $ | (2) |
式中:σij, j(t), bi(t), üi(t),
文中是以方管水平型、方管上字型以及方棒上字型复合横担作为研究对象,建立这3种不同形式复合横担的有限元模型进行数值计算。输电线路档距采用80 m,塔型为直线塔,导线采用JKLYJ系列铝芯交联聚乙烯绝缘架空电缆,参数见表 1。
|
|
表 1 10 kV绝缘导线参数 Table 1 10 kV insulated wire parameter |
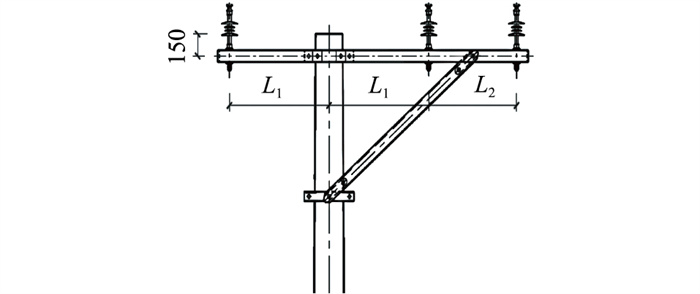
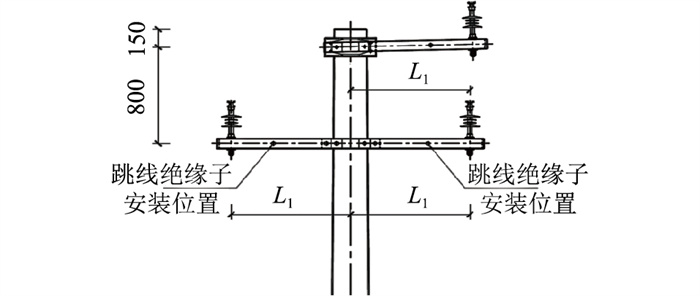
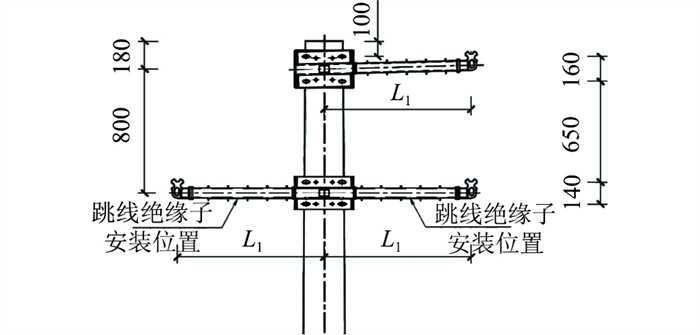
复合横担均采用高性能纤维增强树脂基材料,3种不同形式的复合横担如图 1—图 3所示。
|
图 1 方管水平型 Fig. 1 Square tube horizontal type |
|
图 2 方管上字型 Fig. 2 Square tube upward type |
|
图 3 方棒上字型 Fig. 3 Square stick upward type |
在实际情况中,横担与电线杆的连接通常可以看成是固接,其余节点的连接可以根据实际情况采用节点耦合的方式设计为固接或铰接。文中在构建复合横担模型时采用空间梁单元beam l88进行模拟。beam l88梁单元的各端节点包含X,Y,Z方向的位移和绕这3个轴的扭转,共6个自由度,能够满足横担实际变形的要求。
2 复合横担的动力计算 2.1 断线分析在对导线进行断线工况的模拟时,首先需要完成结构在自重和覆冰作用下的静力分析[18]。然后分别对线路断1根、2根和3根导线的工况进行对比分析[19-20]。一般在进行有限元分析时,为了方便处理问题都会作出假设,文中的分析主要基于以下假设进行:
(1) 材料特性符合胡克定律;
(2) 输电杆塔塔底与地基的连接按固接处理,复合横担与输电杆塔的连接也按固接处理;
(3) 断线在较短的时间内发生;
(4) 不考虑导线落地后与地面的接触冲击作用;
(5) 断线发生于导线和横担的连接位置。
根据文献[18]的研究,对于塔线体系发生断线时对结构体系的冲击作用可采用冲击系数来反映,即:
| $ \delta = \frac{{\left| {{N_m} - {N_0}} \right|}}{{\left| {{N_0}} \right|}} $ | (3) |
式中:Nm为塔线体系在发生断线工况下的构件最大轴向应力值;N0为塔线体系在正常运行情况下杆件的轴线应力值[21]。
2.2 复合横担在断线工况下的数值计算文中对方管水平型横担在不同位置断1根、2根、3根导线的情况进行分析,发生断裂的导线都为方管水平型横担的同侧导线。由于断线一般发生在线路覆冰的情况下[22],所以断线工况的模拟计算选用线路覆冰工况下的荷载。
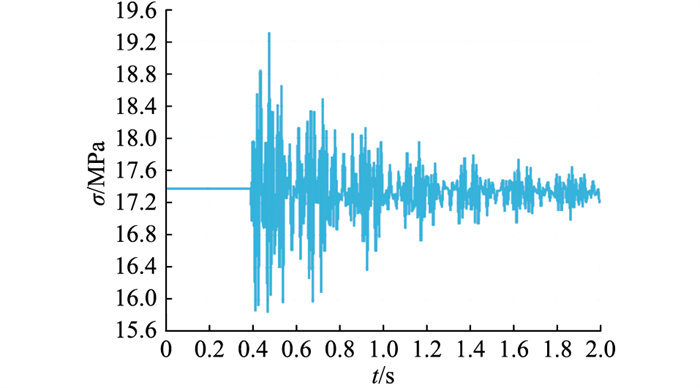
2.2.1 断1根导线在ANSYS中采用瞬态动力分析来模拟断线过程。以垂直方向(y方向)荷载为例,在0~0.4 s时,荷载保持不变以模拟未断线情况,在0.4 s时,荷载突然下降,模拟断线瞬间荷载突然变化,在0.4~2 s时,荷载为断线后的情况。首先对方管水平型横担左侧导线进行断线处理,得到其斜撑左侧单元最大截面点应力的时程曲线,如图 4所示。此单元截面上动态最大应力为19.31 MPa,相比覆冰工况下此单元上的最大应力17.37 MPa,增大了1.1倍。
|
图 4 斜撑左侧单元最大截面点应力时程曲线(断线点位于横担最左侧) Fig. 4 Maximum section point stress time history curve of left strut (the break point is on the leftmost side of the crossarm) |
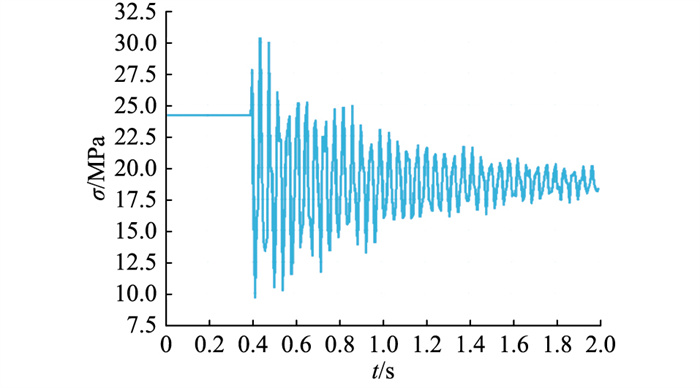
其次考虑在方管水平型横担最右侧断1根导线,在此情况下其根部右侧单元最大截面点应力的时程曲线如图 5所示。此单元截面上动态最大应力为30.35 MPa,相比覆冰工况下此单元上的最大应力24.18 MPa,增大了1.3倍。
|
图 5 根部右侧单元最大截面点应力时程曲线(断线点位于横担最右侧) Fig. 5 Maximum section point stress time history curve of right side unit (the break point is on the far right side of the crossarm) |
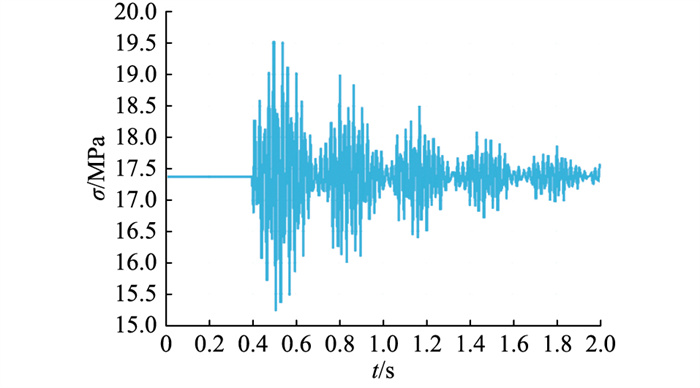
最后考虑在方管水平型横担右侧中间断1根导线,此时其斜撑左侧单元最大截面点应力的时程曲线如图 6所示。此单元截面上动态最大应力为19.53 MPa,相比覆冰工况下此单元上的最大应力17.37 MPa,增大了1.2倍。
|
图 6 斜撑左侧单元最大截面点应力时程曲线(断线点位于横担右侧中间) Fig. 6 Maximum section point stress time history curve of left strut unit (the break point is located in the middle of the right side of the crossarm) |
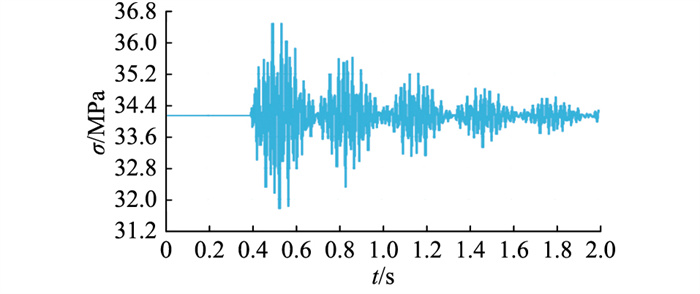
下面考虑方管水平型横担断右侧2根导线的情况,方管水平型横担根部左侧单元最大截面点应力的时程曲线如图 7所示,此单元截面上动态最大应力为36.50 MPa,相比覆冰工况下此单元上的最大应力34.14 MPa,增大了1.1倍。
|
图 7 根部左侧单元最大截面点应力时程曲线(断2根导线) Fig. 7 Maximum section point stress time history curve of left side unit (break two wires) |
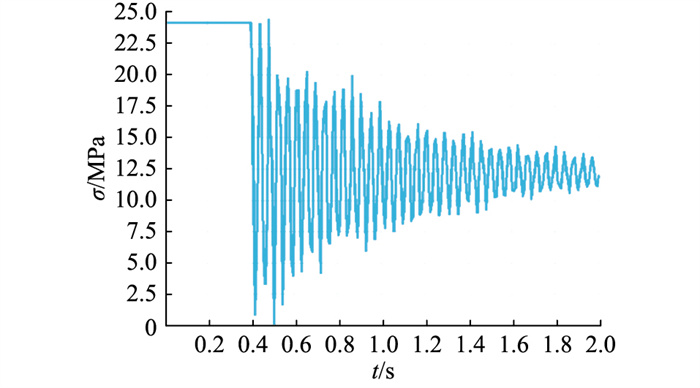
最后考虑方管水平型横担断3根导线(即两侧导线全断)的情况,方管水平型横担根部右侧单元最大截面点应力的时程曲线如图 8所示,此单元截面上动态最大应力为24.48 MPa,相比覆冰工况下此单元上的最大应力24.18 MPa,略有增大。
|
图 8 根部右侧单元最大截面点应力时程曲线(断3根导线) Fig. 8 Maximum section point stress time history curve of right side unit (break three wires) |
当导线发生断线时,复合横担关键截面应力会有不同程度的增加,对与断点位置有直接联系的复合横担根部影响较大,在设计中应加以考虑;对与断点位置无直接联系的复合横担根部影响较小,断线后横担上关键截面危险点的应力放大系数一般为1.1~1.3;多根导线同时发生断线时导线之间的相互影响较小,因此断线之间的互相作用基本可以忽略。由于断线过程本身是一个卸载过程,断线稳定后横担上关键截面危险点的应力应当是减小的。如果3根导线同时断裂相当于在横担上3个加载点的位置同时卸载,而断1根导线的情况是只有1个加载点卸载,其余2个加载点都是满载,所以断线数目多反而动力放大系数会更小。
断线工况下3种形式的复合横担最危险位置位于横担与杆塔连接的根部两侧,而方管水平型横担与斜撑连接的位置也是重点关注区域,所以在强度设计时应当采取相应的加固措施。相比而言,方管水平型横担和方管上字型横担能够满足工程应用安全冗余度的要求,而方棒上字型横担不能满足工程应用安全冗余度的要求。
由于不同电压等级的输电线路复合横担的结构形式不同,文中仅对10 kV复合绝缘横担进行了仿真分析,因此得到的结论若要推广到更高等级的输电线路复合横担中还需进一步研究。
| [1] |
陈强, 王建, 熊小伏, 等. 一种降雨诱发滑坡灾害下输电杆塔的监测与预警方法[J]. 电力系统保护与控制, 2020, 48(3): 147-155. CHEN Qiang, WANG Jian, XIONG Xiaofu, et al. Monitoring and early warning method for transmission tower under rainfall-induced landslide disaster[J]. Power System Protection and Control, 2020, 48(3): 147-155. (  0) 0) |
| [2] |
曹宁. 110 kV输电线路复合材料杆塔的应用研究[D]. 广州: 华南理工大学, 2012. CAO Ning. The applied research on composite material towers of 110 kV transmission line[D]. Guangzhou: South China University of Technology, 2012. (  0) 0) |
| [3] |
张栋. 复合材料构件疲劳性能试验研究[D]. 西安: 西安理工大学, 2016. ZHANG Dong. Experimental research on fatigue properties of composite material component[D]. Xi'an: Xi'an University of Technology, 2016. (  0) 0) |
| [4] |
LEE S W, CHO Y H, KIM J H, et al. Mechanical performance evaluation of composite hybrid pantograph upper arm under environmental cyclic conditions: experimental verification[J]. Composite Structures, 2019, 210: 599-607. DOI:10.1016/j.compstruct.2018.11.076 (  0) 0) |
| [5] |
SELVARAJ M, KULKARNI S, BABU R R. Analysis and experimental testing of a built-up composite cross arm in a transmission line tower for mechanical performance[J]. Composite Structures, 2013, 96: 1-7. DOI:10.1016/j.compstruct.2012.10.013 (  0) 0) |
| [6] |
单青. 新型复合横担在特高压输电铁塔中的应用研究[D]. 北京: 华北电力大学, 2017. SHAN Qing. Study on the application of the new composite cross load in UHV transmission tower[D]. Beijing: North China Electric Power University, 2017. (  0) 0) |
| [7] |
胡超, 冯衡, 徐彬. 750 kV输电线路复合材料横担塔的适用性研究[J]. 电力勘测设计, 2016(1): 65-71. HU Chao, FENG Heng, XU Bin. Research on the applicability of composite cross arm tower for 750 kV transmission line[J]. Electric Power Survey & Design, 2016(1): 65-71. DOI:10.3969/j.issn.1671-9913.2016.01.018 (  0) 0) |
| [8] |
吴昊, 孙珍茂, 刘勇. 复合横担在1000 kV特高压交流输电双回路铁塔中的应用探讨[J]. 电力与能源, 2018, 39(1): 45-48, 62. WU Hao, SUN Zhenmao, LIU Yong. Application of composite cross arm in 1000 kV UHV AC overhead transmission line tower[J]. Power & Energy, 2018, 39(1): 45-48, 62. (  0) 0) |
| [9] |
何健, 杨振国, 冯文礼, 等. 辽宁电网"11.7"覆冰灾害分析[J]. 吉林电力, 2016, 44(1): 46-49. HE Jian, YANG Zhenguo, FENG Wenli, et al. 11.7 icing disaster analyses in Liaoning power system[J]. Jilin Electric Power, 2016, 44(1): 46-49. DOI:10.3969/j.issn.1009-5306.2016.01.014 (  0) 0) |
| [10] |
马天男. 基于大数据的电网覆冰灾害预测与风险管理研究[D]. 北京: 华北电力大学, 2017. MA Tiannan. Prediction and risk management of power grid icing disaster based on big data[D]. Beijing: North China Electric Power University, 2017. (  0) 0) |
| [11] |
杜雅昕, 张婷婷, 张文. 极端天气下计及电-气互联影响的配电网弹性评估[J]. 供用电, 2019, 36(5): 8-13. DU Yaxin, ZHANG Tingting, ZHANG Wen. Resilience assessment for distribution systems considering interconnections with gas systems under extreme weather[J]. Distribution & Utilization, 2019, 36(5): 8-13. (  0) 0) |
| [12] |
张宇, 徐宁, 邓静伟, 等. 山区输电塔线体系覆冰断线效应研究[J]. 武汉理工大学学报, 2016, 38(6): 61-65, 72. ZHANG Yu, XU Ning, DENG Jingwei, et al. Research on icing wire-breaking effects of transmission tower-line systems in mountain areas[J]. Journal of Wuhan University of Technology, 2016, 38(6): 61-65, 72. DOI:10.3963/j.issn.1671-4431.2016.06.010 (  0) 0) |
| [13] |
张志强, 黄增浩. 配网线路覆冰断线力学特性及加固措施分析[J]. 电力科学与工程, 2019, 35(3): 52-58. ZHANG Zhiqiang, HUANG Zenghao. Mechanical property of distribution network line breaking under icing status and reinforcement measures analysis[J]. Electric Power Science and Engineering, 2019, 35(3): 52-58. DOI:10.3969/j.ISSN.1672-0792.2019.03.008 (  0) 0) |
| [14] |
杨风利. 重冰区导线断线响应及荷载取值分析[J]. 振动与冲击, 2013, 32(24): 169-173, 186. YANG Fengli. Dynamic responses and tensions of broken conductors for suspension towers in heavy icing area[J]. Journal of Vibration and Shock, 2013, 32(24): 169-173, 186. DOI:10.3969/j.issn.1000-3835.2013.24.029 (  0) 0) |
| [15] |
李嘉祥. 覆冰导线的力学特性及塔-线体系动力响应分析[D]. 大连: 大连理工大学, 2017. LI Jiaxiang. Mechanical characteristics of iced conductor and dynamic response analysis of tower-line system[D]. Dalian: Dalian University of Technology, 2017. (  0) 0) |
| [16] |
SHEN G H, SUN B N, YIN Y E, et al. Broken wire analysis and broken wire load calculation of high voltage transmission tower[J]. Journal of Zhejiang University, 2011, 45(4): 678-683. (  0) 0) |
| [17] |
鲍立华. 输电塔线体系的断线分析[D]. 杭州: 浙江大学, 2008. BAO Lihua. Broken wire analysis of transmission line systems[D]. Hangzhou: Zhejiang University, 2008. (  0) 0) |
| [18] |
李妍, 刘红军, 李正良, 等. 输电塔线体系断线非线性动力分析[J]. 振动与冲击, 2017, 36(7): 70-79, 85. LI Yan, LIU Hongjun, LI Zhengliang, et al. Nonlinear dynamic analysis for a transmission tower-line system subjected to wire breakage[J]. Journal of Vibration and Shock, 2017, 36(7): 70-79, 85. (  0) 0) |
| [19] |
谢云云, 金颖, 黄琳雁, 等. 适用于有高差线路的覆冰输电导线ANSYS找形方法[J]. 电力工程技术, 2017, 36(2): 9-13, 50. XIE Yunyun, JIN Ying, HUANG Linyan, et al. Form-finding method of transmission lines consulting the lowest point[J]. Electric Power Engineering Technology, 2017, 36(2): 9-13, 50. DOI:10.3969/j.issn.1009-0665.2017.02.002 (  0) 0) |
| [20] |
刘红军, 周佳林, 赵亚新. 基于断线作用的输电塔线体系动力效应影响分析[J]. 湖南大学学报(自然科学版), 2018, 45(3): 62-71. LIU Hongjun, ZHOU Jialin, ZHAO Yaxin. Analysis on dynamic effect of transmission line system based on wire breakage[J]. Journal of Hunan University (Natural Sciences), 2018, 45(3): 62-71. (  0) 0) |
| [21] |
HAN G D, WU Z Q, WAN S T, et al. Fracture analysis of 500 kV composite insulators suspension clamp[J]. Applied Mechanics and Materials, 2014, 556-562531-534. (  0) 0) |
| [22] |
陈勇, 李鹏, 张忠军, 等. 基于PCA-GA-LSSVM的输电线路覆冰负荷在线预测模型[J]. 电力系统保护与控制, 2019, 47(10): 110-119. CHEN Yong, LI Peng, ZHANG Zhongjun, et al. Online prediction model for power transmission line icing load based on PCA-GA-LSSVM[J]. Power System Protection and Control, 2019, 47(10): 110-119. DOI:10.7667/PSPC20191015 (  0) 0) |
2. Jiangsu Electric Power Industrial Management Co., Ltd., Nanjing 210024, China
 2021, Vol. 40
2021, Vol. 40


 陆兴华(1994), 男, 硕士, 研究方向为工程中关键力学问题的建模、分析理论及计算方法(E-mail:
陆兴华(1994), 男, 硕士, 研究方向为工程中关键力学问题的建模、分析理论及计算方法(E-mail: