文章编号: 2096-3203(2021)05-0017-08 中图分类号: TM71
2. 东南大学电气工程学院, 江苏 南京 210096
面对日益严峻的能源危机与环境污染问题,电动汽车(electric vehicle, EV)作为环境友好型交通工具迎来了发展机遇[1-2]。然而规模化EV的随机充电行为会导致负荷峰值增加、电能质量降低等问题,给配电网的安全与经济运行带来了挑战[3-4]。同时,面对规模化电动汽车调度算力要求高、计算复杂的问题,传统优化模型无法满足实时调度需求。因此,研究充光储一体化能源站的区域电动汽车优化调度策略,已成为亟待解决的重要问题。
目前,国内外学者在针对光储能源站的电动汽车调度方面已取得一定成果。考虑光伏发电等可再生能源对优化调度策略的影响,文献[5]以能源站运行成本为优化目标,基于多模态近似动态规划进行求解,在不同定价模型与光伏出力情况下均表现出较强鲁棒性。文献[6]以减少微电网与配电网交换功率以及微电网网络损耗为优化目标,采用序列二次规划算法进行求解。通过对EV进行充放电调度使日负荷曲线跟踪发电曲线,并网模式下的网络损耗及离网模式下的所需储能系统容量均得到降低。文献[7]考虑能源站源荷互补特性,提出了一种考虑不确定性风险的能源站多时间尺度调度模型。文献[8-9]考虑光伏出力预测误差等不确定性,建立了以充光储能源站日运行成本最小为目标的充电站日前优化模型,并在此基础上建立实时
滚动优化模型。文献[10]以大规模EV接入的配电网运行成本最小和负荷曲线方差最小为目标建立EV优化调度模型,在保证系统运行成本的同时有效降低了负荷峰谷差。
上述研究均建立单/多目标-多约束优化模型解决EV调度问题,但应用在实时调度方面均面临着海量计算的压力,无法满足实时调度的需求。同时,上述研究过度依赖模型,当实际应用中包含模型未考虑的不确定性因素时,模型的优化结果得不到保证,算法的鲁棒性与泛化能力有待改进。随着机器学习算法的逐渐成熟,已有少量学者开展了深度强化学习(deep reinforcement learning,DRL)应用于EV充电调度的研究。文献[11]提出一种基于竞争深度Q网络的充电控制方法,在含高渗透率分布式电源的系统中能够兼顾配电网的安全运行与用户出行需求。文献[12]考虑EV行驶距离限制,以最小化EV总充电时间为目标,建立DRL模型进行训练求解。文献[13]考虑用户用电需求,将EV充放电能量边界作为部分状态空间,建立了以最小化功率波动与充放电费用为目标的实时调度模型。文献[14]考虑电价与用户通勤行为的不确定性,从充电电价中提取特征训练Q网络,并采用Q值最大化原则执行动作。文献[15]以最小化EV用户行驶时间与充电成本为目标,利用最短路径法提取当前环境状态训练智能体。
虽然上述研究理解了DRL方法的本质,以用户充放电时间或费用作为目标,将车辆与充电站参数作为环境状态进行求解。然而,作为车辆行驶与充电行为的最终执行者,EV车主对充电方案的感知效应尤为重要,影响调度策略的可执行性与适用性。为此,文中提出了一种考虑人类行为心理的能源站EV调度方法。基于后悔理论刻画EV用户心理状态,建立智能体"人-车-站"全状态环境感知模型。同时,引入时变ε-greedy策略作为智能体动作选择方法以提高算法收敛速度。最后结合南京市实际道路与能源站分布设计了多场景算例仿真,验证文中所提策略的有效性与实用性。
1 EV调度问题构建充光储一体化能源站[16]结构如图 1所示,按功能可分为:配电网系统、光伏发电系统、储能系统、AC/DC模块、DC/DC模块、充电桩、通信管理机以及能量管理系统。

|
图 1 充光储能源站架构 Fig. 1 PV-storage-charging integrated energy station |
光伏系统由多组太阳能电池板串并联组成,电池板接收太阳能发电经DC/DC变换器接入直流母线,电能主要用于EV充电。储能系统由电池组构成,通过双向DC/DC变换器接入直流母线。当光伏系统发电有剩余时,其储存电能;当光伏发电不足时,其释放电能。AC/DC模块为配电网系统与能源站的连接单元,当能源站内部电能不能满足充电需求时由配电网经AC/DC接入充电负荷。
针对充光储一体化能源站,考虑能源站光伏消纳能力与EV用户利益,可以建立EV充电调度模型如下:
| $ \min {f_1} = \frac{1}{{{N_{\rm{e}}}}}\sum\limits_{i = 1}^{{N_{\rm{e}}}} {\left( {{\omega _1}{T_i} + {\omega _2}{C_i}} \right)} $ | (1) |
| $ \max {f_2} = \frac{1}{{{T_{\rm{s}}}}}\sum\limits_{t = 1}^{{T_{\rm{s}}}} {{P_{{\rm{PV}}}}} (t)\Delta t $ | (2) |
约束条件为:
| $ {S^{\min }} \le S(t) \le {S^{\max }} $ | (3) |
| $ \frac{{{P_{{\rm{EV}}}}(t)}}{{{\eta _1}}} + \frac{{{P_{\rm{B}}}(t)}}{{{\eta _1}}} = {P_{{\rm{PV}}}}(t){\eta _1} + {P_{\rm{D}}}(t){\eta _2} $ | (4) |
| $ \left| {{P_{\rm{B}}}(t)} \right| \le P_{\rm{B}}^{\max } $ | (5) |
| $ 0 \le {P_{\rm{D}}}(t) < P_{\rm{D}}^{\max } $ | (6) |
| $ \sum\limits_{i = 1}^{{N_{\rm{s}}}} {{\varphi _i}} = 1 $ | (7) |
| $ \sum\limits_{j \in {W_i}} {{u_{ij}}} = 1 $ | (8) |
式中:Ne为EV总数量;Ti为用户i的总时间,包括路程时间、等待时间与充电时间,其中路程时间为用户从充电触发位置出发直至抵达目标能源站的路程耗时;Ci为用户i的费用,包括充电费用与服务费用;ω1,ω2分别为用户时间与费用系数;Ts为仿真总时间;PEV(t), PPV(t), PD(t), PB(t)分别为t时刻站内充电负荷、光伏出力、配电网出力以及储能充放电功率,其中储能充电时PB(t)值为正,放电时PB(t)值为负;η1,η2分别为站内DC/DC模块及AC/DC模块效率;Smin,Smax分别为储能系统荷电状态(state of charge,SOC)下限与上限;PBmax为储能最大充放电功率;PDmax为充电桩最大购电功率;Ns为区域范围内能源站数量;φi为能源站选择变量;Wi为所有与节点i相连的道路节点集合;uij为用户在节点i处的道路选择变量。
针对充光储能源站的EV调度模型属于多目标多约束优化问题,基于规划的方法以及启发式算法虽然可以进行求解,但这些算法均为离线运算且面对实际交通拓扑网络运算耗时较长。同时,不同日期下天气条件、用户充电需求等均存在较大差异,模型均需要重新求解,耗时较长且难以实现在线实时调度。
2 基于DRL的EV调度方法 2.1 DRL基本原理DRL是一种结合深度学习的感知能力与强化学习的决策能力的人工智能算法。通过智能体不断与环境进行交互,并采取一定的动作使得累计奖励最大化[17-18]。智能体本质上是一个状态空间到动作空间的映射关系。强化学习算法以马尔科夫过程(Markov decision process, MDP)为数学基础,即环境下一时刻状态仅与当前状态有关,与前序状态无关。
强化学习算法采用状态-动作值函数Qπ(s, a)来评价状态s时采取动作a的好坏,Q函数的贝尔曼方程可表示为:
| $ {Q^\pi }(s, a) = E\left( {r\left( {s, a, s'} \right) + \gamma \mathop {\max }\limits_\pi {Q^\pi }\left( {s', a'} \right)} \right) $ | (9) |
式中:r(s, a, s′)为智能体采取动作a,状态s转变为s′对应的即时奖励;π为智能体在当前状态s下决定下一动作a的策略函数;E为数学期望;γ∈[0, 1],为折扣率,γ接近于0时,智能体更在意短期回报,γ接近于1时,智能体更在意长期回报。
在传统Q学习过程中,状态-动作-Q值以表格的实行进行记录,智能体在状态s下查找Q表并采取最大Q值对应的动作a*。然而,实际问题中状态空间及动作空间往往很大,Q学习方法难以实践。在Q学习框架基础上,深度Q网络(deep Q net-work, DQN)以深度神经网络代替Q表进行函数逼近[19],拟合状态-动作与Q值的映射关系,其贝尔曼迭代方程可表示为:
| $ \begin{array}{l} Q\left( {s, a;{\theta ^ + }} \right) = Q\left( {s, a;{\theta ^ + }} \right) + \alpha \left( {r\left( {s, a, s'} \right) + } \right.\\ \;\;\;\;\;\left. {\gamma \mathop {\max }\limits_{a'} Q\left( {s', a';{\theta ^ - }} \right) - Q\left( {s, a;{\theta ^ + }} \right)} \right) \end{array} $ | (10) |
式中:α∈[0, 1],为学习率;θ+为评价网络参数;θ-为目标网络参数。学习过程中,评价网络每隔一定回合数将参数复制给目标网络,通过2个网络的配合以提高算法稳定性。
2.2 人类行为决策理论EV用户在充电过程中不仅仅追求预期效用的最大化,也会受限于认知水平及主观心理情绪等因素的影响,因此很难选择出全局最优或个人利益最大的充电选择方案。事实上,个体往往寻求决策后的正面情绪,从而规避决策可能带来的负面情绪。为此,文中引入后悔理论建立人类行为决策心理模型,刻画用户在EV充电调度过程中的心理状态,作为DRL智能体"人-车-站"环境状态感知的一部分。
后悔理论最早由Bell提出,其将后悔描述为一件给定事件的结果或状态与他将要选择的状态进行比较所产生的情绪[19]。依据人类在离散事件选择中的后悔规避心理,当所选方案优于备选方案时,决策者会感到欣喜,反之则会感到后悔。因此,决策者个体更倾向于选择预期后悔最小的方案。后悔理论通过式(11)量化决策者在选择过程中对所选方案与备选方案的感知效应[20]:
| $ {U_i} = {F_i} + {\sigma _i} = \sum\limits_{j = 1, j \ne i}^{{N_{\rm{s}}}} {\sum\limits_{k = 1}^{{N_{\rm{a}}}} {\ln } } \left( {1 + {{\rm{e}}^{{\xi _k}\left( {{x_{j, k}} - {x_{i, k}}} \right)}}} \right) + {\sigma _i} $ | (11) |
式中:Ui为选择方案i的随机效用值;Fi为选择方案i的可确定效用值;xj, k为随机效应误差;Ns为总方案个数,即能源站个数;Na为总属性因素个数;xj, k为j方案在属性k上的取值;ξk为属性k的估计参数,反应决策者对该属性的偏重;σi为随机效用值。当σi服从独立同分布式时,决策者选择方案i的概率可表述为:
| $ {P_u}(i) = {\mathop{\rm prob}\nolimits} \left( {{F_i} > {F_j}, \forall j \ne i} \right) = \frac{{{{\rm{e}}^{{F_i}}}}}{{\sum\limits_{j = 1}^{{N_{\rm{s}}}} {{{\rm{e}}^{{F_j}}}} }} $ | (12) |
可见,后悔理论的实质是通过比较不同方案效用差xj, k-xi, k,模拟人类在多方案选择中的思维过程,最终按照一定概率做出方案选择。文中基于后悔理论将EV用户参与调度总时间与总费用作为2个属性,将所有能源站作为方案集,通过计算用户对各方案的效用值Ui作为智能体对环境状态感知的一部分,其具体模型如式(13)所示。
| $ \begin{array}{l} {U_i} = \sum\limits_{j = 1, j \ne i}^{{N_{\rm{s}}}} {\left( {\ln \left( {1 + {{\rm{e}}^{{\xi _1}\left( {{T_{{\rm{sche }}, j}} - {T_{{\rm{sche }}, i}}} \right)}}} \right) + } \right.} \\ \;\;\;\;\left. {\ln \left( {1 + {{\rm{e}}^{{\xi _2}\left( {{C_{{\rm{sche }}, j}} - {C_{{\rm{sche }}, i}}} \right)}}} \right)} \right) + {\sigma _i} \end{array} $ | (13) |
式中:ξ1,ξ2分别为用户对时间与费用偏重;Tsche, i为用户选择能源站i的总时间,包括路程时间、等待时间与充电时间;Csche, i为用户选择能源站i的费用,包括充电费用与服务费用,其计算公式详见文献[21]。
2.3 DQN实现EV充电调度针对能源站的EV充电调度问题每一个时刻的状态仅与前一时刻状态及智能体动作有关,符合马尔科夫决策过程,因此,文中采用DQN方法建立EV充电调度模型,利用智能体进行"人-车-站"多主体状态感知,通过不断地探索与利用,建立状态-动作与Q值的映射关系,实现EV实时调度。模型中对状态、动作及奖励的定义如下。
(1) 状态。为实现智能体对环境状态的有效感知,文中定义环境状态由EV"时-空-能量"状态、能源站"充-光-储"运行状态及用户心理状态构成,因此可建立状态st,如式(14)所示。
| $ {s_t} = \left( {t, {L_{{\rm{EV}}, t}}, {E_{{\rm{EV}}, t}}, {P_{{\rm{EV}}, t}}, {P_{{\rm{PV}}, t + 1}}, {E_{{\rm{B}}, t}}, {U_{{\rm{U}}, t}}} \right) $ | (14) |
式中:t为当前时刻;LEV, t为当前时刻EV位置;EEV, t为当前时刻EV动力电池SOC;PEV, t为当前时刻各能源站EV的充电负荷;PPV, t+1为各能源站t+1时刻光伏出力预测值;EB, t为当前时刻各能源站储能系统SOC;UU, t为用户对各备选能源站的感知效用值。
(2) 动作。为实现EV的充电调度,将目标能源站与导航路径的选择作为智能体的动作,则t时刻智能体动作at可表示为:
| $ {a_t} = \left( {{x_{{\rm{ES}}, t}}, {x_{{\rm{link}}, t}}} \right)\;\;\;\;\;\;\;{x_{{\rm{ES}}, t}} \in D, {x_{{\rm{link}}, t}} \in L $ | (15) |
式中:xES, t为智能体选择的能源站;xlink, t为智能体选择的当前道路;D为能源站位置集合;L为与当前道路节点相连的节点集合。
(3) 奖励。由于调度过程涉及到途中导航与到站充电,因此可将智能体与环境交互所得的奖励分为途中奖励与到站奖励。其中,途中奖励主要考虑用户方面路程花费时间与动力电池能量代价,到站后奖励由光伏消纳功率及用户在站时间决定。
| $ {r_t} = \left\{ {\begin{array}{*{20}{l}} { - {\lambda _1}{d_{ij}}\alpha - {\lambda _2}{d_{ij}}/{v_{ij}}\;\;\;\;{L_{{\rm{EV}}, t}} \ne {x_{{\rm{ES}}, t}}}\\ {{\delta _1}{{\bar P}_{{\rm{PV}}, t}} - {\delta _2}\left( {{T_{{\rm{wait}}}} + {T_{{\rm{charge}}}}} \right)\;\;\;\;{L_{{\rm{EV}}, t}} = {x_{{\rm{ES}}, t}}} \end{array}} \right. $ | (16) |
式中:LEV, t为当前时刻EV位置;xES, t为目标能源站位置;dij为道路节点i至j的距离;vij为道路节点i至j的平均行驶速度;α为EV单位距离耗电量;λ1,λ2分别为能耗与时间奖励系数;Twait,Tcharge分别为EV在站等待时间与充电时间;PPV, t为各能源站平均光伏消纳功率;δ1,δ2分别为能源站光伏消纳系数与用户充电时间代价系数。
由于智能体在学习前期缺少历史样本,如果采用确定性的贪心策略进行动作选择,容易造成局部收敛甚至不收敛。因此,文中引入时变ε-greedy策略,在前期的学习中增大智能体探索能力,在后期的学习中有效利用前期历史样本进行决策,如式(17)所示。
| $ {a_t} = \left\{ {\begin{array}{*{20}{l}} {{\rm{ random}}\;A\;\;\;\;\beta < (N - n)\varepsilon /N}\\ {\arg \;\mathop {\max }\limits_{{a_t} \in A} Q\left( {{s_t}, {a_t}} \right)\;\;\;\;\beta \ge (N - n)\varepsilon /N} \end{array}} \right. $ | (17) |
式中:N为总训练回合数;n为当前训练回合数;β为(0, 1)随机数;ε为比例参数;random为随机函数,即从A中随机抽取动作;arg max为求解函数值最大化,即返回使得Q值最大的动作。因此,在训练前期智能体有更大概率是从动作集合A中随机选取动作,而在训练中后期,则更有可能选取最优动作。同时,时变ε-greedy策略逐步减小ε,可以提高算法的收敛速度。
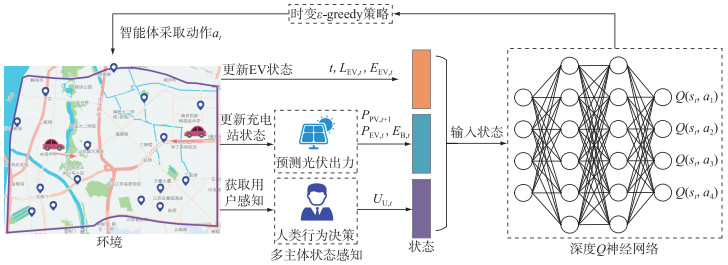
3 EV充电调度框架基于DRL的EV充电调度实现框架如图 2所示。该过程可分为以下3个步骤:
|
图 2 优化调度策略实现流程 Fig. 2 Flow chart of optimized scheduling strategy |
(1) 智能体通过更新时间、EV位置及动力电池SOC获取车辆状态,更新各能源站运行状态并预测下一时刻光伏出力,通过后悔理论感知EV用户的心理状态,得到当前时刻环境状态st。
(2) 智能体将感知到的环境状态输入深度神经网络,得到各备选动作的Q值,通过时变ε-greedy策略选择动作at。
(3) 智能体执行所选动作,重复上述步骤直至车辆抵达所选能源站。
4 算例分析 4.1 参数设置为验证文中所提策略的有效性与实用性,选取南京市部分区域,范围为经度(东经)118.735 152~118.784 076,纬度(北纬)32.059 057~32.092 003作为算例路网。同时,选取该区域已经投入运营的15座能源站, 假设该区域能源站均配置了光伏发电及储能系统,且站内充电桩均为快充,具体配置详见表 1。
|
|
表 1 能源站基本参数表 Table 1 Basic parameters of energy station |
根据文献[22]EV出行规律,文中在该区域一天中引入1 000辆EV,设EV动力电池容量为40 kW ·h,并设初始SOC服从对数均值为3.2,对数标准差为0.48的对数正态分布。考虑电池充放电深度对其寿命的影响,取EV结束充电时的终止SOC均为90%。
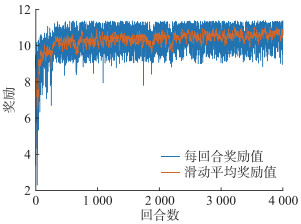
4.2 智能体训练过程设置DQN算法中智能体学习率α=0.85,奖励折扣率γ=0.85,ε-greedy策略中ε初值为0.5,每回合递减7.5×10-4直至为0,Q网络采用150×120全连接神经网络。总训练回合数设置为4 000次,可得训练过程中智能体训练过程中平均奖励值如图 3所示。
|
图 3 训练过程奖励值 Fig. 3 Reward value of training process |
由图 3可知,在训练前期智能体每回合奖励呈现一个明显的上升阶段,并在500回合左右实现收敛,奖励值稳定于10.44。这是因为ε-greedy策略的存在,使得智能体在前期能够不断探索环境,而当n=500时,(N-n)ε/N=0.11,表明500回合之后智能体更大概率是根据当前学习到的历史经验进行动作选择。由于每一回合中EV初始时空分布存在差异,且光伏出力存在一定波动,所以智能体所得奖励存在一定波动,但训练后期平均奖励明显高于训练前期,表明智能体已拟合状态-动作与Q值的映射关系,并能够进行最优动作的选取。
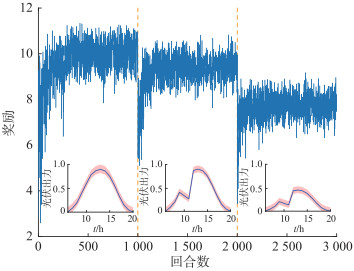
4.3 泛化能力分析为分析所提DRL算法泛化能力,考虑能源站日常运行状态,设置晴天、突变天气及阴雨天光伏出力如图 4所示,其中红色宽带为光伏出力概率区间。设置训练1~1 000回合对应晴天,1 001~2 000回合对应突变天气,2 001~3 000回合对应阴雨天气,可得训练奖励如图 4所示。
|
图 4 考虑泛化能力的训练奖励 Fig. 4 Training reward considering generalization ability |
由图 4可知,不同天气类型对智能体所获得奖励值有较大影响,3种天气下智能体平均奖励分别为9.95,9.38,7.23,特别地,阴雨天气奖励值较晴天降低27.34%。这是由于智能体的到站奖励与区域内能源站平均光伏消纳功率有较大关系,虽然阴雨天气智能体所得奖励较晴天更低,但此时智能体已经实现了最优策略的学习。同时,观察算法收敛速度可见,所提DQN方法在前2种场景下分别在400与200回合达到稳定,而在第3种场景下训练约80回合即实现收敛,表明智能体能够有效利用前期累积的经验,当环境状态发生较大改变时,其能够调整神经网络参数以快速适应当前环境状态。
进一步,在上述3种场景下,EV分别采取无序充电及文中所提DQN方法所得光伏消纳率如表 2所示。
|
|
表 2 不同场景光伏消纳率 Table 2 Objective value of different scheduling scale |
从表 2可见,在场景1中,无序充电情况下各能源站平均光伏消纳率仅为75.31%,而文中DQN方法只涉及EV用户对能源站的选择及导航问题,在时间维度不存在调度关系,因此基于DQN方法的光伏消纳率也仅提高了6.02%。3种不同场景下文中所提方法平均提高光伏消纳率7.94%,其中场景3效果最为明显,提高11.73%。可见,所提方法能够适应不同场景下的能源站运行状态,有效提高光伏消纳水平。
4.4 算法实时性分析进一步地,为了分析所提DQN方法的计算效率以及实时性,文中将常规的规划方法和启发式算法与DQN算法进行比较。文中所提EV调度问题可以采用商业Cplex求解器以及粒子群优化算法(particle swarm optimization, PSO)进行求解。为体现算法在实际应用中是实时性,不同求解方法的单辆EV平均计算耗时如表 3所示。
|
|
表 3 不同算法计算耗时对比 Table 3 Comparison of computation time of different algorithms |
由表 3可知,训练好的DQN模型在计算速度上具有较大优势。PSO通过粒子群逐步迭代寻优,计算结果可能收敛于局部最优。同时,每次求解重复迭代直至收敛的过程,使得PSO的决策时间较长。当环境状态发生改变时,传统的优化算法均需要重新进行优化求解,而DQN模型只需将当前时刻的环境状态作为输入,通过训练好的网络即可得到EV的动作输出,能够在毫秒级完成调度策略的制定,满足实时调度的需求。
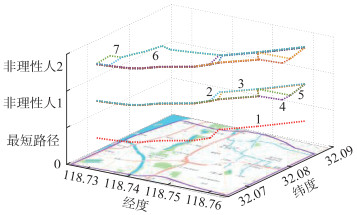
4.5 非理性人心理分析上述智能体训练过程中,后悔理论中EV用户对时间成本与费用成本的感知系数均为0.5。为探究人类非理性状态感知对智能体决策的影响,分别定义2种非理性人:非理性人1更在意费用成本(ξ1=0.2, ξ2=0.8);非理性人2更在意时间成本(ξ1=0.8, ξ2=0.2),分别与最短路径法导航结果相比较,图 5给出了不同非理性人在同一起讫点时模型所推荐的导航路径。
|
图 5 不同情况下导航路径 Fig. 5 Navigation path in different situations |
由图 5可知,针对2种非理性人,智能体共选取出7条路线,其中均包含了最短路径。对于非理性人1,智能体共推荐出行驶路线5条,平均路程4.37 km,平均行驶时间8.54 min。对于非理性人2,智能体共推荐路线7条,平均路程4.62 km,较前者增长5.72%,平均行驶时间8.61 min,较前者增加0.82%。通过对比可知,若用户表现出更在意时间成本,智能体则会更倾向于具有探索精神,以极小的时间代价,进而探索可能的最佳路线。可见,由于不同行为人在后悔理论中对各因素感知权重不同,智能体能够通过状态感知获取st,并在训练过程中不断学习与调整Q网络参数与映射关系,实现考虑用户异质性的EV充电导航与调度。
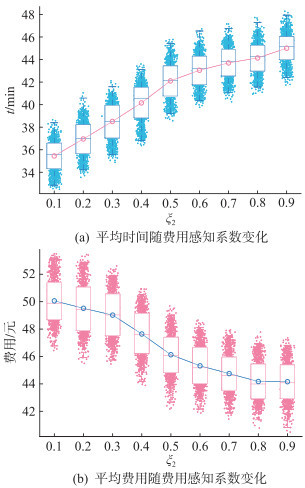
最后,为探究不同非理性人心理状态对智能体调度策略的影响,分别设用户的费用感知偏重ξ2= 0.1, 0.2, …, 0.9(时间感知偏重ξ1=0.9, 0.8, …, 0.1),可得基于DRL方法的用户平均时间与费用变化曲线如图 6所示。
|
图 6 不同感知偏重对用户影响 Fig. 6 The impact of different perception bias on users |
由图 6可知,随着用户费用感知系数的增大,用户平均费用逐渐减小,平均用时逐渐增大。特别地,当ξ2=0.1,即用户特别在意时间成本时,此时平均耗时35.44 min,平均费用50.06元;当ξ2=0.9,即用户特别在意费用时,平均耗时45.01 min,较前者增加了27%,而平均费用44.16元,较前者降低了11.79%。由时间与费用变化趋势可以看出,不同特质车主对于充电所用时间与费用的预期存在一定差异,当费用感知系数每增加0.1时,用户费用平均降低1.55%,而时间感知系数每增加0.1时,用户时间平均降低2.93%。可见,EV用户对于充电过程所用时间感知更为敏感。
5 结论针对能源站EV充电导航与调度问题,提出基于DRL方法的调度策略。算例从多角度分析了优化调度策略,得到如下结论:(1) DQN方法中智能体对EV状态、能源站运行状态以及用户心理状态进行全状态感知,通过学习状态-动作与Q值的映射关系能够有效进行充电调度。(2) 在晴天与阴雨天等能源站常见运行场景下,所提方法均能够兼顾用户心理感知进行调度,同时有效提高了能源站光伏利用率,具有较强的实用性与泛化能力。(3) 不同行为人对时间与费用的感知效用会影响智能体状态感知与策略参数,进而影响所提方法对其的导航与调度策略。
尽管如此,限于篇幅文中并未分析DQN算法参数对调度策略的影响,在下一步的工作中DQN算法参数的选择可以继续完善。此外,基于用户感知异质性的研究,可以进一步改进所提策略。
| [1] |
肖定垚, 王承民, 曾平良, 等. 电力系统灵活性及其评价综述[J]. 电网技术, 2014, 38(6): 1569-1576. XIAO Dingyao, WANG Chengmin, ZENG Pingliang, et al. A survey on power system flexibility and its evaluations[J]. Power System Technology, 2014, 38(6): 1569-1576. (  0) 0) |
| [2] |
刘洪, 阎峻, 葛少云, 等. 考虑多车交互影响的电动汽车与快充站动态响应[J]. 中国电机工程学报, 2020, 40(20): 6455-6468. LIU Hong, YAN Jun, GE Shaoyun, et al. Dynamic response of electric vehicle and fast charging stations considering multi-vehicle interaction[J]. Proceedings of the CSEE, 2020, 40(20): 6455-6468. (  0) 0) |
| [3] |
邵尹池, 穆云飞, 余晓丹, 等. "车-路-网"模式下电动汽车充电负荷时空预测及其对配电网潮流的影响[J]. 中国电机工程学报, 2017, 37(18): 5207-5219, 5519. SHAO Yinchi, MU Yunfei, YU Xiaodan, et al. A spatial-temporal charging load forecast and impact analysis method for distribution network using EVs-traffic-distribution model[J]. Proceedings of the CSEE, 2017, 37(18): 5207-5219, 5519. (  0) 0) |
| [4] |
江明, 许庆强, 季振亚. 基于时序差分学习的充电站有序充电方法[J]. 电力工程技术, 2021, 40(1): 181-187. JIANG Ming, XU Qingqiang, JI Zhenya. Coordinated charging approach for charging stations based on temporal difference learning[J]. Electric Power Engineering Technology, 2021, 40(1): 181-187. (  0) 0) |
| [5] |
KORKAS C D, BALDI S, YUAN S, et al. An adaptive learning-based approach for nearly optimal dynamic charging of electric vehicle fleets[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(7): 2066-2075. DOI:10.1109/TITS.2017.2737477 (  0) 0) |
| [6] |
CAI H, CHEN Q Y, GUAN Z J, et al. Day-ahead optimal charging/discharging scheduling for electric vehicles in microgrids[J]. Protection and Control of Modern Power Systems, 2018, 3(1): 1-15. DOI:10.1186/s41601-017-0075-8 (  0) 0) |
| [7] |
阎怀东, 马汝祥, 柳志航, 等. 计及需求响应的电动汽车充电站多时间尺度随机优化调度[J]. 电力系统保护与控制, 2020, 48(10): 71-80. YAN Huaidong, MA Ruxiang, LIU Zhihang, et al. Multi-time scale stochastic optimal dispatch of electric vehicle charging station considering demand response[J]. Power System Protection and Control, 2020, 48(10): 71-80. (  0) 0) |
| [8] |
高昇宇, 柳志航, 卫志农, 等. 城市智能光储充电塔自适应鲁棒日前优化调度[J]. 电力系统自动化, 2019, 43(20): 39-48. GAO Shengyu, LIU Zhihang, WEI Zhinong, et al. Adaptive robust day-ahead optimal dispatch for urban smart photovoltaic storage and charging tower[J]. Automation of Electric Power Systems, 2019, 43(20): 39-48. DOI:10.7500/AEPS20181002001 (  0) 0) |
| [9] |
李睿雪, 胡泽春. 电动公交车光储充电站日运行随机优化策略[J]. 电网技术, 2017, 41(12): 3772-3780. LI Ruixue, HU Zechun. Stochastic optimization strategy for daily operation of electric bus charging station with PV and energy storage[J]. Power System Technology, 2017, 41(12): 3772-3780. (  0) 0) |
| [10] |
肖浩, 裴玮, 孔力. 含大规模电动汽车接入的主动配电网多目标优化调度方法[J]. 电工技术学报, 2017, 32(S2): 179-189. XIAO Hao, PEI Wei, KONG Li. Multi-objective optimization scheduling method for active distribution network with large scale electric vehicles[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 179-189. (  0) 0) |
| [11] |
杜明秋, 李妍, 王标, 等. 电动汽车充电控制的深度增强学习优化方法[J]. 中国电机工程学报, 2019, 39(14): 4042-4049. DU Mingqiu, LI Yan, WANG Biao, et al. Deep reinforcement learning optimization method for charging control of electric vehicles[J]. Proceedings of the CSEE, 2019, 39(14): 4042-4049. (  0) 0) |
| [12] |
ZHANG C, LIU Y, WU F, et al. Effective charging planning based on deep reinforcement learning for electric vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(1): 542-554. DOI:10.1109/TITS.2020.3002271 (  0) 0) |
| [13] |
李航, 李国杰, 汪可友. 基于深度强化学习的电动汽车实时调度策略[J]. 电力系统自动化, 2020, 44(22): 161-167. LI Hang, LI Guojie, WANG Keyou. Real-time dispatch strategy for electric vehicles based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2020, 44(22): 161-167. (  0) 0) |
| [14] |
WANZ Q, LI H P, HE H B, et al. Model-free real-time EV charging scheduling based on deep reinforcement learning[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 5246-5257. DOI:10.1109/TSG.2018.2879572 (  0) 0) |
| [15] |
QIAN T, SHAO C C, WANG X L, et al. Deep reinforcement learning for EV charging navigation by coordinating smart grid and intelligent transportation system[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1714-1723. (  0) 0) |
| [16] |
何阳, 张宇, 王育飞, 等. 考虑负荷优化的电动汽车光伏充电站储能容量配置[J]. 现代电力, 2019, 36(5): 76-81. HE Yang, ZHANG Yu, WANG Yufei, et al. Energy storage capacity configuration of PV-integrated EV charging station considering load optimization[J]. Modern Electric Power, 2019, 36(5): 76-81. (  0) 0) |
| [17] |
张自东, 邱才明, 张东霞, 等. 基于深度强化学习的微电网复合储能协调控制方法[J]. 电网技术, 2019, 43(6): 1914-1921. ZHANG Zidong, QIU Caiming, ZHANG Dongxia, et al. A coordinated control method for hybrid energy storage system in microgrid based on deep reinforcement learning[J]. Power System Technology, 2019, 43(6): 1914-1921. (  0) 0) |
| [18] |
刘全, 翟建伟, 章宗长, 等. 深度强化学习综述[J]. 计算机学报, 2018, 41(1): 1-27. LIU Quan, ZHAI Jianwei, ZHANG Zongchang, et al. A survey on deep reinforcement learning[J]. Chinese Journal of Computers, 2018, 41(1): 1-27. (  0) 0) |
| [19] |
BELL D E. Regret in decision making under uncertainty[J]. Operations Research, 1982, 30(5): 961-981. (  0) 0) |
| [20] |
高玉芳. 基于后悔理论的城市轨道交通动态配流模型研究[D]. 北京: 北京交通大学, 2018. GAO Yufang. Research on dynamic assignment model of urban rail transit based on regret theory[D]. Beijing: Beijing Jiaotong University, 2018. (  0) 0) |
| [21] |
邢强, 杨祺铭, 范军太, 等. 基于数据驱动方式和行为决策的电动汽车快充需求预测模型[J]. 电网技术, 2020, 44(7): 2439-2453. XING Qiang, YANG Qiming, FAN Juntai, et al. Electric vehicle fast charging demand forecasting model based on data-driven approach and human behavior decision-making[J]. Power System Technology, 2020, 44(7): 2439-2453. (  0) 0) |
| [22] |
程骏. 电动汽车充电站运行调度策略研究[D]. 南京: 东南大学, 2016. CHENG Jun. Research on operation scheduling strategy for electric vehicle charging station[D]. Nanjing: Southeast University, 2016. (  0) 0) |
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2021, Vol. 40
2021, Vol. 40


 孙广明(1979), 男, 硕士, 高级工程师, 从事电动汽车充换电设施监控与运营管理工作(E-mail:
孙广明(1979), 男, 硕士, 高级工程师, 从事电动汽车充换电设施监控与运营管理工作(E-mail: