文章编号: 2096-3203(2021)05-0071-07 中图分类号: TM71
柔性直流电网(以下简称柔直电网)具有功率解耦控制、无换相失败、无需大容量无功补偿装置等优点,是解决可再生能源并网、异步交流电网互联、海上孤岛供电、城市配电网增容等问题的重要手段,亦是现代直流输电技术发展和变革的主要趋势之一[1-5]。然而,由于柔直电网含有大量电感、分布电容以及电力电子元件,其故障后的电磁暂态过程十分复杂,易引发系统过电压等问题,这是制约该技术快速发展的重要因素之一[6-12]。
针对柔直电网的故障暂态特性及过电压分析,已有研究按故障发生区域,一般将故障分为直流侧故障、换流站内故障和交流侧故障。文献[13-15]分析了对称单极柔直电网直流侧单极接地故障的暂态过程和过电压大小,提出非故障极充电是导致直流侧过电压的主要原因,并详细分析了接地方式、换流站闭锁、故障距离等因素对过电压的影响。文献[16]基于±500 kV张北柔直工程仿真模型,揭示健全极过电压的根本原因是中性点电位抬升。文献[17-18]对交流系统不对称情况下的柔直输电系统故障暂态特性进行研究,分析零序分量对直流电压波动的影响,提出了二倍频直流电压波动抑制策略。
相对于输电线路,换流站内故障率相对较低,但故障后果十分严重,可能导致整个直流电网闭锁,应给予足够重视。文献[19]分析了单变压器柔直系统交流单相接地和直流单极接地故障特性,并提出了过电压抑制策略。文献[20]分析了对称双极柔直电网站内交流接地的故障传播机理,研究发现故障会导致换流器内子模块(sub-module,SM)过充电,进而引发严重的操作过电压。文献[21]对舟山五端柔直工程站内交流短路故障进行仿真分析,过电压计算结果可为相关工程的绝缘配合及设备选型提供重要依据。目前针对换流站内接地故障的研究已取得些许成果,但对故障传播机理及故障过电压的定量分析仍有不足。
为此,文中针对对称单极接线型柔直输电系统开展研究。分别从交流故障区和直流故障区分析换流站内单相接地的故障特性、传播规律及过电压机理,并提出一种过电压抑制策略,有效抑制直流侧过电压幅值及过电压传播,提升系统故障后的连续运行能力。此外,文中基于PSCAD搭建柔直电网仿真模型,仿真分析站内单相接地故障机理,并对文中理论分析的正确性及过电压抑制策略的有效性进行验证。
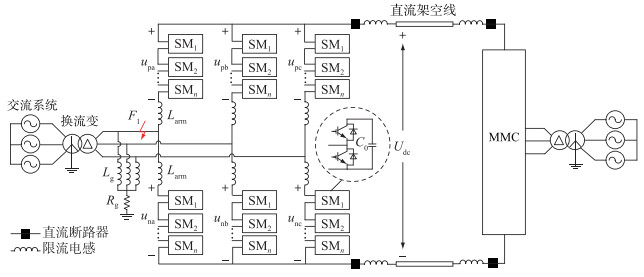
1 故障机理分析基于模块化多电平换流器(modular multilevel converter, MMC)的柔直电网拓扑如图 1所示。其中每个桥臂均由n个SM构成;C0为SM电容;upx,unx分别为x(x=a, b, c)相上、下桥臂投入SM的电压和;Larm为桥臂电感;Udc为直流侧电压;接地方式为换流变阀侧Y型电抗接地;Lg,Rg分别为接地系统的电感和电阻;F1为站内单相接地故障(以a相为例)。MMC采用dq坐标系下的双闭环控制策略,包含正序和负序电流控制。
|
图 1 柔直电网拓扑 Fig. 1 The topology of flexible DC grid |
由图 1可知,故障F1将系统划分为2个故障区域,分别为交流故障区域(交流电源至故障点)和直流故障区域(故障点至直流线路)。
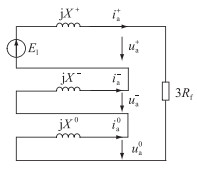
1.1 交流故障区分析采用传统复合序网络法对交流故障区进行分析,等效电路如图 2所示。图中,E1为交流侧等效电源;Xj为交流电源至故障点的阻抗,j=+, -, 0分别表示正序、负序和零序分量;uaj,iaj分别为故障点对地电压和电流的序分量;Rf为故障电阻。
|
图 2 交流故障区等效电路 Fig. 2 The equivalent circuit of the AC fault area |
换流变一般采用Y/Δ接线,因此零序阻抗X0趋于无穷大,电流序分量满足:
| $ i_{\mathrm{a}}^{+}=i_{\mathrm{a}}^{-}=i_{\mathrm{a}}^{0}=0 $ | (1) |
由式(1)可知,系统发生站内单相接地故障时,由于未形成有效对地放电通路,各相对地故障电流均为0。根据式(1)和图 2进一步推导得:
| $ \left\{\begin{array}{l} u_{\mathrm{a}}^{+}=-u_{\mathrm{a}}^{0} \\ u_{\mathrm{a}}^{-}=0 \end{array}\right. $ | (2) |
定义z=ej120,故障点b相和c相电压为:
| $ \left\{\begin{array}{l} u_{\mathrm{b}}=z^{2} u_{\mathrm{a}}^{+}+z u_{\mathrm{a}}^{-}+u_{\mathrm{a}}^{0}=u_{\mathrm{b}}-u_{\mathrm{a}} \\ u_{\mathrm{c}}=z u_{\mathrm{a}}^{+}+z^{2} u_{\mathrm{a}}^{-}+u_{\mathrm{a}}^{0}=u_{\mathrm{c}}-u_{\mathrm{a}} \end{array}\right. $ | (3) |
根据交流故障区分析可以得出:(1) 换流站内单相接地故障不会引起系统过电流,但会导致非故障相电压幅值上升至线电压;(2) 站内交流系统负序电压分量幅值为0,零序电压分量与故障相电压幅值相等、方向相反;(3) 由于换流变阀侧一般采用Δ接线方式,零序电压不会影响换流变网侧交流系统。
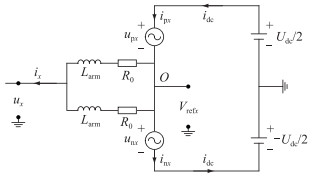
1.2 直流故障区分析在1.1节基础上进一步分析直流故障区。根据MMC工作原理,可以将其等效为图 3所示电路[22]。其中O为上、下桥臂电抗器的虚拟等位点;Vrefx为虚拟等位点电压;ux,ix分别为MMC交流输出电压和电流;idc为直流侧电流;R0为桥臂等效电阻。
|
图 3 MMC单相基波等效电路 Fig. 3 The fundamental equivalent circuit for single phase of MMC |
MMC一般采用dq坐标系下的双闭环控制策略,在确定上、下桥臂SM个数时仅考虑虚拟等位点正序和负序电压分量之和,可得:
| $ \left\{\begin{array}{l} u_{\mathrm{p} x}=\frac{1}{2} U_{\mathrm{dc}}-\left(V_{\mathrm{ref} x}^{+}+V_{\mathrm{ref} x}^{-}\right) \\ u_{\mathrm{n} x}=\frac{1}{2} U_{\mathrm{dc}}+\left(V_{\mathrm{ref} x}^{+}+V_{\mathrm{ref} x}^{-}\right) \end{array}\right. $ | (4) |
则O点实际电压可表示为:
| $ V_{\mathrm {ref }x}=V_{\mathrm {ref }x}^{+}+V_{\mathrm {ref }x}^{-}+V_{\mathrm {ref }x}^{0} $ | (5) |
根据基尔霍夫电压定律,进一步推导可得:
| $ \left\{\begin{array}{l} u_{\mathrm{p}}=V_{\mathrm{ref} x}+u_{\mathrm{p} x} \\ u_{\mathrm{n}}=V_{\mathrm{ref} x}-u_{\mathrm{n} x} \end{array}\right. $ | (6) |
| $ \left\{\begin{array}{l} u_{x}^{+}-V_{\mathrm{ref} x}^{+}=-\frac{1}{2}\left(L \frac{\mathrm{d} i_{x}^{+}}{\mathrm{d} t}+R_{0} i_{x}^{+}\right) \\ u_{x}^{-}-V_{\mathrm{ref} x}^{-}=-\frac{1}{2}\left(L \frac{\mathrm{d} i_{x}^{-}}{\mathrm{d} t}+R_{0} i_{x}^{-}\right) \\ u_{x}^{0}-V_{\mathrm{ref} x}^{0}=-\frac{1}{2}\left(L \frac{\mathrm{d} i_{x}^{0}}{\mathrm{~d} t}+R_{0} i_{x}^{0}\right) \end{array}\right. $ | (7) |
式中:up,un分别为直流侧正极和负极电压。
根据复合序网络分析结果可知,零序电流分量为0,即ix0=0,因此联立式(4)—式(7)可得:
| $ \left\{\begin{array}{l} u_{\mathrm{p}}=u_{x}^{0}+\frac{1}{2} U_{\mathrm{dc}} \\ u_{\mathrm{n}}=u_{x}^{0}-\frac{1}{2} U_{\mathrm{dc}} \end{array}\right. $ | (8) |
由式(8)可知,在系统发生换流站内单相接地故障后,直流侧正、负极会在原极电压基础上出现零序电压大小的共模振荡。由于零序电压分量与故障相电压大小相等、方向相反,因此直流侧最大过电压幅值umax为:
| $ u_{\max } =U_{\mathrm{dc}}(1+m) / 2 $ | (9) |
| $ m =U_{\mathrm{ac}} /\left(U_{\mathrm{dc}} / 2\right) $ | (10) |
式中:m为电压调制比,0<m≤1;Uac为MMC输出交流电压幅值。
因此,非故障换流站MMC交流输出电压u′x为:
| $ u_{x}^{\prime}=u_{\mathrm{p}}-\left(u_{\mathrm{p} x}^{\prime}+L_{\mathrm{arm}} \frac{\mathrm{d} i_{\mathrm{p} x}^{\prime}}{\mathrm{d} t}\right) $ | (11) |
式中:u′px,i′px分别为非故障换流站x相上桥臂电压和电流。
将式(8)代入式(11)可得:
| $ u_{x}^{\prime}=\frac{U_{\mathrm{dc}}}{2}-\left(u_{\mathrm{p} x}^{\prime}+L_{\mathrm{arm}} \frac{\mathrm{d} i_{\mathrm{p} x}^{\prime}}{\mathrm{d} t}\right)+u_{x}^{0} $ | (12) |
可以看出,零序电压会叠加到非故障换流站MMC正常输出电压上,从而引起非故障换流站内产生工频过电压。
根据直流故障区域分析可知:(1) 换流站内单相接地故障会导致直流线路发生幅值为零序电压大小的共模振荡,最大过电压为极电压的m+1倍;(2) 零序电压会通过换流器传播至其他非故障换流站内,从而引发站内交流系统工频过电压。
2 直流过电压抑制策略当系统发生站内单相接地故障后,虽然直流侧会产生周期振荡的过电压,但在该故障条件下,交、直流侧不会出现明显过电流,且极间电压基本保持不变,直流电网仍能正常传输功率。若能有效降低直流侧过电压水平和传播范围,则能提升系统在故障条件下的连续运行能力,为故障换流站安全退出提供更多准备和处理时间,提升整个系统的安全稳定运行水平。因此,文中提出一种零序过电压控制方法。
2.1 控制原理控制目标是消除故障后直流侧极电压的零序电压振荡,即:
| $ u_{\mathrm{p}}-\frac{1}{2} U_{\mathrm{dc}}=0 $ | (13) |
假设增加零序电压控制器后,换流器的输出参考电压为fx,可以得到:
| $ \left\{\begin{array}{l} u_{\mathrm{p} x}=\frac{1}{2} U_{\mathrm{dc}}-f_{x} \\ u_{\mathrm{n} x}=\frac{1}{2} U_{\mathrm{dc}}+f_{x} \end{array}\right. $ | (14) |
将式(5)、式(6)和式(13)代入式(14)可得:
| $ f_{x}=V_{\mathrm {ref } x}^{+}+V_{\mathrm {ref } x}^{-}+V_{\mathrm {ref } x}^{0} $ | (15) |
由于ix0=0,根据式(7)可知ux0=Vrefx0。因此,式(15)可进一步表示为:
| $ f_{x}=V_{\mathrm {ref } x}^{+}+V_{\mathrm {ref } x}^{-}+u_{x}^{0} $ | (16) |
可以看出,理论上只需在原参考电压的基础上叠加零序电压分量就能有效消除直流侧过电压振荡。
然而,根据第1章分析结果,单相接地故障时非故障相输出参考电压幅值将上升至线电压,因而式(16)中的fx可能超过MMC的最大输出能力,过大的fx可能引起交直流侧电气量出现较大波动。因此,需要对叠加的零序电压进行一定的限幅处理,即:
| $ f_{x}=V_{\mathrm {ref } x}^{+}+V_{\mathrm {ref } x}^{-}+k u_{x}^{0} $ | (17) |
式中:k为限幅系数。
2.2 限幅系数计算以fx满足MMC最大交流输出能力时的限幅系数计算值k′作为k值下限,即:
| $ \left|V_{\mathrm {ref } x}^{+}+V_{\mathrm {ref }x}^{-}+k^{\prime} u_{0}\right|=\left|f_{x}\right| \leqslant \frac{U_{\mathrm{dc}}}{2} $ | (18) |
假设故障相为a相,则式(18)可进一步表示为:
| $ \left|U_{\mathrm{ac}} \cos \left(\omega t \pm \frac{2 {\rm{ \mathsf{ π} }}}{3}\right)-k^{\prime} U_{\mathrm{ac}} \cos \omega t\right| \leqslant \frac{U_{\mathrm{dc}}}{2} $ | (19) |
进一步推导可得:
| $ k^{\prime} \leqslant \sqrt{\frac{1}{m^{2}}-\frac{3}{4}}-\frac{1}{2} $ | (20) |
综合以上分析,k取值范围为:
| $ \sqrt{\frac{1}{m^{2}}-\frac{3}{4}}-\frac{1}{2} \leqslant k \leqslant 1 $ | (21) |
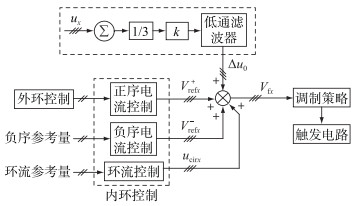
综合以上分析,文中提出的直流侧零序过电压控制器如图 4所示。
|
图 4 直流侧零序过电压控制器 Fig. 4 The DC zero-sequence overvoltage controller |
由图 4可知,零序电压控制首先通过MMC交流输出电压ux求和并乘以1/3得到零序电压分量,然后乘以k进行限幅处理,再经过二阶低通滤波器得到零序电压的最终参考值Δu0,最后将Δu0叠加在内环控制器输出的参考电压上,得到最终参考电压Vfx。
3 仿真分析 3.1 测试系统基于PSCAD搭建如图 1所示的柔性直流输电系统。系统采用对称单极接线和半桥SM拓扑,换流站之间采用长度为60 km的直流架空线路连接,直流线路的两端均配置10 mH的限流电感。系统采用dq坐标系下的双闭环控制策略,并增加了环流控制和负序电流控制,采用最近电平逼近调制(nearest level modulation, NLM)方式。MMC1为功率控制站,最大传输功率为20 MW。MMC2为电压控制站,额定直流电压为±20 kV,详细的换流站参数如表 1所示。
|
|
表 1 测试系统参数 Table 1 The parameters of test system |
m取0.82,计算得到k取值范围为[0.36,1],仿真分析时k取0.7。滤波器采用二阶低通滤波器,截止频率为2 000 Hz。
3.2 单相接地故障仿真在测试系统MMC1内设置换流变阀侧a相接地故障F1,Rf为0.01 Ω,故障始于0.7 s,持续时间为0.2 s,零序电压控制器在0.8 s时投入,仿真结果如图 5所示。
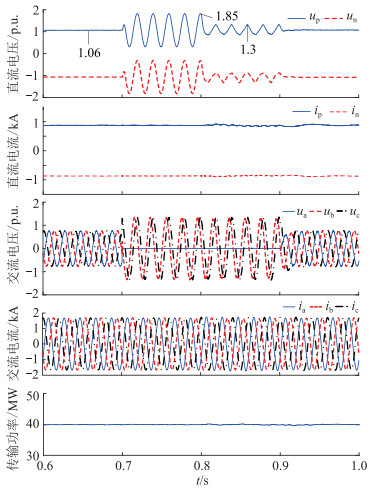
|
图 5 单相接地故障时交、直流侧的仿真结果 Fig. 5 The simulation results of the AC and DC side when single-phase-to-ground fault occurs |
由图 5可知,故障后非故障相电压上升为线电压,而直流侧正负极产生了零序电压大小的共模振荡,最大过电压幅值约为1.82 p.u.,与理论值1.88 p.u.即1.06+0.82 p.u.基本一致。零序电压控制器投入后,直流侧电压振荡得到了明显抑制,最大过电压值降低至1.3 p.u.。在零序电压控制器投入期间,输出的交流电流和系统功率均未发生明显改变。零序电压控制无法改变站内交流过电压,因此在故障穿越期间,故障站内交流系统需要具备一定的耐压能力。
图 6给出了交流电压序分量及其与直流侧电压增量Δu的对比结果。由图 6可知,故障后的零序电压分量与故障相电压大小相等,极性相反,并且与Δu几乎吻合,验证了理论分析的正确性。
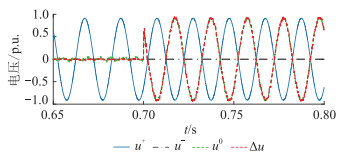
|
图 6 交流电压序分量和直流侧电压增量 Fig. 6 AC voltage sequence component and DC side voltage increment |
正常运行时零序电压分量为0,因此在故障消失后,交、直流侧电压和电流迅速恢复至故障前状态。附加零序电压控制器不会对系统正常运行产生影响。
MMC2中的交流电压如图 7所示。由图 7可知,故障后零序电压会叠加在原MMC2交流输出电压上,使交流系统产生一定的操作过电压。随着零序电压控制器的投入,过电压明显改善。
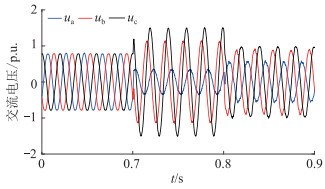
|
图 7 MMC2交流电压 Fig. 7 The AC voltage of MMC2 |
为了验证文中所提过电压抑制策略,以故障F1为例,分别选取不同限幅系数k进行对比分析。图 8给出了不同k值下极电压(以正极为例)和系统传输功率。图 9、图 10分别给出了不同k值下MMC1的输出交流电流和b相电流快速傅里叶变换分解后的谐波分量幅值。
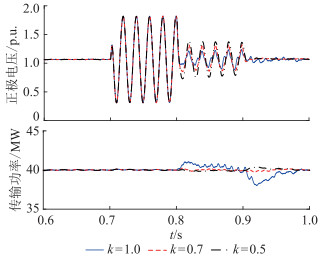
|
图 8 不同k值下的正极电压和传输功率 Fig. 8 The positive pole voltage and transmission power under different k |
|
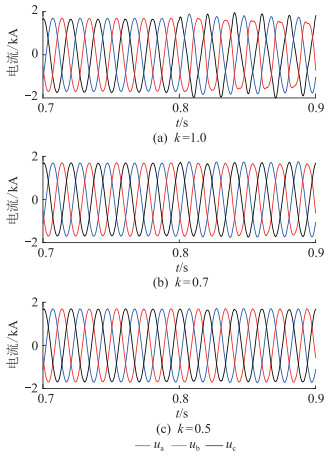
图 9 不同k值下的交流电流 Fig. 9 The AC current under different k |
|
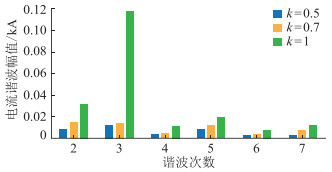
图 10 不同k值下b相电流的谐波幅值 Fig. 10 The amplitude of b phase harmonic current under different k |
由图 8—图 10可知,k值越大, 即叠加的零序电压幅值越大, 对过电压的抑制效果越好,但过大的k值会导致输出功率波动和交流电流畸变,其中畸变电流主要包含3次谐波分量。因此,实际应用时需在合理范围内选择限幅系数。
4 结论文中针对对称单极柔直电网的站内单相接地故障,基于交流复合序网络和换流器控制方程推导故障传播规律和过电压产生机理。研究结果表明:
(1) 换流站内单相接地故障会使站内交流系统非故障相电压上升至线电压,故障产生的零序电压分量与故障相电压大小相等、方向相反。
(2) 零序电压会通过换流器传播至直流侧和其他换流站,并产生工频过电压,直流侧过电压表现为零序电压大小的共模振荡。
(3) 文中提出一种直流侧过电压抑制策略,通过在原控制器输出电压上叠加经限幅后的零序电压实现过电压抑制,并给出了限幅系数的选取方法。仿真结果证明了理论分析的正确性及过电压抑制策略的有效性。
| [1] |
ZHANG Y Z, RAVISHANKAR J, FLETCHER J, et al. Review of modular multilevel converter based multi-terminal HVDC systems for offshore wind power transmission[J]. Renewable and Sustainable Energy Reviews, 2016, 61: 572-586. DOI:10.1016/j.rser.2016.01.108 (  0) 0) |
| [2] |
崔嘉奇. 海外柔性直流输电工程项目质量管理体系及成熟度评价[J]. 发电技术, 2020, 41(4): 361-368. CUI Jiaqi. Quality management system and maturity evaluation of overseas flexible HVDC transmission project[J]. Power Generation Technology, 2020, 41(4): 361-368. (  0) 0) |
| [3] |
张静, 高冲, 许彬, 等. 海上风电直流并网工程用新型柔性直流耗能装置电气设计研究[J]. 中国电机工程学报, 2021, 41(12): 4081-4091. ZHANG Jing, GAO Chong, XU Bin, et al. Research on electrical design of novel flexible DC energy consuming device for offshore wind power DC grid connection project[J]. Proceedings of the CSEE, 2021, 41(12): 4081-4091. (  0) 0) |
| [4] |
祁琪, 姜齐荣, 许彦平. 智能配电网柔性互联研究现状及发展趋势[J]. 电网技术, 2020, 44(12): 4664-4676. QI Qi, JIANG Qirong, XU Yanping. Research status and development prospect of flexible interconnection for smart distribution networks[J]. Power System Technology, 2020, 44(12): 4664-4676. (  0) 0) |
| [5] |
段军, 谢晔源, 朱铭炼, 等. 模块化多电平换流阀子模块旁路方案设计[J]. 电力工程技术, 2020, 39(4): 207-213. DUAN Jun, XIE Yeyuan, ZHU Minglian, et al. Bypass scheme design for value sub-module of modular multi-level converter[J]. Electric Power Engineering Technology, 2020, 39(4): 207-213. (  0) 0) |
| [6] |
彭宇锋, 张英敏, 李俊松, 等. 考虑线路电容的MMC-HVDC系统直流接地故障电流计算方法[J]. 电力系统保护与控制, 2020, 48(23): 57-63. PENG Yufeng, ZHANG Yingmin, LI Junsong, et al. Ground fault current calculation method for an MMC-HVDC system considering line capacitance[J]. Power System Protection and Control, 2020, 48(23): 57-63. (  0) 0) |
| [7] |
李泓志, 贺之渊, 杨杰, 等. 模块化多电平换流器操作过电压分析[J]. 高电压技术, 2017, 43(4): 1144-1151. LI Hongzhi, HE Zhiyuan, YANG Jie, et al. Switching overvoltage analysis for modular multilevel converters[J]. High Voltage Engineering, 2017, 43(4): 1144-1151. (  0) 0) |
| [8] |
WU L, FAN X, XU M, et al. Research and application of a power-flow-calculation method in multiterminal VSC-HVDC power grid[J]. Global Energy Interconnection, 2019, 2(1): 37-44. DOI:10.1016/j.gloei.2019.06.005 (  0) 0) |
| [9] |
赵创业, 卢铁兵, 陈宁, 等. 直流断路器对张北柔直电网中单极接地过电压的影响分析[J]. 高压电器, 2019, 55(9): 111-118. ZHAO Chuangye, LU Tiebing, CHEN Ning, et al. Analysis on the influence of DC circuit breaker on single-pole-to-ground overvoltage in Zhangbei flexible DC power grid[J]. High Voltage Apparatus, 2019, 55(9): 111-118. (  0) 0) |
| [10] |
张文嘉, 王荃荃, 李海坤, 等. 基于对称双极接线的全桥型MMC-HVDC直流侧短路故障穿越控制方法[J]. 电力系统保护与控制, 2020, 48(16): 147-154. ZHANG Wenjia, WANG Quanquan, LI Haikun, et al. DC short circuit fault ride-through method based on symmetrical bipolar FBSM-MMC HVDC system[J]. Power System Protection and Control, 2020, 48(16): 147-154. (  0) 0) |
| [11] |
聂男峰. 特高压多端直流系统操作过电压研究[D]. 杭州: 浙江大学, 2020. NIE Nanfeng. Research on operating overvoltage of multi-terminal ultra HVDC system[D]. Hangzhou: Zhejiang University, 2020. (  0) 0) |
| [12] |
范雪峰, 黄金海, 宋延涛, 等. 柔性直流交流连接区故障分析[J]. 电力系统保护与控制, 2020, 48(11): 151-159. FAN Xuefeng, HUANG Jinhai, SONG Yantao, et al. Fault analysis of flexible DC/AC connection area[J]. Power System Protection and Control, 2020, 48(11): 151-159. (  0) 0) |
| [13] |
赵西贝, 许建中, 卢铁兵, 等. 采用架空线的MMC-HVDC单极接地过电压分析[J]. 电力系统自动化, 2018, 42(7): 44-49. ZHAO Xibei, XU Jianzhong, LU Tiebing, et al. Overvoltage analysis on overhead line based MMC-HVDC system under single-pole-to-ground[J]. Automation of Electric Power Systems, 2018, 42(7): 44-49. (  0) 0) |
| [14] |
BADRKHANI AJAEI F, IRAVANI R. Cable surge arrester operation due to transient overvoltages under DC-side faults in the MMC-HVDC link[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 1213-1222. DOI:10.1109/TPWRD.2015.2477493 (  0) 0) |
| [15] |
李岩, 黄豫, 龚雁峰, 等. 柔性直流电网直流线路故障的过电压机理分析[J]. 电力系统自动化, 2020, 44(5): 146-153. LI Yan, HUANG Yu, GONG Yanfeng, et al. Analysis on overvoltage mechanism of DC line fault in flexible DC grid[J]. Automation of Electric Power Systems, 2020, 44(5): 146-153. (  0) 0) |
| [16] |
赵翠宇, 齐磊, 陈宁, 等. ±500 kV张北柔性直流电网单极接地故障健全极母线过电压产生机理[J]. 电网技术, 2019, 43(2): 530-536. ZHAO Cuiyu, QI Lei, CHEN Ning, et al. Research on producing mechanism of healthy pole bus overvoltage for monopolar grounding fault in ±500 kV Zhangbei flexible DC power grid[J]. Power System Technology, 2019, 43(2): 530-536. (  0) 0) |
| [17] |
ZHOU Y B, JIANG D Z, GUO J, et al. Analysis and control of modular multilevel converters under unbalanced conditions[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 1986-1995. DOI:10.1109/TPWRD.2013.2268981 (  0) 0) |
| [18] |
SHI X J, WANG Z Q, LIU B, et al. Characteristic investigation and control of a modular multilevel converter-based HVDC system under single-line-to-ground fault conditions[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 408-421. DOI:10.1109/TPEL.2014.2323360 (  0) 0) |
| [19] |
周杨, 尹昌新, 贺之渊, 等. 单变压器分区互联装置接地故障特性研究及控制保护策略设计[J]. 中国电机工程学报, 2017, 37(23): 6901-6909, 7080. ZHOU Yang, YIN Changxin, HE Zhiyuan, et al. Characteristic investigation and control of single transformer interconnecting device under grounding fault condition[J]. Proceedings of the CSEE, 2017, 37(23): 6901-6909, 7080. (  0) 0) |
| [20] |
周杨, 贺之渊, 庞辉, 等. 双极柔性直流输电系统站内接地故障保护策略[J]. 中国电机工程学报, 2015, 35(16): 4062-4069. ZHOU Yang, HE Zhiyuan, PANG Hui, et al. Protection of converter grounding fault on MMC based bipolar HVDC systems[J]. Proceedings of the CSEE, 2015, 35(16): 4062-4069. (  0) 0) |
| [21] |
邓旭, 王东举, 沈扬, 等. 舟山多端柔性直流输电工程换流站内部暂态过电压[J]. 电力系统保护与控制, 2013, 41(18): 111-119. DENG Xu, WANG Dongju, SHEN Yang, et al. Research on transient overvoltage for converter station of Zhoushan multi-terminal VSC-HVDC project[J]. Power System Protection and Control, 2013, 41(18): 111-119. DOI:10.7667/j.issn.1674-3415.2013.18.019 (  0) 0) |
| [22] |
徐政, 屠卿瑞, 管敏渊. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2013. XU Zheng, TU Qingrui, GUAN Minyuan. Flexible DC transmission system[M]. Beijing: China Machine Press, 2013. (  0) 0) |
 2021, Vol. 40
2021, Vol. 40


 李岩(1990), 男, 博士, 工程师, 从事能源电力规划研究工作(E-mail:
李岩(1990), 男, 博士, 工程师, 从事能源电力规划研究工作(E-mail: