文章编号: 2096-3203(2021)05-0078-09 中图分类号: TM743
2. 安徽省电力有限公司电力科学研究院, 安徽 合肥 230601
近年来,高压直流输电(high voltage direct current, HVDC)技术应用广泛[1-3],国内已投运和在建的直流输电线路已超过18条。其中,在大功率直流输电的场合下,以晶闸管为核心的电网换相换流器(line-commuted converter, LCC)仍然是首选[4]。
直流输电系统的参数设计、稳定性研究、交直流系统相互作用研究以及基于故障分析的控保系统设计依赖于对换流器的准确建模,受大功率LCC-HVDC的元件数量和复杂程度限制,包含阀过程的电磁暂态仿真难以在普通计算设备中进行。目前已有多种简化模型被提出,包括准稳态模型、阻抗模型、以开关函数为核心的开关函数模型和动态相量模型等[5-8]。准稳态模型本质上是一种平均值模型,忽略了阀的换相过程,常应用于直流输电系统规划设计和小信号稳定性分析[9]。阻抗模型建立在准稳态模型的基础上,通常用于研究直流输电系统的振荡稳定性[10]。开关函数模型和动态相量模型更关注阀的换相过程,利用开关函数数值的变化来表示阀的不同状态,以此简化模型的计算量,开关函数模型保留了换流器的动态过程,其精度高于准稳态模型和阻抗模型,广泛应用于直流输电系统暂态分析。动态相量模型在开关函数模型的基础上,引入动态相量的概念,根据精度需要,保留开关函数傅里叶系数中特定的项,以此简化模型,降低计算复杂度[11-12]。
开关函数模型和动态相量模型由于物理概念清晰、运行效率高而得到广泛应用,但传统开关函数无法准确反映三相不对称和换相失败下的阀过程,因此需要对传统开关函数进行修正。文献[13]分析了三相不对称下自然换相点的偏移,并计算出相位修正量,以此修正开关函数。文献[14]详细分析了单次换相失败和多次换相失败下的阀过程及相应的预期开关函数,通过实时测量换相电压或熄弧角,判断是否发生换相失败,进而通过前一时刻的开关函数,判断换相失败的类型和故障相,以此为依据将原开关函数替换为预期开关函数。目前已提出的方法都是基于特定故障的分析和修正,未能将多种故障对开关函数的影响进行统一,且无法应对更为复杂的组合故障。
为此,文中首先分析了LCC的运行原理,在开关函数模型的基础上建立LCC的常微分方程(ordinary differential equation, ODE)模型。利用换相方程,将换流器的多种故障统一到阀的层面,并提出一种同时适用于三相不对称故障和换相失败的开关函数调制策略。最后,建立昌吉古泉±1 100 kV直流输电系统的ODE模型和详细模型(detailed model, DM)。通过稳态、动态和故障下的仿真对比,验证开关函数调制策略的准确度和ODE模型的运行效率。
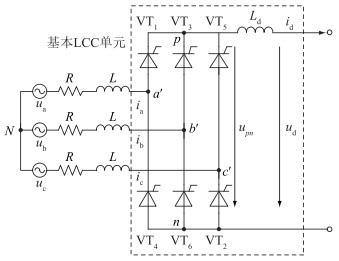
1 ODE描述与封装方法 1.1 开关函数模型的ODE描述LCC的基本单元为三相桥式电路,包括VT1—VT6共6组换流阀,直流侧出口串联平波电抗器Ld,为便于理解和说明,桥臂阀组统一用单个晶闸管的电气符号表示,如图 1所示。其中ua,ub,uc分别为三相交流电压源的电压;ia,ib,ic分别为三相交流电流;R,L分别为交流等效电阻和交流等效电感;upn为直流侧出口电压;ud为直流电压;id为直流电流。
|
图 1 基本LCC拓扑 Fig. 1 Topology of basic LCC |
根据开关函数模型原理[15],可获得三相六脉波换流器的开关函数模型:
| $ \left[\begin{array}{c} u_{\mathrm{a}}^{\prime} \\ u_{\mathrm{b}}^{\prime} \\ u_{\mathrm{c}}^{\prime} \end{array}\right]=\left[\begin{array}{c} u_{\mathrm{a}} \\ u_{\mathrm{b}} \\ u_{\mathrm{c}} \end{array}\right]-R\left[\begin{array}{c} i_{\mathrm{a}} \\ i_{\mathrm{b}} \\ i_{\mathrm{c}} \end{array}\right]-L\left[\begin{array}{c} \mathrm{d} i_{\mathrm{a}} / \mathrm{d} t \\ \mathrm{~d} i_{\mathrm{b}} / \mathrm{d} t \\ \mathrm{~d} i_{\mathrm{c}} / \mathrm{d} t \end{array}\right] $ | (1) |
| $ u_{\mathrm{d}}=\left[\begin{array}{l} S_{\mathrm{ua}} \\ S_{\mathrm{ub}} \\ S_{\mathrm{uc}} \end{array}\right]^{-1}\left[\begin{array}{c} u_{\mathrm{a}}^{\prime} \\ u_{\mathrm{b}}^{\prime} \\ u_{\mathrm{c}}^{\prime} \end{array}\right]-L_{\mathrm{d}} \frac{\mathrm{d} i_{\mathrm{d}}}{\mathrm{d} t} $ | (2) |
| $ \left[\begin{array}{c} i_{\mathrm{a}} \\ i_{\mathrm{b}} \\ i_{\mathrm{c}} \end{array}\right]=\left[\begin{array}{c} S_{\mathrm{ia}} \\ S_{\mathrm{ib}} \\ S_{\mathrm{ic}} \end{array}\right] i_{\mathrm{d}} $ | (3) |
式(1)为交流电压方程,式(2)为直流电压方程,Sua,Sub,Suc分别为a、b、c相电压开关函数,由阀电压开关函数Su1,Su2,Su3,Su4,Su5,Su6获得,即Sua= Su1- Su4,Sub= Su3- Su6,Suc= Su5- Su2;式(3)为交流电流输出方程,Sia,Sib,Sic为a、b、c相电流开关函数,由阀电流开关函数Si1,Si2,Si3,Si4,Si5,Si6获得,即Sia= Si1- Si4,Sib= Si3- Si6,Sic= Si5- Si2。
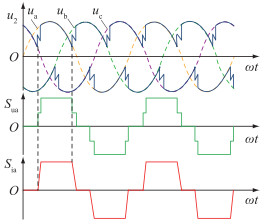
三相电压、电流开关函数反映了换流阀的电压、电流状态,开关函数的调制需要准确反映LCC的换相状态,同时,为降低计算量,也需要对换相过程中交流电流的变化过程作线性化处理。以a相电压、电流开关函数的调制过程为例,具体如图 2所示。
|
图 2 a相电压和电流开关函数波形 Fig. 2 Voltage and current switching function waveforms for phase a |
为进一步简化LCC模型,使其更加直观,需要将式(1)—式(3)进行变形。
首先,将交流电压方程与直流电流方程代入直流电压方程中,可获得:
| $ u_{\mathrm{d}}=\left[\begin{array}{c} S_{\mathrm{ua}} \\ S_{\mathrm{ub}} \\ S_{\mathrm{uc}} \end{array}\right]^{-1}\left[\begin{array}{l} u_{\mathrm{a}}-i_{\mathrm{a}} R-L \frac{\mathrm{d}\left(S_{\mathrm{ia}} i_{\mathrm{d}}\right)}{\mathrm{d} t} \\ u_{\mathrm{b}}-i_{\mathrm{b}} R-L \frac{\mathrm{d}\left(S_{\mathrm{ib}} i_{\mathrm{d}}\right)}{\mathrm{d} t} \\ u_{\mathrm{c}}-i_{\mathrm{c}} R-L \frac{\mathrm{d}\left(S_{\mathrm{ic}} i_{\mathrm{c}}\right)}{\mathrm{d} t} \end{array}\right]-L_{\mathrm{d}} \frac{\mathrm{d} i_{\mathrm{d}}}{\mathrm{d} t} $ | (4) |
式(4)中存在项Sumd(Simid)/dt(m=a,b,c),而该项可展开成如下形式:
| $ S_{\mathrm{u} m} \frac{\mathrm{d}\left(S_{\mathrm{i}m} i_{\mathrm{d}}\right)}{\mathrm{d} t}=S_{\mathrm{u}m} i_{\mathrm{d}} \frac{\mathrm{d} S_{\mathrm{i}m}}{\mathrm{d} t}+S_{\mathrm{u}m} S_{\mathrm{i}m} \frac{\mathrm{d} i_{\mathrm{d}}}{\mathrm{d} t} $ | (5) |
在式(5)等号右边第一项存在输入量的微分,为避免微分计算带来的不稳定,需对该项进行处理,现作如下讨论:
(1) 在非换相过程中,均有dSim/dt=0,此时有:
| $ S_{\mathrm{ua}} i_{\mathrm{d}} \frac{\mathrm{d} S_{\mathrm{ia}}}{\mathrm{d} t}+S_{\mathrm{ub}} i_{\mathrm{d}} \frac{\mathrm{d} S_{\mathrm{ib}}}{\mathrm{d} t}+S_{\mathrm{uc}} i_{\mathrm{d}} \frac{\mathrm{d} S_{\mathrm{ic}}}{\mathrm{d} t}=0 $ | (6) |
(2) 在换相过程中,以共阴极组a-b换相过程为例,有Sua=Sub=0.5,Suc=-1,且dSia/dt=-dSib/dt,dSic/dt=0,那么,对于任意换相过程,式(6)仍成立。因此可忽略式(5)中的SumiddSim/dt,式(4)可进一步简化为:
| $ \begin{array}{c} \left(L_{\mathrm{d}}+L\left[\begin{array}{c} S_{\mathrm{ua}} \\ S_{\mathrm{ub}} \\ S_{\mathrm{uc}} \end{array}\right]^{-1}\left[\begin{array}{c} S_{\mathrm{ia}} \\ S_{\mathrm{ib}} \\ S_{\mathrm{ic}} \end{array}\right]\right) \frac{\mathrm{d} i_{\mathrm{d}}}{\mathrm{d} t}=\left[\begin{array}{c} S_{\mathrm{ua}} \\ S_{\mathrm{ub}} \\ S_{\mathrm{uc}} \end{array}\right]^{-1}\left[\begin{array}{c} u_{\mathrm{a}} \\ u_{\mathrm{b}} \\ u_{\mathrm{c}} \end{array}\right]-u_{\mathrm{d}}- \\ R\left[\begin{array}{c} S_{\mathrm{ua}} \\ S_{\mathrm{ub}} \\ S_{\mathrm{uc}} \end{array}\right]^{-1}\left[\begin{array}{l} S_{\mathrm{ia}} \\ S_{\mathrm{ib}} \\ S_{\mathrm{ic}} \end{array}\right] i_{\mathrm{d}} \end{array} $ | (7) |
式(7)即为LCC开关函数模型的ODE形式,即ODE模型。
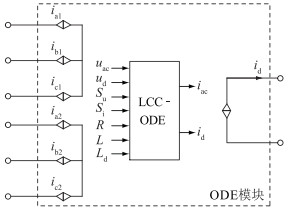
1.2 LCC-HVDC系统的ODE封装在实际LCC-HVDC系统中,为减小直流纹波,通常将2个或4个6脉波换流器的直流侧串联、交流侧接移相30°构成12脉波换流器和双12脉波换流器,其ODE模型可由式(7)推导而得。而系统中的交、直流滤波器组、接地极、直流线路等不是本次研究的重点,且难以统一建模,因此将数学建模范围限制在换流器部分,利用受控电流源或受控电压源将信号量转换为电气量,构成与外部电路的电气接口,实现换流器ODE模型的封装,建立换流器的模块化ODE模型,其余电路则采用详细模型建模。
对ODE模型进行封装需选取合适的输入、输出量,以避免出现电流源与电感串联、电压源与电容并联的情况。针对前文所述的基本LCC单元,直流输出量为直流电流,交流输出量为三相交流电流;12脉波换流器以及双12脉波换流器由2个或4个基本LCC级联而成,其直流输出量同样应为直流电流,交流输出量为三相交流电流,均由受控电流源作为电气接口,整流侧12脉波换流器的ODE封装形式如图 3所示。逆变侧封装模块受控电流源的正方向与整流侧封装相同,但直流端口的电压极性与整流侧封装模块相反。
|
图 3 12脉波换流器的ODE封装 Fig. 3 ODE package of 12-pulse converter |
前文所述的开关函数调制过程为传统调制方法,只适用于三相对称下的稳态运行,在非理想工作状态下,如发生不对称故障以及换相失败时,传统开关函数调制将失效,需对其进行修正,以准确反映换流器真实运行状态。
文中首先分析故障状态对换相过程的影响,然后提出相应的开关函数调制策略。
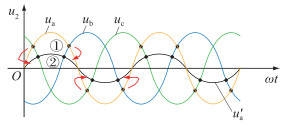
2.1 自然换相点偏移以a相接地短路为例,故障发生后,a、b、c的自然换相点发生偏移,如图 4所示,其中u′a为a相接地短路后a相电压波形。
|
图 4 a相接地短路 Fig. 4 Short circuit to ground of phase a |
a相幅值的降低导致a与b的自然换相点从点①转移至点②,以a-b换相过程为例,对a-b换相过程的影响体现在以下方面:
(1) 换相电压uba的过零点相对于b相电压过零点发生偏移,换相开始时刻uba相对于过零点的相位不再是导通角α;
(2) 换相电压uba的幅值发生变化。
uba的相位和幅值的改变会引起换相角和熄弧角的改变,进而影响开关函数的波形。要使开关函数准确反映三相电压不对称带来的影响,核心在于对换相电压uba的过零点的相位实时修正:设ua=Uasin ωt,ub=Ubsin(ωt-2π/3),令ua=ub|ωt=ωtab,可解得:
| $ \omega t_{\mathrm{ab}}=\tan ^{-1} \frac{-\sqrt{3}}{2 U_{\mathrm{a}} / U_{\mathrm{b}}+1} $ | (8) |
式(8)即为图 4中点②的相位,点②超前点①的角度即为换相电压uba过零点的相位偏移角θab。
| $ \theta_{\mathrm{ab}}=-\frac{{\rm{ \mathsf{ π} }}}{6}-\tan ^{-1} \frac{-\sqrt{3}}{2 U_{\mathrm{a}} / U_{\mathrm{b}}+1} $ | (9) |
同理可得b-c,c-a的相位偏移角为:
| $ \theta_{\mathrm{bc}}=-\frac{{\rm{ \mathsf{ π} }}}{6}-\tan ^{-1} \frac{-\sqrt{3}}{2 U_{\mathrm{b}} / U_{\mathrm{c}}+1} $ | (10) |
| $ \theta_{\mathrm{ca}}=-\frac{{\rm{ \mathsf{ π} }}}{6}-\tan ^{-1} \frac{-\sqrt{3}}{2 U_{\mathrm{c}} / U_{\mathrm{a}}+1} $ | (11) |
以上桥臂a-b换相过程为例,具体如图 5所示。其中,isc为换相短路电流,且有:
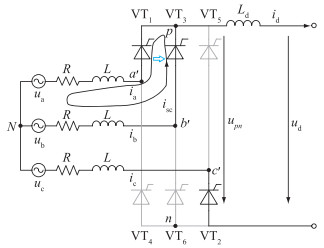
|
图 5 上桥臂a-b换相过程 Fig. 5 a-b commutation process of upper arm |
| $ i_{\mathrm{a}}=i_{\mathrm{d}}-i_{\mathrm{sc}} $ | (12) |
| $ i_{\mathrm{b}}=i_{\mathrm{sc}} $ | (13) |
交流等效电阻R为变压器等效电阻与交流电网等效电阻之和,其数值通常较小,引起的压降可以忽略不计。因此,为简化换相过程的求解,文中忽略交流等效电阻R,则换相过程中a、b相电压回路方程为:
| $ u_{\mathrm{a}}-L \frac{\mathrm{d} i_{\mathrm{a}}}{\mathrm{d} t}=u_{\mathrm{b}}-L \frac{\mathrm{d} i_{\mathrm{b}}}{\mathrm{d} t} $ | (14) |
设:
| $ u_{\mathrm{b}}=\sqrt{2} U_{\mathrm{b}} \sin (\omega t+{\rm{ \mathsf{ π} }} / 6) $ | (15) |
考虑三相电压不对称的影响,换相电压uba为:
| $ u_{\mathrm{ba}}=\sqrt{2} U_{\mathrm{ba}} \sin \left(\omega t+\theta_{\mathrm{ab}}\right) $ | (16) |
将式(12)、式(13)、式(16)代入式(14)中,可解得换相电路电流isc为:
| $ i_{\mathrm{sc}}=\frac{\sqrt{2} U_{\mathrm{ba}}}{2 \omega L}\left[\cos \left(\alpha+\theta_{\mathrm{ab}}\right)-\cos \left(\omega t+\theta_{\mathrm{ab}}\right)\right] $ | (17) |
令isc|ωt=α+μab =id,可解得换相角μab和熄弧角γab为:
| $ \mu_{\mathrm{ab}}=\cos ^{-1}\left[\cos \left(\alpha+\theta_{\mathrm{ab}}\right)-\frac{2 \omega L i_{\mathrm{d}}}{\sqrt{2} U_{\mathrm{ba}}}\right]-\left(\alpha+\theta_{\mathrm{ab}}\right) $ | (18) |
| $ \gamma_{\mathrm{ab}}={\rm{ \mathsf{ π} }}-\cos ^{-1}\left[\cos \left(\alpha+\theta_{\mathrm{ab}}\right)-\frac{2 \omega L i_{\mathrm{d}}}{\sqrt{2} U_{\mathrm{ba}}}\right] $ | (19) |
当三相不对称时,也可能会出现换相电压过零点滞后的情况,此时若导通角α<-θab,实际触发时刻将由滞后角度-θab决定,实际导通角αreal=-θab,将其代入式(18)—式(19)中,可得实际换相角和熄弧角为:
| $ \mu_{\mathrm{ab}}=\arccos \left(1-\frac{2 \omega L i_{\mathrm{d}}}{\sqrt{2} U_{\mathrm{ba}}}\right) $ | (20) |
| $ \gamma_{\mathrm{ab}}={\rm{ \mathsf{ π} }}-\arccos \left(1-\frac{2 \omega L i_{\mathrm{d}}}{\sqrt{2} U_{\mathrm{ba}}}\right) $ | (21) |
特别地,当α<-θab时,换流器通常运行在整流状态,通常不会发生换相失败,因此无需考虑换相失败的情况。
2.2 换相失败换相失败的特征在于晶闸管无法有效关断,单个晶闸管持续导通[16-17]。以上桥臂a-b换相过程为例,a相晶闸管因熄弧角过小或阀短路等故障,在换相电压过零前没有有效关断,因此在换相电压由正变负后A相晶闸管重新开通,b相晶闸管继而关断,发生倒换相,这个过程称为换相失败[18];当c相晶闸管触发脉冲到来后,往往由于uca<0而无法开通,a相晶闸管持续导通,直至b相晶闸管的触发脉冲再次到来;如果此时故障消失,则a-b能够正常换相,该过程称为单次换相失败;如果此时故障仍然存在,则a-b仍无法成功换相,换流器将重复上述状态,该过程称为连续换相失败[19]。换相失败最直接的判据是熄弧角γ是否小于晶闸管的最小熄弧角γmin,而根据熄弧角γ是否小于0,换相失败又可分为以下情况:
(1) 当0<γab<γmin≈7°时,在uba<0前,a相晶闸管关断,b相晶闸管完成开通;但在uba<0后,a相晶闸管重新开通,b相晶闸管继而关断,发生倒换相,此时,电压、电流开关函数如图 6所示。其中up为图 5中p点电位。
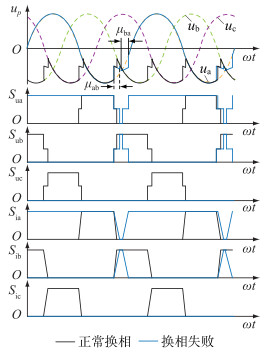
|
图 6 0<γab<γmin时电压和电流开关函数 Fig. 6 Voltage and current switching functions when 0 < γab<γmin |
这种情况下包含2个换相过程,在uba<0前的换相过程的换相角μab以及熄弧角γab可利用式(18)—式(19)计算得出;uba<0后,令ia=isc,ib=id-isc,根据A-B相电压回路方程,可计算出换相短路电流isc为:
| $ i_{\mathrm{sc}}=\frac{\sqrt{2} U_{\mathrm{ba}}}{2 \omega L}\left[\cos \left(\omega t+\theta_{\mathrm{ab}}\right)+\cos \theta_{\mathrm{ab}}\right] $ | (22) |
令isc|ωt=π+μba =id,进而可解得换相角μba为:
| $ \mu_{\mathrm{ba}}=\arccos \left(\cos \theta_{\mathrm{ab}}-\frac{2 \omega L i_{\mathrm{d}}}{\sqrt{2} U_{\mathrm{ba}}}\right)-\theta_{\mathrm{ab}} $ | (23) |
(2) 当γab<0时, a相电流始终大于零,换相过程将延续到uba<0之后,且式(18)无解,此时,电压、电流开关函数如图 7所示。
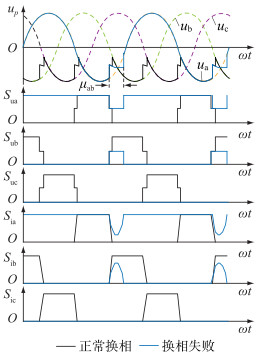
|
图 7 γab<0时电压和电流开关函数 Fig. 7 Voltage and current switching functions when γab<0 |
此时,仍可利用式(17)计算换相短路电流isc,令:
| $ \left.i_{\mathrm{sc}}\right|_{\omega t=\alpha+\mu_{\mathrm{ab}}}=0 $ | (24) |
可解得:
| $ \mu_{\mathrm{ab}}=2 {\rm{ \mathsf{ π} }}-2 \alpha-2 \theta_{\mathrm{ab}} $ | (25) |
且ωt=π-θab时,isc有最大值:
| $ \left.i_{\mathrm{sc}}\right|_{\max }=\frac{\sqrt{2} U_{\mathrm{ba}}}{2 \omega L}\left[\cos \left(\alpha+\theta_{\mathrm{ab}}\right)-\cos {\rm{ \mathsf{ π} }}\right] $ | (26) |
基于前文的分析,可根据换相电压相位偏移角、换相角和熄弧角等状态变量对换流器运行状态进行判断,并根据当前的运行状态,对开关函数采取相应的调制过程,可按照图 8所示流程对开关函数进行调制。调制流程主要分为3个步骤:
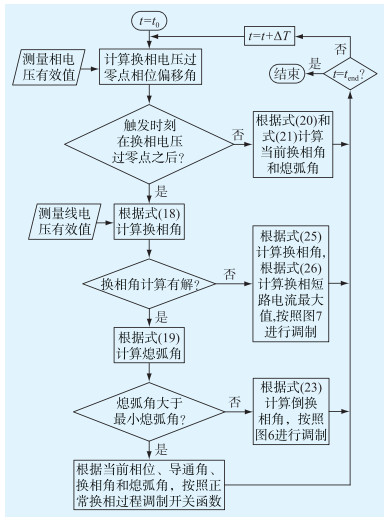
|
图 8 开关函数调制流程 Fig. 8 Modulation process of switching function |
(1) 计算换相电压相位偏移角、换相角和熄弧角;
(2) 根据计算结果,判断当前换相过程的状态;
(3) 根据当前换相状态选取对应的换相过程计算模块,输出包括换相角、熄弧角、换相电流最大值等状态变量,结合当前电压相位角,输出开关函数。
3 仿真分析 3.1 仿真算例为验证LCC-HVDC系统ODE模型的准确性和开关函数调制策略的有效性,文中以昌吉古泉±1 100 kV直流输电系统实际工程参数为依据,分别设置逆变侧交流不对称故障、对称故障以及直流线路故障仿真算例。
算例1:1.6 s时刻在500 kV交流母线处设置a相接地故障,持续0.1 s,采用定触发角控制,整流侧和逆变侧的触发角整定值分别为8°和145°;
算例2:1.6 s时刻在500 kV交流母线处设置三相短路故障,持续0.1 s,采用定触发角控制,整流侧和逆变侧的触发角整定值分别为8°和145°;故障发生后,逆变侧触发角增加10°;
算例3:1.6 s时刻在直流线路靠近整流侧的某一点设置接地故障,持续0.1 s,采用定触发角控制,整流侧和逆变侧的触发角整定值分别为8°和145°;故障发生后,整流站触发角增加到164°。
仿真时间均为2 s,算例中涉及的直流系统为双极双12脉波LCC-HVDC,如图 9所示。其中送端接入750 kV交流电网,受端分层接入500 kV和1 000 kV交流电网,直流系统参数如表 1所示。
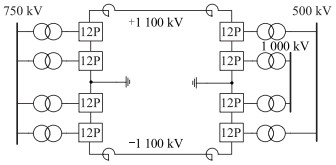
|
图 9 仿真系统结构 Fig. 9 Structure of simulation system |
|
|
表 1 直流系统参数 Table 1 Parameters of DC system |
基于文中提出的LCC-HVDC系统ODE模型,在Matlab/Simulink中建立相应的HVDC系统模型,对直流系统500 kV交流母线a相接地故障进行仿真,并将结果与其相应的DM进行比较[20-24]。
3.2 仿真结果算例1:在故障发生时刻附近,详细模型中逆变站阀电压波形以及对应的电压开关函数调制波形如图 10所示,其中阀电压为标幺值,其基准值为500 kV;详细模型与ODE模型的直流线路电流id,整流侧直流电压udr,逆变侧直流电压udi见图 11。
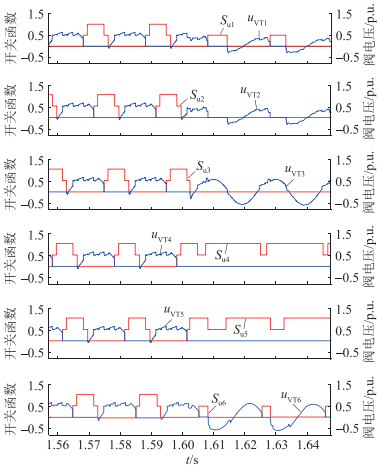
|
图 10 阀电压与电压开关函数仿真波形 Fig. 10 Simulation waveforms of valve voltage and voltage switching function |
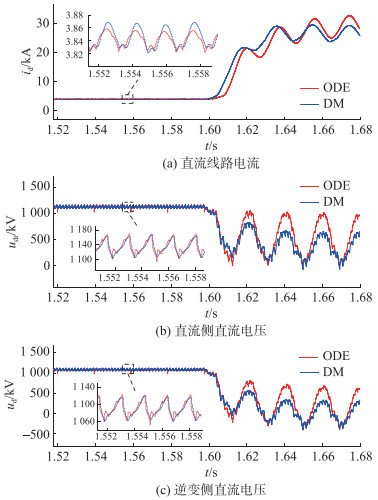
|
图 11 直流线路仿真波形(算例1) Fig. 11 Simulation waveforms of DC line(example 1) |
从仿真波形中可以看出,换相电压相位偏移角修正策略能够准确跟踪不对称故障带来的相位偏差;在系统发生换相失败后,开关函数调制策略能够根据实际系统的运行状况确定当前工作状态,并正确判断连续导通的相。
直流线路仿真波形反映了ODE模型在相位以及波形变化趋势上与DM较为接近。但由于ODE模型忽略阀缓冲电路的影响,并且将换流变压器等效为交流阻抗,ODE模型的直流电压和直流电流在幅值上与详细模型出现偏差。
算例2:在故障发生时刻附近,详细模型与ODE模型的直流线路电流id,整流侧直流电压udr,逆变侧直流电压udi如图 12所示。
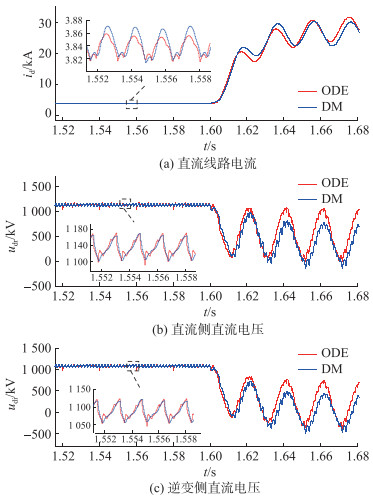
|
图 12 直流线路仿真波形(算例2) Fig. 12 Simulation waveforms of DC line (example 2) |
在1.6 s时刻,500 kV交流母线发生三相短路故障,逆变侧直流电压迅速跌落,直流电流迅速增加,换相角随之增大。为了弥补直流电压跌落,在控制器的作用下,逆变侧触发角增大10°,这导致熄弧角进一步减小,从而发生了换相失败。由仿真结果可见,在发生对称故障时,ODE模型精度高于不对称故障。
算例3:在故障发生时刻附近,详细模型与ODE模型的整流侧的换流器电流idr,整流侧直流电压udr,逆变侧直流电压udi如图 13所示。
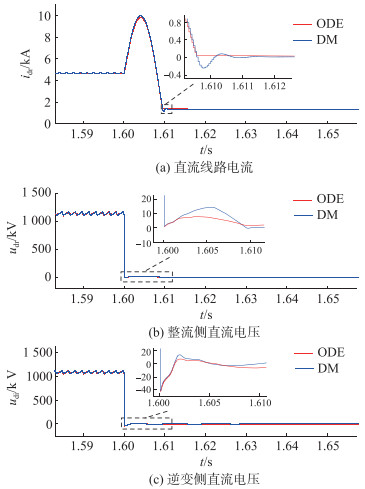
|
图 13 直流线路仿真波形(算例3) Fig. 13 Simulation waveforms of DC line (example 3) |
故障发生后,整流侧触发角迅速增大至164°,直流电流和直流电压迅速降为0。由于ODE模型忽略了换流阀的开关损耗以及相关寄生参数,直流电流在过零之后没有振荡过程。由仿真结果可见,在相同的运行参数下,ODE模型能够较为准确地模拟直流电路故障以及触发角突变的情况。
上述3个算例中详细模型和ODE模型的运行时间如表 2所示,直流电流id(idr)的误差在正常运行(0~1.6 s)和故障运行(1.6~2.0 s)期间的平均值如表 3所示。
|
|
表 2 模型运行时间 Table 2 The running time of models |
|
|
表 3 直流电流平均误差 Table 3 Average error of DC current |
文中提出一种基于开关函数的LCC-HVDC系统ODE模型,通过对开关函数进行故障状态的修正,准确模拟了HVDC系统在交流故障和直流故障下的换流阀动态过程,主要结论如下:
(1) 将LCC的开关函数模型表示为ODE形式,并结合开关函数特性剔除ODE中与系统运行无关的项,使模型具有明确的输入、输出量,也提高了ODE模型的运行速度。仿真结果表明,与详细模型相比,ODE模型在运行速度上有明显的优势,且仿真误差最大不超过7%。
(2) 以换相方程作为换流阀状态判断的依据,使得文中提出的开关函数调制策略相比于传统开关函数修正策略更加灵活,具有相位误差小、能适应多种故障状态的特点。仿真结果表明,在发生自然换相点偏移以及换相失败时,开关函数波形均能准确“跟踪”DM中阀的状态。
考虑故障状态的ODE模型可应用于多端混合直流输电等大规模输电系统的建模,模型的仿真精度保证了仿真结果的可靠性;而模型在仿真效率上的优势能够显著降低对仿真设备性能的要求,提高仿真速度,缩短直流输电系统参数设计的时间周期。
本文得到国网安徽省电力有限公司科技项目(521205180020)资助,谨此致谢!
| [1] |
孔祥平, 李鹏, 高磊, 等. 基于深度学习的特高压直流控制保护系统可视化技术[J]. 电网与清洁能源, 2020, 36(2): 29-37. KONG Xiangping, LI Peng, GAO Lei, et al. The visualization technology of the UHVDC control and protection system based on deep learning[J]. Power System and Clean Energy, 2020, 36(2): 29-37. (  0) 0) |
| [2] |
袁博, 王颖, 邵华, 等. (特)高压直流线路单极故障隔离策略[J]. 电网与清洁能源, 2020, 36(12): 9-18. YUAN Bo, WANG Ying, SHAO Hua, et al. Isolation strategy for pole-to-ground fault of (U)HVDC lines[J]. Power System and Clean Energy, 2020, 36(12): 9-18. DOI:10.3969/j.issn.1674-3814.2020.12.002 (  0) 0) |
| [3] |
张怿宁, 孟令军, 王越杨. 基于非接触式行波采集的分布式高压直流故障测距方法[J]. 电网与清洁能源, 2020, 36(4): 55-59, 65. ZHANG Yining, MENG Lingjun, WANG Yueyang. A fault location method for distributed hvdc high resistance fault based on non-contact traveling wave collecting[J]. Power System and Clean Energy, 2020, 36(4): 55-59, 65. DOI:10.3969/j.issn.1674-3814.2020.04.008 (  0) 0) |
| [4] |
董朝阳, 吉攀攀, 冯敏, 等. 基于LCC-FHMMC混合直流输电的控制策略研究及试验验证[J]. 电力系统保护与控制, 2019, 47(13): 148-155. DONG Chaoyang, JI Panpan, FENG Min, et al. Control strategies and experimental verification for hybrid HVDC system based on LCC and FHMMC[J]. Power System Protection and Control, 2019, 47(13): 148-155. (  0) 0) |
| [5] |
PROBST L, HAHN C, LUTHER M. A novel approach for analytical modeling of line commutated converter based HVDC systems for electromagnetic transient analysis[C]//2015 IEEE Eindhoven Power Technology Eindhoven, Netherlands. IEEE, 2015: 1-7.
(  0) 0) |
| [6] |
LIU H C, SUN J. Modeling and analysis of DC-link harmonic instability in LCC HVDC systems[C]//2013 IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL). Salt Lake City, UT, USA. IEEE, 2013: 1-9.
(  0) 0) |
| [7] |
LI B H, LIU T Q, XU W H, et al. Research on technical requirements of line-commutated converter-based high-voltage direct current participating in receiving end AC system's black start[J]. IET Generation, Transmission & Distribution, 2016, 10(9): 2071-2078. (  0) 0) |
| [8] |
HAHN C, SEMEROW A, LUTHER M, et al. Generic modeling of a line commutated HVDC system for power system stability studies[C]//2014 IEEE PEST&D Conference and Exposition. Chicago, IL, USA. IEEE, 2014: 1-6.
(  0) 0) |
| [9] |
OSAUSKAS C M, WOOD A R. Small signal dynamic modeling of HVDC systems[J]. IEEE Power Engineering Review, 2002, 22(7): 62-63. (  0) 0) |
| [10] |
LIU H K, XIE X R, LIU W. An oscillatory stability criterion based on the unified dq-frame impedance network model for power systems with high-penetration renewables[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3472-3485. DOI:10.1109/TPWRS.2018.2794067 (  0) 0) |
| [11] |
戚庆茹, 焦连伟, 严正, 等. 高压直流输电动态相量建模与仿真[J]. 中国电机工程学报, 2003, 23(12): 31-35. QI Qingru, JIAO Lianwei, YAN Zheng, et al. Modeling and simulation of hvdc with dynamic phasors[J]. Proceedings of the CSEE, 2003, 23(12): 31-35. (  0) 0) |
| [12] |
DARYABAK M, FILIZADEH S, JATSKEVICH J, et al. Modeling of LCC-HVDC systems using dynamic phasors[J]. IEEE Transactionson Power Delivery, 2014, 29(4): 1989-1998. DOI:10.1109/TPWRD.2014.2308431 (  0) 0) |
| [13] |
NGANDUI E, OLIVIER G, APRIL G E, et al. Comprehensive switching functions approach to calculate harmonics produced by multipulse thyristor converters operating under unbalanced supply[C]//8th International Conference on Harmonics and Quality of Power Proceedings (Cat. No. 98EX227). Athens, Greece. IEEE, 1998: 837-843.
(  0) 0) |
| [14] |
王超. 考虑换相失败的换流站开关函数模型[D]. 北京: 华北电力大学, 2012. WANG Chao. Modeling of switch function considering commutation failure effects for converter[D]. Beijing: North China Electric Power University, 2012. (  0) 0) |
| [15] |
HU L, YACAMINI R. Harmonic transfer through converters and HVDC links[J]. IEEE Transactions on Power Electronics, 1992, 7(3): 514-525. DOI:10.1109/63.145139 (  0) 0) |
| [16] |
刘建坤, 王蒙, 张宁宇, 等. 基于UPFC抑制HVDC换相失败的控制方法研究[J]. 电力工程技术, 2018, 37(5): 86-91, 120. LIU Jiankun, WANG Meng, ZHANG Ningyu, et al. The control method of HVDC commutation failure based on UPFC[J]. Electric Power Engineering Technology, 2018, 37(5): 86-91, 120. (  0) 0) |
| [17] |
周前, 张潮, 张宁宇, 等. 2018年多直流馈入江苏规划电网连锁换相失败分析[J]. 电力工程技术, 2018, 37(1): 51-57. ZHOU Qian, ZHANG Chao, ZHANG Ningyu, et al. Analysis on commutation failures in multi-infeed HVDC system in planning power grid of Jiangsu in 2018[J]. Electric Power Engineering Technology, 2018, 37(1): 51-57. (  0) 0) |
| [18] |
许韦华, 陈争光, 汤广福, 等. 换流阀设备换相失败故障的暂态分析[J]. 电网技术, 2013, 37(6): 1759-1763. XU Weihua, CHEN Zhengguang, TANG Guangfu, et al. Analysis on transient commutation failure fault on converter valve[J]. Power System Technology, 2013, 37(6): 1759-1763. (  0) 0) |
| [19] |
JAFAR M, MOLINAS M. Transformer-less series voltage injection for reactive power compensation of line-commutated HVDC[C]//2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC). NoviSad, Serbia. IEEE, 2012.
(  0) 0) |
| [20] |
刘泽洪, 余军, 郭贤珊, 等. ±1100 kV特高压直流工程主接线与主回路参数研究[J]. 电网技术, 2018, 42(4): 1015-1022. LIU Zehong, YU Jun, GUO Xianshan, et al. Study on main connection line and main circuit parameters of ±1100 kV UHVDC[J]. Power System Technology, 2018, 42(4): 1015-1022. (  0) 0) |
| [21] |
郭焕, 曹均正, 汤广福, 等. ±1100 kV特高压直流换流系统主电路优化设计[J]. 电网技术, 2013, 37(9): 2383-2389. GUO Huan, CAO Junzheng, TANG Guangfu, et al. Optimization design of main circuit of converter system for ±1100 kV UHVDC transmission system[J]. Power System Technology, 2013, 37(9): 2383-2389. (  0) 0) |
| [22] |
郝婧. 基于EMTDC仿真平台的特高压直流输电控制系统建模的研究[D]. 北京: 华北电力大学, 2012. HAO Jing. Research on UHVDC control system modeling based on EMTDC[D]. Beijing: North China Electric Power University, 2012. (  0) 0) |
| [23] |
翁华. 大规模交直流系统电磁暂态仿真和稳定控制技术研究[D]. 杭州: 浙江大学, 2014. WENG Hua. Research on electromagnetic transient simulation and stability control for large-scale AC/DC power systems[D]. Hangzhou: Zhejiang University, 2014. (  0) 0) |
| [24] |
KUMAR R, LEIBFRIED T. Analytical modelling of HVDC transmission system converter using Matlab/Simulink[C]//IEEE Systems Technical Conference on Industrial and Commercial Power 2005. SaragotaSprings, NY, USA. IEEE, 2005: 140-146.
(  0) 0) |
2. State Grid Anhui Electric Power Co., Ltd. Research Institute, Hefei 230601, China
 2021, Vol. 40
2021, Vol. 40


 王梓懿(1996), 男, 硕士, 研究方向为特高压直流输电系统建模(E-mail:
王梓懿(1996), 男, 硕士, 研究方向为特高压直流输电系统建模(E-mail: