文章编号: 2096-3203(2021)05-0121-07 中图分类号: TM854
随着柔性直流输电工程的发展,绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)已应用于高压换流阀[1]。现有IGBT电压等级已提高到了6.5 kV以上[2-3],其绝缘性能是关系到换流阀能否正常安全运行的重要因素[4]。不同于常规的交/直流电应力,IGBT器件承受高电压脉冲电应力作用,其绝缘状态检测和老化评估与高压脉冲参数息息相关。其中,局部放电特性对绝缘状态检测与老化评估至关重要。因此,研究脉冲电应力作用下IGBT绝缘材料的局部放电特性尤为重要。
脉冲电压幅值、频率、上升沿、占空比是影响局部放电特性的关键因素。文献[5]指出在实验温度28 ℃,频率1 kHz的脉冲电压下,聚酰亚胺薄膜在0.7~2 kV脉冲电压幅值变化范围内平均放电量和单个周期内的放电次数随着电压的增大而增加。文献[6]指出在电压峰峰值3 kV,实验温度160 ℃条件下,电机绞线在脉冲频率1~15 kHz范围内,随着频率增大,电应力会造成局部放电平均放电量增大;文献[7]在电压峰峰值3 kV,实验温度25 ℃条件下,对聚酰胺酰亚胺绞线进行实验,发现在脉冲频率0.5~10 kHz范围内,随着频率升高局部放电幅值显著减小而局部放电相位增加。文献[8]在脉冲频率1 kHz,电压峰峰值3 kV,上升沿10~100 ns的实验条件下,发现随着上升沿时间增加,双绞线局部放电幅值减小,相位增大;文献[9-10]指出在脉冲频率50 Hz,电压3 kV,实验温度100 ℃的条件下,在上升沿20 ns~1 μs的范围内,随上升沿时间的缩短,双绞线放电幅值增大,单个周期放电总量减少。文献[11-12]指出在脉冲频率50 Hz,实验温度25 ℃,聚酰亚胺漆包线在脉冲持续时间8~100 μs条件下,上升沿放电相位随占空比增加而减小,下降沿放电相位随占空比增加而增大;文献[13]指出在脉冲频率10 kHz,实验温度25 ℃的条件下,漆包线在占空比5%~50%的范围内,上升沿附近的局部放电幅值随占空比增加而减小且分散性逐渐减小,下降沿附近的放电幅值随电压占空比增加而增大且分散性逐渐增大。
综上所述,脉冲参数对绝缘材料的局部放电特性影响研究已较为成熟,但仍存在以下不足:(1) 现有研究的脉冲频率局限在50 Hz~15 kHz范围内,无法反映脉冲频率为20 kHz及以上时的局部放电特性;(2) 上升沿对局部放电特性的研究主要集中在脉冲频率1 kHz以下,无法反映1 kHz以上的频率条件对局部放电的影响;(3) 占空比对局部放电特性的影响的研究对象集中于电机匝间漆包线,未展开针对其他材料的研究。
因此,文中选取IGBT器件中聚酰亚胺薄膜为研究对象,研究了宽脉冲参数范围下电压幅值、频率、上升沿、脉宽对聚酰亚胺薄膜局部放电特性的影响。
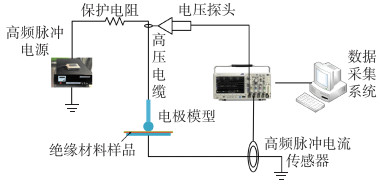
1 局部放电实验平台局部放电实验平台示意如图 1所示,该平台包含纳秒脉冲电源系统、球板电极放电装置、固体绝缘材料(100 μm厚的聚酰亚胺薄膜)、局部放电传感系统,以及温湿度控制系统。利用具有干燥、控温功能的空调控制环境温度和湿度,将电极附近(0.5 m)的环境温度和湿度分别始终保持为(23±2) ℃和(50±5)%。
|
图 1 局部放电实验平台 Fig. 1 Partial discharge experimental platform |
高频脉冲电源与球板电极装置之间接入了2个并联的5 kΩ电阻,电极的另一端直接接地。利用高压探头测试放电装置两端的电压,高频脉冲电流传感器测量由电极流入大地的电流,并将电压与电流信号传入示波器,再通过示波器的USB端口将数据传至PC系统。结合PC计算机系统的LabVIEW局放统计程序,可以获得局部放电统计图谱。
利用高压探头Tektronix P6015A测量球板电极两端电压。利用电流探头Pearson 2877测量接地侧的电流,其带宽为200 MHz,响应时间为2 ns,能够对局部放电信号进行精确测量。所采集的电压、电流信号由TektronixMDO3034示波器进行记录。采用的高频高压脉冲电源输出参数范围为:电压0~15 kV,频率1 Hz~100 kHz,上升沿50~500 ns,脉宽500 ns~1 ms,有利于研究大参数范围内的脉冲电应力对局部放电特性的影响。
选取0.1 mm的Kapton聚酰亚胺薄膜为绝缘材料。根据GB/T 22689—2008,提前一天取出厚0.1 mm、宽80 mm的聚酰亚胺薄膜卷,裁出长80 mm的聚酰亚胺薄膜试样,用在96%乙醇浸泡5 min并自然晾干的软毛刷清洁试样表面,将空调开至25 ℃除湿模式,使试样保持在温度为(23±2) ℃,相对湿度为(50±5)%的标准环境大气中处理至少24 h。
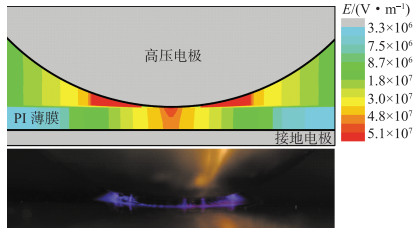
为了模拟IGBT器件封装中金属镀膜表面凸点(缺陷)与绝缘材料之间构成的稍不均匀电场,文中设计了不均匀系数[14]为1.7的球板放电装置。基于COMSOL有限元仿真软件,搭建了放电装置的电场仿真二维模型,模拟了固体介质为100 μm厚聚酰亚胺薄膜的球板电极放电装置的静电场空间分布,如图 2所示,最大电场强度达到5.1×107 V/m。
|
图 2 电场的仿真结果及实际放电现象 Fig. 2 Simulation results of electric field and actual discharge phenomena |
仿真发现,电场最强的位置位于电极与聚酰亚胺薄膜之间的空气间隙中,而不是球电极的顶端。实验过程中紫色光圈放电出现在靠近球电极顶端附近的空气间隙中,与仿真结果中最大电场强度位置相同,并伴随放电声。
2 局部放电信号测量在实际局部放电测量过程中,即使未发生局部放电,电流探头也能测到峰值高达数百毫安的位移电流,远大于局部放电引起的放电电流。另外,位移电流主要集中在电压脉冲的上升沿和下降沿处,与局部放电引起的放电电流位置重叠。因此,为了能够获得真实的局部放电信号,必须去除位移电流的影响。
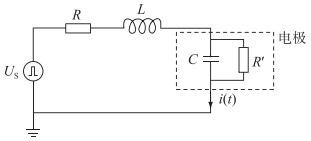
实验装置可进行RLC电路等效,其示意见图 3。其中,R为保护电阻;L为线路电感;C为电极间的等效电容;R′为电极间的等效电阻(远远大于保护电阻);US为电源电压。
|
图 3 实验平台等效RLC电路 Fig. 3 Equivalent RLC circuit of experimental platform |
从电路的时域分析角度计算,当US为阶跃函数时,流经负载电极装置的电流[15]为:
| $ \mathit{i}{\rm{(}}\mathit{t}{\rm{) = }}\frac{{{\mathit{U}_{\rm{S}}}}}{{\mathit{L}({\mathit{p}_1} - {\mathit{p}_2})}}({{\rm{e}}^{{\mathit{p}_{{1^\mathit{t}}}}}} - {{\rm{e}}^{{\mathit{p}_{{2^\mathit{t}}}}}}) $ | (1) |
式中:p1,p2为特征根,其数值由电路自身RLC参数决定。由式(1)可见,同一时刻的位移电流与施加的电压幅值呈线性关系,并且进行了实验验证。因此,通过测量未发生局部放电情况下的位移电流,再乘以比例系数k,即可获得发生局部放电时的位移电流。然后,在总电流波形中减去位移电流,获得真实局部放电引起的放电电流。
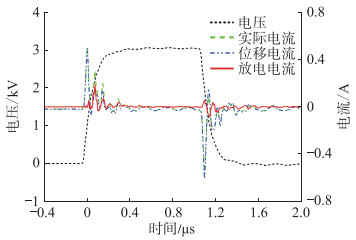
如图 4所示,放电电流与位移电流都为脉冲波形,都主要集中在电压脉冲的上升沿和下降沿,两者发生了重叠。另外,放电电流的幅值约为0.2 A,远小于位移电流幅值。值得注意的是,以电压脉冲上升沿为相对时间起点,位移电流波形峰值比放电电流波形峰值出现更早,大约为71.2 ns。该发现可为去除位移电流波形影响提供新的解决方案。
|
图 4 干扰电流和全电流及放电电流波形 Fig. 4 Interference current, full current and discharge current waveform |
另外,通过电流波形的傅里叶分析,发现位移电流的频谱主要集中在13.5 MHz,20.5 MHz,28 MHz,而放电电流的频谱主要集中在13.5 MHz,20.5 MHz,28 MHz,33 MHz,49 MHz,62 MHz,两者有相互重叠部分,因此难以使用超高频传感方法直接测量脉冲电应力下的局部放电信号。
为尽量减少纳秒脉冲电源引起的空间电磁辐射和传导干扰,采取下述措施:(1) 将采集系统的地与高压脉冲电源的地分开,避免共地带来的脉冲传导干扰;(2) 在电流信号传感部分,采用带屏蔽金属网的射频线缆传输信号,并在末端进行了50 Ω阻抗匹配,减少了空间电磁辐射耦合进入线缆和电磁波来回反射;(3) 为进一步减弱空间电磁辐射对采集系统的干扰,将采集系统放置在金属屏蔽箱内,理论上能够对0.1~1 GHz电磁信号实现30 dB衰减。
3 高电压脉冲参数对聚酰亚胺薄膜局放特性的影响分析采用局部放电统计谱图法,研究电压幅值、脉冲重复频率、脉宽及上升沿对局部放电特性的影响。在统计谱图绘制过程中,每个电压脉冲内固定为2次放电(上升沿和下降沿处各1次),只考虑放电电流峰值大小及出现的延时。其中,延时为相对电压脉冲上升沿信号触发的电流峰值出现时间。相对幅值是放电电流幅值除以采集的多个脉冲周期内最大放电电流幅值。
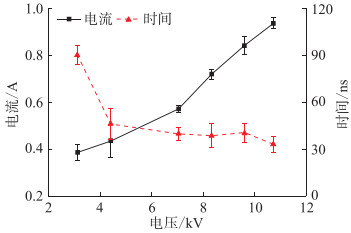
3.1 电压幅值对聚酰亚胺薄膜局放特性的影响固定脉冲频率为3 kHz,脉宽为1 μs,上升沿和下降沿时间都为136 ns,采集聚酰亚胺薄膜在不同电压幅值下500个周期内的放电时延及放电电流幅值。以数百个周期内的放电电流幅值的平均值和放电时延平均值为数据点,对6组不同电压幅值下的上升沿放电幅值以及放电时延进行统计分析,得到局部放电统计特性与电压幅值的关系,即图 5。可见,随着薄膜两端电压幅值的增大,上升沿局部放电幅值由0.38 A逐渐增大至0.95 A。当电压幅值由3.12 kV上升至4.4 kV时,上升沿放电时延明显减小;当电压幅值继续升高时,上升沿时延变化不明显。
|
图 5 不同电压幅值下的放电幅值与放电时延 Fig. 5 Discharge amplitude and discharge delay at different voltage amplitudes |
固定电压幅值3 kV,脉宽为500 ns,上升沿和下降沿时间都为136 ns,采集聚酰亚胺薄膜在不同脉冲频率(1 kHz, 20 kHz, 100 kHz)下500个周期内的放电时延及放电电流幅值。
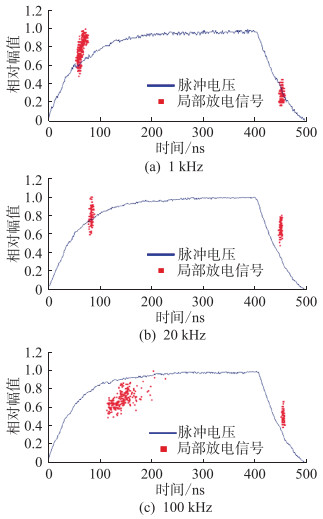
如图 6所示,上升沿处放电电流相对幅值主要分布在0.5~1.0范围内,受脉冲频率的影响较小,下降沿处放电电流幅值比上升沿处放电电流幅值相对更小。频率1 kHz下上升沿处放电电流峰值出现的时间位置主要集中在50~70 ns;20 kHz频率下上升沿处放电电流峰值出现的时间位置主要集中在75~100 ns;100 kHz下上升沿处放电电流峰值出现的时间位置主要集中在110~200 ns。因此,随着脉冲频率的增大,上升沿处局部放电引起的放电电流幅值分布更加分散,放电时延增大。
|
图 6 不同电压频率下局部放电散点图 Fig. 6 Scatter plots of partial discharges at different voltage frequency |
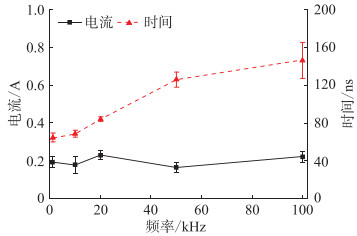
以数百个周期内的放电电流幅值的平均值和放电时延平均值为数据点,对5组不同脉冲频率下的上升沿放电幅值及放电时延进行统计分析,得到局部放电统计特性与电压幅值的关系曲线,即图 7。随着脉冲频率的增大,上升沿的放电时延由60 ns逐渐增大至140 ns,放电时延明显增大;脉冲频率对放电幅值影响微弱,局部放电电流幅值基本稳定在0.2 A。
|
图 7 不同电压频率下的放电幅值与放电时延 Fig. 7 Discharge amplitude and discharge delay at different voltage frequency |
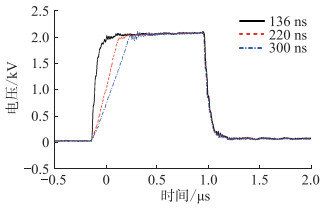
为了研究脉冲上升沿变化对局部放电特性的影响,将电压幅值、下降沿及频率等参数保持不变,结果见图 8。由图 8可知,脉冲电压上升沿时间从136 ns增长至300 ns,其余参数保持不变。
|
图 8 脉冲电源在不同上升沿下的空载输出 Fig. 8 No-load output of pulse power under different rising edges |
固定脉冲电压3 kV,脉冲频率3 kHz,脉宽为1 μs,下降沿时间为50 ns。由于电极装置为容性负载,电极两端的电压上升时间受电容影响,与电源空载输出的脉冲上升沿不一致。文中分析讨论的数据为电极两端实际承受的脉冲电压上升沿。在不同上升沿时间(230 ns, 330 ns, 400 ns)下,采集聚酰亚胺薄膜在500个周期内的放电时延及放电电流幅值,结果见图 9。
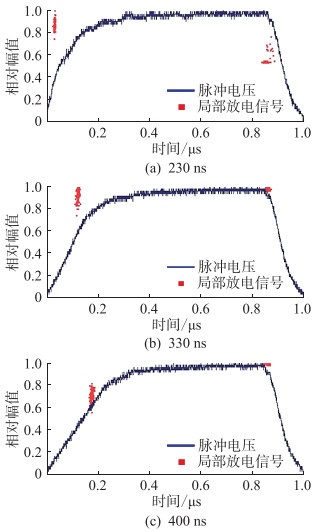
|
图 9 不同上升沿时间下局部放电散点图 Fig. 9 Scatter plots of partial discharges at different rising edge time |
如图所示,放电电流相对幅值基本分布在0.8~1.0范围内,受上升沿时间影响较小。当上升沿时间为230 ns时,上升沿处放电电流峰值出现的时间位置主要集中在放电时延为25~50 ns;当上升沿时间为330 ns时,上升沿处放电电流峰值出现的时间位置主要集中在放电时延为100~130 ns;当上升沿时间为400 ns时,上升沿处放电电流峰值出现的时间位置主要集中在放电时延为140~190 ns。因此,随着上升沿时间增大,放电时延明显增大,放电次数分布更分散。
以数百个周期内的放电电流幅值的平均值和放电时延平均值为数据点,对8组不同上升沿时间下的上升沿放电幅值以及放电时延进行统计分析,得到局部放电统计特性与电压幅值的关系曲线,即图 10。可见,随着上升沿时间的增大,放电电流由0.44 A逐渐降低到0.09 A,平均放电时延由0.04 μs逐渐升高到0.34 μs。因此,随着上升沿的增大,放电幅值逐渐减小且分布越来越紧密,放电时延逐渐增大且分布越来越分散。
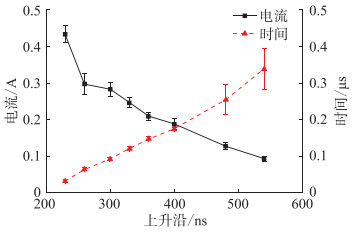
|
图 10 不同上升沿下的放电幅值与放电时延 Fig. 10 Discharge amplitude and discharge delay under different rise time |
文中对比研究脉宽为500 ns和1 μs的局部放电特性,并分析不同脉宽下频率对局部放电特性的影响。固定脉冲电压幅值3 kV,上升沿和下降沿时间为136 ns,在不同电压频率(1 kHz, 10 kHz, 20 kHz, 50 kHz, 100 kHz)下,采集聚酰亚胺薄膜在500个周期内的放电数据,共10组数据。选取500 ns及1 μs脉宽下局部放电量的平均值及标准差作为数据点进行统计分析并绘制曲线,如图 11所示。
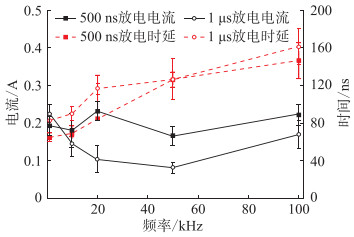
|
图 11 不同脉宽下的放电幅值与放电时延 Fig. 11 Discharge amplitude and discharge delay under different pulse widths |
脉冲频率为20 kHz时,脉宽500 ns下的放电电流幅值约0.23 A,放电时延为84 ns,脉宽1 μs下的放电电流幅值约0.14 A,放电时延为89.5 ns;脉冲频率为50 kHz时,脉宽500 ns下的放电电流幅值约0.17 A,放电时延为125 ns,脉宽1 μs下的放电电流幅值约0.08 A,放电时延为126 ns;当脉冲频率为100 kHz时,脉宽500 ns下的放电电流幅值约0.22 A,放电时延为146 ns,脉宽1 μs下的放电电流幅值约0.17 A,放电时延为160.9 ns。因此,在不同脉冲频率下,脉宽500 ns下的放电时延比1 μs下的放电时延快约20 ns;当脉冲频率在10~100 kHz时,脉宽越大,局部放电幅值越小,局部放电时延越大。
4 局放特性影响因素分析文中研究了电压幅值、脉冲重复频率、上升沿时间和占空比对聚酰亚胺薄膜局部放电特性的影响规律。发现放电时延随着脉冲频率增加而增大,与文献[6-7]相似。然而,研究发现局部放电信号幅值随着脉冲频率的增大而保持基本不变,与文献[6-7]结果显著不同。这可能与研究的频率范围和电极结构不同有关。文中将脉冲重复频率拓展至100 kHz,远大于文献[6-7]研究的频率范围。另外,文中采用了球板电极,而不是双绞线结构。这两者都会导致空间电荷运动和热量扩散不同,使得局部放电信号幅值存在一些差异。
研究发现随着上升沿增大,放电幅值逐渐减小且放电时延逐渐增大,与文献[8]研究结果相似。此外,关于占空比对局部放电特性影响,研究发现:在脉冲重复频率为10~100 kHz范围内,上升沿处局部放电信号幅值随脉宽增大而减小,与文献[13]的研究结果相似;然而,上升沿处局部放电时延随着脉宽增大而增大,与文献[11-12]在50 Hz下的研究结果相反。因此,下文从局部放电机理分析脉冲重复频率、上升沿时间及脉宽的影响。
4.1 脉冲重复频率对局放特性的影响通常来讲,脉冲频率升高导致局部放电处的温度升高,致使击穿电压更低,局部放电更容易发生。然而,由于文中脉宽短至500 ns,局部放电发生次数少,总体温度并未大幅上升。采用红外测温仪发现脉冲重复频率为100 kHz时局部放电位置处薄膜温度稍微高于环境温度。因此,频率导致的温升效应不显著。此外,当脉冲重复频率增大时,2次放电的时间间隔缩短,电荷复合过程时间减少,导致更多的空间电荷残留下来[16-17],容易阻碍电子崩的发展和初始电子的产生,使得表面可脱陷的电子减少,放电延迟时间增大。
4.2 上升沿时间对局放特性的影响当脉冲电压上升沿时间减小时,意味着电压变化速度较快,绝缘材料承受的电压能够迅速超过起始放电电压,但是由于并未产生激发电子崩的初始电子,在等待初始电子产生的时间中过电压增大。在过电压作用下,空间电场增强,电子崩发展过程的延时会显著缩短,导致放电时延减小和局部放电信号幅值增大,与文献[9-10]结果类似。
4.3 脉宽对局放特性的影响图 12为稍不均匀场下的电荷分布。当脉宽增大时,会同时加速空间正负离子复合、薄膜表面电荷积累、电荷自身径向极型扩散这3个过程,而这3个过程互相之间是呈竞争关系。其中,电荷扩散速度为毫秒至秒量级,而空间正负离子的复合为微秒至毫秒量级。当脉宽增大时,增加了电荷扩散的可能性,相对而言电荷复合的影响会减弱,因此在下次放电时薄膜表面积累的正电荷数量会增多,削弱了空间电场,使得脉宽增大时放电幅值减小。同时,空间电场减小后,放电时延更大。
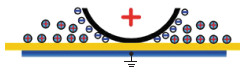
|
图 12 稍不均匀场下的电荷分布 Fig. 12 Charge distribution in a slightly uneven field |
为探索脉冲电应力作用下高压IGBT器件绝缘材料的局部放电特性,建立适用于高频高压脉冲作用下局部放电测量的平台,文中研究了脉冲电压幅值、上升沿、脉宽及频率对聚酰亚胺薄膜局部放电特性的影响,获得如下结论:(1) 随着电压幅值增大,上升沿处局部放电信号幅值增大,放电时延减小,下降沿处放电时延基本不变;(2) 随着脉冲重复频率增大,上升沿处放电时延增大,局部放电引起的放电电流幅值分布更加分散;(3) 随着上升沿时间增大,放电时延增大且更加分散,局部放电信号幅值减小且更加紧密;(4) 相比于脉宽为1 μs的情况,脉宽为500 ns时局部放电信号幅值更大,放电时延更小。上述研究不仅可为高压大功率IGBT器件的局部放电检测和绝缘老化状态评估提供重要科学依据,而且有利于指导更高频、开断速度更快的新型半导体开关器件的绝缘优化设计,对新一代柔性直流输电工程的换流阀绝缘设计与状态检测具有参考意义。
本文得到中央高校基本科研业务费(NT2020007),台达电力电子科教发展计划青年项目(DREG2017008)资助,谨此致谢!
| [1] |
汪涛, 李汉杰, 张茂强, 等. 柔性直流输电换流器子模块程序远程升级研究与应用[J]. 电力工程技术, 2018, 37(6): 103-108, 114. WANG Tao, LI Hanjie, ZHANG Maoqiang, et al. Research and application of program remote upgrade for sub-modules in VSC-HVDC converter[J]. Electric Power Engineering Technology, 2018, 37(6): 103-108, 114. (  0) 0) |
| [2] |
殷冠贤, 朱铭炼, 谢晔源, 等. MMC阀子模块IGBT损耗与结温计算[J]. 电力工程技术, 2018, 37(3): 129-133, 150. YIN Guanxian, ZHU Minglian, XIE Yeyuan, et al. A calculating method for loss and junction temperature of IGBT based on MMC[J]. Electric Power Engineering Technology, 2018, 37(3): 129-133, 150. (  0) 0) |
| [3] |
欧阳有鹏, 谢晔源, 朱铭炼, 等. 换流阀子模块IGBT短路测试系统分析与设计[J]. 电力工程技术, 2018, 37(4): 109-113. OUYANG Youpeng, XIE Yeyuan, ZHU Minglian, et al. Analysis and design of IGBT short circuit test system for sub modular of converter valve[J]. Electric Power Engineering Technology, 2018, 37(4): 109-113. (  0) 0) |
| [4] |
唐新灵, 张朋, 陈中圆, 等. 高压大功率压接型IGBT器件封装技术研究综述[J]. 中国电机工程学报, 2019, 39(12): 3622-3638. TANG Xinling, ZHANG Peng, CHEN Zhongyuan, et al. Review of high voltage high power press pack IGBT package technology[J]. Proceedings of the CSEE, 2019, 39(12): 3622-3638. (  0) 0) |
| [5] |
周凯, 吴广宁, 雷克刚, 等. 脉冲电压下局部放电对聚酰亚胺膜寿命的影响[J]. 材料科学与工程学报, 2008, 26(3): 361-364, 384. ZHOU Kai, WU Guangning, LEI Kegang, et al. Effects of partial discharge under square pulse voltage on lifetime of polyimide film[J]. Journal of Materials Science and Engineering, 2008, 26(3): 361-364, 384. (  0) 0) |
| [6] |
张作钦, 孙传铭. 方波脉冲电压频率对变频牵引电机绞线对绝缘特性的影响[J]. 电气开关, 2014, 52(4): 78-80, 83. ZHANG Zuoqin, SUN Chuanming. Effect of square impulse voltage frequency on insulating characteristics of inverter-fed traction motor twisted pair[J]. Electric Switchgear, 2014, 52(4): 78-80, 83. (  0) 0) |
| [7] |
杨能, 王鹏, 赵政嘉, 等. 重复短脉冲及方波电压频率对变频电机绝缘局部放电统计特性影响[J]. 绝缘材料, 2018, 51(11): 56-63. YANG Neng, WANG Peng, ZHAO Zhengjia, et al. Effect of repetitive short impulse and square wave voltage frequency on partial discharge statistical properties of inverter-fed motor insulation[J]. Insulating Materials, 2018, 51(11): 56-63. (  0) 0) |
| [8] |
郑昌江, 雷勇, 王鹏, 等. 重复短脉冲上升时间对变频电机绝缘局部放电统计特性的影响[J]. 绝缘材料, 2018, 51(10): 50-56. ZHENG Changjiang, LEI Yong, WANG Peng, et al. Influence of repetitive short impulsive voltage rise time on partial discharge statistical properties of inverter-fed motor insulation[J]. Insulating Materials, 2018, 51(10): 50-56. (  0) 0) |
| [9] |
王剑, 周凯, 王鹏, 等. 重复脉冲电压上升时间对变频电机绝缘局部放电起始电压影响研究[J]. 绝缘材料, 2018, 51(8): 37-42. WANG Jian, ZHOU Kai, WANG Peng, et al. Influence of repetitive impulse voltage rise time on partial discharge inception voltage of inverter-fed motors insulation[J]. Insulating Materials, 2018, 51(8): 37-42. (  0) 0) |
| [10] |
王剑, 王燕, 赵世林, 等. 重复脉冲上升时间对变频电机绝缘局部放电特征的影响[J]. 绝缘材料, 2015, 48(1): 53-58. WANG Jian, WANG Yan, ZHAO Shilin, et al. Effect of repetitive impulse voltage rise time on partial discharge characteristics of inverter-fed motor insulation[J]. Insulating Materials, 2015, 48(1): 53-58. (  0) 0) |
| [11] |
徐洪英, 赵莉华, 王鹏, 等. 重复脉冲占空比对变频电机绝缘局部放电统计特性的影响[J]. 中国电机工程学报, 2017, 37(7): 2159-2167. XU Hongying, ZHAO Lihua, WANG Peng, et al. Influence of repetitive impulse wave voltage duty cycle on partial discharge statistics in inverter-fedmotor insulation[J]. Proceedings of the CSEE, 2017, 37(7): 2159-2167. (  0) 0) |
| [12] |
WANG P, XU H Y, WANG J, et al. Effect of repetitive impulsive voltage duty cycle on partial discharge features and insulation endurance of enameled wires for inverter-fed low voltage machines[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(4): 2123-2131. (  0) 0) |
| [13] |
王鹏, 陈波, 徐洪英, 等. 重复脉冲占空比对变频电机匝间绝缘耐电晕寿命影响研究[J]. 绝缘材料, 2020, 53(1): 64-69. WANG Peng, CHEN Bo, XU Hongying, et al. Effect of duty cycle of repetitive impulsive voltage on corona-resistant lifetime of turn-to-turn insulation for inverter-fed motors[J]. Insulating Materials, 2020, 53(1): 64-69. (  0) 0) |
| [14] |
邱毓昌. 棒-板间隙电场不均匀系数的近似计算式[J]. 高压电器, 1985, 21(5): 38-40. QIU Yuchang. Approximate calculation formula of electric field unevenness coefficient in bar-plate clearance[J]. High Voltage Apparatus, 1985, 21(5): 38-40. (  0) 0) |
| [15] |
潘双来, 邢丽冬, 龚余才. 电路理论基础[M]. 北京: 清华大学出版社, 2007. PAN Shuanglai, XING Lidong, GONG Yucai. Fundamentals of circuit theory[M]. Beijing: Tsinghua University Press, 2007. (  0) 0) |
| [16] |
王鹏. 方波脉冲电压对局部放电特性及电机绝缘寿命影响机理研究[D]. 成都: 西南交通大学, 2013. WANG Peng. Influence and mechanism of square wave voltage on partial discharge and motor insulation life[D]. Chengdu: Southwest Jiaotong University, 2013. (  0) 0) |
| [17] |
吴琦, 王鹏, 郑昌江, 等. 重复方波脉冲和短脉冲电压下变频电机匝间绝缘耐电晕特性对比研究[J]. 绝缘材料, 2020, 53(3): 34-40. WU Qi, WANG Peng, ZHENG Changjiang, et al. Comparative study on corona resistance of turn to turn insulation in inverter-fed motor under repetitive square wave and short pulse voltage[J]. Insulating Materials, 2020, 53(3): 34-40. (  0) 0) |
 2021, Vol. 40
2021, Vol. 40


 刘畅(1997), 女, 硕士在读, 研究方向为局部放电检测(E-mail:
刘畅(1997), 女, 硕士在读, 研究方向为局部放电检测(E-mail: