文章编号: 2096-3203(2021)04-0010-08 中图分类号: TM46
模块化多电平换流器(modular multilevel converter, MMC)凭借输出波形质量高、开关损耗低、扩容维修灵活方便等优点[1-5],广泛应用于风力发电系统中。绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)模块是MMC的核心部件,其成本约占设备投入总成本的20%~30%[6]。因此,合理设计IGBT模块能够降低换流器设备的一次投入,同时可以改善系统的效率、温升等性能,降低系统运行成本,提高工程的经济效益。
传统的工程设计方法中一般会根据最严峻工况下IGBT和二极管所承受的电流、电压应力选择功率器件,以保证结温不超过所允许的最大值。这种方法往往要求反复尝试不同型号的半导体器件,更多的是依靠设计人员的经验,缺乏系统的设计准则,且一般情况下留有较大的裕量,存在明显浪费模块容量的现象。文献[7]基于上述选型原则,针对多端直流输电系统,直流电网这类场合进行分析,此时,IGBT模块的各个功率器件在最恶劣工况下承受的电流应力大致相同,因此选择上、下桥臂对称相等的IGBT半桥模块。但在一些特殊应用中,例如新能源发电汇集并网或者是向无源海岛供电等场合中,IGBT模块内不同开关管的电流有效值差距很大,若继续沿用文献[7]的方法进行设计,采用芯片面积对称的IGBT模块,会造成模块芯片成本方面的浪费,因此可以结合各场合的特点优选IGBT模块。
在电力电子系统中,为使IGBT模块处于合适的工作状态,一方面可优化变流器运行时的开关频率、调制方式、负载电流等电气参数来降低IGBT模块的损耗与热应力[8-9];另一方面,可根据应用场合的特点去优选IGBT模块。如文献[10]根据效率与寿命为光伏逆变器优选功率器件的芯片面积;文献[11]基于直接搜索法,从效率、可靠性及成本的角度为电动汽车变流器优选IGBT及开关频率;文献[12]对比Si与SiC功率器件,为双有源桥拓扑提供了一种效率高、成本低、功率密度高的设计方案。
基于此,文中针对风电MMC中IGBT模块电流应力不均衡的特性,结合多目标优化的思想,在兼顾变流器可靠性的前提下,定制化设计IGBT模块,通过提高器件利用率、减小裕量来实现IGBT成本和损耗的综合最优。
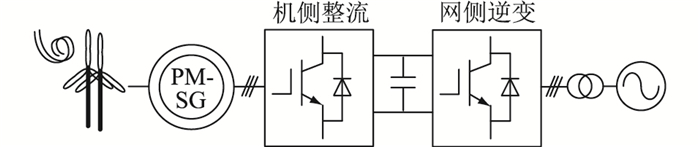
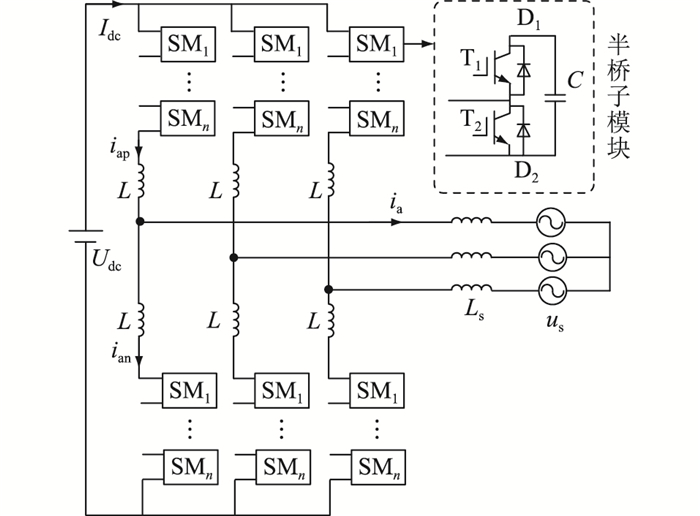
1 IGBT模块应力不均衡特性分析为说明定制化设计方案,文中以某海上风力发电MMC直流输电系统为例进行分析。图 1为典型的风力发电系统,机侧和网侧的变流器均采用如图 2所示的MMC拓扑。MMC的6个桥臂均由n个子模块与桥臂电抗器串联而成。半桥子模块由2个IGBT(T1与T2),2个二极管(D1与D2)以及子模块电容C组成。虽然机侧与网侧的换流器在控制与运行上有一定差异,但二者仍可以采用类似的分析方法,限于文章篇幅,将聚焦于网侧的逆变器进行分析,其具体参数见表 1。
|
图 1 风力发电直流输电系统 Fig. 1 HVDC system for wind power generation |
|
图 2 MMC拓扑 Fig. 2 The structure of a three phase MMC |
|
|
表 1 网侧变流器具体参数 Table 1 Parameters for the grid side converter |
理想情况下,各桥臂的情况相似,为简化分析,文中以a相上桥臂电流iap为例进行分析。由文献[13]可知,iap可用式(1)表示。不难发现,桥臂电流随着换流器运行时的容量和功率因数角变化而变化。不同于直流电网这类柔性直流输电场合,在风力发电应用中,功率器件的最大电流应力将出现在满容量传输有功功率和满容量传输无功功率这2种极端工况中[7, 14]。根据表 1的参数,计算出这2种极端工况下IGBT模块的电流有效值,见表 2。结果显示IGBT模块存在应力不均衡的特性。
| $ i_{\mathrm{ap}}=\frac{1}{2} \frac{U_{\mathrm{ac}}}{U_{\mathrm{dc}}} I_{\mathrm{ac}} \cos \varphi+\frac{1}{2} I_{\mathrm{ac}} \sin (\omega t-\varphi) $ | (1) |
|
|
表 2 IGBT模块电流有效值 Table 2 The RMS current of the IGBT module |
式中:Udc为直流电压;Uac,Iac分别为相电压、相电流的幅值;ω为角频率;φ为功率因数角。
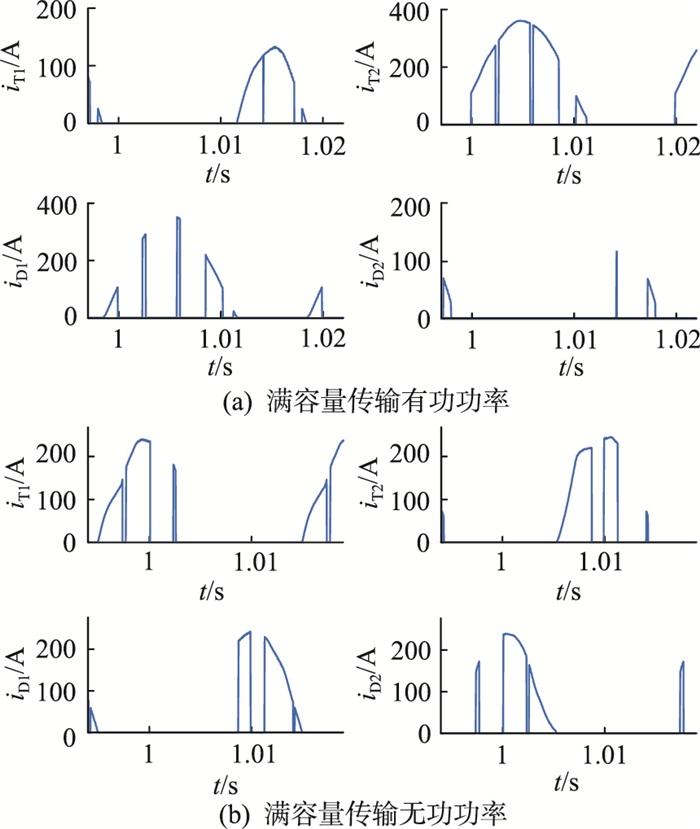
观察式(1)可发现,在满容量传输无功功率的工况下,桥臂电流的直流分量为零,因此各开关管电流处于均衡状态。而随着φ的减小,桥臂电流的直流分量逐渐增大,流过各开关管的电流差异变大,直到功率因数角为零,即满容量传输有功功率时,这种电流不均衡现象最为明显。该应力不均衡现象本质上是因为MMC桥臂电流存在直流分量。图 3(a)和(b)分别为满容量传输有功功率和满容量传输无功功率的工况仿真中IGBT模块的电流波形。仿真中采用表 1的参数,采用载波移相脉宽调制方式。从仿真波形能直观地看出,在最恶劣的工况下,IGBT模块的电流应力是不对称的。
|
图 3 MMC仿真电流波形 Fig. 3 Simulation current waveforms of MMC |
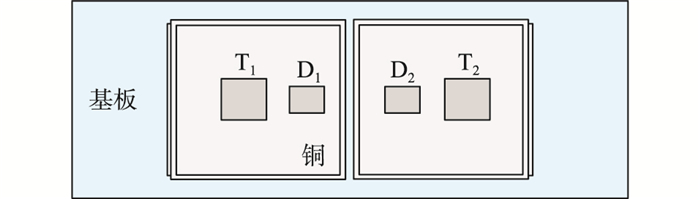
在风电场合中,目前基本都是选择如图 4所示的上、下桥臂芯片面积对称相等的IGBT模块。但根据上述分析,模块内流过不同芯片的最大电流应力并不相同,若继续沿用该设计方法,将会造成部分器件,如T1芯片面积方面的浪费,因此有必要对IGBT模块进行定制化设计。
|
图 4 某IGBT模块内部结构布局 Fig. 4 The layout of an IGBT module |
由于MMC各个子模块具有相似的特性,为简化分析,以单个子模块中的IGBT模块为例,对IGBT模块的芯片面积进行定制化设计,使IGBT模块的成本和损耗达到综合最优。其中,定制化方案包括模块定制化和分立元件定制化。
2.1 设计变量IGBT模块的主要设计参数包括芯片面积、布局及封装等。布局、封装及工艺等会影响寄生参数、可靠性及成本等参数。可近似认为,采用相同封装不同芯片面积的模块在寄生参数等方面具有相似的表现。而芯片面积主要改变了通流能力以及功率处理能力,也与损耗结温等直接相关,是文中的主要设计参数。
定义设计变量x见式(2),即为图 4所示的各开关管芯片面积,包括IGBT模块上、下管的IGBT芯片面积AT1,AT2,上、下管的二极管芯片面积AD1,AD2。在后续设计中,对4个芯片进行独立优化。
| $ x=\left(A_{\mathrm{T} 1}, A_{\mathrm{D} 1}, A_{\mathrm{T} 2}, A_{\mathrm{D} 2}\right) $ | (2) |
IGBT的设计直接影响着系统的成本以及损耗等性能指标,文中将芯片成本和年平均损耗率这2个指标作为定制化设计的目标函数。
IGBT模块的成本包括芯片和封装,其中硅芯片约占IGBT模块成本的82%[15],占比很高。因此,为简化分析,仅考虑相同封装技术下IGBT模块的芯片成本σ,即图 4所示IGBT模块中所有芯片的成本。损耗是换流器的关键指标,不仅关系到系统长期运行的成本,还关系到散热的设计和器件寿命等。对于风电换流器而言,单一工况的损耗并不能准确反映设计的优劣,因此采用年平均损耗率作为设计的另一性能指标。
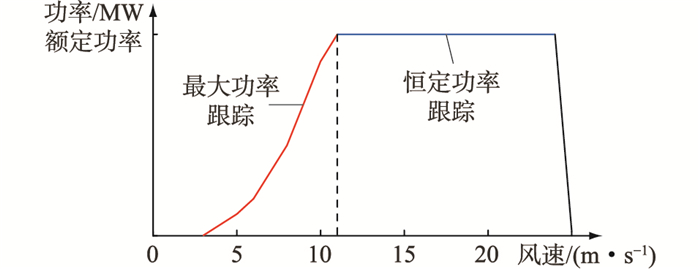
为高效利用风能,系统采用最大功率跟踪策略[16],其风电系统功率特性曲线如图 5所示,文中的切入风速、额定风速和切除风速分别为3 m/s,11 m/s,25 m/s。
|
图 5 风电系统功率特性曲线 Fig. 5 Output curve of a wind power system |
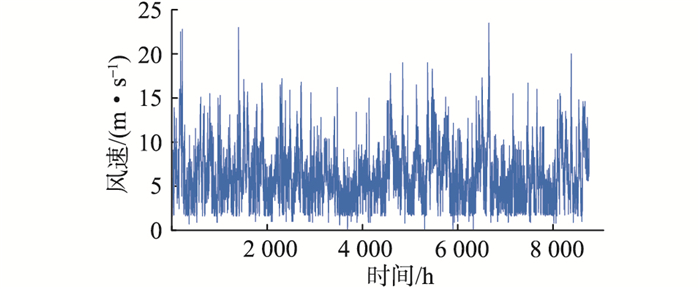
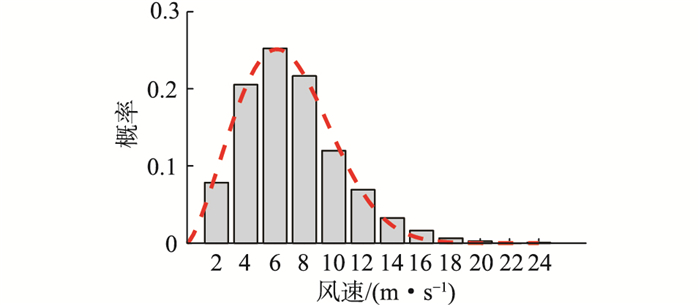
图 6为浙江某风电场全年风速曲线,由于风速经常随机波动,可根据全年风速数据评估风电场的风速概率分布,具体如图 7所示。
|
图 6 浙江某风电场全年风速曲线 Fig. 6 Annual wind speed curve of a wind farm |
|
图 7 某风电场风速概率分布 Fig. 7 Probability distributions of wind speed in a wind farm |
按2 m/s的间隔,可将风速划分成12个区间,即1~3 m/s,3~5 m/s, …, 23~25 m/s。用每个区间的平均风速表示这个区间的风能大小,如用2 m/s的风速表示1~3 m/s这个区间的风能大小。为简化分析,文中以某风速区间的平均风速评估此区间内IGBT模块的损耗以及换流器传输功率的大小。假设MMC的各子模块损耗相同,定义MMC的年平均损耗率ε为所有IGBT模块一年的总损耗与换流器一年传输总功率的比值,即:
| $ \varepsilon=6 n \frac{\sum\limits_{i=1}^{12} h_{i} S P_{\mathrm{L}, 2 i}}{\sum\limits_{i=1}^{12} h_{i} S P_{2 i}} \times 100 \% $ | (3) |
式中:hi为一年内风速处于(2i-1)~(2i+1) m/s区间的概率;n为桥臂的子模块数;S为一年的总小时数;P2i为平均风速为2i m/s时变流器传输的功率大小;PL, 2i为平均风速为2i m/s时单个IGBT模块的损耗。
根据上述分析,对IGBT模块进行定制化设计的目标函数可表示为成本函数和损耗函数的综合最优,即:
| $ \left\{\begin{array}{l} \min \sigma(x) \\ \min \varepsilon(x) \end{array}\right. $ | (4) |
为确保IGBT模块的长期可靠运行,要确保模块因损耗引起的发热保持在允许的范围内。因此,在最恶劣的情况下,IGBT模块的最高结温不能高于结温限制Tjmax,可表示为:
| $ \max T_{\mathrm{j}} \leqslant T_{\mathrm{jmax}} $ | (5) |
式中:Tj为结温。综上所述,IGBT模块的定制化设计目标是在满足约束条件下,使成本与损耗达到综合最优。
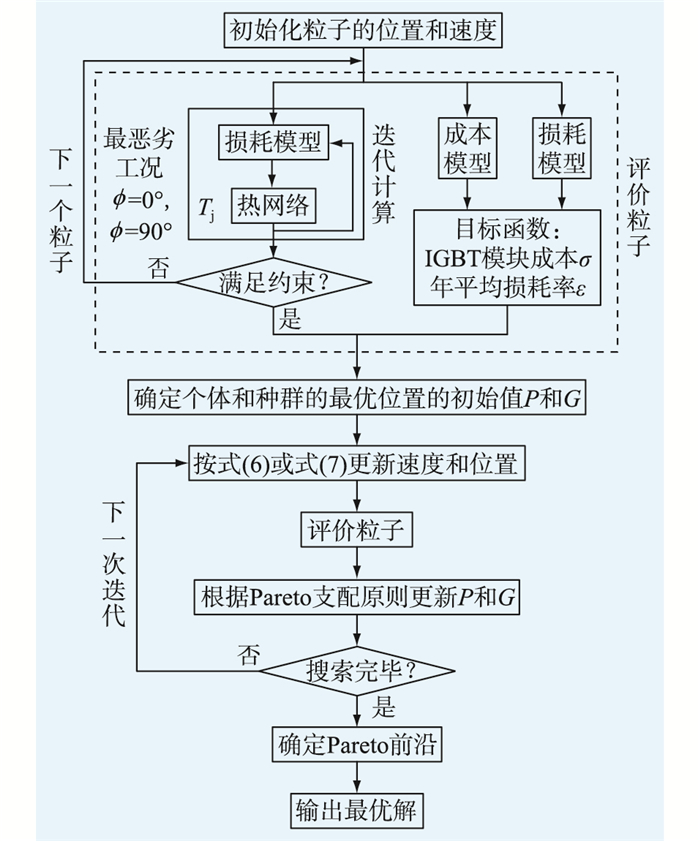
2.3 基于粒子群的优化流程在换流器的多目标优化问题中,粒子群算法具有简单、搜索高效等优点[9],文中采用该方法来寻找最优解。具体设计流程如图 8所示。在每次迭代中,粒子先根据自身的最优值P以及种群的最优值G来调整自己的速度v和位置g,如式(6)和式(7)所示;然后根据成本、损耗去评价粒子所处位置的优劣,并按Pareto支配原则选出非劣解[17];最后不断迭代搜索,直到满足终止条件。
|
图 8 粒子群算法流程 Fig. 8 The flow chart of particle swarm optimization |
| $ \begin{gathered} v_{N, t+1}=w v_{N, t}+c_{1} R_{1}\left(P_{N, t}-g_{N, t}\right)+ \\ c_{2} R_{2}\left(G_{N, t}-g_{N, t}\right) \end{gathered} $ | (6) |
| $ g_{N, t+1}=g_{N, t}+v_{N, t+1} $ | (7) |
式中:vN, t为粒子N在第t次迭代时的速度;PN, t为粒子N在第t次迭代时的自身最优值;GN, t为粒子N在第t次迭代时种群的最优值;gN, t粒子N在第t次迭代时的位置;w为惯性权重;c1,c2为学习因子;R1,R2均为[0, 1]的随机数。
3 功率模块的损耗和成本模型定制化设计中,要先建立芯片面积与MMC的损耗、温度及成本等指标的联系。此过程中,不同芯片面积的IGBT模块采用相同的布局、封装及工艺,即寄生电感等可近似认为不变。本节是基于英飞凌34 mm封装的IGBT模块而进行的分析。
3.1 损耗模型文献[11]引入了芯片单位面积的电流、导通压降和开关损耗的概念,通过数据拟合的方法建立关系,采用该方法来研究配置不同面积芯片时,IGBT模块中各个开关管的损耗特性。以T1为例进行研究,由于其他开关管的计算过程类似,故文中不再赘述。
IGBT模块损耗包括IGBT和二极管的导通损耗和开关损耗,由于MMC的开关频率一般很低,开关损耗基本可以忽略[18],则T1的损耗PT1可表示为:
| $ P_{\mathrm{T} 1} \approx A_{\mathrm{T} 1} f \int_{0}^{1 / f} d_{\mathrm{T1}} v_{\mathrm{on}, \mathrm{T} 1}\left(i_{\text {chip }, \mathrm{T} 1}, T_{\mathrm{j}, \mathrm{T} 1}\right) i_{\text {chip }, \mathrm{T1}} \mathrm{d} t $ | (8) |
式中:AT1为T1的芯片面积;f为基波频率;dT1为占空比;von, T1(ichip, T1, Tj, T1)为在结温Tj, T1时T1芯片单位面积的导通损耗;ichip, T1=iT1/AT1,为芯片电流密度;iT1为流过芯片的电流;。
芯片结温Tj, T1是影响损耗的重要因素,而结温与模块热阻有关。对于带基板的IGBT模块,器件的平均结温可表示为[11]:
| $ T_{\mathrm{j}, \mathrm{T} 1}=T_{\mathrm{h}}+P_{\mathrm{T} 1} R_{\mathrm{jc}}+\left(P_{\mathrm{T} 1}+P_{\mathrm{D} 1}\right) R_{\mathrm{ch}} $ | (9) |
式中:Rjc,Rch分别为IGBT结至壳,壳至散热器的热阻;PD1为D1的损耗;Th为散热器温度。文中采用水冷散热器,假设其温度维持在50 ℃。
制造商一般会给出四阶Foster网络参数,可通过曲线拟合的方法来提取同一封装的模块中T1的各阶热阻与芯片面积之间的关系,如式(10)所示。
| $ R_{\mathrm{jc}, k}=\frac{\beta_{k}}{A_{\mathrm{T} 1}} $ | (10) |
式中:βk为第k阶热阻与芯片面积间的拟合参数。
FFxxR12RT4系列模块T1的各阶热阻与面积参数如图 9所示,可见采用相同封装的模块中T1各阶热阻与芯片面积基本满足图中曲线关系,该曲线即为式(10)所示的反比例关系。图 9中各阶曲线的拟合参数β1,β2,β3,β4分别为1.59,8.74,8.48,7.68。可以采用同样的方法去提取二极管的热阻参数。
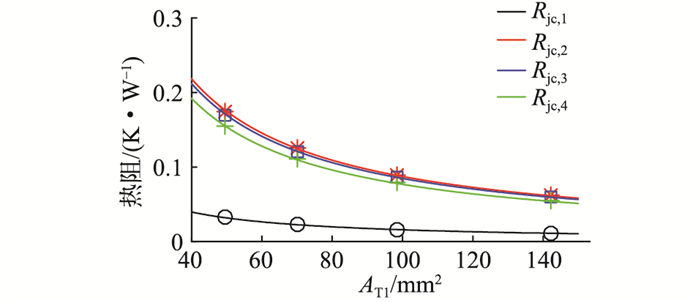
|
图 9 IGBT热阻与芯片面积的关系 Fig. 9 The relationship between IGBT thermal resistance and chip area |
IGBT模块的芯片成本σ可表示为:
| $ \sigma=\sum\limits_{s=\mathrm{T} 1, \mathrm{T} 2}\left(\lambda_{\mathrm{T}} A_{s}+p_{\mathrm{T}}\right)+\sum\limits_{s=\mathrm{D1}, \mathrm{D} 2}\left(\lambda_{\mathrm{D}} A_{s}+p_{\mathrm{D}}\right) $ | (11) |
式中:λT,pT为IGBT芯片成本的系数;λD,pD为二极管芯片成本的系数。可通过对同一系列的IGBT或二极管的芯片面积和售价进行线性拟合得出这些系数,拟合曲线见图 10。其中拟合系数λT,pT分别为1.16,11.2,λD,pD分别为1.07,4.32。另外,芯片售价受供应商、采购量以及运费等影响,文中芯片售价均来自德捷电子公司。
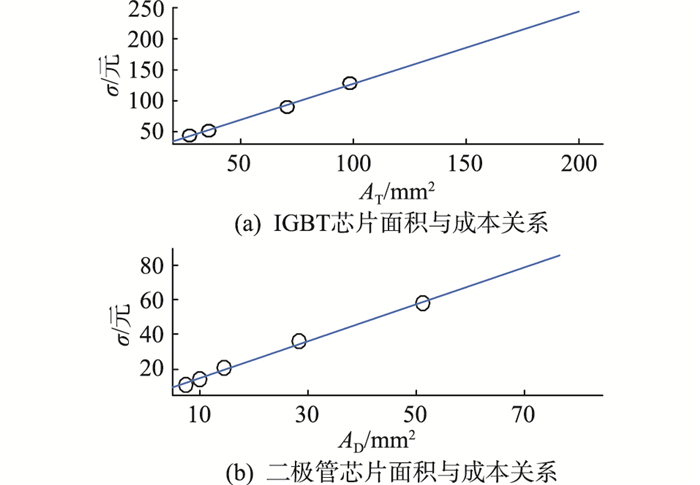
|
图 10 IGBT模块芯片价格 Fig. 10 Prices of chips in IGBT modules |
使用Matlab分别对IGBT模块以及分立元件这2种方案进行定制化设计。
4.1 模块定制化设计结果根据图 8的流程,获得如图 11所示的Pareto前沿。前沿上的解都是多目标优化中的综合最优解,并无优劣之分。以3个最优解为例进行说明,方案具体参数见表 3。A是最便宜的方案,但其损耗是最大的。随着芯片面积的增大,损耗减小而成本逐渐提高,C是最昂贵的方案,而损耗是最小的。不难发现,在前沿上选择方案时,实质是在性能指标之间进行折中选择,在改善成本指标时,就必然会使年平均损耗率指标变差,反之亦然。在最终决策的时候,先按重要性对目标函数进行排序,例如损耗的重要性高于成本。假设设计时的硬性要求为IGBT模块芯片的投入不得超过400元,则可以在芯片成本小于400元的前沿上选择损耗最低的最优解,即方案B。方案的具体指标见图 12。
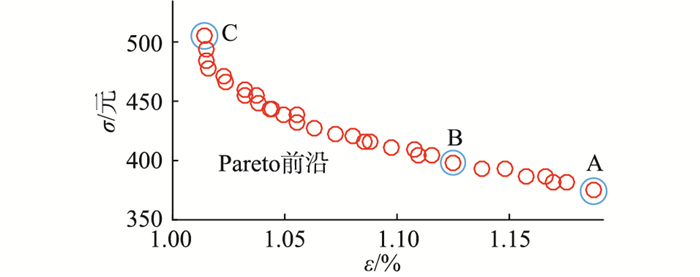
|
图 11 模块定制化设计的Pareto前沿 Fig. 11 Pareto front of the design for IGBT module |
|
|
表 3 模块定制化设计的Pareto最优解参数 Table 3 Pareto parametric optimal solutions for the design of IGBT module |
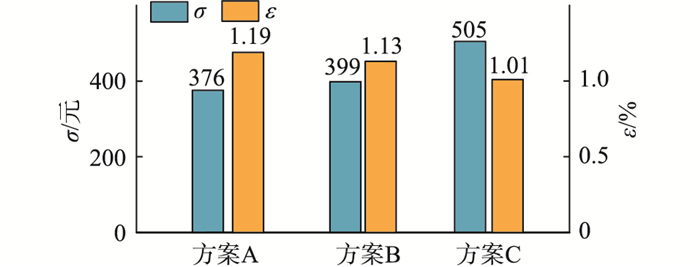
|
图 12 模块定制化设计的最优解指标 Fig. 12 Performance of optimal solutions of the design for IGBT module |
从可靠性与便利性等方面考虑,大功率场合一般会选择IGBT模块作为开关器件。然而,采用分立元件,如TO247封装的开关器件,设计方案成本优势明显,且可以灵活地串并联,因此,有必要分析基于分立元件的功率器件定制化设计。
分立元件定制化方案中,子模块中的功率器件由多个单管并联组成。因此,分立元件定制化设计的设计变量是单管的芯片面积(AT1, AD1, AT2, AD2)以及分立元件的并联数量(NT1, ND1, NT2, ND2),芯片成本σ指单个子模块全部芯片的成本。其他设计思路和流程与模块定制化设计相似。设计流程中的损耗、成本模型等是基于英飞凌TO247封装的IGBT和TO220封装的二极管而进行分析设计的。由此可得图 13所示的Pareto前沿,前沿上的最优解D,E,F,G的具体参数见图 14和表 4。
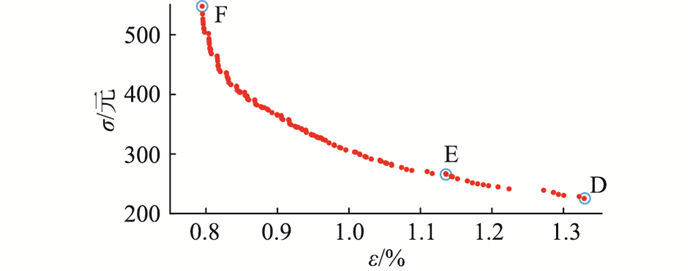
|
图 13 分立元件定制化设计的Pareto前沿 Fig. 13 Pareto front of the design for discrete IGBT |
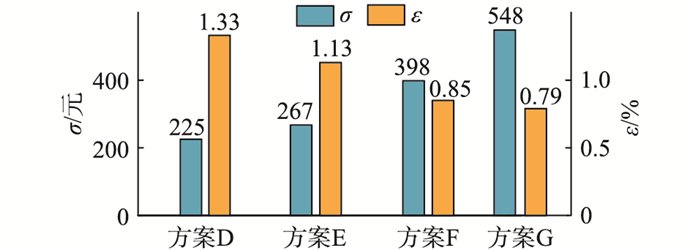
|
图 14 分立元件定制化设计的最优解指标 Fig. 14 Performance of optimal solutions of the design for discrete IGBT |
|
|
表 4 分立元件定制化设计的Pareto最优解参数 Table 4 Pareto parametric optimal solutions of the design for discrete IGBT |
对模块定制优化解、分立元件定制优化解以及传统设计方法的设计结果进行对比。
在实际设计中,有时难以选购到与模块定制化设计方案中芯片面积完全一样的芯片,因此为方案B中的4个器件选择市面上最接近的芯片面积,以此作为最终IGBT模块的定制优化解,并记作方案H。在方案H中,T1,T2,D1,D2分别选择型号为IGC70T120T8,IGC189T120T8,IDC40D120T8,IDC40D120T8,即方案H的x=(70, 40, 189, 40)与方案B的x=(70, 40, 190, 35)接近。若按传统的设计方法,IGBT模块的选择主要取决于电流应力最大的开关器件T2,选择与方案H中T2面积相近的IGBT模块FF200R12RT4, 即x=(189, 105, 189, 105)。
图 15为不同方案间性能指标的对比,其中成本和损耗的计算如前文所述。表 5为不同方案间参数的对比,表中E的芯片面积是指分立元件的芯片总面积。为验证3种方案的可靠性,计算了开关器件的寿命(LT1, LD1, LT2, LD2)。先根据年风速曲线以及MMC的模型提取开关器件的年结温曲线,例如方案H中T2的年结温曲线如图 16所示,然后通过雨流算法提取热循环的次数、幅值与均值等,最后借助IGBT的寿命模型预测开关器件的寿命,具体计算方式可以参考文献[13, 19-20]。IGBT模块寿命主要取决于寿命最短的开关管,因此方案H和模块FF200R12RT4中IGBT模块的寿命分别是23 a和24 a。即尽管减小了芯片面积,但模块定制优化解的可靠性指标基本维持不变,可见该方法是在保证可靠性的前提下,对IGBT模块进行的定制化设计,可实现芯片成本和年平均损耗率的综合最优。
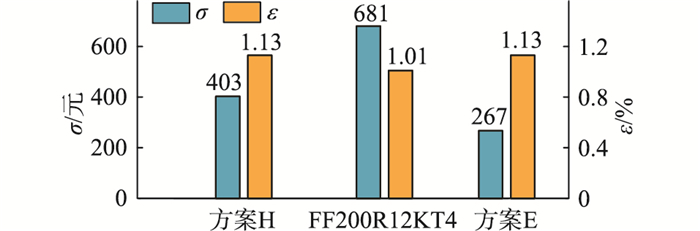
|
图 15 性能指标对比 Fig. 15 Comparisons of performance |
|
|
表 5 方案参数对比 Table 5 Comparisons of parameters |
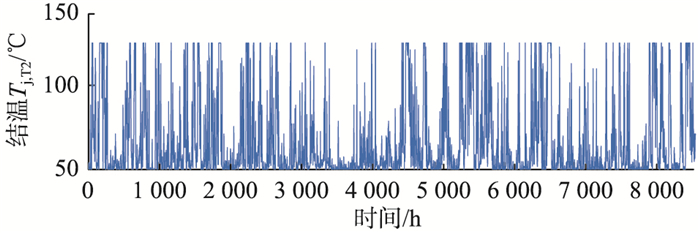
|
图 16 方案G中T2的年结温曲线 Fig. 16 Annual junction temperature curve of T2 in solution G |
对比方案H和模块FF200R12RT4,可以发现方案H的芯片成本大幅降低至403元,下降了约40%,而芯片面积减小,其损耗会略微增大,但仅增加了0.12%。
对比方案F和方案H,在成本接近的情况下,采用分立元件的定制化设计方案损耗率更低。对比方案H和方案E,在损耗率一样的情况下,采用分立元件的定制化设计方案成本优势更明显。方案E中部分开关器件的芯片面积更小,寿命反而比方案G略有增加,这是因为模块的芯片和分立元件的芯片型号不同,二者的导通压降、热阻等参数有一定区别。相比于传统的设计方案,这2种设计方案都具有明显的成本优势。
5 结论在风电MMC中,存在开关器件应力不均衡现象,采用标准的IGBT模块会存在芯片成本方面的浪费。针对该问题,提出一种IGBT定制化设计方法。首先定义了定制化设计中的优化目标,即实现成本和损耗的综合最优;然后结合实际工况评估年平均损耗,并且基于双目标粒子群寻优算法求得Pareto前沿。最后,将IGBT模块定制化设计方案、分立元件定制化设计方案以及传统设计方案进行对比。结果表明,在保证变流器性能及可靠性的前提下,该定制化设计方法能够降低IGBT成本,提高MMC工程的经济效益。且该方法不依赖于设计者的经验,便于比较不同方案之间的优劣,决策者只需在性能指标之间进行权衡选择,对MMC的IGBT模块的设计有一定的参考价值。
| [1] |
DEKKA A, WU B, FUENTES R L, et al. Evolution of topologies, modeling, control schemes, and applications of modular multilevel converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1631-1656. DOI:10.1109/JESTPE.2017.2742938 (  0) 0) |
| [2] |
徐政, 屠卿瑞, 管敏渊. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2013. XU Zheng, TU Qingrui, GUAN Minyuan. Flexible direct current transmission system[M]. Beijing: China Machine Press, 2013. (  0) 0) |
| [3] |
白雪, 高瑞雪, 闻福岳, 等. 特定次谐波注入抑制模块化多电平换流器电容电压波动[J]. 电网与清洁能源, 2020, 36(9): 8-14. BAI Xue, GAO Ruixue, WEN Fuyue, et al. Suppression of Capacitor Voltage Fluctuation of the Modular Multilevel Converter by Specific Sub-Harmonic Injection[J]. Power System and Clean Energy, 2020, 36(9): 8-14. DOI:10.3969/j.issn.1674-3814.2020.09.002 (  0) 0) |
| [4] |
肖超, 韩伟, 李琼林, 等. 柔性直流输电系统交流侧线路继电保护适应性研究[J]. 智慧电力, 2020, 48(4): 1-8. XIAO Chao, HAN Wei, LI Qionglin, et al. Adaptability of MMC-HVDC System on relay protection of AC transmission lines[J]. Smart Power, 2020, 48(4): 1-8. DOI:10.3969/j.issn.1673-7598.2020.04.001 (  0) 0) |
| [5] |
吕佳宁, 叶小晖, 杨明玉. 混合级联多端直流输电系统的功率协调控制策略[J]. 智慧电力, 2020, 48(9): 9-15. LYU Jianing, YE Xiaohui, YANG Mingyu. Power coordination control strategy for hybrid cascaded multi-terminal HVDC system[J]. Smart Power, 2020, 48(9): 9-15. DOI:10.3969/j.issn.1673-7598.2020.09.003 (  0) 0) |
| [6] |
钱照明, 张军明, 盛况. 电力电子器件及其应用的现状和发展[J]. 中国电机工程学报, 2014, 34(29): 5149-5161. QIAN Zhaoming, ZHANG Junming, SHENG Kuang. Status and development of power semiconductor devices and its applications[J]. Proceedings of the CSEE, 2014, 34(29): 5149-5161. (  0) 0) |
| [7] |
徐政, 肖晃庆, 张哲任. 模块化多电平换流器主回路参数设计[J]. 高电压技术, 2015, 41(8): 2514-2527. XU Zheng, XIAO Huangqing, ZHANG Zheren. Design of main circuit parameters of modular multilevel converters[J]. High Voltage Engineering, 2015, 41(8): 2514-2527. (  0) 0) |
| [8] |
段军, 谢晔源, 姜田贵, 等. 模块化多电平换流阀可靠性研究与设计优化[J]. 电力工程技术, 2018, 37(2): 38-43. DUAN Jun, XIE Yeyuan, JIANG Tiangui, et al. Reliability research and design optimization of modular multilevel converter[J]. Electric Power Engineering Technology, 2018, 37(2): 38-43. (  0) 0) |
| [9] |
SHEN K, ZHAO D, MEI J, et al. Elimination of harmonics in a modular multilevel converter using particle swarm optimization-based staircase modulation strategy[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5311-5322. DOI:10.1109/TIE.2013.2297301 (  0) 0) |
| [10] |
SHEN Y F, WANG H, YANG Y H, et al. Mission profile based sizing of IGBT chip area for PV inverter applications[C]//2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG). Vancouver, BC, Canada. IEEE, 2016: 1-8.
(  0) 0) |
| [11] |
罗旭, 王学梅, 吴海平. 基于多目标优化的电动汽车变流器IGBT及开关频率的选择[J]. 电工技术学报, 2020, 35(10): 2181-2193. LUO Xu, WANG Xuemei, WU Haiping. Selections of IGBTs and switching frequency of the electric vehicle converter based on multi-objective optimization[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2181-2193. (  0) 0) |
| [12] |
BURKART R M, KOLAR J W. Comparative life cycle cost analysis of Si and SiC PV converter systems based on advanced η-ρ-σ multiobjective optimization techniques[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4344-4358. DOI:10.1109/TPEL.2016.2599818 (  0) 0) |
| [13] |
WANG L J, XU J Y, WANG G, et al. Lifetime estimation of IGBT modules for MMC-HVDC application[J]. Microelectronics Reliability, 2018, 82: 90-99. DOI:10.1016/j.microrel.2018.01.009 (  0) 0) |
| [14] |
CUNICO L M, LAMBERT G, DACOL R P, et al. Parameters design for modular multilevel converter (MMC)[C]//2013 Brazilian Power Electronics Conference. Gramado, Brazil. IEEE, 2013: 264-270.
(  0) 0) |
| [15] |
曾正, 李晓玲, 林超彪, 等. 功率模块封装的电-热-力多目标优化设计[J]. 中国电机工程学报, 2019, 39(17): 5161-5171, 5297. ZENG Zheng, LI Xiaoling, LIN Chaobiao, et al. Electric-thermal-stress oriented multi-objective optimal design of power module package[J]. Proceedings of the CSEE, 2019, 39(17): 5161-5171, 5297. (  0) 0) |
| [16] |
ZARAGOZA J, POU J, ARIAS A, et al. Study and experimental verification of control tuning strategies in a variable speed wind energy conversion system[J]. Renewable Energy, 2011, 36(5): 1421-1430. DOI:10.1016/j.renene.2010.11.002 (  0) 0) |
| [17] |
COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256-279. DOI:10.1109/TEVC.2004.826067 (  0) 0) |
| [18] |
屠卿瑞, 徐政. 基于结温反馈方法的模块化多电平换流器型高压直流输电阀损耗评估[J]. 高电压技术, 2012, 38(6): 1506-1512. TU Qingrui, XU Zheng. Dissipation analysis of MMC-HVDC based on junction temperature feedback method[J]. High Voltage Engineering, 2012, 38(6): 1506-1512. (  0) 0) |
| [19] |
WANG X P, LI Z G, YAO F, et al. Simplified estimation of junction temperature fluctuation at the fundamental frequency for IGBT modules considering mission profile[J]. IEEE Access, 2019, 7: 149308-149317. DOI:10.1109/ACCESS.2019.2947346 (  0) 0) |
| [20] |
LIU H, MA K, QIN Z A, et al. Lifetime estimation of MMC for offshore wind power HVDC application[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 504-511. DOI:10.1109/JESTPE.2015.2477109 (  0) 0) |
 2021, Vol. 40
2021, Vol. 40


 何伟冬(1996), 男, 硕士在读, 研究方向为换流器的可靠性分析及其优化设计(E-mail:
何伟冬(1996), 男, 硕士在读, 研究方向为换流器的可靠性分析及其优化设计(E-mail: