文章编号: 2096-3203(2021)04-0018-08 中图分类号: TM461
2. 江苏省配用电与能效工程技术研究中心, 江苏 南京 211100;
3. 国网江苏省电力有限公司, 江苏 南京 210024
船舶停港期间利用岸电系统替代柴油发电机继续供电可减少废气排放,有助于保护环境。目前,对于应用于岸电系统的模块化多电平变换器(modular multilevel converter, MMC),亟需建立其相关温升模型来验证温升控制技术的有效性,需要针对岸电系统这种工程领域展开基于损耗所建立温升模型的研究。文中得出的损耗模型和温升模型可以检验温升抑制措施的有效性,从而选择合理的温升抑制措施应用在岸电系统中。岸电系统的温度控制不仅仅是选用一个调制方式,后续研究工作可以在文中研究的基础上展开,提出合理且有效的温升抑制措施,从而促进岸电系统的稳定运行。
载波移相(carrier phase shift, CPS)和最近电平逼近(near level modulation, NLM)2种调制策略均可应用于MMC中[1-3]。由于调制方式不同,上述2种调制作用下的开关器件损耗不同,系统温升也有差异,最终对MMC整流器的运行可靠性产生不同影响[4]。
专家和学者们已对电力电子开关器件运行时的温升进行了研究,旨在寻找尽可能降低温升的方法。文献[5-7]基于电力电子器件损耗研究了温升,并从开关器件散热器材料的角度进一步分析了影
响散热的原因,但仅基于两电平变换器,未涉及MMC结构。文献[8]研究了变流器在整流和逆变2种状态下的温升情况,分析了水冷条件下开关器件的温升分布,但只分析了2种不同运行方式下开关器件温升的差异,没有研究调制方式对温升的影响。文献[9]分析了MMC变流器损耗与温升的关系,利用电热转化原理,给出了电力电子器件的瞬态温升模型,但没有给出开关器件的损耗计算和分析模型。文献[10-11]从绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)散热片与外环境热交换优化的角度研究了减少IGBT温升的方法,并基于系统成本、散热效率、系统寿命等多目标综合优化,设计了一种IGBT散热优化方案,但未考虑如何通过调制降低IGBT损耗和温升,以及不同调制方式对开关器件损耗的影响。
为此,文中研究CPS调制与NLM调制对半桥型MMC整流器中开关器件损耗和温升的影响。在给出MMC整流器拓扑的基础上,分析2种调制方式的工作原理,建立IGBT和反并联二极管的损耗模型和表达式;结合实际IGBT模块的参数和电热转化原理,得到开关器件损耗与温升的数学关系。
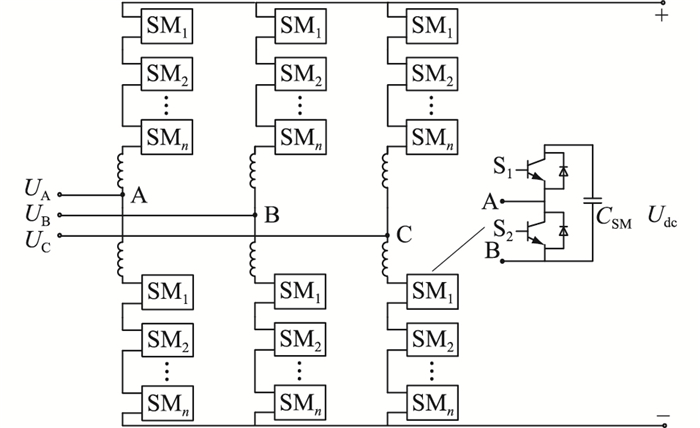
1 半桥型MMC整流器开关器件工作原理 1.1 拓扑结构半桥子模块的MMC整流器拓扑如图 1所示,每相包括上、下2个桥臂,单个桥臂上由n个子模块和1个抑制环流的缓冲电感直接串联构成。故总子模块数为N,即N=2n[12]。
|
图 1 MMC整流器拓扑结构 Fig. 1 Topology of MMC rectifier |
其子模块的结构如图 1中的放大部分所示,子模块电容CSM用以支撑直流侧电压,通过端子A和端子B构成的端口,子模块可与主电路连接。
通过对子模块中上管S1和下管S2的控制,可将子模块分为3种运行状态。
(1) 投入状态:S1开通、S2关断时,电容投入主电路;
(2) 切除状态:S1关断、S2开通时,电容被旁路;
(3) 闭锁状态:S1和S2都关断。
闭锁状态只在整流器故障或者启动时出现。在不考虑闭锁状态的情况下,子模块只在投入和切除状态之间切换,子模块上、下2个桥臂作互补的通断状态[13]。
对于MMC整流器,每相上、下2个桥臂构成一个相单元,由于每个子模块中的电容电压为恒定值,可通过控制上、下桥臂在每个时刻投入子模块的数量进而控制每相的输出电压,通常上、下桥臂投入的子模块数量之和为定值。例如:在任一时刻,对于A相来说,上桥臂投入子模块数为npa,下桥臂投入子模块数为nna,有:
| $ n_{\mathrm{pa}}+n_{\mathrm{na}}=n_{\mathrm{a}} $ | (1) |
式中:na为A相任一时刻上、下桥臂投入子模块数之和,一般为一个相单元总模块数的一半,即na=n[14]。
1.2 调制方式MMC整流器通过控制子模块的投入和切除,使MMC型整流器输出直流电压,通常采用CPS调制和NLM调制2种方式。
1.2.1 CPS调制CPS调制具有等效开关频率高、谐波特性好、控制相对简洁等特点。由于每相桥臂上投入运行的子模块数量为n,故采用n组三角载波,每相载波之间的移相角为θ=2π/n。将n组三角载波分别与同一个调制波进行比较后得到n个PWM调制信号[15],单独子模块的调制方式为双极型SPWM调制[16-17]。
令:
| $ \left\{\begin{array}{l} V_{\mathrm{T}}=U_{\mathrm{dc}} \\ V_{\mathrm{P}}=\sqrt{2} U_{\mathrm{s}} / \sqrt{3} \end{array}\right. $ | (2) |
式中:VT为载波幅值;VP为调制波幅值;Udc为直流侧电压;Us为交流侧电压。
可得电压调制比M为:
| $ M=V_{\mathrm{P}} / V_{\mathrm{T}}=\frac{\sqrt{2} U_{\mathrm{s}} / \sqrt{3}}{U_{\mathrm{dc}}} $ | (3) |
可推导出在同一个子模块中,S1,S2中IGBT的占空比函数分别为:
| $ \left\{\begin{array}{l} D_{1}(t)=\frac{1+M \sin \omega t}{2} \\ D_{2}(t)=\frac{1-M \sin \omega t}{2} \end{array}\right. $ | (4) |
式中:D1,D2分别为S1和S2的占空比;ω为实际电流的角频率。
对于同一组IGBT和续流二级管而言,IGBT的导通时间与反并联二极管的导通时间互补,所以同一组IGBT的占空比和续流二级管的占空比也互补。
1.2.2 NLM调制NLM调制的本质是任意时刻投入的若干数量子模块叠加的方波尽可能逼近于调制波[18]。假设单相上、下桥臂投入子模块数量分别为np,nn,VC为一个子模块的电容电压,则当前时刻的电压幅值为(np-nn)VC。
对于这种调制方式中的占空比D,可以通过式(5)求得:
| $ D=t_{\mathrm{on}} / T $ | (5) |
式中:ton为开关管的导通时间;T为载波周期。
2 半桥型MMC整流器的温升模型 2.1 损耗模型开关管IGBT和反并联二极管所产生的通态和开关损耗是MMC整流器的主要损耗,调制方式所产生的电流谐波引起的损耗较小,故建立损耗模型时不考虑谐波电流及其他因素所产生损耗的影响,在一定程度上简化整流器的损耗模型,便于后续温升模型的搭建和计算。
忽略电感损耗,MMC整流器的损耗主要包括主电路损耗和辅助电路损耗[19]。主电路损耗包括IGBT模块损耗和子模块电容损耗;辅助电路损耗包括门极驱动损耗和缓冲电路损耗,其中IGBT模块损耗占主导[20]。故文中主要对IGBT模块损耗进行研究,并分为IGBT及其反并联二极管损耗。
2.1.1 IGBT的损耗IGBT的功率损耗包含通态损耗PSS,开通损耗PSW(on),关断损耗PSW(off)(开关损耗PSW为开通损耗与关断损耗之和)和截止损耗4个部分,其中IGBT的截止损耗很小可忽略。
(1) 通态损耗[21]。在MMC子模块SM中,利用IGBT通态损耗的计算公式,可得S1中的单个IGBT通态损耗PSS1为:
| $ P_{\mathrm{SS} 1}=\frac{1}{T} \int_{0}^{T} v_{\mathrm{CE}}(t) i_{\mathrm{C}}(t) D_{1}(t) \mathrm{d} t $ | (6) |
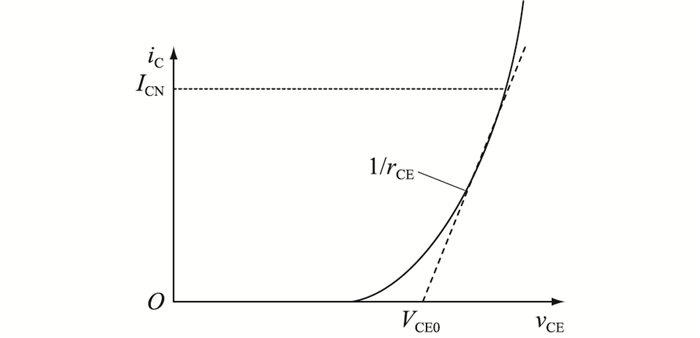
式中:vCE为IGBT的集-射极电压;iC为集电极电流。vCE和iC之间的典型曲线如图 2所示。
|
图 2 IGBT输出特性 Fig. 2 Output characteristic of IGBT |
由图 2可知,vCE和iC是非线性关系,为了便于分析计算,将对其进行线性拟合,可得到:
| $ v_{\mathrm{CE}}(t)=V_{\mathrm{CE} 0}+r_{\mathrm{CE}} i_{\mathrm{C}}(t) $ | (7) |
式中:VCE0为集-射极通态等效门槛电压;rCE为IGBT的通态等效电阻,可从输出特性曲线中获得。
采用CPS时,假设电流iC(t)=Issin ωt,可得:
| $ P_{\mathrm{SS} 1}=\left(\frac{1}{2 {\rm{ \mathsf{ π} }}}+\frac{M}{8}\right) V_{\mathrm{CE} 0} I_{\mathrm{s}}+\left(\frac{1}{8}+\frac{M}{3 {\rm{ \mathsf{ π} }}}\right) r_{\mathrm{CE}} I_{\mathrm{s}}^{2} $ | (8) |
式中:Is为实际通过电流的幅值。
同理可得,S2的通态损耗为:
| $ P_{\mathrm{SS} 2}=\left(\frac{1}{2 {\rm{ \mathsf{ π} }}}-\frac{M}{8}\right) V_{\mathrm{CE} 0} I_{\mathrm{s}}+\left(\frac{1}{8}-\frac{M}{3 {\rm{ \mathsf{ π} }}}\right) r_{\mathrm{CE}} I_{\mathrm{s}}^{2} $ | (9) |
采用NLM时,假设电流iC(t)=Issin ωt,可得:
| $ P_{\mathrm{SS} 1}=D V_{\mathrm{CE} 0} I_{\mathrm{s}}+D r_{\mathrm{CE}} I_{\mathrm{s}}^{2} $ | (10) |
| $ P_{\mathrm{SS} 2}=(1-D) V_{\mathrm{CE} 0} I_{\mathrm{s}}+(1-D) r_{\mathrm{CE}} I_{\mathrm{s}}^{2} $ | (11) |
无论采用CPS或NLM,单个SM模块的IGBT通态损耗都可以表示为:
| $ P_{\mathrm{SS}}=P_{\mathrm{SS} 1}+P_{\mathrm{SS} 2} $ | (12) |
(2) 开关损耗[21]。假设IGBT的开关频率为fSW,半个周期内开通和关断的次数总和为nSW,开通次数为nSW/2。单个IGBT的开关损耗PSW为:
| $ P_{\mathrm{SW}}=\left(E_{\mathrm{SW}(\mathrm{on})}+E_{\mathrm{SW}(\mathrm {off})}\right) \frac{1}{2 f_{\mathrm{o}}} f_{\mathrm{SW}} \frac{I_{\mathrm{s}}}{I_{\mathrm{sN}}} \frac{U_{\mathrm{dc}}}{U_{\mathrm{dcN}}} $ | (13) |
式中:ESW(on)为IGBT开通一次损耗的能量;ESW(off)为IGBT关断一次损耗的能量;IsN为额定的工作电流;UdcN为额定的直流侧电压;fo为基波频率。
开关频率存在如式(14)所示的关系:
| $ n_{\mathrm{SW}}=f_{\mathrm{SW}} / f_{\mathrm{o}} $ | (14) |
结合式(13)与式(14),可得:
| $ P_{\mathrm{SW}}=\left(E_{\mathrm{SW}(\mathrm{on})}+E_{\mathrm{SW}(\mathrm { off })}\right) \frac{n_{\mathrm{SW}}}{2} \frac{I_{\mathrm{s}}}{I_{\mathrm{sN}}} \frac{U_{\mathrm{dc}}}{U_{\mathrm{deN}}} $ | (15) |
二极管的功率损耗包含二极管的通态损耗PDC,开通损耗PDiode(on),反向恢复损耗PDiode(off)(开关损耗Prr为开通损耗与反向恢复损耗之和)和截止损耗4个部分,其中二极管的截止损耗和开通损耗很小,可以忽略不计。
(1) 通态损耗[21]。MMC子模块SM中,S1的反并联二极管通态损耗PDC1为:
| $ P_{\mathrm{DC1}}=\left(\frac{1}{2 {\rm{ \mathsf{ π} }}}-\frac{M}{8}\right) V_{\mathrm{F} 0} I_{\mathrm{s}}+\left(\frac{1}{8}-\frac{M}{3 {\rm{ \mathsf{ π} }}}\right) r_{\mathrm{F}} I_{\mathrm{s}}^{2} $ | (16) |
式中:vF为反并联二极管正向压降;iF为反并联二极管正向电流。
vF和iF是非线性关系,其典型曲线与IGBT的输出特性类似,对其线性拟合可得:
| $ v_{\mathrm{F}}(t)=V_{\mathrm{F} 0}+r_{\mathrm{F}} i_{\mathrm{F}}(t) $ | (17) |
式中:VF0为反并联二极管的门槛电压;rF为通态等效电阻,可从输出特性曲线中获得。
采用CPS时,假设iF(t)=iC(t)=Issin ωt,可得:
| $ P_{\mathrm{DC} 1}=\left(\frac{1}{2 \pi}-\frac{M}{8}\right) V_{\mathrm{F} 0} I_{\mathrm{s}}+\left(\frac{1}{8}-\frac{M}{3 \pi}\right) r_{\mathrm{F}} I_{\mathrm{s}}^{2} $ | (18) |
同理可得,S2的反并联二极管通态损耗为:
| $ P_{\mathrm{DC} 2}=\left(\frac{1}{2 {\rm{ \mathsf{ π} }}}+\frac{M}{8}\right) V_{\mathrm{F} 0} I_{\mathrm{s}}+\left(\frac{1}{8}+\frac{M}{3 {\rm{ \mathsf{ π} }}}\right) r_{\mathrm{F}} I_{\mathrm{s}}^{2} $ | (19) |
采用NLM时,假设iF(t)=iC(t)=Issin ωt,可得:
| $ P_{\mathrm{DC} 1}=(1-D) V_{\mathrm{F} 0} I_{\mathrm{s}}+(1-D) r_{\mathrm{F}} I_{\mathrm{s}}^{2} $ | (20) |
| $ P_{\mathrm{DC} 2}=D V_{\mathrm{F} 0} I_{\mathrm{s}}+D r_{\mathrm{F}} I_{\mathrm{s}}^{2} $ | (21) |
无论采用CPS或NLM,单个SM模块的反并联二极管通态损耗都可以表示为:
| $ P_{\mathrm{DC}}=P_{\mathrm{DC} 1}+P_{\mathrm{DC} 2} $ | (22) |
(2) 开关损耗[21]。二极管的开通损耗可以忽略不计,仅计算其关断损耗。反并联二极管的开关损耗Prr为:
| $ P_{\mathrm{rr}}=E_{\mathrm{Diode}(\mathrm { off)P }} \frac{1}{2 f_{\mathrm{o}}} f_{\mathrm{SW}} \frac{I_{\mathrm{s}}}{I_{\mathrm{sN}}} \frac{U_{\mathrm{dc}}}{U_{\mathrm{deN}}} $ | (23) |
式中:EDiode(off)P为反并联关断一次损耗的能量。
经过简化,可得:
| $ P_{\mathrm{rr}}=E_{\mathrm{Diode}(\mathrm { off }) \mathrm{P}} \frac{n_{\mathrm{SW}}}{2} \frac{I_{\mathrm{s}}}{I_{\mathrm{sN}}} \frac{U_{\mathrm{dc}}}{U_{\mathrm{dcN}}} $ | (24) |
在上文建立的各类损耗模型基础上,获得IGBT和反并联二极管各自总的损耗,结合电热转换原理进一步搭建MMC整流器的温升分析模型,确立开关损耗与温升的数学关系式,有助于后续研究不同调制方式下的温升情况。
对于一个应用于工程实际的IGBT模块成品,其内部结构是确定的。文中所研究的模块结构由2个IGBT开关组串联而成,对应了MMC整流器中的一个SM子模块,其结构如图 3所示。

|
图 3 IGBT模块内部接线 Fig. 3 The internal circuit of IGBT-module |
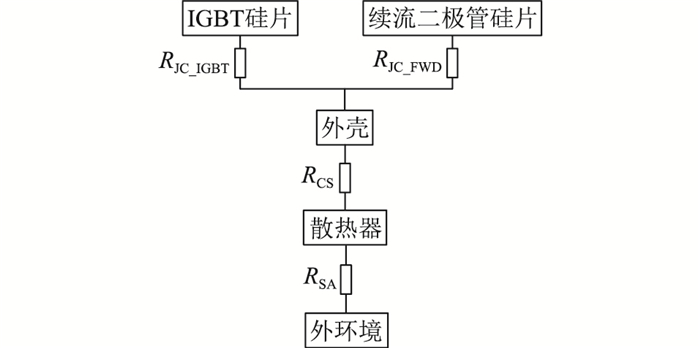
单个IGBT模块的温升模型如图 4所示[22-23],对于同一个IGBT模块中的2种开关器件而言,IGBT的硅片和反并联二极管的硅片分别通过不同的材料连接至外壳,再连接至散热器上。
|
图 4 IGBT模块温升分析模型 Fig. 4 Temperature rise analysis model of IGBT-module |
图 4中,RJC_IGBT为IGBT硅片与外壳之间的热阻;RJC_FWD为反并联二极管硅片与外壳之间的热阻;RCS为外壳与散热器之间的热阻;RSA为散热器与外环境之间的热阻。
热阻与功率损耗之间的关系可以通过温升来反映:
| $ R=\Delta T / P $ | (25) |
式中:R为热阻;P为功率损耗;ΔT为温升。利用电气量来进行类比,则可得:热阻类比于电阻,温升类比于电位差,损耗类比于电流。
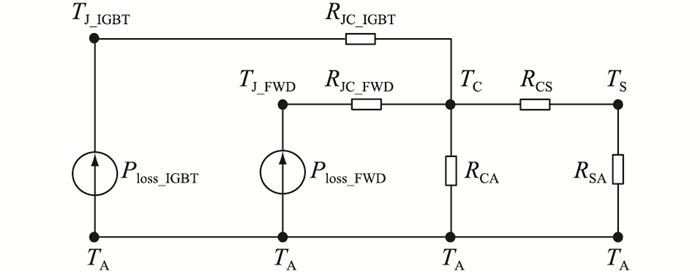
|
图 5 IGBT模块等效热阻电路 Fig. 5 Equivalent thermal resistance circuit of IGBT-module |
图 5中,Ploss_IGBT,Ploss_FWD分别为IGBT和反并联二极管的损耗;TJ_IGBT,TJ_FWD分别为IGBT和反并联二极管的结温;TC,TS,TA分别为IGBT模块外壳、IGBT散热器和外环境的温度;RCA为模块外壳与外环境之间的热阻。由于RCA远大于RCS,即开关器件散热方式主要是通过设备中的散热器向外散热[24],因此,在等效电路中,RCA与RCS、RSA并联时,可以被视为开路。由此可以将图 5简化为图 6。
|
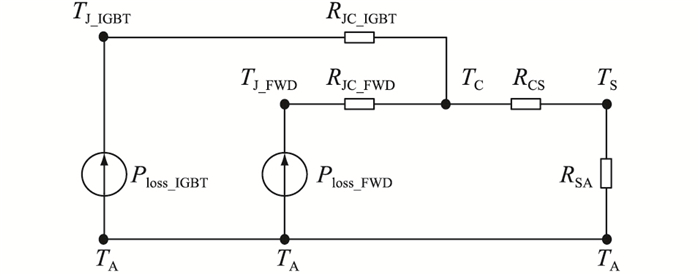
图 6 简化等效热阻电路 Fig. 6 Simplified equivalent thermal resistance circuit of IGBT-module |
由图 6和式(25)可得各个节点处的温度为:
| $ \left\{\begin{array}{l} T_{\mathrm{J}\_{\mathrm{IGBT}}}=P_{\mathrm{loss\_IGBT}} R_{\mathrm{JC\_IGBT}}+T_{\mathrm{C}} \\ T_{\mathrm{J}\_{\mathrm{FWD}}}=P_{\mathrm {loss\_FWD }} R_{\mathrm{JC\_FWD}}+T_{\mathrm{C}} \\ T_{\mathrm{C}}=\left(P_{\text {loss_IGBT }}+P_{\text {loss_FWD }}\right) R_{\mathrm{CS}}+T_{\mathrm{S}} \\ T_{\mathrm{S}}=\left(P_{\text {loss_IGBT }}+P_{\text {loss_FWD }}\right) R_{\mathrm{SA}}+T_{\mathrm{A}} \end{array}\right. $ | (26) |
对于同一个IGBT模块中的2种开关器件的损耗,有如下关系:
| $ \left\{\begin{array}{l} P_{\text {loss_IGBT }}=P_{\mathrm{SS}}+2 P_{\mathrm{SW}} \\ P_{\text {loss_FWD }}=P_{\mathrm{DC}}+2 P_{\mathrm{rr}} \end{array}\right. $ | (27) |
由于外环境的初始温度为已知,利用式(26)求出TJ_IGBT和TJ_FWD的温度,便可求得IGBT和反并联二极管的温升。
3 仿真分析 3.1 仿真参数和模型搭建仿真采用三相半桥型MMC结构的整流器,每相上、下桥臂各24个SM子模块串联,IGBT模块为Infineon型FF450R17ME4模块,参数如表 1所示。IGBT模块的热阻参数如表 2所示。MMC整流器的实际运行参数如表 3所示。
|
|
表 1 IGBT模块参数 Table 1 Parameters of IGBT-module |
|
|
表 2 IGBT模块热阻参数表 Table 2 Thermal resistances of IGBT-module |
|
|
表 3 MMC整流器运行参数表 Table 3 Operation parameters of MMC rectifier |
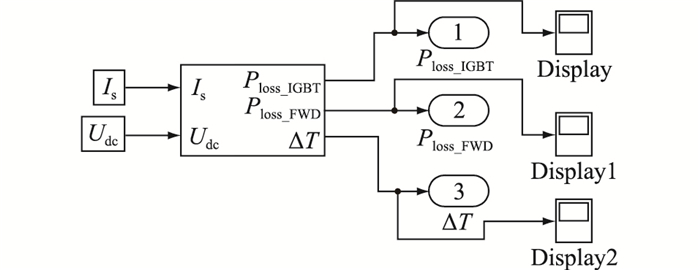
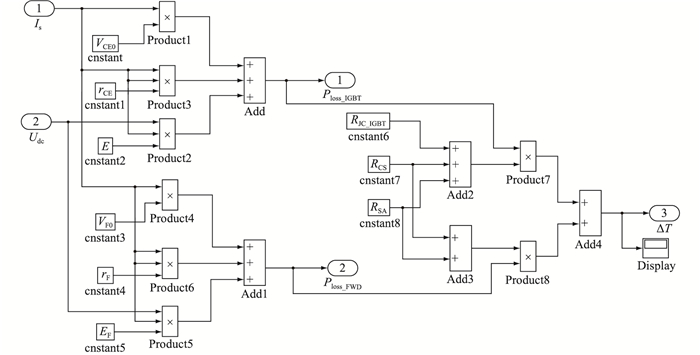
根据仿真参数在Matlab中搭建仿真模型,所搭建的CPS调制下的仿真模型图外部封装如图 7所示,内部结构如图 8所示,NLM调制下的仿真模型搭建与此类似。
|
图 7 CPS调制下仿真模型的外部封装 Fig. 7 The external package of the simulation model under CPS modulation |
|
图 8 CPS调制下仿真模型的内部结构 Fig. 8 The internal structure of the simulation model under CPS modulation |
根据建立的开关损耗模型可知,开关损耗会受到调制方式的影响。文中建立开关损耗和温升的数学关系,故调制方式的不同会间接影响温升情况。分别对采用CPS和NLM的半桥型MMC整流器的每个桥臂子模块温升进行对比分析。
3.2.1 采用载波移相调制在采用8倍频调制,且调制比为$\sqrt{2} / \sqrt{3}$时,结合式(12)、式(15)和式(27)可得Ploss_IGBT,结合式(22)、式(24)和式(27)可得Ploss_FWD,通过计算可得到单个SM子模块的开关器件损耗与实际电流和电压之间的关系为:
| $ \left\{\begin{aligned} P_{\mathrm {loss\_IGBT }}=&0.371\ 4 I_{\mathrm{s}}+4.629\ 6 \times 10^{-4} I_{\mathrm{s}}^{2}+ \\ & 4.009\ 9 \times 10^{-6} U_{\mathrm{dc}} I_{\mathrm{s}}\\ P_{\mathrm {loss\_FWD }}=&0.363\ 8 I_{\mathrm{s}}+3.571\ 4 \times 10^{-4} I_{\mathrm{s}}^{2}+ \\ & 1.185\ 2 \times 10^{-6} U_{\mathrm{dc}} I_{\mathrm{s}} \end{aligned}\right. $ | (28) |
结合式(28)和式(26)可得:
| $ \left\{\begin{aligned} \Delta T_{\mathrm{J}\_{\mathrm{IGBT}}}=&0.067\ 9 I_{\mathrm{s}}+7.862\ 4 \times 10^{-5} I_{\mathrm{s}}^{2}+\\ &4.406\ 2 \times 10^{-7} U_{\mathrm{dc}} I_{\mathrm{s}} \\ \Delta T_{\mathrm{J}\_\mathrm{FWD}}=&0.082\ 0 I_{\mathrm{s}}+8.656\ 0 \times 10^{-5} I_{\mathrm{s}}^{2}+ \\ &4.406\ 2 \times 10^{-7} U_{\mathrm{dc}} I_{\mathrm{s}} \end{aligned}\right. $ | (29) |
式中:ΔTJ_IGBT,ΔTJ_FWD分别为IGBT和反并联二极管的损耗温差。
3.2.2 采用最近电平逼近调制在采用最近电平逼近调制时,结合式(12)、式(15)和式(27)可得Ploss_IGBT,结合式(22)、式(24)和式(27)可得Ploss_FWD,通过计算单个SM子模块的开关器件损耗与实际电流和电压之间的关系为:
| $ \left\{\begin{array}{c} P_{\mathrm {loss\_GBT }}=0.583\ 3 I_{\mathrm{s}}+9.250\ 0 \times 10^{-4} I_{\mathrm{s}}^{2}+ \\ 5.0124 \times 10^{-7} U_{\mathrm{dc}} I_{\mathrm{s}} \\ P_{\mathrm {loss }\_{\mathrm{FW} \mathrm{D}}}=0.571\ 4 I_{\mathrm{s}}+7.125\ 0 \times 10^{-4} I_{\mathrm{s}}^{2}+ \\ 1.481\ 5 \times 10^{-7} U_{\mathrm{dc}} I_{\mathrm{s}} \end{array}\right. $ | (30) |
结合式(30)和式(26)可得:
| $ \left\{\begin{array}{c} \Delta T_{\mathrm{J}\_{\mathrm{IGBT}}}=0.106\ 6 I_{\mathrm{s}}+1.570\ 3 \times 10^{-4} I_{\mathrm{s}}^{2}+ \\ 7.033\ 7 \times 10^{-8} U_{\mathrm{dc}} I_{\mathrm{s}} \\ \Delta T_{\mathrm{J\_{\mathrm{FWD }}}}=0.128\ 7 I_{\mathrm{s}}+1.727\ 8 \times 10^{-4} I_{\mathrm{s}}^{2}+ \\ 5.507\ 7 \times 10^{-8} U_{\mathrm{dc}} I_{\mathrm{s}} \end{array}\right. $ | (31) |
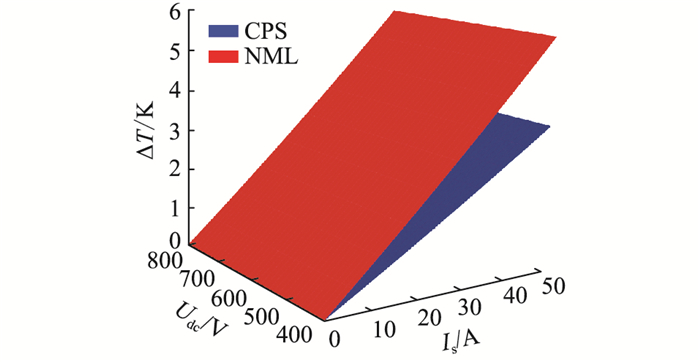
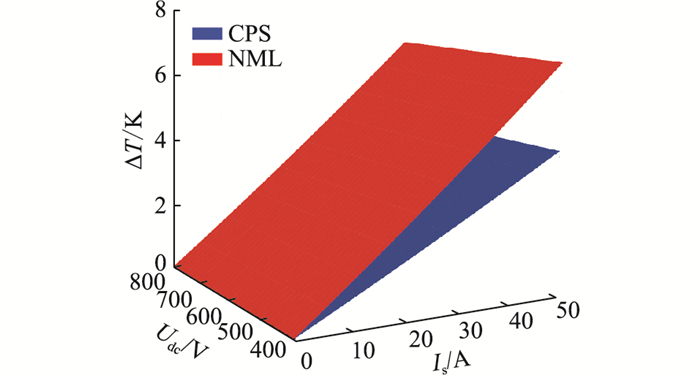
基于已建立的开关损耗和温升模型,代入参数计算开关器件损耗和温升与实际电流与电压之间的关系。通过在Matlab中仿真得出采用2种调制方式后的温升与实际电压电流的关系分别如图 9和图 10所示,图 9为IGBT的温升,图 10为反并联二极管的温升。
|
图 9 不同电压电流下IGBT温升 Fig. 9 Temperature rise of IGBT with different voltages and currents |
|
图 10 不同电压电流下反并联二极管温升 Fig. 10 Temperature rise of FWD with different voltages and currents |
可以看出,相对NLM,CPS调制下的IGBT和反并联二极管温升均较低,故CPS调制更适用于文中所述MMC工程样机。
将表 3中MMC工程样机的实际工作条件代入式(29)和式(31),分别得到CPS和NLM调制下实际的开关器件损耗结果,如表 4所示。CPS调制下的IGBT和反并联二极管的温升与NLM调制相比均较低,与上述结论一致,验证了所建立的开关器件损耗和温升模型的正确性。
|
|
表 4 开关器件温升情况表 Table 4 Temperature rise of electronic power switches |
文中通过对半桥型MMC整流器的开关器件进行分析,提出了电力电子开关器件损耗模型,并将该模型与电热转换的原理相结合建立了开关器件的温升模型。基于建立的温升模型,仿真分析和对比了CPS和NLM 2种调制方法所导致的温升情况。结果表明,相对于NLM,CPS调制时的IGBT和反并联二极管温升更低,同时根据工程样机的实际数据验证了模型的正确性。考虑实际工程应用条件的复杂性,可参考选用CPS调制来抑制MMC整流器的温升。然而温升的抑制不仅仅局限于调制方式的选择,文中建立的开关器件损耗及温升模型可用于验证后续研究相关温升抑制措施的可行性及有效性。
| [1] |
关金萍, 徐永海. 电力电子变压器在风力发电系统中的应用研究综述[J]. 电工电能新技术, 2019, 38(2): 88-96. GUAN Jinping, XU Yonghai. Research review of power electronic transformer applications in wind energy conversion systems[J]. Advanced Technology of Electrical Engineering and Energy, 2019, 38(2): 88-96. (  0) 0) |
| [2] |
易灵芝, 黄晓辉, 黄守道, 等. 基于最近电平逼近调制的模块化多电平变换器中高压变频调速系统运行控制[J]. 电工技术学报, 2020, 35(6): 1303-1315. YI Lingzhi, HUANG Xiaohui, HUANG Shoudao, et al. A medium-voltage motor drive with modular multilevel converter based on nearest level modulation[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1303-1315. (  0) 0) |
| [3] |
公铮, 伍小杰, 王钊, 等. 基于载波移相调制的模块化多电平变换器变频运行控制[J]. 中国电机工程学报, 2015, 35(11): 2822-2830. GONG Zheng, WU Xiaojie, WANG Zhao, et al. Variable frequency operation control of modular multilevel converter based on carrier phase-shift modulation[J]. Proceedings of the CSEE, 2015, 35(11): 2822-2830. (  0) 0) |
| [4] |
张江勇, 杜明星, 魏克新. IGBT模块结温变化下的电磁干扰特性研究[J]. 电力电子技术, 2019, 53(1): 84-86, 100. ZHANG Jiangyong, DU Mingxing, WEI Kexin. Study of electromagnetic interference characteristics of IGBT module under junction temperature change[J]. Power Electronics, 2019, 53(1): 84-86, 100. (  0) 0) |
| [5] |
马汉卿. 基于热敏感电参数法的IGBT模块结温检测[J]. 浙江电力, 2019, 38(4): 13-19. MA Hanqing. IGBT module junction temperature detection based on thermal-sensitive electrical parameters[J]. Zhejiang Electric Power, 2019, 38(4): 13-19. (  0) 0) |
| [6] |
戴超, 陈向荣. 碳化硅IGBT电力电子器件封装和绝缘研究综述[J]. 浙江电力, 2019, 38(10): 26-33. DAI Chao, CHEN Xiangrong. A review of research on SiC IGBT power electronic device packaging and insulation[J]. Zhejiang Electric Power, 2019, 38(10): 26-33. (  0) 0) |
| [7] |
郭庆奎, 张洪阳, 张志锋, 等. 风机并网变流器温升分析与控制参数优化[J]. 电力系统保护与控制, 2018, 46(24): 173-179. GUO Qingkui, ZHANG Hongyang, ZHANG Zhifeng, et al. Temperature rise evaluation and control parameter optimization of wind power grid converter[J]. Power System Protection and Control, 2018, 46(24): 173-179. (  0) 0) |
| [8] |
王雷, 杨璐, 李守蓉. 大功率变流装置IGBT模块冷却性能分析研究[J]. 电力电子技术, 2018, 52(8): 56-58. WANG Lei, YANG Lu, LI Shourong. Research and analysis of cooling performance of IGBT module for high power converters[J]. Power Electronics, 2018, 52(8): 56-58. (  0) 0) |
| [9] |
王希平, 李志刚, 姚芳. 模块化多电平换流阀IGBT器件功率损耗计算与结温探测[J]. 电工技术学报, 2019, 34(8): 1636-1646. WANG Xiping, LI Zhigang, YAO Fang. Power loss calculation and junction temperature detection of IGBT devices for modular multilevel valve[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1636-1646. (  0) 0) |
| [10] |
米高祥, 郭勇, 李旭, 等. 大功率变流器热设计的多目标优化研究[J]. 电力电子技术, 2018, 52(8): 48-51. MI Gaoxiang, GUO Yong, LI Xu, et al. Research on multi-objective optimization of high power converter thermal design[J]. Power Electronics, 2018, 52(8): 48-51. (  0) 0) |
| [11] |
边少聪, 王宇. 基于PSO-BP神经网络模型的IGBT老化预测[J]. 浙江电力, 2019, 38(11): 58-64. BIAN Shaocong, WANG Yu. Ageing prediction of IGBT based on PSO-BP neural network model[J]. Zhejiang Electric Power, 2019, 38(11): 58-64. (  0) 0) |
| [12] |
孙广星, 苟锐锋, 孙伟. 基于MMC结构的电力电子变压器拓扑结构及控制策略研究[J]. 高压电器, 2016, 52(1): 142-147, 153. SUN Guangxing, GOU Ruifeng, SUN Wei. Research on topology and control strategy of power electronic transformer based on MMC structure[J]. High Voltage Apparatus, 2016, 52(1): 142-147, 153. (  0) 0) |
| [13] |
张芳, 杜雪靓, 陈堃. MMC-HVDC系统换流器桥臂短路故障暂态特性分析[J]. 电力自动化设备, 2020, 40(5): 180-189. ZHANG Fang, DU Xuejing, CHEN Kun. Transient characteristic analysis of converter bridge arm short circuit fault in MMC-HVDC system[J]. Electric Power Automation Equipment, 2020, 40(5): 180-189. (  0) 0) |
| [14] |
孙永忠, 姜毅龙. 载波移相PWM调制下的MMC电压平衡控制策略[J]. 电气传动, 2020, 50(2): 47-54, 62. SUN Yongzhong, JIANG Yilong. Voltage balance control strategy for modular multilevel converters with phase-shifted carrier-based pulse width modulation[J]. Electric Drive, 2020, 50(2): 47-54, 62. DOI:10.3969/j.issn.1005-7277.2020.02.012 (  0) 0) |
| [15] |
王晓鹏, 杨晓峰, 范文宝, 等. 模块组合多电平变换器的脉冲调制方案对比[J]. 电工技术学报, 2011, 26(5): 28-33. WANG Xiaopeng, YANG Xiaofeng, FAN Wenbao, et al. A comparative study of multi-pulse modulation schemes for modular multilevel converters[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 28-33. (  0) 0) |
| [16] |
刘喜梅, 王宁, 张硕博. 基于CPS-SPWM的模块化多电平整流器的研究与应用[J]. 电力系统保护与控制, 2020, 48(22): 180-179. LIU Ximei, WANG Ning, ZHANG Shuobo. Research and application of a modular multilevel rectifier based on CPS-SPWM[J]. Power System Protection and Control, 2020, 48(22): 180-179. (  0) 0) |
| [17] |
赵鲁, 李耀华, 葛琼璇, 等. 特定谐波消除及优化脉宽调制单相整流器的研究[J]. 电工技术学报, 2014, 29(10): 57-64. ZHAO Lu, LI Yaohua, GE Qiongxuan, et al. Study of selective harmonic elimination and optimization pulse width modulation single-phase rectifier[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 57-64. DOI:10.3969/j.issn.1000-6753.2014.10.007 (  0) 0) |
| [18] |
张国荣, 韩慧颖, 王啸飞, 等. 模块化多电平变换器最近电平调制研究[J]. 电测与仪表, 2017, 54(23): 1-9. ZHANG Guorong, HAN Huiying, WANG Xiaofei, et al. Research on nearest level modulation for multilevel converter[J]. Electrical Measurement & Instrumentation, 2017, 54(23): 1-9. DOI:10.3969/j.issn.1001-1390.2017.23.001 (  0) 0) |
| [19] |
廖敏, 许韦华, 杨杰, 等. 考虑子模块均压约束的混合型模块化多电平换流器功率极限分析[J]. 电力系统保护与控制, 2019, 47(5): 17-25. LIAO Min, XU Weihua, YANG Jie, et al. Analysis of maximum power operating region for hybrid MMC considering sub-module balancing constraint[J]. Power System Protection and Control, 2019, 47(5): 17-25. (  0) 0) |
| [20] |
ROHNER S, BERNET S, HILLER M, et al. Modulation, losses, and semiconductor requirements of modular multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2633-2642. DOI:10.1109/TIE.2009.2031187 (  0) 0) |
| [21] |
YUE Q Y, LI C B, CAO Y J, et al. Comprehensive power losses model for electronic power transformer[J]. IEEE Access, 2018, 6: 14926-14934. (  0) 0) |
| [22] |
JANG S H, SHIN M W. Thermal characterization of junction in solar cell packages[J]. IEEE Electron Device Letters, 2010, 31(7): 743-745. (  0) 0) |
| [23] |
杨中宇, 朱志明, 刘博, 等. 稳压式变极性焊接电源中的IGBT功率损耗和温升模型[J]. 清华大学学报(自然科学版), 2017, 57(5): 471-475, 482. YANG Zhongyu, ZHU Zhiming, LIU Bo, et al. Power loss and temperature rise model for an IGBT in a variable polarity welding power supply with a reverse voltage stabilizer[J]. Journal of Tsinghua University (Science and Technology), 2017, 57(5): 471-475, 482. (  0) 0) |
| [24] |
江超, 唐志国, 李荟卿, 等. 电机控制器IGBT用风冷散热器设计[J]. 汽车工程学报, 2015, 5(3): 179-186. JIANG Chao, TANG Zhiguo, LI Huiqing, et al. Design of air cooled heat sink for IGBT in motor controller[J]. Chinese Journal of Automotive Engineering, 2015, 5(3): 179-186. (  0) 0) |
2. Jiangsu Province Power Distribution and Energy Efficiency Engineering Technology Research Center, Nanjing 211100, China;
3. State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210024, China
 2021, Vol. 40
2021, Vol. 40


 余昆(1978), 男, 博士, 副教授, 研究方向为智能配电网自愈控制与优化调度、配用电系统多能互补与高效运行、能效评估与用能模式优化(E-mail:
余昆(1978), 男, 博士, 副教授, 研究方向为智能配电网自愈控制与优化调度、配用电系统多能互补与高效运行、能效评估与用能模式优化(E-mail: