文章编号: 2096-3203(2021)04-0136-06 中图分类号: TM715
2. 南京豪庆信息科技有限公司, 江苏 南京 210006
20世纪80年代初,文献[1]首次提出空间负荷预测概念,即在规划用电区域内,将用地按照一定规则划分为相同大小或不同大小的小区(也可称为元胞),通过对小区历史负荷以及土地利用特征、发展规律的分析,预测小区的电力负荷情况[2]。空间负荷预测结果关系配电网规划的合理性,预测值过大或过小都会带来不利影响,因此对空间负荷预测结果的精度有着较高的要求[3]。
目前,空间负荷预测方法主要有用地仿真法、趋势法、多元变量法和负荷密度指标法[2]。用地仿真法采用大小相同的网格划分小区,故仅能得到小区的理论负荷值,无法得到实际负荷值,对预测结果检验造成一定困难[4-5]。趋势法简单方便,数据需求量小,但其受负荷数据波动和外部环境变化的影响较大[6-7]。多元变量法对数据的质量和数量都有较高要求,且有效预测期较短[8]。负荷密度指标法在用地性质较为明确的规划区域,具有较好的预测精度和较强的适应性[9-11],在国内应用较为广泛。
近年来,采用负荷密度指标法的空间负荷预测不断发展,预测精度有所提高,但仍需完善。文献[12]提出基于最小二乘支持向量机(least square support vector machine,LS-SVM)的负荷密度指标法。该方法采用聚类后与待预测小区负荷密度指标较为接近的一类小区负荷密度指标作为LS-SVM模型的训练样本,训练样本中夹杂部分相似度较低的样本,且可能会漏掉部分较好的样本。文献[13-14]引入灰色关联分析(grey relational analysis,GRA),选取与待预测小区负荷密度指标关联度较高的样本作为LS-SVM模型的训练样本,进一步提高了预测精度,但未考虑各影响因素指标对负荷密度影响程度不一的问题,且LS-SVM模型计算相对复杂,影响预测模型的整体运行速度。
文中针对以上问题,提出一种基于负荷密度指标优化与GRA-ELM的空间负荷预测方法。应用熵权法优化负荷密度指标的影响权重,引入极限学习机(extreme learning machine,ELM)降低算法复杂度,提高模型运算速度,并应用GRA为ELM选取训练样本。通过实例分析可知,文中所提方法空间负荷预测精度较其他方法有所提高。
1 熵权法熵权法根据被评价对象指标值构成的判断矩阵确定指标权重,是一种客观赋权法,能有效避免专家意见主观性的影响[15]。当样本中某项指标值变化较大时,其熵值较小,说明该指标提供的有效信息量大,权重相应较大;反之,指标的熵值较大,则该指标的权重较小。一组数据的信息熵定义为:
| $ E_{j}=-\ln \frac{1}{n} \sum\limits_{i=1}^{n}\left(p_{i j} \ln p_{i j}\right) $ | (1) |
式中:n为样本总数;pij为样本i的第j个指标信息量在n个样本总指标信息量中的比例。
| $ p_{i j}=Y_{i j} / \sum\limits_{i=1}^{n} Y_{i j} $ | (2) |
式中:Yij为样本数据标准化值。
对各指标进行信息熵计算,假设评价对象的指标共有k个,则各指标对评价对象影响权值为:
| $ w_{j}=\frac{1-E_{j}}{k-\sum\limits_{j=1}^{k} E_{j}} j=1, 2, \cdots, k $ | (3) |
利用熵权法可以确定负荷密度指标体系中不同类型负荷各指标的影响程度,并以权重分配的形式表现出来。
2 GRA-ELM模型 2.1 GRA算法GRA算法的基本思路是根据序列曲线几何形状的相似程度判断其联系是否紧密[15]。曲线相似度越高,则相应序列之间关联度越大;反之,曲线相似度越低,则相应序列之间关联度越小。
根据关联度定义,已知序列Y和其相关序列Zi在第j项的关联系数为:
| $ g\left(\boldsymbol{Y}_{j}, \boldsymbol{Z}_{i j}\right)=\frac{\min \Delta_{i j}-\lambda \max \Delta_{i j}}{\Delta_{i j}+\lambda \max \Delta_{i j}} $ | (4) |
| $ \Delta_{i j}=\left|\boldsymbol{Y}_{j}-\boldsymbol{Z}_{i j}\right| $ | (5) |
式中:λ为分辨系数,取值为[0, 1];Δij为Y和Zi在第j项的绝对差;min Δij,max Δij分别为第j项绝对差值的最小和最大值。
则Yj和Zi的关联度为:
| $ G\left(\boldsymbol{Y}_{j}, \boldsymbol{Z}_{i}\right)=\sum\limits_{j} g\left(\boldsymbol{Y}_{j}, \boldsymbol{Z}_{i j}\right) $ | (6) |
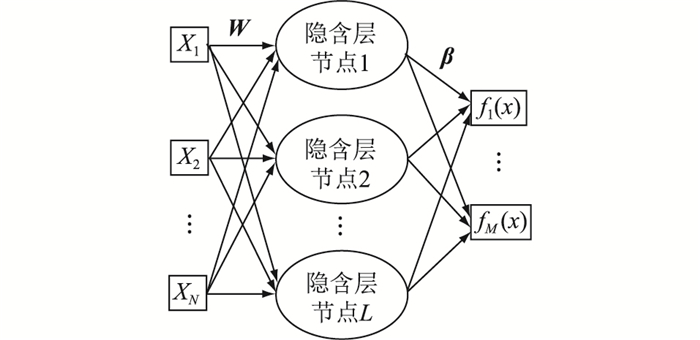
ELM算法是一种单隐含层前馈神经网络学习算法[16],该算法随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值,且在训练过程中无需调整,通过求解广义逆矩阵得出输出权重矩阵。与LS-SVM相比,该算法无需选取核函数,且计算相对简单,因而训练速度较快[16]。
假设共有N组训练样本(Xj, tj),其中Xj=[xj1 xj2 … xjn]T∈ R n,tj=[tj1 tj2 … tjm]T∈ R m, j=1, 2, …, N,ELM隐含层含L个神经元,则ELM的输出为:
| $ f(x)=\sum\limits_{i=1}^{L}\left[\boldsymbol{\beta}_{i} e\left(\boldsymbol{W}_{i} \boldsymbol{X}_{j}+b_{i}\right)\right] $ | (7) |
式中:e(·)为激励函数;Wi=[wi1 wi2 … win]为隐含层第i个神经元与各个输入层神经元间的连接权值;βi=[βi1 βi2 … βim]T为隐含层第i个神经元与各个输出层神经元间的连接权值;bi为隐含层第i个神经元的阈值。ELM结构如图 1所示,其中M为输出层节点数。
|
图 1 ELM结构 Fig. 1 Structure of ELM |
为使单隐含层的输出误差达到最小学习目标,式(7)可表示为:
| $ \boldsymbol{H} \boldsymbol{\beta}=\boldsymbol{T} $ | (8) |
式中: B为隐含层与输出层的连接权值矩阵; T为期望输出;H为神经网络的隐含层输出矩阵,如式(9)所示。
| $ \boldsymbol{H}(\boldsymbol{W}, \boldsymbol{X}, \boldsymbol{b})=\left[\begin{array}{ccc} e\left(\boldsymbol{W}_{1} \boldsymbol{X}_{1}+b_{1}\right) & \cdots & e\left(\boldsymbol{W}_{L} \boldsymbol{X}_{1}+b_{L}\right) \\ \vdots & & \vdots \\ e\left(\boldsymbol{W}_{1} \boldsymbol{X}_{N}+b_{1}\right) & \cdots & e\left(\boldsymbol{W}_{L} \boldsymbol{X}_{N}+b_{L}\right) \end{array}\right] $ | (9) |
| $ \boldsymbol{\beta}=\left[\begin{array}{c} \beta_{1}^{\mathrm{T}} \\ \vdots \\ \beta_{L}^{\mathrm{T}} \end{array}\right]_{L \times m}, \boldsymbol{T}=\left[\begin{array}{c} t_{1}^{\mathrm{T}} \\ \vdots \\ t_{L}^{\mathrm{T}} \end{array}\right]_{N \times m} $ | (10) |
式中:W为输入层与隐含层之间的连接值;b为隐含层神经元阈值。
ELM参数无需全部给定,W和b在训练过程中随机给定,H在训练过程中保持不变。因此,整个神经网络的训练过程相当于寻找式(8)线性系统的最小二乘解
| $ \|\boldsymbol{H} \hat{\boldsymbol{\beta}}-\boldsymbol{T}\|=\min \limits_{\boldsymbol{\beta}}\|\boldsymbol{H} \boldsymbol{\beta}-\boldsymbol{T}\| $ | (11) |
通常L < N,故此时H奇异,可通过广义逆矩阵求解奇异矩阵的逆矩阵,即式(11)的解为:
| $ \hat{\boldsymbol{\beta}}=\boldsymbol{H}^{+} \boldsymbol{T} $ | (12) |
式中:H+为H的广义逆。
考虑到ELM中,W和b均为随机给定,对未知输入参数识别能力差,无法保证预测精度为模型最优。因此引入粒子群优化(particle swarm optimization,PSO)算法对ELM的输入参数寻优,提高模型预测精度。
PSO算法中每个粒子就是d维空间的一个潜在解,记为Qi=[qi1 qi2 … qid],第i个粒子的速度记为Vi=[vi1 vi2 … vid]。在迭代过程中,第i个粒子搜索到的最佳位置为Piopt=[pi1 pi2 … pid],所有粒子搜索到的最佳位置为Pg=[pg1 pg2 … pgd]。粒子按式(13)更新速度和位置。
| $ \left\{\begin{array}{l} \boldsymbol{V}_{i, t+1}=\omega_{0} \boldsymbol{V}_{i, t}+c_{1} r_{1}\left(\boldsymbol{P}_{\mathrm{iopt}, t}-\boldsymbol{Q}_{i, t}\right)+c_{2} r_{2}\left(\boldsymbol{P}_{\mathrm{g}, t}-\boldsymbol{Q}_{i, t}\right) \\ \boldsymbol{Q}_{i, t+1}=\boldsymbol{Q}_{i, t}+\boldsymbol{V}_{i, t+1} \end{array}\right. $ | (13) |
式中:i=1, 2, …, I,I为粒子总数;t为迭代次数;ω0为惯性权重因子;非负常数c1,c2为学习因子;r1,r2为[0, 1]之间的随机数。
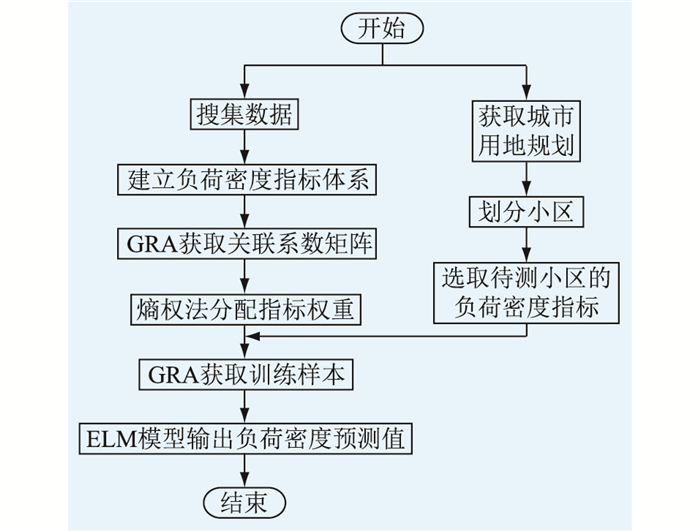
2.3 GRA-ELM建模步骤GRA-ELM建模步骤为:首先,利用GRA计算所有样本与待预测小区指标值之间的灰色关联度,选取灰色关联度较高的样本作为训练样本;然后,将挑选后的训练样本输入到ELM模型,并采用PSO算法对ELM模型的W和b进行寻优;最后,由模型输出预测值。
3 空间负荷预测实施方法基于熵权法与GRA-ELM的空间负荷预测方法,利用熵权法对负荷密度指标进行权重分配,应用GRA为ELM挑选训练样本,并采用PSO算法对ELM的参数进行寻优,主要步骤如下。
3.1 数据搜集在规划区域内,根据实际用地情况划分小区,搜集小区的历史负荷、面积、经济、人口等基础数据,为空间负荷预测奠定基础。
3.2 建立负荷密度指标体系建立负荷密度指标体系是为了确定不同类型负荷的影响因素和这些影响因素组成的样本库,为空间负荷预测提供参考依据及有效的数据基础,避免因数据收集不足、输入模型杂乱无序而降低预测精度[14]。
根据《城市用地分类与规划建设用地标准》[17]给定的小区用地、用电性质,将规划区域内的负荷划分为4~10类(具体可按实际情况确定),即商业负荷、居民负荷、工业负荷、物流负荷、教育科研负荷、公共负荷等。通过搜集到的数据,统计分析不同类型负荷的相关影响因素。建立负荷密度指标体系,得到不同类型负荷的密度值和影响因素数据库。不同类型负荷的影响因素如图 2所示。

|
图 2 不同类型负荷的影响因素 Fig. 2 Influencing factors of different types of loads |
应用熵权法对3.2节中的负荷密度指标进行权重分配,使得负荷密度指标体系更好地反映各因素对负荷密度值的影响。将权重分配结果具体应用在样本挑选和ELM中的数据输入上。若直接采用影响因素样本信息作为熵权法的输入,可能会掩盖影响因素信息与负荷密度值之间的某些联系。因此,利用GRA获取影响因素与负荷密度值之间的关联系数矩阵,作为熵权法的输入。
根据关联系数矩阵,应用熵权法获得负荷密度指标之间的权重分配。按式(1)计算关联系数矩阵的信息熵Ej,而后按式(3)计算各负荷密度指标权重wj。
3.4 基于GRA挑选训练样本为给ELM模型提供准确有效的训练样本,利用GRA对样本进行精选。以待预测小区的负荷密度指标为已知序列Y,样本的负荷密度指标为相关序列Xi,则二者之间的关联度为:
| $ G\left(\boldsymbol{Y}, \boldsymbol{X}_{i}\right)=\sum\limits_{j=1}\left[w_{j} g\left(\boldsymbol{Y}_{j}, \boldsymbol{X}_{i j}\right)\right] $ | (14) |
需要注意的是,在负荷密度指标权重分配中,GRA是用来获取影响因素与负荷密度的关联系数矩阵,为熵权法确定指标权重提供可靠的数据。在GRA-ELM模型中,GRA是用来挑选与待测小区负荷密度指标较为相近的样本,为ELM提供有效的训练数据,二者的使用方式和作用皆不相同。
3.5 ELM模型输出负荷密度值将GRA挑选的样本数据进行如式(15)所示的归一化处理,并将负荷密度指标数据乘上相应的指标权重wj,作为ELM模型的输入x′ i。
| $ x_{i}^{\prime}=\frac{x_{i}}{x_{\max }} $ | (15) |
式中:xi为第i个样本数据; xmax为各指标属性值中对应的最大值。
利用PSO算法优化ELM模型的W,b。将参数W,b编码为粒子,按式(14)迭代获取粒子最优位置,并解码得到最优解。将处理后的训练样本数据和优化后的参数输入到ELM中,得到待测区域的负荷密度预测值。
3.6 负荷值计算根据获得的小区负荷密度预测值yi和收集的小区面积si,可求得小区负荷预测值Pi。
| $ P_{i}=y_{i} s_{i} $ | (16) |
对不同类型负荷的小区求取负荷预测值,得到分类负荷预测值。将分类负荷预测值相加,则可得规划区域内的总负荷预测值。空间负荷预测流程如图 3所示。
|
图 3 空间负荷预测流程 Fig. 3 Process of spatial load forecasting |
以居民类小区为例,搜集上海市某居民类小区的负荷及影响因素数据,分析基于熵权法与GRA-ELM的空间负荷预测实际效果。在居民负荷中,选取的负荷密度指标为人口密度A1, 人均月收入A2, 人均负荷用电量预期A3, 电价A4。整理各指标数据,并计算小区负荷密度C,作为空间负荷预测模型的输入样本。小区样本总数为163,样本具体指标数据如表 1所示。
|
|
表 1 样本的各指标数据 Table 1 Each indicator data of the sample |
将上述样本输入GRA中,得到各指标与负荷密度值的关联系数矩阵,再将关联系数矩阵输入到熵权法模型中,得到各影响因素指标对负荷密度值的影响权重,结果如表 2所示。
|
|
表 2 影响因素对负荷密度值的影响权重 Table 2 The influence weight of influencing factors on the load density value |
由表 2可知,在居民负荷中,人口因素对小区负荷密度值的影响程度较高,电价因素对小区负荷密度值的影响程度较低。这与居民负荷中人口密度增大时用电需求随之增加,以及居家用电刚性需求受电价影响相对较小的实际情况相符。
计算待预测小区负荷密度指标数据与样本的灰色关联度,选取关联度大于0.9的样本进行训练。表 3为待预测小区指标数据与样本的灰色关联度。
|
|
表 3 待预测小区指标与样本的灰色关联度 Table 3 The gray correlation degree between the index of the community to be predicted and samples |
将训练样本输入ELM模型,输出待预测小区的负荷密度值,并根据式(16)计算小区负荷预测值。不同方法得到的预测值对比如表 4所示,负荷实际值为15.60 MW,相对误差为预测值相对实际值的误差大小。
|
|
表 4 不同方法的负荷预测结果 Table 4 Load forecasting results of different methods |
由表 4可知,文中方法预测值的相对误差为1.73%,精度较高;未引入熵权法进行负荷密度指标权重分配的方法预测精度稍低,相对误差为2.88%;未使用GRA挑选训练样本的方法预测精度较低,相对误差为8.01%。由此表明,训练样本的选择对模型的预测结果有重要影响。同时,负荷密度指标权重的合理分配,有助于提高预测精度。
进一步与文献[12]、文献[13]的负荷预测结果进行对比,结果见表 5。文献[12]采用模糊C-均值(fuzzy C-means,FCM)聚类算法挑选训练样本,利用LS-SVM得到预测结果。文献[13]采用GRA挑选训练样本,利用LS-SVM得到预测结果。
|
|
表 5 3种方法的负荷预测结果 Table 5 Load forecasting results of three methods |
由表 5可知,文中方法预测精度最高,其次为文献[13]采用GRA挑选样本的LS-SVM方法,最后为文献[12]采用FCM挑选样本的LS-SVM方法。对比不同方法的运行时间(6次运行时间的平均值),文中方法耗时最短。由此表明,文中所提方法预测精度较高,且具有较快的运行速度。
5 结语文中提出了基于熵权法与GRA-ELM的空间负荷预测方法,先引入熵权法对负荷密度指标进行了客观权重分配,而后利用ELM学习能力强、速度快的优势,采用GRA为ELM挑选高质量训练样本,并使用PSO算法对ELM参数进行优化,提高预测精度。实例分析表明,与未引入熵权法、未引入GRA或采用LS-SVM的方法相比,文中方法的空间负荷预测精度较高。
| [1] |
WILLIS H L. Spatial electric load forecasting[M]. New York: Marcel Dekker, 2002.
(  0) 0) |
| [2] |
肖白, 周潮, 穆钢. 空间电力负荷预测方法综述与展望[J]. 中国电机工程学报, 2013, 33(25): 78-92, 14. XIAO Bai, ZHOU Chao, MU Gang. Review and prospect of the spatial load forecasting methods[J]. Proceedings of the CSEE, 2013, 33(25): 78-92, 14. (  0) 0) |
| [3] |
周潮, 邢文洋, 李宇龙. 电力系统负荷预测方法综述[J]. 电源学报, 2012, 10(6): 32-39. ZHOU Chao, XING Wenyang, LI Yulong. Summarization on load forecasting method of electrical power system[J]. Journal of Power Supply, 2012, 10(6): 32-39. (  0) 0) |
| [4] |
马星河, 娄晨阳, 赵军营, 等. 基于人工蜂群算法的空间负荷预测[J]. 电力系统及其自动化学报, 2018, 30(8): 102-107. MA Xinghe, LOU Chenyang, ZHAO Junying, et al. Spatial load forecasting based on artificial bee colony algorithm[J]. Proceedings of the CSU-EPSA, 2018, 30(8): 102-107. DOI:10.3969/j.issn.1003-8930.2018.08.017 (  0) 0) |
| [5] |
程其云, 张晓星, 周湶, 等. 基于粗糙集数据挖掘的配电网小区空间负荷预测方法研究[J]. 电工技术学报, 2005, 20(5): 98-102. CHENG Qiyun, ZHANG Xiaoxing, ZHOU Quan, et al. Spatial load forecasting method for distribution net based on rough set data mining approach[J]. Transactions of China Electrotechnical Society, 2005, 20(5): 98-102. (  0) 0) |
| [6] |
肖白, 杨欣桐, 田莉, 等. 计及元胞发展程度的空间负荷预测方法[J]. 电力系统自动化, 2018, 42(1): 61-67. XIAO Bai, YANG Xintong, TIAN Li, et al. Spatial load forecasting method based on development degree of cell[J]. Automation of Electric Power Systems, 2018, 42(1): 61-67. (  0) 0) |
| [7] |
张纪伟, 刘晓明, 贡卓, 等. 基于城市用地性质及开发时间的改进空间负荷预测方法研究[J]. 供用电, 2019, 36(7): 65-70. ZHANG Jiwei, LIU Xiaoming, GONG Zhuo, et al. Research on improved spatial load forecasting method based on land use and development time[J]. Distribution & Utilization, 2019, 36(7): 65-70. (  0) 0) |
| [8] |
肖白, 杨修宇, 穆钢, 等. 基于多变量分析的城市电网空间负荷预测方法[J]. 东北电力大学学报, 2013, 33(Z1): 39-44. XIAO Bai, YANG Xiuyu, MU Gang, et al. Spatial electric load forecasting of urban power system based on multivariate analysis[J]. Journal of Northeast Dianli University, 2013, 33(Z1): 39-44. (  0) 0) |
| [9] |
梁荣, 杨波, 马润泽, 等. 利用多源信息和深度置信神经网络的配电系统空间负荷预测[J]. 电力建设, 2018, 39(10): 12-19. LIANG Rong, YANG Bo, MA Runze, et al. Spatial electric load forecasting for distribution systems using multi-source information and deep belief network-deep neural network[J]. Electric Power Construction, 2018, 39(10): 12-19. (  0) 0) |
| [10] |
杨军胜, 彭石, 王承民, 等. 基于城市用地性质的配网空间负荷预测研究[J]. 电测与仪表, 2018, 55(11): 30-34. YANG Junsheng, PENG Shi, WANG Chengmin, et al. Research of spatial load forecasting in distribution network based on grid partition of urban land-use property[J]. Electrical Measurement & Instrumentation, 2018, 55(11): 30-34. (  0) 0) |
| [11] |
吴争荣, 孔祥玉, 董旭柱, 等. 基于配用电信息分区分类的短期空间负荷预测[J]. 电力系统及其自动化学报, 2019, 31(2): 26-31. WU Zhengrong, KONG Xiangyu, DONG Xuzhu, et al. Short-term spatial load forecasting based on partition and classification of power distribution information[J]. Proceedings of the CSU-EPSA, 2019, 31(2): 26-31. (  0) 0) |
| [12] |
周湶, 孙威, 任海军, 等. 基于最小二乘支持向量机和负荷密度指标法的配电网空间负荷预测[J]. 电网技术, 2011, 35(1): 66-71. ZHOU Quan, SUN Wei, REN Haijun, et al. Spatial load forecasting of distribution network based on least squares support vector machine and load density index system[J]. Power System Technology, 2011, 35(1): 66-71. (  0) 0) |
| [13] |
唐玮, 钟士元, 舒娇, 等. 基于GRA-LSSVM的配电网空间负荷预测方法研究[J]. 电力系统保护与控制, 2018, 46(24): 76-82. TANG Wei, ZHONG Shiyuan, SHU Jiao, et al. Research on spatial load forecasting of distribution network based on GRA-LSSVM method[J]. Power System Protection and Control, 2018, 46(24): 76-82. (  0) 0) |
| [14] |
刘业峰, 王婷. 基于GRA-LSSVM密度法的配电网空间负荷预测方法研究[J]. 计算机测量与控制, 2018, 26(11): 256-260. LIU Yefeng, WANG Ting. Research on spatial load forecasting of distribution network based on GRA-LSSVM density method[J]. Computer Measurement & Control, 2018, 26(11): 256-260. (  0) 0) |
| [15] |
周俊峰, 胡诗尧, 安佳坤, 等. 基于熵权法和灰色关联度的中压配电网供电水平关键性指标研究[J]. 科技通报, 2019, 35(12): 101-104. ZHOU Junfeng, HU Shiyao, AN Jiakun, et al. Research on key indexes of power supply level of medium-voltage distribution network based on entropy-weighted method and grey relational degree[J]. Bulletin of Science and Technology, 2019, 35(12): 101-104. (  0) 0) |
| [16] |
牟多铎, 刘磊. ELM与SVM在高光谱遥感图像监督分类中的比较研究[J]. 遥感技术与应用, 2019, 34(1): 115-124. MOU Duoduo, LIU Lei. Comparative study of ELM and SVM in hyperspectral image supervision classification[J]. Remote Sen-sing Technology and Application, 2019, 34(1): 115-124. (  0) 0) |
| [17] |
中华人民共和国住房和城乡建设部. 城市用地分类与规划建设用地标准: GB 50137-2011[S]. 北京: 中国计划出版社, 2012. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for classification of urban land use and planning standards of development land: GB 50137-2011[S]. Beijing: China Planning Press, 2012. (  0) 0) |
2. Nanjing Hao-qing Information Technology Co., Ltd., Nanjing 210006, China
 2021, Vol. 40
2021, Vol. 40


 邓燕国(1997), 男, 硕士在读, 研究方向为空间负荷预测、新能源技术(E-mail:
邓燕国(1997), 男, 硕士在读, 研究方向为空间负荷预测、新能源技术(E-mail: