文章编号: 2096-3203(2021)04-0182-07 中图分类号: TM75
2. 国网山西省电力公司, 山西 太原 030021;
3. 国电南瑞科技股份有限公司, 江苏 南京 211106
电力输电线路作为电力输送的重要通道,其可靠性、稳定性对电网的安全稳定运行至关重要。然而,采空区地质塌陷造成的杆塔倾斜与基础不均匀沉降问题严重威胁着输电线路的可靠性,杆塔倾斜与沉降产生的非荷载应力极有可能导致杆塔构件破坏、断裂、变形等事故,甚至导致输电线路被迫停运等[1-2]。因此,采空区输电线路杆塔稳定性研究已成为全国电力行业关注的热点安全问题[3]。
目前已有部分专家学者在输电杆塔设计优化方面展开研究,虽然取得了不少进展,但在输电线路杆塔结构的优化设计中,一些重要附加因素仍未在实际应用中予以考虑[4-5]。文献[6]讨论了采空区输电线路杆塔的优化问题,该结构承受多个荷载工况和条件约束,但实验条件较为理想,杆塔四面均为对称,得出的最佳杆塔结构难以适用于采空区。文献[7]研究了输电线路杆塔在多工况和规范约束下的形状优化问题,由于该方法是基于连续变量设计的,因此无法保证最终杆塔结构能够满足采空区沉降和倾斜等特殊外部环境要求。文献[8]对大型输电线路铁塔进行了尺寸、形状和拓扑优化,优化后的结构在横风的作用下不会发生较大形变。
以上研究大多基于局部优化措施以改进拓扑结构,最终设计可能改进有限,从结构角度来看对采空区的使用场景还是较难适应[9]。并且输电杆塔结构中不包含钢结构,很难正确评估有效屈曲长度[10]。此外,在全尺寸输电线路塔的设计中,所有结构的对称性很难实现,为此,在传统输电塔的设计中常采用交错支撑非对称结构,作为给定输电线路中结构的主体部分。文献[11]在考虑横截面积离散值和规范约束的情况下,对承受多个荷载的输电线路塔进行了尺寸和形状优化,通过将结构分块进行优化。而块体的几何结构是独立更改的,因此最终设计会显示每个块体中支腿坡度之间的差异。文献[12]提出一种先设计塔体形状,后优化构件类型的方法,该方法考虑了横截面积的离散值,并在塔身形状修改过程中考虑应力和稳定性约束,对塔节数、各节高度和所用隔板的类型进行了优化。
但上述方法未充分考虑采空区沉降导致杆塔倾斜所带来的输电杆塔应力变化,因此文中提出一种结合应力、位移、长细比等标准设计约束,并基于混合启发式的输电线路杆塔设计优化方法。(1) 针对采空区的地势特点以及输电线路杆塔的拓扑结构,将杆塔分成3个部分,并提出其拓扑优化的方法,即选择最合适的杆塔支撑形式、边缘形式、内层数以及冗余数。(2) 传统输电线路杆的材料弹性较差,在采空区发生杆塔倒塌的可能性更大。因此,采用纤维增强复合材料(fiber reinforced plastic,FRP)设计杆塔横担,保证在多向荷载作用下,杆塔受力性能良好,以提高其承载力,更好地适用于采空区。(3) 现有输电线路杆塔难以满足应力、位移、重量等约束条件,而文中方法利用回溯搜索算法(backtracking search algorithm,BSA)求解杆塔结构优化问题,实现了杆塔尺寸、形状和拓扑的优化,能够满足采空区的应用需求。
1 输电杆塔的拓扑结构设计目前输电线路杆塔结构设计的工业实践通常采用三维桁架或框架单元进行线弹性(或几何非线性)分析,虽然简化了模型,但可能会出现一些非线性效应,主要与杆塔连接件的实际性能有关。由于缺乏可靠的实验数据,最初的研究侧重于评估螺栓滑移对结构性能的影响,而非开发实际的模型,且研究表明螺栓的滑移对结构的挠度有一定影响,但对结构的极限强度影响不大。
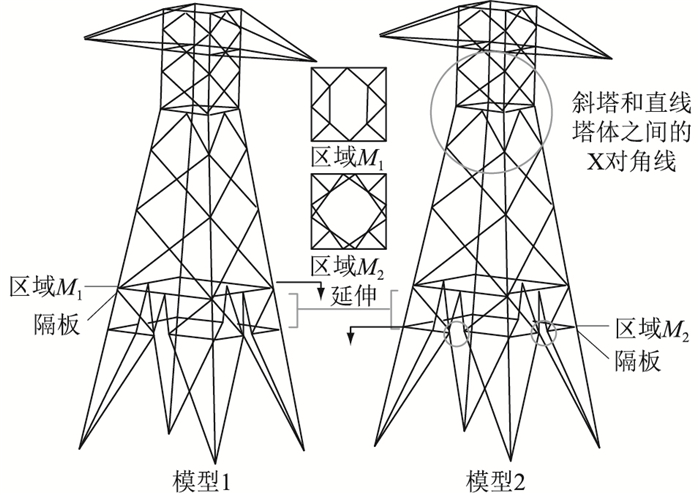
CIGRÉ设计了一个原始输电线路杆塔结构并进行内力测试,以更好地了解其结构特性。基于此,CIGRÉ提出并测试了3种拓扑结构差异较小的新型原型结构,虽然差别很小,但其对结构的刚度起着重要作用。并利用Ungkurapinan确定的典型塔角实验荷载-滑移关系,将实验原型结构的连接件建模为非线性弹簧,2种刚度结构的结构预测值与实验观测值接近。此外,CIGRÉ实验研究证实了杆塔结构刚度越大,螺栓滑移对塔架性能的影响就越大,随着结构刚度的增加,简单模型的预测结果在某些构件中有较大差异。因此,在实践中,横担的位置和对角线的配置会使杆塔更灵活,从而减少螺栓滑移的影响。其中,输电线路杆塔中横隔板位置和对角线配置如图 1所示,图中展示了2种不同结构的杆塔模型。
|
图 1 不同的输电线路杆塔拓扑结构 Fig. 1 Different transmission line tower topologies |
斜塔体和直塔体之间的对角线配置以及截面配置使模型2的刚度显著增加,因为“X”结构的对角线边缘增强了杆塔刚度。而文中方法针对输电线路杆塔结构的影响因素展开研究。
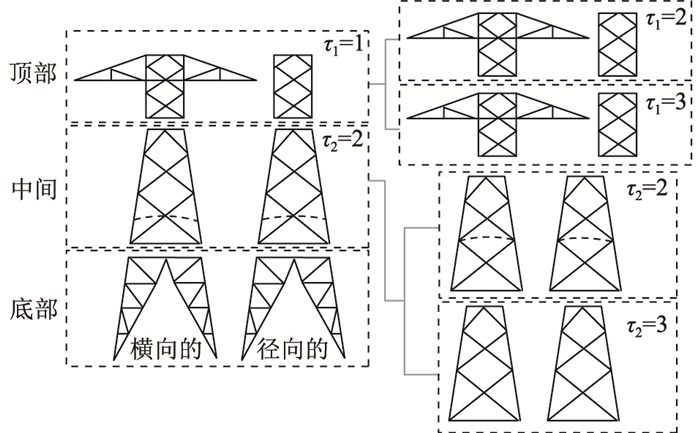
1.1 拓扑优化方法文中方法中的输电线路杆塔结构被划分为3个模块:高级、中级和低级[13],这些模块可以假设为不同预先建立的拓扑,利用预先建立的拓扑模块进行拓扑优化的流程如图 2所示。在优化过程中,通过在可能的模板组合中选择能够提供较轻结构并满足约束条件的模板组合,同时对拓扑结构的大小和形状进行优化。
|
图 2 基于模块进行拓扑优化 Fig. 2 Topology optimization based on modules |
拓扑优化中也可以使用交错支撑的结构,但会导致结构支腿中长度屈曲,即采用交错支撑时,正确的屈曲长度并不是简单地由相邻节点之间的距离确定。因此,有必要规定正确的有效屈曲长度和结构拓扑。现有方法中屈曲长度大多直接从结构模型中计算2个相邻节点之间的距离获得。文中方法中屈曲长度可与每个可用的模板共同定义,从而允许在优化过程中正确建模局部屈曲,即使在交错支撑的复杂情况下也是如此。
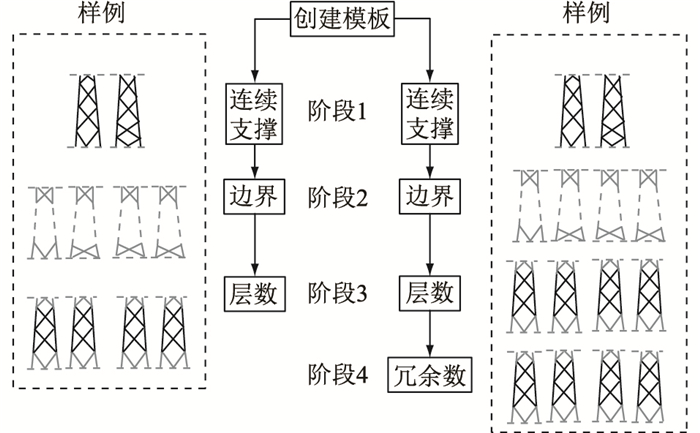
正如CIGRÉ的实验证明和以上论述的,拓扑结构在全尺寸实验中起着重要作用,即使是结构上的微小变化也会直接影响结构性能和与设计所采用的机械模型的兼容性。基于所有因素的考虑,输电线路杆塔结构模板创建规则如图 3所示,主要包括4个阶段。
|
图 3 输电线路杆塔结构模板的创建规则 Fig. 3 Rules for the creation of transmission line tower structure template |
阶段1:支撑形式的选择,连续或交错,是中高输电杆塔中最常见的支撑形式。交错支撑的优点在于不需要多余的构件,但通常需要更多的对角线。
阶段2:边缘的选择。支撑边缘的微小变化也会对结构性能产生重大影响,从而影响优化结果,通过此过程,可以选择所有的配置可能性。
阶段3:内部层的数量。结构承载力的增加(因屈曲长度的减少)与总重量的增加之间存在权衡。
阶段4:冗余数的选择。冗余构件负责减少屈曲长度,但仅适用于具有连续支撑的塔,其屈曲长度及其最终重量直接影响最终结构承载力。
1.2 FRP复合材料横担结构FRP作为一种新型复合材料,主要原料包含纤维增强材料和基体树脂,经过一定的比例混合后按特定工艺复合而成,能够充分发挥不同组分间材料的优势,甚至产生新的优越性能。FRP材料制作的输电杆塔能够大幅度降低运输和安装成本,同时能够提高杆塔承载力。
横担通常位于输电杆塔顶部,是一种横向固定的桁架体系。传统横担通常使用钢结构,为改进横担性能,提出了一种使用FRP复合材料设计的横担构架,不仅能够减轻横担导线悬挂位置所承受张力,还能够增加主塔或者主杆上吊杆的柔性,以增强杆塔稳定性。
在工程实际中,需要对杆塔的应力作近似分析,将杆塔立体结构转化为平面形式。目前存在多种近似计算,文中方法采用矩形横担进行应力分析。假设前后两平面桁架主要承受垂直荷载,下平面主要承受横向荷载,纵向荷载有2种假设。
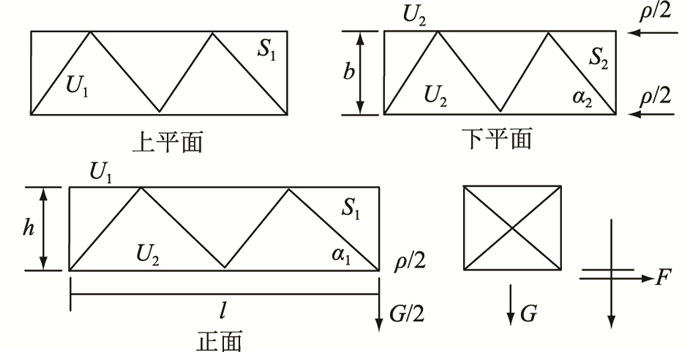
(1) 上平面不承受纵向张力时,如图 4所示。
|
图 4 矩形横担(上平面不承受纵向张力) Fig. 4 Rectangular cross arm (upper plane does not bear longitudinal tension) |
| $ \left\{\begin{array}{l} U_{1}=G l /(2 h) \\ U_{2}=-G l /(2 h) \pm(F l) / b \\ S_{1}=G /\left(2 \sin a_{1}\right) \\ S_{2}=F / \sin a_{2} \end{array}\right. $ | (1) |
式中:F为横担受到的外界压力;U1,U2分别为上、下平面承受的压力;S1,S2分别为上、下平面承受的张力;G为重力;h为横担的高;b为横担的宽;l为横担的宽;α为力的夹角。
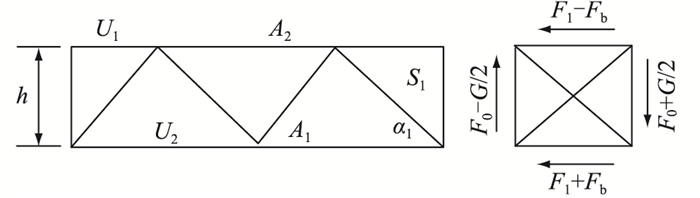
(2) 上平面承受纵向张力时,如图 5所示。
|
图 5 矩形横担(上平面承受纵向张力) Fig. 5 Rectangular cross arm (the upper plane bears longitudinal tension) |
横担并不是对称的截面,则计算横担截面的重心距离x为:
| $ x=\frac{A_{1}\left(h-Z_{1}\right)+A_{2} Z_{2}}{A_{1}+A_{2}} $ | (2) |
式中:Z1,Z2分别为上、下主角钢的重心距离;A1,A2分别为上、下主角钢截面积。
作用在上、下平面的剪力分别为F1,F2:
| $ \left\{\begin{array}{l} F_{1}=\frac{A_{1}}{A_{1}+A_{2}\left(l_{2} / l_{1}\right)^{3}} F \\ F_{2}=F-\frac{A_{1}}{A_{1}+A_{2}\left(l_{2} / l_{1}\right)^{3}} F \end{array}\right. $ | (3) |
式中:l1,l2分别为横担上、下平面的宽。则杆塔受力为:
| $ \left\{\begin{array}{l} U_{1}=-\left(F_{2}-F_{\mathrm{b}}\right) l / b-\left(F_{\mathrm{a}}-G / 2\right) l / h \\ \text {或 } U_{1}=\left(F_{2}-F_{\mathrm{b}}\right) l / b+\left(F_{\mathrm{a}}+G / 2\right) l / h \\ U_{2}=-\left(F_{1}+F_{\mathrm{b}}\right) l / b+\left(F_{\mathrm{a}}-G / 2\right) l / h \\ \text {或 } U_{2}=\left(F_{1}+F_{\mathrm{b}}\right) l / b-\left(F_{\mathrm{a}}+G / 2\right) l / h \\ S_{1}=\pm\left(G / 2+F_{\mathrm{a}}\right) / \sin a_{1} \\ S_{2}=\pm\left(F_{1}+F_{\mathrm{b}}\right) / \sin a_{2} \end{array}\right. $ | (4) |
式中:Fa,Fb为作用在各面的扭力。
1.3 基于混合启发式的输电线路杆塔结构优化拓扑优化在于输电线路杆塔的尺寸和形状优化。对于尺寸优化,将结构构件的横截面积作为设计变量,并存储在矢量A中;将所选节点的坐标作为形状优化的设计变量,并存储在矢量ζ中。出于实际目的,将与节点坐标有关的设计变量作为离散值,并使用拓扑向量τ来存储结构的每个模块中所使用的模板。设计变量的最终向量为x。
优化目标是在满足约束条件的前提下,使结构重量最小化,则问题描述为:
| $ \boldsymbol{x}=\{\boldsymbol{A}, \boldsymbol{\zeta}, \boldsymbol{\tau}\}=\left\{A_{1}, \cdots, A_{m}, \zeta_{1}, \cdots, \zeta_{q}, \tau_{1}, \cdots, \tau_{s}\right\} $ | (5) |
最小化:
| $ W(x)=\sum\limits_{i=1}^{m} \rho_{i} l_{i}(x) A_{i}(x) $ | (6) |
受压力约束:
| $ y_{i}(x)=\left|\sigma_{i}(x)\right|-\bar{\sigma}_{i} \leqslant 0 \quad i=1,2, \cdots, m $ | (7) |
长细比约束:
| $ y_{i+m}(x)=v_{i}(x)-\bar{v}_{i} \leqslant 0 \quad i=1,2, \cdots, m $ | (8) |
横截面约束:
| $ y_{i+2 m}(x)=\frac{w_{i}(x)}{h_{i}(x)}-w / h_{\max } \leqslant 0 \quad i=1,2, \cdots, m $ | (9) |
式中:m为横截面数目;q为节点坐标数目;s为作为设计变量的拓扑变化数目;W为结构重量;ρi为第i根FRP材料的比重;li为第i根FRP材料的长度;σi为第i根FRP材料的轴向应力;σi为第i根FRP材料的允许应力;υi为第i根FRP材料的细长率;υi为第i根FRP材料的允许细长率;hi为第i根FRP材料的厚度;wi为第i根FPR材料角轮廓腿的扁平宽度;w/hmax为h和w之间的允许关系。
对于优化问题中的约束条件,采用惩罚方法将其转化为不受约束的问题,可避免搜索算法的收敛问题。其惩罚函数Pt为:
| $ \begin{gathered} P_{t}(x)=a\left[\sum\limits_{i=1}^{m}\left(\frac{\left|\sigma_{i}(x)\right|-\bar{\sigma}_{i}}{\bar{\sigma}_{i}}\right)^{+}+\right. \\ \sum\limits_{i=1}^{m}\left(\frac{\left|\boldsymbol{v}_{i}(x)\right|-\overline{\boldsymbol{v}}_{i}}{\overline{\boldsymbol{v}}_{i}}\right)^{+}+ \\ \left.\sum\limits_{i=1}^{m}\left(\frac{w_{i}(x) / h_{i}(x)-w / h_{\max }}{w / h_{\max }}\right)^{+}\right] \end{gathered} $ | (10) |
式中:a为一个正常数参数,a=108;(·)+表示操作,(·)+= (·) +(·)/2。选择合适的惩罚函数对文中方法的性能影响很大,Pt太大会阻止算法收敛,而Pt太小可能不足以避免不可行的解决方案。
离散变量以及优化问题存在非凸性和非线性特性,因此采用BSA进行求解。BSA是Civicioglu开发的基于多主体的进化算法,能够解决无约束的非凸优化问题[14]。其主要步骤如下:
(1) 初始化。BSA的初始种群Q生成为:
| $ (Q)_{i j} \sim U\left(x_{j}^{\min }, x_{j}^{\max }\right) $ | (11) |
式中:U为统一随机变量;xjmax,xjmin分别为第j个设计变量的上、下限。i=1, …, ttop,j=1, …, nv,其中ttop为种群大小,nv为问题维度。构造初始种群后,生成实验种群并对其进行更新,直到达到某个收敛准则,此时启动算法。
(2) 构建种群Qpert。对种群Qpert进行建模,首先需要利用历史种群Qold评估将应用于当前种群的扰动方向,其中Qold有2种可能的情况,每种情况的发生概率均为50%。被扰动的总体评估为:
| $ Q_{\text {pert }}=Q+\boldsymbol{M}\left[\alpha\left(Q_{\text {old }}-Q\right)\right] $ | (12) |
式中:α为控制搜索方向的随机参数,α=3N,其中N为标准正态随机变量;M设置为ttop×nv零矩阵。
(3) 选择新种群。评估种群Qpert的每个个体的适应度值,将被扰动种群的第Qpert, i个个体的目标值与Qi的第i个个体的目标值进行比较。如果Qpert, i的目标函数比Qi的目标函数好,则在新算法中后者被前者替换,以此得到算法的最优解。
2 实验结果与分析为了说明文中方法的性能,采用Matlab中开发的有限元程序对输电线路杆塔的结构设计进行实验论证。
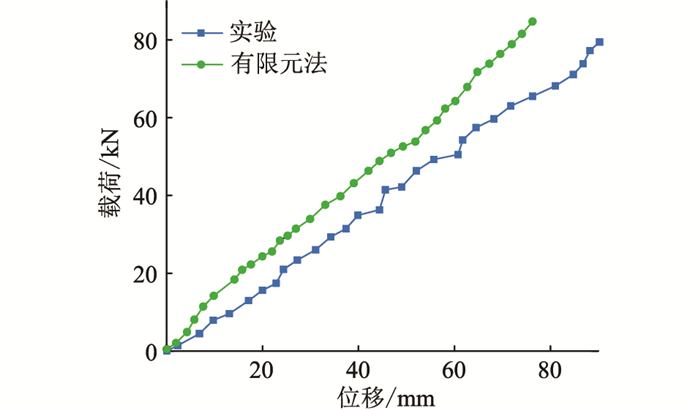
2.1 输电线路杆塔的有限元分析对横担体系进行有限元模拟[15-16],在75 kN合力作用下,将FRP的荷载-应变曲线与实验结果进行对比分析,结果如图 6及表 1所示。
|
图 6 FRP横担体系试件荷载-位移曲线 Fig. 6 Load displacement curve of FRP cross arm system |
|
|
表 1 有限元模拟结果对比 Table 1 Comparison of finite element simulation results |
由于有限元模拟FRP横担体系时没有考虑部件原有的不足,模拟中各个部件均较为理想[17],因此实验与有限元模拟的载荷在大小和方向上均会存在一定的误差。从表 1可看出:施加载荷一端的最大位移相对误差是16.68%。此外,横担体系应变数值与实验值相差不大,相对误差均小于5%。输电线路杆塔采用FRP横担增加其弹性,提高了杆塔承载力,满足了预期需求。
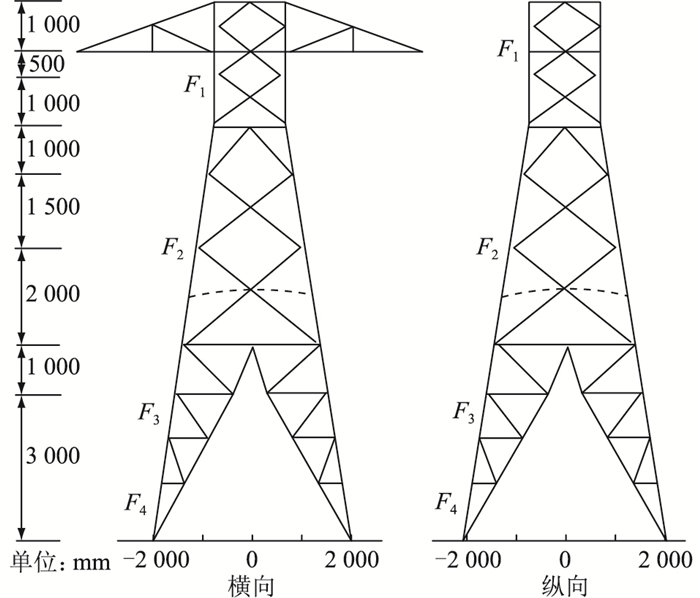
2.2 输电线路杆塔结构优化的对比分析基于CIGRÉ描述的输电线路杆塔结构,利用文中方法对杆塔的尺寸和形状进行优化。输电线路杆塔的设计如图 7所示。其中横担采用FRP复合材料,螺栓直径为12 mm,每个构件中使用角度剖面及其特性、多余构件的位置、施加的荷载情况以及每个荷载情况等数据信息监控关键构件上的确定应力。
|
图 7 杆塔设计 Fig. 7 Tower design |
为了清楚地了解优化过程对最终结果的影响,分别进行3项研究:(1) 尺寸优化;(2) 尺寸和形状优化;(3) 尺寸、形状和拓扑优化。在所有场景中,分别使用BSA方法和文献[6]、文献[8]、文献[11]方法。文献[6]中输电线路杆塔优化结构能够承受多个荷载工况和条件约束,但在采空区的复杂环境下性能不佳;文献[8]中输电线路铁塔实现了尺寸、形状和拓扑优化,且优化后的结构抵抗横风的干扰能力较强,但实际环境中风向不可控,因此性能不稳定;文献[11]中提出了结构分块的优化方式,对承受多个荷载的输电线路塔进行了尺寸和形状优化。而文中方法考虑的因素更为全面,基于分块优化的模式进行输电杆塔的尺寸、形状和拓扑优化,适用于复杂环境。
此外,为更准确地评估各优化水平对塔减重的影响,将(2)和(3)中提供的结果与(1)中获得的结果进行比较。其中BSA算法的参数为:总体Q=50,循环次数5 000。
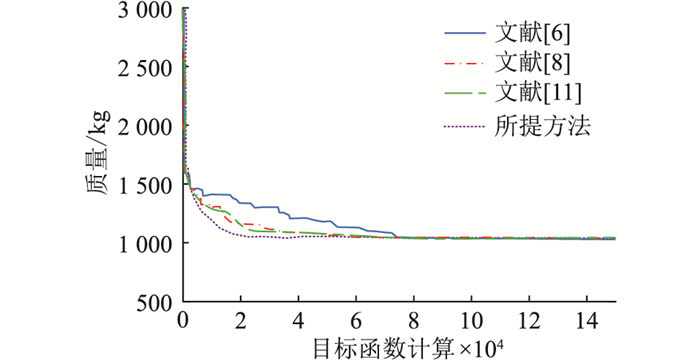
(1) 尺寸优化。应尽可能减少设计变量,根据其相似性和结构要求对钢材进行分组,总共有35个设计变量,其向量定义为x= A1, …, A35,其中Ai是每组的横截面积。不同优化算法的尺寸优化结果如图 8所示。
|
图 8 不同优化算法的尺寸优化结果 Fig. 8 Size optimization results of different optimization algorithms |
由图 8可知,文中方法的收敛速度最快,得到的输电线路杆塔总质量最小为1 046.7 kg,且经过30次迭代后,标准差为0.66 kg,相比于文献[6]、文献[8]和文献[11]的标准差9.82 kg,7.69 kg,3.75 kg,文中方法在尺寸优化方面效果较为理想。
(2) 尺寸和形状优化。对于尺寸和形状优化,节点坐标也作为设计变量,其中变量1水平应用于4个基础节点,变量2水平应用于20个顶部节点,变量3垂直应用于4个中间节点,所有节点均位于塔腰。设计向量为x={A1, …, A35, ζ1, ζ2, ζ3},其中ζi为节点通过优化算法从其原始位置偏移的距离。
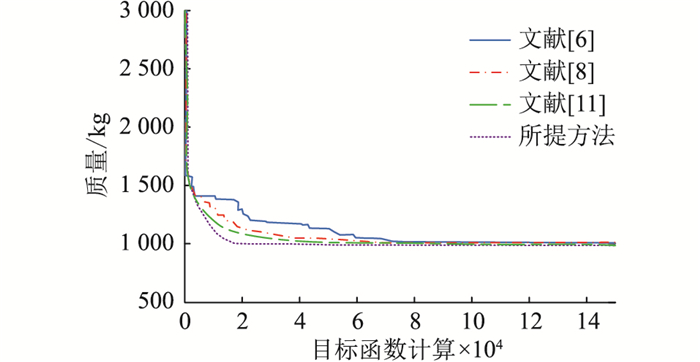
施加在变量ζ1,ζ2,ζ3的上下限分别为[-20 cm, 20 cm],[-10 cm, 10 cm],[-20 cm, 20 cm],均可在每1 cm处假设离散值。每个优化算法的实验结果如图 9所示。
|
图 9 不同优化算法的尺寸和形状优化结果 Fig. 9 Size and shape optimization results of different optimization algorithms |
图 9中可得出,文中方法的结果最佳,输电杆塔总质量为1 032.2 kg,平均值为1 035.6 kg,标准差为2.55 kg。结果表明,用BSA法再次获得了最佳结果,且相比于仅通过尺寸优化获得的结果,结构质量得到了进一步降低。
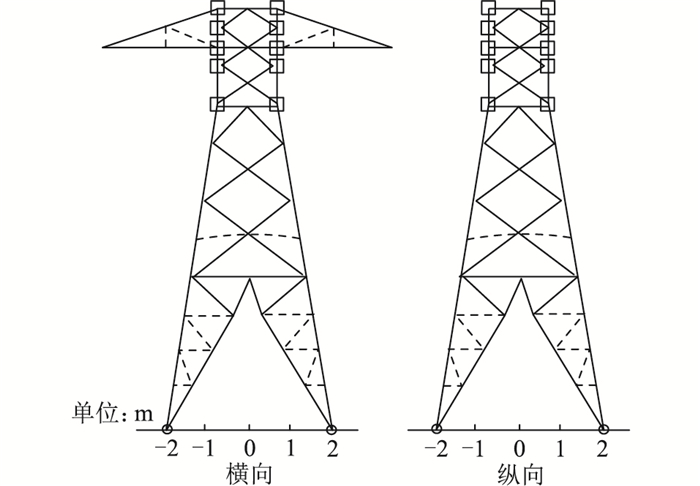
(3) 尺寸、形状和拓扑优化。输电杆塔拓扑结构由2个附加变量τ1和τ2定义,这2个变量可以假设值1, 2, 3表示用于结构每个部分的模板。因此,设计向量现在写为x={A1, …, A35, ζ1, ζ2, ζ3, τ1, τ2}。通过尺寸、形状和拓扑优化获得最佳交错支撑的结构设计,其横向和纵向视图如图 10所示。
|
图 10 横向和纵向面尺寸、形状和拓扑优化的最佳结果 Fig. 10 Optimal results of size, shape and topology optimization of transverse and longitudinal surfaces |
相比于上述2个场景的研究,文中方法得到的总质量为993.4 kg,平均结果为999.1 kg,标准偏差为5.78 kg,相较于其他方法,均是最为理想的。
将上述3种场景的最佳结果进行对比,结果如表 2所示。
|
|
表 2 CIGRÉ塔3个研究场景的最佳结果对比 Table 2 Comparison of the best results of three research scenarios of CIGRÉ tower |
表 2显示了3个场景的最佳结果以及与仅尺寸优化相比的重量减少百分比。可见,拓扑优化确实可以显著改善结构设计,即提出的拓扑优化方法在实际应用中具有有效性。此外,在实例研究中,相对于其他方法,采用文中方法得到的平均值和标准差也表明其具有更优越的性能,证明该方法能够在未来工程研究中推广实施。
3 结语针对现有输电线路杆塔结构难以很好地应用于采空区且杆塔设计方法不理想的问题,提出了一种面向采空区的输电线路杆塔设计优化方法。在明确杆塔拓扑优化流程的基础上,采用FRP材料制作杆塔的横担,以及利用BSA算法求解所提的优化问题,以满足杆塔应力等约束,实现尺寸、形状和拓扑的优化。最后基于有限元方法对文中方法的性能进行实验,结果表明,横担采用FRP材料的输电线路杆塔在多向荷载作用下无明显形变,弹性较好,很大程度上提高了其承载力。此外,与其他优化方法相比,文中方法能够在最短的时间内获得尺寸、形状和拓扑的优化结果,且结果最优,在满足杆塔的多重约束下,降低了杆塔的质量,同时由交错支撑构成的最优拓扑,设计的输电线路杆塔更适用于采空区。
由于横担体系在实际状态中的受力情况较为复杂,实验仅对FRP复合材料横担体系进行了静力过载分析,对横担体系在覆冰荷载、动荷载(风荷载、雪荷载)情况下的受力性能还有待进一步研究。并且在输电线路杆塔拓扑优化问题中,考虑的约束因素并不全面,因此接下来的工作将考虑更多的影响因素,以更好地应用于生产实际。
| [1] |
李岩, 滕云, 冷欧阳, 等. 数据驱动的输电线路在线监测装置可靠性评估[J]. 中国电机工程学报, 2018, 38(15): 4410-4419, 4641. LI Yan, TENG Yun, LENG Ouyang, et al. Reliability evaluation of on-line monitoring device over transmission line based on data driven concept[J]. Proceedings of the CSEE, 2018, 38(15): 4410-4419, 4641. (  0) 0) |
| [2] |
黄明祥, 卞宏志, 林奕夫, 等. 500 kV双回输电线路转角塔附近屋顶畸变电场分析[J]. 电力工程技术, 2019, 38(3): 140-145, 174. HUANG Mingxiang, BIAN Hongzhi, LIN Yifu, et al. The distorted electric field on rooftop near angle tower of 500 kV double circuit transmission lines[J]. Electric Power Engineering Technology, 2019, 38(3): 140-145, 174. (  0) 0) |
| [3] |
TAO G H, FANG L J. A multi-unit serial inspection robot for power transmission lines[J]. Industrial Robot: the International Journal of Robotics Research and Application, 2019, 46(2): 223-234. DOI:10.1108/IR-09-2018-0195 (  0) 0) |
| [4] |
WANG Y, LANG L J, LEE C H, et al. Topologically enhanced harmonic generation in a nonlinear transmission line metamaterial[J]. Nature Communications, 2019, 10(1): 1102. DOI:10.1038/s41467-019-08966-9 (  0) 0) |
| [5] |
刘云. 同塔并架高压直流输电线路故障及保护特性研究[J]. 电力工程技术, 2019, 38(3): 163-169. LIU Yun. Characteristics of fault and protection of the multi HVDC transmission lines on the same tower[J]. Electric Power Engineering Technology, 2019, 38(3): 163-169. (  0) 0) |
| [6] |
ACOSTA J S, TAVARES M C. Multi-objective optimization of overhead transmission lines including the phase sequence optimization[J]. International Journal of Electrical Power & Energy Systems, 2020, 115: 105495. (  0) 0) |
| [7] |
SCHMIDT M K, NIELSEN M G, ENDAHL B, et al. Thor-a new design of overhead transmission line towers[J]. Papers, 2019, 3(3-4): 403-408. (  0) 0) |
| [8] |
JANGID M D. Wind analysis of four legged transmission towers with different bracing systems for angle section & tube section[J]. Recent Trends in Civil Engineering & Technology, 2019, 9(1): 1-11. (  0) 0) |
| [9] |
葛小宁, 庞福滨, 嵇建飞, 等. 采用六相输电技术优化双回高压输电线路电磁环境的研究[J]. 电力工程技术, 2019, 38(1): 1-5. GE Xiaoning, PANG Fubin, JI Jianfei, et al. Improving the electromagnetic environment of a double-circuit high-voltage transmission line using the six-phased technology[J]. Electric Power Engineering Technology, 2019, 38(1): 1-5. (  0) 0) |
| [10] |
刘俊卿, 袁红丽, 文凡, 等. 输电塔结构八地脚螺栓塔座板的抗拉承载力试验与计算方法研究[J]. 土木工程学报, 2019, 52(7): 48-56. LIU Junqing, YUAN Hongli, WEN Fan, et al. Experimental research and calculation method for tensile bearing capacity of the base plate with eight bolts in transmission tower structure[J]. China Civil Engineering Journal, 2019, 52(7): 48-56. (  0) 0) |
| [11] |
CAI C S, WANG J H, JING H, et al. Universal wireless powered terminals for robust overhead transmission line monitoring[J]. IET Power Electronics, 2019, 12(14): 3739-3748. DOI:10.1049/iet-pel.2019.0206 (  0) 0) |
| [12] |
JI Y M, WU F J, ZHANG Y B. Influence of the structure of transmission line on harmonics distribution in DC system[J]. The Journal of Engineering, 2019, 2019(16): 2185-2192. DOI:10.1049/joe.2018.8649 (  0) 0) |
| [13] |
郝宝新, 周志成, 曲广吉, 等. 桁架结构拓扑优化的半定规划建模与求解[J]. 哈尔滨工业大学学报, 2019, 51(10): 11-21. HAO Baoxin, ZHOU Zhicheng, QU Guangji, et al. Modeling and solving of truss topology optimization problems based on semidefinite programming[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 11-21. DOI:10.11918/j.issn.0367-6234.201901070 (  0) 0) |
| [14] |
CHATZIPAVLIS A, TSEKOURAS G E, TRYGONIS V, et al. Modeling beach realignment using a neuro-fuzzy network optimized by a novel backtracking search algorithm[J]. Neural Computing and Applications, 2019, 31(6): 1747-1763. DOI:10.1007/s00521-018-3809-2 (  0) 0) |
| [15] |
秦会来, 周予启, 周同和, 等. 预留土基坑支护性状的有限元分析[J]. 岩土工程学报, 2019, 41(S1): 9-12. QIN Huilai, ZHOU Yuqi, ZHOU Tonghe, et al. Retaining traits of berm-retained excavations by FEM[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S1): 9-12. (  0) 0) |
| [16] |
杨富磊, 张玉婵, 祁志远, 等. 基于有限元的预绞式耐张金具发热故障分析[J]. 电气技术, 2019, 20(1): 24-26, 30. YANG Fulei, ZHANG Yuchan, QI Zhiyuan, et al. Analysis of preheated tension fittings on high voltage transmission lines[J]. Electrical Engineering, 2019, 20(1): 24-26, 30. (  0) 0) |
| [17] |
DEMESHKO I, WATKINS J, TEZAUR I K, et al. Toward performance portability of the Albany finite element analysis code using the Kokkos library[J]. The International Journal of High Performance Computing Applications, 2019, 33(2): 332-352. DOI:10.1177/1094342017749957 (  0) 0) |
2. State Grid Shanxi Electric Power Company, Taiyuan 030021, China;
3. NARI Technology Co., Ltd., Nanjing 211106, China
 2021, Vol. 40
2021, Vol. 40


 宰红斌(1971), 男, 学士, 高级工程师, 从事输电线路防灾减灾, 运行维护与带电作业等工作(E-mail:
宰红斌(1971), 男, 学士, 高级工程师, 从事输电线路防灾减灾, 运行维护与带电作业等工作(E-mail: