文章编号: 2096-3203(2021)03-0092-07 中图分类号: TM711
拓扑结构分析是配电系统各类高级分析功能的基础,因此拓扑结构的准确性对配电网潮流计算和状态估计等计算结果的合理性有重要影响。为了达到运行灵活和供电可靠的目的,配电网通常装设大量开关,且开关的开合状态会根据不同的需要而发生改变,加之配电网量测冗余度很低,这就导致得到的配电网拓扑结构不可信,从而影响其他配电网高级分析功能的应用。因此,有必要寻找一种能够适应配电网结构动态变化的拓扑识别方法。
目前,国内外相关学者在配电网拓扑检错方面开展了许多研究工作,提出了一些识别方法,如贝叶斯公式迭代法[1-3]、支路电流状态估计法[4-6]、信息损失最小法[7]等,但这些方法均存在各自的局限性。文献[8-9]提出规则法,模拟人工操作步骤,通过一套基于因果原理的规则来判断开关的位置。其优点是简单、快速、收敛性好,并且已经应用于欧洲电网的控制中心,取得了较好的实用效果;缺点是对于规模庞大的电网而言,其结构复杂且开关的开合状态经常发生改变,因此很难形成完备的规则库,单一的规则很难清楚地表示出较为复杂的拓扑错误。此外,各规则之间也会存在一定的矛盾冲突,该方法的应用受到了一定限制。文献[10-12]提出残差法,将计算结果中的大残差归结为是由拓扑结构的不准确导致的。该假设较为合理,因此也被应用于实际电网,但遥信信息损失会对拓扑结构产生一定影响,而该方法忽略了这一点,因而开关变化的随机性和误判的风险性大大提高,其数学基础有待探讨。文献[13-14]提出人工神经网络法,以标准化新变量作为输入变量,在预滤波阶段识别不良数据。由于标准化新变量比其他变量(原始测量数据和标准化残差)具有更好的误差识别能力,因此这种方法在区分拓扑误差和模拟误差、识别支路或母线错误配置以及不良数据等方面是非常有效的。但该方法不适用于规模庞大且结构复杂的电网,而且需要有大量的训练范本,因此很难在实际电网中应用。
由此可见,上述的网络结构分析方法并未很好地适应配电网开关变化频繁和量测冗余度低的特点。文中提出一种基于支路有功功率的配电网拓扑结构识别方法,与现有的分析方法相比,该方法对配电网结构的动态变化有更好的适应性,并且合理利用了配电网计量系统中的负荷数据以及各支路的实时量测数据。算例表明,该方法合理有效,快速简便,且具有较好的实用性。
1 支路有功功率残值 1.1 支路有功功率残值概念配电网多采用环状结构辐射状运行,若任意断开某环网内的一条支路,此时由拓扑结构改变所引起的潮流变化可以通过在该环网内引入特定回路功率的方式来模拟[11]。配电网支路有功功率一定程度上可以反应开关的运行状态,例如当开关处于断开状态时,其所在支路的有功功率真值为0,因此可以通过回路功率叠加的方式来寻找配电网中断开可能性最大的支路,具体方法如下。
首先闭合全网开关,形成若干环网,通过潮流计算得到各支路初始功率;然后调整各个环网的回路功率,将各支路的初始功率和各环网的回路功率叠加,使装有量测装置的支路有功功率与该条支路的有功功率实时量测数据最接近,此时得到的支路有功功率称作支路有功功率残值;最后通过比较各支路有功功率残值的大小来确定各环网中断开的支路(取残值最小的),按此方法得到的拓扑结构与当前实时量测数据的匹配度最高。
1.2 支路有功功率残值算法首先需要计算各回路有功功率的最优解,使支路有功功率实际量测值与支路有功功率残值匹配度最高,因此其应满足以下关系:
| $ \min S=\sum\limits_{j \in M} w_{j}\left(P_{m, j}-P_{j}\right)^{2} $ | (1) |
式中:S为目标函数;wj为支路功率实时量测的权重,wj=1/δ2;M为设置功率量测装置的支路集合;Pm, j为支路有功功率量测实际值;Pj为支路有功功率残值。为使S最小,对式(1)求偏导:
| $ \frac{\partial S}{\partial P_{j}}=0 $ | (2) |
式(2)经数学推导可得,各支路此时的有功功率残值为:
| $ P_{\mathrm{opt}, j}=\sum\limits_{j \in M} w_{j} P_{m, j} / \sum\limits_{j \in M} w_{j} $ | (3) |
Popt, j为各回路有功功率与各支路初始有功功率叠加后的支路有功功率残值,因此始终满足式(4):
| $ P_{\mathrm{opt}, j}=P_{0, j}+\sum\limits_{i=1}^{n} \Delta P_{\mathrm{opt}, \mathrm{L} i} b_{i j} $ | (4) |
式中:P0, j为支路初始有功功率,即闭合全网开关,经潮流计算所得功率;ΔPopt, Li为各环网有功功率最优解;bij为配电网中支路与独立回路关系矩阵B[15]中元素(当支路j属于独立回路i且两者方向相同时取1,当支路j属于独立回路i且两者方向相反时取-1,当支路j不属于独立回路i时取0)。
在电气工程领域,根据已知的数据,拟合出变量之间的关系,拟合效果较好的方法是最小二乘拟合[16-18]。其拟合方法如下:
设n个变量x与变量y之间存在线性关系, 要对其做形如式(5)的线性拟合, 则拟合重点在于求出aj(j=0, 1, …, n)的值。
| $ y=a_{0}+\sum\limits_{j=1}^{n} a_{j} x_{j} y=a_{0}+\sum\limits_{j=1}^{n} a_{j} x_{j} $ | (5) |
设xij是变量xj的第i次量测值, 其对应的函数值为yi(i=0, 1, …, m), 则残差平方和为:
| $ \begin{gathered} s\left(a_{0}, a_{1}, \cdots a_{n}\right)=\sum\limits_{i=1}^{m}\left(y_{i}-y\right)^{2}= \\ \sum\limits_{i=1}^{m}\left(y_{i}-a_{0}-\sum\limits_{j=1}^{n} a_{j} x_{i j}\right)^{2} \end{gathered} $ | (6) |
为使变量y与实际值yi的残差平方和最小,对式(6)求偏导,将测量数据(xij, yi)代入可得出未知参数aj(j=0, 1, …, n)。
由式(4)可知,Popt, j与n+1个变量(P0, j, b1j, …, bnj)存在线性关系,经函数的线性拟合,可建立基于最小二乘法的支路有功功率残值的目标函数:
| $ \min J=\sum\limits_{j \in M} w_{j}\left[P_{\mathrm{opt}, j}-\left(P_{0, j}+\sum\limits_{i=1}^{n} \Delta P_{\mathrm{opt}, \mathrm{L} i} b_{i j}\right)\right]^{2} $ | (7) |
为了使J最小,对式(7)求偏导,并代入已知数据,可得各回路有功功率最优解为ΔPopt, L1, …, ΔPopt, Ln,拟合后可得各支路有功功率残值方程为:
| $ P=P_{0}+\sum\limits_{i=1}^{n} b_{i} \Delta P_{\text {opt }, \text { L} i} $ | (8) |
通过第1章介绍的算法可以算出各支路有功功率残值。根据各支路有功功残值大小,选择可能断开的支路(考虑到计算效率,建议每个独立回路选择可能断开支路为2~4条),得到若干种可能拓扑结构,再通过状态估计和计算拓扑结构匹配目标函数值,从可能拓扑结构集中找到可能性最高的拓扑结构作为可信拓扑结构。
在选择可能断开支路的过程中,由于各个独立回路间可能存在公共支路,因此在选择的过程中可能出现以下3种特殊情况: (1) 2个独立回路选择的可能断开支路为同一条支路,即公共支路;(2) 2个独立回路选择的可能断开支路不是同一条支路,但都是公共支路;(3) 2个独立回路选择的可能断开支路一条是公共支路,另一条不是公共支路。
由于配电网多采用环状结构辐射状运行,(1)和(2)选出的拓扑结构明显不符合该规范,所以排除不予考虑。(3)选出的拓扑结构符合该规范,继续看作可能拓扑结构进行分析计算。此外,装有实时量测装置的支路不作为可能断开的支路来考虑,这样进一步减少了可能拓扑结构的数量,提高了计算效率。
2.2 支路有功功率状态估计考虑到快速性的要求,选取支路有功功率为状态变量,并引入快速潮流直流法[19]消除节点的相角差,各量测函数的表达式以及对应的雅可比矩阵元素如下:
(1) 支路有功功率。
| $ P_{i j}=X $ | (9) |
| $ \frac{\partial P_{i j}}{\partial X}=1 $ | (10) |
式中:Pij为有功的量测类型;X为状态变量。
(2) 支路无功功率。
| $ Q_{i j}=-\left(b+y_{\mathrm{c}}\right)+g \sin (X / b)+b \cos (X / b) $ | (11) |
| $ \frac{\partial Q_{i j}}{\partial X}=\frac{g}{b} \cos (X / b)-\sin (X / b) $ | (12) |
式中:Qij为无功的量测类型;g,b分别为支路电导和电纳;yc为对地电纳。
(3) 注入节点有功功率。
| $ P_{i}=\sum\limits_{j \in i} P_{i j} $ | (13) |
| $ \frac{\partial P_{i}}{\partial X}=\frac{\partial \sum\limits_{j \in i} P_{i j}}{\partial X} $ | (14) |
式中:Pi为有功注入量测。
(4) 注入节点无功功率。
| $ Q_{i}=\sum\limits_{j \in i} Q_{i j} $ | (154) |
| $ \frac{\partial Q_{i}}{\partial X}=\frac{\partial \sum\limits_{j \in i} Q_{i j}}{\partial X} $ | (16) |
式中:Qi为无功注入量测。
(5) 节点电压幅值。
| $ U_{i}^{2} \approx \frac{P_{i j}}{g-g \cos (X / b)-b \sin (X / b)} $ | (17) |
| $ \begin{gathered} \frac{\partial U_{i}^{2}}{\partial X}=\{g-g \cos (X / b)+b \sin (X / b)- \\ \left.X_{P i j}[g / b \sin (X / b)+\cos (X / b)]\right\} / \\ {[g-g \cos (X / b)+b \sin (X / b)]^{2}} \end{gathered} $ | (18) |
式中:Ui2为电压幅值型量测。
(6) 支路电流幅值。
| $ \begin{gathered} I_{i j}^{2}=\left(2 g^{2}+2 b^{2}+y_{\mathrm{c}}^{2}+2 b y_{\mathrm{c}}\right)- \\ 2\left[\left(g^{2}+b^{2}+b y_{\mathrm{c}}\right) \cos (X / b)+g y_{\mathrm{c}} \sin (X / b)\right] \end{gathered} $ | (19) |
| $ \frac{\partial I_{i j}^{2}}{\partial X}=\frac{2\left(g^{2}+b^{2}+b y_{\mathrm{c}}\right)}{b} \sin (X / b)-\frac{2 g y_{\mathrm{c}}}{b} \cos (X / b) $ | (20) |
式中:Iij2为电流幅值型量测。
2.3 拓扑结构匹配目标函数根据第2.2节介绍的方法可以算出每个可能拓扑结构下各支路的有功功率估计值,从这若干种可能拓扑结构中寻找可能性最高的拓扑结构作为可信拓扑结构。首先构建拓扑结构匹配目标函数:
| $ J=\sum\limits_{i \in H} w_{i}\left|P_{\text {true }}-P_{\text {esti }}\right| $ | (21) |
式中:wi为实时量测权重,wi=1/δ2;H为实时量测集合;Ptrue为有功功率测量值;Pesti为有功功率估计值。
用相同实时量测值和负荷伪量测值在选出每个可能拓扑结构下分别进行状态估计,代入式(15)计算目标函数值。目标函数值越小,代表状态估计结果与真实值越接近,即该拓扑结构可信度越高。
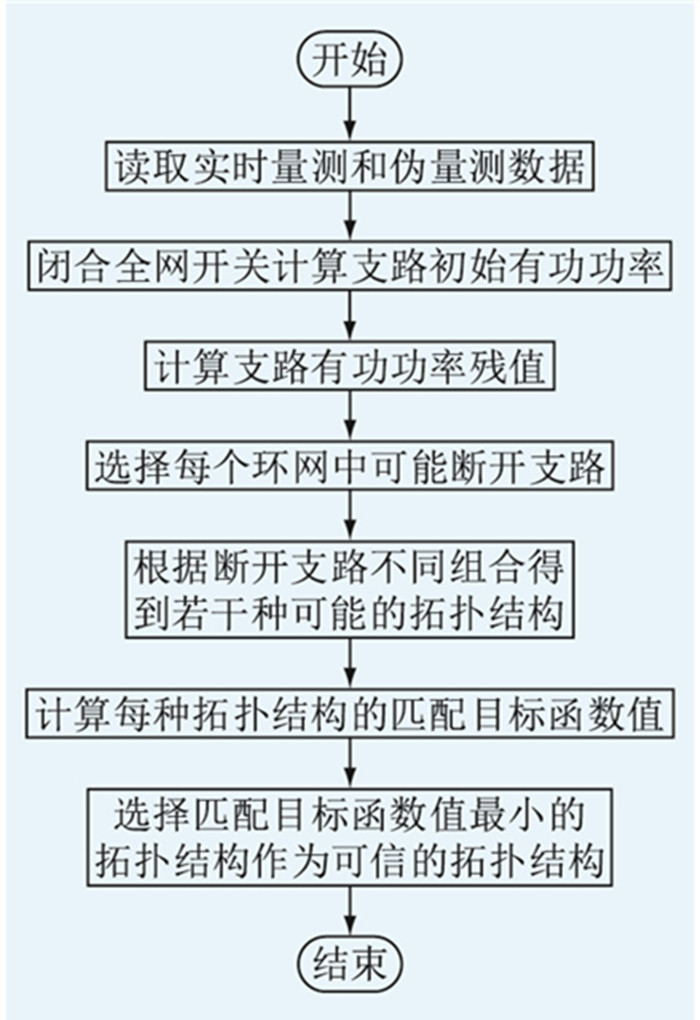
2.4 拓扑辨识方法流程配电网拓扑结构辨识方法的流程如图 1所示,具体步骤如下。
|
图 1 拓扑结构识别方法流程 Fig. 1 Flow chart of topological structure identification method |
(1) 读取实时量测值和负荷伪量测值,闭合全网开关,求得各支路的初始功率;
(2) 计算各支路的有功功率残值。选取各回路可能断开的支路;
(3) 根据各环网可能断开支路的不同组合确定可能拓扑结构集;
(4) 分别在每一个可能的拓扑结构下进行状态估计和算出目标函数值;
(5) 选取可能拓扑集中目标函数值最小的拓扑作为可信拓扑结构。
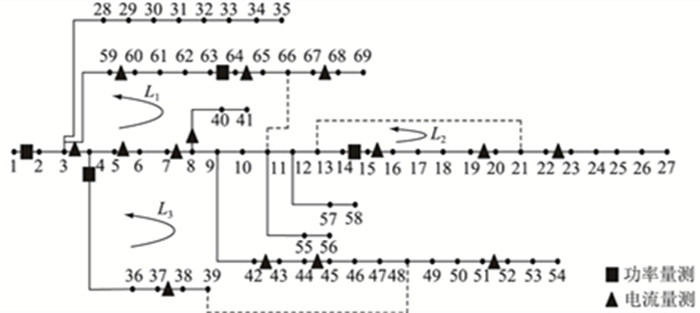
3 算例仿真 3.1 69节点配网算例文中采用PG & E 69节点系统进行算例分析,系统基准功率为20 MV ·A,基准电压为10 kV,其系统接线和量测分布如图 2所示。
|
图 2 69节点系统接线及量测分布 Fig. 2 69-bus system wiring and measurement distribution diagram |
将环网1、环网2、环网3内的支路ln11-66、ln13-21、ln39-48断开时的拓扑结构作为基准拓扑,并在此基准拓扑结构下进行潮流计算。文中所提实时量测数据均由潮流计算添加高斯误差求得。
对于一个服从高斯分布的变量,在(μ-3δ, μ+3δ)的范围内可以包含其所有可能取值的99.73%。其中,μ为变量均值,δ为误差标准差。由于量测值一般服从高斯分布,因此可以根据式(16)求得量测标准差。在求得量测标准差后,可以通过高斯分布生成量测值。
| $ {\delta _{\rm{z}}} = \frac{{{\mu _{\rm{z}}}{e_{\rm{z}}}}}{3} $ | (22) |
式中:μz为量测均值;ez为量测误差。
量测误差的设置如表 1所示,由于实时量测的精度较高,负荷伪量测的误差比较大,故将实时量测的权重设为90,负荷伪量测的权重设为10。
|
|
表 1 量测误差设置 Table 1 Measurement error setting |
算例采用Matlab进行编程计算,在Case1-Case5的情况下分别进行分析:
闭合全网开关,按照前面所述方法分别计算Case1-Case5情况下各支路有功功率残值。通过计算分析,环网L1、L2、L3在带有不同量测误差的情况下,支路有功功率残值最小的前3条支路见表 2。
|
|
表 2 各环网在Case1-Case5下支路有功功率残值最小的前3条支路 Table 2 The first three branches with minimum residual active power under Case1-Case5 of each ring network |
由表 2可以看到,在Case1-Case5的情况下各环网可能断开支路的结果相同,即在量测值误差不同时得到的可能拓扑结构相同。由于支路ln59-60、ln15-16和ln42-43上带有电流量测,所以这3条支路不看作可能断开的支路。因此,各回路中可能断开的支路由3条变为2条,可能拓扑结构一共有8种,具体如表 3所示。
|
|
表 3 可能拓扑结构 Table 3 Possible topology |
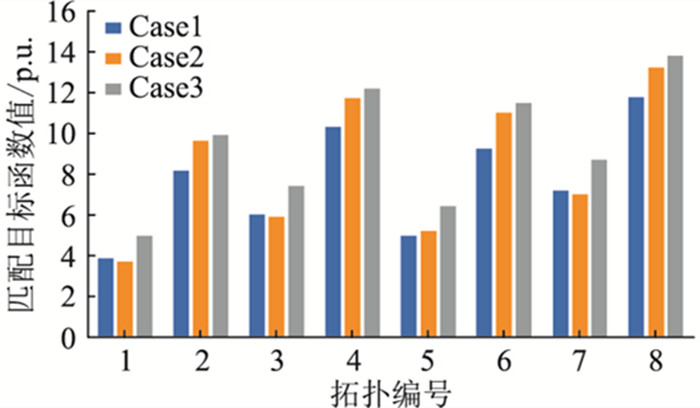
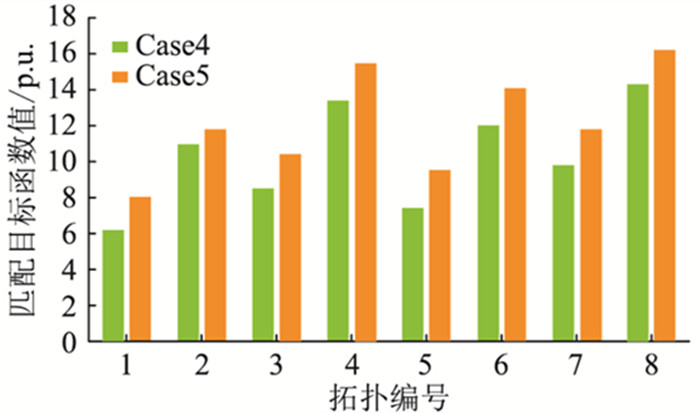
采用同一实时量测数据和负荷伪量测值,在这8种拓扑结构下分别进行状态估计,并根据式(14)算出匹配目标函数值,具体结果见图 3和图 4。
|
图 3 不同拓扑结构在Case1-Case3下的目标函数值 Fig. 3 Objective function values of different topologies under Case1-Case3 |
|
图 4 不同拓扑结构在Case4和Case5下的目标函数值 Fig. 4 Objective function values of different topologies under Case4 and Case5 |
由图 3和图 4可以看出,在Case1-Case5这5种带有不同量测误差的情况下,拓扑结构1的目标函数值均为最小,即拓扑结构1为可信拓扑结构。而拓扑结构1为支路ln11-66、ln13-21、ln39-48断开时的拓扑结构,与设定的基准拓扑结构一致,从而证明了该方法合理有效。此外,由表 1可知,该方法在功率量测值和负荷伪量测值误差较大时也有很好的适应性,从而更加证明了该方法的可靠性和准确性。
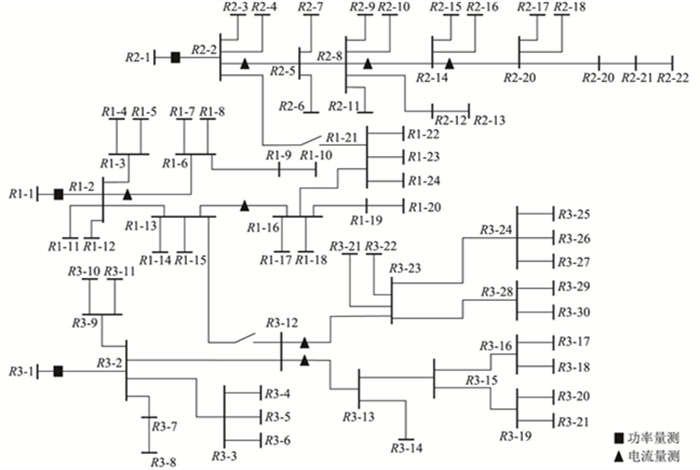
3.2 实际配网算例为验证所提出的拓扑辨识方法对实际配网的实用性,选取某地区10 kV电压等级下的3条馈线R1、R2、R3进行分析,其网络结构如图 5所示。
|
图 5 某城区局部配电网结构 Fig. 5 Structure of local distribution network in an urban area |
算例中,选用某一天上午八点A相的量测数据作为实时量测和负荷伪量测, 将电量计费系统采集的负荷数据作为负荷量测,将计量系统采集的中压负荷以15 min为周期更新的功率量测作为实时量测。
正常运行下,支路lnR1-21-R2-2和lnR1-13-R3-12是断开的。闭合全网开关,按照上述方法计算各支路有功功率残值。通过计算分析,馈线R1和R2、馈线R1和R3所形成的环网中有功功率残值最小的前3条支路如表 4所示。
|
|
表 4 各环网支路有功功率残值最小的前3条支路 Table 4 The first three branches with minimum residual active power of each ring network |
由于支路lnR1-13-R1-16上带有电流量测,所以该支路不看作可能断开支路。因此可能拓扑结构一共有6种,具体如表 5所示。
|
|
表 5 可能拓扑结构 Table 5 Possible topology |
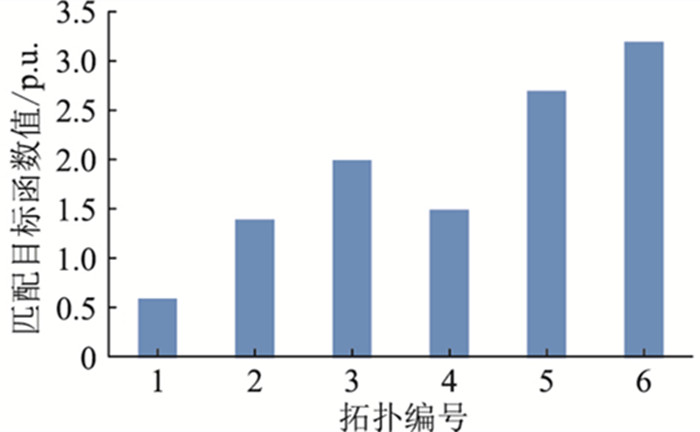
分别计算6种拓扑结构的目标函数值,计算结果见图 6。
|
图 6 不同拓扑结构的目标函数值 Fig. 6 Objective function values of different topologies |
观察图 6可知,1号拓扑结构的目标函数值最小,即认为支路lnR1-21-R2-2和lnR1-13-R3-12断开的情况下为可信拓扑,这与假设的基准网络拓扑结构相同,证明了该方法在实际配网中可以准确识别拓扑结构。
4 结语针对配电网拓扑检错困难的现状,文中提出了基于支路有功功率的配电网拓扑结构识别方法,通过引入最小二乘法来计算支路有功功率残值,大大降低了配电网拓扑结构分析的解空间,并引入快速潮流直流法来计算各支路有功功率的状态估计值,是对以往研究的丰富与突破,有很强的创新性。算例表明,该方法能有效地辨识出配电网准确的拓扑结构,且在带有较大量测误差的情况下也有很好的适应性,实现简单快速,尤其适用规模不大的配电网。
本文得到江苏省高等学校自然科学研究重大项目"含高渗透率分布电源配电网电压暂降鲁棒状态估计及应用"(19KJA510012)资助,谨此致谢!
| [1] |
AHMAD F, RASOOL A, OZSOY E E, et al. Successive-over-relaxation based recursive Bayesian approach for power system configuration identification[J]. COMPEL-the International Journal for Computation and Mathematics in Electrical and ElectronicEngineering, 2017, 36(4): 1043-1058. DOI:10.1108/COMPEL-10-2016-0462 (  0) 0) |
| [2] |
刘健, 张志华, 张小庆, 等. 基于配电自动化系统的单相接地定位[J]. 电力系统自动化, 2017, 41(1): 145-149. LIU Jian, ZHANG Zhihua, ZHANG Xiaoqing, et al. Single phase to ground fault location based on distribution automation systems[J]. Automation of Electric Power Systems, 2017, 41(1): 145-149. (  0) 0) |
| [3] |
罗群, 刘春雨, 顾强, 等. 基于最优匹配回路功率的配电网拓扑辨识方法[J]. 电测与仪表, 2019, 56(19): 1-6. LUO Qun, LIU Chunyu, GU Qiang, et al. A topology identification method of distribution network based on optimal matching loop power[J]. Electrical Measurement & Instrumentation, 2019, 56(19): 1-6. (  0) 0) |
| [4] |
王珊珊, 王克文, 王君亮, 等. 利用支路参数的状态估计法辨识拓扑错误[J]. 电测与仪表, 2016, 53(13): 10-13, 74. WANG Shanshan, WANG Kewen, WANG Junliang, et al. State estimation method of the branch parameter for topology error identification[J]. Electrical Measurement & Instrumentation, 2016, 53(13): 10-13, 74. DOI:10.3969/j.issn.1001-1390.2016.13.003 (  0) 0) |
| [5] |
姬源, 杨欣, 王燕, 等. 基于支路等值的拓扑辨识方法[J]. 电力系统保护与控制, 2015, 43(10): 129-134. JI Yuan, YANG Xin, WANG Yan, et al. A topology estimation method based on branch equivalence[J]. Power System Protection and Control, 2015, 43(10): 129-134. DOI:10.7667/j.issn.1674-3415.2015.10.021 (  0) 0) |
| [6] |
张占龙. 配电网量测配置优化与拓扑结构检错研究[D]. 北京: 华北电力大学, 2014. ZHANG Zhanlong. Research of measure placement optimization and topology error identification in distribution system[D]. Beijing: North China Electric Power University, 2014. (  0) 0) |
| [7] |
孙宏斌, 高峰, 张伯明, 等. 最小信息损失状态估计中潮流和拓扑统一估计的通用理论[J]. 中国电机工程学报, 2005, 25(17): 1-4. SUN Hongbin, GAO Feng, ZHANG Boming, et al. Minimum information loss based state estimation: general theory for unified estimation of power flow and topology[J]. Proceedings of the CSEE, 2005, 25(17): 1-4. DOI:10.3321/j.issn:0258-8013.2005.17.001 (  0) 0) |
| [8] |
SINGH N, GLAVITSCH H. Detection of identification of topological errors in online[J]. IEEE Power Engineering Review, 1991, 11(2): 70. (  0) 0) |
| [9] |
黄滔, 卢建刚, 张辉. 广东省调提高状态估计计算精度的措施[J]. 电网技术, 2004, 28(16): 78-81. HUANG Tao, LU Jiangang, ZHANG Hui. Measures to improve state estimation calculation accuracy in Guangdong provincial power dispatching centre[J]. Power System Technology, 2004, 28(16): 78-81. DOI:10.3321/j.issn:1000-3673.2004.16.017 (  0) 0) |
| [10] |
CLEMENTS K A, DAVIS P W. Detection and identification of topology errors in electric power systems[J]. IEEE Transactions on Power Systems, 1988, 3(4): 1748-1753. DOI:10.1109/59.192991 (  0) 0) |
| [11] |
WU F F, LIU W H E. Detection of topology errors by state estimation (power systems)[J]. IEEE Transactions on Power Systems, 1989, 4(1): 176-183. DOI:10.1109/59.32475 (  0) 0) |
| [12] |
ALSAC O, VEMPATI N, STOTT B, et al. Generalized state estimation[J]. IEEE Transactions on Power Systems, 1998, 13(3): 1069-1075. DOI:10.1109/59.709101 (  0) 0) |
| [13] |
SOUZA J C S, LEITE DA SILVA A M, ALVES DA SILVA AP. Data debugging for real-time power system monitoring based on pattern analysis[J]. IEEE Transactions on Power Systems, 1996, 11(3): 1592-1599. DOI:10.1109/59.535702 (  0) 0) |
| [14] |
SOUZA J C S, LEITE DA SILVA A M, ALVESDA SILVA A P. Online topology determination and bad data suppression in power system operation using artificial neural networks[J]. Proceedings of the 20th International Conference on Power Industry Computer Applications, 1997, 46-53. (  0) 0) |
| [15] |
吴文传, 张伯明. 配网潮流回路分析法[J]. 中国电机工程学报, 2004, 24(3): 72-76. WU Wenchuan, ZHANG Boming. Study on loopanalysis theorem of distribution system power flow[J]. Proceedings of the CSEE, 2004, 24(3): 72-76. DOI:10.3321/j.issn:0258-8013.2004.03.014 (  0) 0) |
| [16] |
莫小琴. 基于最小二乘法的线性与非线性拟合[J]. 无线互联科技, 2019, 16(4): 128-129. MO Xiaoqin. Linear and nonlinear fitting based on least squa- res method[J]. Wireless Internet Technology, 2019, 16(4): 128-129. (  0) 0) |
| [17] |
孙炯, 梁锦强, 刘凯. 一种基于最小二乘法的广义加权组合预测模型[J]. 科技通报, 2013, 29(8): 10-12. SUN Jiong, LIANG Jinqiang, LIU Kai. A combined forecasting model based on optimal weighted method and east-squares method[J]. Bulletin of Science and Technology, 2013, 29(8): 10-12. DOI:10.3969/j.issn.1001-7119.2013.08.004 (  0) 0) |
| [18] |
卢秀和, 朱加勉, 宫文文. 分段最小二乘拟合法在变压器测温中的应用[J]. 电测与仪表, 2016, 53(3): 105-108. LU Xiuhe, ZHU Jiamian, GONG Wenwen. Piecewise least square fitting method used in the temperature measurement of transformer[J]. Electrical Measurement & Instrumentation, 2016, 53(3): 105-108. DOI:10.3969/j.issn.1001-1390.2016.03.019 (  0) 0) |
| [19] |
季禹舜. 基于配电网状态估计的量测配置优化与拓扑辨识[D]. 南京: 南京工程学院, 2020: 43-55. JI Yushun. Robust measurement placement and topology identification method based on state estimation in distribution networks[D]. Nanjing: Nanjing Institute of Technology, 2020: 43-55. (  0) 0) |
 2021, Vol. 40
2021, Vol. 40


 刘迪(1994),女,硕士,研究方向为电力系统运行与控制(E-mail:
刘迪(1994),女,硕士,研究方向为电力系统运行与控制(E-mail: