文章编号: 2096-3203(2021)03-0072-06 中图分类号: TM614
随着大规模风电接入电网,准确预测风电功率对确保电力系统安全经济运行具有重要意义[1]。传统风电功率预测主要采用点预测方法,此方法仅能给出单一的具体数值,无法计及未来风电功率可能的波动范围,在涉及风电不确定性分析的问题上难以满足实际需求,因此风电功率概率预测应运而生。概率预测方法能够预测未来某一时间点上风电功率的置信区间或概率密度函数[2-3],实现对风电功率不确定性的定量描述,在电力系统风险评估、风险决策与优化调度等方面具有一定的应用价值[4-6]。
目前风电功率概率预测方法有预测误差分布统计法[7]、区间上下限估计法[8-9]和分位数回归法[10]等。文献[7]提出通过Beta分布估计任意概率水平的预测误差区间,由于事先假设服从特定分布,可能与实际情况存在较大偏差。文献[8]采用预测区间覆盖率(prediction interval coverage percentage, PICP)、预测区间归一化平均宽度(prediction interval normalized average width, PINAW)和累积带宽偏差(accumulated width deviation, AWD) 3种指标作为目标函数,并通过调整权重系数将多目标问题转化为单目标问题,但权重系数设定依赖主观经验,影响预测精度。文献[9]提出利用多目标优化模型解决系数选择不合理问题,但未考虑目标值在区间外的偏离程度。文献[10]建立了基于分位数回归与神经网络相结合的预测模型,实现月度风电功率概率预测。分位数回归法能够有效避免概率分布构造的主观性与先验性,预测效果很大程度上受智能算法本身的影响。
近年来,深度学习的兴起极大促进了智能算法的发展,已被不少学者应用于新能源等电力系统领域的相关预测[11]。文献[12]在简化长短期记忆神经网络内部结构的基础上提出门控循环单元(gated recurrent unit, GRU)神经网络,不仅提高了计算效率,而且相比传统机器学习,加强了对时间序列内在特征的学习能力。文中在分位数回归与深度学习的基础上,提出一种基于变分模态分解(variational mode decomposition, VMD)与改进门控循环单元分位数回归(quantile regression gated recurrent unit, QRGRU)的超短期风电功率概率预测方法。该方法通过VMD实现原始风电功率序列的分解,降低样本训练的复杂程度,并采用变量间的网络结构约束作为QRGRU模型目标函数的惩罚项,提高预测的稳健性。结合某风电场实测数据开展具体的算例分析,验证了所提方法能够有效提高风电功率概率预测精度,为风电功率的不确定性分析提供可靠依据。
1 VMD原理风电功率序列含有大量噪声,具有较高的非平稳性,在预测前可通过分解方法对其进行预处理,典型的方法有小波变换(wavelet transform, WT)、经验模态分解(empirical mode decomposition, EMD)和集合经验模态分解(ensemble empirical mode decomposition, EEMD)等[2]。VMD是一种自适应、非递归的新型信号分解方法,具有良好的鲁棒性[13]。该方法不仅可解决WT在基函数选择过程中的自适应差问题,还可克服EMD的端点效应和模态混叠现象,分解的模态个数也小于EEMD[14]。鉴于VMD的优点,文中将其用于风电功率序列的预处理,通过降低输入数据的复杂度提高概率预测精度。
VMD的目的是将原始信号序列f分解成若干个有限带宽的模态函数,使得每个模态函数估计的带宽之和最小。其核心思想在于变分问题的构造与求解。VMD具体实现过程可参考文献[13-14]。
2 改进QRGRU原理 2.1 GRU原理GRU是一种特殊的循环神经网络,凭借特有的门限策略和状态记忆解决传统循环神经网络在训练过程中易出现的梯度爆炸和梯度消失问题,在分析处理时间序列数据时具有较优异的泛化性能[15-16]。与长短期记忆网络结构相比,GRU将元胞状态与门结构耦合,集中实现了数据传递与状态记忆。GRU内部结构如图 1所示。

|
图 1 GRU内部结构 Fig. 1 Internal structure of GRU |
图 1展示了GRU的2个重要门结构,分别为更新门和重置门。GRU前向传播为:
| $ \boldsymbol{z}_{t}=\sigma\left(\boldsymbol{W}_{\mathrm{z}} \boldsymbol{x}_{t}+\boldsymbol{U}_{\mathrm{z}} \boldsymbol{h}_{t-1}\right) $ | (1) |
| $ \boldsymbol{r}_{t}=\sigma\left(\boldsymbol{W}_{\mathrm{r}} \boldsymbol{x}_{t}+\boldsymbol{U}_{\mathrm{r}} \boldsymbol{h}_{t-1}\right) $ | (2) |
| $ \tilde{\boldsymbol{h}}_{t}=\tanh \left[\boldsymbol{W}_{\mathrm{h}} \boldsymbol{x}_{t}+\boldsymbol{U}_{\mathrm{h}}\left({\boldsymbol{r}_{t}}^{\circ} \boldsymbol{h}_{t-1}\right)\right] $ | (3) |
| $ \boldsymbol{h}_{t}=\left(1-\boldsymbol{z}_{t}\right){ }^{\circ} \boldsymbol{h}_{t-1}+\boldsymbol{z}_{t}{ }^{\circ} \tilde{\boldsymbol{h}}_{t} $ | (4) |
式中:x t,h t分别为当前t时刻GRU的输入和输出;z t,r t分别为更新门和重置门的输出;
QRGRU保留了GRU原有的网络结构与功能,旨在通过最优化目标函数实现非线性分位数回归。目标函数为:
| $ \begin{gathered} \min \limits_{\boldsymbol{W}(\tau), \boldsymbol{U}(\tau)} \frac{1}{T} \sum\limits_{i=1}^{T}\left\{\rho_{\tau}\left[y_{i}-\hat{Q}_{y_{i}}(\tau)\right]\right\}= \\ \frac{1}{T} \sum\limits_{i=1}^{T}\left\{\left\{\tau-I\left[y_{i}-\hat{Q}_{y_{i}}(\tau)\right]\right\}\left[y_{i}-\hat{Q}_{y_{i}}(\tau)\right]\right\} \end{gathered} $ | (5) |
式中:T为样本数;yi为样本i实际值;
指示函数I(u)为:
| $ I(u)=\left\{\begin{array}{ll} 0 & u \geqslant 0 \\ 1 & u<0 \end{array}\right. $ | (6) |
式中:
QRGRU综合了神经网络和分位数回归两方面优势,通过调节τ的取值,给出相应变量在不同分位点上的条件分位数。
2.3 改进QRGRU原理GRU网络结构具有数据流向自身的状态记忆功能,对历史时刻的信息反馈较为敏感。相较传统机器学习而言,GRU加强了对数据内在特征的反馈调节能力,但由于自身的敏感性,在训练过程中也不可避免会受到风电功率异常噪声的影响,降低模型泛化性。
为克服上述问题,文中采用网络结构约束作为目标函数的惩罚项,根据变量间的相关程度平滑网络权重在迭代修正过程中的偏离程度,提高预测的稳健性[17-19]。网络结构约束是基于图论的拉普拉斯矩阵L的非负二次型,如式(7)所示。
| $ \boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{\beta}=\sum\limits_{1 \leqslant i<j \leqslant p}\left[\left|a_{i j}\right|\left({\beta}_{i}-s_{i j} {\beta}_{j}\right)^{2}\right] $ | (7) |
式中:aij为通过变量间网络结构表示的邻接矩阵A的元素,即A =[aij]p×p,aij用来度量变量之间的相关关系;sij=sgn(aij);β为将网络权重W和U转换后的向量形式。
将此惩罚项加入目标函数,构建含网络结构约束的改进QRGRU网络,则式(5)改写为:
| $ \min \limits_{\boldsymbol{W}(\tau), \boldsymbol{U}(\tau)} \frac{1}{T} \sum\limits_{i=1}^{T}\left\{\rho_{\tau}\left[y_{i}-\hat{Q}_{y_{i}}(\tau)\right]\right\}+\boldsymbol{\beta}^{\mathrm{T}}(\tau) \boldsymbol{L} \boldsymbol{\beta}(\tau) $ | (8) |
非参数核密度估计无需任何先验假设,通过一组随机变量的观测值估计概率密度分布。若改进QRGRU输出得到的条件分位数估计值为
| $ \hat{f}(y)=\frac{1}{n h} \sum\limits_{i=1}^{n} K\left[\frac{y-\hat{Q}_{y}\left(\tau_{i}\right)}{h}\right] $ | (9) |
式中:n为分位点个数;K(·)为核函数,文中采用高斯核函数;h为窗宽,采用经验法则来选取合适的窗宽值[20]。
完成核密度估计之后,根据所得概率密度函数,计算得到某一置信区间的上、下限U,L。风力发电在接近零发或满发时由预测得到的置信区间有可能超出风电实际出力范围,如出现负值或大于额定功率,则不符合实际情况。因此需要对置信区间进行如式(10)所示的校正,使其位于风电出力范围内。
| $ \left\{\begin{array}{l} U_{2}=\min \left\{U_{1}, U\right\} \\ L_{2}=\max \left\{L_{1}, L\right\} \end{array}\right. $ | (10) |
式中:U1,L1分别为风电出力的上、下限;U2,L2分别为校正后置信区间的上、下限。
3 超短期风电功率概率预测 3.1 概率预测流程文中所提基于VMD与改进QRGRU的超短期风电功率概率预测步骤主要为:
(1) 采用VMD对原始风电功率序列进行预处理,分解得到若干个模态函数;
(2) 对每个模态函数分别建立改进QRGRU预测模型,在模型训练完成后,对测试样本进行预测,得到模态函数在不同分位数条件下的预测值;
(3) 将每个模态函数的预测值进行叠加,并采用核密度估计得到未来风电功率的概率密度函数;
(4) 根据所得到的概率密度函数,通过计算求得某一置信水平下的风电功率预测区间,并校正。
3.2 概率预测评价指标文中采用3个指标,PICP用于评价区间的可靠性,其值越大,说明可靠性越高;PINAW用于评价区间宽度的精锐程度,一般其值越小越好;温克勒分数(Winkler score, WS)是二者的综合评价,集中考虑了区间的覆盖率与宽度,其值越小,说明概率预测效果越好。
3.2.1 PICP指标| $ e_{\mathrm{PICP}}=\frac{1}{N} \sum\limits_{i=1}^{N} c_{i} $ | (11) |
| $ c_{i}=\left\{\begin{array}{ll} 1 & y_{i} \in\left[L_{i}, U_{i}\right] \\ 0 & y_{i} \notin\left[L_{i}, U_{i}\right] \end{array}\right. $ | (12) |
式中:N为预测点个数;Ui,Li分别为预测区间的上、下限。
3.2.2 PINAW指标| $ e_{\mathrm{PINAW}}=\frac{1}{N R} \sum\limits_{i=1}^{N}\left(U_{i}-L_{i}\right) $ | (13) |
式中:R为预测目标值的取值范围,用以归一化区间平均宽度。
3.2.3 WS指标| $ e_{\mathrm{WS}}=\frac{1}{N} \sum\limits_{i=1}^{N} e_{\mathrm{Winkler}, i} $ | (14) |
| $ e_{\text {Winkler }, i}=\left\{\begin{array}{ll} \delta \quad L_{i} \leqslant y_{i} \leqslant U_{i} & \\ \delta+2\left(L_{i}-y_{i}\right) / \alpha & y_{i}<L_{i} \\ \delta+2\left(y_{i}-U_{i}\right) / \alpha & y_{i}>U_{i} \end{array}\right. $ | (15) |
式中:δ=Ui-Li为置信水平为(1-α)×100%时预测区间的宽度[21],α为显著性水平。
4 算例分析文中实验数据采用GEFCom 2014比赛提供的某风电场2013年3月至6月连续90 d的风电功率实测数据[22],采样间隔为1 h,数据如图 2所示。其中纵轴为风电功率的标幺值, 即风电实测输出功率与机组容量的比值。将前90%数据作为训练样本,用于训练模型,后10%数据作为测试样本,用于验证概率预测效果。

|
图 2 风电功率实测数据 Fig. 2 Actual data of wind power |
文中基于Python编程环境的Tensorflow深度学习框架进行仿真实验。改进QRGRU模型采用单个隐含层;隐含层神经元个数为32;激活函数选取ReLU函数;采用的优化算法为Adam算法;训练次数为1 000;τ取值范围为[0.01, 0.99];间隔为0.01;VMD的惩罚因子取默认值2 000;收敛判据为10-6;模态函数个数取4。
4.2 概率预测结果在进行概率预测之前,采用VMD对原始风电功率序列进行分解,结果如图 3所示。

|
图 3 VMD分解结果 Fig. 3 Decomposition results of VMD |
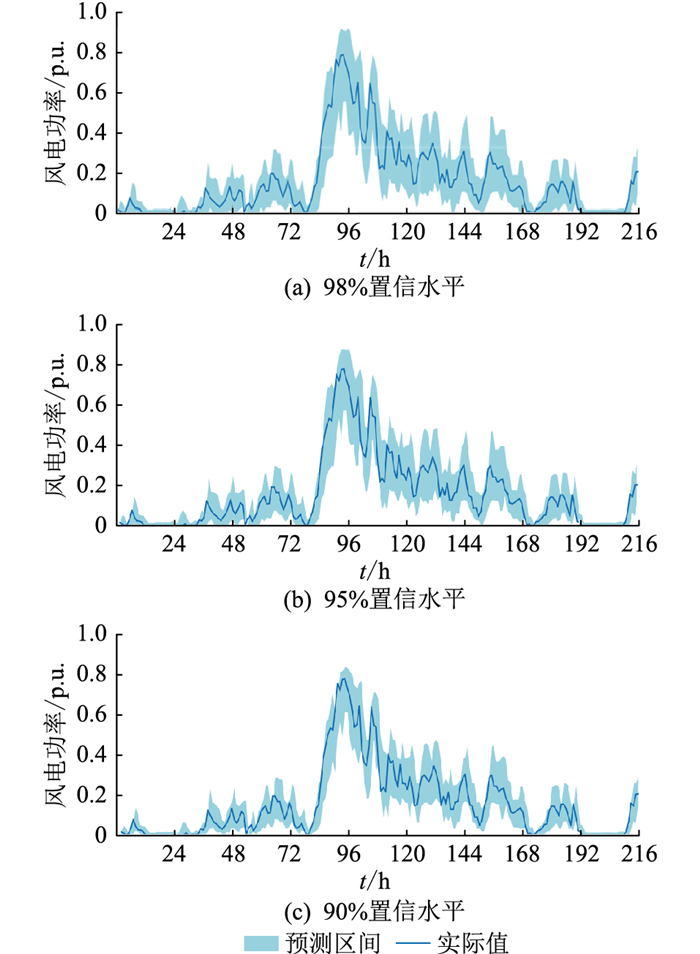
对每个模态函数分别建立改进QRGRU模型,在训练完成之后,对测试样本进行提前一步的风电功率概率预测。置信水平为98%, 95%, 90%时的概率预测结果如图 4所示。
|
图 4 风电功率概率预测 Fig. 4 Prediction of wind power probability |
由图 4可知,预测区间的变化趋势与实际风电功率曲线较为相似。在风电功率波动较平缓时区间宽度尽可能变窄,而在风电功率波动较剧烈时区间宽度变宽,尽可能提高了区间覆盖程度,客观反映了风电功率在不同时刻受到的不确定性影响不同。3种置信水平下的预测区间都能较好地覆盖风电功率实际值,测得ePICP在98%,95%,90%置信水平下的数值分别为98.61%,96.76%,92.59%。说明区间覆盖率均与各自置信水平相吻合,验证了文中概率预测方法的正确性。
4.3 VMD对概率预测的影响为了校验VMD对概率预测效果的影响,在98%,95%,90%置信水平下的单步概率预测中,对有无VMD的预测方法进行对比,预测区间的评价结果如表 1所示。
|
|
表 1 不同置信水平下预测区间评价结果 Table 1 Evaluation results of prediction interval under different confidence levels |
由表 1可知,在3种高置信水平下,VMD对概率预测效果均有不同程度的改善。尤其是在98%和95%置信水平下,保证较高区间覆盖率的同时取得了较小的区间宽度。而在90%置信水平下,无VMD的预测方法虽拥有较高的覆盖率,但牺牲了过多的区间宽度。总体而言,有VMD作用时,eWS在98%,95%,90%置信水平下分别提升了11.6%,8.9%,4.3%,VMD能有效提升整体概率预测效果。
4.4 不同预测步长时预测性能的对比为进一步验证文中方法的预测性能,选择传统神经网络分位数回归(quantile regression neural network, QRNN)、QRGRU与文中方法进行预测精度对比。当给定95%置信水平时,3种方法在不同步长预测中的区间评价结果如表 2所示。
|
|
表 2 不同预测步长对应的预测区间评价结果 Table 2 Evaluation results of prediction interval corresponding to different prediction steps |
由表 2可知,随着预测步长增加,3种方法的整体预测效果均随之出现不同程度的降低,原因主要在于不同时间点的风电功率具有较高的随机性,时间间隔越长,可预测性越弱,这与“近大远小”的预测原则有一定联系。文中方法在PICP评价上与其他方法差异不大,均能满足可靠性要求,而在PINAW评价上有相对明显的优势,在不同预测步长中都能保持较窄的区间宽度。综合而言,相较于QRNN和QRGRU,文中方法的eWS在单步预测中分别提升了10.6%,6.3%;在2步预测中分别提升了6.5%,4.6%;在3步预测中分别提升了6.8%,4.4%。说明文中方法在改进后具有较稳健的预测性能,能够较好地提升概率预测精度,验证了文中方法的优越性。
5 结语文中采用VMD对风电功率序列进行预处理,在传统GRU中引入网络结构约束作为目标函数的惩罚项,并结合分位数回归,提出了一种基于VMD与改进QRGRU的超短期风电功率概率预测方法。实验结果表明,文中所提VMD和改进QRGRU方法均能一定程度上提高概率预测精度,与其他方法相比,概率预测效果更好。值得注意的是,文中方法不仅可以得到未来风电功率的概率密度函数,也可以得到任意置信水平下的风电功率区间,避免了传统构造概率分布的主观性与先验性。文中主要围绕深度学习与分位数回归的结合与应用,下一步将深入研究VMD在不同模态函数上的差异化精细化建模。文中为风电功率概率预测提供了新方法,对解决风电功率不确定性问题具有一定的借鉴意义。
| [1] |
陶玉波, 陈昊, 秦晓辉, 等. 短期风电功率预测概念和模型与方法[J]. 电力工程技术, 2018, 37(5): 7-13. TAO Yubo, CHEN Hao, QIN Xiaohui, et al. A review of the short-term wind power forecasting theory, model and approach[J]. Electric Power Engineering Technology, 2018, 37(5): 7-13. DOI:10.3969/j.issn.1009-0665.2018.05.004 (  0) 0) |
| [2] |
吴问足, 乔颖, 鲁宗相, 等. 风电功率概率预测方法及展望[J]. 电力系统自动化, 2017, 41(18): 167-175. WU Wenzu, QIAO Ying, LU Zongxiang, et al. Methods andprospects for probabilistic forecasting of wind power[J]. Automation of Electric Power Systems, 2017, 41(18): 167-175. DOI:10.7500/AEPS20160914002 (  0) 0) |
| [3] |
ZHANG Y, WANG J X, WANG X F. Review on probabilistic forecasting of wind power generation[J]. Renewable and Sustainable Energy Reviews, 2014, 32: 255-270. DOI:10.1016/j.rser.2014.01.033 (  0) 0) |
| [4] |
刘德伟, 郭剑波, 黄越辉, 等. 基于风电功率概率预测和运行风险约束的含风电场电力系统动态经济调度[J]. 中国电机工程学报, 2013, 33(16): 9-15, 24. LIU Dewei, GUO Jianbo, HUANG Yuehui, et al. Dynamic economic dispatch of wind integrated powersystem based on wind power probabilistic forecasting and operation risk constraints[J]. Proceedings of the CSEE, 2013, 33(16): 9-15, 24. (  0) 0) |
| [5] |
TEWARI S, GEYER C J, MOHAN N. A statistical model for wind power forecast error and its application to the estimation of penalties in liberalized markets[J]. IEEE Transactions on Power Systems, 2011, 26(4): 2031-2039. DOI:10.1109/TPWRS.2011.2141159 (  0) 0) |
| [6] |
黄海煜, 于文娟. 考虑风电出力概率分布的电力系统可靠性评估[J]. 电网技术, 2013, 37(9): 2585-2591. HUANG Haiyu, YU Wenjuan. Power grid reliability assessment considering probability distribution of wind farm power output[J]. Power System Technology, 2013, 37(9): 2585-2591. (  0) 0) |
| [7] |
杨宏, 苑津莎, 张铁峰. 一种基于Beta分布的风电功率预测误差最小概率区间的模型和算法[J]. 中国电机工程学报, 2015, 35(9): 2135-2142. YANG Hong, YUAN Jinsha, ZHANG Tiefeng. A model and algorithm for minimum probability interval of wind power forecast errors based on Beta distribution[J]. Proceedings of the CSEE, 2015, 35(9): 2135-2142. (  0) 0) |
| [8] |
杨锡运, 关文渊, 刘玉奇, 等. 基于粒子群优化的核极限学习机模型的风电功率区间预测方法[J]. 中国电机工程学报, 2015, 35(S1): 146-153. YANG Xiyun, GUAN Wenyuan, LIU Yuqi, et al. Prediction intervals forecasts of wind power based on PSO-KELM[J]. Proceedings of the CSEE, 2015, 35(S1): 146-153. (  0) 0) |
| [9] |
陈杰, 沈艳霞, 陆欣, 等. 一种风电功率概率区间多目标智能优化预测方法[J]. 电网技术, 2016, 40(8): 2281-2287. CHEN Jie, SHEN Yanxia, LU Xin, et al. An intelligent multi-objective optimized method for wind power prediction intervals[J]. Power System Technology, 2016, 40(8): 2281-2287. (  0) 0) |
| [10] |
李丹, 任洲洋, 颜伟, 等. 基于因子分析和神经网络分位数回归的月度风电功率曲线概率预测[J]. 中国电机工程学报, 2017, 37(18): 5238-5247, 5522. LI Dan, REN Zhouyang, YAN Wei, et al. Month-ahead wind power curve probabilistic prediction based on factor analysis and quantile regression neural network[J]. Proceedings of the CSEE, 2017, 37(18): 5238-5247, 5522. (  0) 0) |
| [11] |
万灿, 宋永华. 新能源电力系统概率预测理论与方法及其应用[J]. 电力系统自动化, 2021, 45(1): 2-16. WAN Can, SONG Yonghua. Theories, methodologies and applications of probabilistic forecasting for power systems with renewable energy sources[J]. Automation of Electric Power Systems, 2021, 45(1): 2-16. (  0) 0) |
| [12] |
CHO K, VAN MERRIENBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[C]//Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). 2014.
(  0) 0) |
| [13] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 (  0) 0) |
| [14] |
武小梅, 林翔, 谢旭泉, 等. 基于VMD-PE和优化相关向量机的短期风电功率预测[J]. 太阳能学报, 2018, 39(11): 3277-3285. WU Xiaomei, LIN Xiang, XIE Xuquan, et al. Short-term wind power forecasting based onvariational mode decomposition-permutation entropyand optimized relevance vector machine[J]. Acta Energiae Solaris Sinica, 2018, 39(11): 3277-3285. (  0) 0) |
| [15] |
王增平, 赵兵, 纪维佳, 等. 基于GRU-NN模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 53-58. WANG Zengping, ZHAO Bing, JI Weijia, et al. Short-term load forecasting method based on GRU-NN model[J]. Automation of Electric Power Systems, 2019, 43(5): 53-58. (  0) 0) |
| [16] |
陈海文, 王守相, 王绍敏, 等. 基于门控循环单元网络与模型融合的负荷聚合体预测方法[J]. 电力系统自动化, 2019, 43(1): 65-72. CHEN Haiwen, WANG Shouxiang, WANG Shaomin, et al. Aggregated load forecasting method based on gated recurrent unit networks and model fusion[J]. Automation of Electric Power Systems, 2019, 43(1): 65-72. (  0) 0) |
| [17] |
LI C, LI H. Variable selection and regression analysis for graph-structured covariates with anapplication to genomics[J]. The Annals of Applied Statistics, 2010, 4(3): 1498-1516. (  0) 0) |
| [18] |
HUANG J, MA S, LI H, et al. The sparse Laplacian shrinkage estimator for high-dimensional regression[J]. Annals of Statistics, 2011, 39(4): 2021-2046. (  0) 0) |
| [19] |
王小燕, 姚佳含, 袁欣. 带网络结构的自适应Lasso分位数回归及其应用[J]. 系统工程理论与实践, 2019, 39(8): 1954-1965. WANG Xiaoyan, YAO Jiahan, YUAN Xin. Adaptive Lasso quantile regression with network structure and its application[J]. Systems Engineering-Theory & Practice, 2019, 39(8): 1954-1965. (  0) 0) |
| [20] |
杨秀, 陈斌超, 朱兰, 等. 基于相关性分析和长短期记忆网络分位数回归的短期公共楼宇负荷概率密度预测[J]. 电网技术, 2019, 43(9): 3061-3071. YANG Xiu, CHEN Binchao, ZHU Lan, et al. Short-term public building load probability density prediction based on correlation analysis and long- and short-term memory network quantileregression[J]. Power System Technology, 2019, 43(9): 3061-3071. (  0) 0) |
| [21] |
LIU B D, NOWOTARSKI J, HONG T, et al. Probabilistic load forecasting via quantile regression averaging on sister forecasts[J]. IEEE Transactions on Smart Grid, 2017, 8(2): 730-737. (  0) 0) |
| [22] |
HONG T, PINSON P, FAN S, et al. Probabilistic energy forecasting: global energy forecasting competition 2014 and beyond[J]. International Journal of Forecasting, 2016, 32(3): 896-913. DOI:10.1016/j.ijforecast.2016.02.001 (  0) 0) |
 2021, Vol. 40
2021, Vol. 40


 刘云凯(1995),男,硕士在读,研究方向为大数据在智能电网中的应用、电力系统运行分析和电网规划(E-mail:
刘云凯(1995),男,硕士在读,研究方向为大数据在智能电网中的应用、电力系统运行分析和电网规划(E-mail: