文章编号: 2096-3203(2021)03-0084-08 中图分类号: TM715
2. 国家电网有限公司华东分部,上海 200120
电力负荷预测是根据历史负荷数据及其他外界影响因素对将来的负荷需求进行科学预测的过程[1]。电力系统瞬时供需平衡的特点决定了其预测工作的紧迫性,构建精准的负荷功率模型并进行准确的负荷预测是电力系统进行安全调度和经济运转的重要前提条件。然而负荷功率呈现多样的时空变化特性,受多因素(如气象、日期类型等)影响。随着各种储能设备、电动汽车、分布式电源等大规模接入电网,以及基于激励措施、电价等需求侧管理方案的实施,负荷预测的复杂度增加[2]。
构建负荷功率模型并进行负荷预测的关键因素之一是确定模型的输入特征量。国内外大部分短期负荷预测研究是对模型和方法的探索[3-4]。近年来,许多专家学者将电力负荷预测相关影响因素作为研究重点[5-9],这些研究也表明对负荷特征的深入挖掘分析可有效提高预测效果。
特征选择(feature selection,FS)是通过移除无关、冗余特征,从一组给定的特征集合中选出最有效的相关特征子集从而实现特征空间维数降低的过程[10]。经过特征选择后的低维数据在后期聚类分析或机器学习中能降低复杂度,提高精度和稳定性。就数据类型而言,特征选择分类包括监督式、无监督式和半监督式;从机制层面来看,又可以分为过滤式(Filter)、封装式(Wrapper)和嵌入式(Embedded)。Filter法用评价准则来增强特征与类的相关性或削减特征之间的相关性[10];Wrapper法直接采用学习器分类性能作为特征子集的评价标准;而Embedded法将特征选择与学习算法相结合,在训练过程中自主完成了特征选择。快速消除冗余特征,提高算法分类性能是特征选择重要的研究方向[11]。结合子算法的优势,混合方法通常比传统方法更稳健,因此成为解决特定问题的新策略。文献[12]提出了一种混合的过滤器和包装器方法,采用自举策略创建特征子集,通过计算每个特征子集的分类精度找到优化子集。
文中首先以气象、日期及历史负荷等因素作为初始输入特征集,并引入负荷和温度的导数以刻画变量之间的非线性影响;接着,分别采用基于Filter、Wrapper和Embedded的方法进行负荷功率模型的特征选择;最后,基于各方法选择结果的明显差异提出基于遗传算法的最优特征集搜索策略,实现了输入特征集的最优化,并通过算例进行验证。
1 数据处理 1.1 数据预处理负荷预测往往都是实时采集数据,而动态的数据采集可能存在通道拥堵、故障等现象,导致相应数据采集程序发生中断,从而原始数据会出现错误与不真实的情况。同时可能因为天气突变、特殊突发事件等引起数据异常,造成大量伪数据的存在[13],这必定会严重影响预测精度,因此须对负荷数据进行加工、完善。
(1) 插值法补全缺失值。文中取某地区220 kV变电站能量管理系统(energy management system,EMS)记录数据,数据缺失情况非常少,个别空缺数据采用线性插值法补全,具体是将空缺点前后两点数据取平均作为空缺点的缺失值。
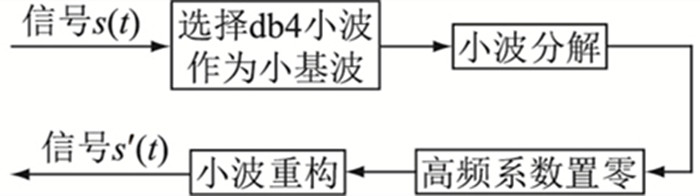
(2) 小波去噪法处理异常值。文中算例的母线负荷预测量级小,随机性与波动性较强,且往往掺杂部分坏数据,从而对预测精度产生较大影响。文中选择db4小波作为小基波,利用小波去噪处理负荷数据的异常波动。该方法首先在各尺度上将含噪声的信号进行小波分解,得到小波系数和尺度系数;然后对高频系数置零,去除噪声信号;最后利用重构算法、小波系数和尺度系数重构出估计信号[14],具体流程如图 1所示。
|
图 1 db4小波去噪流程 Fig. 1 Flow chart of db4 wavelet denoising |
(3) 归一化。由于样本气象数据、负荷数据单位不一致,在进行负荷功率模型构建和训练前,应对其进行归一化处理,将数据取值范围定在[0, 1]或[-1, 1]之间,计算公式为:
| $ x{'_i} = \frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $ | (1) |
式中:xi,x'i分别为归一化之前和之后的数值;xmin,xmax分别为该组数据中的最小值与最大值。
1.2 输入特征集负荷功率模型的输入特征集考虑气象、历史负荷等36个特征,符号表示及其含义如表 1所示。左边一栏为气象、日期等负荷相关的外部因素,右边一栏为历史负荷特征,其中前一时刻负荷为预测值。
|
|
表 1 相关特征命名 Table 1 Nomenclature of the related features |
气象因素中加入了前3 d的温度特征,以充分考虑温度对负荷的影响和气温的累积效应[15]。实际值往往不及一阶导或二阶导能够捕捉到变量的基本趋势[16],考虑将负荷和温度曲线的日动态变化趋势作为新的预测因素以系统地解释不同特征量之间的非线性相互作用,特征中加入温度和负荷的一阶和二阶导数,计算公式为:
| $ L'(t) = \frac{1}{2}[L(t + 1) - L(t - 1)] $ | (2) |
式中: L'(t)为t时刻的负荷一阶导数; L(t+1), L(t-1)分别表示t+1,t-1时刻的负荷值。利用差分法同样可求负荷二阶导数和温度相关导数。
2 特征选择方法性能比较 2.1 特征选择方法文中采用Filter法中的最大信息系数(maximal information coefficient,MIC)、Wrapper法中基于支持向量机的递归特征消除(support vector machine based recursive feature elimination,SVM-RFE)和Embedded法中的随机森林(random forest,RF)。
MIC主要利用互信息和网格划分方法进行计算,互信息是衡量变量之间相关程度的指标[17],对于给定样本数为n的变量,X={xi, i=1, 2, …, n}和Y={yi, i=1, 2, …, n},互信息定义为:
| $ {I_{{\rm{MI}}}}(X, Y) = \sum\limits_{x \in X} {\sum\limits_{y \in Y} p } (x, y){\log _2}\frac{{p(x, y)}}{{p(x)p(y)}} $ | (3) |
式中:p(x, y)为X和Y的联合概率密度;p(x),p(y)分别为X和Y的边缘概率密度。
假设Z={(xi, yi), i=1, 2, …, n}为一有限的有序对的集合,定义G为a×b的网格,将X,Y的值域分别分成a段和b段。MIC定义为:
| $ {I_{{\rm{MIC}}}}(Z) = \mathop {\max }\limits_{ab < B(n)} \left\{ {\frac{{\max {I_{{\rm{MI}}}}(Z\mid G)}}{{{{\log }_2}\min \{ a, b\} }}} \right\} $ | (4) |
式中:max IMI(Z|G)为划分G下Z的最大互信息,取不同划分方式中的IMI(X, Y)最大值作为划分G的互信息值。B(n)为网格划分a×b的上限值,当B=n0.6时效果较好。
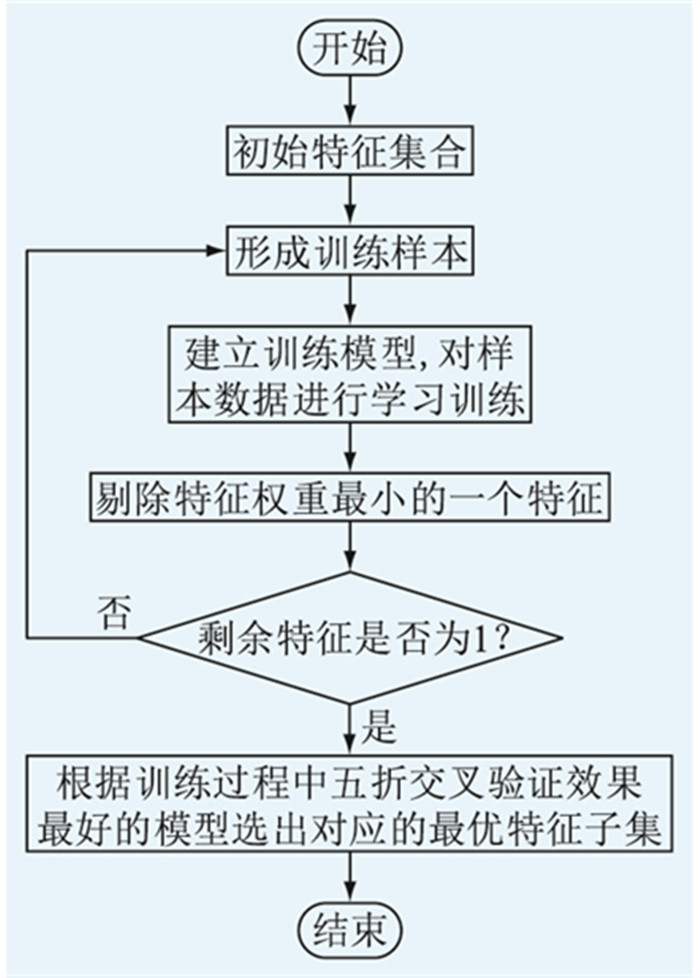
SVM-RFE是将SVM作为递归特征消除过程中的分类器,通过调节SVM模型的各项参数以确定特征排序的标准,算法流程如图 2所示。
|
图 2 SVM-RFE算法流程 Fig. 2 Flow chart of SVM-RFE algorithm |
SVM-RFE是一个向后消去特征的迭代过程,需经过多轮训练,每次迭代都要经过以下3步:
(1) 利用当前数据集对SVM进行训练,获得与分类器特征相关的信息;
(2) 按照评估准则计算特征权重值;
(3) 移除特征重要性排名最靠后的特征。
当特征集中只剩1个特征时,结束循环,输出五折交叉验证得分最高时所对应的特征集合。
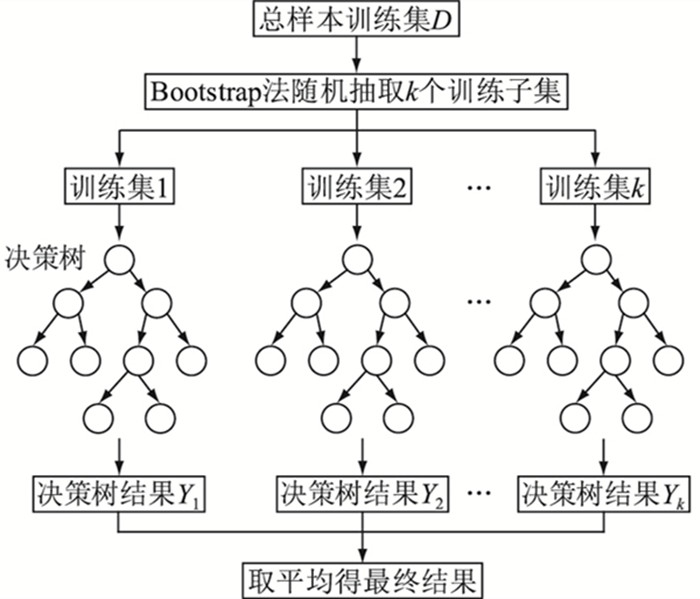
RF算法结构示意如图 3所示,核心思想是从样本M维特征中随机抽取m个特征组成分裂特征集,进行节点分裂,每个决策树不进行剪枝处理[18],使其最大程度地生长,最终生成一片森林,森林中的所有决策树投票得出最终结果。
|
图 3 随机森林结构 Fig. 3 Structure of random forest |
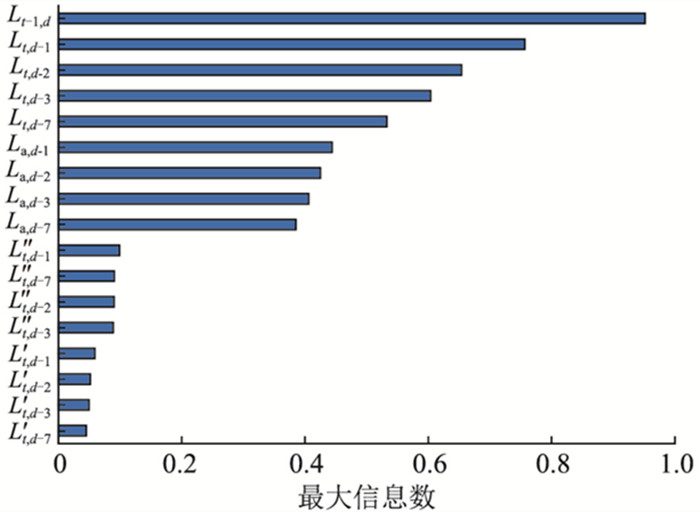
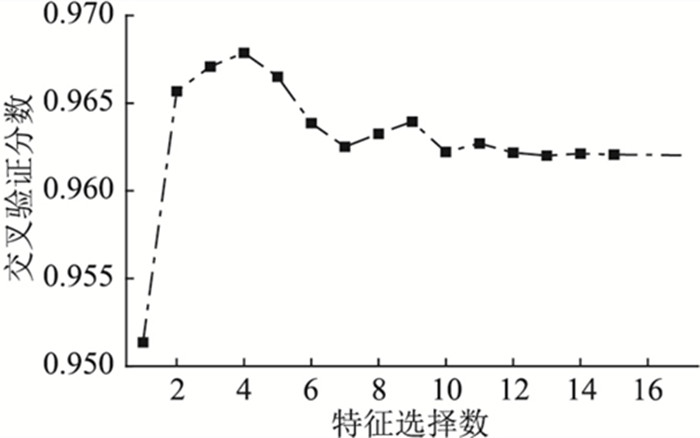
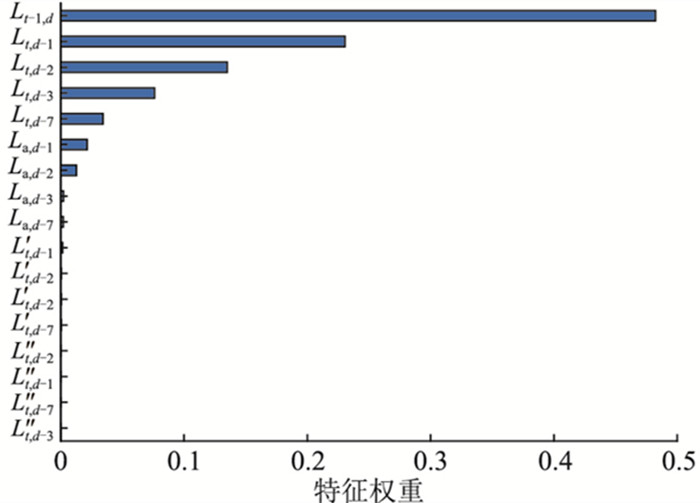
在进行特征选择时,历史负荷特征往往会掩盖其他特征,故将历史负荷特征单独考虑,利用以上3种方法对表 1中历史负荷特征进行选择,得到的MIC、RFE算法中不同特征数的交叉验证分数、RF模型特征权重值分别如图 4-图 6所示。
|
图 4 最大信息数 Fig. 4 Maximum information coefficient |
|
图 5 递归特征消除交叉验证分数 Fig. 5 Cross-validation scores of SVM-RFE |
|
图 6 随机森林特征权重 Fig. 6 Feature weights of random forest |
随着我国经济持续增长,人民生活水平不断提高,大功率家用电器也越来越普及,导致各种降温取暖负荷(特别是空调负荷)在社会总用电负荷中所占比例越来越大,故气象因素对于电力负荷的影响也是愈加显著。为此,同样应用以上3种方法对气表 1左栏气象、日期类型等特征进行选择,根据每个特征的MIC值、SVM-RFE算法中每个特征的得分和RF特征权重,将特征重要性按由大到小排序,所得特征排名如表 2所示。
|
|
表 2 3种方法的负荷外部因素特征排名 Table 2 Ranking of load-related external features in three methods |
根据以上特征选择结果可得如下结论:
(1) MIC与RF的历史负荷特征排序相差不大,虽然3种方法选择结果略有不同,但前一时刻负荷和1 d前时刻负荷的重要性排名都是位于第一和第二,可见这2个特征对于负荷预测的重要性。
(2) 相较于时刻负荷特征,各种日平均负荷排名相对靠后。对于负荷导数特征,除了SVM-RFE,其他2种方法中几乎排在末尾;MIC方法中负荷二阶导数排名普遍高于一阶导数,RF中则相反。
(3) 由于气象因素的随机多变、不确定性,且对于负荷功率的影响存在延时和累积效应,各方法的特征排名存在明显差异,选择结果也不尽相同,但可知外部因素中温度特征均占有较大权重。
(4) 据历史负荷和温度特征的排名,可知同一类型特征中,特征所在时间与预测日越近,重要性排名越高,这也体现了负荷影响因素的近因效应。
综上,尽管对比结果说明了部分历史负荷和温度特征的重要性,但负荷导数特征的重要性也未得到体现且3种方法的特征排名结果之间存在明显差异,仅靠设定阈值或是排名难以统一所选特征集,因此需要进一步对输入特征集进行优化搜索和验证分析。
3 基于遗传算法的最优特征集搜索针对以上3种特征选择方法结果的差异性,文中提出利用遗传算法对36个特征优化搜索得到最优特征子集。
3.1 个体染色体编码与生物遗传概念相对应,遗传算法里个体指优化问题的可行解,为1个变量序列,可行解中每一分量代表的特征就是基因[19]。根据具体问题通过1种编码方式,将可行解域中的每个解都表示为简单的字符串或数字符串,即染色体。
待选特征集中共有36个特征,对应染色体中36个基因,每个个体都代表 1种可能的特征组合,采用二进制对个体基因编码,1代表选中该特征,0代表没有选中,因此每个特征组合都可由1个长度为36的二进制串表示。
3.2 适应性函数计算为找出使负荷预测准确率达到最高的最优特征子集,预测模型采用极限梯度提升XGBoost模型,通过1组弱分类器的迭代计算实现准确的分类效果[20-23]。目标函数采用负荷预测模型日负荷平均引用误差的倒数,具体公式为:
| $ f\left( {{X_i}} \right) = \frac{1}{{\frac{1}{N}\sum\limits_{j = 1}^N {\left( {\frac{1}{{96}}\sum\limits_{t = 1}^{96} {{E_t}} } \right)} }} = \frac{{96N}}{{\sum\limits_{j = 1}^N {\sum\limits_{t = 1}^{96} {{E_t}} } }} $ | (5) |
其中:
| $ {E_t} = \frac{{\left| {{P_t} - P{'_t}} \right|}}{{{P_{\rm{B}}}}} \times 100\% $ | (6) |
式中:Xi为第i个遗传个体,即1个可能的特征子集;Et为t时刻母线的负荷预测的引用误差;N为测试集中的天数。文中日负荷曲线采用96点,时间间隔为15 min;Pt为t时刻母线负荷的实际值;P't为t时刻母线负荷的预测值;PB为负荷基准值,220 kV母线的负荷基准值为305 MV ·A。
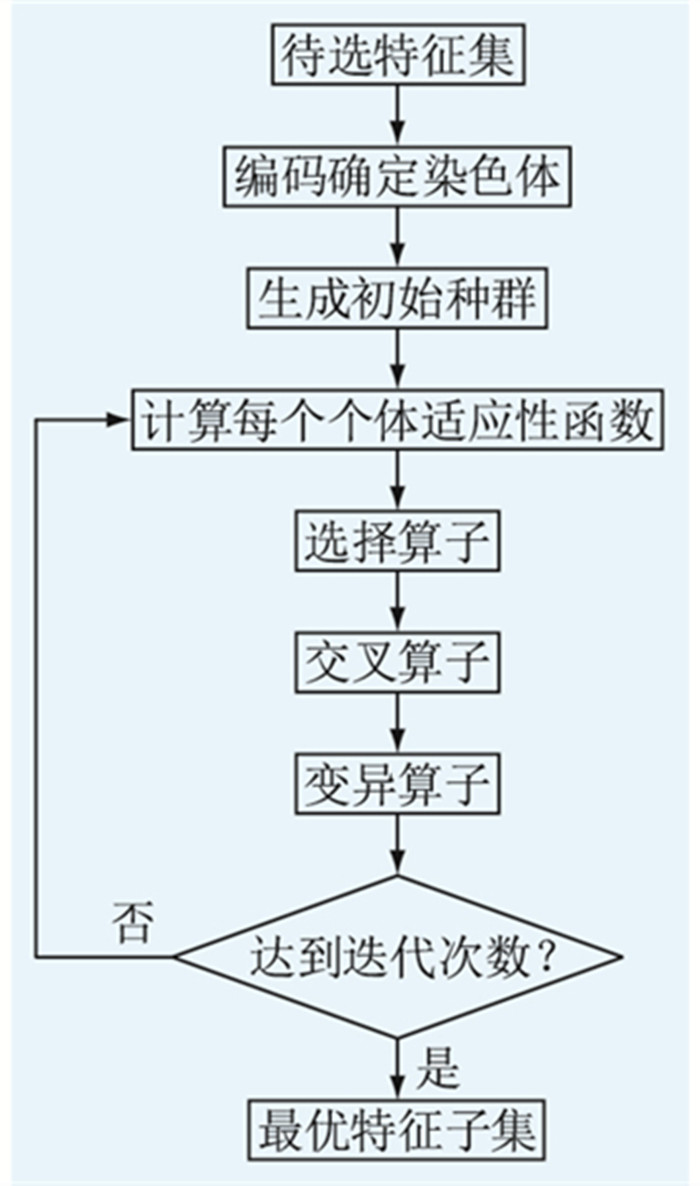
3.3 算法流程文中基于遗传算法的最优特征集搜索流程如图 7所示。由图 7可知,首先对待选特征集进行染色体编码,接着随机生成具有一定数量个体的初始种群。在每一代中,通过适应性函数计算值评价每一个体,并按照适应度高低进行排序。根据排名将优良个体挑选出来,通过交叉和变异过程实现种群的遗传进化。该过程不断重复,直至达到迭代次数,最终输出最优特征子集。
|
图 7 遗传算法流程 Fig. 7 Flow chart of genetic algorithm |
文中采用某地区220 kV高压侧母线2017-01-01-2018-10-23的负荷数据作为算例,根据国网公司发布的《电网母线负荷预测工作考核管理办法》,采用了母线的负荷预测引用误差作为负荷预测相关考核指标,具体计算公式见式(5)和式(6)。除此之外,文中还采用平均绝对百分误差(mean absolute percentage error,MAPE)来描述模型的预测性能。
| $ {E_{{\rm{MAPE}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{P_i} - P{'_i}}}{{{P_i}}}} \right|} \times 100\% $ | (7) |
式中:Pi为i时刻负荷的真实值;P'i为i时刻负荷的预测值;N为每日预测点总数。
4.2 遗传算法结果依照以上遗传算法流程,将交叉概率设为0.7,变异概率设为0.1,种群进化迭代次数设为100,每生成新一代种群,选择其中最优个体输出,种群进化100次后,共有18个特征,其中包含负荷导数特征,输出的最优特征集如表 3所示。
|
|
表 3 遗传算法输出最优特征集 Table 3 Optimal feature set obtained by genetic algorithm |
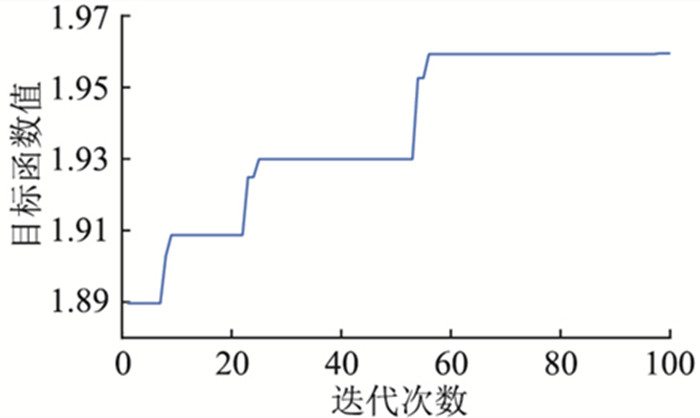
遗传算法迭代100次的目标函数值变化曲线如图 8所示。从迭代曲线和相应输出结果数据中得出,当迭代次数达到56次,算法已经收敛。
|
图 8 遗传算法目标函数变化曲线 Fig. 8 Curve of genetic algorithm objective function |
表 4列出了部分迭代次数后种群中最优个体的目标函数和相关负荷预测评价指标值。
|
|
表 4 评价指标变化情况 Table 4 Change of evaluation index values |
由表 4可知,算法每轮的输出结果表明当前最优特征组合在逐步向最终的最优特征集合靠拢,目标函数值不断增大,而日负荷平均引用误差和预测模型的平均绝对百分比误差在逐渐减小,最终得到最优特征子集。
4.3 有效性分析在第2节中,已经得到MIC、SVM-RFE、RF的特征排名,考虑到阈值的设定会对各方法所选特征数量产生较大影响,选定3种特征选取方案对比上述3种方法与遗传算法的特征选择效果,具体分别为:
方案一:不做任何特征选择,分别选取仅含历史负荷因素和仅含负荷外部因素的特征集以及所有36个特征组成的特征集。
方案二:3种方法单独考虑历史负荷时,从历史负荷排名结果中选取前9位,其他外部相关因素排名中选前9位,18个特征组成各自的输入集。
方案三:3种方法将所有特征一起考虑,选择总排名前18位特征作为输入集。
为体现导数特征对于负荷预测的影响,增加一组对比量,利用遗传算法对不含导数特征的输入特征集进行优化搜索。
分别将上述方案中各方法的特征选择结果作为负荷功率模型的特征输入集,采用与遗传算法中相同的XGBoost预测模型对算例中相同的训练集和测试集分别进行训练和负荷预测,各评价指标统计结果如表 5所示。
|
|
表 5 各特征选择方法的负荷预测误差统计 Table 5 Load forecasting error statistics of various feature selection methods |
由表 5可知:
(1) 由方案一的3组结果对比得到历史负荷因素对于负荷预测精度的重要性明显高于外部因素。从3种方法的总排名中也可以得到验证,其中历史负荷特征排名总体相对靠前,导数特征中温度导数特征重要性明显弱于负荷导数特征。
(2) 后2种方案中,MIC结果变动不大,误差结果较大;SVM-RFE结果同样差距不大,且误差较小;RF方法中3种方案的负荷预测误差跨距最大。这说明历史负荷特征与外部因素特征分开或合并选择对MIC和RFE影响不大,对RF影响较大。
(3) 将不考虑导数特征的遗传算法输出结果作为负荷预测输入特征时,误差指标明显增加,即负荷预测准确性下降,说明负荷导数特征一定程度上能描述负荷的变化趋势,对负荷预测具有重要意义。
(4) SVM-RFE的2种方案选择结果中均含有负荷导数,RF总排名前18位中也含有负荷导数特征。方案一中当仅有历史负荷特征作为输入和所有特征作为输入时,模型的输入特征集中包含了负荷导数特征,且预测效果有很大提升,与遗传算法结果较为接近,进一步验证了负荷导数特征的重要性,也对(2)中现象做出了合理解释。但是,递归特征消除方法在所有特征一起考虑时仅仅选择了3个,其中并不包含负荷导数特征,说明该方法利用交叉验证分数存在一定的局限性。
(5) 综合以上误差统计情况,就日负荷平均引用误差和MAPE而言,遗传算法对应的数值结果都是所在行的最小值,说明遗传算法所选特征集的预测结果要优于MIC、SVM-RFE和RF这3种方法所有特征选取方案和不做特征选择时的预测结果,表明文中基于遗传算法的最优特征集搜索方法对于负荷功率模型的特征输入集确实有一定的优化效果,能够有效提升负荷预测效果。
5 结语文中研究了短期功率模型的输入特征集的选择,针对MIC、SVM-RFE和RF 3种特征选择方法结果存在差异性这一情况,进一步提出利用遗传算法优化搜索最优特征集。对比各特征选择方法和特征选取方案,误差结果表明基于遗传算法得到的最优特征集作为输入可有效提高负荷预测精度,有助于确定负荷功率模型的输入特征集,并验证特征选择相关研究在短期负荷预测方面的有效性。
| [1] |
薛琳, 黄南天, 赵树野, 等. 基于条件互信息的低冗余短期负荷预测特征选择[J]. 东北电力大学学报, 2019, 39(2): 30-38. XUE Lin, HUANG Nantian, ZHAO Shuye, et al. Low redundancy feature selection using conditional mutual information for short-term load forecasting[J]. Journal of Northeast Electric Power University, 2019, 39(2): 30-38. (  0) 0) |
| [2] |
孔祥玉, 李闯, 郑锋, 等. 基于经验模态分解与特征相关分析的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 46-52. KONG Xiangyu, LI Chuang, ZHENG Feng, et al. Short-term load forecasting method based on empirical mode decomposition and feature correlation analysis[J]. Automation of Electric Power Systems, 2019, 43(5): 46-52. (  0) 0) |
| [3] |
何忠华, 张涛, 胡娱欧, 等. 考虑大气污染防治措施影响的短期电力负荷预测模型研究[J]. 智慧电力, 2019, 47(5): 1-9. HE Zhonghua, ZHANG Tao, HU Yu'ou, et al. Short-term electric load forecasting model considering the influence of air pollution prevention and control policy[J]. Smart Power, 2019, 47(5): 1-9. DOI:10.3969/j.issn.1673-7598.2019.05.001 (  0) 0) |
| [4] |
徐诗鸿, 张宏志, 林湘宁, 等. 基于改进评价指标的波动性负荷短期区间预测[J]. 电力系统自动化, 2020, 44(2): 156-163. XU Shihong, ZHANG Hongzhi, LIN Xiangning, et al. Improved evaluation index based short-term interval prediction of fluctuation load[J]. Automation of Electric Power Systems, 2020, 44(2): 156-163. (  0) 0) |
| [5] |
林志坚, 鲁迪, 林锐涛, 等. 基于k-means聚类和变分位鲁棒极限学习机的短期负荷预测方法[J]. 智慧电力, 2019, 47(3): 46-53. LIN Zhijian, LU Di, LIN Ruitao, et al. Short-term load forecasting method based on k-means clustering and varied quantile outlier robust extreme learning machine[J]. Smart Power, 2019, 47(3): 46-53. (  0) 0) |
| [6] |
李闯, 孔祥玉, 朱石剑, 等. 能源互联环境下考虑需求响应的区域电网短期负荷预测[J]. 电力系统自动化, 2021, 45(1): 71-78. LI Chuang, KONG Xiangyu, ZHU Shijian, et al. Short-term load forecasting of regional power grid considering demand response in energy interconnection environment[J]. Automation of Electric Power Systems, 2021, 45(1): 71-78. (  0) 0) |
| [7] |
郭亦宗, 冯斌, 岳铂雄, 等. 负荷聚合商模式下考虑需求响应的超短期负荷预测[J]. 电力系统自动化, 2021, 45(1): 79-87. GUO Yizong, FENG Bin, YUE Boxiong, et al. Ultra-short-term load forecasting considering demand response in load aggregator mode[J]. Automation of Electric Power Systems, 2021, 45(1): 79-87. (  0) 0) |
| [8] |
陈玉辰, 王子健, 姜宁, 等. 基于径向基函数优化的短期负荷预测方法[J]. 电力需求侧管理, 2019, 21(2): 36-40. CHEN Yuchen, WANG Zijian, JIANG Ning, et al. Short-term load forecasting method based on RBF parameter optimization[J]. Power Demand Side Management, 2019, 21(2): 36-40. (  0) 0) |
| [9] |
陈纬楠, 胡志坚, 岳菁鹏, 等. 基于长短期记忆网络和LightGBM组合模型的短期负荷预测[J]. 电力系统自动化, 2021, 45(4): 91-97. CHEN Weinan, HU Zhijian, YUE Jingpeng, et al. Short-term load prediction based on combined model of long short-term memory network and light gradient boosting machine[J]. Automation of Electric Power Systems, 2021, 45(4): 91-97. (  0) 0) |
| [10] |
姚旭, 王晓丹, 张玉玺, 等. 特征选择方法综述[J]. 控制与决策, 2012, 27(2): 161-166, 192. YAO Xu, WANG Xiaodan, ZHANG Yuxi, et al. Summary of feature selection algorithms[J]. Control and Decision, 2012, 27(2): 161-166, 192. (  0) 0) |
| [11] |
裴作飞, 李兆玉, 王云锋, 等. 基于自适应遗传算法的混合特征选择方法[J]. 计算机应用与软件, 2020, 37(8): 256-259, 306. PEI Zuofei, LI Zhaoyu, WANG Yunfeng, et al. Hybrid feature selection method based on adaptive genetic algorithm[J]. Computer Applications and Software, 2020, 37(8): 256-259, 306. DOI:10.3969/j.issn.1000-386x.2020.08.044 (  0) 0) |
| [12] |
ZHANG J X, XIONG Y M, MIN S G. A new hybrid filter/wrapper algorithm for feature selection in classification[J]. Analytica Chimica Acta, 2019, 1080: 43-54. DOI:10.1016/j.aca.2019.06.054 (  0) 0) |
| [13] |
周晨. 基于负荷特性的电力系统短期负荷预测实现[D]. 重庆: 重庆大学, 2008. ZHOU Chen. The realization of short term load foreeasting for power system based on load characteristic[D]. Chongqing: Chongqing University, 2008. (  0) 0) |
| [14] |
李光珍, 刘文颖, 云会周, 等. 母线负荷预测中样本数据预处理的新方法[J]. 电网技术, 2010, 34(2): 149-154. LI Guangzhen, LIU Wenying, YUN Huizhou, et al. A new data preprocessing method for bus load forecasting[J]. Power System Technology, 2010, 34(2): 149-154. (  0) 0) |
| [15] |
李嘉龙, 李小燕, 刘思捷, 等. 考虑气温累积效应的短期负荷预测[J]. 华北电力大学学报(自然科学版), 2013, 40(1): 49-54. LI Jialong, LI Xiaoyan, LIU Sijie, et al. Short-term load forecasting considering the accumulative effects of temperatures[J]. Journal of North China Electric Power University (Natural Science Edition), 2013, 40(1): 49-54. DOI:10.3969/j.ISSN.1007-2691.2013.01.010 (  0) 0) |
| [16] |
KHOSHROU A, PAUWELS E J. Short-term scenario-based probabilistic load forecasting: a data-driven approach[J]. Applied Energy, 2019, 238: 1258-1268. DOI:10.1016/j.apenergy.2019.01.155 (  0) 0) |
| [17] |
孙广路, 宋智超, 刘金来, 等. 基于最大信息系数和近似马尔科夫毯的特征选择方法[J]. 自动化学报, 2017, 43(5): 795-805. SUN Guanglu, SONG Zhichao, LIU Jinlai, et al. Feature selection method based on maximum information coefficient and approximate Markov blanket[J]. Acta Automatica Sinica, 2017, 43(5): 795-805. (  0) 0) |
| [18] |
荀港益. 基于聚类分析与随机森林的短期负荷滚动预测[J]. 智能城市, 2018, 4(9): 9-11. XUN Gangyi. A short-term load rolling prediction model based on cluster analysis and random forest(K-RF)[J]. Intelligent City, 2018, 4(9): 9-11. (  0) 0) |
| [19] |
辛宇, 童孟军, 华宇婷. 一种基于最优特征选择改进的遗传算法[J]. 传感技术学报, 2018, 31(11): 1747-1752. XIN Yu, TONG Mengjun, HUA Yuting. An improved genetic algorithm based on optimal feature selection[J]. Chinese Journal of Sensors and Actuators, 2018, 31(11): 1747-1752. DOI:10.3969/j.issn.1004-1699.2018.011.022 (  0) 0) |
| [20] |
LI G, LI W, TIAN X, et al. Short-term electricity load forecasting based on the XGBoost algorithm[J]. Smart Grid, 2017, 7(4): 274-285. DOI:10.12677/SG.2017.74031 (  0) 0) |
| [21] |
巢政, 温蜜. 一种基于SMOTE和XGBoost的窃电检测方案[J]. 智慧电力, 2020, 48(11): 97-102. CHAO Zheng, WEN Mi. Scheme for electricity theft detection based on SMOTE and XGBoost[J]. Smart Power, 2020, 48(11): 97-102. DOI:10.3969/j.issn.1673-7598.2020.11.017 (  0) 0) |
| [22] |
臧海祥, 刘冲冲, 滕俊, 等. 基于CNN-GRU分位数回归的短期母线负荷概率密度预测[J]. 智慧电力, 2020, 48(8): 24-30, 69. ZANG Haixiang, LIU Chongchong, TENG Jun, et al. Short-term bus load probability density forecasting based on CNN-GRU quantile regression[J]. Smart Power, 2020, 48(8): 24-30, 69. (  0) 0) |
| [23] |
段炼, 乡立, 吴琼, 等. 基于数据驱动的差分-RBF神经网络的台区短期负荷预测方法[J]. 广东电力, 2020, 33(11): 66-74. DUAN Lian, XIANG Li, WU Qiong, et al. Short-term load forecasting method based on data-driven difference RBF neural network[J]. Guangdong Electric Power, 2020, 33(11): 66-74. DOI:10.3969/j.issn.1007-290X.2020.011.009 (  0) 0) |
2. East China Grid Corporation, Shanghai 200120, China
 2021, Vol. 40
2021, Vol. 40


 严雪颖(1997),女,硕士在读,研究方向为电力系统分析(E-mail:
严雪颖(1997),女,硕士在读,研究方向为电力系统分析(E-mail: