文章编号: 2096-3203(2021)03-0186-07 中图分类号: TM615
2. 国家电网有限公司西北分部,陕西 西安 710048;
3. 西安交通大学电气工程学院,陕西 西安 710049
光热发电(concentrating solar power,CSP)技术具有清洁、调节性能好、配有储能系统等特点[1—3]。极端天气时光热发电不足,故评估光热机组参与电力平衡的容量成为规划运行人员的新挑战,这使得新能源发电的容量效益逐渐成为热点[4]。文献[5]考虑光伏发电与负荷相关性,分别计算昼夜光伏发电置信容量。文献[6]从电源侧考虑,采用中点分割法迭代求解在一定可靠性指标下,光伏机组的置信容量。文献[7—8]提出了光热机组可配合风电运行,降低风电机组的不确定性,进而降低系统的辅助服务需求并提高系统可靠性。文献[9—10]从可靠性的角度分析了含有储热及不含储热的光热机组的容量可信度。此外,文献[11—13]对光热机组建立优化运行模型。光热电站替代常规电源的容量效益将比光伏和风电要强,但其容量效益的发挥与资源特性、储热时长、调峰方式等因素密切相关。在电力系统规划设计阶段,光热发电大规模参加装机平衡,这对于系统规划设计与调度运行至关重要[14—16]。
目前对于光热电站容量效益的研究大多采用典型日的分析方法。该方法时间尺度短,无法模拟光热跨日调节导致的效益评估失真的问题,且对储热时长、光热运行方式的分析较少。故文中提出了一种全面分析光热电站容量效益的新方法,考虑光热电站的调峰方式、储热时长、新能源比例、光热电站规模等因素。该方法采用基于数学优化的生产模拟仿真,以周为尺度,计算全年8 760 h的系统运行状态,计及了机组启停、水电跨日调节、抽蓄跨日调节、光热电站的跨日调节等因素。
1 光热电站容量效益评估方法光热电站的容量效益是指光热电站可替代常规电源的容量。当系统中含有新能源发电、抽水蓄能、电化学储能电站时,光热电站的容量效益评估十分复杂,文中给出了一种采用等可靠性指标法评估光热电站的容量效益和电量效益的方法。即计算在可靠性指标不变的情况下,光热电站投入运行后,系统可降低的火电装机容量。光热电站容量效益示意如图 1所示。
|
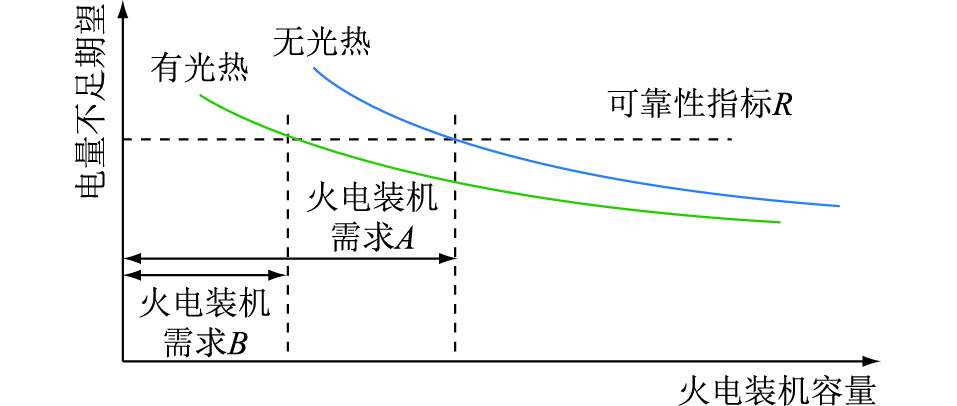
图 1 光热电站容量效益示意 Fig. 1 Schematic diagram of CSP station capacity efficiency |
由图 1可知,若没有光热电站,则在可靠性指标R的约束下,系统的火电装机需求为A,加入光热电站后,在相同的可靠性指标约束下,系统的火电装机需求为B,则火电装机需求A与火电装机需求B的差值反映了由于光热电站投入运行而使系统可减少的火电装机,此火电需求的差值即为光热电站的容量效益。
可靠性指标R取研究周期内由于供电不足造成的用户停电所损失的电量,即由于系统电源不可靠而使得用户减少的用电量。当已知停电单位电量的经济损失时,R指标可以转变为经济指标,便于方案比较。
| $ R=\sum\limits_{i=1}^{L} \Delta E_{i} $ | (1) |
式中:L为计算周期;ΔEi为i时刻系统的电量不足。
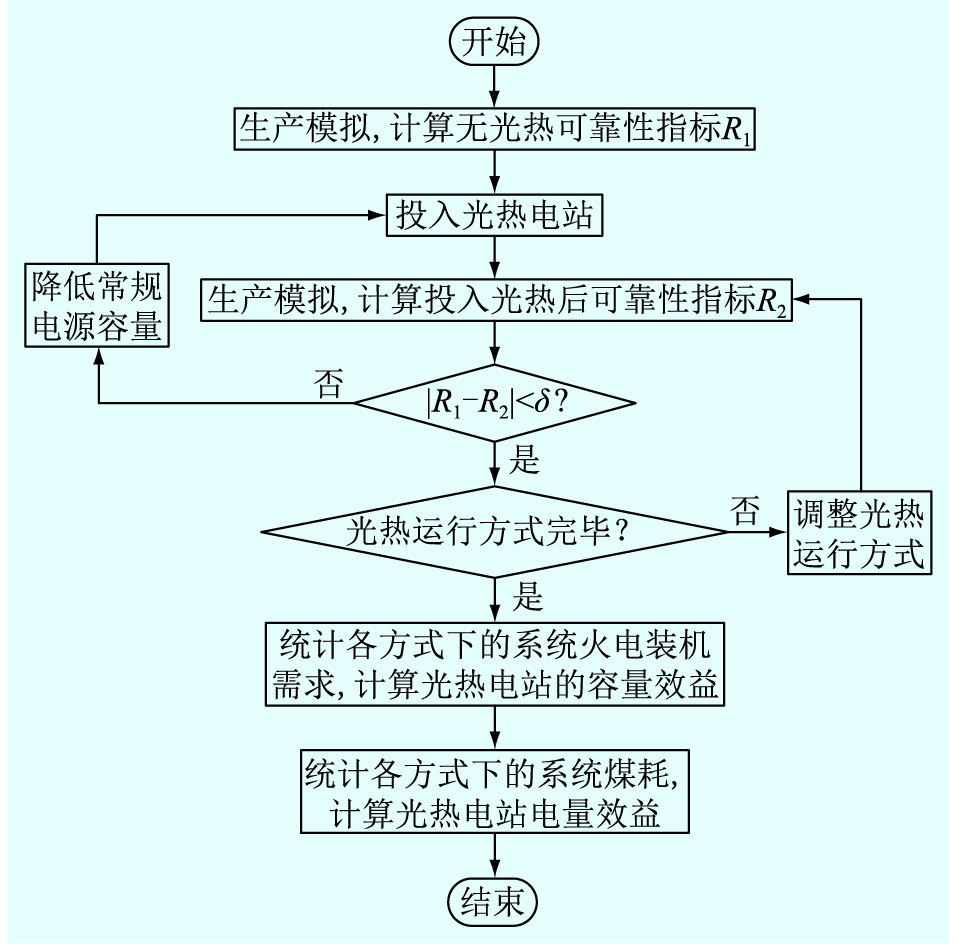
图 2为基于等可靠性指标的光热电站容量效益计算流程,R1和R2分别为投入光热电站前后系统的供电可靠性指标,δ为光热投入前后系统可靠性指标收敛值。
|
图 2 光热电站容量效益计算流程 Fig. 2 Flow chart of calculating capacity benefit of CSP station |
综合考虑新能源弃电量和发电煤耗,在满足负荷需求约束下,尽量减少新能源弃电量和系统发电煤耗,目标函数为:
| $ \min \left\{f_{1}+\lambda_{1} f_{2}+\lambda_{3} f_{3}+\lambda_{4} f_{4}+\lambda_{5} f_{5}+\lambda_{6} f_{6}\right\} $ | (2) |
式中:f1为火电机组的发电成本;f2为新能源发电的弃电量;f3为水电弃水电量;f4为光热机组发电成本;f5损失负荷成本;f6为损失备用成本; λ1,λ2,λ3,λ4分别为弃风、弃光、弃水以及因光热机组调峰运行而造成效率降低的惩罚因子;λ5为失负荷惩罚因子;λ6为失备用惩罚因子。各系数f的求解方式具体如下:
| $ \left\{\begin{array}{l} f_{1}=\sum\limits_{t=1}^{L} \sum\limits_{i=1}^{G}\left(C_{i, t}\left(P_{i, t}, U_{i, t}\right)+Q_{i, t, \text { up }}\left(U_{i, t-1}, U_{i, t}\right)+\right. \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.Q_{i, t, \text { off }}\left(U_{i, t-1}, U_{i, t}\right)\right) \\ f_{2}=\sum\limits_{t=1}^{L} \sum\limits_{b=1}^{B}\left(W_{b, t}^{(0)}-W_{b, t}\right)+\lambda_{2} \sum\limits_{t=1}^{T} \sum\limits_{b=1}^{B}\left(S_{b, t}^{(0)}-S_{b, t}\right) \\ f_{3}=\sum\limits_{t=1}^{L} \sum\limits_{i=1}^{Y} E_{i, t} \\ f_{4}=\sum\limits_{t=1}^{L} \sum\limits_{i=1}^{N}\left(H_{i, t}\left(P_{i, t}^{\mathrm{s}}, U_{i, t}^{\mathrm{s}}\right)+M_{i, t, \mathrm{up}}\left(U_{i, t-1}^{\mathrm{s}}, U_{i, t}^{\mathrm{s}}\right)+\right. \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.M_{i, t, \text { off }}\left(U_{i, t-1}^{\mathrm{s}}, U_{i, t}^{\mathrm{s}}\right)\right) \\ f_{5}=\sum\limits_{t=1}^{L} \sum\limits_{b=1}^{B} l_{b, t} \\ f_{6}=\sum\limits_{t=1}^{L} \sum\limits_{b=1}^{B} h_{b, t} \end{array}\right. $ | (3) |
式中:Ci, t为煤电机组i在时刻t的发电成本函数;Pi, t为机组i在时刻t的有功出力;Qi, t, up,Qi, t, off分别为机组i在时刻t的启动和停机费用;Ui, t,Ui, t-1分别为机组i在时刻t和时刻t-1的运行状态;Wb, t为时刻t节点b的风电场出力;Wb, t(0)为时刻t节点b的风电场的预测出力;Sb, t为时刻t节点b的光伏电站出力;Sb, t(0)为时刻t节点b的光伏电站预测出力;Ei, t为水电机组i时刻t的弃水量;lb, t,hb, t分别为时刻t节点b的失负荷量和失备用量;Hb, t为光热机组i在时刻t的效率;Mi, t, up,Mi, t, off分别为光热机组i在时刻t的启动和停机费用;Ui, ts,Ui, t-1s分别为光热机组i在时刻t和时刻t-1的运行状态;Pi, t为光热机组i在时刻t的有功出力;G为所有火电机组的集合;Y为所有水电机组的集合;N为所有光热机组的集合;B为所有节点的集合。
目标函数的约束条件包括系统平衡约束、电站/机组运行约束、地区间联络线功率约束等,具体可见文献[17—18],文中主要介绍光热电站约束。
2.2 光热电站数学模型以塔式熔盐光热电站为例,光热发电系统均分为3个部分:聚光集热部分、储热部分和发电部分。
聚光集热部分热量平衡约束如下:
| $ H_{i, t}^{\mathrm{sf}}=H_{i, t}^{\mathrm{D}}+H_{i, t}^{\mathrm{in}}-H_{i, t}^{\text {out }}+H_{i, t}^{\mathrm{gen}}+H_{i, t}^{\mathrm{SU}} $ | (4) |
式中:Hi, tsf为光热机组i的聚光集热系统在t时刻接收到的太阳光热能;Hi, tD为光热机组i的聚光集热系统在t时刻的弃热;Hi, tin为光热机组i时刻t流入储热罐的净热量;Hi, tout为光热机组i时刻t流出储热罐的净热量;Hi, tgen为光热机组i在t时刻进入汽轮机的用于发电的热量;Hi, tSU为光热机组i在t时刻进入汽轮机的用于启动的热量。
光热储热罐约束有进热和出热速率限制,总储热量限制和前后时刻热量流动关系表达式,即:
| $ 0 \leqslant H_{i, t}^{\text {out }} \leqslant H_{i, \max }^{\text {out }} u_{i, t}^{\mathrm{s}} $ | (5) |
| $ 0 \leqslant H_{i, t}^{\text {in }} \leqslant H_{i, \max }^{\mathrm{in}}\left(1-u_{i, t}^{\mathrm{s}}\right) $ | (6) |
| $ T_{i, \min } \leqslant T_{i, t} \leqslant T_{i, \max } $ | (7) |
| $ T_{i, t+1}=T_{i, t}+H_{i, t}^{\mathrm{in}} \eta_{i n}-H_{i, t}^{\text {out }} \eta_{\text {out }} $ | (8) |
式中:Hi, maxout为光热机组i的热罐的单时刻最大净出热量;Hi, maxin为光热机组i的热罐的单时刻最大净进热量;ui, ts为热罐在t时刻是否可以流出热量的0-1整数状态变量;Ti, t为光热机组i的热罐在t时刻的储热量;Ti, min为光热机组i的热罐的最小储热量;Ti, max为光热机组i的热罐的最大储热量;ηin为光热机组i的热罐的进热效率;ηout为光热机组i的热罐的出热效率。
光热机组储热罐的初态值约束和末态值约束,可表示为:
| $ \left\{\begin{array}{l} T_{i, 0}=T_{i, \text { init }} \\ T_{i, L}+H_{i, L}^{\mathrm{in}} \eta_{\mathrm{in}}-H_{i, L}^{\text {out }} \eta_{\mathrm{out}}=T_{i, \mathrm{end}} \end{array}\right. $ | (9) |
式中:Ti, init为光热机组i的热罐的初始储热;Ti, end为光热机组i的热罐的末态储热。
光热机组通常需要2 h积累的热量才能满足启动需求,其中任一时段积累的热量既取决于允许进热最大值,也取决于该时段的光照和热罐储存的可用热量,需要满足的约束,可表示为:
| $ H_{i, t}^{\mathrm{SU}} \leqslant\left(y_{i, t}^{\mathrm{csp}}+y_{i, t+1}^{\mathrm{csp}}\right) H_{i, \max }^{\mathrm{SU}} $ | (10) |
| $ H_{i, t}^{\mathrm{SU}}+H_{i, t+1}^{\mathrm{SU}} \geqslant H_{i, \mathrm{req}}^{\mathrm{SU}} y_{i, t}^{\mathrm{csp}} $ | (11) |
| $ H_{i, t}^{\mathrm{SU}}+H_{i, t+1}^{\mathrm{SU}} \leqslant H_{i, \mathrm{req}}^{\mathrm{SU}} $ | (12) |
| $ u_{i, 0}^{\mathrm{csp}}-u_{i, \mathrm{init}}^{\mathrm{csp}}=-z_{i, 0}^{\mathrm{csp}} $ | (13) |
| $ u_{i, t}^{\mathrm{csp}}-u_{i, t-1}^{\mathrm{csp}}=y_{i, t-1}^{\mathrm{csp}}-z_{i, t}^{\mathrm{csp}} $ | (14) |
| $ 0 \leqslant y_{i, t-1}^{\mathrm{csp}}+z_{i, t}^{\mathrm{csp}} \leqslant 1 $ | (15) |
| $ 0 \leqslant y_{i, t}^{\mathrm{csp}}+z_{i, t}^{\mathrm{csp}} \leqslant 1 $ | (16) |
| $ \sum\limits_{\tau=t}^{t+{T_{\min }^{\mathrm{on}}}-1} u_{i, \tau}^{\mathrm{csp}}-y_{i, t}^{\mathrm{csp}} T_{i, \min }^{\mathrm{on}} \geqslant 0 $ | (17) |
| $ \sum\limits_{\tau=t}^{t+{T_{\min }^{\mathrm{on}}}-1}\left(1-u_{i, \tau}^{\mathrm{csp}}\right)-z_{i, t}^{\mathrm{csp}} T_{i, \min }^{\mathrm{off}} \geqslant 0 $ | (18) |
式中:yi, tcsp为光热机组i的汽轮机在t时刻是否有启动动作的0-1整数变量;Hi, maxSU为光热机组i启动热量允许最大输入量;Hi, reqSU为光热机组i的汽轮机启动所需热量;Hi, tSU为t时刻光热机组i的启动热量;Hi, t+1SU为t+1时刻光热机组i的启动热量;ui, tcsp为光热机组i的汽轮机在t时刻的开机0-1整数状态变量;ui, 0csp为光热机组i的初始开停机状态;zi, tcsp为光热机组i在时刻t的关机0-1整数变量;ui, initcsp为光热机组i的汽轮机的初始开机状态;zi, tcsp为光热机组i的汽轮机在t时刻的关机0-1整数动作变量;Ti, minon为光热机组i的汽轮机的最小开机时间;Ti, minoff为光热机组i的汽轮机的最小关机时间。
式(10)-式(12)为启动热量约束,表示在有了启动动作的第二个时段,所积累的启动热量才能达到启动要求,达到开机状态。式(13)和式(14)表示光热机组汽轮机前后时刻状态切换整数变量约束。式(15)和式(16)表示汽轮机任意时刻的开机动作和关机动作不能同时发生,也不能前一时刻有开机动作,后一时刻立即关机。式(17)和式(18)表示最小开停机时间约束。
光热机组汽轮机发电功率满足最大值与最小值限制。
| $ p_{i, \min }^{\mathrm{csp}} u_{i, t}^{\mathrm{csp}} \leqslant p_{i, t}^{\mathrm{csp}} \leqslant p_{i, \max }^{\mathrm{csp}} u_{i, t}^{\mathrm{csp}} $ | (19) |
式中:pi, tcsp为光热电站i时刻t的发电功率;pi, mincsp为光热机组i的最小发电功率;pi, maxcsp为光热机组i的最大发电功率。
2 案例分析 2.1 系统参数及运行方式以我国某省区电网为算例进行验证,该电网负荷28 000 MW,直流外送16 000 MW,内用电量1 800亿kW ·h,外送电量1 024亿kW ·h,电源结构如表 1所示。
|
|
表 1 某实际电网电源装机 Table 1 Power supply of practical grid |
光热电站容量效益的发挥,与光热电站的调峰方式、储热时长、装机规模、风电和光伏比例等因素密切相关,考虑多种场景,如表 2所示。
|
|
表 2 光热电站容量效益分析场景 Table 2 Scenario of capacity benefit analysis of CSP |
采用1.1节光热电站容量效益的计算流程和1.2节生产模拟程序,计算光热电站加入系统后,火电装机需求的变化,结果如表 3和表 4所示。
|
|
表 3 容量效益分析 Table 3 Capacity benefit analysis |
|
|
表 4 生产模拟运行结果 Table 4 Production simulation results |
由表 3和表 4可知,无光热电站情况下(场景A),系统需要火电装机39 970 MW;新能源弃电率为6%;煤耗5 851万t。考虑2 000 MW光热装机后(光热不参与调峰,场景B)后,系统火电装机维持不变,即光热电站不参与调峰情况下,系统并没有因光热电站增加2 000 MW而降低了常规火电的装机需求,其容量效益为0,且由于光热电站不参与调峰,新能源弃电率有所提高,弃电率增加至8.1%。系统煤耗降低了170万t。当场景B中2 000 MW光热参与调峰时(场景C),系统火电装机需求为39 070 MW,火电装机需求降低900 MW,即光热电站容量效益为900 MW,容量替代率为45%;煤耗降低286万t;新能源弃电率5.0%。
为了分析储热时长对容量效益的影响,场景D将场景C中光热电站储热时长降低2 h,计算结果显示,系统火电装机需求为39 270 MW,光热电站容量效益为700 MW,容量替代率为35%;煤耗降低279万t;新能源弃电率5.2%。可以看出,储热时长降低后,光热电站的调节性能有所降低,容量效益的发挥也有所降低。
为分析其他新能源发电规模对光热发电容量效益的影响,场景E为场景C中光伏规模增加5 000 MW的情况。光伏规模增加了5 000 MW以后,系统新能源弃电率有所提高,系统火电装机需求为38 870 MW,即光热电站容量效益为1 100 MW,容量替代率为55%;煤耗降低288万t;新能源弃电率7.5%。
为分析光热发电自身规模对其容量效益的影响,场景F该场景为场景C中增加了2 000 MW光热的情况,可以看出,系统中加入4 000 MW光热装机后,火电装机需求为38 470 MW,光热电站容量效益为1 500 MW,容量替代率为37.5%;煤耗降低了557万t;新能源弃电率4.4%。
(1) 光热电站发挥容量效益与调峰方式相关。在该算例中,光热电站不参与调峰的情况下(场景B),光热电站的容量效益为0,即光热电站的加入仅降低系统煤耗的电量效益,2 000 MW的光热降低了179万t标煤,但并不能降低火电的装机规模。光热电站参与调峰后(场景C),光热电站具有了容量效益,可降低系统所需火电装机规模。该算例中2 000 MW的光热电站降低了900 MW的火电,容量替代率为45%。
(2) 光热电站发挥容量效益与储热时长相关。该算例中,光热电站储热时长12 h,调峰运行方式下(场景C),容量效益为900 MW,而储热时长为10 h的情况下(场景D),容量效益为700 MW。由于光热电站储热时长的增加,可以降低火电装机需求200 MW。
(3) 光热电站容量效益的发挥,与系统中新能源规模相关。对比场景C和场景E,在光热电站规模和调峰方式相同的情况下,系统光伏规模从11 500 MW增加至16 500 MW后,新能源弃电率增加2.5%,系统火电装机需求从39 070 MW降低至38 870 MW。由于光伏夜间不发电,而文中算例系统负荷高峰在晚上9点左右,因此可认为系统火电装机需求的降低是由光热发电引起,并不是增加光伏引起的,即光热电站容量效益增加至1 100 MW,光热发电容量效益增加了200 MW。
(4) 光热电站发挥容量效益和光热电站自身规模相关。光热电站规模越大,能够替换下来的火电规模也越大,但是其容量替代率不一定继续增加。对比场景C和场景F,在其他所有条件都相同的情况下,光热电站规模从2 000 MW增加至4 000 MW,容量效益从900 MW增加至1 500 MW,但其容量替代率却从45%降低至37.5%。
综合上述分析,影响光热电站容量效益的因素有储热时长、光热本身规模、调峰方式,并且随着光热规模的增加,光热容量替代率有一个先增加后下降的过程,尽管容量效益的绝对值仍在增加。表 5给出了光热电站容量效益替代率的拐点计算结果。对于文中算例系统而言,2 500 MW光热发电的容量替代率最大。
|
|
表 5 光热电站容量效益最大替代率计算结果 Table 5 Calculation results of maximum replace-ment rate of capacity benefit of CSP station |
在文中算例中,光热不参与调峰时候容量效益为0,对于其他系统也有大于0的情况。文中算例中列出光热不参与调峰的容量效益,是为了反映光热电站调峰运行方式对其容量效益具有重要影响。光热电站的典型日运行方式如图 3—图 5所示。
|
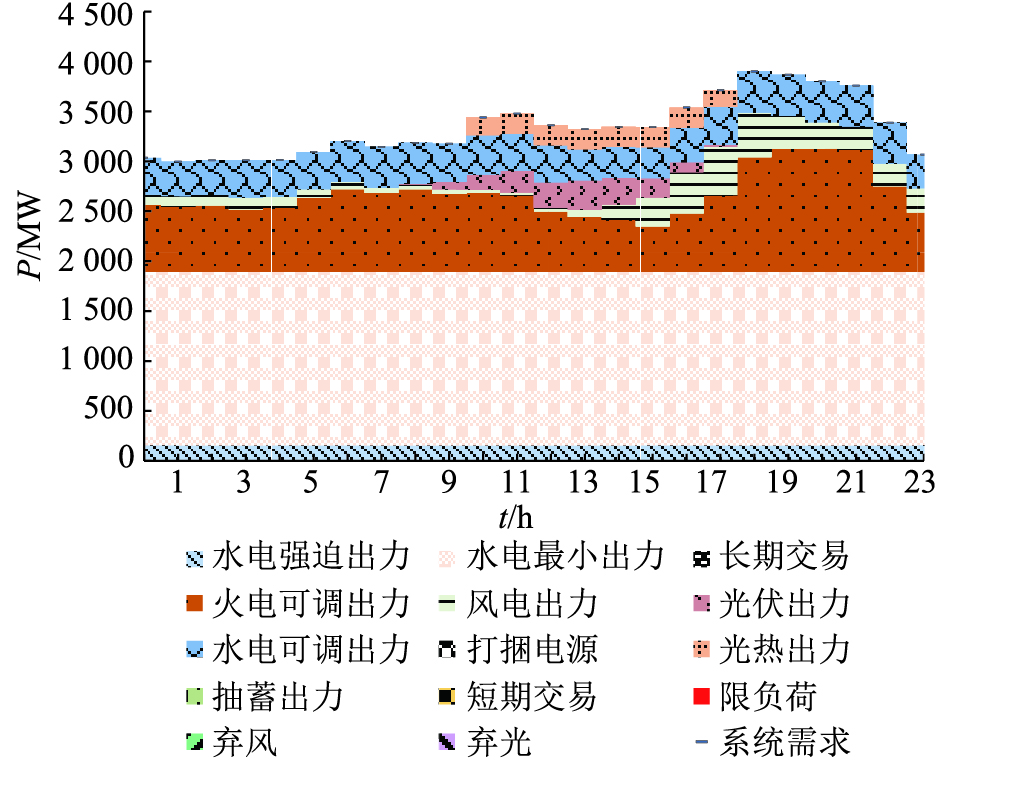
图 3 日模拟(光热2 000 MW,储热12 h,不参与调峰) Fig. 3 Simulation of daily operation (2 000 MW CSP, heat storage for 12 h, not participating in load peaking) |
|
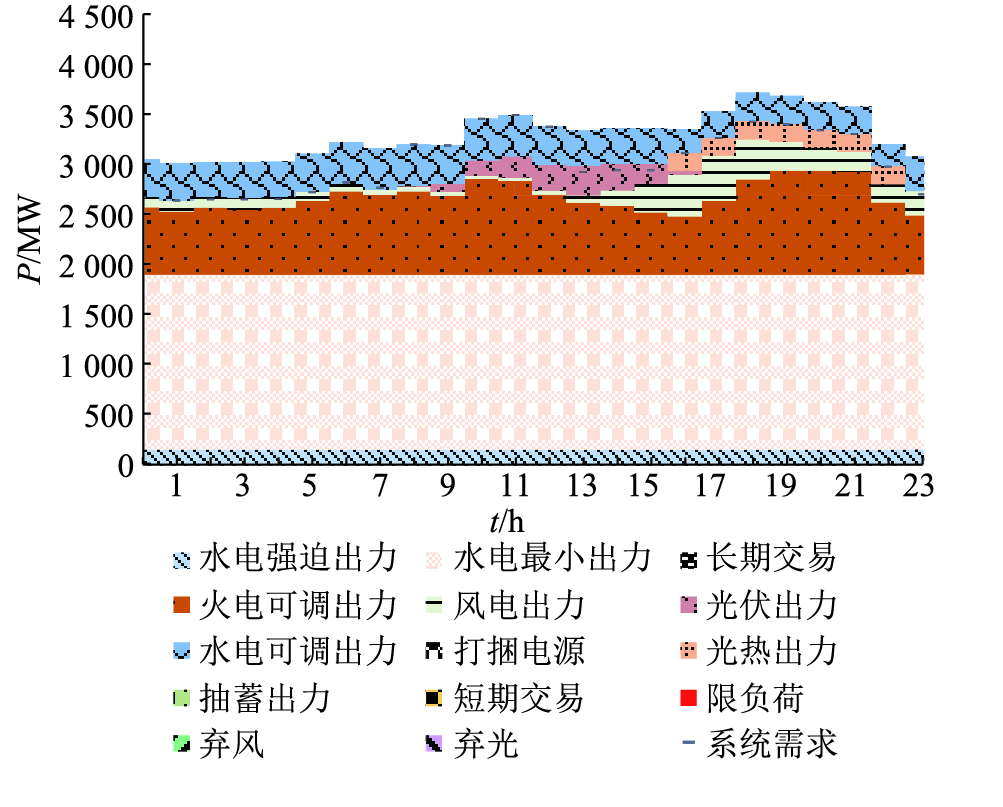
图 4 日模拟(光热2 000 MW,储热12 h,参与调峰) Fig. 4 Simulation of daily operation (2 000 MW CSP, heat storage for 12 h, participating in load peaking) |
|
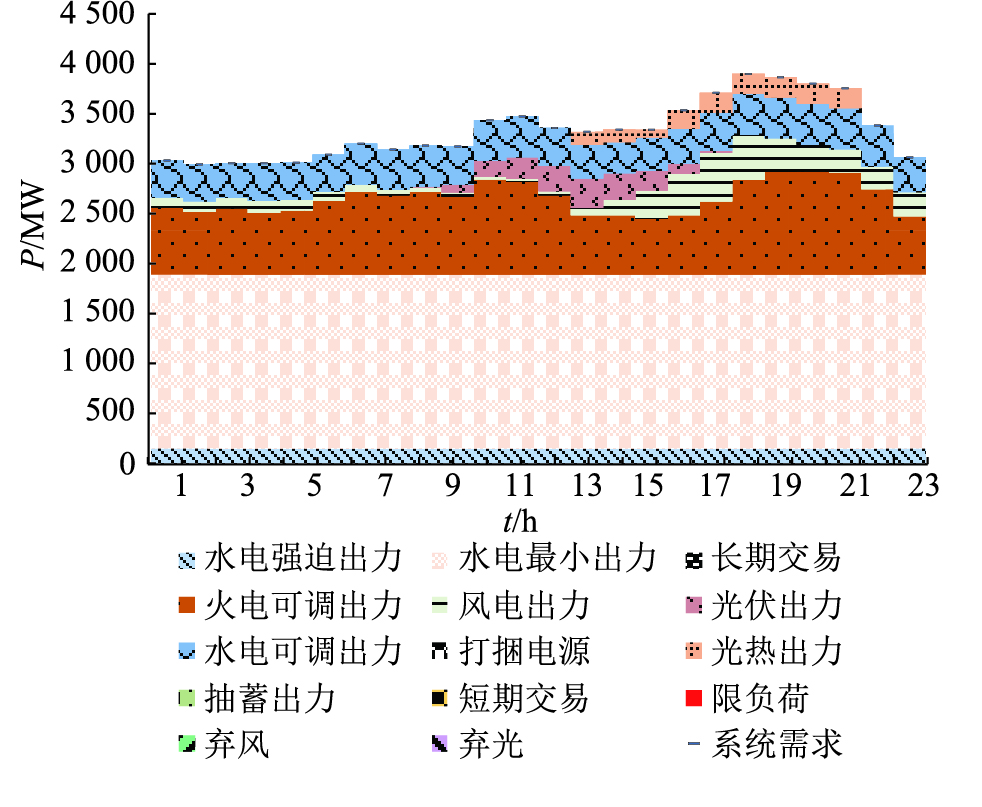
图 5 日模拟(光热2 000 MW,储热10 h,参与调峰) Fig. 5 Simulation of daily operation (2 000 MW CSP, he- at storage for 10 h, participating in load peaking) |
由图 3可知,当光热电站不参与调峰时,其出力集中在10~16点,即太阳能资源最好的时候出力最多。当光热电站参与调峰情况下,如图 4所示,光热发电白天没有发电,而在晚上负荷高峰时候,光热电站发电,系统可降低常规电源的装机容量,光热电站发挥了容量效益。图 5给出光热规模2 000 MW、储热时长为10 h的运行模拟情况。与图 4类似,光热晚间发电,发挥容量效益。
通过上述分析,光热电站的容量配置方案涉及许多因素,包括光热本体、调度运行方式、系统的规模和电源结构。在目前调度策略下,光热电站以自身发电量最大为目标,配置10~12 h的储热时长,不参与系统调峰较为合理,当光热资源充足时,光热电站满出力运行,并将多余的热量存储起来,其他时段发电。一个大型系统中最佳的光热装机规模,与系统对新能源发电量配额指标的要求相关。当系统消纳新能源目标要求过高时,如完全依靠风电光伏,将导致弃电率升高。光热系统的装设,增加了新能源消纳量,且不对系统调峰造成影响。
3 结论(1) 提出了一种评估光热电站容量效益的等可靠性法,分析了调峰方式、储热时长、新能源规模、光热电站规模等因素对光热电站容量效益的影响。
(2) 对含有光热的复杂系统进行8 760 h生产模拟,考虑光热电站跨日调节,避免了典型日生产模拟无法模拟光热跨日调节导致的效益评估失真的问题。
(3) 随着光热发电规模的增加,光热发电容量效益增加,但光热发电容量替代率有一个先增加后下降的过程。
| [1] |
杜尔顺, 张宁, 康重庆, 等. 太阳能光热发电并网运行及优化规划研究综述与展望[J]. 中国电机工程学报, 2016, 36(21): 5765-5775, 6019. DU Ershun, ZHANG Ning, KANG Chongqing, et al. Reviews and prospects of the operation and planning optimization for grid integrated concentrating solar power[J]. Proceedings of the CSEE, 2016, 36(21): 5765-5775, 6019. (  0) 0) |
| [2] |
冯陈佳, 邵成成, 王雅楠, 等. 考虑启动热量约束的光热机组优化运行模型[J]. 电力系统自动化, 2019, 43(13): 29-35. FENG Chenjia, SHAO Chengcheng, WANG Ya′nan, et al. Optimal operation model of concentrating solar power units considering startup heat constraints[J]. Automation of Electric Power Systems, 2019, 43(13): 29-35. DOI:10.7500/AEPS20181026004 (  0) 0) |
| [3] |
魏炜, 贾皓越, 穆云飞, 等. 光电-光热区域综合能源系统太阳能消纳能力评估模型[J]. 电力系统自动化, 2019, 43(20): 16-23, 38. WEI Wei, JIA Haoyue, MU Yunfei, et al. Assessment model of solar energy accommodation capability of regional integrated energy system with PVs and solar collectors[J]. Automation of Electric Power Systems, 2019, 43(20): 16-23, 38. DOI:10.7500/AEPS20181008008 (  0) 0) |
| [4] |
高英, 谢开贵, 胡博, 等. 考虑光伏出力与负荷相关性的光伏电站容量可信度评估[J]. 电力系统保护与控制, 2013, 41(14): 1-6. GAO Ying, XIE Kaigui, HU Bo, et al. Photovoltaic power capacity credit evaluation model considering the correlation between photovoltaic power generation and system load[J]. Power System Protection and Control, 2013, 41(14): 1-6. DOI:10.7667/j.issn.1674-3415.2013.14.001 (  0) 0) |
| [5] |
方鑫, 郭强, 张东霞, 等. 并网光伏电站置信容量评估[J]. 电网技术, 2012, 36(9): 31-35. FANG Xin, GUO Qiang, ZHANG Dongxia, et al. Capacity credit evaluation of grid-connected photovoltaic generation[J]. Power System Technology, 2012, 36(9): 31-35. (  0) 0) |
| [6] |
张宁, 康重庆, 陈治坪, 等. 基于序列运算的风电可信容量计算方法[J]. 中国电机工程学报, 2011, 31(25): 1-9. ZHANG Ning, KANG Chongqing, CHEN Zhiping, et al. Wind power credible capacity evaluation model based on sequence operation[J]. Proceedings of the CSEE, 2011, 31(25): 1-9. (  0) 0) |
| [7] |
CHEN R Z, SUN H B, GUO Q L, et al. Reducing generation uncertainty by integrating CSP with wind power: an adaptive robust optimization-based analysis[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 583-594. DOI:10.1109/TSTE.2015.2396971 (  0) 0) |
| [8] |
XU T, ZHANG N. Coordinated operation of concentrated solar power and wind resources for the provision of energy and reserve services[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1260-1271. (  0) 0) |
| [9] |
MADAENI S H, SIOSHANSI R, DENHOLM P. Estimating the capacity value of concentrating solar power plants: a case study of the southwestern United States[J]. IEEE Transactions on Power Systems, 2012, 27(2): 1116-1124. DOI:10.1109/TPWRS.2011.2179071 (  0) 0) |
| [10] |
MADAENI S H, SIOSHANSI R, DENHOLM P. Estimating the capacity value of concentrating solar power plants with thermal energy storage: a case study of the southwestern United States[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1205-1215. DOI:10.1109/TPWRS.2012.2207410 (  0) 0) |
| [11] |
陈润泽, 孙宏斌, 李正烁, 等. 含储热光热电站的电网调度模型与并网效益分析[J]. 电力系统自动化, 2014, 38(19): 1-7. CHEN Runze, SUN Hongbin, LI Zhengshuo, et al. Grid dispatch model and interconnection benefit analysis of concentrating solar power plants with thermal storage[J]. Automation of Electric Power Systems, 2014, 38(19): 1-7. DOI:10.7500/AEPS20140313001 (  0) 0) |
| [12] |
晋宏杨, 孙宏斌, 郭庆来, 等. 含大规模储热的光热电站-风电联合系统多日自调度方法[J]. 电力系统自动化, 2016, 40(11): 17-23. JIN Hongyang, SUN Hongbin, GUO Qinglai, et al. Multi-day self-scheduling method for combined system of CSP plants and wind power with large-scale thermal energy storage contained[J]. Automation of Electric Power Systems, 2016, 40(11): 17-23. DOI:10.7500/AEPS20150826012 (  0) 0) |
| [13] |
孙沛, 傅旭, 李富春, 等. 含有电加热装置的光热机组运行策略研究[J]. 智慧电力, 2018, 46(3): 38-43. SUN Pei, FU Xu, LI Fuchun, et al. Study on operation strategy of concentrating solar power plant with electric heating device[J]. Smart Power, 2018, 46(3): 38-43. DOI:10.3969/j.issn.1673-7598.2018.03.007 (  0) 0) |
| [14] |
宋汶秦, 吕金历, 赵玲霞, 等. 光热-风电联合运行的电力系统经济调度策略研究[J]. 电力系统保护与控制, 2020, 48(5): 95-102. SONG Wenqin, LYU Jinli, ZHAO Lingxia, et al. Study on the economic dispatch strategy of power system with combined operation of concentrated solar power and wind farm[J]. Power System Protection and Control, 2020, 48(5): 95-102. (  0) 0) |
| [15] |
贠韫韵, 董海鹰, 陈钊, 等. 考虑随机性及光热电站参与的多源发电系统两阶段随机优化调度[J]. 电力系统保护与控制, 2020, 48(4): 30-38. YUN Yunyun, DONG Haiying, CHEN Zhao, et al. A two-stage stochastic scheduling optimization for multi-source power system considering randomness and concentrating solar power plant participation[J]. Power System Protection and Control, 2020, 48(4): 30-38. (  0) 0) |
| [16] |
张宏, 董海鹰, 陈钊, 等. 基于模型预测控制的光热-光伏系统多时间尺度无功优化控制策略研究[J]. 电力系统保护与控制, 2020, 48(9): 135-142. ZHANG Hong, DONG Haiying, CHEN Zhao, et al. Multi-time scale reactive power optimal control strategy of a CSP-PV system based on model predictive control[J]. Power System Protection and Control, 2020, 48(9): 135-142. (  0) 0) |
| [17] |
朱少杰, 刘皓明, 唐宇, 等. 含多个能源站的区域综合能源系统建模及协同优化运行策略[J]. 电力需求侧管理, 2019, 21(4): 60-66. ZHU Shaojie, LIU Haoming, TANG Yu, et al. Modeling and collaborative optimal operation strategy for multiple energy stations of regional integrated energy system[J]. Power Demand Side Management, 2019, 21(4): 60-66. (  0) 0) |
| [18] |
荀挺, 雷胜华, 丁晓辰, 等. 区域综合能源系统的多目标最优潮流算法研究[J]. 智慧电力, 2019, 47(9): 19-28. XUN Ting, LEI Shenghua, DING Xiaochen, et al. Multi-objec-tive optimal power flow algorithms for integrated community energy systems[J]. Smart Power, 2019, 47(9): 19-28. (  0) 0) |
2. Northwest Branch of State Grid Corporation of China, Xi′an 710048, China;
3. School of Electrical Engineering, Xi′an Jiaotong University, Xi′an 710049, China
 2021, Vol. 40
2021, Vol. 40


 傅旭(1976),男,博士,研究员级高级工程师,从事电力系统规划分析工作(E-mail:
傅旭(1976),男,博士,研究员级高级工程师,从事电力系统规划分析工作(E-mail: