文章编号: 2096-3203(2021)03-0035-07 中图分类号: TM734
2. 南瑞集团有限公司(国网电力科学研究院),江苏 南京 211106;
3. 国网江苏省电力有限公司,江苏 南京 210024
随着工业结构的调整和节能减排方针政策的实施,电网逐步淘汰落后产能、关停老旧火电机组。电化学储能以技术成熟、建设周期短的特点成为替代电源的首选。通过储能电站建设,可弥补火电机组退役后的供电紧张局面[1-3]。
电网调度机构依据地域将电网划分为若干子区域以降低调度控制的复杂度,形成由1个或多个500 kV变电站为中心,带动220 kV地区负荷分片运行的网络格局[4-5]。近年来清洁能源迅速发展,其出力不确定性和不同于常规电源的调峰特性引发潮流倒送和输变电设备过载,加大了电网分区内输变电潮流的控制难度[6-8]。通过储能资源的集中管理,可实现削峰填谷和电能量时移,解决分布式电源的就近消纳和并网问题,提升电网的运行安全。储能电站单站容量小难以形成有效的调控资源,因此电网分区的平衡分析和调度控制应关注整个分区或断面下多电站聚合后整体的充放电特性。目前尚缺乏有效的可为调度机构提供辅助决策的储能资源聚合监测手段,因此如何融合多储能电站的电力和电量信息,拟合储能资源整体的充放电能力,成为规模化储能调度控制中亟需解决的问题。
规模化储能的优化控制技术在国内外学术领域已有广泛而深入的研究。文献[9-11]中的混合能源系统利用储能平滑风电、光伏功率波动,提升清洁能源的并网接入能力和市场交易的可行性。文献[12-13]中的联网型微电网利用负荷和清洁能源预测优化储能系统的充放电行为,促进了本地电力市场交易,节约了购电成本。文献[14-15]通过日前和实时两阶段优化、可变充放电功率控制,减小了峰谷差,实现了平滑负荷的目的。文献[16-17]分析了储能在不同调度应用场景下参与大功率缺失故障的快速调频及与负荷协同的需求侧响应,并提出了容量配置方法。
文中针对规模化储能电站接入的电网分区,利用聚合分析算法,从电力和电量2个维度分析多储能电站的充放电能力,为调度主站端的储能电站集群的快速功率控制、负荷趋势跟踪提供决策依据;在归纳电网分区控制目标的基础上,提出储能电站参与分区控制的分配策略,以满足电网分区正常情况下的发用电平衡、紧急情况下的断面安全要求。
1 规模化储能聚合特性分析电池单体以荷电状态(state of charge, SOC)和健康度(state of health, SOH)评估电池的潜在电能,衡量储存和输送电能的能力。电池管理系统和能量管理系统对站内电池和电池组进行测量分量和充放电管理控制。调度主站从储能电站上进行信息抽取和建模,其上传信息包括:有功功率、SOC量测、SOC上/下限、最大充/放电功率、充/放电闭锁等。调度主站自动发电控制(automatic generation control, AGC)控制建模的接入信息,如表 1所示。遥测量约定充电功率为负,放电功率为正。
|
|
表 1 调度主站AGC控制接入储能电站信息 Table 1 Energy storage station information for AGC of dispatching center |
差异化储能电站的聚合并非电力和电量的简单累加,取决于各电站的运行约束和电站间的功率分配策略。因此,以电能量最大化利用为目标,将储能聚合后的电力和电量属性转换为功率与时间特性,并拟合特性曲线。
1.1 功率与可用时间特性功率与可用时间特性可描述满足某一有功功率的最大持续可用时间,该特性主要取决于分配策略下可用时间最短的储能电站。通过站间动态聚合和分解协调计算,可提高计算效率且减少分配策略导致的调节资源浪费。计算流程如图 1所示。

|
图 1 多储能电站聚合功率与可用时间特性计算流程 Fig. 1 Computing flow of power and available time characteristics for energy storage stations cluster |
多储能电站聚合功率与可用时间特性计算步骤为:
(1) 计算电站集群聚合后在设定功率Pset下的理论可用时间t0。
| $ t_{0}=\left\{\begin{array}{ll} \frac{\sum\limits_{j=0}^{n} P_{\text {cap }, j}\left(S_{j}-S_{\min , j}\right)}{P_{\text {set }}} & P_{\text {set }}>0 \\ \frac{\sum\limits_{j=0}^{n} P_{\text {cap }, j}\left(S_{j}-S_{\max , j}\right)}{P_{\text {set }}} & P_{\text {set }}<0 \end{array}\right. $ | (1) |
式中:Pcap, j为电站j的容量,MW ·h;Sj,Smin, j,Smax, j分别为电站j的SOC实测、SOC上限和SOC下限;n为集群C的电站数量。
(2) 计算储能电站的理论功率Pj。
| $ P_{j}=\left\{\begin{array}{ll} \frac{P_{\text {cap }, j}\left(S_{j}-S_{\min , j}\right)}{t_{0}} & P_{\text {set }}>0 \\ \frac{P_{\text {cap }, j}\left(S_{j}-S_{\max , j}\right)}{t_{0}} & P_{\text {set }}<0 \end{array}\right. $ | (2) |
(3) Pj与最大充/放电功率校验。
| $ P_{j}=\left\{\begin{array}{ll} P_{\mathrm{cmx}, j} & P_{j}<P_{\mathrm{cmx}, j} \\ P_{\mathrm{dmx}, j} & P_{j}>P_{\mathrm{dmx}, j} \end{array}\right. $ | (3) |
式中:Pcmx, j,Pdmx, j分别为电站j的最大充、放电功率。
当Pj < Pcmx, j或Pj > Pdmx, j时,Pj分别降低充放电功率为Pcmx, j或Pdmx, j,储能电站j在当前SOC条件下,降低充放电功率延长可用时间。电站j退出初始化集群并更新设定功率Pset(k)为:
| $ P_{\text {set }}(k)=P_{\text {set }}(k-1)-P_{j} $ | (4) |
式中:k为设定功率Pset的迭代次数,为更新后集群的设定功率,其中Pset(0)=Pset。
(4) 返回(1)迭代直到满足各电站运行约束。更新后集群的理论可用时间为Pset的可用时间。
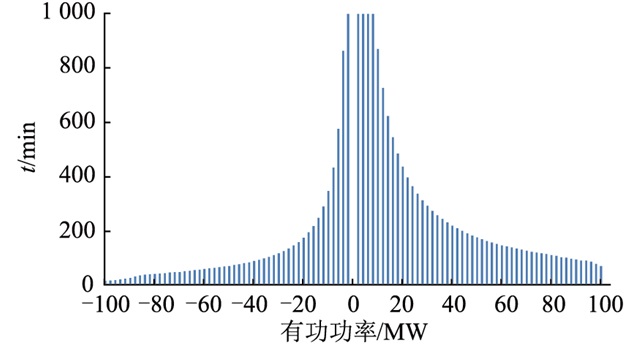
计算覆盖多电站聚合后不同充/放电功率之间的可用时间如图 2所示。
|
图 2 多储能电站聚合功率与可用时间特性 Fig. 2 Power and available time characteristics of energy storage stations cluster |
功率与可用时间特性可应用在断面越限、不平衡功率的调整中,根据确定的功率调节需求预估电能量支撑时间。
1.2 时间与可用功率特性时间与可用功率,描述满足某一时间要求的最大可用充放电功率,由储能电站根据时间反推理论充放电功率校验后得到。
电站j满足时间tset的最大可用充放电功率分别为:
| $ \left\{\begin{array}{l} P_{\mathrm{c}, j}=\max \left\{\frac{P_{\text {cap }, j}\left(S_{j}-S_{\max , j}\right)}{t_{\mathrm{set}}}, P_{\mathrm{cmx}, j}\right\} \\ P_{\mathrm{d}, j}=\min \left\{\frac{P_{\text {cap }, j}\left(S_{j}-S_{\min , j}\right)}{t_{\mathrm{set}}}, P_{\mathrm{dmx}, j}\right\} \end{array}\right. $ | (5) |
式中:Pc, j为电站j的最大可用充电功率,取负值;Pd, j为电站j的最大可用放电功率,取正值。
储能电站集群聚合后的最大可用充电和放电功率则分别由各电站的Pc, j和Pd, j累加得到:
| $ \left\{\begin{array}{l} P_{\mathrm{c}, \mathrm{ESC}}=\sum\limits_{j=0}^{n} P_{\mathrm{c}, j} \\ P_{\mathrm{d}, \mathrm{ESC}}=\sum\limits_{j=0}^{n} P_{\mathrm{d}, j} \end{array}\right. $ | (6) |
聚合储能资源在不同时计算聚合后的最大可用充放电功率,如图 3所示。

|
图 3 多储能电站聚合时间与可用功率特性 Fig. 3 Time and charging/discharging power characteristics of energy storage stations cluster |
时间与可用功率特性可用在已知负荷高峰或低谷持续时间,用于评估储能资源的削峰填谷能力或调峰深度。
2 储能分区聚合控制在电网分区电力平衡紧张状态下,省级电网实时调度运行可通过分区间负荷快速转移等预控措施维持分区内发用电平衡,避免稳态及N-1故障下主变或输电断面潮流越限,确保电网安全运行。
直调机组、清洁能源、需求侧响应负荷和储能电站是电网分区内的主要调度控制手段。规模化储能集中接入的电网分区,可在分区负荷高峰和低谷、清洁能源大发且火电机组深度调峰、清洁能源出力波动及火电调节能力不足等时段,通过规模化储能的集中控制,实施合理的电能量调度,解决输电线路阻塞、变压器峰值负荷与潮流控制问题。
2.1 分区控制目标根据电网分区发用电平衡、输变电潮流控制需求,分区内储能资源聚合调度控制的目标可归纳为:越限主变或输电线路的潮流调整、计划平衡的削峰填谷和清洁能源波动平抑。
2.1.1 输变电潮流控制根据分区内的网络拓扑建立储能电站与输变电断面的关联模型,分解分区内受电断面实时潮流的发电和负荷成分,并将断面潮流控制在限值范围以内,相关关系可表示为:
| $ P_{\mathrm{T}}=P_{\mathrm{Ld}}-P_{\mathrm{Tg}}-P_{\mathrm{St}} $ | (7) |
式中:PT为分区断面实时潮流;PLd为分区负荷;PTg为分区内除储能外的电源总有功功率;PSt为分区内储能参与输变电潮流控制的目标。当PT > PT, max时,有:
| $ P_{\mathrm{St}}=P_{\mathrm{Ld}}-P_{\mathrm{Tg}}-P_{\mathrm{T}, \mathrm{max}} $ | (8) |
式中:PT, max为分区断面限额。
2.1.2 计划削峰填谷在非越限时段,各储能电站可自行决策跟踪日前或日内发电计划,或由分区统一调配执行调度削峰填谷发电计划,并提前预留充足的电量,以备发用电平衡紧张时段使用。削峰填谷计划编制方法可见文献[14-15],此处不再赘述。
| $ P_{\mathrm{Ss}}=P_{\mathrm{Splan}} $ | (9) |
式中:PSs为分区内储能参与计划削峰填谷的目标;PSplan为储能分区削峰填谷计划。
2.1.3 清洁能源波动平抑利用多储能电站聚合可形成可观的调节资源,其用于风光平滑控制,缓解分区内清洁能源出力大幅度波动引起的电能质量持续恶化。
利用清洁能源出力的滤波结果[9]或计划值作为控制目标参考值,计算平抑分区内清洁能源出力的储能调节容量需求。
| $ P_{\mathrm{Sr}}=P_{\mathrm{Ref}}-P_{\mathrm{C}{\mathrm{s}}} $ | (10) |
式中:PSr为分区内储能参与清洁能源波动平抑的目标;PRef为分区清洁能源出力目标参考值;PCs为分区清洁能源有功出力。
2.2 储能电站控制目标分区控制目标的分配考虑各储能电站的运行状态和运行约束,兼顾充放电状态和SOC一致性要求,计算满足分区控制目标的最小调整容量。为避免电池充放电效率和性能衰减等因素引起SOC变化不一致的问题,实时滚动更新各储能电站控制目标,实现聚合后分区控制目标的闭环调整。
2.2.1 储能电站间功率分配流程分区内储能电站的功率分配流程如图 4所示。

|
图 4 电网分区储能电站功率分配数据流程 Fig. 4 Data flow of power dispatching among energy storage stations in power subarea division |
(1) 统计分区内不可控储能电站的总有功功率,并计算可控储能资源的调节目标,计算公式为:
| $ P_{\mathrm{Ss}}^{\prime}=P_{\mathrm{Ss}}-\sum\limits_{j=0}^{l} P_{\mathrm{gen}, j} $ | (11) |
式中:PSs′为分区内可控储能的调节目标;l为分区内不可控储能电站数;Pgen, j为电站j的实际出力。
(2) 根据可控储能资源的调节目标,按充放电状态转换、功率调整的原则依次调用可控储能电站,计算电站控制目标,以确保可控储能电站出力调整方向一致且控制目标处于相同的充放电状态。
状态转换:筛选出储能电站实际出力与可控储能资源的调节目标方向反向的储能电站,按照实际出力幅值递减的顺序依次调用,直到调节目标分配结束为止。若调节目标为正,将处于充电状态的储能电站依次转为静止(即0功率);反之,若调节目标为负,将处于放电状态的储能电站转为依次静止。
储能电站j控制目标Pdes, j为:
| $ \begin{array}{c} P_{\mathrm{des}, j}=\\ \left\{\begin{array}{ll} \min \left\{0, P_{\mathrm{Ss}}^{\prime}(u)+P_{\mathrm{gen}, j}\right\} & P_{\mathrm{Ss}}^{\prime}(u)>0, P_{\mathrm{gen}, j}<0 \\ \max \left\{0, P_{\mathrm{Ss}}^{\prime}(u)+P_{\mathrm{gen}, j}\right\} & P_{\mathrm{Ss}}^{\prime}(u)<0, P_{\mathrm{gen}, j}>0 \end{array}\right. \end{array} $ | (12) |
式中:u为与PSs′反向的储能电站j按照实际出力幅值由大到小排序的调用序号;PSs′(0)=PSs′;PSs′(u)=PSs′(u-1)+Pgen, u-1(u≥1)。
功率调整:若状态转换无法满足调节目标要求,则在各可控储能电站间采用可用电量比例或SOC裕度优先级的原则分配剩余的调节目标。
2.2.2 储能电站间功率分配策略储能电站间功率分配考虑电站间SOC的差异化分布,提出了可用电量比例和SOC裕度优先级2种分配策略,以确保分区内储能电站SOC趋于一致和提升分区内储能资源的利用效率。
(1) 可用电量比例。可用电量定义为:
| $ \gamma_{j}=\left\{\begin{array}{ll} P_{\text {cap }, j}\left(S_{j}-S_{\min , j}\right) & P_{\mathrm{Ss}}^{\prime \prime}>0 \\ P_{\text {cap }, j}\left(S_{\max , j}-S_{j}\right) & P_{\mathrm{Ss}}^{\prime \prime}<0 \end{array}\right. $ | (13) |
式中:γj为储能电站j的可用电量;PSs"为经状态转换后剩余的待分配容量。
储能电站控制目标的初始分配结果为:
| $ P_{\mathrm{des}, j}=P_{\mathrm{Ss}}^{\prime \prime} \frac{\gamma_{j}}{\sum\limits_{k=0}^{n} \gamma_{k}} $ | (14) |
式中:Pdes, j为储能电站j的控制目标;n为可控储能电站总数。
对初始分配结果与储能电站最大充/放电功率进行校验,对初始分配结果迭代修正:
① 当分配结果Pdes, j≤Pcmx, j或Pdes, j≥Pdmx, j时,则Pdes, j分别修正为Pcmx, j或Pdmx, j。
② 当分配结果Pdes, j > Pcmx, j或Pdes, j < Pdmx, j时,
| $ P_{\text {des }, j}^{\prime}=P_{\text {des }, j}+\frac{\gamma_{j}}{\sum\limits_{i=1}^{m} \gamma_{i}} \sum\limits_{k=1}^{n-m}\left(P_{\text {des }, k}-P_{\text {des }, k}^{\prime}\right) $ | (15) |
式中:Pdes, j′为电站j的控制目标;m为有可调裕度的电站总数;n-m为已修正电站总数。
(2) SOC裕度优先级。SOC裕度定义为:
| $ \eta_{j}=\left\{\begin{array}{ll} S_{j}-S_{\min , j} & P_{\mathrm{Ss}}^{\prime \prime}>0 \\ S_{\max , j}-S_{j} & P_{\mathrm{Ss}}^{\prime \prime}<0 \end{array}\right. $ | (16) |
式中:ηj为储能电站j的SOC裕度。
按照SOC裕度从大到小的顺序依次调用,储能电站控制目标为:
| $ P_{\operatorname{des}, j}=\left\{\begin{array}{ll} \min \left\{P_{\mathrm{dmx}, j}, P_{\mathrm{Ss}}^{\prime \prime}-\sum\limits_{i=0}^{m-1} P_{\mathrm{dmx}, i}\right\} & P_{\mathrm{Ss}}^{\prime \prime}>0 \\ \max \left\{P_{\mathrm{cmx}, j}, P_{\mathrm{Ss}}^{\prime \prime}-\sum\limits_{i=0}^{m-1} P_{\mathrm{cmx}, i}\right\} & P_{\mathrm{Ss}}^{\prime \prime}<0 \end{array}\right. $ | (17) |
式中:m为SOC裕度从大到小排序的序号。
3 算例分析文中所提的方法已应用于国内某省电力调度控制中心,目前运行情况良好,能够充分发挥储能资源的规模聚合特性,解决分区发用电平衡和断面安全问题。储能电站分区聚合控制,除具备输变电潮流控制、计划削峰填谷功能外,增加了调度人工干预的“一键充电”、“一键放电”和“设定目标”,实现分区内可控储能电站一键满功率充电或放电,设定目标的快速跟踪调节,以适应突发情况的调度紧急控制需求。某时段电网分区内的4个可控储能电站的运行信息如表 2所示。
|
|
表 2 可控储能电站的运行信息 Table 2 Operational information of controllable energy storage station |
利用第1章储能聚合特性分析方法,考虑SOC上限和下限、充放电功率约束,计算绘制其功功率与可用时间、时间与可用功率的特性曲线见图 5。

|
图 5 电网分区储能聚合特性 Fig. 5 Aggregation characteristic of energy storage stations cluster in power subarea division |
由图 5可知,聚合电源60 MW放电功率可维持89 min,由于各储能电站SOC处于高位,60 MW充电功率可维持21 min。在1 h的调峰时段,最大可提供22 MW的充电功率或62 MW的放电功率。
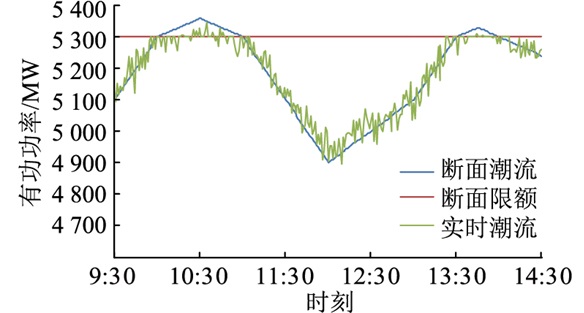
某个时段储能参与电网分区的输变电潮流控制,断面限额、负荷预测趋势和实时潮流曲线见图 6。
|
图 6 分区断面潮流历史 Fig. 6 Section power flowin power subarea division |
由图 6可知,2个越限时段持续时间分别为1 h和20 min左右,预测峰值负荷的越限容量分别为60 MW和35 MW,为顺利支撑2个越限时段的功率调整,2个时段之间各储能电站跟踪发电计划,充电蓄能使SOC恢复。在断面越限时段,则以输电潮流的越限调整量作为储能聚合的控制目标。
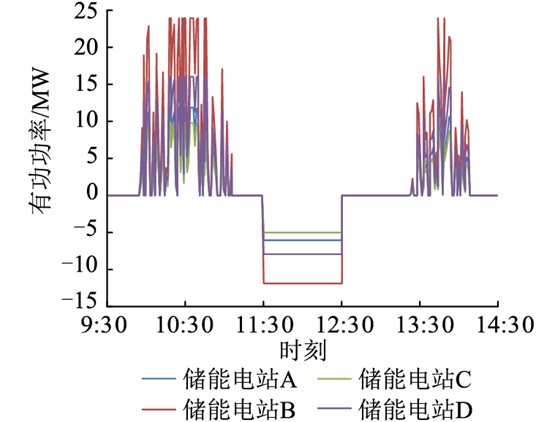
采用可用电量比例分配策略,各储能电站的有功出力在最大充放电功率范围内调整如图 7所示,根据越限断面的调节需求,各储能电站出力同增同减并处于同一充放电状态,以配合解除断面越限。
|
图 7 储能电站有功出力 Fig. 7 Active power of energy storage stations |
可用电量比例和SOC裕度优先级策略均可在实时调节过程中缩小站间SOC差异,2种方法在不同聚合功率控制目标下各储能电站的SOC与SOC平均值(不考虑储能电站的装机容量权重)的平均绝对误差随时间变化曲线,如图 8所示。

|
图 8 储能电站间SOC平均绝对误差 Fig. 8 Mean absolute error of SOC among energy storage stations |
图 8(a)反映SOC裕度优先级策略在充放电功率大于最大充放电功率的90%时,SOC均衡作用减弱,这主要是由于储能电站接近满功率运行,策略对出力的调整空间有限。图 8(b)反映可用电量比例策略的SOC均衡作用,随着充放电功率的增大,功率分配的差异化愈加明显而增强。在SOC均衡效果上,SOC裕度优先级策略优于可用电量比例策略,这是由于后者基于分配系数同步调用各储能电站会导致储能电站SOC同向变化,SOC变化趋于一致对收敛性要求较高。因此,在电站间SOC差异过大时,建议优先采用SOC裕度优先级分配,以快速缩小电站间SOC差异;在电网分区断面越限调整或快速功率控制时,宜采用可用电量比例分配,以充分发挥多储能电站协同的快速功率调节优势。
4 结语针对电网分区的大规模清洁能源接入,文中从电网调度角度探讨了多储能电站聚合后用于平衡控制的资源特性和电站间的功率分配策略。与常规能源机组相比,储能电量空间有限且与充放电行为密切相关。参与电网调节的过程将涉及复杂的能量转化和功率自变量与电量因变量交互影响的过程,通过拟合储能的功率与时间特性可动态提取其可调度能力信息。调度人员根据当前电网运行工况决定分区内储能电源聚合的控制目标,站间功率分配则在策略层面规避了多储能电站充放电状态不一致和SOC过于分散化的问题。由于储能电站调度控制涉及调度计划优化、调频和调峰辅助服务等一系列课题,未来将在储能调度控制行为优化和频率协调控制等方面展开进一步的研究。
本文得到国网江苏省电力有限公司科技项目“规模化储能电站有功功率广域协调控制技术”资助,谨此致谢!
| [1] |
胡娟, 杨水丽, 侯朝勇, 等. 规模化储能技术典型示范应用的现状分析与启示[J]. 电网技术, 2015, 39(4): 879-885. HU Juan, YANG Shuili, HOU Chaoyong, et al. Present condition analysis on typical demonstration application of large-scale energy storage technology and its enlightenment[J]. Power System Technology, 2015, 39(4): 879-885. (  0) 0) |
| [2] |
李建林, 牛萌, 王上行, 等. 江苏电网侧百兆瓦级电池储能电站运行与控制分析[J]. 电力系统自动化, 2020, 44(2): 28-35. LI Jianlin, NIU Meng, WANG Shangxing, et al. Operation and control analysis of 100 MW class battery energy storage station on grid side in Jiangsu power grid of China[J]. Automation of Electric Power Systems, 2020, 44(2): 28-35. (  0) 0) |
| [3] |
李建林, 袁晓冬, 郁正纲, 等. 利用储能系统提升电网电能质量研究综述[J]. 电力系统自动化, 2019, 43(8): 15-24. LI Jianlin, YUAN Xiaodong, YU Zhenggang, et al. Comments on power quality enhancement research for power grid by energy storage system[J]. Automation of Electric Power Systems, 2019, 43(8): 15-24. (  0) 0) |
| [4] |
严干贵, 刘莹, 段双明, 等. 电池储能单元群参与电力系统二次调频的功率分配策略[J]. 电力系统自动化, 2020, 44(14): 26-34. YAN Gangui, LIU Ying, DUAN Shuangming, et al. Power distribution strategy for battery energy storage unit group participating in secondary frequency regulation of power system[J]. Automation of Electric Power Systems, 2020, 44(14): 26-34. (  0) 0) |
| [5] |
徐贤, 丁涛, 万秋兰. 限制短路电流的220 kV电网分区优化[J]. 电力系统自动化, 2009, 33(22): 98-101. XU Xian, DING Tao, WAN Qiulan. 220 kV power grid district-dividing optimization for limiting fault current[J]. Automation of Electric Power Systems, 2009, 33(22): 98-101. (  0) 0) |
| [6] |
傅旭, 李富春, 刘飞, 等. 高比例新能源系统储能需求优化研究[J]. 电力需求侧管理, 2020, 22(6): 26-32. FU Xu, LI Fuchun, LIU Fei, et al. Research on energy storage demand optimization of high proportion new energy system[J]. Power Demand Side Management, 2020, 22(6): 26-32. DOI:10.3969/j.issn.1009-1831.2020.06.007 (  0) 0) |
| [7] |
徐帆, 葛朝强, 吴鑫, 等. 区域电网省间调峰辅助服务的市场机制与出清模型[J]. 电力系统自动化, 2019, 43(16): 109-115. XU Fan, GE Zhaoqiang, WU Xin, et al. Market mechanism and clearing model of inter-provincial peak regulation ancillary service for regional power grid[J]. Automation of Electric Power Systems, 2019, 43(16): 109-115. DOI:10.7500/AEPS20180824004 (  0) 0) |
| [8] |
陈炜, 艾欣, 吴涛, 等. 光伏并网发电系统对电网的影响研究综述[J]. 电力自动化设备, 2013, 33(2): 26-32, 39. CHEN Wei, AI Xin, WU Tao, et al. Influence of grid-connected photovoltaic system on power network[J]. Electric Power Automation Equipment, 2013, 33(2): 26-32, 39. (  0) 0) |
| [9] |
任洛卿, 白泽洋, 于昌海, 等. 风光储联合发电系统有功控制策略研究及工程应用[J]. 电力系统自动化, 2014, 38(7): 105-111. REN Luoqing, BAI Zeyang, YU Changhai, et al. Research on active power control strategy for wind/photovoltaic/energy storage hybrid power system and its engineering application[J]. Automation of Electric Power Systems, 2014, 38(7): 105-111. (  0) 0) |
| [10] |
ABEGAZ B W, MAHAJAN S M. Optimal dispatch control of energy storage systems using forward-backward induction[C]//2015 International Conference on Clean Electrical Power (ICCEP). Taormina, Italy. IEEE, 2015: 731-736.
(  0) 0) |
| [11] |
OTHMAN A M, GABBAR H A. Design of resilient energy storage platform for power grid substation[C]//2018 IEEE International Conference on Smart Energy Grid Engineering (SEGE). Oshawa, ON, Canada. IEEE, 2018: 226-229.
(  0) 0) |
| [12] |
SANDGANI M R, SIROUSPOUR S. Coordinated optimal dispatch of energy storage in a network of grid-connected microgrids[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 1166-1176. DOI:10.1109/TSTE.2017.2664666 (  0) 0) |
| [13] |
杨锡运, 董德华, 李相俊, 等. 商业园区储能系统削峰填谷的有功功率协调控制策略[J]. 电网技术, 2018, 42(8): 2551-2561. YANG Xiyun, DONG Dehua, LI Xiangjun, et al. Active power coordinated control strategy of peak load shifting for energy storage system in business park[J]. Power System Technology, 2018, 42(8): 2551-2561. (  0) 0) |
| [14] |
郭莉, 薛贵元, 吴晨, 等. 储能系统应用于削峰填谷的经济效益分析研究[J]. 电力需求侧管理, 2019, 21(5): 31-34. GUO Li, XUE Guiyuan, WU Chen, et al. Research on economic evaluation of energy storage applied to load shift[J]. Power Demand Side Management, 2019, 21(5): 31-34. (  0) 0) |
| [15] |
孟娅, 李欣然, 黎淑娟, 等. 电池储能参与配电网削峰填谷的变功率控制策略[J]. 电力建设, 2018, 39(4): 45-50. MENG Ya, LI Xinran, LI Shujuan, et al. Variable power control strategy of battery energy storage system participating in distribution network peak load shifting[J]. Electric Power Construction, 2018, 39(4): 45-50. (  0) 0) |
| [16] |
樊海锋, 俞智鹏, 刘文龙, 等. 储能参与电力系统快速调频的需求评估方法[J]. 电力工程技术, 2019, 38(2): 18-24. FAN Haifeng, YU Zhipeng, LIU Wenlong, et al. A demand assessment approach of energy storage for participating in fast frequency regulation of power system[J]. Electric Power Engineering Technology, 2019, 38(2): 18-24. (  0) 0) |
| [17] |
李兆伟, 方勇杰, 李威, 等. 电化学储能应用于电网频率安全防御三道防线的探讨[J]. 电力系统自动化, 2020, 44(8): 1-7. LI Zhaowei, FANG Yongjie, LI Wei, et al. Discussion on application of electrochemical energy storage in three defense lines of power grid frequency[J]. Automation of Electric Power Systems, 2020, 44(8): 1-7. (  0) 0) |
2. NARI Group (State Grid Electric Power Research Institute) Co., Ltd., Nanjing 211106, China;
3. State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210024, China
 2021, Vol. 40
2021, Vol. 40


 陈兵(1975),男,硕士,高级工程师,从事电力系统调度与运行工作(E-mail:
陈兵(1975),男,硕士,高级工程师,从事电力系统调度与运行工作(E-mail: