文章编号: 2096-3203(2021)02-0154-08 中图分类号: TM723
2. 中国南方电网有限责任公司超高压输电公司, 广东 广州 510663
特高压直流输电(high voltage direct current,UHVDC)具有传输容量大、距离远、损耗低等优点,是实现能源优化配置的有效途径。国内已投运的UHVDC工程普遍采用基于电网换相换流器(line commutate converter,LCC)串联的方式[1-3]。随着柔性直流输电技术的发展,模块化多电平换流器(modular multilevel converter,MMC)的电压及容量已逐步接近LCC的水平。送受端分别采用LCC换流阀组串联、MMC换流阀组串联构成的特高压混合直流输电系统已进入工程实施阶段[4]。
目前,基于LCC的阀组在线投入技术已成熟并工程应用[5-10]。采用阀组串联技术的基本要求是能够实现“阀组在线投入”。由于换流器工作原理的差别,基于LCC的阀组在线投入策略并不能直接用于MMC,需要结合MMC的工作特性来制定相应的策略。
为简化阀组区域的开关刀闸配置及在线投入的顺控操作流程,在MMC换流器解锁前的充电阶段推荐采用阀组直流侧经旁路开关(bypass switch,BPS)短接后充电的方式[11-12]。针对常规基于半桥子模块(half bridge sub-module,HBSM)的半桥MMC,如在直流侧短接状态下充电,将出现短路过流而导致充电失败,因此须采用具有直流短路阻断能力的MMC拓扑,如基于全桥子模块(full bridge sub-module,FBSM)的全桥MMC或基于全桥、半桥子模块混合的混合型MMC。
混合型MMC综合了半桥与全桥MMC的优点。目前,针对混合型MMC的研究主要集中在运行控制特性、交直流故障穿越等方面[13-18],而对阀组在线投入的研究成果偏少。文献[11-12]分别研究了混合型MMC在线投入前的充电策略,可实现直流侧短接充电。文献[19]研究了混合型MMC阀组投入过程中的子模块电容均压问题,提出了基于环流注入的均压策略,但实现较为复杂。针对混合型MMC阀组在线投入机理及关键策略的实现方式尚未有深入报道。
首先,文中阐述基于混合型MMC的特高压柔直阀组在线投入过程及关键点;其次,分析混合型MMC阀组的控制特性及在线投入过程的等效回路;然后,结合等效回路对阀组在线投入过程关键策略进行详细分析,并提出基于直流调制度的特高压柔直阀组在线投入策略的实现方案;最后,通过实时数字仿真平台试验验证所提策略的有效性。
1 特高压柔直阀组在线投入过程及关键点文中以±kV特高压混合直流输电系统为研究对象,如图 1所示。在整流侧特高压常直站中,每极由2个十二脉动LCC阀组串联组成;在逆变侧特高压柔直站中,每极由2个混合型MMC阀组串联组成。两侧阀组区域采用相同开关刀闸配置,即每个阀组配置BPS、旁路刀闸(bypass isolator,BPI)、阳极隔刀(anode isolator,AI)及阴极隔刀(cathode isolator,CI)各1把。
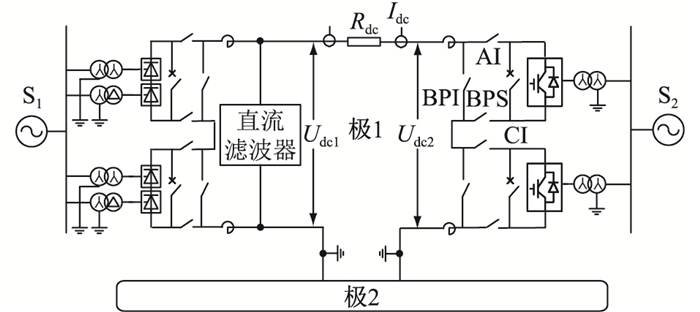
|
图 1 特高压混合直流输电系统拓扑 Fig. 1 Topology structure of the hybrid UHVDC transmission system |
逆变站混合型MMC拓扑结构如图 2所示。每个桥臂由NFB个FBSM、NHB个HBSM和1个桥臂电抗器串联而成,两种类型子模块的电容值C及工作电压额定值UcN相同。UdV为混合型MMC直流电压;IdV为直流电流;ujo(j=a,b,c)为交流相电压;o为假想的电压中性点;ij为交流电流;upj,unj分别为上、下桥臂电压;ipj,inj分别为上、下桥臂电流;L0为桥臂电抗器电感;R0为桥臂等效电阻。
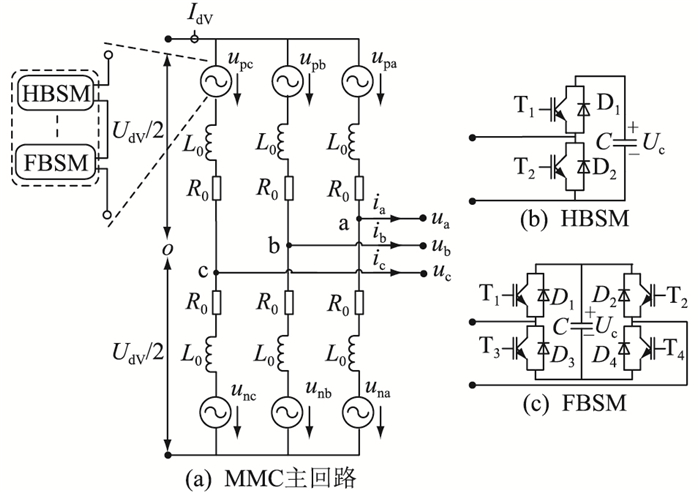
|
图 2 混合型MMC拓扑 Fig. 2 Topology of the hybrid MMC |
文中以高压MMC阀组在线投入为例进行分析。阀组投入前其BPS、AI、CI均为合位,BPI为分位,直流电流经高压阀组BPS流入运行中的低压阀组。参考成熟的LCC阀组在线投入过程,高压MMC阀组在线投入可采用如下步骤:
(1) 合上交流进线开关,通过直流侧短接充电方式将MMC阀组子模块电容电压充至接近额定值,该步骤可参照文献[11]中提出的方案实现;
(2) 在直流侧短接状态下解锁MMC阀组;
(3) 先控制流过MMC阀组BPS的直流电流,使之降至零,之后将其拉开;
(4) 抬升MMC阀组直流电压至最终的稳态目标值,阀组投入过程结束。
由于MMC与LCC的工作特性存在较大差异,对于MMC阀组在线投入步骤中的关键控制策略须进行专门研究,具体包括:
(1) 关键点一。在步骤2中,解锁后须避免直流侧出现过流并保持稳定运行。这是由于高压MMC阀组直流侧经旁路开关短接,其直流侧回路阻抗很小,且全桥、半桥子模块均存在电容储能元件。
(2) 关键点二。在步骤3中,为尽可能减小在线投入过程对直流传输功率造成的扰动, 须实现直流电流由旁路开关向MMC的快速平滑转移。同时应引起注意的是:旁路开关通常所采用的常规交流开关须借助电流过零点才能熄弧断开,故应保证旁路开关在分闸前存在可靠电流过零点,以避免无电流过零点而分闸失败。
(3) 关键点三。在MMC阀组在线投入全过程中,须保证全桥、半桥子模块的电容电压均衡,避免因子模块欠压、过压导致阀组投入失败。
文中将结合混合型MMC控制特性,对上述阀组在线投入过程关键策略进行分析,并给出实现方案。
2 基于直流调制度的特高压柔直阀组在线投入策略 2.1 混合型MMC阀组控制特性分析对于混合型MMC,全桥子模块可通过负电平输出使其具有过调制能力,实现直流降压运行。在此,定义直流调制度mdV为:
| $ {m_{{\rm{dv}}}} = \frac{{{U_{{\rm{dv}}}}}}{{{U_{{\rm{dVN}}}}}} $ | (1) |
式中:UdVN为混合型MMC的额定直流电压。
由式(1)可知,当mdV=1时,混合型MMC按额定直流电压运行;当0 < mdV < 1时,直流降压运行;当mdV=0时,零直流电压运行;当mdV < 0时,直流负压运行。
根据混合型MMC的子模块连接特征,假设各桥臂的工作子模块电容电压平均值相同。在稳态运行下可忽略L0,R0压降,混合型MMC直流电压可表示为:
| $ {U_{{\rm{dV}}}} = {u_{{\rm{p}}j}} + {u_{{\rm{n}}j}} = ({N_{{\rm{p}}j}} + {N_{{\rm{n}}j}}){U_{\rm{c}}} $ | (2) |
式中:Npj,Nnj分别为各相上、下桥臂投入的子模块数;Uc为子模块电容电压平均值。
由式(2)可知,在子模块电容电压稳定的情况下,混合型MMC直流电压由各相上、下桥臂投入子模块的等效总电平数确定。
引入直流调制度后,设定mdV为控制目标,直流电压目标值即为mdVUdVN,混合型MMC直流电压可表示为:
| $ {U_{{\rm{dV}}}} = ({N_{{\rm{p}}j}} + {N_{{\rm{n}}j}}){U_{\rm{c}}} = \frac{{{m_{{\rm{dV}}}}{U_{{\rm{dVN}}}}}}{{{U_{{\rm{cN}}}}}}{U_{\rm{c}}} $ | (3) |
由式(3)可知,在子模块电容电压稳定于额定值时,调整mdV可实现对混合型MMC直流电压的控制。因此,维持子模块电容电压的稳定是控制混合型MMC直流电压的关键。
从能量平衡角度来看,MMC换流器交流侧与直流侧的能量差等于换流器所有工作子模块电容储能的变化量[20-22]。对于逆变站MMC,直流侧输入MMC的能量Wdc、MMC输出至交流侧的能量Wac及MMC所有工作子模块电容储能变化量ΔWMMC之间满足:
| $ {W_{{\rm{dc}}}} = {W_{{\rm{ac}}}} + \Delta {W_{{\rm{MMC}}}} $ | (4) |
如控制各工作子模块电容平均储能恒定,则ΔWMMC可趋近于0,换流器交流侧与直流侧能量进入平衡状态。各工作子模块电容平均储能Wc可表示为:
| $ {W_{\rm{c}}} = CU_{\rm{c}}^2/2 $ | (5) |
由式(5)可知,控制Wc恒定可同时维持子模块电容电压的稳定。
2.2 特高压柔直阀组在线投入过程等效回路为便于分析基于混合型MMC的特高压柔直阀组的在线投入过程,需建立相应的一次等效回路。混合型MMC的桥臂电流方程[23-24]为:
| $ \left\{\begin{array}{l} i_{\mathrm{p} j}=i_{j} / 2+I_{\mathrm{dV}} / 3+i_{\mathrm{cir}} \\ i_{\mathrm{nj}}=-i_{j} / 2+I_{\mathrm{dV}} / 3+i_{\mathrm{cir}} \\ i_{\mathrm{com}}=I_{\mathrm{dV}} / 3+i_{\mathrm{cir}} \end{array}\right. $ | (6) |
式中:icom为同时流经上、下桥臂的电流,其包含直流电流分量及内部相间环流分量icir。
根据基尔霍夫电压定律,桥臂电压方程为:
| $ \left\{\begin{array}{l} u_{\mathrm{p} j}=\frac{U_{\mathrm{dV}}}{2}-u_{j o}-\left(L_{0} \frac{\mathrm{d} i_{\mathrm{p} j}}{\mathrm{~d} t}+R_{0} i_{\mathrm{p} j}\right) \\ u_{\mathrm{n} j}=\frac{U_{\mathrm{dV}}}{2}+u_{j o}-\left(L_{0} \frac{\mathrm{d} i_{\mathrm{n} j}}{\mathrm{~d} t}+R_{0} i_{\mathrm{n} j}\right) \end{array}\right. $ | (7) |
式(7)上、下两式相加可得直流侧电压方程:
| $ U_{\mathrm{dV}}=u_{\mathrm{p} j}+u_{\mathrm{n} j}+2\left(L_{0} \frac{\mathrm{d} i_{\mathrm{com}}}{\mathrm{d} t}+R_{0} i_{\mathrm{com}}\right) $ | (8) |
在环流抑制措施起效条件下,icom中的icir分量可以忽略,式(8)可以表示为:
| $ U_{\mathrm{dV}}=u_{\mathrm{com}}+\frac{2}{3}\left(L_{0} \frac{\mathrm{d} i_{\mathrm{dV}}}{\mathrm{d} t}+R_{0} i_{\mathrm{dV}}\right) $ | (9) |
式中:ucom=upj+unj。
根据式(9),待投入高压MMC解锁后其直流侧等效回路可表示为图 3(a),其中换流器等效电阻Req和等效电感Leq分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{R_{{\rm{eq}}}} = 2/3{R_0}}\\ {{L_{{\rm{eq}}}} = 2/3{L_0}} \end{array}} \right. $ | (10) |
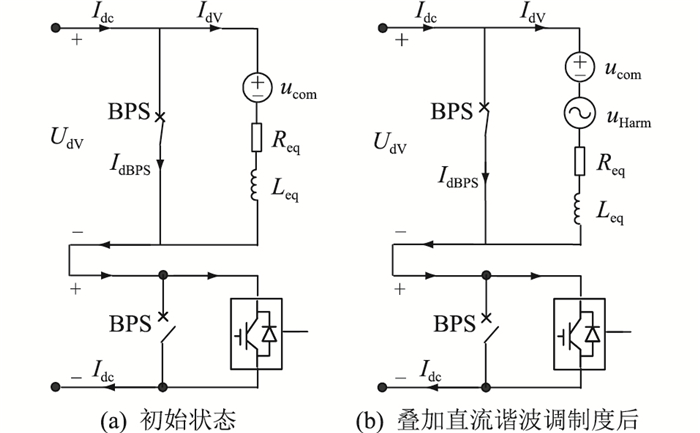
|
图 3 高压MMC阀组解锁后的直流回路 Fig. 3 DC circuit after high voltage MMC deblocked |
式中:桥臂等效电阻R0包括桥臂电抗器电阻RL和桥臂开关管导通电阻RB。在不计及子模块旁路退出的情况下,混合型MMC不论处于投入还是退出状态,各桥臂中的半桥子模块均有1组开关管串于桥臂中, 全桥子模块均有2组开关管串于桥臂中,因此R0为:
| $ R_{0}=R_{\mathrm{L}}+R_{\mathrm{B}}=R_{\mathrm{L}}+\left(N_{\mathrm{HB}}+2 N_{\mathrm{FB}}\right) R_{\mathrm{on}} $ | (11) |
式中:Ron为单个开关管的导通电阻。
在图 3(a)中,高压MMC解锁且BPS分开前,直流侧回路满足:
| $ U_{\mathrm{dV}}=u_{\mathrm{com}}+I_{\mathrm{dV}} R_{\mathrm{eq}}+L_{\mathrm{eq}} \frac{\mathrm{d} I_{\mathrm{dV}}}{\mathrm{d} t}=I_{\mathrm{dBPS}} R_{\mathrm{BPS}} $ | (12) |
式中:IdBPS为旁路开关电流;RBPS为旁路开关通态电阻,一般不大于1 mΩ。
2.3 特高压柔直阀组在线投入过程策略分析针对第1章所述各关键点进行策略分析:
(1) 关键点一。结合图 3(a),在高压MMC的初始解锁阶段,BPS处于合位,MMC直流侧回路电阻由Req与RBPS串联组成,其阻值一般为百毫欧级。为避免直流侧出现过流,高压MMC解锁后须稳定输出零直流电压。
由2.1节分析可知,在子模块电容电压稳定于额定值的前提下, 将混合型MMC的mdV设定为0后解锁可实现输出零直流电压。在mdV解锁状态下,各相上、下桥臂电压分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{u_{{\rm{p}}j}} = - {u_{jo}}}\\ {{u_{{\rm{n}}j}} = {u_{jo}}} \end{array}} \right. $ | (13) |
即各相上桥臂电压与交流电压反相、下桥臂电压与交流电压同相。
(2) 关键点二。在高压MMC进入零压解锁状态后,可启动直流电流转移过程。在高压MMC解锁且BPS分开前,直流电流Idc,阀组电流IdV,旁路开关电流IdBPS满足:
| $ {I_{{\rm{dc}}}} = {I_{{\rm{dV}}}} + {I_{{\rm{dBPS}}}} $ | (14) |
由式(14)可知,如将IdV平滑控制至与Idc相等,IdBPS将下降至0,旁路开关将具备执行分闸操作的条件。由式(12)可知,为使直流电流由旁路开关全部转移至换流器,逆变站MMC阀须输出负直流电压。由2.1节知,当控制混合型MMC的mdV至负值时,可使其输出负直流电压并达到相应控制目标。
在直流电流转移过程结束后,流过旁路开关的电流将接近于0,但该状态不能确保旁路开关存在可靠的电流过零点。经分析,通过在高压MMC的mdV叠加一个直流谐波调制度mHarm,可使其在直流侧主动输出一个具有谐波特性的电压uHarm。该电压在直流侧回路中产生的谐波电流可使旁路开关电流产生持续交替的正、负向过零点,对应的直流侧等效回路如图 3(b)所示。直流谐波调制度mHarm的频率可设置为工频的正整数倍,其表达式如下:
| $ m_{\text {Harm }}=M_{\mathrm{H}} \sin \left(n \omega_{\mathrm{N}} t\right) $ | (15) |
式中:MH为直流谐波调制度峰值;ωN为工频角频率;n为谐波次数。
根据电路叠加原理,该直流谐波调制度在高压MMC直流侧回路中产生的谐波电流如下:
| $ \dot{I}_{\text {Harm }}=\frac{\dot{m}_{\text {Harm }}}{R_{\mathrm{eq}}+{\text {j }} n \omega_{\mathrm{N}} L_{\mathrm{eq}}} U_{\mathrm{dVN}} $ | (16) |
式中:
由于MMC直流侧回路中
| $ I_{\mathrm{H}}=\frac{M_{\mathrm{H}} U_{\mathrm{dVN}}}{n \omega_{\mathrm{N}} L_{\mathrm{eq}}}=\frac{3 M_{\mathrm{H}} U_{\mathrm{dVN}}}{4 {\rm{ \mathsf{ π}}} n f_{\mathrm{N}} L_{0}} $ | (17) |
为保证旁路开关电流存在可靠过零点,谐波电流须达到一定幅值。由式(17)可知,在相同的谐波电流峰值下,直流谐波调制度的峰值与其设定频率成反比,且直流谐波调制度产生的谐波电流峰值与直流功率大小无关。
(3) 关键点三。在高压MMC阀组BPS分开后的直流电压升压起始阶段,由于阀组直流电压接近0,故换流器的交、直流侧功率均接近0,其桥臂电流主要成分为流过换流器的直流电流。对逆变站MMC而言,其桥臂电流在该阶段会持续为正。全桥子模块由于可以输出负电平,在正向桥臂电流下仍可维持子模块电容电压稳定;从而半桥子模块将被持续充电,这易引发子模块过压导致阀组投入失败,须采取必要的均压控制策略。
2.4 特高压柔直阀组在线投入策略实现方案为实现2.3节阀组在线投入相关策略,文中设计的基于直流调制度的特高压柔直阀组控制器如图 4所示。图中QV为MMC阀组的无功实际值;usd,usq分别为交流电压的d,q轴分量;isd,isq分别为交流电流的d,q轴分量。
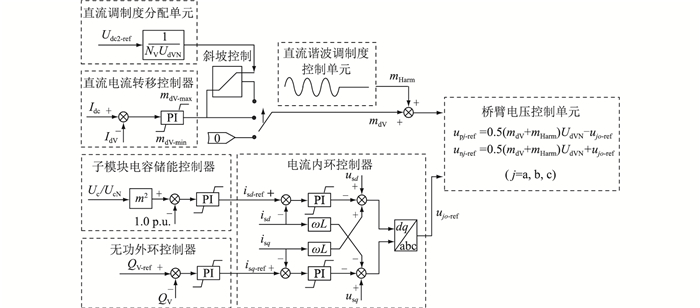
|
图 4 特高压柔直阀组控制器结构 Fig. 4 Structure of VSC-UHVDC valve group controller |
子模块电容储能控制器以子模块平均储能恒定于1.0 p.u.为控制目标,并作为MMC控制器的有功外环,保证子模块电容电压在阀组投入过程中稳定于额定值。
直流电流转移控制器以IdV与Idc相等为控制目标,输出为直流调制度,通过动态调整负向直流调制度实现逆变站直流电流由旁路开关向换流器的快速转移。由于MMC直流侧回路阻抗较小,该控制器的输出须进行必要限幅,避免换流器输出过大的直流负压。
直流谐波调制度控制单元在直流电流转移过程结束后启动,主动叠加的直流谐波调制度须预设合适的频率及峰值。较高的频率可以降低直流谐波调制度的峰值,并缩短可靠过零的检测时间。如考虑到控制系统控制频率的限制,过高的频率会导致谐波拟合失真。以控制频率10 kHz为例,直流谐波调制度的频率选定300 Hz较合适。
检测旁路开关电流是否出现稳定交替的正、负向过零点且电流峰值大于设定值,该特征的持续时间达到设定的延时后发出分开旁路开关命令。开关分开后,可立即将叠加的直流谐波调制度撤除。之后,当控制高压MMC直流调制度按斜率爬升至稳态目标值时,阀组在线投入过程完成。稳态目标值由直流调制度分配单元依据逆变站出口的本极直流电压目标值Udc2-ref与1/NVUdVN的乘积确定,其中NV为本极实际运行的阀组数量。基于直流调制度的特高压柔直阀组在线投入完整流程见图 5。
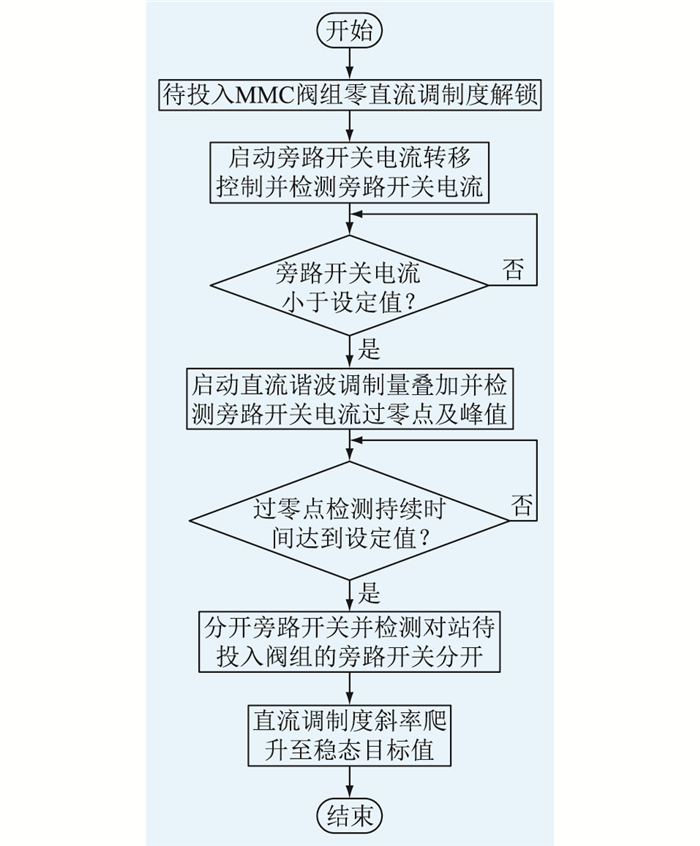
|
图 5 特高压柔直阀组在线投入流程 Fig. 5 Entry processof VSC-UHVDC valve group |
对于阀组在线投入过程中全桥、半桥子模块的电容均压控制,采用的原则与文献[13-14]相同,即在任何时刻,桥臂内不允许同时存在正投入模块和负投入模块。文中对文献[14]中所提策略进行了优化,基于全桥、半桥子模块电容电压进行统一排序控制,提高了半桥子模块投入的灵活性,取得更好的均压效果,具体实现如图 6所示。
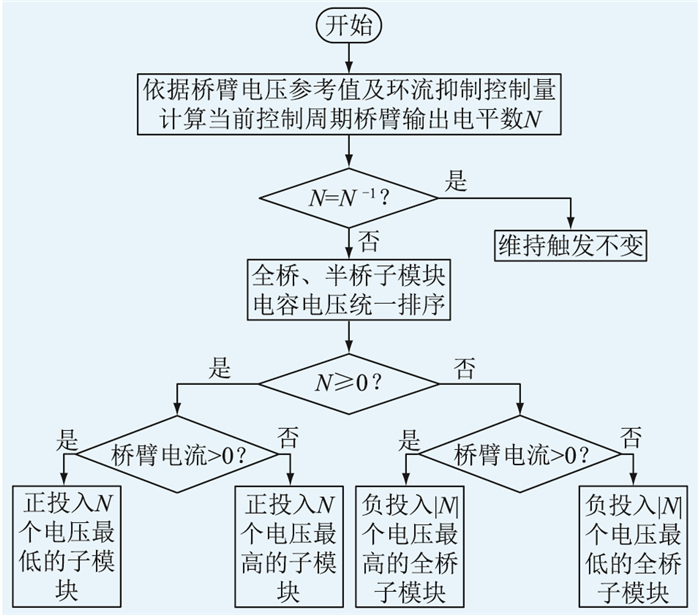
|
图 6 子模块电容电压均压策略 Fig. 6 Voltage balancing strategy for the sub-module capacitors |
当桥臂输出电平数N为正值时,全桥及半桥子模块均可参与正投入,当桥臂输出电平数为负值时,只有全桥子模块参与负投入,实际投入的子模块依据图 6中全桥、半桥子模块电容电压统一排序的结果确定。
3 仿真系统建立与验证 3.1 仿真系统建立为了验证文中提出的基于直流调制度的特高压柔直阀组在线投入策略,基于实时数字仿真器(real time digital simulator,RTDS)、实际控制保护设备搭建闭环试验系统开展了仿真验证。试验采用图 1的一次系统结构。该特高压混合直流系统的基本控制模式为整流站LCC控制直流功率/电流、逆变站MMC控制直流电压;双极直流额定功率为3 000 MW;直流额定电压为±800 kV;直流额定电流为1 875 A。换流站主要参数如表 1所示。
|
|
表 1 混合型MMC换流器参数 Table 1 Parameters of the hybrid MMC converter |
极1在直流电压400 kV、直流电流1 875 A的低压阀组额定运行工况下进行高压阀组在线投入测试,逆变站高压MMC仿真波形如图 7所示。图 7中Ucpj-FB,Ucpj-HB分别为三相上桥臂全桥、半桥子模块电容电压平均值;mharmUdVN为直流谐波调制度对应电压值;mdVUdVN为直流调制度对应电压值。
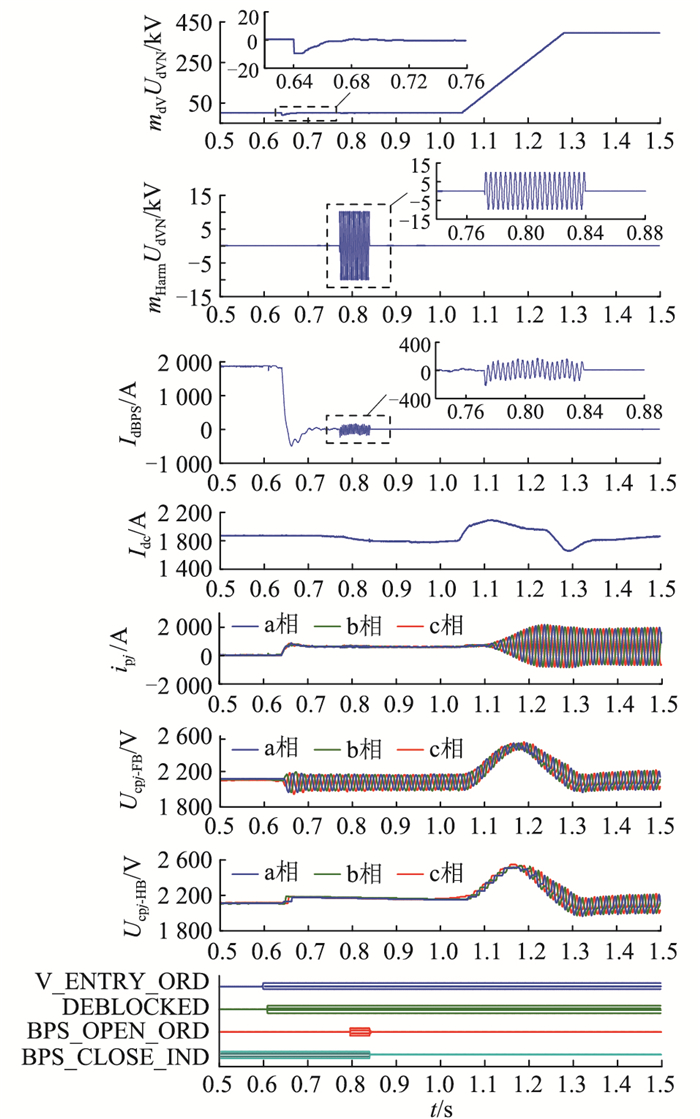
|
图 7 额定工况下高压MMC在线投入波形 Fig. 7 Waveforms for high voltage MMC entry under rated condition |
在待投入高压MMC解锁前,先采用直流侧短接充电方式将各子模块电容电压充至接近额定值。
0.6 s时阀组投入指令信号(V_ENRTY_ORD)到达,10 ms后高压MMC阀组以零直流调制度解锁(DEBLOCKED)并进入零直流电压状态, 阀组电流稳定、未出现过流现象。
0.64 s时启动直流电流转移控制,在转移起始阶段,高压MMC阀组输出较大负向直流调制度以加快直流电流转移。随着旁路开关电流IdBPS的下降,负向直流调制度逐渐减小,在转移过程完成时旁路开关电流降至接近零电流,负向直流调制度对应电压值mdVUdVN用于匹配等效电阻Req的压降。
0.77 s时启动直流谐波调制度叠加,其频率为300 Hz,对应电压值mHarmUdVN的峰值为10 kV。在直流谐波调制度作用下,旁路开关电流中出现同频率的谐波电流,其峰值约为142 A,与按照式(16)计算的理论值145 A基本一致,旁路开关电流持续交替正、负向过零。
0.8 s时旁路开关电流过零点检测完成后发出分开旁路开关命令(BPS_OPEN_ORD),在旁路开关合位信号(BPS_CLOSE_IND)消失后,直流谐波调制度撤除。
1.05 s时启动直流调制度斜率爬升,在1.28 s直流电压升至稳态目标值,阀组在线投入过程结束,整个过程在700 ms内平稳完成。
在直流电压爬升前,ipj持续为正,Ucpj-FB,Ucpj-HB均被稳定控制在安全水平;在直流电压爬升阶段,整流站高压LCC阀组同步进行触发角恢复控制,该控制的角度下降过程会引起直流电流Idc产生一个小幅先升后降的过程,逆变站高压MMC的子模块电容电压也对应出现先升后降的变化;在直流电压爬升完成后,电容电压恢复至额定水平。上述过程中子模块电容电压均压良好。
为验证所提策略在低功率水平下的适应性,在极1直流电压400 kV、直流电流500 A工况下进行了高压阀组在线投入测试,叠加的直流谐波调制度参数设定与额定工况下相同。试验结果表明,低功率水平下阀组在线投入过程特性保持良好,直流谐波调制度产生的旁路开关谐波电流峰值与额定工况下基本一致,与2.2节理论分析结果吻合。
4 结论基于阀组串联技术的特高压柔性直流输电系统要求柔直阀组需具备在线投入的能力。针对该需求,文中提出了基于直流调制度的特高压柔直阀组在线投入策略,通过调整待投入混合型MMC阀组的直流调制度,实现在线投入的全过程控制。由仿真结果,可以得到如下结论:
(1) 在直流侧短接状态下,采用子模块电容储能控制及零直流调制度,混合型MMC阀组可实现零直流电压稳定解锁。
(2) 逆变站混合型MMC通过输出负向直流调制度,可以实现直流电流由旁路开关向换流器的快速转移。
(3) 通过在直流调制度上叠加直流谐波调制度,可使旁路开关电流产生持续的过零点并实现旁路开关的可靠分断。采用同一组直流谐波调制度参数即可适应不同的直流传输功率水平。
后续将在实际换流阀系统上对文中提出的策略进行更全面的验证。
| [1] |
张文亮, 于永清, 李光范, 等. 特高压直流技术研究[J]. 中国电机工程学报, 2007, 27(22): 1-7. ZHANG Wenliang, YU Yongqing, LI Guangfan, et al. Researches on UHVDC technology[J]. Proceedings of the CSEE, 2007, 27(22): 1-7. DOI:10.3321/j.issn:0258-8013.2007.22.001 (  1) 1) |
| [2] |
SUN Xin, LIU Zehong, GAO Liying, et al. Practice and innovation in the ±800 kV UHVDC demonstration project[J]. Proceedings of the CSEE, 2009, 29(22): 35-45. (  0) 0) |
| [3] |
卢东斌, 田杰, 李海英, 等. 电网换相换流器和电压源换流器串联组成的混合直流换流器控制和保护研究[J]. 电力系统保护与控制, 2020, 48(15): 92-101. LU Dongbin, TIAN Jie, LI Haiying, et al. Control and protection of series hybrid DC converters with a line-commutated converter and a voltage source converter[J]. Power System Protection and Control, 2020, 48(15): 92-101. (  1) 1) |
| [4] |
饶宏, 许树楷, 周月宾, 等. 特高压柔性直流主回路方案研究[J]. 南方电网技术, 2017, 11(7): 1-4, 67. RAO Hong, XU Shukai, ZHOU Yuebin, et al. Research on main circuit scheme of VSC-UHVDC[J]. Southern Power System Technology, 2017, 11(7): 1-4, 67. (  1) 1) |
| [5] |
李新年, 李涛, 吕鹏飞, 等. 向家坝至上海特高压直流输电工程换流器的投退策略分析[J]. 高电压技术, 2011, 37(5): 1232-1238. LI Xinnian, LI Tao, LYU Pengfei, et al. Analysis on the strategy of converter entry/exit for Xiangjiaba to Shanghai UHVDC project[J]. High Voltage Engineering, 2011, 37(5): 1232-1238. (  1) 1) |
| [6] |
张庆武, 王永平, 陈小军, 等. 特高压直流控制保护系统设计与开发[J]. 电力系统自动化, 2013, 37(21): 88-93. ZHANG Qingwu, WANG Yongping, CHEN Xiaojun, et al. Design and development of control and protection system for UHVDC[J]. Automation of Electric Power Systems, 2013, 37(21): 88-93. DOI:10.7500/AEPS201210253 (  0) 0) |
| [7] |
谷相宏, 邓凯, 施琳, 等. 特高压直流分层接入方式下阀组在线投入策略研究[J]. 电力工程技术, 2020, 39(5): 92-98. GU Xianghong, DENG Kai, SHI Lin, et al. Online deblocking strategies of valve group for UHVDC system under hierarchical connection mode[J]. Electric Power Engineering Technology, 2020, 39(5): 92-98. (  0) 0) |
| [8] |
陈灏泽, 范若萱, 王金玉, 等. VSC-LCC型混合直流输电系统启动控制策略研究[J]. 智慧电力, 2020, 48(11): 62-67. CHEN Haoze, FAN Ruoxuan, WANG Jinyu, et al. Research on startup control strategy for VSC-LCC hybrid HVDC system[J]. Smart Power, 2020, 48(11): 62-67. (  0) 0) |
| [9] |
肖超, 韩伟, 李琼林, 等. 柔性直流输电系统交流侧线路继电保护适应性研究[J]. 智慧电力, 2020, 48(4): 1-8. XIAO Chao, HAN Wei, LI Qionglin, et al. Adaptability of MMC-HVDC system on relay protection of AC transmission lines[J]. Smart Power, 2020, 48(4): 1-8. (  0) 0) |
| [10] |
余昕越, 袁志昌, 田宝烨, 等. 混合双馈入高压直流系统最大传输功率控制方法[J]. 电力系统自动化, 2019, 43(17): 109-116. YU Xinyue, YUAN Zhichang, TIAN Baoye, et al. Control method of maximum transmission power for hybrid dual-infeed HVDC system[J]. Automation of Electric Power Systems, 2019, 43(17): 109-116. (  1) 1) |
| [11] |
梅勇, 史尤杰, 周剑, 等. 特高压柔性直流阀组投入过程中混合型MMC启动充电策略[J]. 电力系统自动化, 2018, 42(24): 113-119. MEI Yong, SHI Youjie, ZHOU Jian, et al. Start-up charging strategy for hybrid MMC in valve switching-on process of VSC-UHVDC system[J]. Automation of Electric Power Systems, 2018, 42(24): 113-119. (  3) 3) |
| [12] |
杨梅娟, 姚为正, 吴金龙, 等. 特高压柔性直流系统单阀组投入时的启动充电控制[C]//全球能源互联网发展合作组织、山东大学. 超/特高压直流输电技术会议论文集. 《全球能源互联网》编辑部, 2018: 83-90. YANG Meijuan, YAO Weizheng, WU Jinlong, et al. Start-up and charging control for input of VSC-UHVDC single converter group[C]//Global Energy Interconnection and College Innovative Development Forum, Shandong University, Editorial department of Global Energy Interconnection, 2018: 83-90. (  2) 2) |
| [13] |
ZENG R, XU L, YAO L Z, et al. Design and operation of a hybrid modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2015, 30(3): 1137-1146. (  2) 2) |
| [14] |
鲁晓军, 向往, 林卫星, 等. 混合型模块化多电平换流器解析建模与功率运行区间分析[J]. 电力系统自动化, 2018, 42(7): 76-84. LU Xiaojun, XIANG Wang, LIN Weixing, et al. Analysis on analytical modeling and power operating zone of hybrid modular multilevel converter[J]. Automation of Electric Power Systems, 2018, 42(7): 76-84. (  2) 2) |
| [15] |
徐雨哲, 徐政, 张哲任, 等. 基于LCC和混合型MMC的混合直流输电系统控制策略[J]. 广东电力, 2018, 31(9): 13-25. XU Yuzhe, XU Zheng, ZHANG Zheren, et al. Control strategy for hybrid HVDC transmission system based on LCC and hybrid MMC[J]. Guangdong Electric Power, 2018, 31(9): 13-25. (  0) 0) |
| [16] |
曹帅, 向往, 姚良忠, 等. 风电经混合型MMC-HVDC并网的交直流故障穿越策略[J]. 电力系统自动化, 2018, 42(7): 37-43, 49. CAO Shuai, XIANG Wang, YAO Liangzhong, et al. AC and DC fault ride-through strategies for wind power integration via hybrid MMC-HVDC[J]. Automation of Electric Power Systems, 2018, 42(7): 37-43, 49. (  0) 0) |
| [17] |
许烽, 徐政. 基于LCC和FHMMC的混合型直流输电系统[J]. 高电压技术, 2014, 40(8): 2520-2530. XU Feng, XU Zheng. Hybrid HVDC system based on LCC and FHMMC[J]. High Voltage Engineering, 2014, 40(8): 2520-2530. (  0) 0) |
| [18] |
李少华, 王秀丽, 李泰, 等. 混合式MMC及其直流故障穿越策略优化[J]. 中国电机工程学报, 2016, 36(7): 1849-1858. LI Shaohua, WANG Xiuli, LI Tai, et al. Optimal design for hybrid MMC and its DC fault ride-through strategy[J]. Proceedings of the CSEE, 2016, 36(7): 1849-1858. (  1) 1) |
| [19] |
杨美娟, 王先为, 姚为正, 等. 特高压混合式MMC低全桥配比下单阀组投退过程中的均压控制[J]. 全球能源互联网, 2018, 1(5): 603-610. YANG Meijuan, WANG Xianwei, YAO Weizheng, et al. Voltage balancing control of hybrid MMC with low ratio of FBSM in UHVDC during group entry/exit process[J]. Journal of Global Energy Interconnection, 2018, 1(5): 603-610. (  1) 1) |
| [20] |
徐政, 屠卿瑞, 管敏渊. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2013: 65-95. XU Zheng, TU Qingrui, GUAN Minyuan. Voltage source converter based high voltage direct current transmission system[M]. Beijing: China Machine Press, 2013: 65-95. (  1) 1) |
| [21] |
郑安然, 郭春义, 崔鹏, 等. 特高压混合多端直流输电系统中串联换流阀组间的电压平衡控制策略[J]. 电网技术, 2019, 43(9): 3408-3414. ZHENG Anran, GUO Chunyi, CUI Peng, et al. Voltage balancing control strategy of series-connected converter valve groups in hybrid multi-terminal UHVDC transmission system[J]. Power System Technology, 2019, 43(9): 3408-3414. (  0) 0) |
| [22] |
曹亚倩, 郑晓冬, 丛新棚, 等. 基于虚拟能量调节偏差的MMC-HVDC输电线路保护方案[J]. 电力系统自动化, 2020, 44(23): 109-116. CAO Yaqian, ZHENG Xiaodong, CONG Xinpeng, et al. Protection scheme for MMC-HVDC transmission line based on virtual energy regulation deviation[J]. Automation of Electric Power Systems, 2020, 44(23): 109-116. (  1) 1) |
| [23] |
罗永捷, 李耀华, 李子欣, 等. 适用于高压大容量MMC-HVDC系统的改进低开关频率均压控制策略[J]. 中国电机工程学报, 2017, 37(5): 1341-1351. LUO Yongjie, LI Yaohua, LI Zixin, et al. An improved reduced switching frequency voltage balancing control strategy for bulk power MMC-HVDC systems[J]. Proceedings of the CSEE, 2017, 37(5): 1341-1351. (  1) 1) |
| [24] |
赵成勇, 许建中, 李探. 全桥型MMC-MTDC直流故障穿越能力分析[J]. 中国科学: 技术科学, 2013, 43(1): 106-114. ZHAO Chengyong, XU Jianzhong, LI Tan. DC faults ride-through capability analysis of full-bridge MMC-MTDC System[J]. Scientia Sinica Technologica, 2013, 43(1): 106-114. (  1) 1) |
2. EHV Power Transmission Company, China Southern Power Grid, Co., Ltd., Guangzhou 510663, China
 2021, Vol. 40
2021, Vol. 40



 鲁江(1979),男,硕士,高级工程师,从事特高压直流输电及柔性直流输电技术工作(E-mail:
鲁江(1979),男,硕士,高级工程师,从事特高压直流输电及柔性直流输电技术工作(E-mail: