0 引言

20世纪80年代，众学者开始对超高次谐波进行探讨，自21世纪起, 将超高次谐波频率定义为2~150 kHz ^[1]。近年来，高比例光伏并网使配电网的超高次谐波问题愈演愈烈。逆变器作为光伏并网及直交流变换的中间环节，其输出的谐波具有宽频域、高频次等特征，是一类重要的超高次谐波源。过高的谐波含量严重威胁电网的安全稳定运行^[2-6]。当多台光伏同时工作时，产生的超高次谐波间的交互影响更加复杂且危害更大^[7-8]。除此之外，配电网背景谐波与光伏之间的交互影响也将导致并网超高次谐波电流畸变愈发严重^[9]。

现有针对光伏超高次谐波的研究大多集中于测试方面，涉及到多点接入光伏与配电网交互影响的研究较少。近几年，众多学者对光伏发射的超高次谐波进行测试^[10-12]，并探究超高次谐波的传递特性。结果显示：光伏发射的谐波电流大多集中于2~20 kHz(40~400次谐波)，开关频率附近的谐波电流局部范围内最大，且整数倍的开关频率附近出现谐波电流升高现象^[2]。在谐波交互影响方面，文献[13]分析了光伏与电网之间的交互影响特性; 文献[14]研究了多台光伏接入时发射的谐波对配电网的影响。但上述研究均未涉及超高次谐波范围。文献[15]分析了逆变器阻抗与线路阻抗的交互影响; 文献[16]研究了逆变器并网的谐振问题。但上述研究均未涉及多逆变器构成的系统与配电网间的谐波交互影响分析。在光伏模型方面，文献[17]考虑了几种典型接入情况下分布式电源(distributed generation, DG)发射的谐波含量对配电网的影响; 文献[18]分析了背景谐波、光伏并网位置对配电网谐波的影响。上述文献均利用逆变器来等效DG，但光伏发电系统的电气特性受光照、温度等因素的影响，用逆变器等效过于简化，分析结果不可信。

针对以上问题，文中首先建立分布式光伏并网的超高次谐波仿真模型，充分考虑光伏阵列输出特性、最大功率跟踪(maximum power point tracking，MPPT)、逆变器开关频率等因素，可精确反映分布式光伏的实际工况。在此基础上，引入简易配电网模型定量分析光伏之间、光伏与配电网之间的超高次谐波交互影响。最后，通过实测结果验证仿真模型以及结论的正确性。

1 多光伏超高次谐波交互影响分析 1.1 单光伏接入系统超高次谐波交互影响分析

在文献[1]提及的超高次谐波交互影响模型基础上，考虑线路及负荷影响，见图 1。将含滤波环节的光伏整体等效为内阻无穷大的谐波电流源^[18]，见图 2。其中Z_i(i=1, 2, …, n)为线路阻抗; Z_Li(i=1，2, …，n)为负荷阻抗; Z_{L, h}为光伏接入点后的电网等效h次谐波阻抗; Z_{s, h}为系统等效h次谐波阻抗; $\dot{I}_{\mathrm{pv}, h}$为光伏发射的h次谐波电流; R为系统阻抗。

定义Z_{i, h}为Z_i等效h次谐波线路阻抗; Z_{Li, h}为Z_Li等效h次谐波负荷阻抗。由于Z_{i, h} < < Z_{Li, h}，则：

${Z_{{\rm{s}},h}} = R + {Z_{1,h}} + {Z_{2,h}} + \cdots + {Z_{k,h}}$

(1)

${Z_{{\rm{L}},h}} = {Z_{{\rm{L}}(k + 1),h}}// \cdots //{Z_{{\rm{L}}n,h}}$

(2)

可得Z_{L, h}> >Z_{s, h}。因此，光伏产生的超高次谐波电流大部分流向系统，较少部分流向负荷。

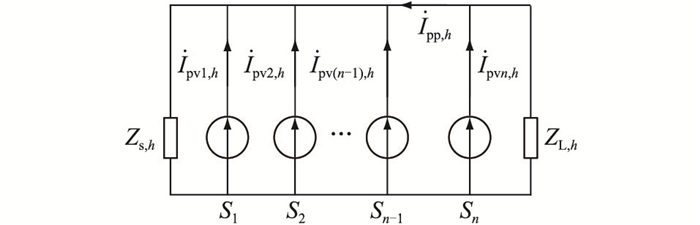
1.2 多光伏接入系统超高次谐波交互影响分析

文献[19]对用户之间以及用户与配电网之间的交互影响进行了深入研究。文中在此基础上，考虑线路阻抗以及负荷因素，构建如图 3所示的模型。

由叠加定理可得，多光伏接入时流入系统的超高次谐波电流为：

$\dot{I}_{\mathrm{g}, h}=\frac{Z_{\mathrm{L}, h}}{Z_{\mathrm{s}, h}+Z_{\mathrm{L}, h}} \sum\limits_{i=1}^{n} \dot{I}_{\mathrm{pv}i, h}$

(3)

式中：$\dot{I}_{{\mathrm{pv}i}, h}$为第i个接入光伏发射的h次超高次谐波电流。

进一步可得：

$\dot{I}_{\mathrm{pp}, h}=\left(Z_{\mathrm{L}, h} \dot{I}_{\mathrm{pv}n, h}-Z_{\mathrm{s}, h} \sum\limits_{i=1}^{n-1} \dot{I}_{\mathrm{pv}i, h}\right) /\left(Z_{\mathrm{s}, h}+Z_{\mathrm{L}, h}\right)$

(4)

式中：$\dot{I}_{\mathrm{pp}, h}$为用户间流动的h次超高次谐波电流。

由式(3)可知，流入系统的超高次谐波电流几乎只与接入光伏发射的超高次谐波电流幅值及相位相关，即流入系统的超高次谐波电流的叠加是矢量相加，叠加结果受相位影响，可能相互助增，也可能相互助减。由式(4)可知，光伏间流动的总超高次谐波电流随光伏并网数量增加呈减小趋势。

1.3 系统背景谐波对多光伏接入的影响

基于文献[20]的网侧变流器单相电路简化模型和光伏控制策略，研究电网背景谐波对光伏网侧变流器输出超高次谐波电流的影响。光伏逆变器控制模型如图 4所示。

图 4中，G_PI(s)为比例积分(proportional integral，PI)控制器的传递函数; G_PWM(s)为脉冲宽度调制(pulse width modulation，PWM)逆变器增益的传递函数; i_ref为参考电流; u_inv，i_inv分别为并网逆变器的输出电压、电流; u_c，i_c分别为滤波电容C的电压、电流; u_g，i_g分别为并网电压、电流; L_g，L_inv分别为网侧和变流器侧电感。则有：

$G_{\mathrm{PI}}(s)=k_{\mathrm{p}}\left[1+1 /\left(k_{\mathrm{i}} s\right)\right]$

(5)

$G_{\mathrm{PWM}}(s)=U_{\mathrm{dc}} /\left(1+T_{\mathrm{s}} s\right)$

(6)

式中：U_dc为直流侧电压; T_s为逆变器的开关周期; k_p，k_i均为PI控制器参数。

为方便后续分析，定义：

$G_{\mathrm{c}}(s)=1 /(C s)$

(7)

$G_{\mathrm{d}}(s)=1 /\left(L_{\mathrm{inv}} s\right)$

(8)

$G_{\mathrm{i}}(s)=1 /\left(L_{\mathrm{g}} s\right)$

(9)

$G_{\mathrm{p}}(s)=G_{\mathrm{PI}}(s) G_{\mathrm{PWM}}(s)$

(10)

因逆变器采用dq解耦控制，结合图 4可得逆变器输出电压u_inv在dq坐标系下的表达式为：

$\begin{array}{c} u_{\mathrm{inv}, d q}=\left[G_{\mathrm{p}}(s) i_{\mathrm{ref}, d q}+\frac{G_{\mathrm{p}}(s) G_{\mathrm{d}}(s) G_{\mathrm{c}}(s) i_{\mathrm{inv}, d q}}{1+G_{\mathrm{c}}(s) G_{\mathrm{i}}(s)}+\right. \\ \left.\frac{G_{\mathrm{p}}(s) G_{\mathrm{d}}(s) G_{\mathrm{c}}(s) G_{\mathrm{i}}(s) u_{\mathrm{g}, d q}}{1+G_{\mathrm{c}}(s) G_{\mathrm{i}}(s)}\right] /\left[1+G_{\mathrm{p}}(s) G_{\mathrm{d}}(s)\right] \end{array}$

(11)

式中：i_{ref, dq}，i_{inv, dq}分别为dq坐标系下逆变器的输出参考电流和输出电流; u_{g, dq}为dq坐标系下逆变器网侧电压。

将式(11)变换到两相静止坐标系αβ中。

$\begin{array}{c} u_{\mathrm{inv}, \alpha \beta}=\left[G_{\mathrm{p}}(s) i_{\mathrm{ref}, \alpha \beta}+H_{0} i_{\mathrm{inv}, \alpha \beta} / H_{3}+\right. \\ \left.H_{1} u_{\mathrm{g}, \alpha \beta} / H_{3}\right] / H_{2} \end{array}$

(12)

其中：

$H_{0}=G_{\mathrm{p}}\left(s \mp \mathrm{j} \omega_{0}\right) G_{\mathrm{d}}\left(s \mp \mathrm{j} \omega_{0}\right) G_{\mathrm{c}}\left(s \mp \mathrm{j} \omega_{0}\right)$

(13)

$\begin{array}{c} H_{1}=G_{\mathrm{p}}\left(s \mp \mathrm{j} \omega_{0}\right) G_{\mathrm{d}}\left(s \mp \mathrm{j} \omega_{0}\right) \times \\ G_{\mathrm{c}}\left(s \mp \mathrm{j} \omega_{0}\right) G_{\mathrm{i}}\left(s \mp \mathrm{j} \omega_{0}\right) \end{array}$

(14)

$H_{2}=1+G_{\mathrm{p}}\left(s \mp \mathrm{j} \omega_{0}\right) G_{\mathrm{d}}\left(s \mp \mathrm{j} \omega_{0}\right)$

(15)

$H_{3}=1+G_{\mathrm{i}}\left(s \mp \mathrm{j} \omega_{0}\right) G_{\mathrm{c}}\left(s \mp \mathrm{j} \omega_{0}\right)$

(16)

式中：ω₀为同步角速度; $s \mp {\rm{j}}{\omega _0}$为dq坐标系的拉普拉斯算子s变换到αβ坐标系的表达式。

由坐标变换理论可得，两相静止坐标系αβ变换为三相静止坐标系abc时，频率不会发生改变，且α轴与a轴重合。因篇幅有限，文中仅对a相电流进行分析。光伏并网的简易电路拓扑如图 5所示。图中u_m，Z_o分别为变流器的戴维南等值电压和阻抗。

根据坐标系理论与等效电路，式(12)可改写为：

$\begin{array}{c} u_{\mathrm{inv}}=u_{\mathrm{m}}-i_{\mathrm{inv}} Z_{\mathrm{o}}=\left[G_{\mathrm{p}}(s) i_{\mathrm{ref}}+\right. \\ \left.H_{0} i_{\mathrm{inv}} / H_{3}+H_{1} u_{\mathrm{g}} / H_{3}\right] / H_{2} \end{array}$

(17)

其中：

$u_{\mathrm{m}}=\left[G_{\mathrm{p}}(s) i_{\mathrm{ref}}+H_{1} u_{\mathrm{g}} / H_{3}\right] / H_{2}$

(18)

$Z_{\mathrm{o}}=-H_{0} /\left(H_{2} H_{3}\right)$

(19)

根据图 5等效电路，利用基尔霍夫电压及电流定律可得：

$u_{\mathrm{inv}}-u_{\mathrm{g}}=i_{\mathrm{g}} s L_{\mathrm{g}}+s L_{\mathrm{inv}} i_{\mathrm{inv}}$

(20)

$i_{c}=\left(u_{\mathrm{g}}+i_{\mathrm{g}} s L_{\mathrm{g}}\right) s C$

(21)

$i_{\mathrm{inv}}=i_{\mathrm{g}}+i_{c}$

(22)

联立式(17)-式(18)、式(20)-式(21)得:

$u_{\mathrm{g}}=G_{\mathrm{p}}(s) i_{\mathrm{ref}} / H_{5}-H_{4} i_{\mathrm{g}} / H_{5}$

(23)

其中:

$H_{4}=s L_{\mathrm{g}} H_{2}+H_{2} s L_{\mathrm{inv}}\left(s L_{\mathrm{g}} C+1\right)-H_{0}\left(s L_{\mathrm{g}} C+1\right) / H_{3}$

(24)

$H_{5}=H_{2} s L_{\mathrm{inv}}-H_{0} s C / H_{3}-H_{1} / H_{3}+H_{2}$

(25)

由图 5模型可得：

$u_{\mathrm{g}}=u_{\mathrm{oc}}-i_{\mathrm{g}} Z_{\mathrm{oc}}$

(26)

式中：u_oc，Z_oc分别为图 5中除系统外的电路戴维南等值电压和阻抗。

联立式(14)-式(15)可得：

$u_{\mathrm{oc}}=G_{\mathrm{p}}(s) i_{\mathrm{ref}} /\left(H_{2} s L_{\mathrm{inv}}-H_{0} s C / H_{3}-H_{1} / H_{3}+H_{2}\right)$

(27)

$\begin{array}{c} Z_{\mathrm{oc}}=\left[s L_{\mathrm{g}} H_{2}+H_{2} s L_{\mathrm{inv}}\left(s L_{\mathrm{g}} C+1\right)-\right. \\ \left.H_{0}\left(s L_{\mathrm{g}} C+1\right) / H_{3}\right] /\left(H_{2} s L_{\mathrm{inv}}-\right. \\ \left.\mathrm{H}_{0} \mathrm{~s} C / \mathrm{H}_{3}-\mathrm{H}_{1} / \mathrm{H}_{3}+\mathrm{H}_{2}\right) \end{array}$

(28)

因光伏逆变器采用直流电压与参考电压进行PI控制获取参考电流，可近似认为参考电流i_ref不受电网背景谐波影响。则u_oc与背景谐波无关，式(26)可改写为：

${i_{{\rm{g}}h}}\left( {{\rm{j}}{\omega _h}} \right) = - \frac{{{u_{{\rm{g}}h}}\left( {{\rm{j}}{\omega _h}} \right)}}{{{Z_{{\rm{oc}}h{\rm{ }}}}\left( {{\rm{j}}{\omega _h}} \right)}}$

(29)

式中：ω_h=2πf为角频率; u_gh为并网点处h次背景谐波电压; i_gh为由u_gh引起的h次谐波电流; Z_och为除系统外的电路戴维南等效模型下h次谐波对应的等值阻抗。

由式(29)可知，光伏输出的谐波电流不仅受自身系统参数的影响，还受系统背景谐波的影响。除此之外，系统背景谐波电压的存在导致光伏额外产生频率与背景谐波电压频率相同、幅值与背景谐波电压幅值成正比的谐波电流。

2 仿真系统搭建与结果分析 2.1 仿真模型 2.1.1 多光伏并网仿真模型

为验证文中所提模型及分析结论的正确性，搭建多光伏并网仿真模型。为模拟背景谐波对分布式光伏的影响，加入其他DG模型(仅在考虑超高次背景谐波时接入)，均使用常见三相电压型SPWM逆变器进行等效，整体结构见图 6。图中，共接入4个光伏发电系统，均采用有功无功(PQ)控制，并网点和接入点均标于图 6中。主要参数见表 1。

2.1.2 光伏系统模型

光伏所处环境是影响光伏输出功率的重要因素。光伏电池板呈非线性，需利用MPPT控制器确保光伏电压始终为最大输出功率对应的电压^[21]。光伏电池将光能转化为直流电，通过变流器转换为交流。逆变器作为中间环节，输入输出均要满足一定条件^[22]。因此，对光伏进行精确建模，研究其与配电网之间的交互影响具有重要意义。

光伏主要由光伏电池模块、DC/DC功率变换模块、DC/AC逆变器模块组成。采用典型的两级拓扑光伏并网发电系统进行建模，如图 7所示。

通过单台光伏仿真可得光伏输出侧超高次谐波发射特性及其与光照、温度的关系。光伏超高次谐波电流发射特征如图 8所示。由图 8可知，光伏在开关频率附近发射的超高次谐波电流幅值最大，且整数倍开关频率附近出现电流幅值变高的现象; 光伏发射的超高次谐波电流随着光照强度降低而减小，随着温度升高而增大，该结论与文献[13]所述基本相符。

2.2 多光伏接入系统的超高次谐波影响

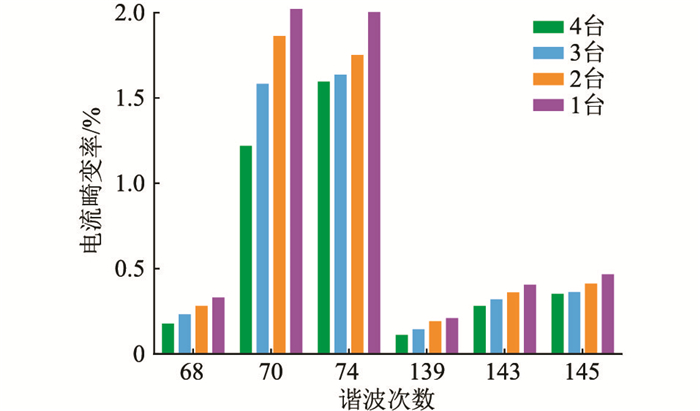
分析光伏运行对电网产生的超高次谐波影响随光伏台数增长的变化关系，分别仿真接入配电网的光伏台数为1~4台时(型号相同)，图 6中的接入点和并网点处的超高次谐波情况。仿真结果分别如图 9、图 10所示。

由图 9可知，随着光伏接入台数增加，单台光伏系统输出的超高次谐波电流畸变率减小。超高次谐波的叠加为矢量叠加，叠加结果受相位影响。超高次谐波电流之间相互助减，即光伏与光伏之间抵消了一部分的超高次谐波电流。此结果与式(4)理论推导相符。

由图 10可知，随着光伏接入台数增加，汇集母线上的超高次谐波电流/电压畸变率呈现显著增加趋势。但4台光伏产生的超高次谐波电流/电压并不是1台光伏的4倍而是低于4倍, 即接入点处超高次谐波的增长小于直接叠加的结果。接入系统的光伏间超高次谐波相互抵消，超高次谐波并不随设备数的增长而同倍增长。

2.3 系统背景谐波对多光伏接入的影响

对无穷大电源设置除基波外的其他低频谐波，以及改变图 6中除光伏外的其他DG的开关频率，实现背景谐波设置，仿真参数如表 2所示。

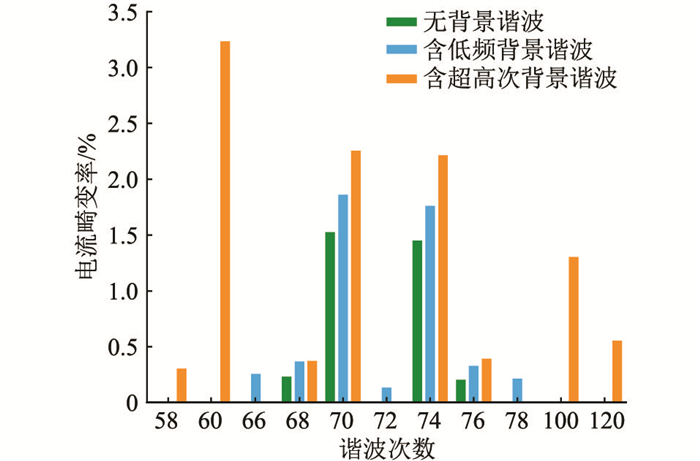
对比分析有无背景谐波时，光伏接入配电网的超高次谐波分布情况，结果如图 11所示。图 11给出了4台光伏接入时，有无背景谐波情况下单台光伏输出(并网点)超高次谐波电流仿真对比结果。

由图 11可知，低频背景谐波改变了单台光伏出口处的超高次谐波分布。对比分析低频背景谐波存在前后光伏输出的超高次谐波分布可知，未考虑低频背景谐波时，超高次谐波分布在开关频率附近(68次，70次，74次，76次); 考虑后，在原来的基础上新增了其他次数的超高次谐波(66次，72次，78次)。结合文献[23]可知，背景谐波电压存在时，光伏并网电流无法完全跟踪参考电流，导致并网电流产生除开关频率之外的超高次谐波电流。

超高次背景谐波的存在为光伏额外引入了其他次数的超高次谐波(60次，100次，120次)。背景谐波电压在光伏出口端产生了同频率的背景谐波电流，使光伏输出出现了其他次数的超高次谐波。这一仿真结果与1.3节中的理论分析相符。

除此之外，对比分析两种背景谐波情况。低频、超高次背景谐波存在时，70次以下的超高次谐波电流畸变率分别为1.857%，2.250%。即超高次背景谐波存在时，光伏发射的超高次谐波电流畸变率高于低频背景谐波存在时的情况。但考虑背景谐波时，单台光伏超高次谐波发射水平比不考虑背景谐波时要高。

3 实测数据验证

为验证文中所提模型及分析结论的正确性，对泉州某屋顶光伏的3台相同型号的光伏逆变器进行为期1 d的超高次谐波连续测试，现场接线示意如图 12所示。

图中，3台光伏并联接入汇集箱，由汇集箱汇总光伏输出电流接入母线，再通过变压器接入系统。目前的电压、电流互感器在超高次谐波频率范围内的测量存在局限性^[1]，因此文中未获得10 kV并网点光伏接入电网的准确谐波电压、电流数据。可将测量点选择为汇集箱0.4 kV出口处。光伏并网逆变器主要参数如表 3所示，3台光伏汇总后接入0.4 kV的低压配电网中。

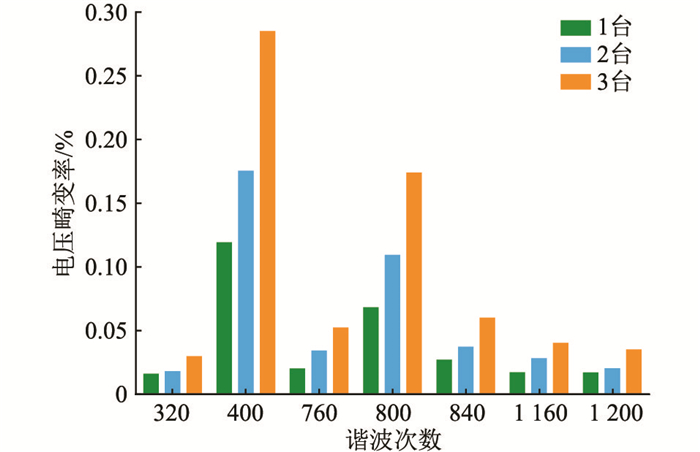
数据采集装置采样频率为409.6 kHz，可用于测量超高次谐波电压。电流探头的带宽为20 kHz, 故只能测到9 kHz的超高次谐波电流。选取3组不同工况的a相实测数据进行对比，测试结果如图 13所示。为了清晰展示，仅给出开关频率及其整数倍附近幅值较大的超高次谐波数据(16~60 kHz)。

由图 13可知，随着光伏逆变器接入配电网的数量增多，汇集母线上超高次谐波电压畸变率呈现不同程度的增大。除此之外，3台光伏产生的谐波电压并不是1台光伏的3倍而是略低于3倍，即汇集母线处超高次谐波电压的增长小于直接叠加的结果。接入系统的光伏之间的超高次谐波相互抵消，超高次谐波并不随设备数的增长而同倍增长。该结论与1.2节的理论推导以及2.2节的仿真结果均相符。

4 结语

文中通过仿真与实测相结合的方法对多接入光伏与配电网超高次谐波的交互影响进行了分析，得到结论如下：

(1) 仿真和实例表明，高比例光伏并网将产生严重的超高次谐波问题。用户间流动的超高次谐波电流畸变率随着并联用户个数的递增呈递减趋势; 汇集母线上的超高次谐波电压/电流畸变率随用户个数的递增呈递增趋势。

(2) 配电网的背景谐波使光伏并网超高次谐波发生更严重、更复杂的畸变。受背景谐波影响，新增的谐波/超高次谐波电流频率与背景谐波电压频率相同，幅值与背景谐波电压幅值成正比。

文中研究成果可为光伏接入规划、配电网光伏接纳能力评估以及超高次谐波治理等提供理论指导。目前电压、电流互感器在超高次谐波频率范围内的测量存在局限性，因此未获得10 kV光伏接入电网的准确数据，下一步将对新型宽频互感器进行研究。