文章编号: 2096-3203(2021)02-0086-07 中图分类号: TM711
2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103
发展至今,高压直流输电(high voltage direct current transmission,HVDC)已成为世界上电力大国解决大容量、远距离输电和电网异步互联等问题的重要手段之一。在我国的“西电东送,南北互供,全国联网”战略中,为解决能源资源和电力负荷分布极度不平衡的问题,HVDC发挥了十分重要的作用[1-3]。
换相失败作为HVDC最为常见的故障之一,其存在对电网的安全稳定运行造成了一定威胁。当系统发生换相失败后,会引起直流电压下降和直流电流迅速上升,且对换流阀产生冲击,并可能引发后续换相失败,严重时造成直流闭锁和设备损坏等后果[4-5]。一定严重程度的交流系统故障后,直流输电的首次换相失败一般无法避免,但可通过合适的控制措施避免直流输电发生后续的换相失败,保障系统的安全稳定运行[6-7]。
国内外关于抑制连续换相失败的研究已经取得了一些成果。文献[8]在低压限流器中增添虚拟电阻控制方法,使系统在故障期间直流电流指令提前减小,从而降低了发生连续换相失败的可能性;文献[9]提出一种渐变恢复策略控制方法,通过延缓单条直流功率恢复速率,降低系统故障时对交流系统的无功需求,并利用延时环节消除暂态不良交互影响,达到抑制连续换相失败的目的;文献[10]以换相电压-时间面积的需求量与提供能力之差作为故障衡量标准,继而提出虚拟换相面积缺乏指标,并将该指标增添到系统原有的直流电流控制环节;文献[11]在柔性直流无功功率控制环节附加上谐波电压补偿分量,以此来提高交流系统的无功功率支撑能力,达到改善同一受端母线常规直流输电连续换相失败的效果。但上述研究均未对常规直流换相失败恢复过程中不同谐波的影响进行深入研究。
文中基于换流母线谐波电压检测,提出一种谐波附加控制抑制直流输电连续换相失败方法,利用换相电压-时间面积的谐波分析法推导得出附加控制回路的各次谐波控制参数,并采用电磁暂态仿真的手段验证其有效性。所提出的附加控制无须增加新的一次设备投资,且不会影响系统的稳态运行。
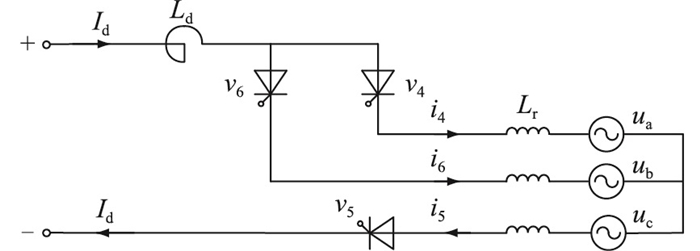
1 谐波电压对换相过程影响 1.1 换相电压-时间面积法为简化分析过程,同时又不影响分析的正确性,以HVDC逆变器中换相过程为例,当电流在a、b两相间由阀4向阀6进行换相时,等效电路如图 1所示。其中,ua,ub,uc为交流系统三相等效电压;Id为直流电流;Ld为直流平波电抗器;Lr为每相的换向等值电抗。
|
图 1 a、b两相换相过程等效图 Fig. 1 Equivalent diagram of a and b phase commutation |
当a、b两相处于换相过程时,电压和电流关系满足式(1)。
| $ \left\{\begin{array}{l} L_{\mathrm{r}} \frac{\mathrm{d} i_{4}}{\mathrm{~d} t}+u_{\mathrm{a}}=L_{\mathrm{r}} \frac{\mathrm{d} i_{6}}{\mathrm{~d} t}+u_{\mathrm{b}} \\ i_{4}+i_{6}=I_{\mathrm{d}} \end{array}\right. $ | (1) |
式中:i4为a相电流;i6为b相电流。由于直流线路中存在平波电抗器,因此Id可看作定值。而在换相过程中,i4不断减小,i6不断增大,直至i4=0,i6=Id,则a、b两相间线电压uab为:
| $ u_{\mathrm{ab}}=L_{\mathrm{r}} \frac{\mathrm{d} i_{6}}{\mathrm{~d} t}-L_{\mathrm{r}} \frac{\mathrm{d}\left(I_{\mathrm{d}}-i_{6}\right)}{\mathrm{d} t}=\frac{2 L_{\mathrm{r}} \mathrm{d} i_{6}}{\mathrm{~d} t} $ | (2) |
对式(2)两边时间t进行积分,即:
| $ 2 L_{\mathrm{r}} I_{\mathrm{d}}=\int_{t_{0}}^{t_{1}} u_{\mathrm{ab}} \mathrm{d} t=A_{\mathrm{CR}} $ | (3) |
其中:
| $ t_{0}=\alpha / \omega $ | (4) |
| $ t_{1}=(\mu+\alpha) / \omega $ | (5) |
式中:ACR为换相电压-时间面积;t0为换相开始时间;t1为换相结束时间;α为逆变侧的延迟触发角;μ为换相重叠角,且与熄弧角γ满足式(6)。
| $ \alpha+\mu+\gamma=180^{\circ} $ | (6) |
假设系统处于正常稳态运行,此时交流线电压uab为:
| $ u_{\mathrm{ab}}=E_{1} \sin \omega t $ | (7) |
式中:E1为交流系统线电压幅值。
将式(7)代入式(3)可得:
| $ A_{\mathrm{CR}}=\int_{\alpha / \omega}^{(\mu+\alpha) / \omega} E_{1} \sin \omega t \mathrm{~d} t $ | (8) |
研究表明,换相失败的本质是当逆变侧熄弧角γ小于临界熄弧角γmin后,晶闸管承受反向电压的时间过短不足以使其恢复阻断能力。临界熄弧角γmin由晶闸管的物理特性决定,其含义为换流阀完成载流子复合及恢复阻断能力的时间所对应的角度[12-13]。文中拟采用熄弧角判断法来判断是否发生换相失败,即当逆变侧熄弧角γ小于临界熄弧角γmin时,认为该系统发生换相失败。不考虑换相失败持续时间的长短,换相失败次数即为逆变侧熄弧角γ小于临界熄弧角γmin的次数。
因此若想换相成功,换相结束时刻t1需要满足的条件为:
| $ \omega t_{1}=\alpha+\mu \leqslant 180-\gamma_{\min } $ | (9) |
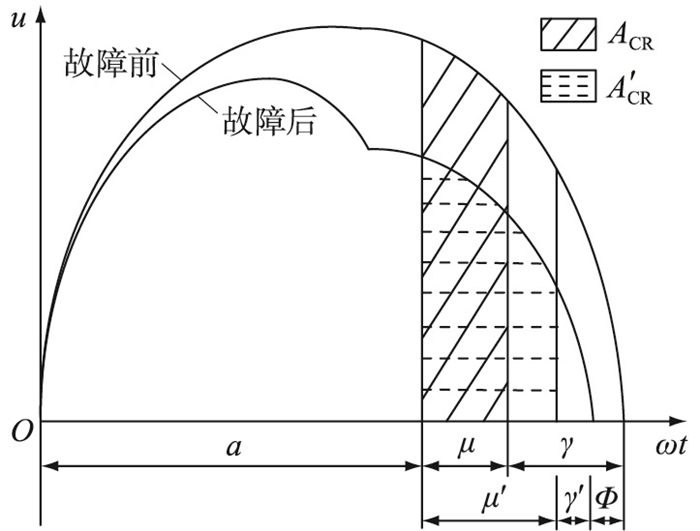
由式(3)可知,换相期间,一定工况下直流电流Id对应的换相电压-时间面积ACR不变;而当电网发生故障后,系统电压会发生幅值和相位上的变化,其对换相电压-时间面积的影响如图 2所示。
|
图 2 谐波对换相电压-时间面积的影响 Fig. 2 Influence of harmonics on commutation voltage-time area |
图 2中,μ,γ,ACR和μ′,γ′,A′CR分别为谐波畸变前后的换相重叠角、熄弧角和换相电压-时间面积,且满足故障前换相电压-时间面积ACR等于故障后的换相电压-时间面积A′CR;Φ为相位移角。可见,扰动造成换相电压的幅值和相位变化可能会导致换相时间延长,进而缩短晶闸管实际的熄弧角γ′,一旦γ′小于晶闸管恢复阻断能力所需的最小熄弧角γmin,则晶闸管将在正向电压的作用下自动恢复导通,直流输电发生换相失败。
1.2 谐波对换相过程影响当系统检测到谐波后,系统交流线电压为:
| $ u_{\mathrm{ab}}=E_{1} \sin \omega t+\sum\limits_{n=2}^{N} E_{n} \sin \left(n \omega t+\varphi_{n}\right) $ | (10) |
式中:En为n次谐波电压幅值;φn为n次谐波相角。
将式(10)代入式(8),可得:
| $ A_{\mathrm{CR}}=\int_{t_{0}}^{t_{1}} E_{1} \sin \omega t+\sum\limits_{n=2}^{N} E_{n} \sin \left(n \omega t+\varphi_{n}\right) \mathrm{d} t $ | (11) |
同时,由换相电压-时间面积法可知,若想成功换相,则必须满足式(9),即换相过程的熄弧角必须大于临界熄弧角:
| $ \begin{aligned} A_{\mathrm{CR}} &<\int_{\alpha / \omega}^{\left(180^{\circ}-\gamma_{\min }\right) / \omega} E_{1} \sin \omega t+\\ &\sum\limits_{n=2}^{N} E_{n} \sin \left(n \omega t+\varphi_{n}\right) \mathrm{d} t \end{aligned} $ | (12) |
为量化评估不同次数谐波对换相过程的影响,设n次谐波的换相电压-时间面积为ACRn,即:
| $ \left\{\begin{array}{l} A_{\mathrm{CR} n}=E_{n} k_{n} \\ k_{n}=\int_{\alpha / \omega}^{\left(180-\gamma_{\min }\right) / \omega} \sin \left(n \omega t+\varphi_{n}\right) \mathrm{d} t \end{array}\right. $ | (13) |
式中:kn为n次谐波影响系数。kn越大,表明该次谐波对换相电压-时间面积的影响越大。
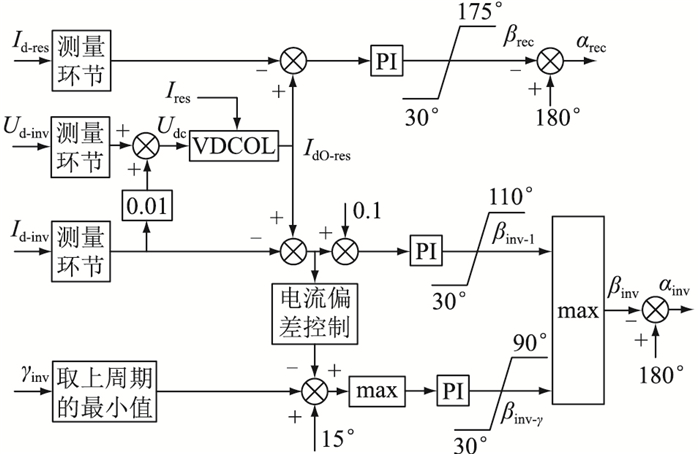
2 直流附加控制抑制连续换相失败方法 2.1 低压限流控制CIGRE HVDC标准测试系统控制器见图 3。整流侧由定电流控制和αmin限制两部分组成,逆变侧配有定电流控制、定关断角γ0控制及电流偏差控制(无定电压控制),整流侧和逆变侧都配有低压限流(voltage dependent current order limiter,VDCOL)控制。其中VDCOL控制对于改善直流输电换相失败的恢复过程具有重要意义。
|
图 3 CIGRE HVDC标准测试系统控制器框图 Fig. 3 Controller block diagram of CIGRE HVDC standard test system |
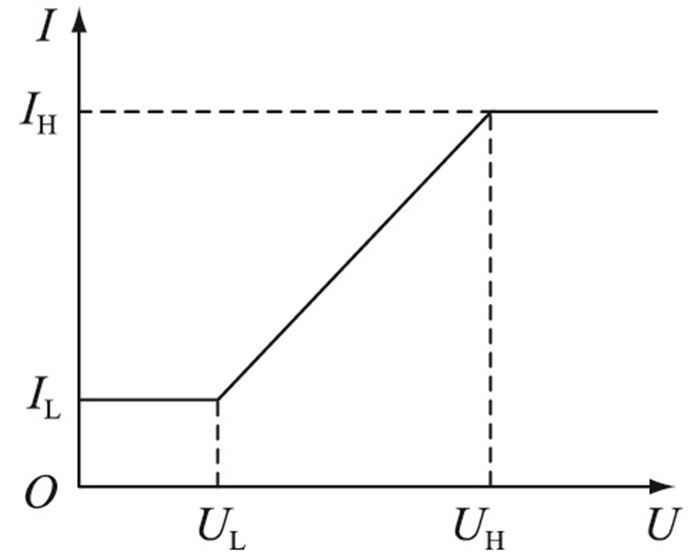
VDCOL控制为直流输电系统中常用的控制策略,其特性曲线如图 4所示。VDCOL作用是在系统电压降低到某一固定值后减少直流电流指令,能够在一定程度上减少逆变站在故障期间的无功需求,同时维持换流母线电压的稳定,减小换相失败发生的可能性[14-17]。
|
图 4 低压限流控制特性曲线 Fig. 4 Characteristic curve of voltage dependent current order limiter |
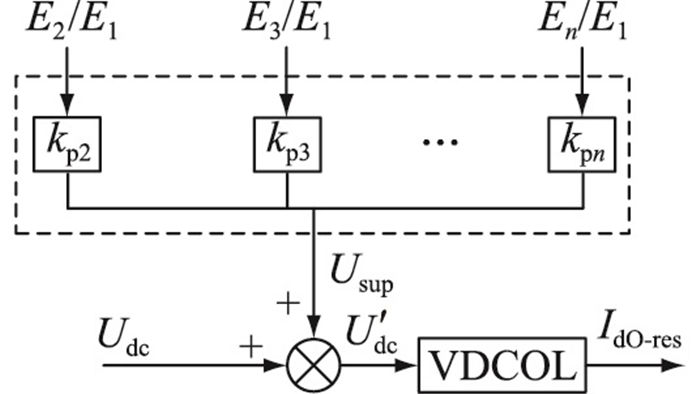
电网故障及直流输电换相失败恢复过程中,电网内将不可避免地产生谐波电压,并进一步造成换相电压-时间面积减少。当换相电压-时间面积小于临界值时,系统即存在发生后续换相失败的风险。传统的低压限流控制在系统电压降低的情况下仅限制直流电流,而并未考虑谐波对直流换相的影响。因此,文中设计了一种谐波附加控制抑制直流输电连续换相失败的方法,通过改进VDCOL控制环节对系统谐波的响应特性,来实现对直流输电连续换相失败的抑制,附加控制器结构及附加信号施加位置如图 5所示。
|
图 5 谐波附加控制回路框图 Fig. 5 Block diagram of the additional harmonic control loop |
图 5中,在原有的低压限流控制系统中引入谐波补偿控制分量,定义包含谐波信息的直流电压等值控制量U′dc,该控制量可由式(14)获取:
| $ \left\{\begin{array}{l} U_{\text {sup }}=\sum\limits_{n=2}^{N} k_{\mathrm{p} n} \frac{E_{n}}{E_{1}} \\ U_{\mathrm{dc}}^{\prime}=U_{\mathrm{dc}}+U_{\mathrm{sup}} \end{array}\right. $ | (14) |
式中:Usup为各次谐波分量影响的总和。
n次谐波控制参数kpn=|kn/k1|,即:
| $ k_{\mathrm{p} n}=\left|\frac{\cos \left(n \alpha+\varphi_{n}\right)-\cos \left(180 n-n \gamma_{\min }+\varphi_{n}\right)}{n\left[\cos \alpha-\cos \left(180-\gamma_{\min }\right)\right]}\right| $ | (15) |
由式(15)可得,当谐波次数n、逆变侧延迟触发角α、临界熄弧角γmin等因素已知时,kpn为常数。
同时由式(14)可知,当系统处于正常工况时,系统中谐波分量较小,Usup值接近于0,附加控制不影响系统正常运行;当系统发生故障导致各次谐波分量急剧增加后,谐波可能会引起换流器的换相电压-时间面积急剧减小,从而造成换相过程的进一步恶化,附加控制回路可以通过减少谐波分量的影响来使换流母线电压快速恢复,避免后续换相失败的发生。
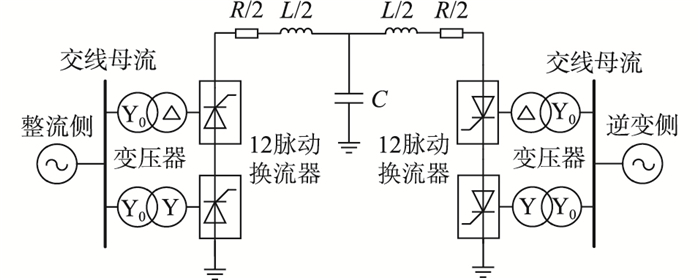
3 控制方法有效性验证 3.1 算例系统采用CIGRE HVDC标准测试系统,验证文中所提直流系统附加控制方法的有效性,系统结构如图 6所示。
|
图 6 CIGRE HVDC标准测试系统结构 Fig. 6 Structure of CIGRE HVDC standard test system |
CIGRE HVDC标准测试系统换流器采用12脉动换流器结构,系统中主要存在12n±1次谐波,且谐波幅值随次数增加而减小[18],该系统整流侧和逆变侧母线上均具有2组高通滤波器,其主要针对11次以上谐波的滤波[19]。
当CIGRE HVDC标准测试系统处于稳态运行时,逆变侧触发角α为141°。此时,晶闸管完成载流子复合及恢复阻断能力的时间约为400 μs,相当于7°的电角度,即γmin=7°。设各次谐波相位φn=0,将γmin=7°,α=141°代入式(15),可得附加控制回路的各次谐波控制参数,2~6次谐波控制参数kpn分别为1.76,2.14,2.08,1.65,1.02。
3.2 仿真分析为验证文中所提控制方法的有效性,在逆变侧换流母线处施加感性接地故障进行仿真验证。当接地电感值Lf越小,表明交流系统故障点距离换流母线越近,故障越严重[20-24]。故障水平fFL的计算方法为:
| $ {f_{\rm{FL}}} = \frac{{{U^2}}}{{{L_{\rm{f}}}\omega {P_{{\rm{dc}}}}}} $ | (16) |
式中:U为换流母线额定线电压;ω为交流系统额定角频率;Pdc为直流系统额定功率。
在不同故障水平下,对以下2种控制方法进行仿真验证。
(1) 控制方法Ⅰ:采用CIGRE HVDC标准测试系统内部所有的控制方法。
(2) 控制方法Ⅱ:在控制方法Ⅰ的基础上,加入文中提出的谐波附加控制。
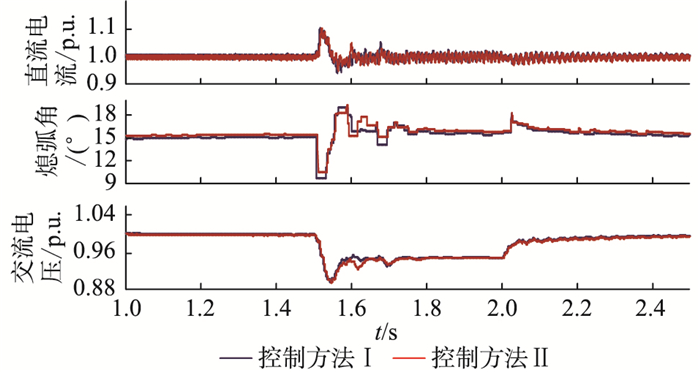
算例1:设t=1.5 s时,系统发生A相接地故障,故障水平为10%,故障持续时间为0.5 s。在此故障条件下,采用控制方法Ⅰ与Ⅱ时,系统直流电流曲线、熄弧角曲线和交流电压曲线结果如图 7所示。
|
图 7 单相故障下10%故障水平时系统响应曲线 Fig. 7 System response curve under single phase fault when fFL=10% |
由图 7可知,在故障较轻,即实际系统中故障点与换流母线电气距离较大的情况下,未加入谐波附加控制时,系统各物理量有较小波动,但并没有发生换相失败;加入谐波附加控制后,各物理量的波动与原有控制系统相比基本没有变化,也不会发生换相失败。
经大量仿真分析可知,当系统发生较轻故障时,若仅有系统原有的控制,系统未发生换相失败,则加入谐波附加控制后,系统亦不会发生换相失败。
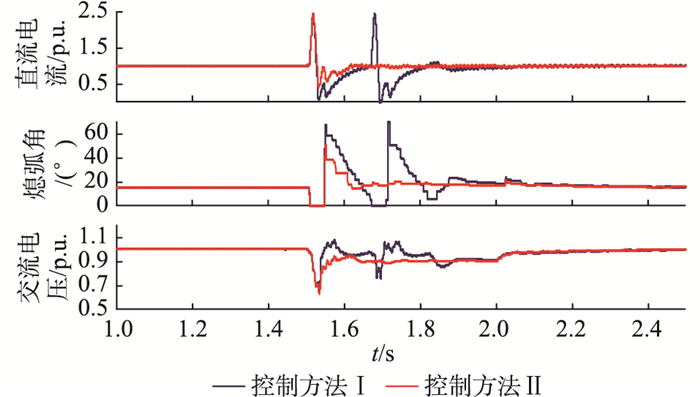
算例2:设t=1.5 s时,系统发生A相接地故障,故障水平为20%,故障持续时间为0.5 s。在此故障条件下,采用控制方法Ⅰ与Ⅱ时。系统直流电流曲线、熄弧角曲线和交流电压曲线结果如图 8所示。
|
图 8 单相故障下20%故障水平时系统响应曲线 Fig. 8 System response curve under single phase fault when fFL=20% |
由图 8可知,当接地电感Lf较小,即实际系统中故障点距离换流母线较近时,容易发生换相失败。若仅有原有控制系统,当发生故障后,直流电流值迅速上升,最大可至基准值的2.5倍,熄弧角迅速降为0°,发生首次换相失败,且在后续的恢复过程中,再一次发生了换相失败;在加入谐波附加控制后,由于故障点距离逆变侧交流系统较近,故障时间较短,直流输电控制系统效果有限,即故障后首次换相失败难以避免,但在加入谐波附加控制后,系统并未发生后续换相失败,连续换相失败得到有效抑制。
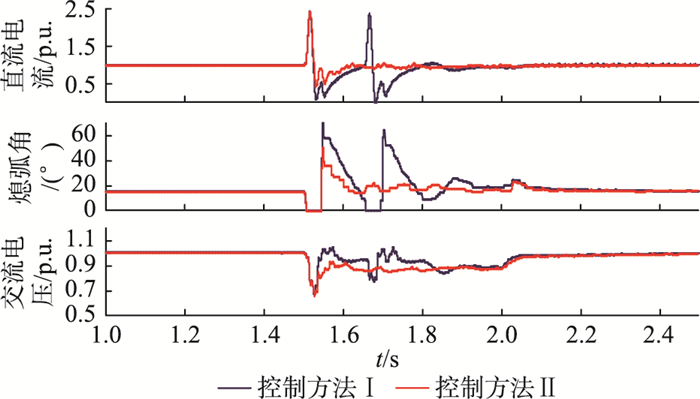
算例3:设t=1.5 s时,系统发生三相接地故障,故障水平为20%,故障持续时间为0.5 s。在此故障条件下,采用控制方法Ⅰ与Ⅱ时,系统直流电流曲线、熄弧角曲线和交流电压曲线结果如图 9所示。
|
图 9 三相故障下20%故障水平时系统响应曲线 Fig. 9 System response curve under three phase fault when fFL=20% |
在系统发生三相故障后,由图 9可知,谐波附加控制在此故障情况下同样可起到抑制直流系统发生连续换相失败的作用,与算例2仿真结果相类似。
为进一步验证谐波附加控制在不同严重程度的故障水平下对直流输电产生连续换相失败的抑制作用,设故障水平以2%为步长进行连续变化,对故障水平fFL在10%~60%之间的逆变侧交流系统故障进行仿真验证,通过比较在同一严重程度故障下2种不同控制方法的直流输电连续换相失败次数,来确定谐波附加控制对于抑制直流输电连续换相失败的作用。
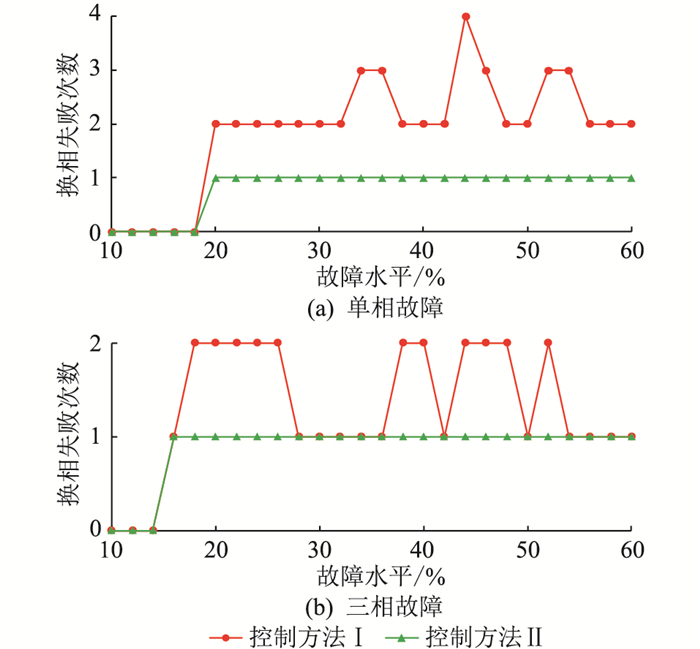
在仿真实验中,均设当t=1.5 s时,系统发生接地故障,且故障持续时间为0.5 s。当系统在不同故障水平下,直流输电系统发生换相失败的次数如图 10所示。
|
图 10 2种控制方法下系统发生换相失败次数 Fig. 10 The number of commutation failures occurred in the system under two control methods |
对图 10中系统在2种控制方法下的换相失败次数进行分析可知:当故障水平较低时,若采用原有的控制策略,直流系统不发生换相失败故障,则采用谐波附加控制也不会造成直流系统换相失败;当故障水平较高时,即原有系统发生2次直至4次连续换相失败时,在加入谐波附加控制后,可将系统换相失败次数降为1,有效抑制了连续换相失败故障。
4 结论文中针对系统谐波造成直流连续换相失败的问题,提出一种基于谐波检测附加控制抑制连续换相失败的方法,并通过理论分析和大量仿真验证分析,得出如下结论:
(1) 所提附加控制不影响系统的稳态运行,系统故障或换相失败后通过附加控制减少谐波分量对换相过程的影响,进而达到抑制连续换相失败的效果,并通过电磁暂态仿真验证了该方法的有效性;
(2) 文中给出了所提附加控制策略的控制参数整定计算方法,可为该方法具体工程应用提供指导;
(3) 文中所提附加控制逻辑仅需对直流输电VDCOL控制进行适当的改造,易于实现且成本较低,可为直流输电连续换相失败抑制提供新的思路和参考。
本文得到江苏省研究生科研创新计划资助项目(KYCX18_1227)资助,谨此致谢!
| [1] |
SHAO Y, TANG Y. Fast evaluation of commutation failure risk in multi-infeed HVDC systems[J]. IEEE Transactions on Power Systems, 2018, 33(1): 646-653. DOI:10.1109/TPWRS.2017.2700045 (  0) 0) |
| [2] |
李春华, 孙宝奎, 赵成勇, 等. 半控型H桥子模块提高HVDC换相失败免疫力的机理[J]. 中国电机工程学报, 2016, 36(9): 2419-2427. LI Chunhua, SUN Baokui, ZHAO Chengyong, et al. Mechanism of semi-controlled H-bridge sub-module to improve commutation failure immunity of HVDC[J]. Proceedings of the CSEE, 2016, 36(9): 2419-2427. (  0) 0) |
| [3] |
李瑞鹏, 李永丽, 陈晓龙. 一种抑制直流输电连续换相失败的控制方法[J]. 中国电机工程学报, 2018, 38(17): 5029-5042, 5300. LI Ruipeng, LI Yongli, CHEN Xiaolong. A control method for suppressing the continuous commutation failure of HVDC transmission[J]. Proceedings of the CSEE, 2018, 38(17): 5029-5042, 5300. (  0) 0) |
| [4] |
邵思语, 黄振琳, 刘永强, 等. 基于交流系统非特征谐波的HVDC换相失败风险评估及抑制策略[J]. 电网技术, 2019, 43(10): 3466-3476. SHAO Siyu, HUANG Zhenlin, LIU Yongqiang, et al. Risk assessment and suppression strategy of HVDC commutation failure based on non-characteristic harmonics in AC system[J]. Power System Technology, 2019, 43(10): 3466-3476. (  0) 0) |
| [5] |
WANG L, WEN J, YU Z, et al. Analysis of the influence of harmonic on commutation failure of thyristor inverter[C]//2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia). Hefei, China. IEEE, 2016: 1296-1301.
(  0) 0) |
| [6] |
GUO C Y, LIU Y C, ZHAO C Y, et al. Power component fault detection method and improved current order limiter control for commutation failure mitigation in HVDC[J]. IEEE Transactions on Power Delivery, 2015, 30(3): 1585-1593. DOI:10.1109/TPWRD.2015.2411997 (  0) 0) |
| [7] |
邵瑶, 汤涌. 采用多馈入交互作用因子判断高压直流系统换相失败的方法[J]. 中国电机工程学报, 2012, 32(4): 108-114, 11. SHAO Yao, TANG Yong. A commutation failure detection method for HVDC systems based on multi-infeed interaction factors[J]. Proceedings of the CSEE, 2012, 32(4): 108-114, 11. (  0) 0) |
| [8] |
郭春义, 李春华, 刘羽超, 等. 一种抑制传统直流输电连续换相失败的虚拟电阻电流限制控制方法[J]. 中国电机工程学报, 2016, 36(18): 4930-4937, 5117. GUO Chunyi, LI Chunhua, LIU Yuchao, et al. A DC current limitation control method based on virtual-resistance to mitigate the continuous commutation failure for conventional HVDC[J]. Proceedings of the CSEE, 2016, 36(18): 4930-4937, 5117. (  0) 0) |
| [9] |
王超, 李兴源, 冯明, 等. 抑制多馈入直流输电系统相继换相失败的协调恢复控制策略[J]. 电测与仪表, 2016, 53(13): 19-24. WANG Chao, LI Xingyuan, FENG Ming, et al. Coordinated recovery strategy for inhibiting continuous commutation failures in multi-infeed HVDC transmission system[J]. Electrical Measurement & Instrumentation, 2016, 53(13): 19-24. (  0) 0) |
| [10] |
刘磊, 林圣, 何正友. 基于虚拟换相面积缺乏量的HVDC系统连续换相失败抑制策略[J]. 中国电机工程学报, 2018, 38(18): 5361-5368. LIU Lei, LIN Sheng, HE Zhengyou. A novel method based on virtual commutation area insufficient to mitigate the continuous commutation failure for HVDC[J]. Proceedings of the CSEE, 2018, 38(18): 5361-5368. (  0) 0) |
| [11] |
何晓峰, 李成翔, 夏成军, 等. 基于谐波电压补偿的混合直流连续换相失败抑制策略[J]. 电力工程技术, 2019, 38(4): 112-117. HE Xiaofeng, LI Chengxiang, XIA Chengjun, et al. Control strategy to suppress hybrid HVDC continuous commutation failure by harmonic voltage compensatio[J]. Electric Power Engineering Technology, 2019, 38(4): 112-117. (  0) 0) |
| [12] |
邵瑶, 汤涌. 一种快速评估多馈入直流系统换相失败风险的方法[J]. 中国电机工程学报, 2017, 37(12): 3429-3436, 3670. SHAO Yao, TANG Yong. A fast assessment method for evaluating commutation failure risk of multi-infeed HVDC systems[J]. Proceedings of the CSEE, 2017, 37(12): 3429-3436, 3670. (  0) 0) |
| [13] |
郭春义, 赵剑, 刘炜, 等. 抑制高压直流输电系统换相失败方法综述[J]. 中国电机工程学报, 2018, 38(S1): 1-10. GUO Chunyi, ZHAO Jian, LIU Wei, et al. A review of methods to mitigate the commutation failure for LCC-HVDC[J]. Proceedings of the CSEE, 2018, 38(S1): 1-10. (  0) 0) |
| [14] |
郭利娜, 刘天琪, 李兴源. 抑制多馈入直流输电系统后续换相失败措施研究[J]. 电力自动化设备, 2013, 33(11): 95-99. GUO Lina, LIU Tianqi, LI Xingyuan. Measures inhibiting follow-up commutation failures in multi-infeed HVDC system[J]. Electric Power Automation Equipment, 2013, 33(11): 95-99. (  0) 0) |
| [15] |
王强, 李天然, 唐小波, 等. 应对多馈入直流换相失败的同步调相机布点方法[J]. 电力系统自动化, 2019, 43(1): 222-227. WANG Qiang, LI Tianran, TANG Xiaobo, et al. Method of site selection for synchronous condenser responding to commutation failures of multi-infeed DC system[J]. Automation of Electric Power Systems, 2019, 43(1): 222-227. (  0) 0) |
| [16] |
王龙飞, 华文, 石博隆, 等. 抑制直流连续换相失败的调相机暂态强励控制策略[J]. 浙江电力, 2020, 39(8): 13-19. WANG Longfei, HUA Wen, SHI Bolong, et al. Research on transient forced excitation control strategy of synchronous condenser for continuous commutations failure mitigation[J]. Zhejiang Electric Power, 2020, 39(8): 13-19. (  0) 0) |
| [17] |
于灿平. 弱送端电网直流群同时换相失败对电网功角稳定特性的影响研究[J]. 浙江电力, 2019, 38(5): 55-61. YU Canping. Research on the stability mechanism under simultaneous commutation failure of UHVDC group in the weak sending end grid[J]. Zhejiang Electric Power, 2019, 38(5): 55-61. (  0) 0) |
| [18] |
徐政. 交直流电力系统动态行为分析[M]. 北京: 机械工业出版社, 2004: 39-42. XU Zheng. Analysis of dynamic behavior of AC/DC power system[M]. Beijing: Machinery Industry Press, 2004: 39-42. (  0) 0) |
| [19] |
王峰, 刘天琪, 周胜军, 等. 谐波对HVDC系统换相失败的影响机理及定量分析方法[J]. 中国电机工程学报, 2015, 35(19): 4888-4894. WANG Feng, LIU Tianqi, ZHOU Shengjun, et al. Mechanism and quantitative analysis method for HVDC commutation failure resulting from harmonics[J]. Proceedings of the CSEE, 2015, 35(19): 4888-4894. (  0) 0) |
| [20] |
SZECHTMAN M, WESS T, THIO C V. A benchmark model for HVDC system studies[C]//International Conference on AC and DC Power Transmission. London, UK. IET, 1991: 374-378.
(  0) 0) |
| [21] |
赵彤, 吕明超, 娄杰, 等. 多馈入高压直流输电系统的异常换相失败研究[J]. 电网技术, 2015, 39(3): 705-711. ZHAO Tong, LYU Mingchao, LOU Jie, et al. Analysis on potential anomalous commutation failure in multi-infeed HVDC transmission systems[J]. Power System Technology, 2015, 39(3): 705-711. (  0) 0) |
| [22] |
王思超, 文俊, 贺冬珊, 等. 受端分层UHVDC换相失败控制和恢复策略[J]. 电力系统保护与控制, 2020, 48(2): 172-179. WANG Sichao, WEN Jun, HE Dongshan, et al. Commutation failure control and recovery strategy of UHVDC with hierarchical connection mode[J]. Power System Protection and Control, 2020, 48(2): 172-179. (  0) 0) |
| [23] |
李晓华, 张陈泽宇, 蔡旺延, 等. 基于三相同时刻采样值算法的HVDC换相失败预测改进[J]. 电力系统保护与控制, 2020, 48(20): 170-176. LI Xiaohua, ZHANG Chenzeyu, CAI Wangyan, et al. Improvement of HVDC CFPREV based on a three phase simultaneity sampling values algorithm[J]. Power System Protection and Control, 2020, 48(20): 170-176. (  0) 0) |
| [24] |
刘建, 李兴源, 吴冲, 等. HVDC系统换相失败的临界指标[J]. 电网技术, 2009, 33(8): 8-12. LIU Jian, LI Xingyuan, WU Chong, et al. Research on critical index of commutation failure in HVDC system[J]. Power System Technology, 2009, 33(8): 8-12. (  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd. Research Institute, Nanjing 211103, China
 2021, Vol. 40
2021, Vol. 40


 陈佳浩(1994),男,硕士,研究方向为电力系统稳定与控制(E-mail:
陈佳浩(1994),男,硕士,研究方向为电力系统稳定与控制(E-mail: