文章编号: 2096-3203(2021)01-0010-07 中图分类号: TM711 文献标识码: A
可再生能源的不确定性和不连续性导致其与用户负荷无法实时匹配,余电上网时会对电力系统安全稳定运行和电能质量管控造成一定冲击[1],产生大量弃风弃光现象。据国家能源局数据显示,2019年全国弃风电量总计169亿kW ·h[2],弃光电量总计46亿kW ·h[3]。电转气(power to gas, P2G)是一种能将电能转换为天然气或氢气的新兴技术[4],利用弃电制氢能够消纳多余电力,降低电网运行风险。我国天然气管道规模庞大,运维和管理技术已经非常成熟,在保证安全的情况下,将氢气掺入天然气管道进行长距离运输是低成本运输氢气的有效途径之一。因此,电-气综合能源系统通过燃气电厂、电驱压缩机组和富余可再生能源电力制氢耦合,耦合程度高,能源综合利用率高,具有较大的节能减排潜力。
针对电-气综合能源系统,文献[5]进行了综合能源系统能量流计算;文献[6-8]研究了电-气综合能源系统协同优化;文献[9-11]研究了电-气综合能源系统的调度问题;文献[12]建立了电-气综合能源系统的分布式状态估计模型。
国外一些学者针对P2G技术在电-气综合能源系统中的应用开展了相关研究:文献[13]建立了英国某地电-气综合能源系统运行优化模型,得到系统最小成本;文献[14]评估了P2G技术对电力和天然气传输网络的运行影响。针对掺混氢气的天然气管网,文献[15]建立了耦合风力发电、电解水制氢以及天然气管网计算的仿真模型,提出了天然气管网输运策略;文献[16]认为混合气中氢气的最大允许体积分数为23%,并认为氢气加入后通过提高输送压力可保证管道输气功率不变;文献[17]计算了氢注入天然气时的热力学关系,探讨了其对能量密度、韦伯数及管道压降的影响;文献[18]对掺氢天然气网进行了建模和评价,并得到最大掺氢比例为6%;文献[19]研究了掺氢天然气对X80钢管道拉伸性能的影响和管道损伤机理。
现有掺氢电-气综合能源系统相关研究仍偏局部性而缺乏系统性,难以综合评价系统的性能。因此文中针对掺氢电-气综合能源系统进行了数学建模,并以经济性为评估目标对系统进行了运行优化,同时与制氢后本地存储的情况进行对比,旨在提高电-气综合能源系统的收益,降低不必要的能源浪费。
1 含可再生能源发电制氢的电-气综合能源系统模型电-气综合能源系统由配电网和天然气网2个子系统构成,通过电网中的燃气电厂、可再生能源富余电力制氢站和气网中的电驱、燃驱压缩机组进行耦合。可再生能源发电富余电力用于电解水制氢,制得的氢气有2条消纳途径:
(1) 将氢气储存于储氢罐中,燃烧发电进行本地消纳;
(2) 将氢气加压后在气网节点处掺混进入天然气,进行混氢天然气(hydrogen and compressed natural gas, HCNG)管道输运,供给相应气用户。
考虑富余可再生能源发电制氢的电-气综合能源系统主要部件有配电网、气网管道、压缩机组,模型还包括氢气与天然气的理想掺混过程及混合气体的物性计算。
1.1 电网模型采用经典的电网功率平衡方程作为电网的稳态模型,节点功率可通过以下公式计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{P_i} = {U_i}\sum\limits_{j \in i} {{U_j}} \left[ {{G_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right) + {B_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right)} \right]}\\ {{V_i} = {U_i}\sum\limits_{j \in i} {{U_j}} \left[ {{G_{ij}}\sin \left( {{\theta _i} - {\theta _j}} \right) - {B_{ij}}\cos \left( {{\theta _i} - {\theta _j}} \right)} \right]} \end{array}} \right. $ | (1) |
式中:Pi,Vi分别为节点i注入的有功功率和无功功率;Ui,Uj分别为节点i和j的电压幅值;Gij,Bij分别为节点导纳矩阵第i行第j列元素的实部和虚部;θi,θj分别为节点i和j的相角。
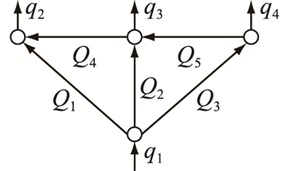
1.2 气网管网模型在实际运行中,天然气由多个输气管道组成的管网进行输送,管道与供气站、电驱及燃驱压缩机站、用气站的交叉口为节点。因此,气网简化模型如图 1所示。
|
图 1 气网简化示意 Fig. 1 Schematic diagram of simplified gas network |
气网管网模型包括流量连续方程和压力环路方程:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{AQ}} = \mathit{\boldsymbol{q}}}\\ {\mathit{\boldsymbol{B}} \times \Delta \mathit{\boldsymbol{P}} = 0} \end{array}} \right. $ | (2) |
式中:A为管网的节点-管段关联矩阵;Q为管道流量向量;q为节点的负载流量向量;B为环路-管段关联矩阵;ΔP为管段压降向量。
1.3 管道输运模型管道稳态输运公式采用Weymouth公式[19],如式(3)所示。
| $ {Q_{0, ij}} = \frac{{\rm{ \mathsf{ π} }}}{4}\frac{{\sqrt {{R_{\rm{a}}}} {T_0}}}{{{P_0}}}\sqrt {\frac{{\left( {P_i^2 - P_j^2} \right){D^5}}}{{\lambda z\Delta {T_0}L}}} $ | (3) |
式中:Q0, ij为节点i和j之间管段的标况体积流量;Pi和Pj分别为管道进口和出口压力;D为管道直径;λ为管道水力摩阻系数;z为气体的压缩因子;Δ为气体的相对密度;L为管道长度;Ra为空气气体常数;P0,T0分别为标况下压力和温度。
水力摩阻系数λ由式(4)计算[20],雷诺数Re由式(5)计算:
| $ {\lambda = 0.067{{\left( {\frac{{2K}}{D} + \frac{{158}}{{Re}}} \right)}^{0.2}}} $ | (4) |
| $ {Re = \frac{{4{Q_{0, ij}}{\rho _0}}}{{{\rm{ \mathsf{ π} }}D\mu }}} $ | (5) |
式中:K为管道的粗糙度;μ为流体的黏度;ρ0为流体的标况密度。
Weymouth公式中混合气体的压缩因子zmix计算如下[21]:
| $ \left\{ {\begin{array}{*{20}{l}} {{z_{{\rm{mix }}}} = 1 + \left( {0.257 - 0.533\frac{{{T_{{\rm{c, mix }}}}}}{{{T_0}}}} \right)\frac{{{{\bar p}_{ij}}}}{{{p_{{\rm{c, mix }}}}}}}\\ {{{\bar p}_{ij}} = \frac{2}{3}\left( {{p_i} + {p_j} - \frac{{{p_i}{p_j}}}{{{p_i} + {p_j}}}} \right)}\\ {{T_{{\rm{c}}, {\rm{ mix }}}} = {T_{{\rm{c}}, {\rm{ng}}}}(1 - \varepsilon ) + {T_{{\rm{c}}, {{\rm{H}}_2}}}\varepsilon }\\ {{P_{{\rm{c}}, {\rm{ mix }}}} = {P_{{\rm{c}}, {\rm{ng}}}}(1 - \varepsilon ) + {P_{{\rm{c}}, {{\rm{H}}_2}}}\varepsilon } \end{array}} \right. $ | (6) |
混合气体的黏度μmix计算如下:
| $ {\mu _{{\rm{mix }}}} = \frac{{{\mu _{{{\rm{H}}_2}}}\varepsilon \sqrt {{M_{{{\rm{H}}_2}}}} + {\mu _{{\rm{ng}}}}(1 - \varepsilon )\varepsilon \sqrt {{M_{{\rm{ng}}}}} }}{{\varepsilon \sqrt {{M_{{{\rm{H}}_2}}}} + (1 - \varepsilon )\sqrt {{M_{{\rm{ng}}}}} }} $ | (7) |
式中:Tc, mix,pc, mix分别为混合气体的临界温度和临界压力;pij为管道两端平均压力;ε为混合气体中氢所占体积比;Tc, ng,Tc, H2分别为天然气和氢气的临界温度;Pc, ng,Pc, H2分别为天然气和氢气的临界压力;Mng,MH2分别为天然气和氢气的摩尔质量;μng,μH2分别为天然气和氢气的黏度。
1.4 压缩机组模型压缩机是天然气管网中常用的控制元件,有2种类型:燃驱压缩机组和电驱压缩机组。前者通过消耗管道内的天然气来增加其压力,后者则消耗电网电力。二者数学模型如下:
(1) 电驱压缩机。
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{{\rm{md}}}} = {n_{{\rm{md}}}}{P_{{\rm{dp}}, {\rm{md}}}} = \frac{{{W_{{\rm{pol}}}}}}{{{\eta _{{\rm{md}}}}}}}\\ {{W_{{\rm{pol}}}} = \frac{m}{{m - 1}}{p_{{\rm{in }}}}{\nu _{{\rm{in }}}}\left[ {{{\left( {\frac{{{p_{{\rm{out }}}}}}{{{p_{{\rm{in }}}}}}} \right)}^{(m - 1)/m}} - 1} \right]}\\ {{\eta _{{\rm{md}}}} = {A_{{\rm{md}}}}{n_{{\rm{md}}}} + {B_{{\rm{md}}}}} \end{array}} \right. $ | (8) |
式中:Pmd,nmd,Pdp, md,ηmd分别为电驱压缩机的耗功、工况、额定功率和电机效率,且ηmd与工况线性相关;Wpol为多变功;νin为进气气体的比体积;pin,pout分别为进、出口气体的压力;m为气体的多变系数;Amd,Bmd均为实际运行数据拟合的修正系数。
(2) 燃驱压缩机。
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{{\rm{gd}}}} = \frac{{{P_{{\rm{op}}}}}}{{{\eta _{{\rm{gd}}}}{H_{{\rm{mix}}}}}}}\\ {{P_{{\rm{op}}}} = {n_{{\rm{gd}}}}{P_{{\rm{dp}}, {\rm{gd}}}} = {Q_{{\rm{gd}}}}{W_{{\rm{pol}}}}}\\ {{\eta _{{\rm{gd}}}} = {A_{{\rm{gd}}}}{n_{{\rm{gd}}}} + {B_{{\rm{gd}}}}} \end{array}} \right. $ | (9) |
式中:Pop,Qgd,ngd,Pdp, gd,ηgd分别为燃驱压缩机的运行功率、消耗燃料量、工况、额定功率和效率,且ηgd与工况线性相关;Hmix为混合气体的热值;Agd,Bgd均为实际运行数据拟合的修正系数。
1.5 电解水制氢模型利用可再生能源的多余电力进行电解水制氢,制氢过程的数学描述为:
| $ {Q_{0, {{\rm{H}}_2}}} = \frac{{{W_{{\rm{pp}}}}{\eta _{{{\rm{H}}_2}}}}}{{{H_{{{\rm{H}}_2}}}}} $ | (10) |
式中:Q0, H2为氢气的标况体积流量;Wpp为可再生能源的富余电力;ηH2为制氢过程的效率;HH2为氢气体积热值。
1.6 氢气理想掺混模型电解水制得的氢气通过加压掺混进入天然气,掺混过程忽略能量损耗和温度变化,混合气体的物性参数计算如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{Q_{{\rm{mix }}}} = \left( {\frac{{{Q_{0, {\rm{ ng }}}}{\rho _{0, {\rm{ng}}}}}}{{{M_{{\rm{ng}}}}}} + \frac{{{Q_{0, {{\rm{H}}_2}}}{\rho _{0, {{\rm{H}}_2}}}}}{{{M_{{{\rm{H}}_2}}}}}} \right)\frac{{R{T_0}}}{P}}\\ {{Q_{0, {\rm{ mix }}}} = {Q_{{\rm{mix }}}}\frac{P}{{{P_0}}}}\\ {{\rho _{{\rm{mix }}}} = \frac{{{Q_{{\rm{ng}}}}{\rho _{0, {\rm{ng}}}} + {Q_{{{\rm{H}}_2}}}{\rho _{0, {{\rm{H}}_2}}}}}{{{Q_{{\rm{mix }}}}}}}\\ {\varepsilon = \frac{{{Q_{{{\rm{H}}_2}}}{\rho _{0, {{\rm{H}}_2}}}}}{{\frac{{{M_{{{\rm{H}}_2}}}}}{{{M_{{\rm{ng}}}}}}{Q_{{\rm{ng}}}}{\rho _{0, {\rm{ng}}}} + {Q_{{{\rm{H}}_2}}}{\rho _{0, {{\rm{H}}_2}}}}} \times 100\% }\\ {\varDelta = \frac{{{\rho _{{\rm{mix }}}}}}{{{\rho _{{\rm{air }}}}}}}\\ {{H_{{\rm{mix }}}} = {H_{{\rm{ng}}}}(1 - \varepsilon ) + {H_{{{\rm{H}}_2}}}\varepsilon } \end{array}} \right. $ | (11) |
式中:Q0, ng,ρ0, ng分别为天然气的标况体积流量和标况密度;Q0, H2,ρ0, H2分别为氢气的标况体积流量和标况密度;Qmix,ρmix,Q0, mix,Hmix分别为混合气体的体积流量、密度、标况体积流量和体积热值;Hng为天然气的体积热值;HH2为氢气的体积热值;R为气体常数;P为混合时的气体压力;ρair为空气密度。
1.7 本地储氢模型可再生能源多余电力进行电解水制氢后,与前文掺入天然气管网不同,考虑将氢气储存在储氢罐中,当电负荷需求较大时,通过燃烧储氢罐中的氢气进行发电,补充电网电力缺口。储氢罐t+1时刻储气量VP2G, t+1计算如下:
| $ {V_{{\rm{P}}2{\rm{G}}, t + 1}} = {V_{{\rm{P}}2{\rm{G}}, t}} - {V_{{\rm{d}}, t}} + {V_{{\rm{g}}, t}} $ | (12) |
式中:VP2G, t为t时刻的储气量;Vd, t,Vg, t分别为t时刻用氢量、加氢量,其计算见式(13)。
| $ \left\{ {\begin{array}{*{20}{l}} {{V_{\rm{d}}} = \frac{{{P_{\rm{d}}}\Delta t}}{{{\eta _{{\rm{ele}}}}{H_{{{\rm{H}}_2}}}}}}\\ {{V_{\rm{g}}} = \frac{{{P_{\rm{g}}}\Delta t{\eta _{{{\rm{H}}_2}}}}}{{{H_{{{\rm{H}}_2}}}}}} \end{array}} \right. $ | (13) |
式中:Pd为电力需求负荷;ηele为氢转化为电过程效率;Pg为富余可再生能源电力;Δt为时间间隔。
2 以经济性为目标的电-气综合能源系统协同优化 2.1 目标函数对电-气综合能源系统进行联合优化,以系统的净收益f作为目标函数,其表达式如下:
| $ f=E_{\mathrm{ele}}+E_{\mathrm{g}}-C_{\mathrm{ele}}-C_{\mathrm{g}} $ | (14) |
式中:Eele,Eg分别为电网和气网的总收益;Cele,Cg分别为电网和气网的成本,其计算见式(15)。
| $ \left\{ {\begin{array}{*{20}{l}} {{E_{{\rm{ele }}}} = \sum\limits_{i = 1}^{{n_{{\rm{ed }}}}} {{k_{\rm{e}}}} {P_{{\rm{d}}, i}}}\\ {{E_{\rm{g}}} = \sum\limits_{i = 1}^{{n_{{\rm{gd}}}}} {\left( {{E_{{\rm{ng}}}} + {L_{{\rm{trans }}, i}}{E_{{\rm{base }}}}} \right)} \frac{{{H_{{\rm{mix }}, i}}}}{{{H_{{{\rm{H}}_2}}}}}{Q_{{\rm{mix }}, i}}}\\ {{C_{{\rm{ele }}}} = {C_{{\rm{re}}}} + {C_{{\rm{nr}}}} = \sum\limits_{i = 1}^{{n_{{\rm{re }}}}} {\left[ {{P_{{\rm{re}}, i}}\left( {{a_{{\rm{re}}}}{P_{{\rm{re}}, i}} + {b_{{\rm{re }}}}} \right) + {d_{{\rm{re}}}}} \right]} + }\\ {\qquad \sum\limits_{i = 1}^{{n_{{\rm{nr}}}}} {\left[ {{P_{{\rm{nr}}, i}}\left( {{a_{{\rm{nr}}}}{P_{{\rm{nr}}, i}} + {b_{{\rm{nr}}}}} \right) + {d_{{\rm{nr}}}}} \right]} }\\ {{C_{\rm{g}}} = \sum\limits_{i = 1}^{{n_{{\rm{ef}}}}} {{h_{\rm{g}}}} \times {Q_{{\rm{f}}, i}}} \end{array}} \right. $ | (15) |
式中:ke为电的单位售价;ned,ngd,nre,nnr,nef分别为电用户、气用户、可再生能源发电、传统能源发电和气网进口的节点数;Eng,Ebase分别为天然气的基准售价和单位长度售价;Ltrans, i为气网入口到i节点的传输长度;Pd, i,Qmix, i分别为i节点的电负荷和气负荷;Cre,Cnr分别为可再生、不可再生能源发电的成本,Cre通过可再生能源发电有功功率Pre, i和其成本函数参数are,bre和dre进行计算,Cnr通过传统能源发电有功功率Pnr, i和其成本函数参数anr,bnr和dnr进行计算;hg为气源处天然气买入价格;Qf, i为买入天然气的量。
特别地,电网和气网的耦合节点收益和成本仅在电网侧或气网侧计算。电驱压缩机的成本由电网侧耗电电价计算,燃气电厂耗气成本体现在气网侧进口买气价格,掺氢收益在气网侧提供气用户混合气体时计算,储氢收益体现在电网侧卖电给电用户所获得的收益。
2.2 约束条件在实际电网中,发电站的有功功率Pi和无功功率Vi需满足以下不等式:
| $ \left\{ {\begin{array}{*{20}{l}} {P_i^{\min } < {P_i} < P_i^{\max }}\\ {V_i^{\min } < {V_i} < V_i^{\max }} \end{array}} \right. $ | (16) |
式中:Pimax,Pimin分别为有功功率上下限;Vimax,Vimin分别为无功功率上下限。
为了保证电网的安全稳定,节点电压幅值Ui必需保持相对稳定,其表达式如下:
| $ U_i^{\min } < {U_i} < U_i^{\max } $ | (17) |
式中:Uimax,Uimin分别为节点电压幅值的上下限。
可再生能源电站的有功功率分为两部分,电网提供电能的部分用Pele表示,用于制氢的部分用Pg表示,需满足以下不等式:
| $ P_{{\rm{re}}}^{\min } < {P_{\rm{g}}} + {P_{{\rm{ele}}}} < P_{{\rm{re}}}^{\max } $ | (18) |
式中:Premax,Premin分别为可再生能源发电有功功率的上下限。
由于可再生能源具有随机性和不稳定性,大量可再生能源接入电网会降低电网的稳定性和安全性,需要对接入电网的可再生能源有功功率进行约束:
| $ {P_{{\rm{ele }}}} < P_{{\rm{ele }}}^{\max } $ | (19) |
式中:Pelemax为接入电网的可再生能源有功功率的最大值。
在气网中,电驱压缩机功率Pmd和燃驱压缩机功率Fgd都存在上下限,其表达式如下:
| $ \left\{ {\begin{array}{*{20}{l}} {P_{{\rm{md}}}^{\min } < {P_{{\rm{md}}}} < P_{{\rm{md}}}^{\max }}\\ {F_{{\rm{gd}}}^{\min } < {F_{{\rm{gd}}}} < F_{{\rm{gd}}}^{\max }} \end{array}} \right. $ | (20) |
式中:Pmdmax,Pmdmin分别为电驱压缩机功率的上下限;Fgdmax,Fgdmin分别为燃驱压缩机功率的上下限。
由于氢气掺入天然气可能会造成氢脆等安全问题,在模型中需要对掺氢比ε的最大值进行约束:
| $ 0 < \varepsilon < {\varepsilon _{\max }} $ | (21) |
式中:εmax为最大掺氢比例。
在本地储氢模型中储氢量VP2G会受到储氢罐容量的约束,可以用以下不等式描述:
| $ 0<V_{\mathrm{P} 2 \mathrm{G}}<V_{\mathrm{P} 2 \mathrm{G}}^{\max } $ | (22) |
式中:VP2Gmax为储氢罐最大存储容量。
每个时间段的用氢量Vd和加氢量Vg会受到送气能力的限制,需要满足下列约束:
| $ \left\{ {\begin{array}{*{20}{l}} {V_{\rm{d}}^{\min } < {V_{\rm{d}}} < V_{\rm{d}}^{\max }}\\ {V_{\rm{g}}^{\min } < {V_{\rm{g}}} < V_{\rm{g}}^{\max }} \end{array}} \right. $ | (23) |
式中:Vdmax,Vdmin分别为每个时间段用氢量的上下限;Vgmax,Vgmin分别为加氢量的上下限。
3 算例分析 3.1 算例系统算例如图 2所示,为IEEE 39节点电网与华中地区部分天然气管网组成的综合能源系统。可再生能源发电包括风电、光伏和水电,其富余电力可通过电解水制氢掺入气网节点2、5和6与天然气进行掺混输运。气网时间尺度大,稳定时间长,因此假设气网需4 h达到稳定状态,全天分为6个时间段进行优化求解。为了客观评价气网掺混输运的电-气综合能源系统的经济性,设计如下场景进行研究。

|
图 2 算例综合能源系统示意 Fig. 2 Schematic diagram of integrated energy system diagram for the case |
场景1:不同最大掺氢比下,气网掺混氢气输运的电-气综合能源系统经济性优化。
场景2:不同储氢容量下,本地储氢的电-气综合能源系统经济性优化。
3.2 气网掺氢情况下的系统经济性优化由于不同地区管道能承受的最大掺氢比例不同,选取不同的掺氢比,分别为2%,4%,5%和6%,以经济性最优为目标对掺氢电-气综合能源系统进行日运行优化,并与不掺氢(储氢)情况进行对比。
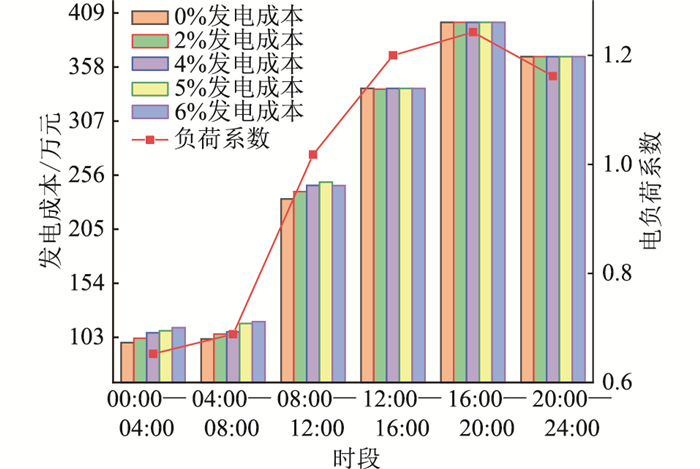
图 3为不同最大掺氢比下电网侧发电总成本及电负荷系数,电负荷系数为实时电负荷与日平均负荷的比值。由图 3可见,发电节点的发电成本与用户电负荷的整体趋势基本匹配,但在12:00-16:00和20:00-24:00,出现了电负荷与发电成本不匹配的情况。这是由于可再生能源发电成本远小于传统能源发电成本,12:00-16:00日照情况较好,可再生能源中发电量较大,而20:00-24:00只能用传统能源满足电负荷需求,因此下午时段的发电成本更低。对比不同最大掺氢比的情况,整体呈掺氢比越大,发电成本越高的趋势。这是由于高掺氢比需要更多可再生电力制氢,在电用户需求不变的情况下需要更多传统能源补足,因此发电成本提高。综上所述,掺氢会导致电网侧总体成本增加,掺氢比例越大,成本呈增大趋势。
|
图 3 不同最大掺氢比时的电网发电总成本与电负荷系数 Fig. 3 Total power generation cost and power load coefficient of the power grid with different maximum hydrogen blending ratio |
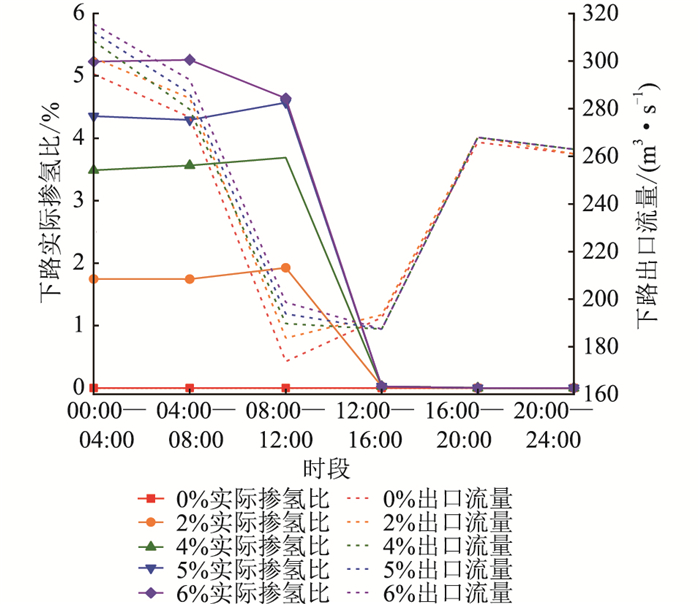
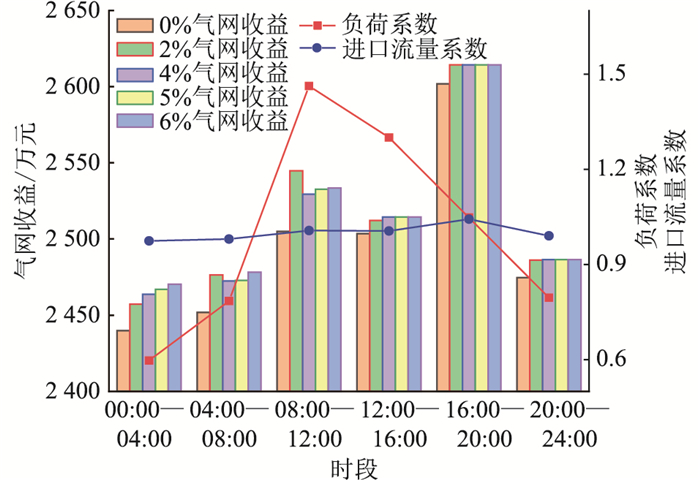
图 4为不同最大掺氢比时的气网下路掺氢比优化结果与出口流量,图 5为不同最大掺氢比时的气网净收益与气负荷及进口流量系数。由图 4和图 5可见,气网收益的整体趋势与出口流量一致,且与进口流量和负荷系数相关:当进口流量较大,负荷较小时,出口流量较大,因此气网收益更高。此外,掺氢比的优化结果表明,并非以最大比例掺氢时的经济性更佳,例如08:00-12:00,最大掺氢比为6%和5%情况中,实际掺氢比的优化结果均为4.5%左右,这是由于掺入更多氢气获得的气网卖气收益小于其导致的发电成本上升。
|
图 4 不同掺氢比时的气网下路实际掺氢比与出口流量 Fig. 4 Actual hydrogen blending ratio and flow rate of gas network lower line with different maximum hydrogen blending ratio |
|
图 5 不同最大掺氢比时的气网收益与气负荷、进口流量系数 Fig. 5 Total gas system net earnings and gas load, inlet flow rate coefficient of the power grid with different maximum hydrogen blending ratio |
表 1列举了不同最大掺氢比情况下的电-气综合能源系统总收益,可以看出掺氢能够提升系统经济性,日收益最高可提升0.6%。由表 1可知,考虑掺氢的电-气综合能源系统整体收益大于不掺氢系统,且在最大掺氢比为2%时,收益达到最大值。这是由于上路整体压力比下路高且掺氢均达到最大掺氢量,在掺氢比例较小时压降较小,节点2的压力较大,而下路实际掺氢量较小,压力差别不大。因此在最大掺氢比为2%时节点2-10的联络线流量较大,更多上路流量从下路出口进行卖气。而模型的单位卖气价格根据相应线路的管输长度进行定价,下路卖气价格高于上路,虽然最大掺氢比为2%时净收益最高,但并非最经济,其收益得益于气网结构和管输长度。
|
|
表 1 不同掺氢比的电-气综合能源系统总收益 Table 1 Total earnings of the integrated energy system with different maximum hydrogen blending ratio |
与3.2节中考虑改变掺氢比例类似,文中考虑改变本地储氢罐的容量(个数),分别设置1~6个储氢罐,每个储氢罐容积为13.9 m3,设计压力为3.2 MPa,正常工作压力在2.4~2.8 MPa之间。以经济性最优为目标,对P2G储氢的电-气综合能源系统进行优化。本地储氢不涉及气网内部输运变化,故气网的压力、流量分布与不掺氢的情况相同。
表 2列举了不同储氢容量时本地储氢电-气综合能源系统优化后的总收益。
|
|
表 2 不同储氢罐个数下电-气综合能源系统总收益 Table 2 Total earnings of integrated energy system with different numbers of hydrogen storage unit |
由表 2可知,本地储氢系统收益高于传统的电-气综合能源系统,但提升并不明显,日收益最高仅提升了0.06%,且该模型未考虑储氢罐的成本,因此总体经济性劣于气网掺氢的电-气综合能源系统。
4 结论文中利用P2G技术消纳富余可再生能源电力,提出了一种考虑可再生能源制氢与气网掺混输运的电-气综合能源系统,建立了以经济性最优为目标的系统运行优化模型,在不同最大掺氢比下进行气网掺氢系统的经济性优化,分析了不同最大掺氢比下的优化结果和收益情况。同时,将其与不同储氢容量的本地储氢系统优化结果进行对比,得到结论:(1)富余可再生能源发电制氢能有效缓解弃风弃光现象,将氢气掺入气网进行掺混运输和储入本地储氢罐均能提高系统经济性,且掺氢经济性更优。(2)在用户需求和进口参数不变的情况下,掺氢可提高气网侧卖气收益,但同时导致电网侧发电成本上升。在文中构建模型中,卖气定价与管输长度有关,实际运行中需综合考虑氢气定价策略与系统的气网结构选择最大掺氢比。(3)采用储氢罐进行本地储氢对经济性的整体优化效果不明显,增加储氢容量后收益并未增加,反而会增加采购成本,可以考虑本地储氢与气网掺混运输共同实施的策略,进一步提升系统的经济性。
文中假设系统在4 h内达到稳态,因气网的时间尺度大,在未来研究中,需对气网进行动态建模,从而研究其达到稳态过程中压力、流量和浓度扩散特性,以此保证优化结果更加符合实际情况。
| [1] |
代贤忠, 韩新阳, 董益华, 等. 能源互联网多源多层次协调优化方法研究[J]. 电力工程技术, 2019, 38(2): 1-9. DAI Xianzhong, HAN Xinyang, DONG Yihua, et al. Multi-source and multi-level coordination optimization method of energy internet[J]. Electric Power Engineering Technology, 2019, 38(2): 1-9. (  0) 0) |
| [2] |
国家能源局. 2019年风电并网运行情况[EB/OL]. [2020-07-31]. http://www.nea.gov.cn/2020-02/28/c_138827910.htm,2020/2/28. National Energy Administration. Grid-connected operation situation of photovoltaic power generation in 2019[EB/OL]. [2020-07-31]. http://www.nea.gov.cn/2020-02/28/c_138827910.htm,2020/2/28. (  0) 0) |
| [3] |
国家能源局. 2019年光伏发电并网运行情况[EB/OL]. [2020-07-31]. http://www.nea.gov.cn/2020-02/28/c_138827923.htm,2020/2/28. National Energy Administration. Grid-connected operation situation of wind power generationin 2019[EB/OL]. [2020-07-31]. http://www.nea.gov.cn/2020-02/28/c_138827923.htm,2020/2/28. (  0) 0) |
| [4] |
孟冰冰, 郭丰慧, 胡林献, 等. 考虑天然气-电力耦合的多能源系统风电消纳分析[J]. 电力工程技术, 2019, 38(6): 1-8. MENG Bingbing, GUO Fenghui, HU Linxian, et al. Wind abandonment analysis of multi-energy systems considering gas-electricity coupling[J]. Electric Power Engineering Technology, 2019, 38(6): 1-8. (  0) 0) |
| [5] |
黄琳妮, 郑宝敏, 殷林飞. 基于ADMM的电气综合能源系统多目标最优能量流分布式计算[J]. 广东电力, 2020, 33(10): 56-63. HUANG Linni, ZHENG Baomin, YIN Linfei. Multi-objective optimal energy flow distributed calculation of electric-gas integrated energy system based on ADMM[J]. Guangdong Electric Power, 2020, 33(10): 56-63. (  0) 0) |
| [6] |
王静, 徐箭, 廖思阳, 等. 计及新能源出力不确定性的电气综合能源系统协同优化[J]. 电力系统自动化, 2019, 43(15): 2-9. WANG Jing, XU Jian, LIAO Siyang, et al. Coordinated optimization of integrated electricity-gas energy system considering uncertainty of renewable energy output[J]. Automation of Electric Power Systems, 2019, 43(15): 2-9. (  0) 0) |
| [7] |
刘天琪, 曾红, 何川, 等. 考虑电转气设备和风电场协同扩建的气电互联综合能源系统规划[J]. 电力自动化设备, 2019, 39(8): 144-151. LIU Tianqi, ZENG Hong, HE Chuan, et al. Planning of integrated gas and electricity system considering coordinated expansion of power-to-gas facilities and wind farms[J]. Electric Power Automation Equipment, 2019, 39(8): 144-151. (  0) 0) |
| [8] |
周贤正, 郭创新, 陈玮, 等. 基于混合整数二阶锥的配电-气网联合规划[J]. 电力自动化设备, 2019, 39(6): 1-11. ZHOU Xianzheng, GUO Chuangxin, CHEN Wei, et al. Joint planning of electricity-gas distribution network based on mixed integer second-order cone programming[J]. Electric Power Automation Equipment, 2019, 39(6): 1-11. (  0) 0) |
| [9] |
周晟锐, 刘继春, 张浩禹, 等. 基于机会约束的多能源枢纽电气互联综合能源系统日前经济调度[J]. 现代电力, 2020, 37(2): 197-204. ZHOU Shengrui, LIU Jichun, ZHANG Haoyu, et al. Day-ahead economic dispatch for electricity-gas integrated energy system with multiple energy hubs based on chance constraints[J]. Modern Electric Power, 2020, 37(2): 197-204. (  0) 0) |
| [10] |
TALEBI A, SADEGHI-YAZDANKHAH A, MIRZAEI M A, et al. Co-optimization of electricity and natural gas networks considering AC constraints and natural gas storage[C]//2018 Smart Grid Conference (SGC). IEEE, 2018: 1-6.
(  0) 0) |
| [11] |
WEITONG Z, JIAN C, HONGKAI Z, et al. Optimal day-ahead scheduling of electricity and natural gas system at the distribution level considering uncertainty of natural gas load[C]//2017 IEEE Conference on Energy Internet and Energy System Integration (EI2). IEEE, 2017: 1-6.
(  0) 0) |
| [12] |
ZHOU D, MA S, HUANG D, et al. An operating state estimation model for integrated energy systems based on distributed solution[J]. Frontiers in Energy, 2020, 14(4): 1-16. DOI:10.1007/s11708-020-0687-y (  0) 0) |
| [13] |
MEYSAM Q, MUDITHA A, MODASSAR C, et al. Role of power-to-gas in an integrated gas and electricity system in Great Britain[J]. International Journal of Hydrogen Energy, 2015, 40(17): 5763-5775. (  0) 0) |
| [14] |
CLEGG S, MANCARELLA P. Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1234-1244. (  0) 0) |
| [15] |
张晓光, 叶茂, 雷马平. 风力发电产氢注入天然气管网仿真计算[J]. 天然气与石油, 2019, 37(5): 13-20. ZHANG Xiaoguang, YE Mao, LEI Maping. The simulation of natural gas networks under hydrogen injection from a wind farm[J]. Natural Gas and Oil, 2019, 37(5): 13-20. (  0) 0) |
| [16] |
黄明, 吴勇, 文习之, 等. 利用天然气管道掺混输送氢气的可行性分析[J]. 煤气与热力, 2013, 33(4): 39-42. HUANG Ming, WU Yong, WEN Xizhi, et al. Feasibility analysis of hydrogen transport in natural gas pipeline[J]. Gas and Heat, 2013, 33(4): 39-42. (  0) 0) |
| [17] |
SCHOUTEN J A, MICHELS J P J, ROSMALEN R J. Effect of H2-injection on the thermodynamicand transportation properties of natural gas[J]. International Journal of Hydrogen Energy, 2004, 29(11): 173-1180. (  0) 0) |
| [18] |
TABKHI F, AZZARO-PANTEL C, PIBOULEAU L, et al. A mathematical framework for modelling and evaluating natural gas pipeline networks under hydrogen injection[J]. International Journal of Hydrogen Energy, 2008, 33(21): 6222-6231. (  0) 0) |
| [19] |
ZHOU D, LI T, HUANG D, et al. The experiment study to assess the impact of hydrogen blended natural gas on the tensile properties and damage mechanism of X80 pipeline steel[J]. International Journal of Hydrogen Energy, 2020, 14(4): 801-806. (  0) 0) |
| [20] |
曾伟. 关于输气公式和水力摩阻系数公式的讨论[J]. 天然气工业, 1989, 9(5): 64-68. ZENG Wei. Discussion of gas transmission equation and friction drag coefficient calculation equation[J]. Natural Gas Industry, 1989, 9(5): 64-68. (  0) 0) |
| [21] |
田立楠. 纯气体、混合气体及液体粘度的计算[J]. 化肥设计, 1997, 35(6): 9-13, 3. TIAN Linan. Viscosity calculation of pure gas, gas mixture and liquid[J]. Chemical Fertilizer Design, 1997, 35(6): 9-13, 3. (  0) 0) |
 2021, Vol. 40
2021, Vol. 40


 严思韵(1997), 女, 硕士在读, 研究方向为综合能源系统建模与仿真(E-mail:
严思韵(1997), 女, 硕士在读, 研究方向为综合能源系统建模与仿真(E-mail: