文章编号: 2096-3203(2021)01-0050-08 中图分类号: TM73 文献标识码: A
2. 东南大学电气工程学院,江苏 南京 210096
自20世纪90年代电力行业解除管制后,国务院高度关注电力市场化改革,发布了《关于进一步深化电力体制改革的若干意见》[1],明确提出推进电价改革和完善市场化交易等举措。在持续推进电力市场改革的同时,热电联产(combined heat and power, CHP)系统基于高能源利用率的巨大优势,被广泛应用于我国北方冬季区域供暖系统[2-6]。芬兰和瑞典已完全开放供热市场,但面临着无法有效刺激投资和维护困难等问题[7]。
目前关于CHP系统的研究大多集中于政府管制下的系统优化运行方面[8-9],缺乏节点电价信息将难以判断电网投资的合理性[10]。现有节点电价计算方法主要有独立计算法和基于Lagrange乘子法。独立计算法包括潮流追踪法、邮票法、费用流法、兆瓦公里法等[10-13],通常在计算潮流分布后计算节点电价。基于Lagrange乘子法的计算方法通常将节点有功平衡约束对应的Lagrange乘子作为节点电价[14],可能出现对偶问题多解的情况,当约束较为复杂时,容易使乘子无法收敛。
我国目前供热定价机制弊端在于热价不能正确反映商品价值和供需的关系。节点热价的计算需遵守“谁受益,谁承担成本”的原则,应体现不同地点消费热能承担的成本差异。文献[15]在考虑热量传输损耗的前提下分析了节点边际热价分布规律。文献[16]使用潮流追踪法计算节点热价,但未考虑热力传输损耗对热价的影响。
近年来,Cournot博弈和Stackelberg博弈常被用来描述寡头垄断市场中理性竞争者的战略行为[17]。Cournot模型通常用于研究发电商的发电投标行为和市场力的大小[18-19];Stackelberg博弈通常用于一部分参与者(领导者)具有先发优势,能在博弈中占据先发有利地位,另一部分参与者(跟随着)须在领导者之后做出决策的情况[20]。文献[21]构建了含一个领导者、多个跟随者的Stackelberg模型,并给出了Stackelberg均衡解存在性的证明,但文中只涉及了电力商品的博弈且采用已知的实时电价。文献[22]基于Stackelberg模型构建了电力与热力的定价模型,但重点在供需博弈过程上,未考虑能源传输网络的拓扑结构。
综上所述,在市场体制下给出快速实用的节点能价计算方法,同时体现用户的需求响应,是文中重点关注的问题。为了高效快速地计算节点能价,文中构建了结构清晰的基于Stackelberg博弈模型的电热联合市场框架,提出求解市场出清的迭代算法,并给出了节点能价计算方法和用户热需求函数的修正方法。通过算例对文中方法的快速性和实用性进行验证。
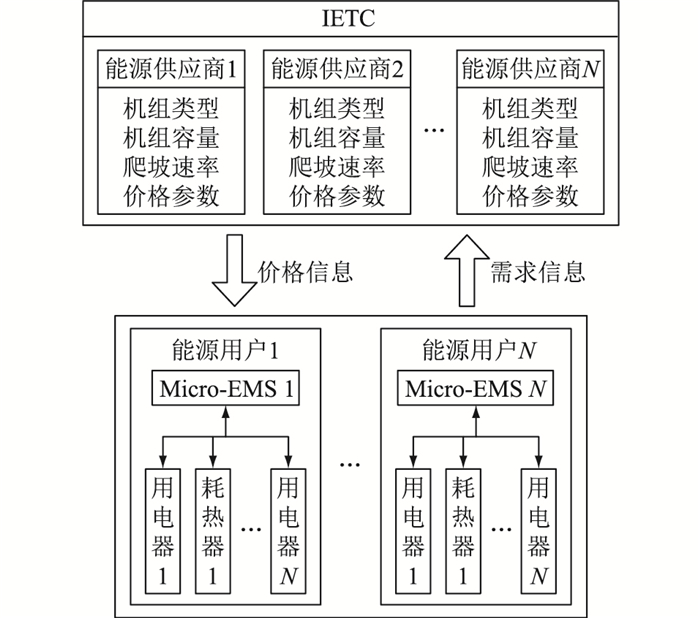
1 电热联合市场框架在传统的电力系统中,电热、电力的供需平衡通过发电侧的多级调度实现。随着CHP技术、智能电网和通信技术的融合发展,以智能电网为物理基础的混合需求响应逐渐加入到CHP系统供需调节体系之中。混合需求响应通过利用先进的控制和通信系统,实现市场参与者之间信息的快速交互,并根据实时能源价格信息制定能源消费计划。电力和热力领域存在较高的进入壁垒,故CHP市场是一个寡头垄断市场。为了充分体现市场环境下用户侧对需求和价格的影响,文中基于Stackelberg模型构建CHP市场主从博弈框架,如图 1所示。
|
图 1 CHP市场交易框架 Fig. 1 Trade framework of CHP market |
CHP市场的领导者是独立能源交易中心(independent energy trading center, IETC)。IETC负责收集能源供应商的基础信息(包括机组类型、机组容量、机组爬坡速率和价格参数等),并在确保系统安全稳定运行的前提下,合理安排机组出力。此外,IETC也负责计算节点能价(包括节点电价和节点热价),并将价格信息广播给所有用户。用户在市场中扮演跟随者角色,并都配备微型能量管理系统(micro energy management system, micro-EMS)。micro-EMS负责接收从IETC广播的价格信号,并根据价格安排用能计划,将需求发送给IETC。IETC汇总最新需求,重新计算能源价格和能源生产计划。将价格和需求经过多次迭代更新,最终得到稳定的市场均衡点。
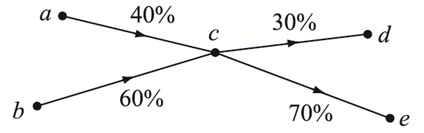
2 基于潮流追踪法的节点电价计算 2.1 潮流追踪法潮流追踪法基于比例共享原则[23],如图 2所示。图 2中,流入节点c的总功率为100 MW,并且由节点a,b流入的功率分别占40%,60%。若潮流Fcd为30 MW,则由节点a,b流入的功率分别为12 MW,18 MW。
|
图 2 比例共享原则 Fig. 2 Proportional sharing principle |
潮流追踪法在电网中主要用于计算潮流分布,确定发电机和负荷对线路潮流的贡献比例。潮流追踪法要求输入数据所有节点满足基尔霍夫电流定律。文中从实用角度出发,忽略直流潮流有功损耗,采用电网直流模型。将节点电价分为2个组成部分:边际发电成本和输电成本。
2.2 节点电价中的发电成本潮流跟踪法包括上游搜索算法和下游搜索算法[23]。文中采用上游搜索算法计算负荷从不同发电机处汲取的功率,可表示为:
| $ {\mathit{\boldsymbol{A}}_{{\rm{up}}}}\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{P}}_{\rm{G}}} $ | (1) |
式中:P=[P1, P2, …, PN]T为节点注入功率,N为网络节点数;PG=[PG1, PG2, …, PGN]T为发电机注入功率;Aup为上游分布矩阵,Aup中元素如式(2)所示。
| $ {\left( {{\mathit{\boldsymbol{A}}_{{\rm{up }}}}} \right)_{ij}} = \left\{ {\begin{array}{*{20}{l}} 1&{i = j}\\ - &{\left| {{F_{ji}}} \right|/{P_j}\quad j \in I_i^{{\rm{up }}}}\\ 0&{{\rm{其他}}} \end{array}} \right. $ | (2) |
式中:Fji为从节点j到节点i的有功功率;Pj为节点j的注入功率;Iiup为与节点i相连的上游节点的集合。
当Aup可逆时,(Aup-1)ji为节点i上的发电机对节点j流入功率的贡献比例,由此可计算节点j的节点电价中边际发电成本为:
| $ p_j^{{\rm{pcost }}} = \frac{1}{{{P_j}}}\sum\limits_{i = 1}^N {\left[ {{{\left( {\mathit{\boldsymbol{A}}_{{\rm{up }}}^{ - 1}} \right)}_{ji}}{P_{{\rm{G}}i}}{C_{{\rm{G}}i}}\left( {{P_{{\rm{G}}i}}} \right)} \right]} $ | (3) |
式中:CGi(PGi)为节点i上发电机组的有功出力为PGi时的边际成本。
2.3 节点电价中的输电成本采用下游搜索算法计算负荷对线路潮流的贡献率,可表示为:
| $ {\mathit{\boldsymbol{A}}_{{\rm{dn}}}}\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{P}}_{\rm{L}}} $ | (4) |
式中:PL=[PL1, PL2, …, PLN]T为节点负荷功率;Adn为下游分布矩阵,Adn中元素如式(5)所示。
| $ {\left( {{\mathit{\boldsymbol{A}}_{{\rm{dn}}}}} \right)_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1\quad i = j}\\ { - \left| {{F_{ij}}} \right|/{P_j}\quad j \in I_i^{{\rm{dn}}}}\\ {0\quad {\rm{ 其他 }}} \end{array}} \right. $ | (5) |
式中:Iidn为与节点i相连的下游节点的集合。
Aup,Adn的关系为:
| $ {\mathop{\rm diag}\nolimits} \left( {{P_1}, {P_2}, \cdots , {P_N}} \right) \cdot \mathit{\boldsymbol{A}}_{{\rm{up }}}^{\rm{T}} = {\mathit{\boldsymbol{A}}_{{\rm{dn}}}} \cdot {\mathop{\rm diag}\nolimits} \left( {{P_1}, {P_2}, \cdots , {P_N}} \right) $ | (6) |
由式(6)可知,Aup,Adn只要确定其中一个即可。
对于线路ij的潮流,有:
| $ {F_{ij}} = \frac{{{F_{ij}}}}{{{P_i}}}\sum\limits_{k = 1}^N {\left[ {{{\left( {\mathit{\boldsymbol{A}}_{{\rm{dn}}}^{ - 1}} \right)}_{ik}}{P_{{\rm{L}}k}}} \right]} $ | (7) |
式中:Fij(Adn-1)ik/Pi即为负荷PLk对潮流Fij的贡献因子。
由此可得到节点k的节点电价中输电成本为:
| $ p_k^{{\rm{ptrans }}} = \sum\limits_{ij \in {I^{\rm{L}}}} {\left[ {{F_{ij}}{C_{{\rm{T}}ij}}{{\left( {\mathit{\boldsymbol{A}}_{{\rm{dn}}}^{ - 1}} \right)}_{ik}}/{P_i}} \right]} $ | (8) |
式中:IL为所有线路ij的集合;CTij为线路ij的单位输电成本。
综上所述,节点k的节点电价可由式(3)和式(8)线性叠加,即:
| $ p_k^{{\rm{ptotal }}} = p_k^{{\rm{post }}} + p_k^{{\rm{prans }}} $ | (9) |
计算热网潮流与计算电网潮流最大的区别在于热网的汇流节点处潮流计算较为复杂,除了流量叠加外,热媒温度也会改变。为简化计算,文中假设热网将应用最为广泛的质调节作为调节方式,热媒的流量和方向均提前确定,假设汇流节点处的热媒可以充分混合,并迅速达到热平衡。此外,影响节点热价的主要因素有生产成本、循环水泵运行成本和热力传输损耗。生产成本、循环水泵运行成本与热价的单位相同,可直接相加构成热价。但热力传输损耗的单位与热价的单位不同,无法直接计入热价。文中在用户需求侧模型构建时将热力传输损耗计入用户总购热量,修正用户热需求响应函数。
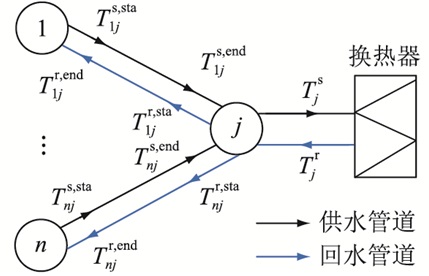
大部分热网处于单热源状态,随着供给侧开放和市场竞争机制的引入,更多的热源连接到热网,热网处于多热源模式。实际热网的物理限制比电网要大很多,一旦热媒的流量和方向确定,负荷分配就随之确定。文中主要讨论图 3所示的城市集中供热系统中供热管网汇流节点处的节点热价计算。
|
图 3 热水传输示意 Fig. 3 Schematic diagram of heat water transmission |
图 3中,节点j为汇流节点,汇流节点处若有负荷,则通过换热器传递热量。Tnjs, sta,Tnjs, end分别为供水管道nj始、末节点的热水温度;Tnjr, sta,Tnjr, end分别为回水管道nj始、末节点的热水温度;Tjs为供水管网中热水在节点j处充分混合后的温度;Tjr为经换热器后回水管网流向节点j的水温。在热网中可以直接测得热水温度,由热水温度变化计算热负荷的热量汲取因子DijF,即汇流节点j从i中汲取的热量占汲取总热量的百分数。
| $ D_{ij}^{\rm{F}} = \frac{{{m_{ij}}\left( {T_{ij}^{{\rm{s}}, {\rm{end}}} - T_{ij}^{{\rm{r}}, {\rm{sta}}}} \right)}}{{\sum\limits_{k \in Z(j)} {\left[ {{m_{kj}}\left( {T_{kj}^{{\rm{s}}, {\rm{end}}} - T_{kj}^{{\rm{r}}, {\rm{sta}}}} \right)} \right]} }} $ | (10) |
式中:mij为节点ij之间的质流量;Z(j)为与汇流节点j直接相连的节点集合;Tkjs, end,Tkjr, sta分别为供水管道kj的末端温度和回水管道kj的始端温度。
3.2 节点热价中的产热成本对于单一热源网络,各节点热价中边际产热成本相同。但2个以上热源同时向某一热负荷供热时,需要根据DijF对不同机组边际产热成本进行线性叠加。产热成本为:
| $ p_j^{{\rm{hcost}}} = \frac{1}{{{H_{{\rm{L}}j}}}}\sum\limits_{i \in Z(j)} {\left[ {D_{ij}^{\rm{F}}{C_{{\rm{H}}i}}\left( {{h_i}} \right){h_i}} \right]} $ | (11) |
式中:HLj为节点j处的热负荷;CHi(hi)为向节点i供热的热源出力为hi时的边际成本。
3.3 节点热价中的水泵运行成本循环水泵为管道中热水的流通提供动力,是热网运行费用中的主要组成部分,保证质调节热网中的热媒以恒定质流量流动。循环水泵的单位成本可用耗电输热比进行估计[12],节点热价中的循环水泵成本为:
| $ p_j^{{\rm{hpump }}} = \sum\limits_{i \in Z(j)} {\left[ {{C_{\rm{e}}}\left( {D_{ij}^{\rm{F}}\sum\limits_{k \in \theta (ij)} {E_k^{{\rm{HR}}}} } \right)} \right]} $ | (12) |
式中:Ce为循环水泵运行电费,该值可选择跟随某一节点电价变化,也可选择与电网签订长期双边合同,得到固定电价,文中算例将该值设为常数;θ(ij)为对管道ij的潮流存在贡献的所有上游水泵的集合;EkHR为第k个水泵的耗电输热比。
综上所述,考虑生产成本和循环水泵运行费用后,节点热价可表示为:
| $ p_j^{{\rm{htotal }}} = p_j^{{\rm{hcost }}} + p_j^{{\rm{hpump }}} $ | (13) |
文中选取单领导者多跟随者结构的主从博弈模型。IETC作为领导者在保证系统安全稳定运行的前提下,安排机组出力,负责将节点能价广播给所有用户。IETC的目标是使能源生产成本最小化,即:
| $ \min \sum\limits_{t \in \varGamma } {\left[ {\sum\limits_{i \in {S^{{\rm{TR}}}}} {C_i^{{\rm{ST}}}} \left( {{p_{i, t}}} \right) + \sum\limits_{i \in {C^{{\rm{TR}}}}} {C_i^{{\rm{CT}}}} \left( {{p_{i, t}}, {h_{i, t}}} \right)} \right]} $ | (14) |
| $ C_i^{{\rm{ST}}}\left( {{p_{i, t}}} \right) = a_i^{{\rm{st}}}p_{i, t}^2 + b_i^{{\rm{st}}}{p_{i, t}} + c_i^{{\rm{st}}}\quad \forall i \in {S^{{\rm{TR}}}} $ | (15) |
| $ \begin{array}{l} C_i^{{\rm{CT}}}\left( {{p_{i, t}}, {h_{i, t}}} \right) = a_{0, i}^{{\rm{ct}}} + a_{1, i}^{{\rm{ct}}}{p_{i, t}} + a_{2, i}^{{\rm{ct}}}{h_{i, t}} + a_{3, i}^{{\rm{ct}}}p_{i, t}^2 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{4, i}^{{\rm{ct}}}h_{i, t}^2 + a_{5, t}^{{\rm{ct}}}{p_{i, t}}{h_{i, t}}\quad \forall i \in {C^{{\rm{TR}}}} \end{array} $ | (16) |
式中:Γ为调度时间集;STR为常规纯凝机组集合;CTR为CHP机组集合;pi, t,hi, t为机组i在t时段内的电出力和热出力;aist,bist,cist为常规纯凝机组i的成本系数;a0, ict-a5, ict为CHP机组i的成本系数。
约束条件主要分为机组约束和系统安全约束。
(1) 机组约束。
| $ {{{\underline p }_i} \le {p_{i, t}} \le {{\bar p}_i}\quad i \in {S^{{\rm{TR}}}} \cup {C^{{\rm{TR}}}}} $ | (17) |
| $ {0 \le {h_{i, t}} \le {{\bar h}_i}\quad i \in {C^{{\rm{TR}}}}} $ | (18) |
| $ {\left| {{p_{i, t}} - {p_{i, t - 1}}} \right| \le {R_i}\Delta t\quad i \in {S^{{\rm{TR}}}} \cup {C^{{\rm{TR}}}}} $ | (19) |
| $ {{p_{i, t}} \le {{\bar p}_i} - {C_{i, 1}}{h_{i, t}}\quad i \in {C^{{\rm{TR}}}}} $ | (20) |
| $ {{p_{i, t}} \ge \max \left\{ {{C_{i, 2}}{h_{i, t}} + {C_{i, 3}}, {{\underline p }_i} - {C_{i, 4}}{h_{i, t}}} \right\}\quad i \in {C^{{\rm{TR}}}}} $ | (21) |
式中:
(2) 系统安全约束。
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i \in {S^{TR}} \cup {C^{{\rm{TR}}}}} {{p_i}} = \sum\limits_{i = 1}^N {{P_{{\rm{L}}i}}} }\\ {\sum\limits_{i \in {C^{{\rm{TR}}}}} {{h_i}} = \sum\limits_{i = 1}^{{H^{\rm{N}}}} {{H_{{\rm{L}}i}}} } \end{array}} \right. $ | (22) |
| $ \sum\limits_{i \in {S^{{\rm{TR}}}} \cup {C^{{\rm{TR}}}}} {\min } \left\{ {{p_{i, t}} - {{\bar p}_i}, \Delta t{R_i}} \right\} \ge {R^{{\rm{up}}}} $ | (23) |
| $ \sum\limits_{i \in {S^{{\rm{TR}}}} \cup {C^{{\rm{TR}}}}} {\min } \left\{ {{p_{i, t}} - {{\underline p }_i}, \Delta t{R_i}} \right\} \ge {R^{{\rm{down }}}} $ | (24) |
| $ \left| {\sum\limits_{i = 1}^N {S_{ki}^{\rm{F}}} \left( {{P_{{\rm{G}}i}} - {P_{{\rm{L}}i}}} \right)} \right| \le F_k^{\max }\quad \forall k \in {N^{\rm{L}}} $ | (25) |
式中:HN为热网节点数量;Rup,Rdown分别为系统需要的向上、向下旋转储备容量;SkiF为节点i的净功率对第k条线上的功率传输分布因子(power transmission distribution factors, PTDF);NL为线路集合;Fkmax为支路k的功率上限。
4.2 用户需求侧模型用户根据最新的能源价格更新自身购能计划。在微观经济学中,效用是对商品偏好的测量,表示消耗商品给消费者带来的满意度。通常用二次函数描述用户效用。
| $ \begin{array}{*{20}{c}} {{W_i}\left( {D_i^{\rm{p}}, D_i^{\rm{h}}} \right) = \beta _i^{\rm{p}}D_i^{\rm{p}} + \beta _i^{\rm{h}}D_i^{\rm{h}} - \left[ {{\alpha ^{\rm{p}}}{{\left( {D_i^{\rm{p}}} \right)}^2}/2} \right] - }\\ {\left[ {{\alpha ^{\rm{h}}}{{\left( {D_i^{\rm{h}}} \right)}^2}/2} \right]\quad \forall i \in C_k^{\rm{N}}} \end{array} $ | (26) |
式中:Dip,Dih分别为用户i消耗的电量和热量;αp,αh,βip,βih为调节用户满意度的参数;CkN为在负荷节点k处的用户集合。
用户的收益Ui可定义为用户效用与购能费用之差。
| $ \begin{array}{*{20}{c}} {{U_i}\left( {D_i^{\rm{p}}, D_i^{\rm{h}}} \right) = {W_i}\left( {D_i^{\rm{p}}, D_i^{\rm{h}}} \right) - p_i^{{\rm{ptotal }}}D_i^{\rm{p}} - }\\ {p_i^{{\rm{hotal }}}D_i^{\rm{h}}\quad \forall i \in C_k^{\rm{N}}} \end{array} $ | (27) |
对式(27)分别求关于Dip和Dih的偏导,并将其累加后可得:
| $ \sum\limits_{i \in Z(k)} {D_i^{\rm{p}}} = \frac{1}{{{\alpha ^{\rm{p}}}}}\left( {\sum\limits_{i \in C_k^{\rm{N}}} {\beta _i^{\rm{p}}} - {N_k}p_i^{{\rm{ptotal }}}} \right) $ | (28) |
| $ \sum\limits_{i \in Z(k)} {D_i^{\rm{h}}} = \frac{1}{{{\alpha ^{\rm{h}}}}}\left( {\sum\limits_{i \in C_k^{\rm{N}}} {\beta _i^{\rm{h}}} - {N_k}p_i^{{\rm{hotal }}}} \right) $ | (29) |
式中:Nk为集合CkN中的元素个数。
式(28)、式(29)即为在某一负荷节点处的用户需求对能源价格的最优反应方程。文中采用直流模型,忽略传输过程中的有功损耗。但热媒在管道中流动不可避免会产生热量损失,导致管道首、末处的温度不同。对于稳态的热力网络,可采用苏霍夫温降式(30)计算管道末端温度。
| $ {T^{{\rm{end }}}} = {T^{{\rm{sta }}}}{{\rm{e}}^{ - 2{\rm{ \mathsf{ π} }}l/\left( {\gamma q\sum R } \right)}} + \left[ {1 - {{\rm{e}}^{ - 2{\rm{ \mathsf{ π} }}l/\left( {\gamma q\sum R } \right)}}} \right]{T_{\rm{e}}} $ | (30) |
式中:Tsta,Tend分别为管道首、末端的热媒温度;l为管段长度;k为比例常数;γ=cρ,c为热媒比热容,ρ为热媒密度;q为热媒流量;∑R为热媒到周围介质间每千米管道的总热阻。
计算管道ij在单个调度时间内的热量损耗为:
| $ Q_{ij}^{{\rm{loss}}} = c{m_{ij}}\left( {T_{ij}^{{\rm{sta}}} - T_{ij}^{{\rm{end}}}} \right)\Delta t $ | (31) |
当一段管道同时为多个负荷传输热量时,可以根据前述比例共享原则对总热损耗进行线性划分。进而对负荷节点k的最优反应函数式(29)进行修正。
| $ \sum\limits_{ij \in {H^{\rm{P}}}(k)} {P_{ij, k}^{{\rm{rop}}}} Q_{ij}^{{\rm{loss}}} + \sum\limits_{i \in Z(k)} {D_i^{\rm{h}}} = \frac{1}{{{\alpha ^{\rm{h}}}}}\left( {\sum\limits_{i \in Z(k)} {\beta _i^{\rm{h}}} - {N_k}p_i^{{\rm{htotal}}}} \right) $ | (32) |
式中:HP(k)为将热水传输至节点k经过的所有管段的集合;Pij, krop为运输到节点k的热量占管段ij传输总热量的百分比。
综上,根据式(28)、式(32)得到节点k处的用户对电力、热力的需求曲线。
4.3 模型的迭代求解过程在计算节点电价时,需要对Aup和Adn求逆,故价格计算不适合放入优化问题中,而应在优化问题求解完毕后进行单独计算。为此,文中采用迭代求解方式,将机组优化调度、节点能价计算和用户需求响应分开计算。当需求不再发生明显变化时,即可判断算法收敛。具体步骤为:
(1) 设置基础参数。例如发电机参数、初始负荷、单位输电成本、循环水泵耗电输热比、合同电价、热源出口温度等。
(2) 求解能源供应商侧的优化问题。
| $ \left\{ {\begin{array}{*{20}{l}} {\min }&{{\rm{ 式 }}(14)}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}}&{{\rm{ 式 }}(17){\rm{ —式}}(25)} \end{array}} \right. $ | (33) |
(3) 根据式(1)-式(9)计算节点电价,根据式(10)-式(13)计算节点热价。
(4) 由式(28)、式(32)计算用户需求曲线,并根据最新的节点能价计算能源需求量。
(5) 判断用户需求量变化是否小于某一限值。若是,则停止迭代;否则,更新负荷,进入步骤(2)。
文中方法可以观测每次迭代中节点能价的变化,清晰展现用户对价格的敏感度。步骤(2)中的优化问题是二次规划问题,求解方法也较为成熟,相较于将节点能价与机组出力联合求解的方法,文中方法计算速度较快,且保证了模型的可求解性。
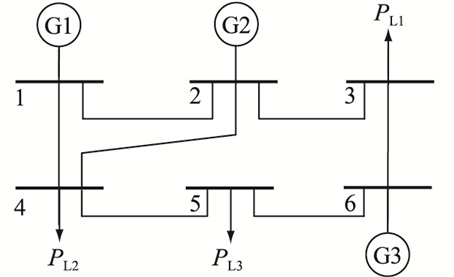
5 算例分析6节点电网模型和8节点热网模型分别如图 4、图 5所示。图 4中,G1和G2均为CHP机组,G3为常规纯凝机组。调度时间间隔Δt为1 h。电网、热网具体参数分别如表 1、表 2所示。
|
图 4 6节点电网模型 Fig. 4 Model of 6-bus power system |
|
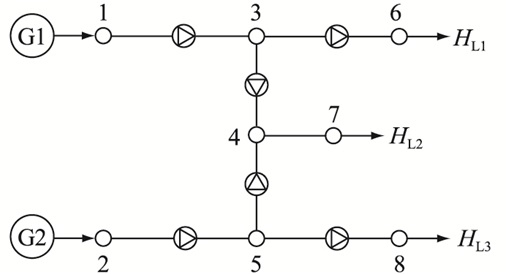
图 5 8节点热网模型 Fig. 5 Model of 8-node heat supply network |
|
|
表 1 电网参数 Table 1 Parameters of power system |
|
|
表 2 热网参数 Table 2 Parameters of heat supply network |
以1号节点为松弛节点,计算电网的PTDF矩阵。假设初始电力需求PL1为40 MW,PL2为80 MW,PL3为80 MW;初始热力需求HL1为20 MW,HL2为50 MW,HL3为50 MW;每条线路的单位输电成本均为10美元/(MW ·h)。根据4.3节中的步骤(2)求解得到优化后的机组出力,根据PTDF计算系统直流潮流。节点注入功率P=[116.8, 99.6, 44.2, 117.6, 80.0, 42.4]T;发电机注入功率PG=[116.8, 45.0, 0, 0, 0, 38.2]T;发电机边际成本CG=[114.2, 118.9, 0, 0, 0, 114.2]T。根据式(2)计算得到上游分布矩阵,随后求其逆矩阵Aup-1。
| $ A_{{\rm{up}}}^{ - 1} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0\\ {0.467{\kern 1pt} {\kern 1pt} 8}&1&0&0&0&0\\ {0.207{\kern 1pt} {\kern 1pt} 8}&{0.444{\kern 1pt} {\kern 1pt} 1}&1&0&0&0\\ {0.792{\kern 1pt} {\kern 1pt} 2}&{0.555{\kern 1pt} {\kern 1pt} {\kern 1pt} 9}&0&1&0&0\\ {0.273{\kern 1pt} {\kern 1pt} 2}&{0.220{\kern 1pt} {\kern 1pt} 4}&{0.096{\kern 1pt} {\kern 1pt} {\kern 1pt} 3}&{0.319{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}&1&1\\ {0.020{\kern 1pt} {\kern 1pt} 0}&{0.042{\kern 1pt} {\kern 1pt} {\kern 1pt} 8}&{0.096{\kern 1pt} {\kern 1pt} {\kern 1pt} 3}&0&0&1 \end{array}} \right] $ | (34) |
以电网3号节点为例,其节点电价为:
| $ \begin{array}{*{20}{c}} {p_3^{{\rm{pcost }}} = \frac{1}{{{P_3}}}\sum\limits_{i = 1}^6 {\left[ {{{\left( {\mathit{\boldsymbol{A}}_{{\rm{up }}}^{ - 1}} \right)}_{3, {\rm{i}}}}{P_{{\rm{G}}i}}{C_{{\rm{G}}i}}} \right]} = }\\ {116.3{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{美元 }}/({\rm{MW}} \cdot {\rm{h}})} \end{array} $ | (35) |
同理得到4号、5号节点电价中的边际成本p4pcost,p5pcost分别为115.2美元/(MW ·h),114.8美元/(MW ·h)。应用式(6)计算Adn-1。
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{A}}_{{\rm{dn}}}^{ - 1} = \\ \left[ {\begin{array}{*{20}{c}} 1&{0.548{\kern 1pt} {\kern 1pt} {\kern 1pt} 2}&{0.548{\kern 1pt} {\kern 1pt} {\kern 1pt} 2}&{0.787{\kern 1pt} {\kern 1pt} {\kern 1pt} 1}&{0.398{\kern 1pt} {\kern 1pt} {\kern 1pt} 8}&{0.055{\kern 1pt} {\kern 1pt} {\kern 1pt} 1}\\ 0&1&1&{0.471{\kern 1pt} {\kern 1pt} {\kern 1pt} 2}&{0.274{\kern 1pt} {\kern 1pt} {\kern 1pt} 6}&{0.100{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}\\ 0&0&1&0&{0.053{\kern 1pt} {\kern 1pt} {\kern 1pt} 3}&{0.100{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}\\ 0&0&0&1&{0.469{\kern 1pt} {\kern 1pt} {\kern 1pt} 6}&0\\ 0&0&0&0&1&0\\ 0&0&0&0&{0.530{\kern 1pt} {\kern 1pt} 4}&1 \end{array}} \right] \end{array} $ | (36) |
根据式(8)计算得到3~5号节点电价的输电成本p3ptrans,p4ptrans,p5ptrans分别为16.4美元/(MW ·h),15.8美元/(MW ·h),13.6美元/(MW ·h)。将节点电价的两部分叠加即可得到3~5号节点电价分别为132.7美元/(MW ·h),131美元/(MW ·h),128.4美元/(MW ·h)。
进而计算节点热价,热网采用质调节方法,流量已提前确定,m34=m54=300 kg/s,根据式(10)计算得到热量汲取因子D34F=D54F=0.5。6号节点的热源只有G1,8号节点的热源只有G2,故其节点热价计算较为方便。文中假设循环水泵的合同电价为90美元/(MW ·h)。
| $ {p_6^{{\rm{htotal }}} = {C_{{\rm{Hl}}}}\left( {{h_1}} \right) + {C_{\rm{e}}}\left( {E_1^{{\rm{HR}}} + E_3^{{\rm{HR}}}} \right)} $ | (37) |
| $ {p_8^{{\rm{hotal }}} = {C_{{\rm{H}}2}}\left( {{h_2}} \right) + {C_{\rm{e}}}\left( {E_4^{{\rm{HR}}} + E_6^{{\rm{HR}}}} \right)} $ | (38) |
为了方便表示汇流节点的出水温度,设立7号节点,7号节点的热源是G1和G2。4号与7号节点之间并无距离,两者的节点热价相同。
| $ \begin{array}{*{20}{c}} {p_4^{{\rm{htotal }}} = p_7^{{\rm{htotal }}} = \left[ {D_{34}^{\rm{F}}{C_{{\rm{Hl}}}}\left( {{h_1}} \right) + D_{54}^{\rm{F}}{C_{{\rm{H}}2}}\left( {{h_2}} \right)} \right] + }\\ {{C_{\rm{e}}}D_{34}^{\rm{F}}\left( {E_1^{{\rm{HR}}} + E_2^{{\rm{HR}}}} \right) + {C_{\rm{e}}}D_{54}^{\rm{F}}\left( {E_4^{{\rm{HR}}} + E_5^{{\rm{HR}}}} \right)} \end{array} $ | (39) |
文中计算可得节点热价p6htotal,p7htotal,p8htotal分别为18.2美元/ (MW ·h),18.6美元/(MW ·h),19.0美元/(MW ·h)。由式(28)、式(29)可知,用户需求函数本质上是向下倾斜的需求曲线,假设
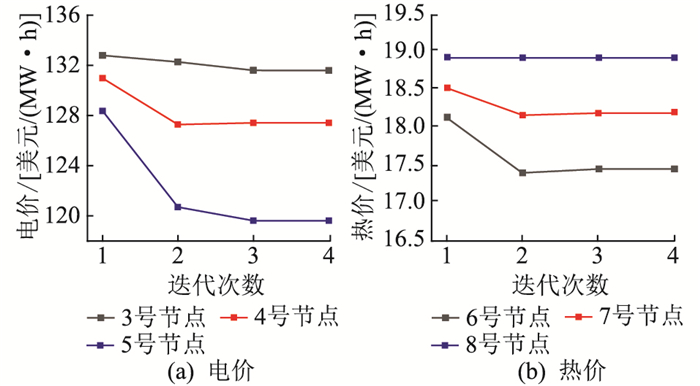
主从博弈模型迭代至收敛的价格变化过程如图 6所示,电、热出力和相应负荷变化分别如表 3、表 4所示,整个博弈过程在迭代4次后收敛。
|
图 6 节点能价变化 Fig. 6 Variation of nodal energy price |
|
|
表 3 电出力与电负荷变化 Table 3 Variation of power generation and demand |
|
|
表 4 热出力与热负荷变化 Table 4 Variation of heat generation and demand |
由图 6、表 3和表 4可知,所提迭代算法在4次迭代后收敛,收敛性较强。
6 结语文中以Stackelberg博弈模型为基础,构建了结构清晰的电热联合市场框架,并基于比例共享原则给出了节点能价的计算方法,使节点的价格信息不仅可反映成本,还可合理反映负荷对传输网络的利用率,充分体现了传输过程对能源价格的影响,以价格信号引导投资规划。文中采用迭代方法求解博弈问题,将优化问题、需求响应和节点能价的计算分开执行,使整个博弈出清过程更加清晰。与基于乘子法的电力定价方法相比,所提方法不受模型复杂度限制,无需求解复杂优化问题获取对偶乘子。相较于传统的仅基于制热成本的定价方式,所提方法将传输损耗和热泵运行成本计入定价,定价方法更加合理。
本文得到国网江苏省电力有限公司科技项目(SGJS0000DKWT2000198)资助,谨此致谢!
| [1] |
中共中央国务院.关于进一步深化电力体制改革的若干意见[EB/OL]. [2020-06-01]. http://www.cec.org.cn/zhuanti/2015nianzhuanti/2015dianlitizhigaigezaichufa/yaowen/2015-06-18/139371.html. General Office of the Communist Party of China. Several opinions on further deepening power system reform[EB/OL]. [2020-06-01]. http://www.cec.org.cn/zhuanti/2015nianzhuanti/2015dianlitizhigaigezaichufa/yaowen/2015-06-18/139371.html. (  0) 0) |
| [2] |
GU W, WANG J, LU S, et al. Optimal operation for integrated energy system considering thermal inertia of district heating network and buildings[J]. Applied Energy, 2017, 199: 234-246. (  0) 0) |
| [3] |
王培汀, 雷杨, 孟政吉. 考虑能源站非线性效率系数的电热综合能源系统运行分析[J]. 广东电力, 2019, 32(10): 12-19. WANG Peiting, LEI Yang, MENG Zhengji. Operation analysis of electric heating integrated energy system considering nonlinear efficiency coefficient of energy station[J]. Guangdong Electric Power, 2019, 32(10): 12-19. (  0) 0) |
| [4] |
邓莉荣, 孙宏斌, 陈润泽, 等. 面向能源互联网的热电联供系统节点能价研究[J]. 中国电机工程学报, 2016, 40(11): 3375-3382. DENG Lirong, SUN Hongbin, CHEN Runze, et al. Research on nodal energy price of combined heat and power system for energy internet[J]. Proceedings of the CSEE, 2016, 40(11): 3375-3382. (  0) 0) |
| [5] |
谭碧飞, 陈皓勇, 梁子鹏, 等. 基于CoPSO-BAS的冷热电联供型微网经济调度[J]. 广东电力, 2019, 32(9): 85-93. TAN Bifei, CHEN Haoyong, LIANG Zipeng, et al. Economic dispatch of CCHP micro-grid based on CoPSO-BAS[J]. Guangdong Electric Power, 2019, 32(9): 85-93. (  0) 0) |
| [6] |
邹泽宇, 刘文泽, 蔡泽祥. 基于增广ε-约束法的冷热电联供系统容量优化配置[J]. 广东电力, 2019, 32(10): 36-44. ZOU Zeyu, LIU Wenze, CAI Zexiang. Research oncapacity optimization configuration of CCHP system based on augmented ε-constraint method[J]. Guangdong Electric Power, 2019, 32(10): 36-44. (  0) 0) |
| [7] |
DIFS K, TRYGG L. Pricing district heating by marginal cost[J]. Energy Policy, 2009, 37(2): 606-616. (  0) 0) |
| [8] |
GU W, WANG Z, WU Z, et al. An online optimal dispatch schedule for CCHP microgrids based on model predictive control[J]. IEEE Transactions on Smart Grid, 2017, 8(5): 2332-2342. (  0) 0) |
| [9] |
顾伟, 陆帅, 王珺, 等. 多区域综合能源系统热网建模及系统优化运行[J]. 中国电机工程学报, 2017, 37(5): 1305-1315. GU Wei, LU Shuai, WANG Jun, et al. Modeling of the heating network for multi-district integrated energy system and its operation optimization[J]. Proceedings of the CSEE, 2017, 37(5): 1305-1315. (  0) 0) |
| [10] |
陈典, 钟海旺, 夏清. 基于全成本电价的安全约束经济调度[J]. 中国电机工程学报, 2015, 36(5): 1190-1199. CHEN Dian, ZHONG Haiwang, XIA Qing. Security constrained economic dispatch based on total cost price[J]. Proceedings of the CSEE, 2015, 36(5): 1190-1199. (  0) 0) |
| [11] |
HAPP H H. Cost of wheeling methodologies[J]. IEEE Transactions on Power System, 1994, 9(1): 147-156. (  0) 0) |
| [12] |
言茂松, 辛洁晴. 在电力市场环境下网嵌入的边际成本输电定价新方法[J]. 中国电机工程学报, 1998, 18(2): 111-116. YAN Maosong, XIN Jieqing. Grid embedded marginal-cost transmission pricing(GEMP) in power market[J]. Proceedings of the CSEE, 1998, 18(2): 111-116. (  0) 0) |
| [13] |
穆钢, 王华伟, 韩学山. 基于费用流法的输电网节点电力成本分析[J]. 中国电机工程学报, 2002, 22(12): 36-40. MU Gang, WANG Huawei, HAN Xueshan. Determining bus electricity cost of transmission system by the cost flow method[J]. Proceedings of the CSEE, 2002, 22(12): 36-40. (  0) 0) |
| [14] |
曹佳, 马洪艳, 刘扬, 等. 基于节点电价的需求响应策略研究[J]. 电网技术, 2016, 40(5): 1536-1542. CAO Jia, MA Hongyan, LIU Yang, et al. Research on demand response strategy based on nodal price[J]. Power System Technology, 2016, 40(5): 1536-1542. (  0) 0) |
| [15] |
方宇娟, 魏韡, 梅生伟, 等. 考虑节点边际价格的热电联产机组主从博弈竞价策略[J]. 控制理论与应用, 2018, 35(5): 682-687. FANG Yujuan, WEI Wei, MEI Shengwei, et al. Stackelberg game strategy for combined heat power unit considering locational marginal prices[J]. Control Theory & Applications, 2018, 35(5): 682-687. (  0) 0) |
| [16] |
PA NG, GU W, WU Z, et al. Optimal design and operation of multi-energy system with load aggregator considering nodal energy prices[J]. Applied Energy, 2019, 239: 280-295. (  0) 0) |
| [17] |
WU C, GU W, BO R, et al. A two-stage game theory model for combined heat and power trading market[J]. IEEE Transactions on Power system, 2019, 34(1): 506-517. (  0) 0) |
| [18] |
OTERO-NOVA I, MESEGUER C, BATTLE C, et al. A simulation model for a competitive generation market[J]. IEEE Transactions on Power system, 2000, 15(1): 250-256. (  0) 0) |
| [19] |
HELMAN U, HOBBS B F. Large-scale market power modeling:Analysis of the U.S. eastern interaction and regulation applications[J]. IEEE Transactions on Power system, 2010, 25(3): 1434-1448. (  0) 0) |
| [20] |
MAHARJAN S, ZHU Q, ZHANG Y, et al. Dependable demand response management in the smart grid:a Stackelberg game approach[J]. IEEE Transactions on Smart Grid, 2013, 4(1): 120-132. (  0) 0) |
| [21] |
YU M, HONG S H. A real-time demand-response algorithm for smart grids:a Stackelberg game approach[J]. IEEE Transactions on Smart Grid, 2013, 7(2): 879-888. (  0) 0) |
| [22] |
LIU N, HE L, YU X, et al. Multiparty energy management for grid-connected microgrids with heat-and electricity-coupled demand response[J]. IEEE Transactions on Industrial Informatics, 2018, 14(5): 1887-1897. (  0) 0) |
| [23] |
BIALEK J. Topological generation and load distribution factors for supplement charge allocation in transmission open access[J]. IEEE Transactions on Power Systems, 1997, 12(3): 1185-1193. (  0) 0) |
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2021, Vol. 40
2021, Vol. 40


 雷震(1979),男,硕士,高级工程师,从事新能源、分布式电源调度运行管理相关工作(E-mail:
雷震(1979),男,硕士,高级工程师,从事新能源、分布式电源调度运行管理相关工作(E-mail: