文章编号: 2096-3203(2021)01-0188-07 中图分类号: TM464 文献标识码: A
2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103
双馈风机(doubly-fed induction generator-based wind turbine, DFIG-WT)通过控制转子侧变换器(rotor-side converter, RSC)和网侧变换器(grid-side converter, GSC)实现变速恒频运行和风能最大功率跟踪[1-3]。变换器故障是DFIG-WT的常见故障,占比达25%[4],而开路故障是电力电子开关管的主要故障类型,故国内外学者针对变换器开路故障展开了大量研究。
研究人员基于变换器模型设计状态观测器[5-6]或提取特征参数[7-8],实现三相变换器单个和双个开关管的故障诊断。国内外学者采用快速傅里叶变换[9]、小波分析[10]、帕克变换[11]等信号处理算法,从风机输出的电压、电流、转速等测量信号中提取故障特征信息,检测并识别变换器的开路故障。但上述模型驱动和信号驱动算法,依赖于模型或者信号模式等先验知识,当DFIG-WT系统运行点变化以及故障类型复杂时,诊断逻辑的设计变得极其困难。而数据驱动方法只需要大量的历史数据,通过人工智能算法从历史数据中提取出故障特征,能够实现多类型复杂故障的识别与分类。
研究人员采用贝叶斯网络[12]、人工神经网络[13]、模糊逻辑[14]分别对永磁同步电机逆变器、全功率变换器、光伏逆变器的开路故障进行诊断。但上述数据驱动方法的故障特征提取和模式识别能力不足,都需要对信号进行预处理,选择对故障敏感的信号进行分析,提取特征量,降低了信息的完整性,不是一种完全数据驱动法,且算法的数据处理能力有限,最终的故障诊断结果准确性不高。此外,上述研究单独考虑GSC或RSC,而没有考虑2个变换器同时故障的相互影响,未能全面系统地考虑DFIG-WT系统的多类型开关开路故障。
针对目前研究的不足,提出了一种基于深度置信网络(deep belief network, DBN)的完全数据驱动的故障诊断方法,应用于DFIG-WT的RSC和GSC开关管开路故障诊断。通过仿真测试与比较,验证了该开路故障诊断算法的有效性和优越性。
1 DFIG-WT系统模型与变换器故障 1.1 系统模型DFIG-WT整体结构如图 1所示,系统由风机叶片、齿轮箱、双馈感应发电机DFIG、GSC和RSC组成,风机的定子和电网连接,转子通过RSC和GSC与电网交换功率。GSC包括6个电力电子IGBT开关器件T1, T2, …, T6,RSC包括6个开关T7, T8, …, T12。其中,vsa, vsb, vsc,isa, isb, isc分别为定子三相电压和定子三相电流;vra, vrb, vrc,ira, irb, irc分别为转子三相电压和转子三相电流;vga, vgb, vgc,iga, igb, igc分别为网侧三相电压和网侧三相电流;vdc为直流电容电压。

|
图 1 双馈风机系统结构 Fig. 1 Structure of DFIG-WT system |
在同步旋转dq轴下,双馈感应发电机DFIG的磁链表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _{{\rm{s}}d}} = {L_{\rm{s}}}{i_{{\rm{s}}d}} + {L_{\rm{m}}}{i_{{\rm{r}}d}}}\\ {{\lambda _{{\rm{s}}q}} = {L_{\rm{s}}}{i_{{\rm{s}}q}} + {L_{\rm{m}}}{i_{{\rm{r}}q}}} \end{array}} \right. $ | (1) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda _{{\rm{r}}d}} = {L_{\rm{r}}}{i_{{\rm{r}}d}} + {L_{\rm{m}}}{i_{{\rm{s}}d}}}\\ {{\lambda _{{\rm{r}}q}} = {L_{\rm{r}}}{i_{{\rm{r}}q}} + {L_{\rm{m}}}{i_{{\rm{s}}q}}} \end{array}} \right. $ | (2) |
磁链动态方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot \lambda }_{{\rm{s}}d}} = {R_{\rm{s}}}{i_{{\rm{s}}d}} - {\omega _{\rm{s}}}{\lambda _{{\rm{s}}q}} - {v_{{\rm{s}}d}}}\\ {{{\dot \lambda }_{{\rm{s}}q}} = {R_{\rm{s}}}{i_{{\rm{s}}q}} + {\omega _{\rm{s}}}{\lambda _{{\rm{s}}d}} - {v_{{\rm{s}}q}}} \end{array}} \right. $ | (3) |
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot \lambda }_{{\rm{r}}d}} = {R_{\rm{r}}}{i_{{\rm{r}}d}} - {\omega _{{\rm{sl}}}}{\lambda _{{\rm{r}}q}} - {v_{{\rm{r}}d}}}\\ {{{\dot \lambda }_{{\rm{r}}q}} = {R_{\rm{r}}}{i_{{\rm{r}}q}} + {\omega _{{\rm{sl}}}}{\lambda _{{\rm{r}}d}} - {v_{{\rm{r}}q}}} \end{array}} \right. $ | (4) |
式中:λsd, λsq分别为定子磁链dq轴分量;λrd, λrq分别为转子磁链dq轴分量;vsd, vsq分别为定子电压dq轴分量;vrd, vrq分别为转子电压dq轴分量;isd, isq分别为定子电压dq轴分量;ird, irq分别为转子电流dq轴分量;Rs,Rr分别为定子、转子电阻;Ls,Lls,Lr,Llr,Lm分别为定子自电感、定子漏电感、转子自电感、转子漏电感、互电感,且Ls=Lls+Lm, Lr=Llr+Lm;ωs,ωr,ωsl分别为同步转速、转子转速、转速差,且ωsl=ωs-ωr。
DFIG-WT的机械传动系统采用单质量块模型:
| $ 2H{\dot \omega _{\rm{r}}} = {T_{\rm{m}}} - {T_{\rm{e}}} - D{\omega _{\rm{r}}} $ | (5) |
式中:H为惯性常数;D为阻尼系数;Tm为机械转矩;Te为电磁转矩。
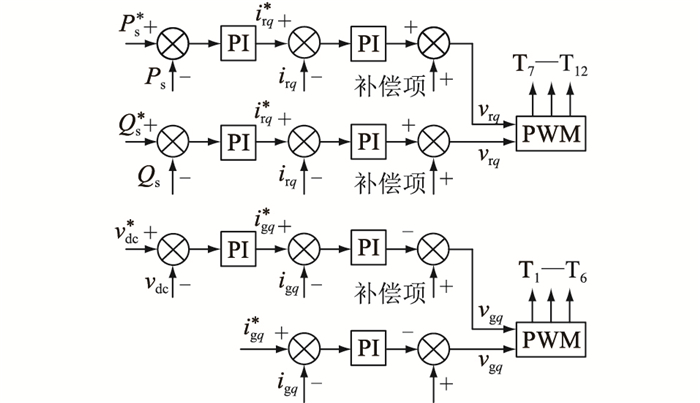
1.2 矢量控制DFIG-WT采用经典的基于比例积分(proportional-integral, PI)的双闭环矢量控制策略,如图 2所示。
|
图 2 双馈风机矢量控制策略 Fig. 2 Vector control scheme for DFIG-WT |
GSC采用电网电压定向,控制器包括网侧电流内环和直流电压外环,通过控制网侧电流dq轴分量igd, igq,将直流电压vdc和网侧电压igq分别调节至参考值vdc*和igq*,网侧电压dq轴分量vgd, vgq用于生成PWM信号驱动IGBT开关T1, T2, …, T6。RSC采用定子电压定向,控制器包括转子电流内环和定子功率外环,电流内环控制器包括PI调节器和补偿项,功率外环产生转子电流参考值ird*, irq*,通过控制转子电流ird, irq实现定子有功功率Ps和定子无功功率Qs的解耦控制,转子电压vrd, vrq经过调制模块产生PWM信号驱动开关T7, T8, …, T12。
1.3 变换器故障类型开路和短路是2种常见的变换器开关器件故障类型,由于短路故障会触发保护装置,导致变换器立刻关断,故只考虑开路故障。以GSC的a相桥臂为例,开关管T1, T2开路故障如图 3所示。g1, g2分别为开关T1, T2的驱动信号,idc为直流电流。定义开关状态为S,则开关管的正常运行状态为:当S=1时,g1=1, g2=0,T1导通,T2关断,此时vga=vdc, idc=iga;当S=0时,g1=0, g2=1,T1关断,T2导通,此时vga=0, idc=0,故存在以下关系:
| $ \left\{ {\begin{array}{*{20}{l}} {{v_{{\rm{ga}}}} = S{v_{{\rm{dc}}}}}\\ {{i_{{\rm{dc}}}} = S{i_{{\rm{ga}}}}} \end{array}} \right. $ | (6) |

|
图 3 GSC开关开路故障示意 Fig. 3 Schematic diagram of open-switch faults on GSC |
由图 3可以看出,在g1=1, g2=0的驱动信号下,当开关管T1开路时,若网侧电流iga>0,有vga=0, idc=0,即开关状态S由正常值1变化为故障值0。同时,在g1=0, g2=1的驱动信号下,当开关管T2开路故障时,若网侧电流iga < 0,有vga=vdc, idc=iga,即开关状态S由正常值0变化为故障值1时。根据上述分析,当开关管T1或T2发生开路故障时,会导致开关状态由正常值变为故障值。由式(6)可知,开关状态S的变化影响网侧电流iga的输出,并进一步导致b相和c相网侧电流的畸变。同理,转子侧变换器开关开路故障也影响转子三相电流的输出。
考虑GSC和RSC总共12个IGBT器件的单开关和双开关故障,统计可得78种故障类型f1, f2, …, f78,正常状态记为f79,详细描述见表 1。
|
|
表 1 双馈风机变换器故障类型 Table 1 Fault types of DFIG-WT converters |
GSC的开关开路故障直接影响网侧三相电流iga, igb, igc的变化,而RSC的开关开路故障影响转子三相电流ira, irb, irc的响应。因此,选择网侧电流iga, igb, igc和转子电流ira, irb, irc作为故障诊断网络的输入信号。定义一维向量表示每个电流传感器的采样数据,表达式为:
| $ {\mathit{\boldsymbol{X}}_i} = \left[ {{x_i}(1),{x_i}(2), \cdots ,{x_i}(n)} \right] $ | (7) |
式中:i=1, 2, …, 6,分别为iga, igb, igc, ira, irb, irc总计6种电流采样信号;n为数据长度。原始采样数据经过归一化后得到
| $ \mathit{\boldsymbol{X}} = {\left[ {\mathit{\boldsymbol{X}}_1^\dagger ,\mathit{\boldsymbol{X}}_2^\dagger , \cdots ,\mathit{\boldsymbol{X}}_6^\dagger } \right]^{\rm{T}}} $ | (8) |
使用滑动窗口从数据X中提取出m个数据集作为训练样本,定义样本对应的标签为Y =[Y1, Y2, …, Ym]T,其中Yi(i=1, 2, …, m)对应变换器开关开路故障类型fi,取值为1到79。因此,故障诊断网络的数据集可表示为D(X, Y)。
2.2 深度置信网络DBN采用分层结构,包括输入层、隐藏层和输出层,是一种完全数据驱动的机器学习算法。其具有优异的特征学习和数据处理能力,能实现多种复杂故障的识别和分类,包括齿轮箱机械故障[15]、汽轮机传感器故障[16]及配电网故障[17]。
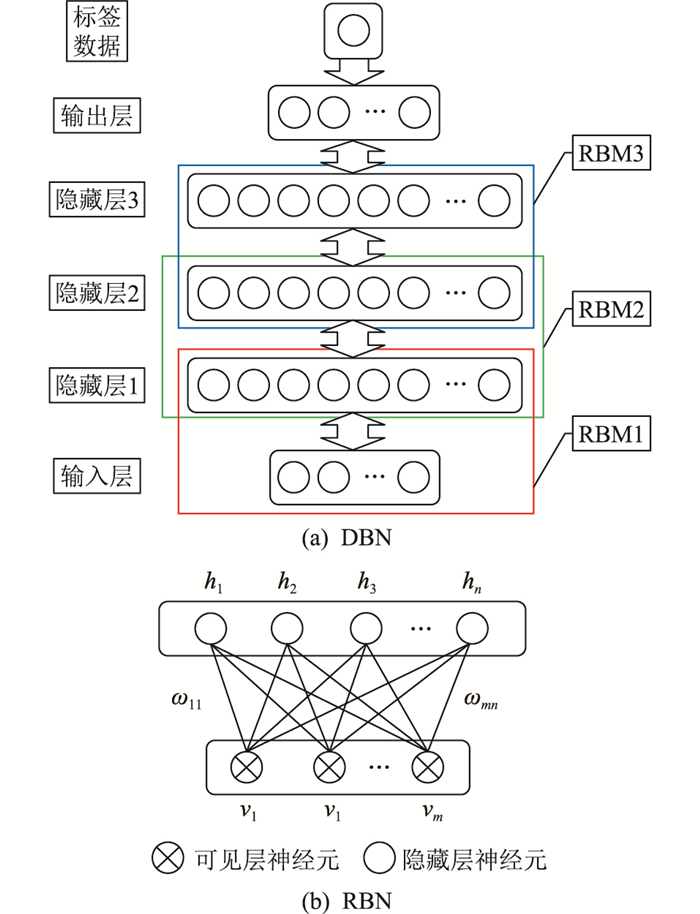
DBN由多个受限玻尔兹曼机(restricted Boltzmann machine, RBM)堆叠组合而成,结构如图 4(a)所示。受限玻尔兹曼机RBM是一个2层神经网络,结构如图 4(b)所示,包括可见层和隐藏层,可见层神经元和隐藏层神经元的联合组态能量函数定义见式(9)。
| $ E(\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}}) = - \sum\limits_{i = 1}^m {{a_i}} {v_i} - \sum\limits_{j = 1}^n {{b_j}} {h_j} - \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{v_j}} } {w_{ij}}{h_j} $ | (9) |
|
图 4 DBN和RBM的结构 Fig. 4 Structure of DBN and RBM |
式中:v =(vi), i=1, 2, …, m,为可见向量;h =(hj), j=1, 2, …, n,为隐藏向量;权重矩阵W =(wij)表示第j个隐藏层神经元和第i个可见层神经元之间的联系。向量A =(ai)和B =(bj)分别为可见层神经元和隐藏层神经元的偏置权重。
在一般的玻尔兹曼机中,隐藏向量和可见向量的概率分布为:
| $ {P(\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}}) = \frac{1}{\varLambda }{{\rm{e}}^{ - E(\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}})}}} $ | (10) |
| $ {\varLambda = \sum\limits_{v,h} {{{\rm{e}}^{ - E(\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}})}}} } $ | (11) |
式中:Λ为归一化因子,保证概率之和为1。可见向量的概率是所有可能的隐藏层组态的总和,即:
| $ P(\mathit{\boldsymbol{v}}) = \frac{1}{\Lambda }\sum\limits_{j = 1}^n {{{\rm{e}}^{ - E\left( {v,{h_j}} \right)}}} $ | (12) |
由于RBM没有层内连接,隐藏层和可见层的各个神经元之间相互独立,故条件概率可表示为:
| $ P(\mathit{\boldsymbol{v}}\mid \mathit{\boldsymbol{h}}) = \prod\limits_{i = 1}^m P \left( {{v_i}\mid \mathit{\boldsymbol{h}}} \right) $ | (13) |
| $ P(\mathit{\boldsymbol{h}}\mid \mathit{\boldsymbol{v}}) = \prod\limits_{i = 1}^n P \left( {{h_i}\mid \mathit{\boldsymbol{v}}} \right) $ | (14) |
而隐藏层和可见层神经元的激活概率分别为:
| $ P\left( {{h_j} = 1\mid \mathit{\boldsymbol{v}}} \right) = \sigma \left( {{b_j} + \sum\limits_{i = 1}^m {{w_{ij}}} {v_i}} \right) $ | (15) |
| $ P\left( {{v_i} = 1\mid \mathit{\boldsymbol{h}}} \right) = \sigma \left( {{a_j} + \sum\limits_{j = 1}^n {{w_{ij}}} {h_i}} \right) $ | (16) |
式中:σ(x)=(1+e-x)-1,为Logistic函数。
可知,概率P(v)是分配给可见层神经元v的概率。故目标函数是负对数似然函数,表达式为:
| $ L(\mathit{\boldsymbol{\theta }},D) = - \sum\limits_{\mathit{\boldsymbol{v}} \in D} {\log } P(\mathit{\boldsymbol{v}},\mathit{\boldsymbol{\theta }}) $ | (17) |
式中:θ =(A, B, W);D为数据集。通过估计优化参数来训练RBM,使得负对数似然函数L (θ, D)最小化,采用经典的对比散度算法进行训练[18]。
2.3 故障诊断网络使用逻辑回归(logistic regression,LR)作为DBN的顶层输出层,同时也作为故障诊断的决策方法。LR是一个概率类型的线性分类器,通过Softmax函数实现数据的分类,故障的概率密度分布为:
| $ {p_i} = {{\rm{e}}^{{S_i}}}/\sum\limits_{k = 1}^{79} {{{\rm{e}}^{{S_k}}}} $ | (18) |
式中:pi为开关故障类型fi发生的概率,i=1, 2, …, 79;Sk为隐藏层输出量。因此,故障诊断结果为:
| $ P = {\mathop{\rm argmax}\nolimits} \left( {{p_1},{p_2}, \cdots ,{p_{79}}} \right) $ | (19) |
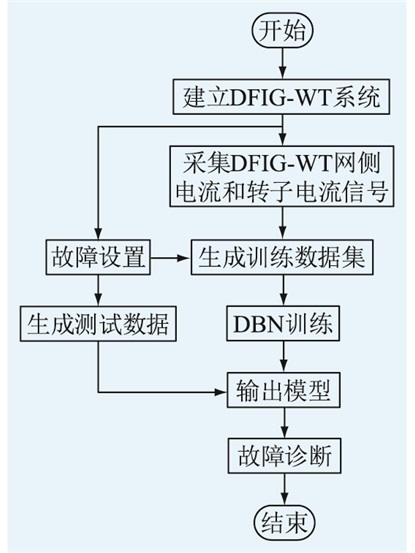
综合以上分析,基于DBN的故障诊断方法如图 5所示。首先,建立DFIG-WT系统的详细模型,设置各种类型的变换器开关开路故障,采集网侧电流和转子电流信号进行预处理,生成训练数据集和测试数据集。训练数据集用于对DBN进行训练,得到网络的输出模型并对测试数据进行分类,输出最终的故障诊断结果。
|
图 5 基于DBN的故障诊断方法 Fig. 5 DBN based fault diagnosis method |
在Matlab/Simulink中搭建图 1所示系统,采用图 2所示的矢量控制方法控制GSC和RSC,DFIG-WT系统的参数见表 2。风机的额定风速为11 m/s,设置初始风速为vw=15 m/s,使得DFIG-WT处在额定运行工况。此外,DFIG-WT的运行参考值为无功功率Qs*=0 p.u.,直流电容电压vdc*=1 150 V,q轴网侧电流igq*=0 p.u.。
|
|
表 2 双馈风机参数 Table 2 Parameters of DFIG-WT |
设计图 4所示的DBN,包括3层隐藏层,每层隐藏层由1 500个神经元组成。设置风速在6 m/s(切入风速)到20 m/s(切出风速)之间变化,同时在双馈风机系统中设置表 1中的78种变换器开关故障状态和正常工作状态,以0.9 kHz的采样频率进行采样,总共得到79 000组数据,数据长度为150。在79 000组数据中随机抽取70 000组作为训练数据,剩下的9 000组作为测试数据。
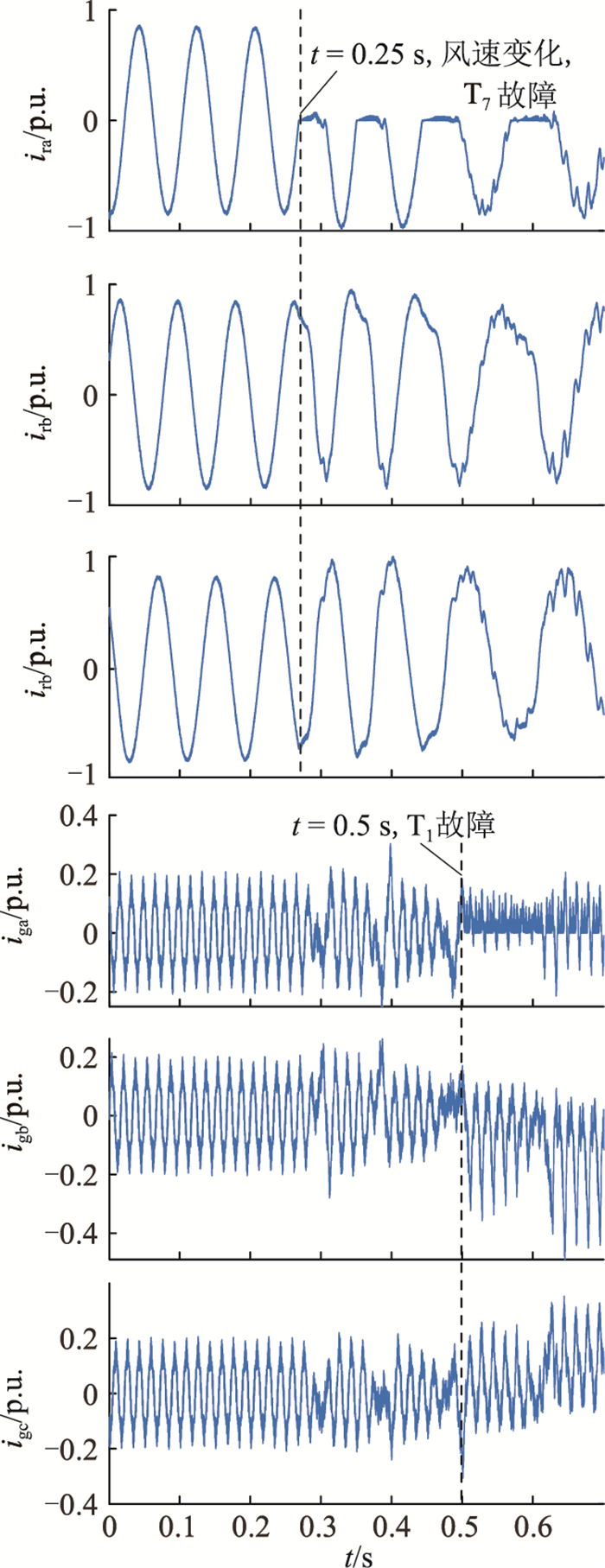
3.2 变换器开路故障特征以GSC的开关T1和RSC的开关T7发生故障为例,仿真结果如图 6所示。在t=0.25 s时,风速从15 m/s阶跃变化为10 m/s,同时设置RSC的开关T7故障。由图 6可见,三相转子电流ira, irb, irc的频率和幅值都随风速变化而发生变化,开关T7故障后a相转子电流ira的上半波被削去,且T7故障导致转子电流irb, irc畸变和网侧电流iga, igb, igc发生波动。在t=0.5 s时,GSC的开关T1发生故障,削去了a相网侧电流的一半波形,并进一步加剧了转子电流ira, irb, irc的畸变和网侧电流igb, igc的波动。
|
图 6 开关T1和T7开路故障仿真波形 Fig. 6 Current waveforms obtained under open-switch faults of T1 and T7 |
针对表 1中的变换器开关开路故障,采用DBN网络进行诊断。进行100次仿真后,计算出准确度Prec(取值0~1,越高越好)、漏检率Reca(取值0~1,越高越好)和综合性能F1(同时考虑准确度和漏检率,取值0~1,越高越好)作为算法的评价指标[19]。将DBN与人工神经网络(back propagation artificial neural network, BPANN)、最小二乘-支持向量机(least-squares support vector machine, LS-SVM)等数据类方法进行对比,3种方法对于部分故障类型的诊断结果见表 3,加粗部分表示3种方法中性能指标的最好结果。
|
|
表 3 故障诊断结果 Table 3 Fault diagnosis results |
从表 3中可以看出,对于GSC的开关T1开路故障,DBN的准确度Prec,漏检率Reca和综合性能F1指标均为1,能够做到对该类型故障的完全精确识别,算法的性能优于BPANN和LS-SVM。其次,对于GSC的开关T1和T4同时故障,DBN的综合性能指标F1=0.93,高于BPANN算法的F1=0.89和LS-SVM算法的F1=0.91。
此外,对于GSC开关T4和RSC开关T10同时故障,由于GSC和RSC的相互影响,故障信号特征复杂,导致BPANN的综合指标F1=0.90和LS-SVM算法的综合指标F1=0.80较低。而DBN算法的深度结构能够提取该类型故障下的特征信息,故障诊断的性能指标值高达F1=0.97,远优于另外2种算法。最后,BPANN、LS-SVM、DBN故障诊断的综合性能指标F1的平均值分别为0.93,0.88,0.96。结果表明,与BPANN、LS-SVM算法相比,DBN算法在绝大部分故障情形下,都具有更好的综合诊断性能。综合以上分析可知,DBN对于双馈风机变换器的单个和双个开关管开路故障的诊断性能都优于BPANN和LS-SVM算法。
4 结语文中基于DBN提出了一种适用于DFIG-WT系统RSC和GSC的电力电子开关管开路的故障诊断方法。
仿真结果表明,DFIG-WT的RSC和GSC开路故障相互影响,导致故障特征复杂,且故障下DFIG-WT输出信号都受风速变化影响。其次,DBN网络采用了多层的RBM,能够提取变换器开关各种故障信号的深度信息,用于DFIG-WT的RSC和GSC单个和双个开关管的复杂故障识别和分类。最后,对于DFIG-WT在风速变化下的单个和双个开关管开路故障,文中所提基于DBN的故障诊断方法,与传统的BPANN和LS-SVM方法相比,具有更高的准确度和更优的诊断性能。
| [1] |
赵洪山, 程亮亮. 基于双线性观测器的双馈风电机组变流器功率管开路故障诊断[J]. 电力自动化设备, 2017, 37(3): 72-79. ZHAO Hongshan, CHENG Liangliang. Open-circuit fault diagnosis based on bilinear observer for converter power-switch of doubly-fed wind turbine[J]. Electric Power Automation Equipment, 2017, 37(3): 72-79. (  0) 0) |
| [2] |
靳现林, 蔡晓宇, 刘其辉, 等. 一种考虑RSC和GSC的双馈风机短路电流实用计算方法[J]. 电力系统保护与控制, 2019, 47(24): 23-30. JIN Xianlin, CAI Xiaoyu, LIU Qihui, et al. A practical calculation method for short-circuit current of DFIG considering RSC and GSC[J]. Power System Protection and Control, 2019, 47(24): 23-30. (  0) 0) |
| [3] |
于淼, 汤亚芳, 黄亦欣, 等. 双馈风机控制方式对继电保护影响的研究[J]. 电力系统保护与控制, 2020, 48(2): 180-187. YU Miao, TANG Yafang, HUANG Yixin, et al. Research on the influence of control mode of DFIG on relay protection[J]. Power System Protection and Control, 2020, 48(2): 180-187. (  0) 0) |
| [4] |
RIBRANT J, BERTLING L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005[J]. IEEE Transactions on Energy Conversion, 2007, 22(1): 167-173. DOI:10.1109/TEC.2006.889614 (  0) 0) |
| [5] |
CAMPOS-DELGADO D U, ESPINOZA-TREJO D R. An observer-based diagnosis scheme for single and simultaneous open-switch faults in induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 671-679. DOI:10.1109/TIE.2010.2047829 (  0) 0) |
| [6] |
ESPINOZA-TREJO D R, CAMPOS-DELGADO D U, BOSSIO G, et al. Fault diagnosis scheme for open-circuit faults in field-oriented control induction motor drives[J]. IET Power Electronics, 2013, 6(5): 869-877. DOI:10.1049/iet-pel.2012.0256 (  0) 0) |
| [7] |
POON J, JAIN P, KONSTANTAKOPOULOS I C, et al. Model-based fault detection and identification for switching power converters[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1419-1430. DOI:10.1109/TPEL.2016.2541342 (  0) 0) |
| [8] |
JUNG S M, PARK J S, KIM H W, et al. An MRAS-based diagnosis of open-circuit fault in PWM voltage-source inverters for PM synchronous motor drive systems[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2514-2526. DOI:10.1109/TPEL.2012.2212916 (  0) 0) |
| [9] |
GAN C, WU J, YANG S, et al. Fault diagnosis scheme for open-circuit faults in switchedreluctance motor drives using fast Fourier transform algorithm with bus current detection[J]. IET Power Electronics, 2016, 9(1): 20-30. DOI:10.1049/iet-pel.2014.0945 (  0) 0) |
| [10] |
沈艳霞, 周文晶, 纪志成, 等. 基于小波包分析的风力发电系统中变流器的故障识别[J]. 电网技术, 2013, 37(7): 2011-2017. SHEN Yanxia, ZHOU Wenjing, JI Zhicheng, et al. Fault identification of converter used in wind power generation based on wavelet packet analysis[J]. Power System Technology, 2013, 37(7): 2011-2017. (  0) 0) |
| [11] |
黄科元, 刘静佳, 黄守道, 等. 永磁直驱系统变流器开路故障诊断方法[J]. 电工技术学报, 2013, 37(7): 2011-2017. HUANG Keyuan, LIU Jingjia, HUANG Shoudao, et al. Converters open-circuit fault-diagnosis methods research for direct-driven permanent magnet wind power system[J]. Transactions of China Electrotechnical Society, 2013, 37(7): 2011-2017. (  0) 0) |
| [12] |
DUAN P, XIE K, ZHANG L, et al. Open-switch fault diagnosis and system reconfiguration of doubly fed wind power converter used in a microgrid[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 816-821. DOI:10.1109/TPEL.2010.2095470 (  0) 0) |
| [13] |
张海霞, 谭阳红, 周野. 风力发电系统变流器故障诊断[J]. 电机与控制学报, 2015, 19(9): 89-94. ZHANG Haixia, TAN Yanghong, ZHOU Ye. Fault diagnoses of converter in wind turbine system[J]. Electric Machines and Control, 2015, 19(9): 89-94. (  0) 0) |
| [14] |
CHEN W, BAZZI A M. Logic-based methods for intelligent fault diagnosis and recovery in power electronics[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5573-5589. DOI:10.1109/TPEL.2016.2606435 (  0) 0) |
| [15] |
CHEN Z, LI C, SANCHEZ R V. Multi-layer neural network with deep belief network for gearbox fault diagnosis[J]. Journal of Vibro-engineering, 2015, 17(5): 2379-2392. (  0) 0) |
| [16] |
FENG D, XIAO M, LIU Y, et al. Finite-sensor fault-diagnosis simulation study of gas turbine engine using information entropy and deep belief networks[J]. Frontiers of Information Technology & Electronic Engineering, 2016, 17(12): 1287-1304. (  0) 0) |
| [17] |
姜有泉, 黄良, 王波, 等. 基于DGA和深度置信网络的变压器内部故障诊断[J]. 武汉大学学报(工学版), 2017, 50(5): 749-753. JIANG Youquan, HUANG Liang, WANG Bo, et al. Transformer internal fault diagnosis based on DGA and deep belief network[J]. Engineering Journal of Wuahn University, 2017, 50(5): 749-753. (  0) 0) |
| [18] |
徐春华, 陈克绪, 马建, 等. 基于深度置信网络的电力负荷识别[J]. 电工技术学报, 2019, 34(19): 4135-4142. XU Chunhua, CHEN Kexu, MA Jian, et al. Recognition of power loads based on deep belief network[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4135-4142. (  0) 0) |
| [19] |
ODGAARD P F, STOUSTRUP J. A benchmark evaluation of fault tolerant wind turbine control concepts[J]. IEEE Transac- tions on Control Systems Technology, 2014, 23(3): 1221-1228. (  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd. Research Institute, Nanjing 211103, China
 2021, Vol. 40
2021, Vol. 40



 夏候凯顺(1991),男,博士,助理研究员,研究方向为新能源发电系统故障诊断与容错控制(E-mail:
夏候凯顺(1991),男,博士,助理研究员,研究方向为新能源发电系统故障诊断与容错控制(E-mail: