文章编号: 2096-3203(2021)01-0079-07 中图分类号: TM714 文献标识码: A
2. 可再生能源发电与并网技术 教育部工程研究中心(新疆大学),新疆维吾尔自治区 乌鲁木齐 830047
随着能源危机和环境污染的加剧,大规模新能源并网成为必然趋势。然而风电等新能源发电固有的随机波动性导致灵活性需求剧增,消纳难度大[1-3]。光热发电作为除光伏发电外另一种太阳能发电技术,拥有良好的可控性和调节特性,未来将发挥支撑高比例可再生能源并网的重要作用[4-6]。
含储热的光热电站能将接收到的太阳能以热能形式储存起来,实现出力灵活可控,使得大规模光热发电并网成为可能。2025年全球光热发电装机容量将达到22 GW,2050年光热发电将满足全球11.3%的电量需求[7]。我国也将逐步在甘肃、青海等地区发展集中式光热发电,2030年光热发电装机容量可达30 GW[8]。为保证系统运行的稳定性和经济性,须合理调度光热电站出力,发挥其良好的调节特性。
目前针对光热电站的调度问题已进行大量研究,主要分为两方面。一方面,联合调度光热与风电以改善联合系统出力的随机波动性。文献[9-12]建立风电-光热联合调度模型,降低了风电不确定性的影响。文献[13-14]在联合系统中加入电加热子系统,将弃风转化为热能储存起来,降低弃风电量。文献[15]通过仿真验证了光热电站对高比例间歇性能源并网的支撑作用。另一方面,光热参与电网的优化调度以提升系统运行灵活性和经济性。文献[16]建立了一种含光热电站的电网调度模型,但未考虑电加热的影响。文献[17-18]在调度模型中考虑了系统综合成本以获得最佳运行效益,但仅考虑了火电机组提供备用容量,未考虑利用光热电站提供备用容量。文献[19-21]从经济性的角度探究了光热电站可调度性带来的经济效益。这些研究考虑了光热电站与风电联合或直接参与电网调度,但未考虑配置储热和电加热的光热电站参与电力系统调度及提供备用的能力。
综上,文中提出一种含大规模风电及光热电站的电力系统优化调度方法。首先分析光热电站运行机理,建立配置储热和电加热的光热电站调度运行模型;然后考虑火电机组、光热电站及电加热共同提供备用、系统安全运行约束等因素,以系统运行成本最小为目标,建立优化调度模型;最后通过IEEE 39节点系统算例仿真验证该方法的有效性。
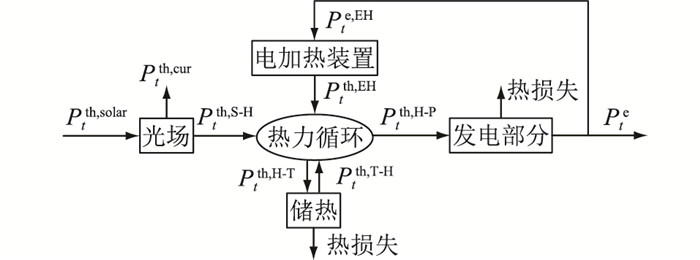
1 光热电站调度运行模型光热电站由光场、储热和发电部分组成[22],通过热力循环将3个部分联系起来,如图 1所示。
|
图 1 光热电站的简化结构 Fig. 1 Simplified structure of CSP |
在光场中,集热装置将太阳能转化为热能,通过传热流体将热能传递到发电部分,产生蒸汽推动汽轮机组发电,同时可将部分热能储存至储热系统,在需要时将热能释放到热力循环系统。电加热装置能够将富裕的风、光等新能源转化成热能储存至储热系统,拓宽光热电站的出力范围,消纳一定的弃风电量[23]。
图 1中,光热电站将接收到的太阳能转化为热能,配合储热系统和电加热装置能够实现系统热功率的储存转化,进而通过热电功率耦合关系实现电出力的灵活调度,系统热力运行约束具体如下。
(1) 热力平衡约束。
| $ P_{c,t}^{{\rm{th}},{\rm{S}} - {\rm{H}}} + P_{c,t}^{{\rm{th}},{\rm{T}} - {\rm{H}}} - P_{c,t}^{{\rm{th}},{\rm{H}} - {\rm{T}}} + P_{c,t}^{{\rm{th}},{\rm{EH}}} - P_{c,t}^{{\rm{h}},{\rm{H}} - {\rm{P}}} = 0 $ | (1) |
式中:Pc, tth, S-H为光热电站c在时段t输入的热功率,后文中c和t的含义相同,不再赘述;Pc, tth, T-H,Pc, tth, H-T分别为储热装置的放热功率和储热功率;Pc, tth, EH为电加热输出的热功率;Pc, tth, H-P为用于发电的热功率。
(2) 光热电站热功率约束。
| $ {P_{c,t}^{{\rm{th}},{\rm{S}} - {\rm{H}}} = P_{c,t}^{{\rm{th}},{\rm{solar}}} - P_{c,t}^{{\rm{th}},{\rm{cur}}}} $ | (2) |
| $ {P_{c,t}^{{\rm{th}},{\rm{solar}}} = {\eta _{c,{\rm{sf}}}}{S_{c,{\rm{sf}}}}{R_{c,t}}} $ | (3) |
式中:Pc, tth, solar为光热电站接收到的热功率;Pc, tth, cur为弃光功率;ηc, sf为光热转换效率;Sc, sf为光热电站光场面积;Rc, t为光照在时段t的直接辐射指数。
(3) 储热装置热量平衡约束。
| $ E_{c,t}^{{\rm{th}}} = \left( {1 - r_c^{{\rm{ts}}}} \right)E_{c,t - 1}^{{\rm{th}}} + \eta _c^{{\rm{ts}},{\rm{cha}}}P_{c,t}^{{\rm{th}},{\rm{H}} - {\rm{T}}} - \frac{{P_{c,t}^{{\rm{th}},{\rm{T}} - {\rm{H}}}}}{{\eta _c^{{\rm{ts}},{\rm{dis}}}}} $ | (4) |
式中:Ec, tth为时段t储能装置中的总热量;rcts为耗散系数;ηcts, cha,ηcts, dis分别为储热装置的储、放热效率。
(4) 储热装置储热容量约束。
| $ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{E}_{c}^{\text{th}}\le E_{c,t}^{\text{th}}\le \frac{{{\rho }^{\text{FLH}}}P_{c,\max }^{\text{CSP}}}{\eta _{c}^{\text{e}}} $ | (5) |
式中:Ecth为储热装置储热量下限;ρFLH为储热装置满负荷小时数,即储热装置在无光照条件下能够支撑光热电站满负荷发电的时间[16];Pc, maxCSP,ηce分别为发电机组最大出力和热电转换效率。
(5) 储热装置储、放热功率约束。
| $ \left\{ {\begin{array}{*{20}{l}} {P_{c,t}^{{\rm{th}},{\rm{ts}}} = P_{c,t}^{{\rm{th}},{\rm{T}} - {\rm{H}}} - P_{c,t}^{{\rm{th}},{\rm{H}} - {\rm{T}}}}\\ {0 \le P_{c,t}^{{\rm{th}},{\rm{H}} - {\rm{T}}} \le I_{c,t}^{{\rm{th}},{\rm{cha}}}P_{c,\max }^{{\rm{th}},{\rm{cha}}}}\\ {0 \le P_{c,t}^{{\rm{th}},{\rm{T}} - {\rm{H}}} \le I_{c,t}^{{\rm{th}},{\rm{dis}}}P_{c,\max }^{{\rm{th}},{\rm{dis}}}}\\ {I_{c,t}^{{\rm{th}},{\rm{cha}}} + I_{c,t}^{{\rm{th}},{\rm{dis}}} \le 1}\\ {x_{c,t}^{{\rm{CSP}}} \ge I_{c,t}^{{\rm{th}},{\rm{dis}}}} \end{array}} \right. $ | (6) |
式中:Pc, tth, ts为储热装置的热出力;Pc, maxth, cha,Pc, maxth, dis分别为储热装置最大储、放热功率;Ic, tth, cha,Ic, tth, dis分别为储热装置储、放热状态;xc, tCSP为发电机组状态变量,1表示开机,0表示停机。
(6) 电加热功率上下限。
| $ {P_{c,t}^{{\rm{th}},{\rm{EH}}} = \eta _c^{{\rm{EH}}}P_{c,t}^{{\rm{e}},{\rm{EH}}}} $ | (7) |
| $ {0 \le P_{c,t}^{{\rm{e}},{\rm{EH}}} \le P_{c,\max }^{{\rm{e}},{\rm{EH}}}} $ | (8) |
式中:ηcEH为电加热的电热转化效率;Pc, te, EH,Pc, maxe, EH分别为电加热的电功率及其功率上限。
(7) 光热电站电出力约束。
| $ {x_{c,t}^{{\rm{CSP}}}P_{c,\min }^{{\rm{CSP}}} \le P_{c,t}^{{\rm{CSP}}} \le x_{c,t}^{{\rm{CSP}}}P_{c,\max }^{{\rm{CSP}}}} $ | (9) |
| $ {P_{c,t}^{{\rm{CSP}}} = \eta _c^{\rm{e}}\left( {P_{c,t}^{{\rm{th}},{\rm{H}} - {\rm{P}}} - u_{c,t}^{{\rm{CSP}}}E_{c,{\rm{su}}}^{\rm{e}}} \right)} $ | (10) |
式中:Pc, minCSP为机组最小出力;uc, tCSP为机组启动变量;Ec, sue为机组启动所需热量。
(8) 最小运行/停运时间约束。
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{c,t}^{{\rm{CSP}}} - x_{c,t - 1}^{{\rm{CSP}}} \le x_{c,\tau }^{{\rm{CSP}}}\\ \forall \tau \in \left[ { + 1,\min \left( {t + T_{c,\min ,{\rm{on}}}^{{\rm{CSP}}} - 1,T} \right)} \right] \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {x_{c,t - 1}^{{\rm{CSP}}} - x_{c,t}^{{\rm{CSP}}} \le 1 - x_{c,\tau }^{{\rm{CSP}}}}\\ {\forall \tau \in \left[ {t + 1,\min \left( {t + T_{c,\min ,{\rm{off}}}^{{\rm{CSP}}} - 1,T} \right)} \right]} \end{array} $ | (12) |
式中:Tc, min, onCSP,Tc, min, offCSP 分别为机组的最小运行和最小停机时间。
(9) 运行状态约束。
| $ \left\{ {\begin{array}{*{20}{l}} {x_{c,t}^{{\rm{CSP}}} - x_{c,t - 1}^{{\rm{CSP}}} = u_{c,t}^{{\rm{CSP}}} - v_{c,t}^{{\rm{CSP}}}}\\ {u_{c,t}^{{\rm{CSP}}} + v_{c,t}^{{\rm{CSP}}} \le 1} \end{array}} \right. $ | (13) |
式中:vc, tCSP为机组的停机变量。
(10) 爬坡约束。
| $ {P_{c,t}^{{\rm{CSP}}} - P_{c,t - 1}^{{\rm{CSP}}} \le r_{c,{\rm{up}}}^{{\rm{CSP}}}\left( {1 - u_{c,t}^{{\rm{CSP}}}} \right) + P_{c,\min }^{{\rm{CSP}}}u_{c,t}^{{\rm{CSP}}}} $ | (14) |
| $ {P_{c,t - 1}^{{\rm{CSP}}} - P_{c,t}^{{\rm{CSP}}} \le r_{c,{\rm{dn}}}^{{\rm{CSP}}}\left( {1 - v_{c,t}^{{\rm{CSP}}}} \right) + P_{c,\min }^{{\rm{CSP}}}v_{c,t}^{{\rm{CSP}}}} $ | (15) |
式中:rc, upCSP,rc, dnCSP分别为机组的向上、向下爬坡速率。
光热电站通过汽轮机组发电,具有良好的快速调节能力,故具备与常规汽轮机组类似的发电运行约束,即式(9)-式(15)。因此光热电站电出力限值及爬坡能力等运行特性由系统热功率(由式(1)-式(8)决定)和汽轮机组运行特性(由式(9)-式(15)决定)共同约束。
2 含光热电站的电力系统调度模型文中综合考虑火电机组运行约束、光热电站运行约束、功率平衡约束、备用容量约束等约束条件,充分利用含储热及电加热的光热电站的日前调度运行灵活性提升系统风电消纳能力和经济性,提供备用容量的调节灵活性应对新能源的波动性和随机性,以系统运行成本最小为目标函数建立优化调度模型。
2.1 目标函数目标函数即系统运行成本由三部分组成,第一部分F1为火电机组发电成本,包括机组的燃料成本和启停成本;第二部分F2为光热发电和风电的运维成本;第三部分F3为弃风惩罚成本。
| $ \left\{ {\begin{array}{*{20}{l}} {\min f = {F_1} + {F_2} + {F_3}}\\ {{F_1} = \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{N_{\rm{g}}}} {\left[ {{a_i}{{\left( {P_{i,t}^{\rm{g}}} \right)}^2} + {b_i}P_{i,t}^{\rm{g}} + {c_i} + } \right.} } }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {C_i^{\rm{U}}u_{i,t}^{\rm{g}} + C_i^{{\rm{up}}}R_{i,t}^{{\rm{up}}} + C_i^{{\rm{dn}}}R_{i,{\rm{t}}}^{{\rm{dn}}}} \right]}\\ {{F_2} = \sum\limits_{t = 1}^T {\left[ {\sum\limits_{c = 1}^{{N_{\rm{c}}}} {\left( {{\delta _{c,{\rm{p}}}}P_{c,t}^{{\rm{CSP}}} + {\delta _{c,{\rm{s}}}}P_{c,t}^{{\rm{hhT}} - {\rm{H}}}} \right)} + } \right.} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\sum\limits_{j = 1}^{{N_j}} {{\delta _{{\rm{w}},{\rm{o}}}}} {P_{{\rm{w}},j,t}}} \right]}\\ {{F_3} = \sum\limits_{t = 1}^T {\sum\limits_{j = 1}^{{N_{\rm{w}}}} {{\delta _{{\rm{w}},{\rm{ cur }}}}} } \left( {{W_{j,t}} - {P_{{\rm{w}},j,t}}} \right)} \end{array}} \right. $ | (16) |
式中:Pi, tg为火电机组的发电功率;ai,bi,ci分别为火电机组的燃料成本参数;ui, tg为火电机组的启动状态变量;Ri, tup,Ri, tdn分别为火电机组向上、向下备用容量;CiU,Ciup,Cidn分别为火电机组的启动成本、正备用容量成本、负备用容量成本;Ng,Nw,Nc分别为火电机组、风电场和光热电站数量;δw, cur为弃风惩罚成本;δc, p,δc, s,δw, o分别为光热发电、储热系统和风电的运行维护成本系数;Pw, j, t,Wj, t分别为风电计划出力及其预测功率。
2.2 约束条件 2.2.1 系统运行约束(1) 功率平衡约束。
| $ \sum\limits_{i = 1}^{{N_{\rm{g}}}} {P_{i,t}^{\rm{g}}} + \sum\limits_{c = 1}^{{N_{\rm{c}}}} {\left( {P_{c,t}^{{\rm{CSP}}} - P_{c,t}^{{\rm{e}},{\rm{EH}}}} \right)} + \sum\limits_{j = 1}^{{N_{\rm{w}}}} {{P_{{\rm{w}},j,t}}} = \sum\limits_{b = 1}^{{N_{\rm{b}}}} {{P_{{\rm{load }},b,t}}} $ | (17) |
式中:Pload, b, t为系统负荷功率;Nb为负荷数量。
(2) 备用容量约束。
| $ {\sum\limits_{i = 1}^{{N_{\rm{g}}}} {R_{i,t}^{{\rm{up}}}} + \sum\limits_{c = 1}^{{N_{\rm{c}}}} {\left( {R_{c,t}^{{\rm{up}}} + R_{c,t}^{{\rm{up}},{\rm{EH}}}} \right)} \ge R_{t,{\rm{sys}}}^{{\rm{up}}}} $ | (18) |
| $ {\sum\limits_{i = 1}^{{N_{\rm{g}}}} {R_{i,t}^{{\rm{dn}}}} + \sum\limits_{c = 1}^{{N_{\rm{c}}}} {\left( {R_{c,t}^{{\rm{dn}}} + R_{c,t}^{{\rm{dn}},{\rm{EH}}}} \right)} \ge R_{t,{\rm{sys}}}^{{\rm{dn}}}} $ | (19) |
式中:Ri, tup,Ri, tdn,Rc, tup,Rc, tdn,Rc, tup, EH,Rc, tdn, EH分别为火电机组、光热电站机组、电加热提供的正、负备用容量;Rt, sysup,Rt, sysdn分别为系统所需的正、负备用容量。
(3) 线路潮流约束。
| $ \begin{array}{*{20}{c}} { - P_l^{\max } \le \sum\limits_{i = 1}^{{N_{\rm{g}}}} {{\pi _{l,i}}} P_{i,t}^{\rm{g}} + \sum\limits_{c = 1}^{{N_{\rm{c}}}} {{\pi _{l,c}}} \left( {P_{c,t}^{{\rm{CSP}}} - P_{c,t}^{{\rm{e,EH}}}} \right) + }\\ {\sum\limits_{j = 1}^{{N_{\rm{w}}}} {{\pi _{l,j}}} {P_{{\rm{w}},j,t}} - \sum\limits_{b = 1}^{{N_{\rm{b}}}} {{\pi _{l,b}}} {P_{{\mathop{\rm load}\nolimits} ,b,t}} \le P_l^{\max }} \end{array} $ | (20) |
式中:πl为节点到线路l的注入功率转移因子;Plmax为线路最大传输容量。
(4) 风电出力约束。
| $ 0 \le {P_{{\rm{w}},j,t}} \le {W_{j,t}} $ | (21) |
(1) 火电机组出力约束。
| $ P_{i,\min }^{\rm{g}}x_{i,t}^{\rm{g}} \le P_{i,t}^{\rm{g}} \le P_{i,\max }^{\rm{g}}x_{i,t}^{\rm{g}} $ | (22) |
式中:Pi, maxg,Pi, ming分别为发电机组的最大、最小出力;xi, tg为发电机组的运行状态变量。
(2) 火电机组最小运行/停机时间约束。
| $ \begin{array}{*{20}{c}} {x_{i,t}^{\rm{g}} - x_{i,t - 1}^{\rm{g}} \le x_{i,\tau }^{\rm{g}}}\\ {\forall \tau \in \left[ {t + 1,\min \left( {t + T_{i,\min ,{\rm{on}}}^{\rm{g}} - 1,T} \right)} \right]} \end{array} $ | (23) |
| $ \begin{array}{*{20}{c}} {x_{i,t - 1}^{\rm{g}} - x_{i,t}^{\rm{g}} \le 1 - x_{i,\tau }^{\rm{g}}}\\ {\forall \tau \in \left[ {t + 1,\min \left( {t + T_{i,\min ,{\rm{ off }}}^{\rm{g}} - 1,T} \right)} \right]} \end{array} $ | (24) |
式中:Ti, min, ong,Ti, min, offg分别为发电机组的最小运行、最小停运时间。
(3) 火电机组运行状态约束。
| $ \left\{ {\begin{array}{*{20}{l}} {x_{i,t}^{\rm{g}} - x_{i,t - 1}^{\rm{g}} = u_{i,t}^{\rm{g}} - v_{i,t}^{\rm{g}}}\\ {u_{i,t}^{\rm{g}} + v_{i,t}^{\rm{g}} \le 1} \end{array}} \right. $ | (25) |
式中:vi, tg为火电机组的停机变量。
(4) 火电机组爬坡约束[24]。
| $ {P_{i,t}^{\rm{g}} - P_{i,t - 1}^{\rm{g}} \le r_{i,{\rm{ up }}}^{\rm{g}}\left( {1 - u_{i,t}^{\rm{g}}} \right) + P_{i,\min }^{\rm{g}}u_{i,t}^{\rm{g}}} $ | (26) |
| $ {P_{i,t - 1}^{\rm{g}} - P_{i,t}^{\rm{g}} \le r_{i,{\rm{dn}}}^{\rm{g}}\left( {1 - v_{i,t}^{\rm{g}}} \right) + P_{i,\min }^{\rm{g}}v_{i,t}^{\rm{g}}} $ | (27) |
式中:ri, upg,ri, dng分别为火电机组向上、向下爬坡速率。
(5)火电机组备用容量约束。
| $ {0 \le R_{i,t}^{{\rm{dn}}} \le \min \left( {r_{i,{\rm{dn}}}^{\rm{g}},P_{i,t}^{\rm{g}} - P_{i,\min }^{\rm{g}}x_{i,t}^{\rm{g}}} \right)} $ | (28) |
| $ {0 \le R_{i,t}^{{\rm{up}}} \le \min \left( {r_{i,{\rm{up}}}^{\rm{g}},P_{i,\max }^{\rm{g}}x_{i,t}^{\rm{g}} - P_{i,t}^{\rm{g}}} \right)} $ | (29) |
光热电站的发电机组及电加热具有良好的调节特性和可调度性,能够为系统提供备用容量以响应可再生能源出力的随机波动,提高系统运行灵活性,如式(30)-式(33)所示。
(1) 光热电站的发电机组备用容量约束。
| $ {0 \le R_{c,t}^{{\rm{up}}} \le \min \left( {r_{c,{\rm{ up }}}^{{\rm{CSP}}},P_{c,\max }^{{\rm{CSP}}}x_{c,t}^{{\rm{CSP}}} - P_{c,t}^{{\rm{CSP}}}} \right)} $ | (30) |
| $ {0 \le R_{c,t}^{{\rm{dn}}} \le \min \left( {r_{c,{\rm{dn}}}^{{\rm{CSP}}},P_{c,t}^{{\rm{CSP}}} - P_{c,\min }^{{\rm{CSP}}}x_{c,t}^{{\rm{CSP}}}} \right)} $ | (31) |
(2) 电加热备用容量约束。
| $ {0 \le R_{c,t}^{{\rm{up}},{\rm{EH}}} \le P_{c,t}^{{\rm{e}},{\rm{EH}}}} $ | (32) |
| $ {0 \le R_{c,t}^{{\rm{dn}},{\rm{EH}}} \le P_{c,\max }^{{\rm{e}},{\rm{EH}}} - P_{c,t}^{{\rm{e}},{\rm{EH}}}} $ | (33) |
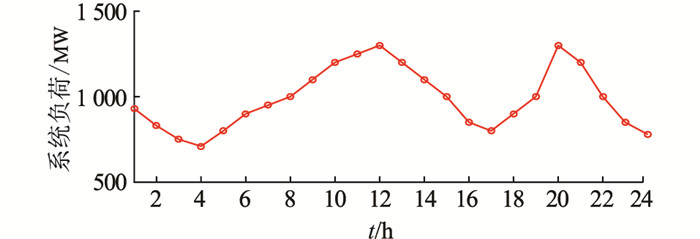
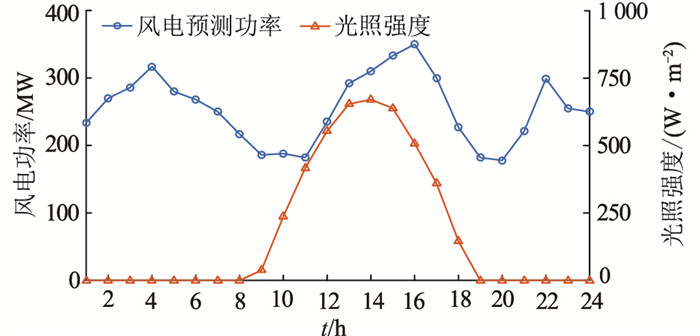
文中采用改进的IEEE 39节点系统对所构建的调度模型进行仿真验证,仿真系统包含10台火电机组,火电机组容量、爬坡速率等运行参数见文献[25],光热电站运行参数及运维成本详见文献[10, 18]。系统负荷、风电和光照强度预测曲线如图 2、图 3所示。文中在Matlab中基于Yalmip工具箱调用优化软件CPLEX对模型进行优化求解。
|
图 2 系统负荷预测曲线 Fig. 2 Load forecast curve of system |
|
图 3 风电功率和光照强度预测曲线 Fig. 3 Forecast curves of wind power and solar irradiation |
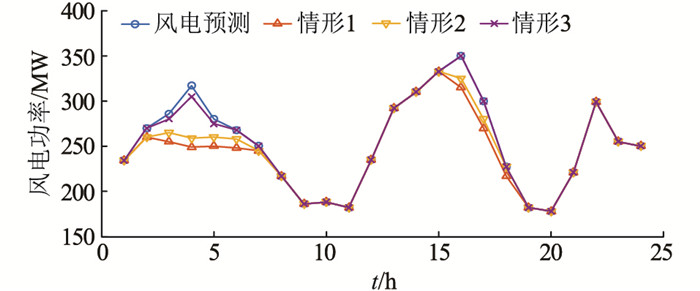
为验证光热电站配置储热和电加热对风电消纳及运行经济性的影响(不考虑光热电站提供备用容量),设置以下3种情形:系统接入光热电站但不配置储热(情形1),系统接入光热电站并配置储热(情形2)和系统接入光热电站并配置储热和电加热(情形3)。调度结果如表 1和图 4所示。
|
|
表 1 不同运行情形下系统成本 Table 1 System cost under different operating scenarios |
|
图 4 不同运行情形下风电计划出力 Fig. 4 Scheduled wind power under different operation conditions |
由表 1和图 4可知,情形2的系统运行成本相比情形1降低了0.7%,经济性得到提升,且弃风电量明显减少,这是由于情形1中光热电站出力受制于光照强度的强弱,可调度性差,而情形2中配置储热后,光热电站具有了良好的可调控性,在负荷需求小而风电出力大时段将部分太阳能以热能的形式储存起来,在负荷需求较大而风电出力和光照强度较小时,将存储的热能释放进行发电,系统运行灵活性增强,提高了系统风电消纳能力和运行经济性。相比于情形1和情形2,情形3的弃风惩罚成本明显降低,这是由于电加热装置能够将部分弃风转化成热能储存起来,对弃风进行时间迁移,提升了系统调度周期内的风电消纳能力,且系统运行成本随着弃风的减少而降低。
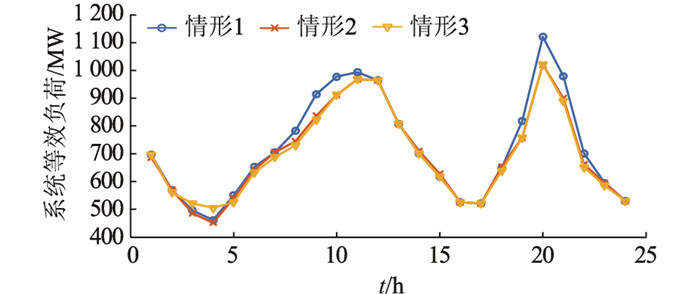
图 5为不同情形下系统的等效负荷曲线,引入配置储热和电加热的光热电站后系统等效负荷曲线的峰谷差相比情形1和情形2分别减少了27.4%和15.9%,由此可知配置储热和电加热的光热电站能够起到一定的“削峰填谷”作用,使得系统等效曲线更为平滑。
|
图 5 不同运行情形下系统等效负荷曲线 Fig. 5 Equivalent load curve of system under different operation conditions |
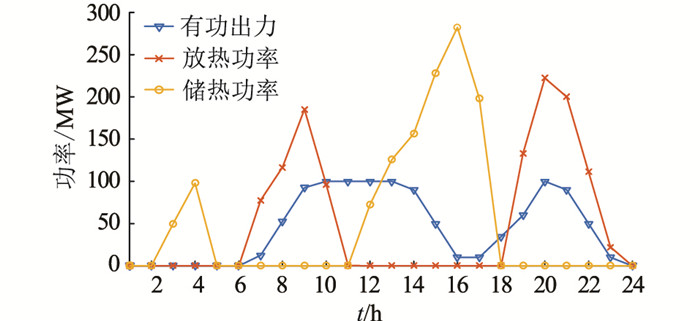
图 6为情形3中光热电站的有功出力和储、放热功率曲线。由图可知,01:00-06:00,负荷较小而风电功率较大,此时光热电站处于停机状态,电加热将部分弃风电量转化成热能储存起来;07:00-11:00,负荷逐渐增加而风电功率较小,此时光照强度也逐渐增强,光热电站综合利用接收到的太阳能和储热装置中的热量增加光热电站有功出力,承担部分负荷;12:00-18:00,风电出力和光照强度均较大,光热电站的储热装置处于储热工作状态,送入系统的有功出力逐渐降低,避免挤占风电出力空间导致弃风。18:00后,风电呈现反调峰特性,光热电站利用储热装置中的热量发电,输出并网友好性更好的高价值电能,能够降低机组运行煤耗并缓解风电反调峰带来的调节压力,提升系统调度运行的经济性。因此,通过光热电站中储热和电加热的协调配合,能够有效提升光热电站的灵活调节能力,削减风电反调峰带来的影响,消纳更多风电。
|
图 6 光伏电站有功出力和储、放热曲线 Fig. 6 Generation and thermal storage/release curves of CSP plant |
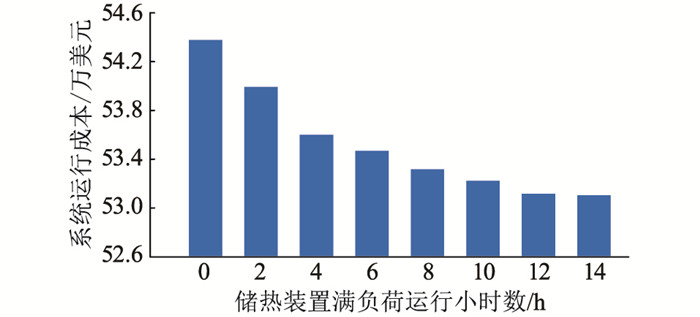
为对比分析光热电站储热容量对系统运行结果的影响,设置储热装置的满负荷小时数在[0, 14]内变化,相应的系统运行成本如图 7所示。
|
图 7 不同储热容量下的系统运行成本 Fig. 7 System operation cost under different heat storage capacity |
随着光热电站配置的储热容量增加,系统的运行成本逐渐降低并趋于稳定。光热电站能够利用储热装置将接收到的能量储存起来,转移到其他时段使用以提高系统的调节能力。随着储热容量的增加,光热电站能够将更多的太阳能储存起来,在需要时转换成更灵活的电能替代常规机组出力,提高调度周期内系统的调节能力和风电消纳能力,提升系统运行的经济性。储热装置满负荷小时数达到12 h后继续增加,则系统运行成本没有进一步降低,是由于受到光照资源的约束,光热电站调节能力达到饱和,增加的储热容量并未被利用,不能继续提升系统运行经济性。
3.3 不同备用容量供给方式下系统调度结果为对比分析不同备用容量供给方式对系统调度结果的影响,光热电站配置储热和电加热装置,设置以下3种方案:(1)仅由火电机组提供备用容量(方案1);(2)由火电机组和光热电站提供备用容量(方案2);(3)由火电机组、光热电站和电加热共同提供备用容量(方案3)。
调度结果如表 2所示,系统运行成本随着备用容量供给来源的增加呈下降趋势。在方案1中,仅由火电机组提供备用容量使得系统备用成本较高,火电机组运行经济性也相对较差;方案2增加光热电站参与提供备用容量,系统运行和备用成本分别降低了3.5%和29.7%;方案3采用火电机组、光热电站和电加热共同提供备用容量,使得火电机组出力降低,煤耗减小,且系统运行成本和备用成本最小,能够保证系统运行可靠性并提升运行经济性。
|
|
表 2 不同运行方案下系统成本 Table 2 System cost under different operating methods |
文中在详细考虑光热电站运行特性的基础上,提出一种含大规模风电及光热电站的电力系统优化调度模型,并通过算例分析验证了该方法的有效性,得到如下结论:
(1) 光热电站能够利用储热和电加热实现灵活调节发电出力,具有良好的调度可控性,通过与火电机组的协调优化能够在保证系统运行可靠性的基础上消纳更多风电及降低系统运行成本。
(2) 随着储热容量增加,系统的运行成本逐渐降低并趋于稳定,故合理的储热容量能够提升光热电站运行灵活性和系统运行经济性,避免不必要的投资成本。
(3) 充分利用光热电站和电加热的备用容量供给能力,能够保证系统运行可靠性并提升运行经济性。
| [1] |
施涛, 朱凌志, 于若英, 等. 电力系统灵活性评价研究综述[J]. 电力系统保护与控制, 2016, 44(5): 146-154. SHI Tao, ZHU Lingzhi, YU Ruoying, et al. Overview on power system flexibility evaluation[J]. Power System Protection and Control, 2016, 44(5): 146-154. (  0) 0) |
| [2] |
王国栋, 卢少锋, 张晓佳, 等. 风电场VSC-HVDC并网不平衡运行改善控制策略[J]. 电力工程技术, 2020, 39(1): 44-50. WANG Guodong, LU Shaofeng, ZHANG Xiaojia, et al. An improved control strategy for wind farm with VSC-HVDC under unbalanced voltage[J]. Electric Power Engineering Technology, 2020, 39(1): 44-50. (  0) 0) |
| [3] |
宁阳天, 罗翠云, 赵梓淇, 等. 计及核电调峰的新能源电力系统两阶段随机优化调度[J]. 电力工程技术, 2020, 39(2): 66-74, 126. NING Yangtian, LUO Cuiyun, ZHAO Ziqi, et al. A two-stage stochastic optimization for power system nuclear power plants participa-ting in peak regulation with the consideration of renewable energy uncertainty[J]. Electric Power Engineering Technology, 2020, 39(2): 66-74, 126. (  0) 0) |
| [4] |
杜尔顺, 张宁, 康重庆, 等. 太阳能光热发电并网运行及优化规划研究综述与展望[J]. 中国电机工程学报, 2016, 36(21): 5765-5775. DU Ershun, ZHANG Ning, KANG Chongqing, et al. Summary and prospect of research on grid-connected operation and optimization planning of solar thermal power generation[J]. Proceedings of the CSEE, 2016, 36(21): 5765-5775. (  0) 0) |
| [5] |
贠韫韵, 董海鹰, 马志程, 等. 考虑需求响应与光热电站参与的多源系统优化经济调度[J]. 电力系统保护与控制, 2020, 48(14): 140-149. YUN Yunyun, DONG Haiying, MA Zhicheng, et al. Optimization economic dispatch of a multi-source system considering the participation of demand response and concentrating solar power plant[J]. Power System Protection and Control, 2020, 48(14): 140-149. (  0) 0) |
| [6] |
贠韫韵, 董海鹰, 陈钊, 等. 考虑随机性及光热电站参与的多源发电系统两阶段随机优化调度[J]. 电力系统保护与控制, 2020, 48(4): 30-38. YUN Yunyun, DONG Haiying, CHEN Zhao, et al. A two-stage stochastic scheduling optimization for multi-source power system considering randomness andconcentrating solar power plant participation[J]. Power System Protection and Control, 2020, 48(4): 30-38. (  0) 0) |
| [7] |
International Energy Agency (IEA). Technology roadmap: concentratng solar power[R/OL].[2020-08-31]. http://www.iea.org/publications/freepublications/publication/csp-roadmap.pdf.
(  0) 0) |
| [8] |
邓友均, 张永熙, 李波, 等. 考虑光热发电的集中充电站有序充电决策[J]. 电力建设, 2018, 39(12): 38-45. DENG Youjun, ZHANG Yongxi, LI Bo, et al. Decision-making of orderly charging of centralized charging station considering concentrating solar power[J]. Electric Power Construction, 2018, 39(12): 38-45. (  0) 0) |
| [9] |
XU Ti, ZHANG Ning. Coordinated operation of concentrated solar power and wind resources for the provision of energy and reserve services[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1260-1271. (  0) 0) |
| [10] |
晋宏杨, 孙宏斌, 郭庆来, 等. 含大规模储热的光热电站-风电联合系统多日自调度方法[J]. 电力系统自动化, 2016, 40(11): 17-23. JIN Hongyang, SUN Hongbin, GUO Qinglai, et al. Multi-day self-scheduling method for combined system of CSP plants and wind power with large-scale thermal energy storage contained[J]. Automation of Electric Power Systems, 2016, 40(11): 17-23. DOI:10.7500/AEPS20150826012 (  0) 0) |
| [11] |
POUSINHO H M I, SILVA H, MENDES V M F, et al. Self-scheduling for energy and spinning reserve of wind/CSP plants by a MILP approach[J]. Energy, 2014(78): 524-534. (  0) 0) |
| [12] |
杨勇, 郭苏, 刘群明, 等. 风电-CSP联合发电系统优化运行研究[J]. 中国电机工程学报, 2018, 38(S1): 151-157. YANG Yong, GUO Su, LIU Qunming, et al. Research on optimization operation for wind-csphybrid power generation system[J]. Proceedings of the CSEE, 2018, 38(S1): 151-157. (  0) 0) |
| [13] |
戴剑丰, 汤奕, 曲立楠, 等. 太阳能光热与风力发电协调优化控制研究[J]. 计算机仿真, 2017, 34(10): 73-77. DAI Jianfeng, TANG Yi, QU Li'nan, et al. Research on coordinated optimization control of solar thermal and wind power generation[J]. Computer Simulation, 2017, 34(10): 73-77. (  0) 0) |
| [14] |
徐欢, 袁越, 张新松, 等. 一种新型风光热电站的风光互补性研究及成本分析[J]. 水电能源科学, 2013(3): 240-243. XU Huan, YUAN Yue, ZHANG Xinsong, et al. Wind-solar complementarjity and cost analysis of new solar-wind hybrid thermal power plant[J]. Water Resources and Power, 2013(3): 240-243. (  0) 0) |
| [15] |
DOMÍNGUEZ R, CONEJO A J, CARRIÓN M. Operation of a fully renewable electric energy system with CSP plants[J]. Applied Energy, 2014(119): 417-430. (  0) 0) |
| [16] |
陈润泽, 孙宏斌, 李正烁, 等. 含储热光热电站的电网调度模型与并网效益分析[J]. 电力系统自动化, 2014, 38(19): 1-7. CHEN Runze, SUN Hongbin, LI Zhengshuo, et al. Grid dispatch model and interconnection benfit analysis of concentrating solar power plants with thermal storage[J]. Automation of Electric Power Systems, 2014, 38(19): 1-7. (  0) 0) |
| [17] |
崔杨, 杨志文, 张节潭, 等. 计及综合成本的风电-光伏-光热联合出力调度策略[J]. 高电压技术, 2019, 45(1): 275-281. CUI Yang, YANG Zhiwen, ZHANG Jietan, et al. Scheduling strategy of wind power-photovoltaic power-concentrating solar power considering comprehensive costs[J]. High Voltage Engineering, 2019, 45(1): 275-281. (  0) 0) |
| [18] |
崔杨, 杨志文, 仲悟之, 等. 基于成本最优的含储热光热电站与火电机组联合出力日前调度[J]. 电力自动化设备, 2019, 39(2): 76-82. CUI Yang, YANG Zhiwen, ZHONG Wuzhi, et al. Day-ahead dispatch for output of combined CSP with thermal storage system and thermal power units based on minimized operation cost[J]. Electric Power Automation Equipment, 2019, 39(2): 76-82. (  0) 0) |
| [19] |
BRAND B, STAMBOULI A B, ZEJLI D. The value of dispatchability of CSP plants in the electricity systems of Morocco and Algeria[J]. Energy Policy, 2012(47): 321-331. (  0) 0) |
| [20] |
SIOSHANSI R, DENHOLM P. The value of concentrating solar power and thermal energy storage[J]. IEEE Transactions on Sustainable Energy, 2010, 1(3): 173-183. (  0) 0) |
| [21] |
DESIDERI U, CAMPANA P E. Analysis and comparison between a concentrating solar and a photovoltaic power plant[J]. Applied Energy, 2014(113): 422-433. (  0) 0) |
| [22] |
CHEN Runze, SUN Hongbin, GUO Qinglai, et al. Reducing generation uncertainty by integrating CSP with wind power:an adaptive robust optimization-based analysis[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 583-594. (  0) 0) |
| [23] |
DU Ershun, ZHANG Ning, HODGE Bri-Mathias, et al. Operation of a high renewable penetrated power system with csp plants:a look-ahead stochastic unit commitment model[J]. IEEE Transactions on Power Systems, 2019, 34(1): 140-151. (  0) 0) |
| [24] |
翟鹤峰, 赵利刚, 戴仲覆, 等. 计及N-k网络安全约束的二阶段鲁棒机组组合[J]. 电力工程技术, 2019, 38(2): 75-85. ZHAI Hefeng, ZHAO Ligang, DAI Zhongfu, et al. Two-stage robust unit commitment considering N-k network security constraints[J]. Electric Power Engineering Technology, 2019, 38(2): 75-85. (  0) 0) |
| [25] |
谢毓广, 江晓东. 储能系统对含风电的机组组合问题影响分析[J]. 电力系统自动化, 2011, 35(5): 19-24. XIE Yuguang, JⅡANG Xiaodong. Impact of energy storage system on the unit commitment problem with volatile wind power[J]. Automation of Electric Power Systems, 2011, 35(5): 19-24. (  0) 0) |
2. Engineering Research Center for Renewable Energy Power Generation and Grid Technology(Xinjiang University), Ministry of Education, Urumqi 830047, China
 2021, Vol. 40
2021, Vol. 40


 陟晶(1985), 男, 硕士, 高级工程师, 从事电网运行技术及政策研究工作(E-mail:
陟晶(1985), 男, 硕士, 高级工程师, 从事电网运行技术及政策研究工作(E-mail: