文章编号: 2096-3203(2021)01-0040-10 中图分类号: TM73 文献标识码: A
光伏等分布式可再生能源是解决能源危机和环境问题的可行方法。可再生能源具有不确定性和随机性,为了减弱其并网给电网造成的影响,设计时应根据光伏装机容量配备相应的储能装置,但大容量的储能装置成本较高。因此,利用源-储-荷协同运行降低可再生能源对储能装置的依赖,并根据系统现有结构制定合理的协调控制策略具有重要意义。
随着能源互联网的发展[1-4],电、气能源的联系愈发紧密,小区能源关系亦是如此。将小区微电网和天然气网组成微网,对微网进行协调控制不仅能提高能源利用率,也能提高微网稳定性[5-7]。在天然气网中,天然气管道在设计时要满足最大负荷流量,但最大流量的运行时间较少,可将天然气管道储存的多余天然气形成储气备用。储气备用量化不仅能稳定天然气网[8],还能作为储能装置用于微网的优化调度[9]。在微网中,负荷侧主动配电网技术日益成熟,控制精度越来越高[10-12],利用需求侧响应技术主动参与能源管理和调度可使微网运行更加灵活多变。已有研究成果以空调负荷为可控负荷参与平抑电网功率波动,文献[13]简化了空调房调温模型,使自适应电网的预测负荷大小进行互补运行,但缺乏实际样机数据支撑。文献[14]提出建立以双耦合偏微分方程组为基础的空调负荷热力学模型,通过对空调设定温度的更改平抑电网中
分布式新能源的波动,但只适用于某些特定场合。文献[15]提出了通过改变双巴特沃兹滤波器中的滤波时间常数,实现空调可控负荷和储能电池的协调控制,但未考虑外界环境对空调负荷的影响。文献[16]提出将空调负荷群聚类,配合储能装置通过模糊控制平抑电网功率波动,但未考虑气、热能源的作用。文献[17]提出建立空调负荷群的虚拟储能聚合模型参与电网能量调度,但未与其他储能装置进行联系。
上述研究建立的天然气储气备用模型只单独作为虚拟储能使用,并未考虑与空调可控负荷产生的虚拟储能相结合。文中在前人的研究成果上,提出将天然气储气备用和空调可控负荷产生的虚拟储能通过控制系统与小区已有储能装置共同参与微网能量管理,并设计多能协调控制策略使源-储-荷微网系统(source-storage-load micro network system,SSLS)可在光伏平抑波动模式、电网有功功率波动模式和峰谷电价套利模式下协调运行。
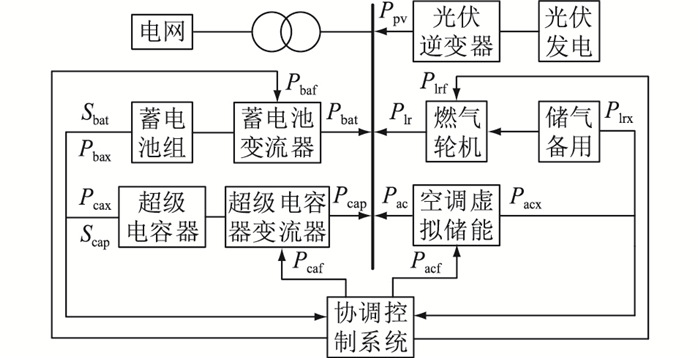
1 SSLS建模 1.1 SSLS结构SSLS由分布式光伏电站、燃气轮机、蓄电池组及超级电容储能装置、空调负荷群和协调控制系统构成,具体如图 1所示。天然气管道储存的天然气通过燃气轮机与微电网耦合,空调虚拟储能由所有住户组成的空调负荷群决定。超级电容和空调虚拟储能适合高频动作,蓄电池组和储气备用适合低频动作。
|
图 1 SSLS结构 Fig. 1 Structure of SSLS |
为实现小区SSLS协调运行,设置一协调控制系统对微网进行功率分配[18]。协调控制系统通过收集燃气轮机的输出功率Plrx和天然气管道储气量计算储气备用虚拟储能; 根据室外温度和空调当前的电功率Pacx计算空调可控负荷的虚拟储能; 根据蓄电池组的荷电状态Sbat,超级电容的荷电状态Scap和最大充放电功率计算输出功率可用范围。在光伏平抑波动模式或电网波动功率模式下,储气备用输出功率Plrf和蓄电池组输出功率Pbaf用于平抑原始功率的中频段,空调可控负荷输出功率Pacf和超级电容输出功率Pcaf用于平抑高频段。在峰谷电价套利模式下,对蓄电池组和超级电容输出功率进行二次调整,使光伏平抑波动模式和电网波动功率模式嵌套在峰谷电价套利模式中。
1.2 空调负荷群 1.2.1 空调负荷的热力学模型空调负荷为可控负荷,快速调节空调温度可改变空调出力。单台空调-建筑系统的等效热力学参数模型为[17]:
| $ \frac{{{\rm{d}}{T_{{\rm{room }}}}(t)}}{{{\rm{d}}t}} = - \frac{{{Q_{{\rm{ac}}}}(t)}}{C} + \frac{{{T_{{\rm{out }}}}(t) - {T_{{\rm{room }}}}(t)}}{{RC}} $ | (1) |
式中:Troom(t)为房间温度;Tout(t)为室外温度;Qac(t)为空调制冷量;C为建筑等效热容;R为建筑等效热阻。
| $ {Q_{{\rm{ac}}}}(t) = \lambda {P_{{\rm{ac}}}}(t) $ | (2) |
式中:λ为空调热电转换系数。
当空调设定温度Tset(t)不变时,空调运行状态s(t)会根据Troom(t)和阈值ΔT调整运行状态[15],具体如式(3)所示。
| $ s(t) = \left\{ {\begin{array}{*{20}{l}} {0\quad {T_{{\rm{set}}}}(t) > {T_{{\rm{room }}}}(t) + \Delta T}\\ {1\quad {T_{{\rm{set }}}}(t) < {T_{{\rm{room }}}}(t) - \Delta T}\\ {s(t - 1)\quad {T_{{\rm{room }}}}(t) - \Delta T < {T_{{\rm{set }}}}(t) < }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{{\rm{room }}}}(t) + \Delta T} \end{array}} \right. $ | (3) |
空调运行一段时间后处于稳态,房间温度会稳定在设置温度的ΔT范围内。
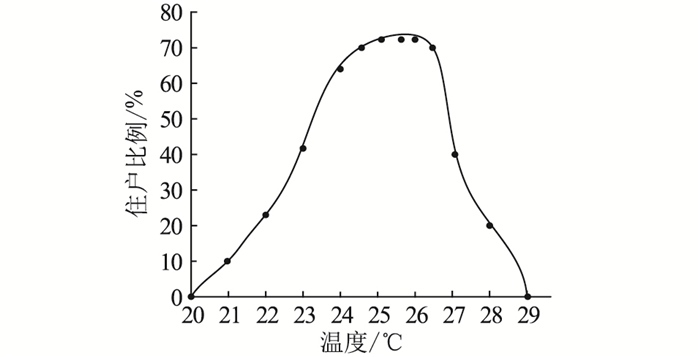
1.2.2 温度变化意愿曲线改变空调设置温度可以调节空调负荷的平均功率。根据住宅用户对空调温度变化敏感度的研究可知,相对于温度降低,住户对温度升高更敏感,希望保持温度不变的住户比例大致服从图 2[19]。
|
图 2 温度变化意愿曲线 Fig. 2 Willingness curve of temperature variation |
由图 2可以看出,当温度处于24.5~26.5 ℃时,至少70%的住户希望保持温度不变。而60%的住户希望保持温度不变的分界温度为24 ℃和27 ℃。因此,设置2个阶段。需要较小空调负荷参与功率调节时,空调温度升高设定为26.5 ℃,空调温度降低设定为24.5 ℃;需要较大空调负荷参与功率调节时,空调温度升高设定为27 ℃,空调温度降低设定为24 ℃。
当Troom(t)为空调初始设置温度时,有:
| $ \frac{{{\rm{d}}{T_{{\rm{room}}}}(t)}}{{{\rm{d}}t}} = 0 $ | (4) |
式(4)代入式(1)得出初始制冷量Qac1(t),改变Tset(t),房间温度在短时间内发生变化。由于建筑的等效热容效应,可近似认为房间散热不变,房间内温度变化为Tset(t)-Troom(t),代入式(1)可得出改变设置温度后的Qac2(t),空调制冷量的变化量ΔQac(t)为:
| $ \Delta {Q_{{\rm{ac}}}}(t) = {Q_{{\rm{ac}}2}}(t) - {Q_{{\rm{ac1}}}}(t) $ | (5) |
通过式(2)将ΔQac(t)转换为空调电功率即得到一个周期内单台空调参与功率分配的功率。
1.2.3 空调负荷群由于单台空调负荷具有随机性,将小区所有空调进行聚类,根据空调的品牌、额定功率、所处环境、住户习惯等进行分类,使不同时段均有稳定的可控负荷参与功率调节。
空调聚类分成不同类别,每个类别空调参与功率调节顺序由空调编号决定,编号依据与空调分类依据相同。空调编号确定后,假定每个住户初始设置的温度即为住户最舒适的温度。在需要较小空调负荷参与功率调节阶段,将空调温度设定值的上
限设定为26.5 ℃,下限设定为24.5 ℃,得到温度改变值,根据等效热力学参数模型得到空调制冷量,再根据式(2)得到可用的空调电功率,称为空调负荷的虚拟储能。若最舒适的温度不在此范围内,则该台空调不参与功率调节。在需要较大空调负荷参与功率调节时,将空调温度设定值上、下限分别设定为27 ℃,24 ℃,按照较小空调负荷参与功率调节的方法得到此时空调负荷的虚拟储能。虚拟储能为负,表示空调从母线获取的功率降低;虚拟储能为正,表示负荷从母线获取的功率增加。每台空调正的虚拟储能值按照从小到大排序,优先使用小虚拟储能值对应的空调。每台空调负的虚拟储能值按照从大到小的顺序排序,优先使用大的虚拟储能值对应的空调。
由于设置了温度上下限,空调在一个控制周期内,不会一直处于工作状态,呈现间歇性的工作特点。为不引起较大的功率变动,将所需参与功率调节的空调分批次进行设置温度调整。
1.3 储气备用天然气管道储气量在管道建成后只由管道两端气压决定,调节管道两端气压可以调节管道的储气量,天然气管道储气曲线可由小区天然气日常使用数据预测得到。设天然气网的一个调度周期为T,在(t0, t0+T)内正储气备用Lru(t0)和负储气备用Lrd(t0)定义为:
| $ {{L_{{\rm{ru}}}}\left( {{t_0}} \right) = a - {L_{\max }}\left( {{t_0}} \right)} $ | (6) |
| $ {{L_{{\rm{rd}}}}\left( {{t_0}} \right) = {L_{\min }}\left( {{t_0}} \right) - b} $ | (7) |
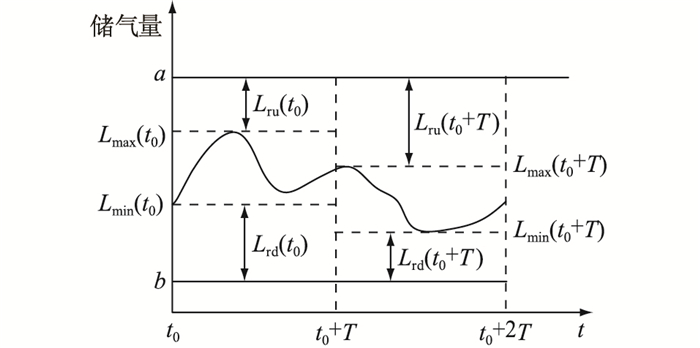
式中:a,b分别为管道最大、最小储气量;Lmax(t0),Lmin(t0)分别为(t0, t0+T)内储气最大、最小值。
图 3为2个周期内天然气正、负储气备用示意。储气备用可提供额外电能的限制条件为管道的储气备用和燃气轮机的爬坡能力。
|
图 3 储气备用示意 Fig. 3 Schematic diagram of the linepack reserve |
假设小区内天然气管道配备的燃气轮机参数相同,则:
| $ \left\{ {\begin{array}{*{20}{l}} {{t_{{\rm{ru}}}} = \left[ {{P_{\max }} - {P_{{\rm{gt}}}}\left( {{t_0}} \right)} \right]/{r_{{\rm{gt}}}}}\\ {{t_{{\rm{rd}}}} = \left[ {{P_{{\rm{gt}}}}\left( {{t_0}} \right) - {P_{\min }}} \right]/{r_{{\rm{gt}}}}} \end{array}} \right. $ | (8) |
式中:tru,trd分别为一个周期内燃气轮机输出功率增加到最大值和输出功率降低到最小值所需的时间;Pmax,Pmin分别为最大、最小输出功率;Pgt(t0)为燃气轮机初始运行状态;rgt为爬坡速率。
进而求出:
| $ {W_{\max }} = \left\{ \begin{array}{l} {r_{{\rm{gt}}}}{T^2}/2\quad {t_{{\rm{ru}}}} > T\\ \left( {{r_{{\rm{gt}}}}t_{{\rm{ru}}}^2/2} \right) + \left[ {{P_{{\rm{max}}}} - {P_{{\rm{gt}}}}\left( {{t_0}} \right)} \right]\left( {T - {t_{{\rm{ru}}}}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {t_{{\rm{ru}}}} \le T \end{array} \right. $ | (9) |
| $ {W_{\min }} = \left\{ {\begin{array}{*{20}{l}} {\left[ {{P_{{\rm{gt}}}}\left( {{t_0}} \right) - {P_{\min }}} \right]T - \left( {{r_{{\rm{gt}}}}t_{{\rm{rd}}}^2} \right)/2\quad {t_{{\rm{rd}}}} < T}\\ {{r_{{\rm{gt}}}}{T^2}/2\quad {t_{{\rm{rd}}}} \ge T} \end{array}} \right. $ | (10) |
式中:Wmax,Wmin分别为燃气轮机输出功率增加到最大值和输出功率降低到最小值的能量变化值。
由式(6)-式(10)可知,在(t0, t0+T)周期内,燃气轮机能提供的额外电能为管道储气备用和燃气轮机最大爬坡力能提供电能的较小值,分别如式(11)、式(12)所示。
| $ {{E_{\rm{u}}}\left( {{t_0}} \right) = \min \left\{ {\eta {L_{{\rm{rd}}}}\left( {{t_0}} \right), {W_{\max }}\left( {{t_0}} \right)} \right\}} $ | (11) |
| $ {{E_{\rm{d}}}\left( {{t_0}} \right) = \min \left\{ {\eta {L_{{\rm{ru}}}}\left( {{t_0}} \right), {W_{\min }}\left( {{t_0}} \right)} \right\}} $ | (12) |
式中:η为管道天然气转化为电能的转化率。
1.4 电池储能装置电池储能装置一般由蓄电池组和超级电容组成,蓄电池组大多采用铅酸蓄电池。蓄电池组适用于大容量、低充放电倍率、少深度循环次数的充放电循环;超级电容适用于小容量、高充放电倍率、多深度循环次数的充放电循环。
在电池储能装置中,铅酸蓄电池和超级电容的荷电状态是储能充放电速率的判断依据,也是整个控制系统功率分配的依据之一。目前,铅酸蓄电池的荷电状态估计常用安时计量算法和卡尔曼滤波法。安时计量算法的优点是简单易测,缺点是误差累积,对荷电状态初始值要求高。卡尔曼滤波法计算准确,但模型相对复杂,计算量大。综合考虑,蓄电池组荷电状态Sbat(t)采用安时计量算法估计。
| $ {S_{{\rm{bat }}}}(t) = {S_0} + \frac{{\int_0^t {\left[ {{\eta _{{\rm{cha }}}}{P_{{\rm{cha }}}}(t) - {P_{{\rm{dis }}}}(t)/{\eta _{{\rm{dis }}}}} \right]} {\rm{d}}t}}{{{E_{\rm{b}}}}} $ | (13) |
式中:S0为蓄电池初始荷电状态;ηcha,ηdis分别为充、放电效率;Pcha(t),Pdis(t)分别为充、放电功率;Eb为蓄电池组容量。
超级电容的荷电状态Scap(t)与端电压V(t)呈近似线性关系。
| $ {S_{{\rm{cap }}}}(t) = \frac{{V(t) - {V_{\min }}}}{{{V_{\max }} - {V_{\min }}}} $ | (14) |
式中:Vmax为超级电容充满电时的端电压;Vmin为超级电容放完电时的端电压。
为延长电池储能系统的使用寿命,不宜充放电过深,充放电功率不宜过大,蓄电池组和超级电容的荷电状态及充放电功率约束为:
| $ \left\{ {\begin{array}{*{20}{l}} {0.2 < {S_{{\rm{bat}}}}(t) < 0.8}\\ {0.1 < {S_{{\rm{cap}}}}(t) < 0.9}\\ {\left| {{P_{{\rm{bat}}}}(t)} \right| \le {P_{{\rm{lim}}, 1}}}\\ {\left| {{P_{{\rm{cap}}}}(t)} \right| \le {P_{\lim , 2}}} \end{array}} \right. $ | (15) |
式中:Pbat,Pcap分别为蓄电池组和超级电容的充放电功率;Plim,1,Plim,2分别为蓄电池组、超级电容充放电功率最大值。
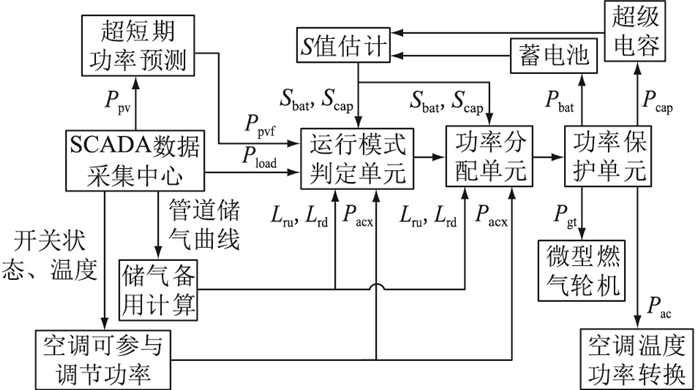
2 多能微网协同控制策略 2.1 整体控制策略文献[18]设计了包含电池储能装置以及光伏的控制系统,文中在此基础上设计一个包含光伏、储气备用、空调负荷、蓄电池组和超级电容的控制系统, 协调控制不同模式,如图 4所示。
|
图 4 协同控制原理 Fig. 4 Principle of coordination control |
利用数据采集与监视控制(supervisory control and data acquisition,SCADA)系统实时采集到的光伏数据Ppv进行超短期功率预测得到Ppvf。收集住户空调开关状态、温度设定值用于计算空调负荷可参与调节的功率Pacx。小区管道储气信息用于计算储气备用值Eu,Ed。结合负荷数据Pload和电网波动功率Pun判定系统运行模式。含有分布式新能源的小区,需要优先保证小区微电网的稳定性,在促进新能源发展的大环境下,优先保证小区光伏发电并网才能作为上级电网调频的备用。而光伏平抑波动模式、电网有功功率波动模式嵌套在峰谷电价套利模式中,3种模式协调运行,既能起虚拟储能作用,又能使储能装置实现峰谷电价套利。
功率分配单元根据运行模式、电池储能信息、储气备用及空调可控负荷的虚拟储能值等信息进行第一次功率分配。功率保护单元对第一次分配的功率进行修正,确保电池储能装置的荷电状态不超过上下限,燃气轮机输出功率不超过允许的最大值,空调设置温度不超过允许值,保证功率分配合理。
2.2 不同控制模式的控制策略系统运行模式有光伏平抑波动模式、电网有功功率波动模式和峰谷电价套利模式,3种模式采用不同的功率分配策略对空调虚拟储能的可用电功率、储气备用、蓄电池组及超级电容的输出功率进行分配。
2.2.1 光伏平抑波动模式目前,针对光伏发电的随机性,处理方法主要有:利用低通滤波器将光伏发电的原始功率简单分成低频和高频部分,通过调节低通滤波环节的时间常数降低铅酸蓄电池组的充放电频率[20];通过小波变换包将光伏发电的原始功率分成低频和高频部分,并将小波包分解后第一个频段的功率作为平抑波动的目标,剩下低频部分由蓄电池组处理,高频由超级电容处理[18]。综合考虑后,文中选择小波包分解将光伏发电的原始功率分解为2个部分,低频能量型部分由储气备用和铅酸蓄电池组平抑,高频功率型部分由空调虚拟储能的可用功率和超级电容平抑。
采用db1小波对光伏发电原始功率进行3层小波包分解,重构分解信号得到8个频段的功率分量。第1,3,4个频段包含原始光伏功率曲线的大部分能量且满足光伏并网条件,将这3个频段的功率分量作为平抑模式的目标功率Pgoal。第2个频段的功率满足储气备用调节周期要求,将此作为储气备用功率调节的参考指令Plrf。剩余需要平抑的功率作为空调虚拟储能可用功率的参考指令Pacf。
为了避免储气备用的输出功率及空调虚拟储能可用功率无法满足参考指令的要求,将蓄电池组功率作为储气备用功率,超级电容作为空调虚拟储能可用功率的备用调节功率。该功率分配属于开环控制,各单元功率分配后仅为参考指令,需校验功率指令是否满足各单元功率约束条件。
一个储气备用功率调整周期内,若储气备用功率参考指令小于燃气轮机能额外提供的功率,则将参考指令作为调整指令;若燃气轮机能额外提供的功率不能满足参考指令,则将燃气轮机能额外提供的功率作为调整指令,再根据Sbat(t)的范围计算蓄电池组充放电功率。
在空调负荷虚拟储能的一个功率调整周期内,若空调虚拟储能参考指令值小于空调可用电功率,则将参考指令作为调整指令;若空调虚拟储能参考指令值大于空调可用电功率,则将空调可用电功率作为调整指令,再根据Scap(t)的范围计算超级电容充放电功率。
将荷电状态即S值分为过充警示区[Sh, 1]、正常区[Sl, Sh]和过放警示区[0, Sl]。当储能装置工作在正常区时,充放电功率无需调整;当储能装置工作在过充警示区时,只需调整充电功率。蓄电池组和超级电容的调整方式为:
| $ {P_{{\rm{bc}}, 1}}(t) = \frac{{{S_{{\rm{bat}}}}(t) - 0.8}}{{{S_{{\rm{bh}}}} - 0.8}}{P_{{\rm{bc}}}}(t) $ | (16) |
| $ {P_{{\rm{cc}}, 1}}(t) = \frac{{{S_{{\rm{cap}}}}(t) - 0.9}}{{{S_{{\rm{ch}}}} - 0.9}}{P_{{\rm{cc}}}}(t) $ | (17) |
式中:Pbc(t)为蓄电池组在正常区的充电功率;Pbc,1(t)为蓄电池组在过充警示区需要调整的充电功率;Sbh为蓄电池组过充警示区的荷电状态标志;Pcc(t)为超级电容在正常区的充电功率;Pcc,1(t)为超级电容在过充警示区需要调整的充电功率;Sch为超级电容过充警示区的荷电状态标志。
当储能装置工作在过放警示区时,只需调整放电功率,调整方式为:
| $ {{P_{{\rm{bd}}, 1}}(t) = \frac{{{S_{{\rm{bat}}}}(t) - 0.2}}{{{S_{{\rm{bl}}}} - 0.2}}{P_{{\rm{bd}}}}(t)} $ | (18) |
| $ {{P_{{\rm{cd}}, 1}}(t) = \frac{{{S_{{\rm{cap}}}}(t) - 0.1}}{{{S_{{\rm{cl}}}} - 0.1}}{P_{{\rm{cd}}}}(t)} $ | (19) |
式中:Pbd(t)为蓄电池组在正常区的放电功率;Pbd, 1(t)为蓄电池组在警示区的放电功率;Sbl为蓄电池组过放警示区的荷电状态标志;Pcd(t)为超级电容在正常区的放电功率;Pcd,1(t)为超级电容在警示区需要调整的放电功率;Scl为超级电容过放警示区的荷电状态标志。
储气备用功率指令Plrf,空调虚拟储能功率指令Pacf,蓄电池组功率指令Pbaf和超级电容功率指令Pcaf经过功率保护单元修正后得到最终的功率输出Plr,Pac,Pbat,Pcap。
2.2.2 电网有功功率波动模式从电网运行需求角度,降低负荷高峰给电网带来的影响及降低辅助设备损耗非常必要,因此提出利用小区可控负荷平抑电网有功功率波动。电网需要调节的有功功率大小一般由上级电网给出,由多个小区共同完成。不同类型的有功功率波动采取不同调节方法。
(1) 上级电网出现阶跃性的有功功率扰动时需要快速响应,可用空调虚拟储能调节功率。
(2) 上级电网出现连续性功率扰动时,利用小波包函数分解扰动信号,将第1个频段的功率作为平抑目标,剩下低频段信号功率作为储气备用的参考指令,高频段信号功率作为空调虚拟储能的参考指令,采取的处理方式与光伏平抑模式相同。
2.2.3 峰谷电价套利模式该模式下,为保证住户使用空调的舒适度,空调虚拟储能的可用功率不用于峰谷电价套利。同时由于我国天然气资源紧张,天然气储气备用也不参与峰谷电价套利。
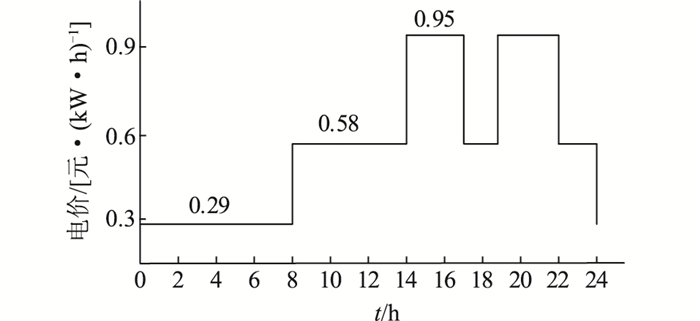
小区配备的蓄电池组和超级电容工作在峰谷套利模式中时,利用峰谷电价获得收益。某市峰谷电价如图 5所示,据峰谷电价的对应时段可知,目前电价低谷一般出现在00:00-08:00。此阶段后,系统可能进入光伏平抑波动模式,而光伏平抑波动模式的优先级比峰谷套利模式高,蓄电池的充电量不宜过大。因此在峰谷套利模式阶段需要将蓄电池的荷电状态区间调整为[0.2, 0.7],超级电容的荷电状态区间调整为[0.2, 0.8]。
|
图 5 某市峰谷电价 Fig. 5 Time of use price of a cartain city |
多模式运行的关键是模式之间的切换控制,保证3种模式协调运行。协调控制系统先判断小区微网的光伏发电是否满足入网要求,满足则进入光伏平抑波动模式,不满足则判断上级电网是否有需要小区调节的Pun。有需要则进入电网有功功率波动模式,否则进入峰谷套利模式。蓄电池组和超级电容只有单独工作在光伏平抑波动模式或电网有功功率波动模式输出功率为0时,才能在电价低谷阶段充电、电价高峰阶段放电,否则蓄电池组和超级电容不参与峰谷电价套利,保证较高优先级的2种模式不受影响。协调控制系统的具体流程如图 6所示。图中,Plrf0为储气备用输出功率的初始指令值;Pacf0为空调虚拟储能输出功率初始指令值;Plrx为储气备用的功率额度;Pacx为空调虚拟储能的功率额度;Plr为储气备用的最终功率指令值;Pac为空调虚拟储能的最终功率指令值。

|
图 6 协调控制系统流程 Fig. 6 Flow chart of coordination control system |
针对上述功率分配策略,采用图 1的拓扑结构在Matlab中进行仿真验证。小区光伏额定容量为150 kW;蓄电池组和超级电容的配置容量分别为60 kW/300 kW ·h,12 kW/10 kW ·h;允许的充放电深度分别为0.2~0.8,0.1~0.9;光伏并网的功率波动要求1 min内不得超过30 kW,10 min内不得超过150 kW;燃气轮机的装机容量为100 kW,发电效率为55%。某小区储气管道的主要参数如表 1所示,小区住户空调房间的主要参数如表 2所示。
|
|
表 1 天然气管道参数 Table 1 Parameters of gas pipes |
|
|
表 2 空调-建筑系统参数 Table 2 Parameters of air condi-tioning-building system |
以某小区光伏数据为算例进行仿真分析。
(1) 验证虚拟储能有效性。对光伏原始功率小波包分解得到2个频段的功率指令,分别利用虚拟储能、储能装置满足功率指令要求。
(2) 对比光伏平抑波动模式和双模式下各部分输出功率、储能装置的S,验证利用虚拟储能可实现光伏平抑波动模式和峰谷电价套利模式协调运行。
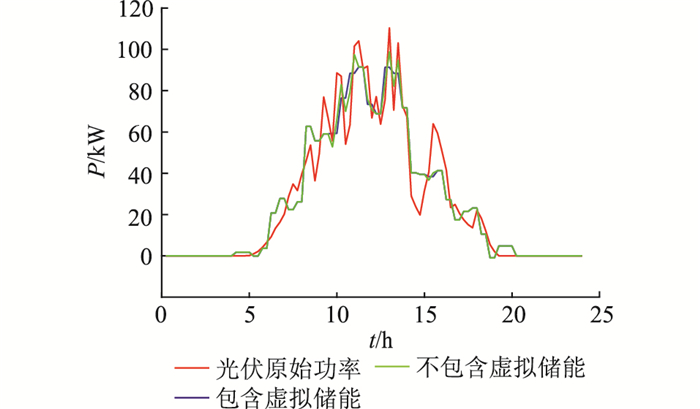
是否包含虚拟储能的光伏平抑波动效果如图 7所示。由图 7可知,当光伏原始功率不满足并网要求时,在储能装置的作用下功率变得相对柔和。在12:00附近,当光照强度发生较大变化时,储能装置由于容量限制并未有效改善功率突变,而虚拟储能降低了原始功率突变的影响。
|
图 7 光伏平抑波动效果对比 Fig. 7 The effect comparison of smoothing PV fluctuation |
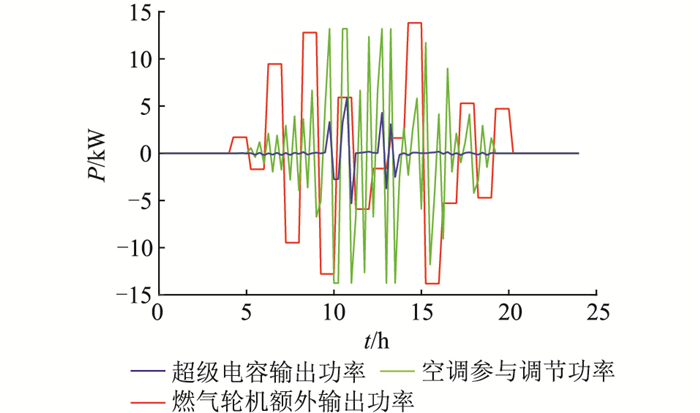
光伏平抑波动中各部分的参与功率如图 8所示。此模式需要平抑的功率较小,参与的空调为96台。天然气管道气压调节周期与铅酸蓄电池组的充放电周期相仿,燃气轮机额外输出功率已经满足了调节要求,故蓄电池组的输出功率为0。而在空调负荷参与光伏平抑波动模式中,超级电容的充放电深度明显降低,表明此功率分配在满足平抑光伏原始功率的前提下,可有效延长蓄电池组和超级电容的使用寿命。由图 8可知,此模式下虚拟储能在大部分时段可以代替储能装置平抑光伏原始功率。
|
图 8 光伏平抑波动各部分的参与功率 Fig. 8 Participating power of each part of smoothing PV fluctuation |
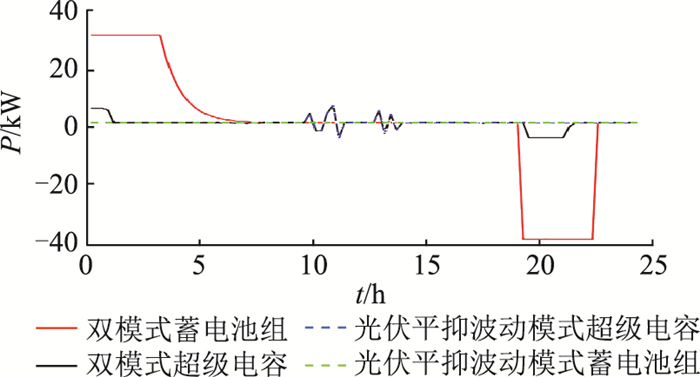
图 9为蓄电池组和超级电容单独工作在光伏平抑波动模式以及工作在光伏平抑波动与峰谷套利双模式下,蓄电池组、超级电容的输出功率对比。只有单独工作在光伏平抑波动模式下输出功率为0时,才能进入峰谷套利模式,在电价低谷阶段充电,电价高峰阶段放电。超级电容由于额定容量小、充电功率大,很快就能充电到允许的最大状态,蓄电池组相对较慢。
|
图 9 光伏平抑波动模式和双模式下储能系统输出功率 Fig. 9 Output power of the energy storage system in smoothing PV fluctuation mode and dual mode |
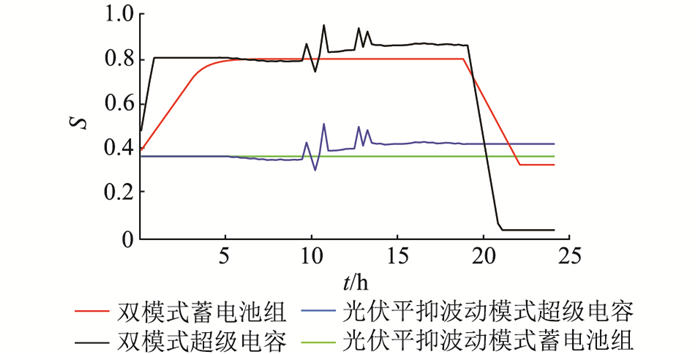
单独工作在光伏平抑波动模式和工作在双模式下, 蓄电池组和超级电容的S如图 10所示。双模式保留了蓄电池组和超级电容S的变化趋势,且在电价低谷阶段充电到允许的最大值,在电价高峰阶段放电,整个过程蓄电池组和超级电容的S始终在允许的变化范围。
|
图 10 光伏平抑波动模式和双模式下储能系统S值 Fig. 10 S of energy torage system in smoothing PV fluctuation mode and dual mode |
以某天风电场发电数据为上级电网扰动,对风力发电原始功率进行小波包分解,得到小区微网各部分输出功率指令。使协调控制系统单独工作在有功功率波动模式以及工作在有功功率波动和峰谷电价套利双模式,对比是否包含虚拟储能的平抑波动效果以及在包含虚拟储能的条件下微网各部分的输出功率和储能系统的荷电状态S值。
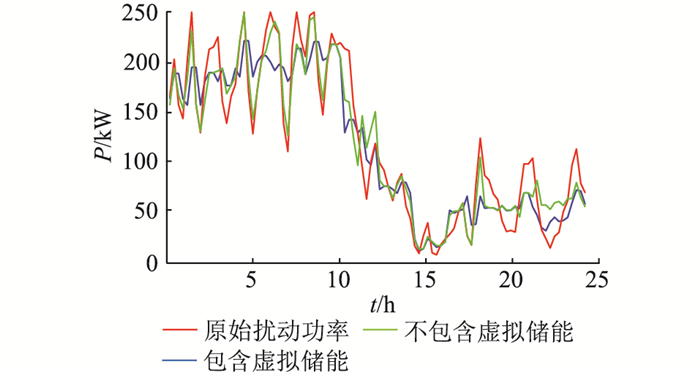
是否包含虚拟储能对平抑上级电网连续性扰动的效果如图 11所示。在扰动功率较大时,不包含虚拟储能的传统储能装置受蓄电池组和超级电容容量影响,平抑效果不明显,而包含虚拟储能的系统具有较好的平抑效果。
|
图 11 电网有功功率波动平抑效果对比 Fig. 11 The effect comparison of smoothing grid active power fluctuation |
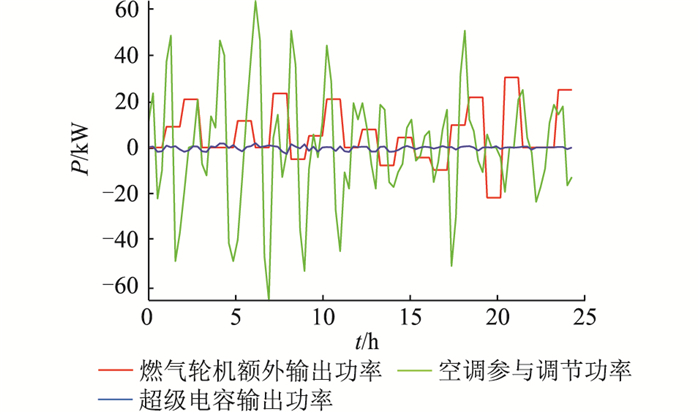
SSLS仅参与电网有功功率波动模式的输出功率如图 12所示。算例中电网波动功率相对较大,为了达到良好的平抑效果,参与平抑功率的空调为960台,此时主要由空调负荷参与电网功率调节。
|
图 12 电网有功功率波动模式各部分的参与功率 Fig. 12 Participating power of each part of smoothing grid active power fluctuation mode |
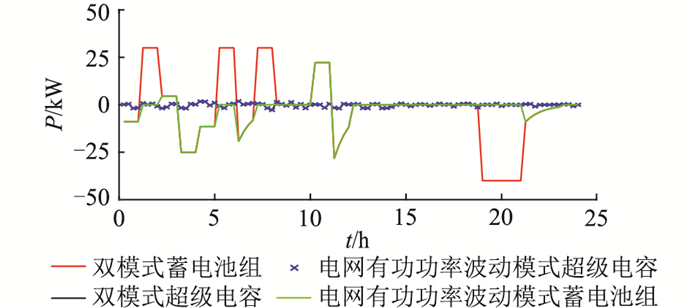
蓄电池组和超级电容参与电网有功功率波动模式以及电网有功功率波动和峰谷电价套利双模式的输出功率对比如图 13所示。电网有功功率波动模式蓄电池组输出功率为0时,蓄电池组在电价低谷时进行充电,在电价高峰时进行放电。超级电容全程参与了电网有功功率波动模式的功率调节,故超级电容未实现峰谷电价套利。
|
图 13 电网有功功率波动模式和双模式下储能系统输出功率 Fig. 13 Output power of the energy storage system in smoothing grid active power fluctuation mode and dual mode |
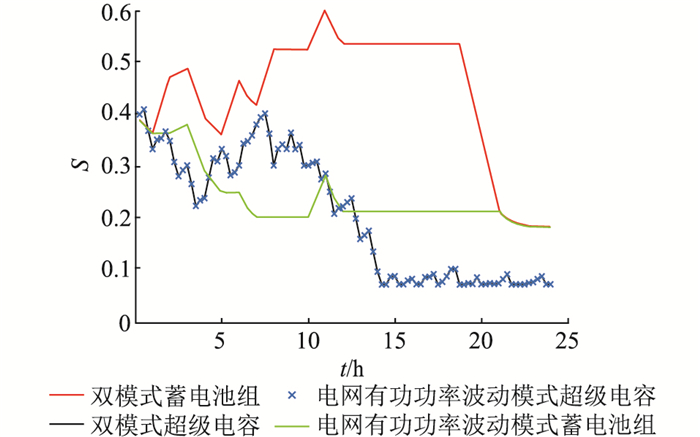
单独工作在电网有功功率波动模式以及工作在电网有功功率波动和峰谷电价套利双模式下蓄电池组、超级电容的S如图 14所示。
|
图 14 电网有功功率波动模式和双模式下储能系统S值 Fig. 14 S of energy torage system in smoothing grid active power fluctuation mode and dual mode |
双模式保留了蓄电池组S值的变化趋势,且在电网有功功率波动单模式蓄电池组S不变时,蓄电池组在电价低谷阶段充电,在电价高峰阶段放电。超级电容在所有时刻都参与了电网有功功率波动模式,故双模式中的S和单模式的相同。蓄电池组和超级电容的S始终在允许范围内变化。
4 结语针对光伏并网和上级电网功率波动带来的微网稳定性和经济性问题,提出构建由空调虚拟储能、储气备用、蓄电池组和超级电容组成的储能系统,实现了光伏平抑波动、电网有功功率波动和峰谷电价套利3种模式协调运行,并通过实例证明了策略的有效性和正确性。
(1) 光伏平抑波动模式下,利用小波包对光伏原始功率进行分解,得到空调可用功率和储气备用的参考指令值,再根据约束条件得到空调可用功率和储气备用最终指令。作为两者备用的蓄电池组和超级电容,结合各自的S确定充放电功率。
(2) 电网有功功率波动模式下,针对波动功率是否连续采取不同的控制方法。非连续型利用空调可用功率的快速响应平抑波动。连续型利用小波包进行分解,与光伏平抑波动模式类似,只是各部分参与功率较大,所需各部分输出功率较大。
(3) 在光伏原始功率满足并网要求,且上级电网无需小区平抑波动功率时,蓄电池组和超级电容在电价低谷时充电,在电价峰值时放电,实现收益。
文中在考虑天然气储气备用时仅考虑了电负荷,并未考虑燃气轮机产生的余热。后续将研究冷热电联供与空调虚拟储能相关联时的优化调度方案。
| [1] |
董朝阳, 赵俊华, 文福拴, 等. 从智能电网到能源互联网:基本概念与研究框架[J]. 电力系统自动化, 2014, 38(15): 1-11. DONG Zhaoyang, ZHAO Junhua, WEN Fushuan, et al. From smart grid to energy internet:basic concept and research framework[J]. Automation of Electric Power Systems, 2014, 38(15): 1-11. DOI:10.7500/AEPS20140613007 (  0) 0) |
| [2] |
马宇辉, 刘念. 用户侧微电网的能量管理方法综述[J]. 电力系统保护与控制, 2017, 45(23): 158-168. MA Yuhui, LIU Nian. Survey on energy management method of community micro-grid[J]. Power System Protection and Control, 2017, 45(23): 158-168. DOI:10.7667/PSPC170782 (  0) 0) |
| [3] |
张延宇, 曾鹏, 臧传治. 智能电网环境下家庭能源管理系统研究综述[J]. 电力系统保护与控制, 2014, 42(18): 144-154. ZHANG Yanyu, ZENG Peng, ZANG Chuanzhi. Review of home energy management system in smart grid[J]. Power System Protection and Control, 2014, 42(18): 144-154. DOI:10.7667/j.issn.1674-3415.2014.18.025 (  0) 0) |
| [4] |
陈永进. 考虑园区能源互联网接入及其需求响应的配电网规划方法[J]. 广东电力, 2019, 32(10): 45-52. CHEN Yongjin. Distribution network planning method considering park energy internetaccess and its demand response[J]. Guangdong Electric Power, 2019, 32(10): 45-52. (  0) 0) |
| [5] |
ClEGG S, MANCARELLA P. Integrated electrical and gas network flexibility assessment in low-carbon multi-energy systems[J]. IEEE Transactions on Sustainable Energy, 2015, 7(2): 1-14. (  0) 0) |
| [6] |
胡殿刚, 潘正婕, 徐昊亮, 等. 大规模可再生能源并网条件下天然气机组调峰空间估算[J]. 电力系统保护与控制, 2017, 45(3): 87-93. HU Diangang, PAN Zhengjie, XU Haoliang, et al. Peaking capacity estimation of natural gas unit under the condition of large-scale renewable energy connecting with power grid[J]. Power System Protection and Control, 2017, 45(3): 87-93. (  0) 0) |
| [7] |
孙可, 吴臻, 尚楠, 等. 以省为实体的区域能源互联网内涵框架及发展方向分析[J]. 电力系统保护与控制, 2017, 45(5): 1-9. SUN Ke, WU Zhen, SHANG Nan, et al. Provincial regional energy internet framework and development tendency analysis[J]. Power System Protection and Control, 2017, 45(5): 1-9. (  0) 0) |
| [8] |
张涛, 张福兴, 张彦. 面向能源互联网的能量管理系统研究[J]. 电网技术, 2016, 40(1): 146-155. ZHANG Tao, ZHANG Fuxing, ZHANG Yan. Study on energy management system of energy internet[J]. Power System Technology, 2016, 40(1): 146-155. (  0) 0) |
| [9] |
汪洋子, 陈茜. 计及冷、热、电联产的气电互联网络最优调度[J]. 电力系统保护与控制, 2019, 47(3): 168-175. WANG Yangzi, CHEN Qian. Optimal dispatch for the integrated electrical and natural gas network with combined cooling, heat and power plant[J]. Power System Protection and Control, 2019, 47(3): 168-175. (  0) 0) |
| [10] |
曾鸣, 杨雍琦, 刘敦楠, 等. 能源互联网"源-网-荷-储"协调优化运营模式及关键技术[J]. 电网技术, 2016, 40(1): 114-124. ZENG Ming, YANG Yongqi, LIU Dunnan, et al. "Generation-grid-load-storage" coordinative optimal operation mode of energy internet and key technologies[J]. Power System Technology, 2016, 40(1): 114-124. (  0) 0) |
| [11] |
马钊, 梁惠施, 苏剑. 主动配电系统规划和运行中的重要问题[J]. 电网技术, 2015, 39(6): 1499-1503. MA Zhao, LIANG Huishi, SU Jian. Important issues in planning and operation of active distribution system[J]. Power System Technology, 2015, 39(6): 1499-1503. (  0) 0) |
| [12] |
IZADKHAST S, GARCIA-GONZALEZ P, PABLO F. An aggregate model of plug-in electric vehicles for primary frequency control[C]//Power & Energy Siety General Meeting. IEEE, 2016.
(  0) 0) |
| [13] |
王栋, 徐青山, 陈亮, 等. 参与调峰控制的空调负荷建模仿真研究[J]. 电力工程技术, 2018, 37(6): 80-86. WANG Dong, XU Qingshan, CHEN Liang, et al. Air conditioning load modeling and simulation of peak load regulation[J]. Electric Power Engineering Technology, 2018, 37(6): 80-86. DOI:10.3969/j.issn.1009-0665.2018.06.013 (  0) 0) |
| [14] |
艾欣, 赵阅群, 周树鹏. 适应清洁能源消纳的配电网直接负荷控制模型与仿真[J]. 中国电机工程学报, 2014, 34(25): 4234-4243. AI Xin, ZHAO Yuequn, ZHOU Shupeng. Direct load control model and simulation for clean energy accommodation in distribution network[J]. Proceedings of the CSEE, 2014, 34(25): 4234-4243. (  0) 0) |
| [15] |
WANG D, GE S, JIA H, et al. A demand response and battery storage coordination algorithm for providing microgrid tie-line smoothing services[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 476-486. DOI:10.1109/TSTE.2013.2293772 (  0) 0) |
| [16] |
屠聪为, 曹军, 于东立, 等. 基于空调负荷的虚拟储能参与调频的控制策略[J]. 电力需求侧管理, 2019, 21(1): 16-21. TU Congwei, CAO Jun, YU Dongli, et al. Control strategy of virtual energy storage system participating in frequency modulation based on air conditioning loads[J]. Power Demand side Management, 2019, 21(1): 16-21. (  0) 0) |
| [17] |
王怡岚, 童亦斌, 黄梅, 等. 基于需求侧响应的空调负荷虚拟储能模型研究[J]. 电网技术, 2017, 41(2): 394-401. WANG Yilan, TONG Yibin, HUANG Mei, et al. Research on virtual energy storage model of air conditioning loads based on demand response[J]. Power System Technology, 2017, 41(2): 394-401. (  0) 0) |
| [18] |
杨子龙, 宋振浩, 潘静, 等. 分布式光伏/储能系统多运行模式协调控制策略[J]. 中国电机工程学报, 2019, 39(8): 2213-2220. YANG Zilong, SONG Zhenhao, PAN Jing, et al. Multi-mode coordinated control strategy of distributed PV and energy storage system[J]. Proceedings of the CSEE, 2019, 39(8): 2213-2220. (  0) 0) |
| [19] |
曹彬.气候与建筑环境对人体热适应性的影响研究[D].北京: 清华大学, 2012. CAO Bin. Research on the impacts of climate and built environment on human thermal[D]. Beijing: Tsinghua University, 2012. (  0) 0) |
| [20] |
程志江, 李永东, 谢永流, 等. 带超级电容的光伏发电微网系统混合储能控制策略[J]. 电网技术, 2015, 39(10): 2739-2745. CHENG Zhijiang, LI Yongdong, XIE Yongliu, et al. Control strategy for hybrid energy storage of photovoltaic generation microgrid system with super capacitor[J]. Power System Technology, 2015, 39(10): 2739-2745. (  0) 0) |
 2021, Vol. 40
2021, Vol. 40


 杨金文(1995), 男, 硕士在读, 研究方向为电力系统运行与控制(E-mail:
杨金文(1995), 男, 硕士在读, 研究方向为电力系统运行与控制(E-mail: