文章编号: 2096-3203(2021)01-0131-07 中图分类号: TM72 文献标识码: A
2. 东南大学电气工程学院, 江苏 南京 210096
随着全球化石能源的逐渐枯竭和生态环境问题的日益严峻, 大量利用可再生资源的分布式发电技术以及使用清洁电能替代传统化石能源的电动汽车产业受到了广泛关注, 并逐渐成为电力行业的研究热点[1-2]。配电系统网络架构相对薄弱, 合理规划分布式电源与电动汽车充电站的安装位置和容量是配电系统安全经济运行的基础, 也是促进可再生能源消纳、提升电动汽车社会认可度的前提[3-5]。因此, 开展分布式电源与电动汽车充电站在配电系统中的协调优化研究具有重要意义。
关于分布式电源与电动汽车充电站在配电系统中的协调配置问题, 文献[6]对其现实意义进行了详细阐述, 并给出了相应的优化模型和优化算法, 有效解决了这一问题。文献[7]考虑了配电系统和交通网络的影响, 建立了包含系统总费用最小、网络损耗最小和交通满意度最高等多个优化目标的配置模型。文献[8]分析了有序充电策略的影响, 提出了以系统建设运行成本、综合净负荷波动指标及网络能量损耗最小为目标的配置模型。文献[9-10]基于耦合的交通-电力网络构建了相应的优化模型。文献[9]采用二阶锥松弛技术处理构建的优化模型, 将其转化为混合整数二阶锥规划模型进行求解。在此基础上, 文献[10]应用加速的广义Benders分解技术提高了优化模型的求解效率。文献[11]充分考虑了电力负荷、分布式电源出力、电动汽车充电负荷的时序波动特性。基于日渐成熟的实时导航技术, 文献[12]计及了电动汽车充电负荷的空间可调度特性, 在配置问题中嵌入了电动汽车的空间优化调度问题。文献[13]充分考虑了不同投资主体的利益诉求, 同时计及了配置方案的技术可行性和经济最优性。
现有研究鲜有考虑风速、光照强度等可再生资源的不确定性, 导致构建的优化模型过于粗糙, 获取的配置方案难以直接应用于工程实际。基于这一背景, 文中应用离散化的多状态模型表征可再生资源的不确定性, 以光伏电站、微型燃气轮机、电动汽车充电站为候选元素, 构建相应的协调配置模型。该模型适用于精确的二阶锥松弛技术, 并最终表征为混合整数二阶锥规划模型进行求解。文中以IEEE 33节点配电系统为算例, 对所提方案的有效性进行验证。
1 协调配置问题中相关资源的建模 1.1 连续时间尺度的离散化为有效降低分布式电源与电动汽车充电站协调配置模型的复杂程度, 文中对连续的时间尺度进行离散化, 同时应用若干个典型日表征协调配置问题中的自然年[12]。具体方法为:
(1) 使用8个典型日(春、夏、秋、冬四季的工作日与周末)代表协调配置问题中的自然年;
(2) 将每个典型日离散为96个时间断面, 每个时间断面为15 min;
(3) 忽略每个时间断面内电力负荷、分布式电源出力、电动汽车充电负荷的波动, 认为其是一个确定性场景。
1.2 可再生资源不确定性的表征在候选元素中, 光伏电站的出力水平与太阳光照强度直接相关, 呈现显著的随机性和间歇性。基于已有研究, Beta分布可以较好表征太阳光照强度的分布情况[14-15], 具体形式为:
| $ f(s) = \frac{{\Gamma (\alpha + \beta )}}{{\Gamma (\alpha )\Gamma (\beta )}}{\left( {\frac{s}{{{s_{\max }}}}} \right)^{\alpha - 1}}{\left( {1 - \frac{s}{{{s_{\max }}}}} \right)^{\beta - 1}} $ | (1) |
式中:f(s)为太阳光照强度s对应的概率; smax为某个时刻太阳光照强度的历史最大值; α, β为Beta分布的形状参数; Γ(α)表示参数为α的Gamma函数值。
对某个时间断面而言, Beta分布的形状参数可以通过历史数据的统计分析得到[16]。
| $ {\alpha = {\mu _{\rm{g}}}\left[ {\frac{{{\mu _{\rm{g}}}\left( {1 - {\mu _{\rm{g}}}} \right)}}{{\sigma _{\rm{g}}^2}} - 1} \right]} $ | (2) |
| $ {\beta = \left( {1 - {\mu _{\rm{g}}}} \right)\left[ {\frac{{{\mu _{\rm{g}}}\left( {1 - {\mu _{\rm{g}}}} \right)}}{{\sigma _{\rm{g}}^2}} - 1} \right]} $ | (3) |
式中:μg, σg分别为该时间断面太阳光照强度历史数据统计的平均值与标准差。
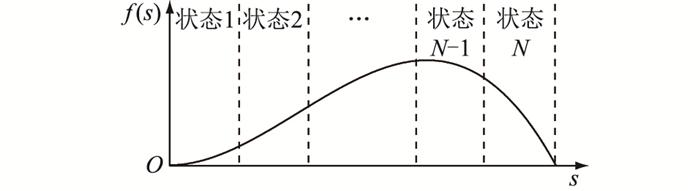
任一时间断面, 太阳光照强度概率密度函数是一个复杂的连续函数, 难以在协调配置模型中进行有效表征。为应对这一问题, 文中应用多状态模型对连续的概率密度函数进行离散化处理, 将太阳光照强度的不确定性表征为一定数量的确定性离散状态, 如图 1所示。图中, N为离散得到的确定性状态数量, 每个确定性状态对应的步长相同[14, 17]。
|
图 1 连续概率密度函数的离散化 Fig. 1 Discretization of the continuous probability density function |
图 1中每个确定性离散状态对应的概率数值可通过积分计算得到, 如式(4)所示。
| $ p\left( {{S_k}} \right) = \int_{{s_{k,\min }}}^{{s_{k,\max }}} f (s){\rm{d}}s $ | (4) |
式中:p(Sk)为太阳光照强度从属于状态k的概率; sk, max, sk, min分别为状态k表征范围的上、下限。
1.3 分布式电源出力建模对于光伏电站, 忽略温度、湿度、光照角度等次要因素影响, 光伏模块的有功功率出力与太阳光照强度间的关系可由式(5)表征[18]。
| $ {P_s} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{P_{s,{\rm{ rated }}}}\;s}}{{{s_{{\rm{rated }}}}}}}&{0 \le s \le {s_{{\rm{rated }}}}}\\ {{P_{s,{\rm{ rated }}}}}&{s > {s_{{\rm{rated }}}}} \end{array}} \right. $ | (5) |
式中:Ps为太阳光照强度s对应的光伏模块有功功率出力; Ps, rated为该光伏模块的额定有功功率出力; srated为该光伏模块的额定太阳光照强度。
考虑到经济性和安全性因素, 文中将光伏电站视作不可控的有功功率源, 其功率因数为1。则在任一太阳光照强度已知的确定性离散状态下, 可推导得到单位光伏装机容量对应的功率出力。
微型燃气轮机具有高效、灵活等特点, 其出力随着配电系统运行状态的改变而改变, 具有良好的调控特性。文中微型燃气轮机被视作可控的分布式电源, 其在每个确定性离散状态下的出力由配电系统运营商根据系统运行状态决定。考虑到装机容量的客观约束, 微型燃气轮机实际出力的可调节范围如式(6)、式(7)所示。
| $ {0 \le {P_{{\rm{MT}}}} \le {S_{{\rm{MT}},{\rm{ rated }}}}} $ | (6) |
| $ { - \sqrt {S_{{\rm{MT}},{\rm{rated}}}^2 - P_{{\rm{MT}}}^2} \le {Q_{{\rm{MT}}}} \le \sqrt {S_{{\rm{MT}},{\rm{rated}}}^2 - P_{{\rm{MT}}}^2} } $ | (7) |
式中:PMT, QMT分别为微型燃气轮机的有功和无功出力; SMT, rated为微型燃气轮机的装机容量。
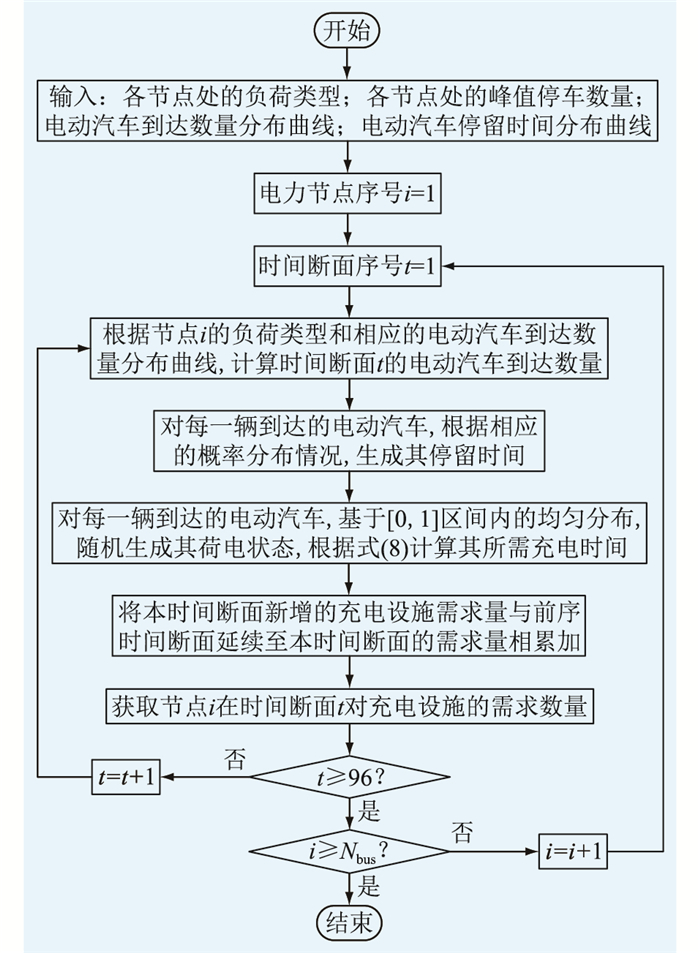
1.4 电动汽车充电负荷建模文中以目的地充电模式下城市内私人电动汽车为研究对象, 首先针对不同类型负荷对应的不同类型停车场(居民小区负荷、商场超市负荷、办公场所负荷)拟合电动汽车到达数量和停留时间的分布曲线, 从而量化表征电动汽车泊车行为。相关曲线的拟合过程见文献[19], 此处不再赘述。基于电动汽车的到达数量和停留时间分布曲线, 可以模拟生成任一典型日特定区域内的电动汽车充电负荷, 具体流程如图 2所示。图中, Nbus为配电系统中的节点数, 任一荷电状态已知的电动汽车所需的充电时间可通过式(8)计算。
| $ {T_{{\rm{ch}}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{E_{{\rm{cap }}}}\left( {1 - {c_{{\rm{SOC}}}}} \right)}}{{{P_{{\rm{EV}},{\rm{ rated }}}}}}\quad \frac{{{E_{{\rm{cap }}}}\left( {1 - {c_{{\rm{SOC}}}}} \right)}}{{{P_{{\rm{EV}},{\rm{ rated }}}}}} \le {T_{{\rm{park }}}}}\\ {{T_{{\rm{park }}}}\quad \frac{{{E_{{\rm{cap }}}}\left( {1 - {c_{{\rm{SOC}}}}} \right)}}{{{P_{{\rm{EV}},{\rm{ rated }}}}}} > {T_{{\rm{park }}}}} \end{array}} \right. $ | (8) |
|
图 2 任一典型日内电动汽车充电负荷的建模流程 Fig. 2 Modeling flow of electric vehicle charging load in a certain typical day |
式中:Tpark, Tch分别为该电动汽车的预计停留时间与所需充电时间; PEV, rated为充电设施的额定充电功率; Ecap, cSOC分别为该电动汽车的电池容量与荷电状态。
1.5 电力负荷建模文中考虑多种类型电力用户(居民小区负荷、商场超市负荷、办公场所负荷), 通过对历史数据拟合得到不同类型电力负荷在不同场景下的分布曲线。有关曲线的拟合过程见文献[19], 此处不再赘述。
2 分布式电源与电动汽车充电站协调配置模型 2.1 目标函数文中构建的分布式电源与电动汽车充电站协调配置模型以网损最小为目标, 网损如式(9)所示。
| $ \begin{array}{l} L = 65.25\sum\limits_{s = 1}^4 {\sum\limits_{t = 1}^{96} {\sum\limits_{k = 1}^N {L_{s,t,k}^{\rm{W}}} } } p\left( {S_{s,t,k}^{\rm{W}}} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 26\sum\limits_{s = 1}^4 {\sum\limits_{t = 1}^{96} {\sum\limits_{k = 1}^N {L_{s,t,k}^{{\rm{WD}}}} } } p\left( {S_{s,t,k}^{{\rm{WD}}}} \right) \end{array} $ | (9) |
式中:s, t, k分别表示季节、时间断面、离散状态; Ls, t, kW, Ls, t, kWD分别为工作日、周末典型日内的系统网损电量; p(Ss, t, kW), p(Ss, t, kWD)为离散状态出现的概率, 满足式(10)。
| $ \sum\limits_{k = 1}^N {\left[ {p\left( {S_{s,t,k}^{\rm{W}}} \right) + p\left( {S_{s,t,k}^{{\rm{WD}}}} \right)} \right]} = 1 $ | (10) |
文中忽略春、夏、秋、冬四季的细微差别, 每个季节包含65.25个工作日及26个周末, 任一离散状态对应的网损电量为:
| $ \left\{ {\begin{array}{*{20}{l}} {L_{s,t,k}^{\rm{W}} = \sum\limits_{i = 1}^{{N_{{\rm{bus }}}}} {\sum\limits_{j \in u(i)} {{{\left( {I_{ij,s,t,k}^{\rm{W}}} \right)}^2}} } {R_{ij}}\Delta t}\\ {L_{s,t,k}^{{\rm{WD}}} = \sum\limits_{i = 1}^{{N_{{\rm{bus }}}}} {\sum\limits_{j \in u(i)} {{{\left( {I_{ij,s,t,k}^{{\rm{WD}}}} \right)}^2}} } {R_{ij}}\Delta t} \end{array}} \right. $ | (11) |
式中:Nbus为配电系统的节点数; u(i)为所有与节点i相连且位于i下游的节点集合; Iij, s, t, kW, Iij, s, t, kWD分别为工作日、周末支路ij上的电流; Rij为支路ij的电阻; Δt为时间断面的持续时间, 文中取15 min。
2.2 约束条件式(12)—式(25)为文中所构建的协调配置模型的约束条件。为了描述方便, 在不引起歧义的前提下省略下标s, t, k及上标W, WD。所述的约束条件对任意典型日内的任一离散状态均具有效力。
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i \in v(j)} {\left( {{P_{ij}} - \frac{{P_{ij}^2 + Q_{ij}^2}}{{U_i^2}}{R_{ij}}} \right)} = \\ \sum\limits_{l \in u(j)} {{P_{jl}}} + {P_{{\rm{Load }},j}} - {P_{{\rm{PV}},j}} - {P_{{\rm{MT}},j}} + {P_{{\rm{EV}},j}}\quad \forall j \in {\varOmega _{\rm{N}}} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {\sum\limits_{i \in v(j)} {\left( {{Q_{ij}} - \frac{{P_{ij}^2 + Q_{ij}^2}}{{U_i^2}}{X_{ij}}} \right)} = }\\ {\sum\limits_{l \in u(j)} {{Q_{jl}}} + {Q_{{\mathop{\rm load}\nolimits} ,j}} - {Q_{{\rm{MT}},j}}\quad \forall j \in {\varOmega _{\rm{N}}}} \end{array} $ | (13) |
| $ \begin{array}{*{20}{l}} {U_j^2 = U_i^2 - 2\left( {{R_{ij}}{P_{ij}} + {X_{ij}}{Q_{ij}}} \right) + }\\ {\left( {R_{ij}^2 + X_{ij}^2} \right)\frac{{P_{ij}^2 + Q_{ij}^2}}{{U_i^2}}\quad \forall ij \in {\varOmega _{\rm{L}}}} \end{array} $ | (14) |
| $ {I_{ij}^2 = \frac{{P_{ij}^2 + Q_{ij}^2}}{{U_i^2}}\quad \forall ij \in {\varOmega _{\rm{L}}}} $ | (15) |
| $ {{U_{\min }} \le {U_i} \le {U_{\max }}\quad \forall i \in {\varOmega _{\rm{N}}}} $ | (16) |
| $ {\left| {{I_{ij}}} \right| \le {I_{ij,\max }}\quad \forall ij \in {\varOmega _{\rm{L}}}} $ | (17) |
| $ {S_{{\rm{PV}},i}^{{\rm{rated }}} = {N_{{\rm{PV}},i}}S_{{\rm{PV}}}^{{\rm{unit }}}\quad \forall i \in {\varOmega _{{\rm{PV}}}}} $ | (18) |
| $ {S_{{\rm{MT}},i}^{{\rm{rated }}} = {N_{{\rm{MT}},i}}S_{{\rm{MT}}}^{{\rm{unit }}}\quad \forall i \in {\varOmega _{{\rm{MT}}}}} $ | (19) |
| $ {\sum\limits_{i \in {\varOmega _{{\rm{PV}}}}} {S_{{\rm{PV}},i}^{{\rm{rated }}}} \ge p_{\min }^{{\rm{PV}}}\sum\limits_{i = 1}^{{N_{{\rm{bus }}}}} {P_{{\rm{Load }},i}^{{\rm{peak }}}} } $ | (20) |
| $ {\sum\limits_{i \in {\varOmega _{{\rm{MT}}}}} {S_{{\rm{MT}},i}^{{\rm{rated}}}} \le p_{\max }^{{\rm{MT}}}\sum\limits_{i = 1}^{{N_{{\rm{bus}}}}} {P_{{\rm{Load}},i}^{{\rm{peak}}}} } $ | (21) |
| $ {0 \le {P_{{\rm{MT}},i}} \le S_{{\rm{MT}},i}^{{\rm{rated}}}\quad \forall i \in {\varOmega _{{\rm{MT}}}}} $ | (22) |
| $ {\sqrt {P_{{\rm{MT}},i}^2 + Q_{{\rm{MT}},i}^2} \le S_{{\rm{MT}},i}^{{\rm{rated }}}\quad \forall i \in {\varOmega _{{\rm{MT}}}}} $ | (23) |
| $ {{P_{{\rm{EV}},j}} = {N_{{\rm{EV}},j}}P_{{\rm{EV}}}^{{\rm{rated }}}\quad \forall j \in {\varOmega _{{\rm{CF}}}}} $ | (24) |
| $ {{N_{{\rm{CF}},j}} = \max \left\{ {{N_{{\rm{EV}},j,s,t,k}}} \right\}\quad \forall s,t,k,\forall j \in {\varOmega _{{\rm{CF}}}}} $ | (25) |
式(12)—式(14)为应用于辐射型配电系统的Distflow潮流方程[20]; 式(15)为支路电流的量化方程; 式(16)、式(17)分别为节点电压和支路电流的越限约束; 式(18)、式(19)为分布式电源容量的离散性约束; 式(20)、式(21)分别为光伏和微型燃气轮机的渗透率约束; 式(22)、式(23)为微型燃气轮机的出力约束; 式(24)为电动汽车充电功率的量化方程; 式(25)为电动汽车充电站充电设施安装数量约束。约束条件中的变量及参数含义见表 1。
|
|
表 1 约束条件中的变量及参数含义 Table 1 Variable and parameter meaning in the constraints |
综上, 得到如式(26)所示的协调配置模型, 其包含连续型和整数型变量、非线性目标函数、线性和非线性约束条件, 为混合整数非线性规划模型。
| $ \left\{ {\begin{array}{*{20}{l}} {\min }&{{\rm{ 式 }}(9)}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}}&{{\rm{ 式 }}(12) - {\rm{式}}(25)} \end{array}} \right. $ | (26) |
采用精确的二阶锥松弛技术对式(26)的协调配置模型进行等价处理, 将混合整数非线性规划模型转换为混合整数二阶锥规划模型进行求解[19]。基于精确二阶锥松弛技术的等价处理步骤为:
(1) 应用式(27)、式(28)所示的变量代换处理优化模型的目标函数和相关的约束条件。
| $ \begin{array}{*{20}{c}} {{{\bar I}_{ij}} = I_{ij}^2}&{\forall ij \in {\varOmega _{\rm{L}}}} \end{array} $ | (27) |
| $ \begin{array}{*{20}{c}} {{{\bar U}_i} = U_i^2}&{\forall i \in {\varOmega _{\rm{N}}}} \end{array} $ | (28) |
则式(11)—式(17)转换为式(29)—式(35)。
| $ L = \sum\limits_{i = 1}^{{N_{{\rm{bus }}}}} {\sum\limits_{j \in u(i)} {{{\bar I}_{ij}}} } {R_{ij}}\Delta t $ | (29) |
| $ \begin{array}{l} \sum\limits_{i \in v(j)} {\left( {{P_{ij}} - {{\bar I}_{ij}}{R_{ij}}} \right)} = \sum\limits_{l \in u(j)} {{P_{jl}}} + {P_{{\rm{Load}},j}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {P_{{\rm{PV}},j}} - {P_{{\rm{MT}},j}} + {P_{{\rm{EV}},j}}\quad \forall j \in {\varOmega _{\rm{N}}} \end{array} $ | (30) |
| $ \begin{array}{l} \sum\limits_{i \in v(j)} {\left( {{Q_{ij}} - {{\bar I}_{ij}}{X_{ij}}} \right)} = \sum\limits_{l \in u(j)} {{Q_{jl}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {Q_{{\rm{load }},j}} - {Q_{{\rm{MT }},j}}\forall j \in {\varOmega _{\rm{N}}} \end{array} $ | (31) |
| $ \begin{array}{*{20}{c}} {{{\bar U}_j} = {{\bar U}_i} - 2\left( {{R_{ij}}{P_{ij}} + {X_{ij}}{Q_{ij}}} \right) + }\\ {\left( {R_{ij}^2 + X_{ij}^2} \right){{\bar I}_{ij}}\quad \forall ij \in {\varOmega _{\rm{L}}}} \end{array} $ | (32) |
| $ {{{\bar I}_{ij}} = \frac{{P_{ij}^2 + Q_{ij}^2}}{{{{\bar U}_i}}}\quad \forall ij \in {\varOmega _{\rm{L}}}} $ | (33) |
| $ {{U_{{{\min }^2}}} \le {{\bar U}_i} \le {U_{{{\max }^2}}}\quad \forall i \in {\varOmega _{\rm{N}}}} $ | (34) |
| $ {{{\bar I}_{ij}} \le I_{ij,\max }^2\quad \forall ij \in {\varOmega _{\rm{L}}}} $ | (35) |
(2) 将式(33)中的“=”松弛为“≥”, 即:
| $ {\bar I_{ij}} \ge \frac{{P_{ij}^2 + Q_{ij}^2}}{{{{\bar U}_i}}}\quad \forall ij \in {\varOmega _{\rm{L}}} $ | (36) |
式(36)的典型二阶锥约束可表示为:
| $ {\left\| {\begin{array}{*{20}{c}} {2{P_{ij}}}\\ {2{Q_{ij}}}\\ {{{\bar I}_{ij}} - {{\bar U}_i}} \end{array}} \right\|_2} \le {\bar I_{ij}} + {\bar U_i}\quad \forall ij \in {\varOmega _{\rm{L}}} $ | (37) |
所构建优化模型的目标函数是关于Iij的单调递增函数, 步骤(2)中的松弛为等价松弛, 并不影响优化模型的最优解。有关该松弛的精确性, 可参考文献[17, 21-22]。
(3) 将式(23)表示为二阶锥形式。
| $ {\left\| {\begin{array}{*{20}{l}} {{P_{{\rm{MT}},i}}}\\ {{Q_{{\rm{MT}},i}}} \end{array}} \right\|_2} \le S_{{\rm{MT}},i}^{{\rm{rated }}}\quad \forall i \in {\varOmega _{{\rm{MT}}}} $ | (38) |
则式(26)的混合整数非线性规划模型转化为式(39)的混合整数二阶锥规划模型, 包含线性的目标函数、线性的约束条件和二阶锥约束条件, 可通过现有的优化算法在多项式时间内寻得最优解。
| $ \left\{ {\begin{array}{*{20}{l}} {\min }&{{\rm{ 式}}(9)}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}}&{{\rm{ 式(}}18){\rm{ — 式 }}(22)}\\ {}&{{\rm{ 式(}}24){\rm{ — 式 }}(25)}\\ {}&{{\rm{ 式(}}30){\rm{ — 式 }}(32)}\\ {}&{{\rm{ 式(34) — 式 }}(35)}\\ {}&{{\rm{ 式(37) — 式 }}(38)} \end{array}} \right. $ | (39) |
文中以IEEE 33节点配电系统为例[20], 验证所提协调配置模型及松弛方法的有效性。在求解算法方面, 基于Matlab环境, 使用Yalmip工具箱调用商业求解器Gurobi对松弛后的混合整数二阶锥规划模型进行求解。
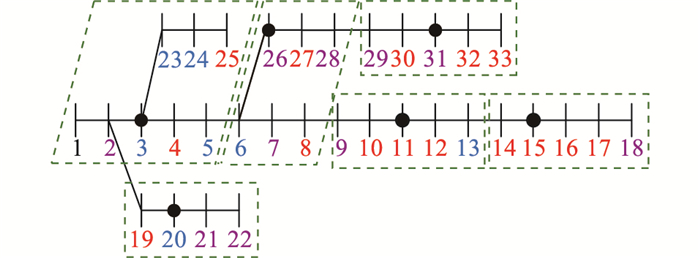
IEEE 33节点配电系统拓扑结构见图 3, 不同颜色的节点序号表示不同的负荷类型, 黑色表示系统根节点, 红色表示居民小区负荷, 紫色表示商场超市负荷, 蓝色表示办公场所负荷。配电系统的3, 11, 15, 20, 26, 31节点处建有电动汽车充电站, 每个电动汽车充电站的服务区域如绿色虚线框所示。
|
图 3 IEEE 33节点配电系统及相关设置 Fig. 3 IEEE 33-bus distribution system and relevant settings |
文中采用美国俄勒冈大学太阳辐射监测实验室统计的俄勒冈州梅德福地区(Medford)历史太阳光照强度数据[23], 将每个时间断面对应的太阳光照强度概率密度函数离散为5个确定性状态。选定节点集6, 12, 15, 21, 24, 32, 4, 7, 16, 22, 25, 29分别作为光伏电站和微型燃气轮机的候选安装节点集合。设定光伏模块和微型燃气轮机的最小单位容量均为10 kW, 并将协调配置中所允许的光伏渗透率下限及微型燃气轮机渗透率上限设定为40%, 系统中节点电压允许范围的下限与上限分别设为0.9 p.u., 1.1 p.u., 每条支路上允许流过的最大电流为500 A。电动汽车充电设施的额定功率、电动汽车充放电行为的相关参数以及电力用户负荷的分布情况均使用真实数据, 详见文献[12]。分布式电源与电动汽车充电站的协调配置结果为:节点6, 12, 15, 21, 24, 32安装光伏容量分别为1 320 kW, 440 kW, 270 kW, 530 kW, 1 110 kW, 960 kW, 合计4 630 kW; 节点7, 16, 29安装微型燃气轮机容量分别为70 kW, 610 kW, 800 kW, 合计1 480 kW; 节点3, 11, 15, 20, 26, 31安装充电设施分别为37套, 17套, 23套, 13套, 25套, 25套, 合计140套; 目标函数值为1.695 3×105 kW·h。
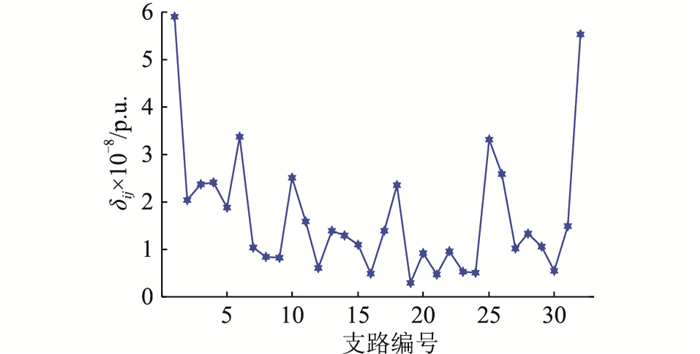
为了有效验证二阶锥松弛的精确性, 即松弛前后分布式电源与电动汽车充电站协调配置模型的等价性, 文中引入偏差变量δij表征对应于支路ij的松弛偏差情况, 如式(40)所示。偏差变量δij分布如图 4所示。。
| $ \begin{array}{*{20}{c}} {{\delta _{ij}} = \max \left\{ {\left| {{{\bar I}_{ij,s,t,k}} - \frac{{P_{ij,s,t,k}^2 + Q_{ij,s,t,k}^2}}{{{{\bar U}_{i,s,t,k}}}}} \right|} \right\}}\\ {\forall s,t,k,\forall ij \in {\varOmega _{\rm{L}}}} \end{array} $ | (40) |
|
图 4 偏差变量δij分布 Fig. 4 Distribution of deviation variable δij |
由图 4可知, 算例分析结果对应的δij均处于10-8这一数量级或更小的数量级, 可认为是复杂计算过程中引入的合理截断误差。这一现象有效验证了文中所采用二阶锥松弛的精确性。即优化模型的最优解是在式(36)左右两部分相等时取得, 引入二阶锥松弛技术并未改变原有协调配置模型的最优解分布。
5 结语文中应用离散化的多状态模型表征可再生资源的不确定性, 构建了以系统网损最小为目标的光伏电站、微型燃气轮机、电动汽车充电站协调配置模型。为降低所建模型的求解难度, 文中采用精确的二阶锥松弛技术对其进行等价处理, 将混合整数非线性规划模型转换为混合整数二阶锥规划模型进行求解。研究成果可在分布式电源与电动汽车充电站的协调配置中有效计及可再生资源不确定性的影响, 得到更加符合工程实际需求的协调配置方案。
本文得到国网江苏省电力有限公司科技项目(J2019100)资助, 谨此致谢!
| [1] |
郭云鹏, 刘伟佳, 文福拴, 等. 智能配电系统的发展现状与展望[J]. 华北电力大学学报(自然科学版), 2014, 41(5): 74-81. GUO Yunpeng, LIU Weijia, WEN Fushuan, et al. State-of-the-art and prospect of smart distribution system development[J]. Journal of North China Electric Power University(Natural Science Edition), 2014, 41(5): 74-81. DOI:10.3969/j.ISSN.1007-2691.2014.05.13 (  0) 0) |
| [2] |
潘明明, 孙晓辉, 于建成. 基于改进Kalman滤波块状态估计方法的分布式光伏发电预测[J]. 供用电, 2019, 36(2): 56-60. PAN Mingming, SUN Xiaohui, YU Jiancheng. A distributed photovoltaic generation prediction based on improved Kalman filter block state estimation method[J]. Distribution & Utilization, 2019, 36(2): 56-60. (  0) 0) |
| [3] |
艾圣芳, 林湘宁, 万云飞, 等. 考虑V2G模式的含多个电动汽车充电站有源配电网规划研究[J]. 中国电机工程学报, 2013, 33(34): 122-129. AI Shengfang, LIN Xiangning, WAN Yunfei, et al. Study of the active distribution network planning considering multiple electric vehicle charging stations participating in V2G applications[J]. Proceedings of the CSEE, 2013, 33(34): 122-129. (  0) 0) |
| [4] |
ZHANG J, LIU C, YUAN R, et al. Design scheme for fast charging station for electric vehicles with distributed photovoltaic power generation[J]. Global Energy Interconnection, 2019, 2(2): 150-159. DOI:10.1016/j.gloei.2019.07.003 (  0) 0) |
| [5] |
所丽, 唐巍, 白牧可, 等. 考虑削峰填谷的配电网集中型充电站选址定容规划[J]. 中国电机工程学报, 2014, 34(7): 1052-1060. SUO Li, TANG Wei, BAI Muke, et al. Locating and sizing of centralized charging stations in distribution network considering load shifting[J]. Proceedings of the CSEE, 2014, 34(7): 1052-1060. (  0) 0) |
| [6] |
PAZOUKI S, MOHSENZADEH A, ARDALAN S, et al. Simultaneous planning of PEV charging stations and DGs considering financial, technical, and environmental effects[J]. Canadian Journal of Electrical & Computer Engineering, 2015, 38(3): 238-245. (  0) 0) |
| [7] |
刘柏良, 黄学良, 李军, 等. 含分布式电源及电动汽车充电站的配电网多目标规划研究[J]. 电网技术, 2015, 39(2): 450-456. LIU Bailiang, HUANG Xueliang, LI Jun, et al. Multi-objective planning of distribution network containing distributed generation and electric vehicle charging stations[J]. Power System Technology, 2015, 39(2): 450-456. (  0) 0) |
| [8] |
田园园, 廖清芬, 徐雨田, 等. 基于有序充电策略的换电站及分布式电源多场景协调规划方法[J]. 电力自动化设备, 2017, 37(9): 62-69. TIAN Yuanyuan, LIAO Qingfen, XU Yutian, et al. Multi-scenario coordinated planning method of EV battery-swapping station and distributed generation based on coordinated charging strategy[J]. Electric Power Automation Equipment, 2017, 37(9): 62-69. (  0) 0) |
| [9] |
ZHANG H, MOURA S, HU Z, et al. Joint PEV charging station and distributed PV generation planning[C]//2017 IEEE PES General Meeting. IEEE, 2017.
(  0) 0) |
| [10] |
ZHANG H, MOURA S J, HU Z, et al. Joint PEV charging network and distributed PV generation planning based on accelerated generalized benders decomposition[J]. IEEE Transactions on Transportation Electrification, 2018, 4(3): 789-803. DOI:10.1109/TTE.2018.2847244 (  0) 0) |
| [11] |
ERDIN O, TACIKARAOLU A, PATERAKIS N G, et al. Comprehensive optimization model for sizing and siting of DG units, EV charging stations, and energy storage systems[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3871-3882. DOI:10.1109/TSG.2017.2777738 (  0) 0) |
| [12] |
LUO L, GU W, WU Z, et al. Joint planning of distributed generation and electric vehicle charging stations considering real-time charging navigation[J]. Applied Energy, 2019(242): 1274-1284. (  0) 0) |
| [13] |
AMINI M H, MOGHADDAM M P, KARABASOGLU O. Simultaneous allocation of electric vehicles' parking lots and distributed renewable resources in smart power distribution networks[J]. Sustainable Cities & Society, 2017(28): 332-342. (  0) 0) |
| [14] |
ATWA Y M, EL-SAADANY E F, SALAMA M M A, et al. Optimal renewable resources mix for distribution system energy loss minimization[J]. IEEE Transactions on Power Systems, 2010, 25(1): 360-370. DOI:10.1109/TPWRS.2009.2030276 (  0) 0) |
| [15] |
ZENG B, ZHANG J, YANG X, et al. Integrated planning for transition to low-carbon distribution system with renewable energy generation and demand response[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1153-1165. DOI:10.1109/TPWRS.2013.2291553 (  0) 0) |
| [16] |
ZOU K, AGALGAONKAR A P, MUTTAQI K M, et al. Distribution system planning with incorporating DG reactive capability and system uncertainties[J]. IEEE Transactions on Sustainable Energy, 2012, 3(1): 112-123. DOI:10.1109/TSTE.2011.2166281 (  0) 0) |
| [17] |
LUO L, GU W, ZHANG X P, et al. Optimal siting and sizing of distributed generation in distribution systems with PV solar farm utilized as STATCOM(PV-STATCOM)[J]. Applied energy, 2018(210): 1092-1100. (  0) 0) |
| [18] |
LIU Z, WEN F, LEDWICH G. Optimal siting and sizing of distributed generators in distribution systems considering uncertainties[J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2541-2551. DOI:10.1109/TPWRD.2011.2165972 (  0) 0) |
| [19] |
LUO L, GU W, ZHOU S, et al. Optimal planning of electric vehicle charging stations comprising multi-types of charging facilities[J]. Applied energy, 2018(226): 1087-1099. (  0) 0) |
| [20] |
BARAN M E, WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407. DOI:10.1109/61.25627 (  0) 0) |
| [21] |
FARIVAR M, LOW S H. Branch flow model: relaxations and convexification[C]//51st IEEE Annual Conference on Decision and Control. IEEE, 2012.
(  0) 0) |
| [22] |
FARIVAR M, LOW S H. Branch flow model:relaxations and convexification—Part I[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2554-2564. DOI:10.1109/TPWRS.2013.2255317 (  0) 0) |
| [23] |
UO solar radiation monitoring laboratory[EB/OL].[2020-05-07]. http://solardat.uoregon.edu/SolarData.html.
(  0) 0) |
2. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2021, Vol. 40
2021, Vol. 40


 钱仲豪(1988), 男, 博士, 工程师, 从事分布式新能源调度运行管理、配网调控运行管理、电力系统运行方式管理等工作(E-mail:
钱仲豪(1988), 男, 博士, 工程师, 从事分布式新能源调度运行管理、配网调控运行管理、电力系统运行方式管理等工作(E-mail: