文章编号: 2096-3203(2021)01-0175-06 中图分类号: TM910.6 文献标识码: A
2. 北京科东电力控制系统有限责任公司,北京 100192
电力系统负荷预测可对未来一段时间的电力需求进行估计,从而根据负荷预测结果安排未来一段时间的机组组合计划、发电计划、联络线交换计划,组织电力现货交易。因此,准确的负荷预测是实现电力系统安全、经济运行的基础[1]。
电力系统负荷受天气、节假日、特殊事件等因素的影响,负荷变化随机性较大[2-4]。分布式电源的接入和电动汽车的广泛应用进一步加大了负荷的随机性和波动性[5-7],增加了负荷精准预测难度。电力负荷预测方法主要分为两大类:统计学方法和基于机器学习的方法。统计学方法采用时间序列方法进行预测[8-9],主要包括多元线性回归(multiple linear regression,MLR)、自回归(auto regression,AR)、自回归移动平均(auto regressive moving average,ARMA)等。该类方法对电力负荷序列的平稳性要求较高,但电力负荷具有较强的随机性,不是平稳时间序列。为了提高负荷预测的准确性,诸多研究将机器学习算法应用在电力负荷预测领域。文献[10]采用K近邻(K-nearest neighbor,KNN)算法实现短期电力负荷预测,提升了负荷预测的精度和计算速度;文献[11]基于深度信念网络构建母线负荷预测模型;文献[12]提出基于改进人工神经网络的短期负荷预测方法;文献[13]将随机森林回归算法应用于短期电力负荷预测;文献[14]应用支持向量机(support vector machines,SVM),并引入实时电价这一影响因素提升负荷预测准确度;文献[15]提出基于多模型融合Stacking集成学习方式的负荷预测方法。机器学习方法从历史负荷数据中学习隐含规律,具备较强的非线性建模能力。传统的机器学习方法仅能学习各类影响因素与负荷之间的非线性关系,未考虑负荷本身的时序依赖关系。
为了兼顾负荷本身的时序依赖关系,采用长短期记忆单元(long short-term memory,LSTM)构建负荷预测模型。利用LSTM替代原有循环神经网络(recurrent neural network,RNN)中的神经元,使普通RNN具备时序记忆能力,实现对负荷本身时序特性、影响因素与负荷之间复杂关系的建模。该方法可以灵活定义历史窗口期、灵活添加负荷影响因素,且预测准确性和稳定性较高。
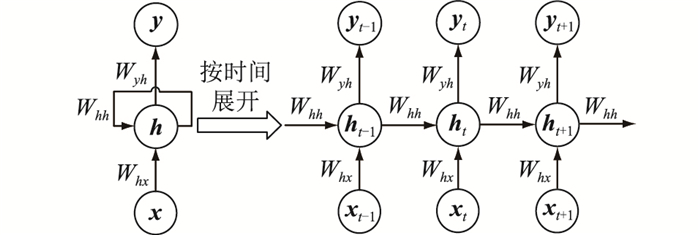
1 RNN 1.1 普通RNNRNN是一种能够处理时间序列数据的神经网络[16],广泛应用于自然语言处理领域[17],在电力系统中也有应用[18]。RNN架构如图 1所示。
|
图 1 RNN架构 Fig. 1 The architecture of RNN |
与前馈神经网络相比,RNN隐藏层中的每个神经元可以通过自链接循环使用。给定输入数据X = x1, x2, …, xt, …, xT,RNN采用式(1)和式(2)计算隐藏状态h = h1, h2, …, ht, …, hT和输出y = y1, y2, …, yt, …, yT。其中T为1 d内根据采样间隔计算的采样点数量。
| $ {{\mathit{\boldsymbol{h}}_t} = f\left( {{W_{hx}}{\mathit{\boldsymbol{x}}_t} + {W_{hh}}{\mathit{\boldsymbol{h}}_{t - 1}} + {\mathit{\boldsymbol{b}}_{\rm{h}}}} \right)} $ | (1) |
| $ {{\mathit{\boldsymbol{y}}_t} = g\left( {{W_{yh}}{\mathit{\boldsymbol{h}}_t} + {\mathit{\boldsymbol{b}}_{\rm{y}}}} \right)} $ | (2) |
式中:xt为t时刻的输入;yt为t时刻的输出;ht为t时刻的隐藏状态;Whx,Whh,Wyh分别为输入、隐藏和输出权重;bh,by分别为隐藏状态和输出的偏置; f(·),g(·)分别为隐藏层和输出层激活函数。
RNN采用ht-1记忆t时刻之前的所有输入信息,t时刻输出yt不但受该时刻输入xt的影响,还受ht-1的影响。RNN采用时间反向传播(back propagation through time,BPTT)算法进行训练[16-17],训练过程中存在梯度消失问题,导致RNN不能学习时间序列的长距离时序依赖关系[19]。LSTM在神经元中加入记忆单元和门控单元,使RNN具备记忆能力,从而可以学习时序数据的长期依赖关系。
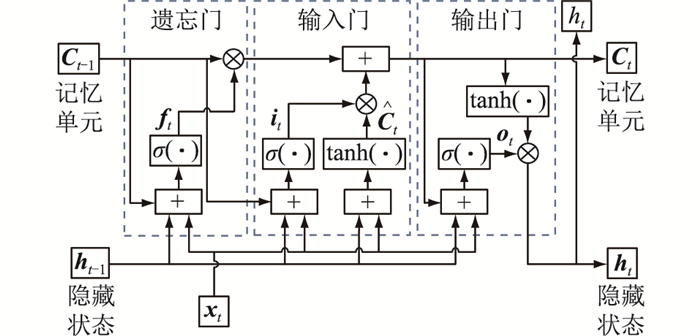
1.2 LSTMLSTM是对普通神经元的改进,在隐藏层的每个神经元引入记忆单元,并采用遗忘门、输入门、输出门3个门控单元控制记忆单元的状态,解决普通RNN不能学习长距离时序依赖的问题[19]。LSTM结构如图 2所示[20-21]。
|
图 2 LSTM结构 Fig. 2 The structure of LSTM |
记忆单元与隐藏状态一起记忆序列数据的历史信息。记忆单元中的信息受3个门控单元的控制。遗忘门根据ht-1和xt删除记忆单元中的信息。遗忘门为:
| $ {\mathit{\boldsymbol{f}}_t} = \sigma \left( {{W_{\rm{f}}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{h}}_{t - 1}}}&{{\mathit{\boldsymbol{x}}_t}} \end{array}} \right]} \right) + {\mathit{\boldsymbol{b}}_{\rm{f}}} $ | (3) |
式中:σ(·)为sigmoid激活函数;Wf为遗忘门权重;bf为遗忘门偏置。
输入门根据ht-1和xt向记忆单元中新增信息,如式(4)、式(5)所示。
| $ {{\mathit{\boldsymbol{i}}_t} = \sigma \left( {{W_{\rm{i}}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{h}}_{t - 1}}}&{{\mathit{\boldsymbol{x}}_t}} \end{array}} \right]} \right) + {\mathit{\boldsymbol{b}}_{\rm{i}}}} $ | (4) |
| $ {{{\mathit{\boldsymbol{\hat C}}}_t} = \tanh \left( {{W_{\rm{c}}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{h}}_{t - 1}}}&{{\mathit{\boldsymbol{x}}_t}} \end{array}} \right]} \right) + {\mathit{\boldsymbol{b}}_{\rm{c}}}} $ | (5) |
式中:it为需要记忆的信息;
遗忘门和输出门计算完成后,采用式(6)更新记忆单元。
| $ {\mathit{\boldsymbol{C}}_t} = {\mathit{\boldsymbol{f}}_t} \circ {\mathit{\boldsymbol{C}}_{t - 1}} + {\mathit{\boldsymbol{i}}_t} \circ {\mathit{\boldsymbol{\hat C}}_t} $ | (6) |
式中:○为哈达玛乘积。
输出门根据ht-1,xt,Ct,决定ht。
| $ {{\mathit{\boldsymbol{o}}_t} = \sigma \left( {{W_{\rm{o}}}\left[ {{\mathit{\boldsymbol{h}}_{t - 1}}\quad {\mathit{\boldsymbol{x}}_t}} \right]} \right) + {\mathit{\boldsymbol{b}}_{\rm{o}}}} $ | (7) |
| $ {{\mathit{\boldsymbol{h}}_t} = {\mathit{\boldsymbol{o}}_t} \circ \tanh {\mathit{\boldsymbol{C}}_t}} $ | (8) |
式中:Wo为输出门权重;bo为输出门偏置。
采用LSTM替换普通RNN中的神经元构建负荷预测模型,利用LSTM能学习长距离时序依赖的优点,对电力负荷中隐藏的历史运行规律进行学习。
2 基于LSTM的负荷预测模型 2.1 基本思路电力系统负荷受人们生产生活规律的影响,具备周期性、趋势性,同时又受天气变化、重大事件等随机因素的影响,具有较大的不确定性。某天某一时刻的负荷lt, d受当天日期类型(周几、是否节假日)和当前时刻天气因素(温度、湿度等)的影响,同时又与当天历史n个时刻的负荷和历史几天同一时刻的负荷有关。利用LSTM能学习长距离时序依赖的优点,在考虑预测日当天相关因素对负荷影响的基础上,从横向上识别预测日当天负荷变化的规律,从纵向上识别历史日期窗口内同一时刻负荷的变化规律。
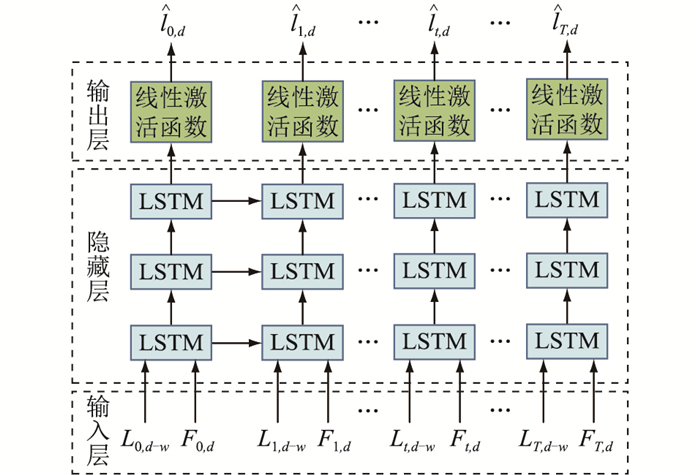
2.2 模型结构基于LSTM网络,用预测日前w天的负荷曲线和负荷影响因素对预测日负荷进行预测,LSTM网络结构如图 3所示。图中,模型输出为预测日的预测负荷,如式(9)所示。
| $ {\hat L_d} = \left\{ {{{\hat l}_{0,d}},{{\hat l}_{1,d}}, \cdots ,{{\hat l}_{t,d}}, \cdots ,{{\hat l}_{T,d}}} \right\} $ | (9) |
|
图 3 用于负荷预测的LSTM网络模型 Fig. 3 LSTM network model for load forecast |
式中:当采样间隔为15 min时, T=96。
历史负荷为:
| $ {L_{t,d - w}} = \left\{ {{l_{t,d - 1}},{l_{t,d - 2}}, \cdots ,{l_{t,d - w}}} \right\} $ | (10) |
式中:lt, d-w为预测日前w天t时刻的负荷。
负荷影响因素为:
| $ {F_{t,d}} = \left\{ {{w_{t,d}},{e_{t,d}}, \cdots ,{h_{t,d}}} \right\} $ | (11) |
式中:wt, d为天气信息;ht, d为0-1变量,为0代表非工作日,为1代表工作日;et, d为影响负荷的特殊事件;Ft, d中还可包含影响负荷的其他因素。
建立的负荷预测模型中,第t时刻的输入由历史负荷和负荷影响因素共同构成,可表示为
预测模型的训练过程包含数据预处理、模型训练、模型评价3个阶段。
2.3.1 数据预处理数据预处理主要包括数据向量化和标准化2个步骤。神经网络基于线性代数理论,不能直接在原始数据上进行训练,在训练之前需要将原始数据转换为向量[22]。数据向量化将Lt, d-w与Ft, d进行拼接,拼接后的数据转化为向量。
神经网络采用基于梯度下降的反向传播算法进行训练[22],数据太大或太小会导致很难寻求到最优解。因此,将数据归一化到标准区间有利于模型求解。采用最小-最大归一化方法将向量中的每个元素归一化到区间[0, 1],如式(12)所示[22]。
| $ X_{\text {norm }}=\frac{X-X_{\min }}{X_{\max }-X_{\min }} $ | (12) |
式中:Xmax, Xmin分别为最大、最小值;X为原始值;Xnorm为归一化后的值。
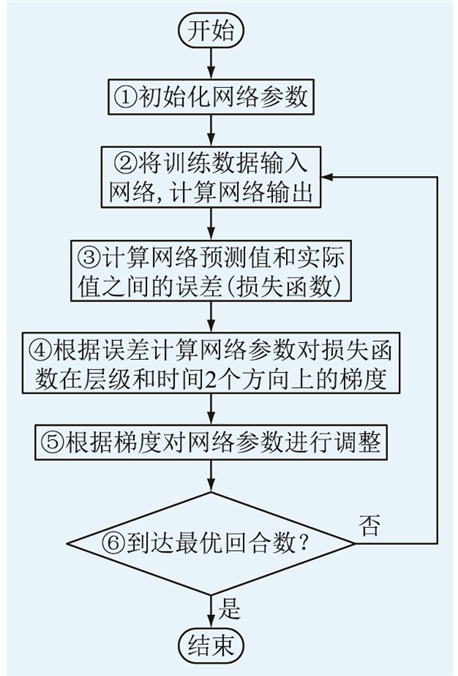
2.3.2 模型训练采用BPTT算法对用于负荷预测的LSTM网络进行训练。训练目标是调整网络参数使网络输出尽可能接近真实值,训练过程如图 4所示。
|
图 4 模型训练流程 Fig. 4 Model training process |
图 4中,②和③为前向推理过程,④和⑤为反向传播过程。损失函数包括均方误差(mean square error,MSE)损失、均方根误差(root mean square error,RMSE)损失、平均绝对误差(mean absolute error,MAE)损失等。文中采用MSE作为损失函数,表示为[18]:
| $ {L_{a,b}} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\hat L}_i} - {L_i}} \right)}^2}} $ | (13) |
式中:N为训练样本总数;
模型训练过程中,将所有数据输入网络并对其参数进行调整,称为一个回合。回合数过少导致网络欠拟合,回合数过多导致网络过度拟合。为了确定合适的回合数,选择最优的模型,需要在每个回合训练结束后对模型进行评价,过程如图 5所示。
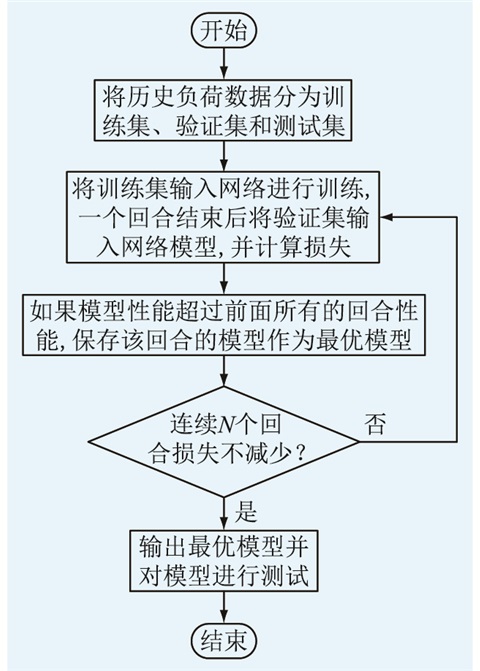
|
图 5 最优训练回合数确定流程 Fig. 5 Determination process of optimal training epoch |
采用美国德州可靠性委员会控制区域2003年-2018年的每小时历史系统负荷数据对文中的模型进行验证[23]。将2003年-2016年的数据作为训练集,2017年的数据作为验证集,2018年的数据作为测试集。验证集用来验证最优训练回合数、最佳网络结构和参数。测试集用来测试模型预测效果。训练预测模型过程中考虑了天气(气温),日期类型(是否工作日,周几等),历史窗口期内同一时刻负荷,历史窗口期内每天的最大、最小负荷等因素,如表 1所示。
|
|
表 1 实验所选取的负荷影响因素 Table 1 Power load influencing factors in the experiment |
常用的负荷预测评价指标包括RMSE、MAE、绝对百分比误差(absolute percentage error,APE)等。通常采用所有样本APE的平均值(mean absolute percentage error,MAPE)eMAPE衡量负荷预测模型的整体性能。与其他方法进行比较时,采用MAE、RMSE、APE对算法性能进行分析,分别如式(14)-式(16)。
| $ {{e_{{\rm{MAE}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{{\hat L}_i} - {L_i}} \right|} } $ | (14) |
| $ {{e_{{\rm{RMSE}}}} = \frac{1}{N}\sqrt {\sum\limits_{i = 1}^N {{{\left( {{{\hat L}_i} - {L_i}} \right)}^2}} } } $ | (15) |
| $ {{e_{{\rm{APE}}}} = \frac{{\left| {{{\hat L}_i} - {L_i}} \right|}}{{{L_i}}} \times 100\% } $ | (16) |
式中:N为训练样本总数;
构建的LSTM网络,隐藏层数和每个隐藏层LSTM的数量对负荷预测精度均有影响。以2017年全年每小时历史负荷数据作为验证集,固定历史日期窗口w为7 d,采用枚举法对隐藏层神经元数量进行逐层选取,确定最优网络结构。首先,确定第1层隐藏神经元的最佳数量并固定;然后,确定下一层隐藏层即第2层隐藏层神经元数量的最佳值;依次类推,直到预测精度不再提高为止。不同网络结构下的预测性能如表 2所示。对每层神经元的数量进行选取时,依次设置为5~40个(间隔为5个),共8个级别。隐藏层的层数依次设置为1,2,3层。
|
|
表 2 不同LSTM网络结构的预测性能 Table 2 Forecasting performance of different LSTM network structures |
由表 2可知,隐藏层数为1,每层神经元数量为5时,eMAPE取得最小值4.6%;隐藏层数为2,每层神经元数为20时,eMAPE取得最小值4.72%;隐藏层为3,每层神经元数为10时,eMAPE取得最小值4.58%。因此,w为7 d且隐藏层数目为3,每层神经元的数目为10时,网络的预测性能较好。
3.4 历史日期窗口选择设置网络层数分别为1, 2, 3层,隐藏单元数分别为5,20, 10。w取1~60 d。同样采用2017年全年每小时历史负荷数据作为验证集。不同网络结构下eMAPE随w的变化曲线见图 6。
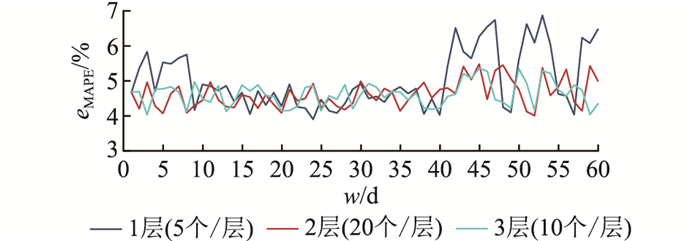
|
图 6 不同LSTM网络结构下eMAPE随w的变化 Fig. 6 The change of eMAPE with w under different LSTM network structures |
由图 6可知,随着w增大,不同网络结构的eMAPE相差不大,无明显下降或上升趋势,但eMAPE的变化在w较大时不太稳定。特别是网络结构为1层,每层5个神经元时,较大的w使eMAPE变化剧烈。3种网络结构下,w为7~30 d时,MAPE都较低,且变化平稳。隐藏层为1,每层神经元数为5,w为23 d时,预测性能最优,eMAPE仅为3.9%。
3.5 结果分析为了验证文中所提方法的性能,选择最优的预测模型(隐藏层为1,每层神经元数为5,w为23 d),采用2018年全年每小时负荷作为测试集对模型预测性能进行测试,并与KNN、SVM算法进行对比。2018年5月的预测结果如图 7所示。图 7(a)为实际负荷与每种方法预测负荷的对比;图 7(b)为每种预测方法每个时间点的APE。由图 7可知,与其他2种方法相比,LSTM算法的APE较小且变化幅度不大,说明LSTM算法的预测性能和预测效果优于其他2种算法。
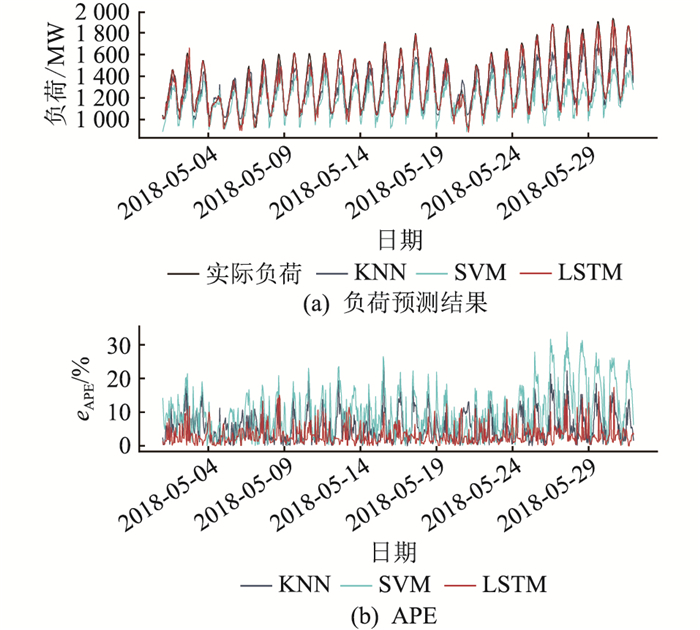
|
图 7 2018年5月负荷预测结果及误差 Fig. 7 Results and errors of load forecast on May 2018 |
为了进一步验证LSTM算法的性能,计算每种算法的APE、MAE和RMSE。APE箱形图见图 8。
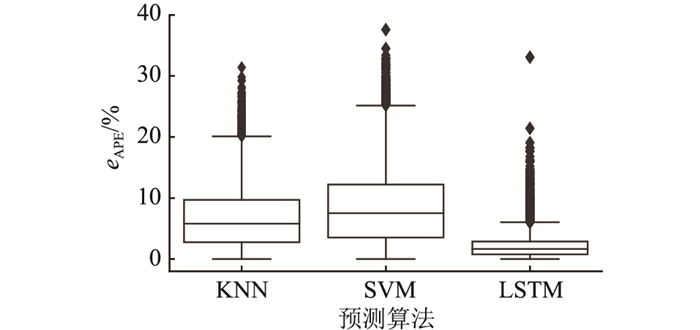
|
图 8 算法的APE分布 Fig. 8 APE distribution of each algorithm |
由图 8可知,LSTM算法与其他2种算法相比,APE明显偏小(箱子偏下),且误差分布相对集中(箱子高度较小)。每种算法的MAPE、MAE和RMSE如表 3所示。
|
|
表 3 不同算法预测性能对比 Table 3 Prediction performance comparison of different algorithms |
由图 8和表 3可知,LSTM算法的负荷预测效果较好,性能较稳定。
4 结语文中采用LSTM构建负荷预测模型,利用LSTM能学习长距离时序依赖的优点,从横向上(时间维度)辨识负荷本身的变化规律,从纵向上(影响因素维度)识别天气、节假日等因素对负荷的非线性影响。采用实际的负荷数据对模型进行验证,比较了不同网络结构、不同历史时间窗口期对预测性能的影响,并与其他2种算法进行了比较。结果表明,所提方法提升了负荷预测准确性,且预测性能较稳定。
目前,深度神经网络无法进行负荷概率区间预测,且预测模型无法对预测结果进行解释。采用深度神经网络对负荷概率区间进行预测,并对预测结果进行解释是未来的研究方向之一。
| [1] |
孔祥玉, 郑锋, 鄂志君, 等. 基于深度信念网络的短期负荷预测方法[J]. 电力系统自动化, 2018, 42(5): 133-139. KONG Xiangyu, ZHENG Feng, E Zhijun, et al. Short-term load forecasting based on deep belief network[J]. Automation of Electric Power Systems, 2018, 42(5): 133-139. (  0) 0) |
| [2] |
戚任远. 上海用电负荷预测中气温累积效应分析[J]. 现代电力, 2018, 35(2): 38-42. QI Renyuan. Analysis on temperature accumulation effect in Shanghai power load forecast[J]. Modern Electric Power, 2018, 35(2): 38-42. (  0) 0) |
| [3] |
龚钢军, 安晓楠, 陈志敏, 等. 基于SAE-ELM的电动汽车充电站负荷预测模型[J]. 现代电力, 2019, 36(6): 9-15. GONG Gangjun, AN Xiaonan, CHEN Zhimin, et al. Model of load forecasting of electric vehicle charging station based on SAE-ELM[J]. Modern Electric Power, 2019, 36(6): 9-15. (  0) 0) |
| [4] |
苏小林, 张艳娟, 武中, 等. 规模化电动汽车充电负荷的预测及其对电网的影响[J]. 现代电力, 2018, 35(1): 45-54. SU Xiaolin, ZHANG Yanjuan, WU Zhong, et al. Forecasting the charging load of large-scale electric vehicle and its impact on the power grid[J]. Modern Electric Power, 2018, 35(1): 45-54. (  0) 0) |
| [5] |
刘青, 戚中译. 考虑空间运动特性的规模化电动汽车接入电网负荷预测模型[J]. 现代电力, 2015, 32(1): 76-82. LIU Qing, QI Zhongyi. The load forecast model for power grid with the accessing of large scale electric vehicles by considering spatial motion characteristics[J]. Modern Electric Power, 2015, 32(1): 76-82. (  0) 0) |
| [6] |
姚建刚, 付强, 叶伦, 等. 考虑峰谷分时电价影响的变电站容量规划方法[J]. 电力系统自动化, 2017, 41(13): 53-61. YAO Jiangang, FU Qiang, YE Lun, et al. Substation capacity planning method considering influence of peak-valley time-of-use power price[J]. Automation of Electric Power Systems, 2017, 41(13): 53-61. (  0) 0) |
| [7] |
LIU H, ZENG P, GUO J, et al. An optimization strategy of controlled electric vehicle charging considering demand side response and regional wind and photovoltaic[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(2): 232-239. DOI:10.1007/s40565-015-0117-z (  0) 0) |
| [8] |
李博, 门德月, 严亚勤, 等. 基于数值天气预报的母线负荷预测[J]. 电力系统自动化, 2015, 39(1): 137-140. LI Bo, MEN Deyue, YAN Yaqin, et al. Bus load forecasting based on numerical weather prediction[J]. Automation of Electric Power Systems, 2015, 39(1): 137-140. (  0) 0) |
| [9] |
郭建鹏, 佘颖铃, 温步瀛. 基于EEMD-ARIMA模型的地区月负荷量预测[J]. 电力工程技术, 2018, 37(6): 28-32, 74. GUO Jianpeng, SHE Yingling, WEN Buying. Regional monthly load forecast based on EEMD-ARIMA model[J]. Electric Power Engineering Technology, 2018, 37(6): 28-32, 74. (  0) 0) |
| [10] |
林芳, 林焱, 吕宪龙, 等. 基于均衡KNN算法的电力负荷短期并行预测[J]. 中国电力, 2018, 51(10): 88-94, 102. LIN Fang, LIN Yan, LYU Xianlong, et al. Short-term parallel power load forecasting based on balanced KNN[J]. Electric Power, 2018, 51(10): 88-94, 102. (  0) 0) |
| [11] |
石天, 梅飞, 陆继翔, 等. 基于PSR和DBN的超短期母线净负荷预测[J]. 电力工程技术, 2020, 39(1): 178-183. SHI Tian, MEI Fei, LU Jixiang, et al. Ultra-short-term bus net load forecasting based on phase space reconstruction and deep belief network[J]. Electric Power Engineering Technology, 2020, 39(1): 178-183. (  0) 0) |
| [12] |
郭威麟, 蒋晓艳, 罗意, 等. 基于EEMD-GABP的某地区短期负荷预测研究[J]. 电力工程技术, 2019, 38(6): 93-98. GUO Weilin, JIANG Xiaoyan, LUO Yi, et al. Short-term load forecasting in a certain area based on EEMD-GABP[J]. Electric Power Engineering Technology, 2019, 38(6): 93-98. (  0) 0) |
| [13] |
吴潇雨, 和敬涵, 张沛, 等. 基于灰色投影改进随机森林算法的电力系统短期负荷预测[J]. 电力系统自动化, 2015, 39(12): 50-55. WU Xiaoyu, HE Jinghan, ZHANG Pei, et al. Power system short-term load forecasting based on improved random forest with grey relation projection[J]. Automation of Electric Power Systems, 2015, 39(12): 50-55. (  0) 0) |
| [14] |
赵佩, 代业明. 基于实时电价和加权灰色关联投影的SVM电力负荷预测[J]. 电网技术, 2020, 44(4): 1325-1332. ZHAO Pei, DAI Yeming. Power load forecasting of SVM based on real-time price and weighted grey relational projection algorithm[J]. Power System Technology, 2020, 44(4): 1325-1332. (  0) 0) |
| [15] |
史佳琪, 张建华. 基于多模型融合Stacking集成学习方式的负荷预测方法[J]. 中国电机工程学报, 2019, 39(14): 4032-4042. SHI Jiaqi, ZHANG Jianhua. Load forecasting based on multi-model by stacking ensemble learning[J]. Proceedings of the CSEE, 2019, 39(14): 4032-4042. (  0) 0) |
| [16] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 (  0) 0) |
| [17] |
MULDER W D, BETHARD S, MOENS M. A survey on the application of recurrent neural networks to statistical language modeling[J]. Computer Speech & Language, 2015, 30(1): 61-98. (  0) 0) |
| [18] |
王卉, 王增平, 刘席洋. 基于深度循环神经网络的换相失败边界检测[J]. 现代电力, 2019, 36(6): 88-94. WANG Hui, WANG Zengping, LIU Xiyang. Commutation failure boundary detection based on deep recurrent neural network[J]. Modern Electric Power, 2019, 36(6): 88-94. (  0) 0) |
| [19] |
BENGIO Y, BOULANGER-LEWANDOWSKI N, PASCANU R, et al. Advances in optimizing recurrent networks[C]//IEEE International Conference on Acoustics. 2012: 8624-8628.
(  0) 0) |
| [20] |
YOSHUA B, PATRICE S, PAOLO F. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166. DOI:10.1109/72.279181 (  0) 0) |
| [21] |
LIPTON, ZACHARY C, BERKOWITZ, et al. A critical review of recurrent neural networks for sequence learning[EB/OL].[2020-06-20]. https://arxiv.org/abs/1506.00019.
(  0) 0) |
| [22] |
GIBSONA, PATTERSON J. Deep learning:a practitioner's approach[M]. Boston: O'Reilly Media, 2017.
(  0) 0) |
| [23] |
Hourly load data archives[EB/OL].[2020-06-20]. http://www.ercot.com/gridinfo/load/load_hist/.
(  0) 0) |
| [24] |
苏运, 卜凡鹏, 郭乃网, 等. 基于低秩表示的多任务短期电力负荷预测的研究[J]. 现代电力, 2019, 36(3): 58-65. SU Yun, BU Fanpeng, GUO Naiwang, et al. Research on short-term load forecast using multi-task with low-rank representation[J]. Modern Electric Power, 2019, 36(3): 58-65. (  0) 0) |
2. Beijing Kedong Power Control System Co., Ltd., Beijing 100192, China
 2021, Vol. 40
2021, Vol. 40


 庞传军(1984),男,硕士,高级工程师,从事电力系统及自动化、人工智能技术在电力系统中的应用相关工作(E-mail:
庞传军(1984),男,硕士,高级工程师,从事电力系统及自动化、人工智能技术在电力系统中的应用相关工作(E-mail: